Ce programme est conçu pour l'analyse de la tolérance des chaînes dimensionnelles bidimensionnelles (2-D) et tridimensionnelles (3-D). Le programme résout les problèmes suivants:
Pendant la conception de la chaîne dimensionnelle, le programme permet de travailler avec des valeurs normalisées de la tolérance.
Ce calcul utilise les données, les méthodes, les algorithmes et l'information de la littérature
spécialisée et des normes ANSI, OIN, DIN et d'autres.
Liste des normes: ANSI B4.1, OIN 286, OIN 2768,
DIN 7186
L’interface d’utilisateur.
A télécharger.
Tarif, Achat.
L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document " commande, structure et syntaxe des calculs ".
L'information sur le but, l'utilisation et la commande du paragraphe "information sur le projet" peut être trouvée dans le document " information sur le projet ".
Une chaîne dimensionnelle est un ensemble de dimensions interdépendantes liées les unes aux autres de façon à créer un circuit géométriquement fermé. Elles peuvent être des dimensions indiquant la position mutuelle des composantes sur une pièce ou les dimensions de plusieurs pièces dans une unité de montage.
Une chaîne dimensionnelle se compose d'éléments partiels séparés
(dimensions initiales) et termine par un élément de fermeture
(dimension résultante). Les composantes
partielles (A, B, C...) sont des dimensions, qui sont cotées directement dans le
dessin ou issues des opérations de production ou de montage précédentes.
La composante de fermeture (Z) représente dans la chaîne donnée la dimension
résultante de production ou de montage, qui est le résultat de la composition
des dimensions partielles comme dimension de production non cotée des pièces
respectivement comme jeu ou interférence d'assemblage. La grandeur, la tolérance
et la déviation limite de la dimension résultante dépendent directement de la
grandeur et de la tolérance des dimensions partielles. Il
y trois types de chaînes dimensionnelles selon la position mutuelle de différentes composantes:
- les chaînes
linéaires (1D) - contiennent rien que les dimensions
parallèles
- les chaînes bidimensionnelles (2D)
- les dimensions sont réparties dans un ou plusieurs plans parallèles
- les chaînes
tridimensionnelles (3D) - les dimensions sont dans des plans
non parallèles
Ce calcul est conçu pour l'analyse de la tolérance des chaînes dimensionnelles
bidimensionnelles et tridimensionnelles.
Dans la solution des relations de tolérance dans les chaînes dimensionnelles, deux types de problèmes se produisent:
Pour résoudre les relations de la tolérance dans les chaînes dimensionnelles, ce
programme utilise deux méthodes de calcul:
-
méthode de
"Worst Case"
- méthode de "Monte Carlo "
Le choix de la méthode de calcul des tolérances et des déviations limites des
composantes des chaînes dimensionnelles affecte la précision de production et
l'interchangeabilité de montage des composantes. Par conséquent, le régime de la
production et de service dépend de ce choix.
La méthode le plus souvent utilisée, parfois appelée méthode de calcul au maximum - minimum. Elle est basée sur la condition de maintenir la déviation limite exigée de la composante de fermeture pour n'importe quelle combinaison des dimensions réelles des composantes partielles, c.-à-d. des dimensions limites supérieures et inférieures. Cette méthode garantit la pleine interchangeabilité de montage et de fonctionnement des composantes. Cependant, la demande d'une précision plus élevée de la composante de fermeture, elle a comme conséquence les tolérances trop limitées des composantes partielles et donc des coûts de production élevés. La méthode de Worst Case est donc adéquate pour le calcul des circuits dimensionnels avec un nombre restreint de composantes ou au cas où une plus large tolérance de la dimension résultante serait acceptable. Elle est le plus souvent utilisée dans la production en pièces ou en petites séries.
Le but de la méthode de "Worst Case" est de trouver les valeurs minimales et maximales qui peuvent être réalisées par la dimension résultante pour une combinaison quelconque des dimensions initiales réelles. L'algorithme de calcul est basé sur un essai progressif de toutes les combinaisons existantes de différentes valeurs (pré-sélectionnées) des dimensions initiales. Pour les chaînes dimensionnelles ordinaires, la dimension résultante atteint souvent ses valeurs limites seulement dans une certaine combinaison des valeurs limites des dimensions initiales. Dans l'analyse de la tolérance, pour les tâches le plus souvent résolues nous pouvons donc nous limiter seulement à examiner les combinaisons des dimensions minimales et maximales des composantes partielles des chaînes.
Pour certains cas (un petit pourcentage), cependant, l'hypothèse mentionnée ci-dessus n'est pas valable et pour trouver les valeurs limites de la dimension résultante, il sera également nécessaire d'effectuer le calcul pour les valeurs des dimensions initiales se trouvant à l'intérieur de l'intervalle de tolérance. Dans ce programme, ce fait est traité par la possibilité du choix du nombre de valeurs des dimensions initiales contrôlées (division de l'intervalle de tolérance).
Bien que l'algorithme de calcul choisi garantisse un succès considérable dans la recherche des valeurs limites de la dimension résultante pour la méthode de "Worst Case", il peut en retour prolonger d'une façon disproportionnée la durée du calcul. La vitesse de calcul dépendra du nombre total des cycles de calcul effectués qui sont nécessaires pour contrôler toutes les combinaisons des dimensions initiales. Le nombre de ces cycles dépend du type choisi de la division de l'intervalle de tolérance et se développe sous forme d'une série géométrique avec un nombre croissant de composantes partielles de la chaîne dimensionnelle. Il est mathématiquement décrit par la relation suivante:
![]()
où:
c... nombre total des cycles de calcul
n... nombre des composantes partielles de la chaîne dimensionnelle
k... nombre des valeurs
contrôlées de
chaque composante partielle
Des faits mentionnés ci-dessus, il découle que la méthode de "Worst Case" est conçue pour résoudre des relations de la tolérance particulièrement dans les chaînes dimensionnelles moins compliquées avec un plus petit nombre de composantes partielles. En pratique, l'usage de cette méthode est limitée par la capacité de l'ordinateur, du nombre de composantes partielles de la chaîne dimensionnelle et de la "précision" choisie de la division d'intervalle de tolérance.
Cette méthode est l'une des méthodes de calcul statistiques des chaînes dimensionnelles. Les méthodes de calcul statistiques sont basées sur le calcul de la probabilité et supposent que dans un choix au hasard des composantes pendant le montage, les valeurs limites des déviations se produisent très rarement dans plusieures composantes partielles simultanément, étant donné qu'il s'agit d'une probabilité combinée. De même l'occurrence de la valeur limite des déviations pendant la production de différentes dimensions d'une composante sera moins probable. Avec un certain, risque de rejet préalablement choisi de quelques composantes, les tolérances des composantes partielles dans la chaîne dimensionnelle peuvent être plus grandes.
La méthode de "Monte Carlo" garantit seulement une interchangeabilité de montage partielle, avec un petit pourcentage des cas non favorables (rebut). Vues les plus grandes tolérances des dimensions partielles, elle résulte en la baisse des coûts de production. Elle est surtout dans les productions massives ou en grandes séries, où l'économie dans les coûts de production est plus importante que le coût élevé de montage et de service issu des conséquences de l'interchangeabilité de montage incomplète des composantes.
Les dimensions de la composante de fermeture accusent une certaine variation du centre de la zone de tolérance. La fréquence de l'apparition de différentes dimensions suit les règles des statistiques mathématiques. La méthode de "Monte Carlo" est donc censée analyser cette fréquence et déterminer le rendement prévu du processus de production.
La méthode de "Monte Carlo" est une méthode de simulation. Son algorithme est basé sur la génération aléatoire des dimensions initiales dans la marge des tolérances choisies selon les fonctions de distribution évaluées. Le calcul des dimensions résultantes est ensuite effectué pour un tel groupe de dimensions initiales généré. Le processus se répète périodiquement pour un nombre de simulations prédéfini. La simulation aura comme conséquence un groupe de statistique des données (dimensions résultantes) généralement décrites par la dimension moyenne:
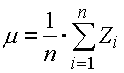
et l'écart type:
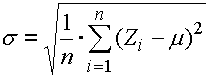
où:
Zi ... valeur de la
dimension résultante au ième
cycle de simulation
n ... nombre total des cycles de simulation
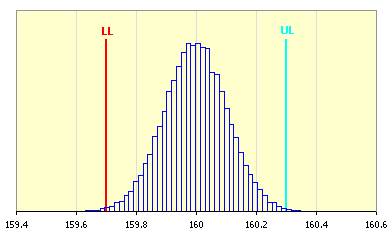
Pour l'évaluation de la fréquence de l'occurrence de la dimension résultante, ce groupe de statistique est en plus transformé en un histogramme.
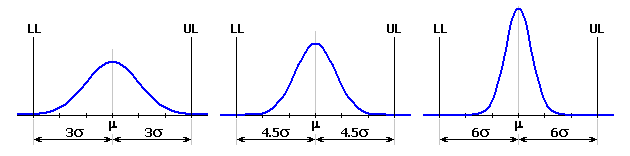
Pour la méthode de "Monte Carlo", le rendement de production prévu sera l'indice décisive dans l'évaluation de la qualité de la conception des chaînes dimensionnelle. Le rendement de production donne le rapport supposé des produits qui remplissent les critères spécifiés, c.à.d. les produits dont la dimension de la composante de fermeture est dans l'intervalle spécifié par les dimensions limites. En construction mécanique, le processus de production est souvent considéré comme suffisamment satisfaisant au niveau 3s, c.-à-d. le processus avec un rendement minimum de 99,73%.
L'exactitude (valeur d'orientation) des résultats statistiques obtenus dépendra du nombre de simulations effectuées. Il est évident que la qualité des résultats monte avec un plus grand nombre de simulations effectuées. Le nombre optimum de simulations dépendra du nombre des dimensions initiales, de la valeur de leur tolérance et de la complexité de la chaîne dimensionnelle. En pratique, une valeur d'approximativement 30 à 50.000 simulations effectuées peut être considérée comme une limite inférieure raisonnable pour les calculs finals.
Cette rangée sert à la conversion des systèmes d'unités de calcul et à choisir les tolérances normalisées.
Choisissez le système d'unités requis pour le calcul sur la liste. Après conversion d'unités, toutes les valeurs seront automatiquement recalculées.
Pendant la définition de la chaîne dimensionnelle dans le paragraphe [1.1], la tolérance est également déterminée pour chaque dimension. Pour simplifier le travail, ce programme contient un outil pour le choix automatique des tolérances normalisées.
Ce programme contient un groupe des tolérances des dimensions de base selon OIN ou ANSI. En rapport avec le type de déviation et la norme appliquée, les tolérances sont reparties en 5 groupes:
Chaque groupe contient un lot des listes et des boutons dans l'entête du cahier de travail. Déterminer les paramètres de tolérance ou respectivement d'ajustement requis (degré de précision, zone de tolérance, ..) sur les listes. A l'aide des boutons, entrez les dimensions de la tolérance choisie dans la cellule appropriée du tableau d'insertion - dans la rangée avec la cellule active.
Les tolérances selon les normes OIN sont définies en [mm] et sont destinées au calcul dans les unités de SI. Les tolérances selon ANSI sont définies en [in] et sont destinées au calcul dans les unités Impériales. En cas d'usage des tolérances normalisées définies dans les unités autres que celles déterminées dans le calcul, les déviations des dimensions seront automatiquement recalculées et arrondies. Les normes OIN 2768 sont destinées à la tolérance des dimensions angulaires.
La conception et l'optimisation d'une chaîne dimensionnelle consistent aux étapes suivantes:
Définissez les paramètres de toutes les composantes partielles de la chaîne dimensionnelle dans ce paragraphe.
Ce tableau sert à définir les paramètres de différentes dimensions initiales (composantes partielles) de la chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. Le sens du tableau est évident dans la description suivante:
Colonne 1 - Le nom de la
composante est un paramètre facultatif.
Colonne
2 – Choisissez le type de la dimension à l'aide des boutons.
Une dimension longitudinale est implicitement supposée pour
toutes les composantes de la chaîne dimensionnelle;
cochez la case pour déterminer une dimension angulaire pour une
composante partielle choisie. Le type
de dimension déterminée ici affecte la
fonction du choix automatique des tolérances normalisées.
Colonne 3 - Déterminez la dimension
nominale de la composante partielle.
Colonne 4 - Déterminez les
déviations supérieure et inférieure de la dimension.
Appuyez sur le bouton choisi dans l'entête du cahier de travail pour insérer les
déviations correspondant aux tolérances choisies dans le tableau.
Pour la tolérance des dimensions
longitudinales, toutes les normes mentionnées ici peuvent
être utilisées; les tolérances des dimensions
angulaires sont normalisées dans OIN 2768.
Colonnes 5..7 – Les
dimensions minimale, maximale
et moyenne de toutes les composantes
partielles sont calculées dans ces colonnes.
Colonne 8 - Choisissez le
type de répartition de la fréquence théorique.
D'habitude, la répartition
normale, qui correspond le mieux à la répartition
réelle des grandeurs occasionnelles du processus est utilisée pour décrire les
procédures de production.
Dans ce paragraphe, définissez les paramètres de toutes les composantes de fermeture de la chaîne dimensionnelle dans le tableau [2.1]. Dans le paragraphe [2.2], choisissez la méthode de calcul requise et déterminez ses paramètres. Démarrez le calcul à l'aide du bouton dans la rangée [2.7].
Ce tableau sert à définir les paramètres de différentes dimensions résultantes (composantes de fermeture) d'une chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. Le sens du tableau est évident dans la description suivante:
Colonne 1 - Le nom de la composante est un paramètre facultatif.
Colonne 2 – Déterminez la relation de calcul utilisée pour définir la dimension résultante. Les formules utilisées (algorithmes) doivent respecter la syntaxe de Microsoft Excel et peut contenir toutes les formules et les fonctions mathématiques définies par Excel (voir l'aide de Excel). Pour marquer les dimensions initiales (composantes partielles) d'une chaîne dimensionnelle, utilisez les symboles composés d'un tiret bas et du nom de la dimension ("_A", "_B", "_C", ...) dans la formule. De même, utilisez les symboles "_Z1", "_Z2", ... pour les noms des dimensions résultantes. Si la relation de calcul est définie correctement, la valeur nominale de la dimension résultante sera calculée ici en temps réel. Sinon, Excel donnera la valeur correspondante à l'erreur.
Colonnes 3, 4 – Définissez les dimensions limites requises de la composante de fermeture telles que définies par les conditions de fonctionnement du produit. Les limites de la dimension résultante données ici sont facultatives et ne servent qu'à comparer les résultats obtenus. Pour la méthode de calcul de "Monte Carlo", les valeur limites admissibles servent à déterminer le rendement de production supposé et le nombre de rebuts.
Dans ce paragraphe, choisissez la méthode de calcul requise et déterminez ses paramètres. Démarrez le calcul à l'aide du bouton dans la rangée [2.7]. Les résultats complets de l'analyse de la tolérance effectuée peuvent être trouvés dans le paragraphe [3].
Le but de la méthode de "Worst Case" est de trouver les valeurs minimales et maximales qui peuvent être réalisées par la dimension résultante pour une combinaison quelconque des dimensions initiales réelles. L'algorithme de calcul est basé sur un essai progressif de toutes les combinaisons existantes de différentes valeurs (pré-sélectionnées) des dimensions initiales. Pour les chaînes dimensionnelles ordinaires, la dimension résultante atteint souvent ses valeurs limites seulement dans une certaine combinaison des valeurs limites des dimensions initiales. Dans l'analyse de la tolérance, pour les tâches le plus souvent résolues nous pouvons donc nous limiter seulement à examiner les combinaisons des dimensions minimales et maximales des composantes partielles des chaînes.
Pour certains cas (un petit pourcentage), cependant, l'hypothèse mentionnée ci-dessus n'est pas valable et pour trouver les valeurs limites de la dimension résultante, il sera également nécessaire d'effectuer le calcul pour les valeurs des dimensions initiales se trouvant à l'intérieur de l'intervalle de tolérance. Dans ce programme, ce fait est traité par la possibilité du choix du nombre de valeurs des dimensions initiales contrôlées (division de l'intervalle de tolérance).
Bien que l'algorithme de calcul choisi garantisse un succès considérable dans la recherche des valeurs limites de la dimension résultante pour la méthode de "Worst Case", il peut en retour prolonger d'une façon disproportionnée la durée du calcul. La vitesse de calcul dépendra du nombre total des cycles de calcul effectués qui sont nécessaires pour contrôler toutes les combinaisons des dimensions initiales. Le nombre de ces cycles dépend du type choisi de la division de l'intervalle de tolérance et se développe sous forme d'une série géométrique avec un nombre croissant de composantes partielles de la chaîne dimensionnelle.
Des faits mentionnés ci-dessus, il découle que la méthode de "Worst Case" est conçue pour résoudre des relations de la tolérance particulièrement dans les chaînes dimensionnelles moins compliquées avec un plus petit nombre de composantes partielles. En pratique, l'usage de cette méthode est limitée par la capacité de l'ordinateur, du nombre de composantes partielles de la chaîne dimensionnelle et de la "précision" choisie de la division de l'intervalle de tolérance.
Les dimensions de la composante de fermeture accusent une certaine variation du centre de la zone de tolérance. La fréquence de l'apparition de différentes dimensions suit les règles des statistiques mathématiques. La méthode de "Monte Carlo" est donc censée analyser cette fréquence et déterminer le rendement prévu du processus de production.
La méthode de "Monte Carlo" est une méthode de simulation et est l'une des méthode statistiques. Son algorithme est basé sur la génération aléatoire des dimensions initiales dans la marge des tolérances choisies selon les fonctions de distribution évaluées. Le calcul des dimensions résultantes est ensuite effectué pour un tel groupe de dimensions initiales généré. Le processus se répète périodiquement pour un nombre de simulations prédéfini. La simulation aura comme conséquence un groupe de statistique des données (dimensions résultantes) généralement décrites par la dimension moyenne m et l'écart type s. Pour la méthode de "Monte Carlo", le rendement de production prévu sera l'indice décisive dans l'évaluation de la qualité de la conception des chaînes dimensionnelle.
L'exactitude (valeur d'orientation) des résultats statistiques obtenus dépendra du nombre de simulations effectuées. Il est évident que la qualité des résultats monte avec un plus grand nombre de simulations effectuées. Le nombre optimum de simulations dépendra du nombre des dimensions initiales, de la valeur de leur tolérance et de la complexité de la chaîne dimensionnelle. En pratique, une valeur d'approximativement 30 à 50.000 simulations effectuées peut être considérée comme une limite inférieure raisonnable pour les calculs finals. Déterminez le nombre de simulations requis sur la liste de la case [2.6].
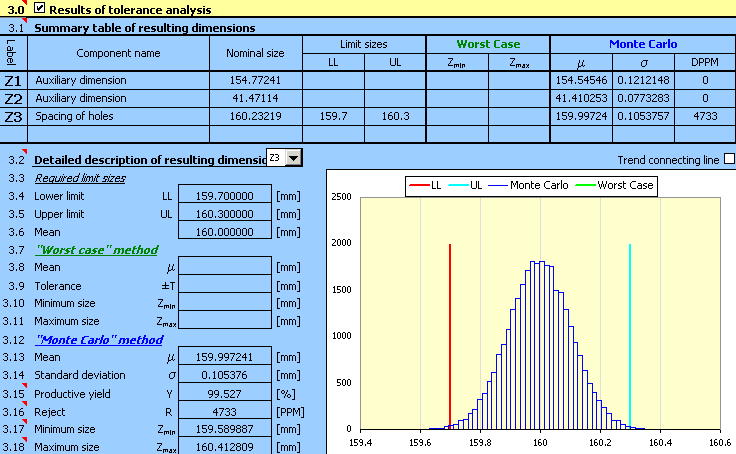
A la fin du calcul [2.7], les résultats de l'analyse de la tolérance de la chaîne dimensionnelle définie ci-dessus seront affichés dans ce paragraphe. Le paragraphe est réparti en deux section. Dans le tableau [3.1], les informations de base concernant toutes les dimensions définies dans le tableau [2.1] sont données sous forme de récapitulation. Les paramètres détaillés de la dimension résultante choisie sont présentés numériquement et graphiquement dans le paragraphe [3.2].
Ce tableau donne un résumé sur les informations de base de toutes les composantes de fermeture de la chaîne dimensionnelle définies dans le tableau [2.1]. Pour le calcul à l'aide de la méthode de "Worst Case", la dimension résultante est décrite par les valeurs minimale et maximale trouvées. Pour la méthode de "Monte Carlo", le groupe statistique caractérisant la fréquence de l'occurrence des dimensions résultantes est donné dans la tableau par la valeur moyenne, l'écart type et le nombre de rebuts par million de pièces produites.
Ce paragraphe présente les paramètres détaillés de la dimension résultante choisie (composante de fermeture) de la chaîne dimensionnelle sous forme graphique et numérique. Sur la liste dans la case, choisissez la dimension résultante requise dont vous voulez afficher les paramètres.
En rapport avec la méthode de calcul utilisée, les résultats de l'analyse de la tolérance sont divisées en deux parties. Pour évaluer la qualité de la conception de la chaîne dimensionnelle, les dimensions limites qui peuvent être atteintes par la dimension résultante [3.10, 3.11] sont décisives pour la méthode de "Worst Case". Pour la méthode de "Monte Carlo", l'indice décisif est donné par le rendement de production prévu [3.15] ou par le nombre de rebuts par million de pièces produites [3.16]. La fréquence de l'occurrence de différentes dimensions est donnée dans l'histogramme joint.
Le rendement de production exprime le rapport prévu des produits qui remplissent les critères spécifiés, c.à.d. les produits dont la dimension résultante de la composante de fermeture se trouve à l'intérieur de l'intervalle donné par les dimensions limites requises. En construction mécanique, un processus de production est souvent considéré comme suffisamment satisfaisant au niveau 3s, c.à.d. un processus avec un rendement minimal de 99.73%.
Le rebut du processus de production exprime le nombre de produits défectueux, c.à.d. les produits dont la dimension résultante de la composante de fermeture se trouve en dehors de l'intervalle donné par les dimensions limites requises. En construction mécanique, le processus de production est souvent considéré comme suffisamment satisfaisant au niveau 3s. Ce qui représente une estimation de 2700 produits défectueux pour un million de pièces produites.
Les dimensions limites données ici ont un caractère informatif seulement. Ces limites ne déterminent pas les valeurs réelles qui peuvent être atteintes par la dimension résultante. Elles ne donnent que les valeurs minimale et maximale de la dimension trouvées pendant le calcul de simulation dans la marge du nombre de simulations choisi. Pour trouver les dimensions limites réelles, il est nécessaire d'utiliser la méthode de calcul de "Worst Case".
Comme illustration des problèmes de l'analyse de la tolérance des chaînes dimensionnelles, le manuel de l'utilisateur (l'aide) contient quelques exemples pratiques sur l'usage de ce calcul:
Pour le système bielle-manivelle excentrique d'un compresseur à piston (voir l'image), résolvez:
A partir de l'illustration graphique de la chaîne dimensionnelle
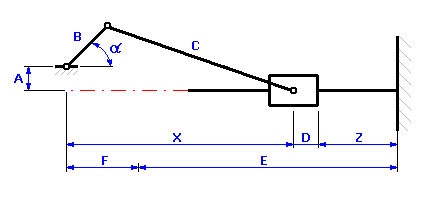
nous pouvons exprimer la valeur de la course du piston pour le mécanisme cinématique donné par la relation:
![]()
où la position du piston par rapport à l'axe X du vilebrequin est une grandeur cinématique qui dépend de l'angle d'orientation a du vilebrequin. Pour le système bielle-manivelle excentrique illustré dans l'image ci-dessus, la position du piston peut être déterminée par la relation suivante:
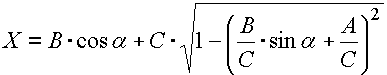
Les positions limites du piston par rapport à l'axe du vilebrequin sont évidentes dans le diagramme suivant
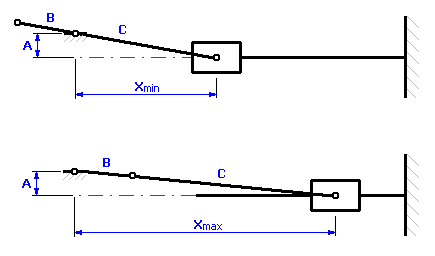
et peuvent être exprimées par ces relations:
![]()
La solution au problème de l'analyse de la tolérance du mécanisme cinématique peut être répartie aux étapes suivantes:
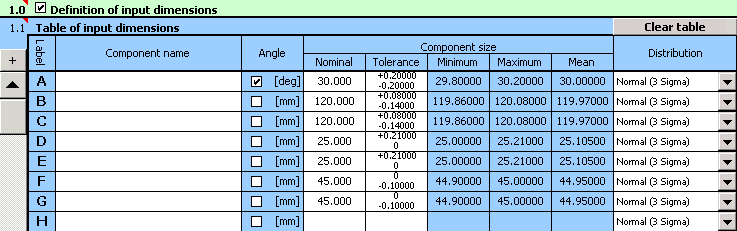
1) Dans le tableau [1.1] nous définirons toutes les dimensions initiales (composantes partielles) de la chaîne dimensionnelle.
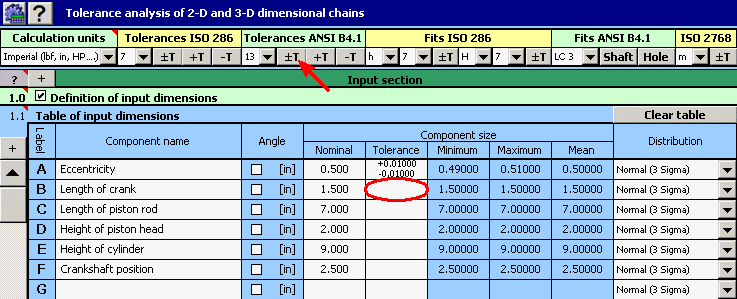
2) Pour les différentes dimensions, nous déterminerons ensuite les tolérances de production prescrites. pour les dimensions B, C et D, les tolérances symétriques normalisées selon ANSI B4.1 avec le degré de précision 13 sont prescrites. Pour leur insertion dans le tableau, nous pouvons utiliser la fonction du choix automatique de la tolérance.
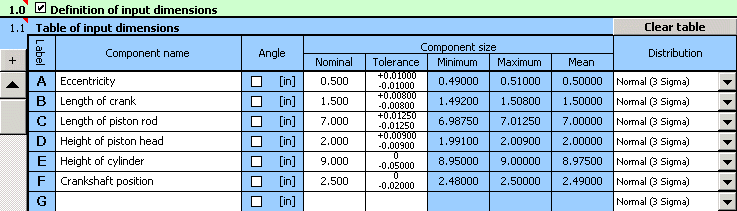
3) Dans le tableau [2.1] nous définirons les paramètres des dimensions résultantes (composantes de fermeture) de la chaîne dimensionnelle. les relations de calcul pour les courses minimale et maximale du piston définies dans le paragraphe précédent doivent être changées en une forme (syntaxe) requise par Excel. Par conséquent, dans la deuxième colonne du tableau, nous inscrirons la relation "=_E+_F-_D-((_C+_B)^2-_A^2)^0.5" pour la course minimale du piston et la relation "=_E+_F-_D-((_C-_B)^2-_A^2)^0.5" pour la course maximale du piston.
4) Dans la rangée [2.3], cochez le bouton à côté de la méthode de calcul de "Worst Case". Sur la liste dans la case [2.4], choisissez ensuite la répartition "la plus brute" de l'intervalle de tolérance (l'article "Min. - Max.") qui est suffisante pour la tâche donnée.
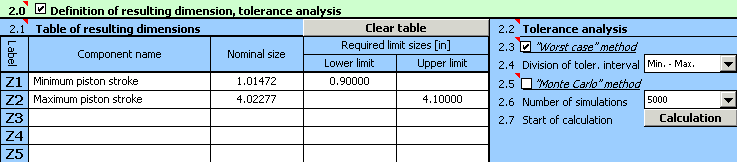
5) Appuyez sur le bouton dans la rangée [2.7] pou démarrer le calcul (analyse de la tolérance) de la chaîne dimensionnelle. les valeurs limites de la course peuvent être trouvées dans le paragraphe [3].
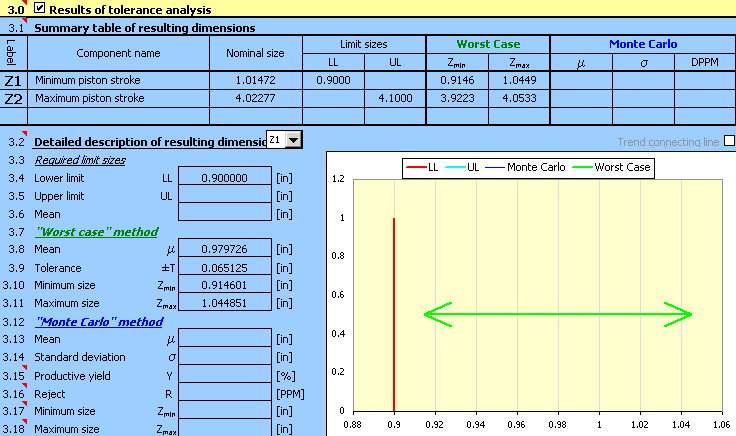
La solution de cette tâche sera similaire à la précédente et peut être répartie aux étapes suivantes:
1) Les dimensions initiales seront définies dans le tableau [1.1] de façon similaire à l'exemple A dans les étapes 1) et 2).

2) L'angle d'orientation du vilebrequin pour lequel nous voulons déterminer la course du piston sera défini comme une constante "Z1" dans la première rangée du tableau [2.1]. "Z2" dans la seconde rangée, ensuite nous inscrirons la relation pour le calcul de la course. La relation de calcul donnée ci-dessus doit être changée en une forme (syntaxe) requise par Excel:
"=_E+_F-_D-(_B*COS(RADIANS(_Z1))+_C*(1-(_B/_C*SIN(RADIANS(_Z1))+_A/_C)^2)^0.5)"
3) Dans la rangée [2.3], cochez le bouton à côté de la méthode de calcul de "Worst Case". Sur la liste dans la case [2.4], choisissez ensuite la répartition "la plus brute" de l'intervalle de tolérance (l'article "Min. - Max.").
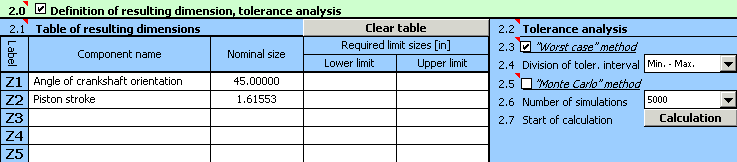
4) Appuyez sur le bouton dans la rangée [2.7] pour démarrer le calcul. Les paramètres de la course pour l'angle donné peuvent être trouvés dans le paragraphe [3].
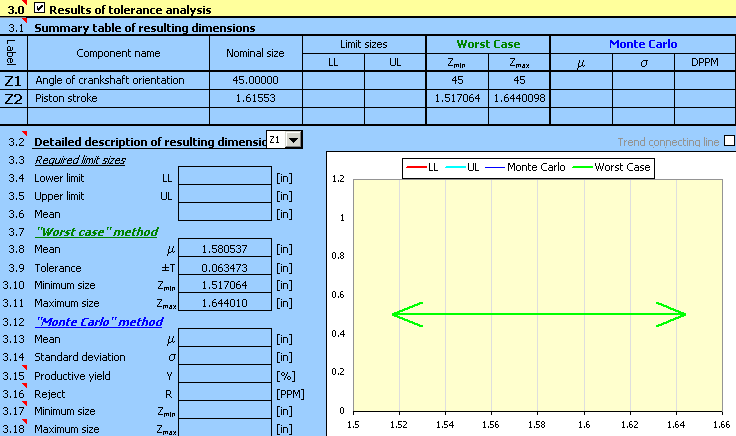
5) Pour déterminer la course pour une autre valeur de l'angle d'orientation, il suffira de changer la valeur de l'angle dans le tableau [2.1] et reprendre le calcul à l'aide du bouton [2.7].
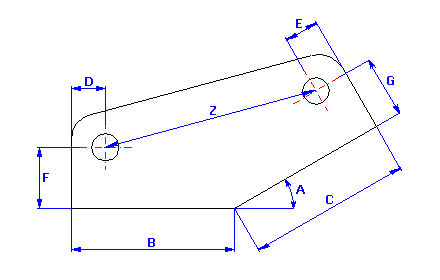
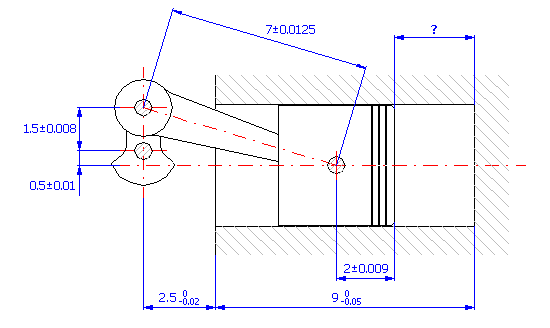
Pour la pièce (voir l'image), procédez à la conception des tolérances de production des dimensions, de sorte que pour un minimum de 99.5% des pièces produites, l'écartement requis de 160±0.3 mm entre les centres des trous soit maintenu.
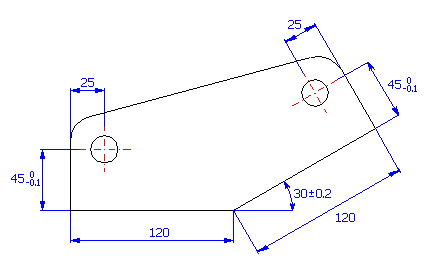
A partir de l'illustration graphique de la chaîne dimensionnelle
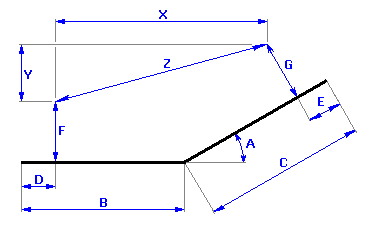
nous pouvons exprimer la dimension résultante pour la pièce donnée par la relation:
![]()
où les relations suivantes s'appliquent pour les variables auxiliaires X, Y:
![]()
![]()
Si la tâche était résolue à l'aide de la méthode traditionnelle de "Worst Case", il aurait été nécessaire d'utiliser les tolérances à un degré de précision d'approximativement 4 pour les dimensions B, C, D et E pour maintenir la tolérance requise de la dimension résultante. Il est évident qu'une production avec un tel degré de précision serait trop coûteuse. Dans ce cas, il sera donc plus convenable d'utiliser la méthode de calcul statistique. Ces méthodes permettent la production de la pièce avec des tolérances sensiblement plus grandes avec un petit pourcentage (déterminé au préalable) de rebut.
La conception de la chaîne dimensionnelle peut être répartie aux étapes suivantes:
1) Dans le tableau [1.1] nous définirons toutes les dimensions initiales (composantes partielles) de la chaîne dimensionnelle.
2) Déterminez ensuite les tolérances de production pour toutes les dimensions. Pour les dimensions avec des tolérances strictement données, déterminez les déviations des dimensions prescrites dans le tableau d'insertion.
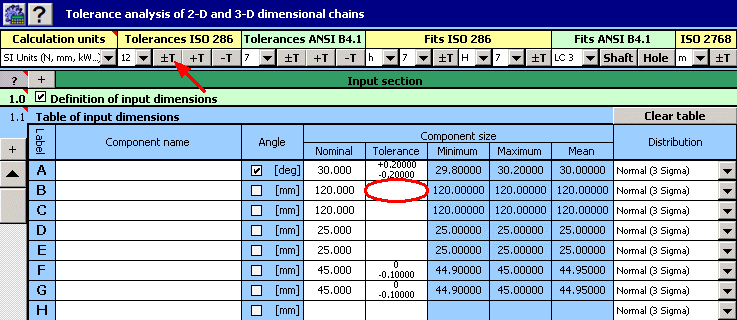
Pour le reste des dimensions, choisissez provisoirement une tolérance symétrique avec 12 comme degré de précision.
3) Sur les listes dans la dernière colonne du tableau, choisissez une répartition normale avec une capacité du processus de production de 3s pour toutes les dimensions.
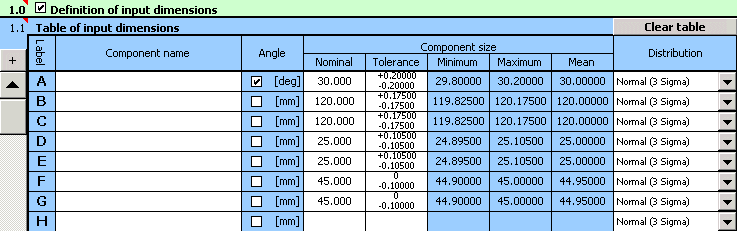
4) Dans le tableau [2.1], définissez les paramètres de la dimension résultante (composante de fermeture) de la chaîne dimensionnelle. Pour rendre le travail plus facile et plus claire, nous répartirons le relation de calcul en trois parties (voir plus haut). Nous utiliserons les deux premières rangées du tableau pour définir les dimensions auxiliaires; les paramètres des dimensions résultantes recherchées seront dans la rangée "Z3". Les relations de calcul données ci-dessus doivent être changées en une forme (syntaxe) requise par Excel. Par conséquent, nous inscrirons le texte suivant dans les différentes rangées de la deuxième colonne du tableau:
Rangée 1 "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
Rangée 2 "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
Rangée 3 "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) Dans la rangée [2.5] cochez le bouton à côté de la méthode de calcul de "Monte Carlo". Sur la liste [2.6] déterminez ensuite le nombre de simulations requis. Pour accélérer le processus de la conception, déterminez un plus petit nombre de simulations dans les premières phases de la conception.
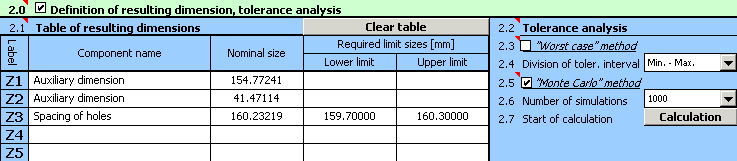
6) Appuyez sur le bouton dans la rangée [2.7] pour démarrer le calcul (analyse de la tolérance). Les paramètres de la dimension résultante peuvent être trouvés dans le paragraphe [3].
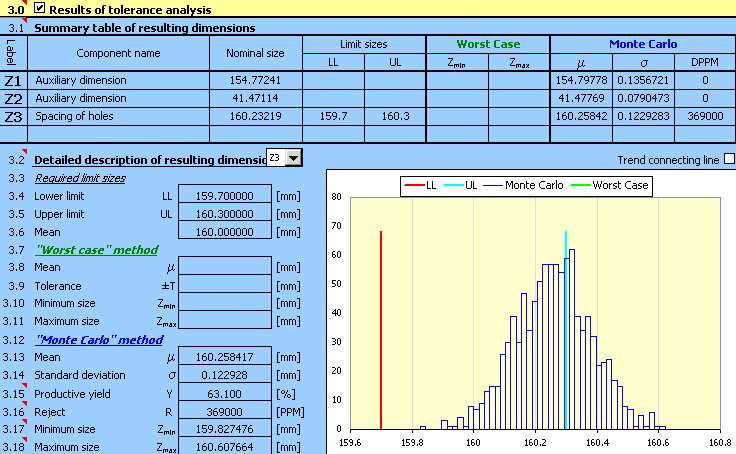
7) Le rendement de production prévu [3.15], ou respectivement le nombre de rebuts [3.16] sera le facteur décisif pour l'évaluation de la qualité de la conception. Les données de cette tâche indiquent un nombre maximum de 5.000 rebuts par million de pièces produites. Les résultats réalisés sont plus élevés, ce qui signifie que les tolérances conçues ne sont pas convenables.
Pour une conception non réussie, la prochaine étape logique serait la réduction des valeurs des tolérances de production utilisées. Après une analyse plus détaillée de cette conception, nous constaterons que le problème se pose au niveau du centrage incorrect de la conception plutôt que les valeurs des tolérances choisies. Dans une conception optimale d'une chaîne dimensionnelle, la dimension moyenne [3.13] devrait être proche de la dimension requise [3.6].
8) Par conséquent, nous ajusterons les positions des zones de tolérance des dimensions B, C, D et E dans l'étape suivante, tout en conservant les valeurs des tolérances originalement conçues. Par les ajustements répétés des déviations de différentes dimensions suivis du recalcula des résultats, nous aboutirons graduellement à la solution

pour laquelle la conception sera centrée
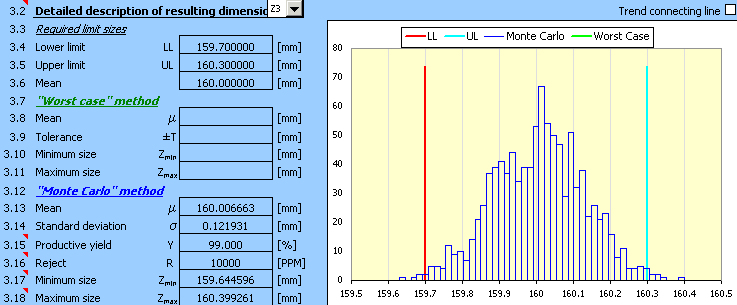
9) Bien que la conception soit déjà bien centrée, le rendement requis n'est pas encore atteint. Dans l'étape suivante, il sera nécessaire de réduire les tolérances provisoirement conçues dans l'étape 2). Après le choix des tolérances des dimensions B et C avec 11 comme degré de précision et après le centrage de la conception, nous obtiendrons le résultat approprié
qui remplit les conditions de fonctionnement déterminées par la tâche donnée.
L'information sur le réglage des paramètres de calcul et le choix de la langue peut être trouvée dans le document "Réglage des calculs, changement de langue".
Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".
^