Analyse de la tolérance d'une chaîne
dimensionnelle 2D à l'aide de la méthode de "Monte Carlo".Analyse de la tolérance d'une chaîne
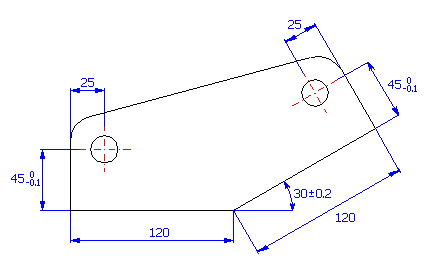
dimensionnelle 2D à l'aide de la méthode de "Monte Carlo".Pour la pièce (voir l'image), procédez à la conception des tolérances de production des dimensions, de sorte que pour un minimum de 99.5% des pièces produites, l'écartement requis de 160±0.3 mm entre les centres des trous soit maintenu.
A partir de l'illustration graphique de la chaîne dimensionnelle
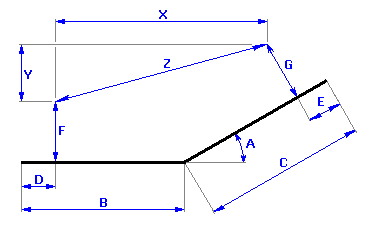
nous pouvons exprimer la dimension résultante pour la pièce donnée par la relation:
où les relations suivantes s'appliquent pour les variables auxiliaires X, Y:
Si la tâche était résolue à l'aide de la méthode traditionnelle de "Worst Case", il aurait été nécessaire d'utiliser les tolérances à un degré de précision d'approximativement 4 pour les dimensions B, C, D et E pour maintenir la tolérance requise de la dimension résultante. Il est évident qu'une production avec un tel degré de précision serait trop coûteuse. Dans ce cas, il sera donc plus convenable d'utiliser la méthode de calcul statistique. Ces méthodes permettent la production de la pièce avec des tolérances sensiblement plus grandes avec un petit pourcentage (déterminé au préalable) de rebut.
La conception de la chaîne dimensionnelle peut être répartie aux étapes suivantes:
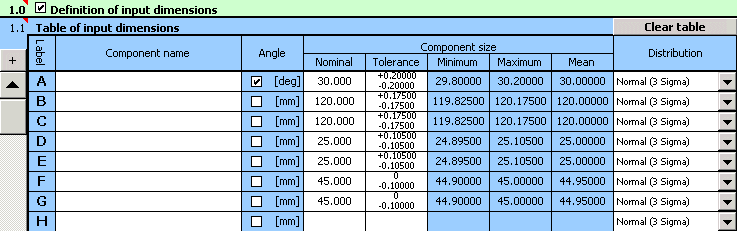
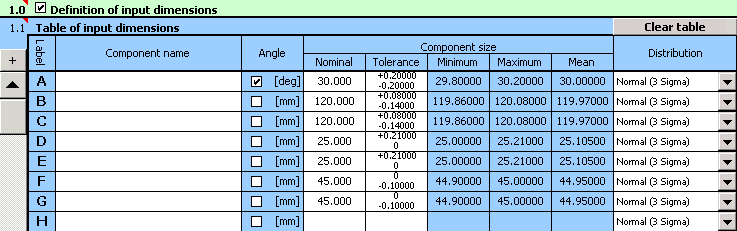
1) Dans le tableau [1.1] nous définirons toutes les dimensions initiales (composantes partielles) de la chaîne dimensionnelle.
2) Déterminez ensuite les tolérances de production pour toutes les dimensions. Pour les dimensions avec des tolérances strictement données, déterminez les déviations des dimensions prescrites dans le tableau d'insertion.
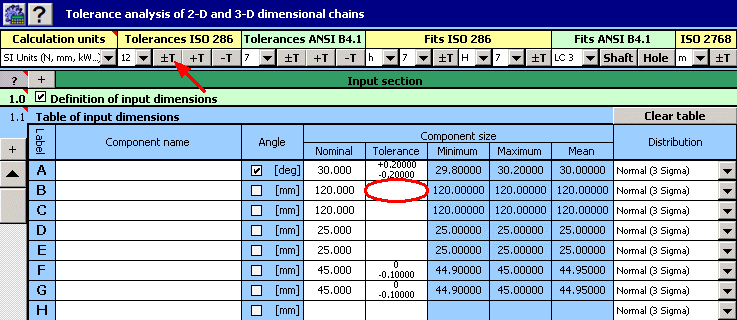
Pour le reste des dimensions, choisissez provisoirement une tolérance symétrique avec 12 comme degré de précision.
3) Sur les listes dans la dernière colonne du tableau, choisissez une répartition normale avec une capacité du processus de production de 3s pour toutes les dimensions.
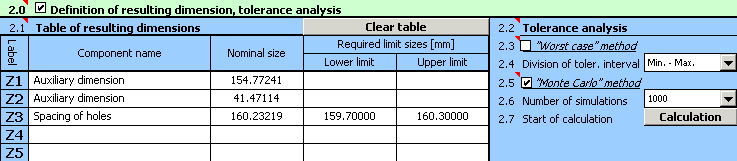
4) Dans le tableau [2.1], définissez les paramètres de la dimension résultante (composante de fermeture) de la chaîne dimensionnelle. Pour rendre le travail plus facile et plus claire, nous répartirons le relation de calcul en trois parties (voir plus haut). Nous utiliserons les deux premières rangées du tableau pour définir les dimensions auxiliaires; les paramètres des dimensions résultantes recherchées seront dans la rangée "Z3". Les relations de calcul données ci-dessus doivent être changées en une forme (syntaxe) requise par Excel. Par conséquent, nous inscrirons le texte suivant dans les différentes rangées de la deuxième colonne du tableau:
Rangée 1 "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
Rangée 2 "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
Rangée 3 "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) Dans la rangée [2.5] cochez le bouton à côté de la méthode de calcul de "Monte Carlo". Sur la liste [2.6] déterminez ensuite le nombre de simulations requis. Pour accélérer le processus de la conception, déterminez un plus petit nombre de simulations dans les premières phases de la conception.
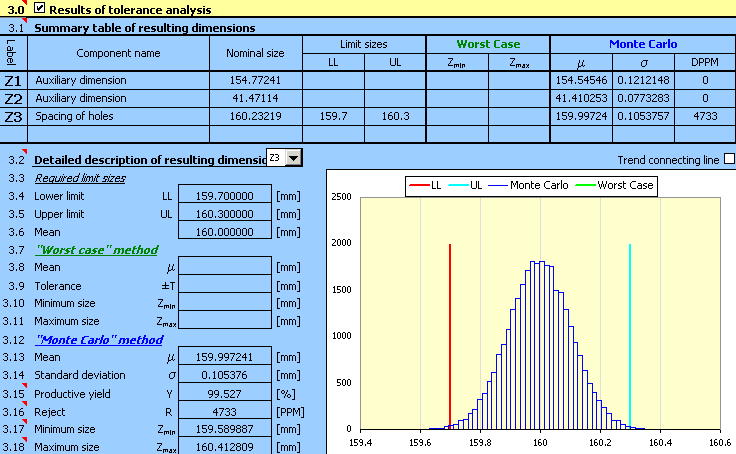
6) Appuyez sur le bouton dans la rangée [2.7] pour démarrer le calcul (analyse de la tolérance). Les paramètres de la dimension résultante peuvent être trouvés dans le paragraphe [3].
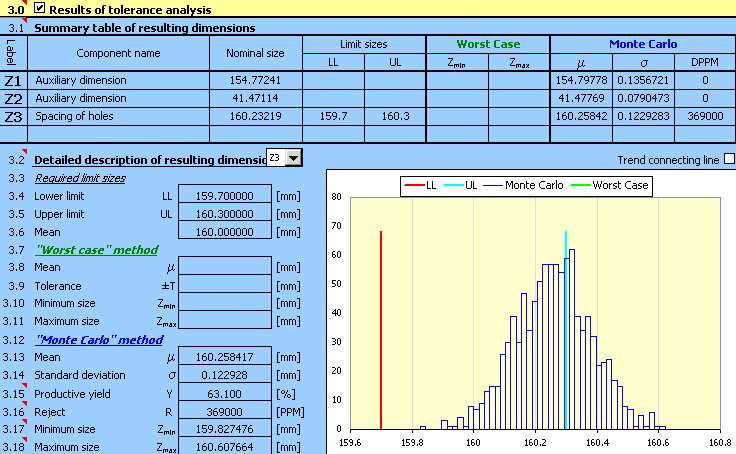
7) Le rendement de production prévu [3.15], ou respectivement le nombre de rebuts [3.16] sera le facteur décisif pour l'évaluation de la qualité de la conception. Les données de cette tâche indiquent un nombre maximum de 5.000 rebuts par million de pièces produites. Les résultats réalisés sont plus élevés, ce qui signifie que les tolérances conçues ne sont pas convenables.
Pour une conception non réussie, la prochaine étape logique serait la réduction des valeurs des tolérances de production utilisées. Après une analyse plus détaillée de cette conception, nous constaterons que le problème se pose au niveau du centrage incorrect de la conception plutôt que les valeurs des tolérances choisies. Dans une conception optimale d'une chaîne dimensionnelle, la dimension moyenne [3.13] devrait être proche de la dimension requise [3.6].
8) Par conséquent, nous ajusterons les positions des zones de tolérance des dimensions B, C, D et E dans l'étape suivante, tout en conservant les valeurs des tolérances originalement conçues. Par les ajustements répétés des déviations de différentes dimensions suivis du recalcula des résultats, nous aboutirons graduellement à la solution
pour laquelle la conception sera centrée
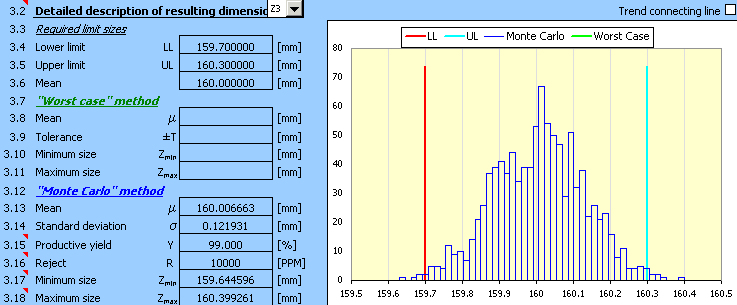
9) Bien que la conception soit déjà bien centrée, le rendement requis n'est pas encore atteint. Dans l'étape suivante, il sera nécessaire de réduire les tolérances provisoirement conçues dans l'étape 2). Après le choix des tolérances des dimensions B et C avec 11 comme degré de précision et après le centrage de la conception, nous obtiendrons le résultat approprié
qui remplit les conditions de fonctionnement déterminées par la tâche donnée.
