Ce programme est destiné à l'analyse de la tolérance (1D) des chaînes dimensionnelles linéaires. Le programme résout les problèmes suivants:
Dans toutes les tâches résolues il est possible de travailler avec des valeurs normalisées de la tolérance, pendant la conception tout comme pendant l'optimisation de la chaîne dimensionnelle.
Le calcul utilise les données, les méthodes, les algorithmes et l'information de la littérature spécialisée et des normes ANSI, OIN, DIN et d'autres. Liste des normes: ANSI B4.1, OIN 286, OIN 2768, DIN 7186
L’interface d’utilisateur.
A télécharger.
Tarif, Achat.
L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document " commande, structure et syntaxe des calculs ".
L'information sur le but, l'utilisation et la commande du paragraphe "information sur le projet" peut être trouvée dans le document " information sur le projet ".
Une chaîne dimensionnelle linéaire est un ensemble de dimensions parallèles indépendantes liées les unes aux autres de façon à créer un circuit géométriquement fermé. Elles peuvent être des dimensions indiquant la position mutuelle des composantes sur une pièce (fig. A) ou les dimensions de plusieurs pièces dans une unité de montage (fig. B).
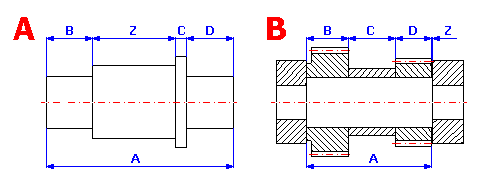
Une chaîne dimensionnelle se compose d'éléments partiels séparés
(dimensions initiales) et termine par un élément de fermeture
(dimension résultante). Les composantes partielles (A, B, C...) sont des
dimensions, qui sont cotées directement dans le dessin ou issues des opérations
de production ou de montage précédentes. La composante de fermeture (Z) représente dans la
chaîne donnée la dimension résultante de production ou de montage,
qui est le résultat de la composition des dimensions partielles comme dimension
de production non cotée des pièces respectivement comme jeu ou interférence
d'assemblage. La grandeur, la tolérance et la déviation limite de la dimension
résultante dépendent directement de la grandeur et de la tolérance des dimensions
partielles. Il y a deux types de composantes dans les
chaînes dimensionnelles, selon la façon dont le changement de la composante partielle affecte le
changement de la composante de fermeture.:
- composantes croissantes - composantes
partielles, dont la croissance a comme conséquence la croissance de la composante
de
fermeture
- composantes décroissantes - composantes partielles, dont
la croissance a comme conséquence la réduction de la composante de fermeture
Dans la solution des relations de tolérance dans les chaînes dimensionnelles, deux types de problèmes se produisent:
Le choix de la méthode de calcul des tolérances et des déviations limites des composantes des chaînes dimensionnelles affecte la précision de production et l'interchangeabilité de montage des composantes. Par conséquent, le régime de la production et de service dépend de ce choix. La solution des relations de la tolérance dans les chaînes dimensionnelles, utilise en pratique trois méthodes de base:
La méthode le plus souvent utilisée, parfois appelée méthode de calcul au maximum - minimum. Elle est basée sur la condition de maintenir la déviation limite exigée de la composante de fermeture pour n'importe quelle combinaison des dimensions réelles des composantes partielles, c.-à-d. des dimensions limites supérieures et inférieures. Cette méthode garantit la pleine interchangeabilité de montage et de fonctionnement des composantes. Cependant, la demande d'une précision plus élevée de la composante de fermeture, elle a comme conséquence les tolérances trop limitées des composantes partielles et donc des coûts de production élevés. La méthode de WC est donc adéquate pour le calcul des circuits dimensionnels avec un nombre restreint de composantes ou au cas où une plus large tolérance de la dimension résultante serait acceptable. Elle est le plus souvent utilisée dans la production en pièces ou en petites séries.
La méthode de WC calcule la tolérance de la dimension résultante comme somme arithmétique de tolérances de toutes les dimensions partielles. Les dimensions de la composante de fermeture sont ainsi déterminées par sa valeur moyenne:
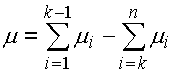
et sa tolérance totale:
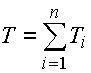
Les dimensions extrêmes de la composante de fermeture sont données par les relations:
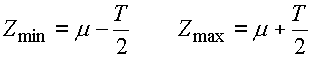
où:
mi - dimension
moyenne de la ième
composante
Ti - tolérance de la ième composante
n - nombre total des composantes partielles
i=1,..,k - nombre de composantes croissantes
i=k,..,n - nombre de composantes décroissantes
Les méthodes de calcul statistiques des chaînes dimensionnelles sont basées sur le calcul de probabilité. Ces méthodes supposent qu'un choix au hasard des pièces pendant le montage, les valeurs limites des déviations apparaissent très rarement dans plusieures composantes partielles simultanément, étant donné qu'il s'agit d'une probabilité combinée. De même les valeurs extrêmes de la déviation dans la production des dimensions particulières d'une composante sont très peu probables. Avec un risque prédéfini de l'élimination de certaines composantes, les tolérances des composantes partielles dans la chaîne dimensionnelle peuvent être plus grandes.
La méthode statistique garantit seulement une interchangeabilité de montage partielle, avec un petit pourcentage des cas non favorables (rebut). Vues les plus grandes tolérances des dimensions partielles, elle résulte en la baisse des coûts de production. Elle est surtout dans les productions massives ou en grandes séries, où l'économie dans les coûts de production est plus importante que le coût élevé de montage et de service issu des conséquences de l'interchangeabilité de montage incomplète des composantes.
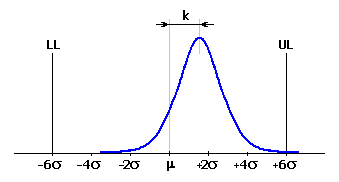
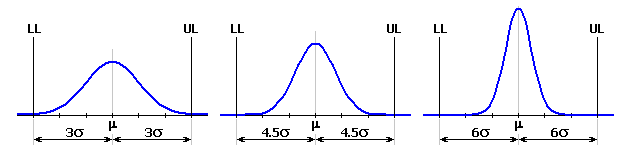
Les dimensions de la composante de fermeture accusent une certaine variation du centre de la zone de tolérance. La fréquence de l'apparition de différentes dimensions suit les règles des statistiques mathématiques et dans la majorité des cas correspond la répartition normale. Cette répartition est décrite par la courbe de la densité de probabilité de Gauss, pour laquelle la fréquence de l'apparition de la dimension donnée "x" s'exprime par la relation:
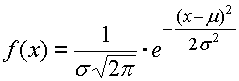
La forme de la coure de Gauss est caractérisée par deux paramètres. La valeur moyenne m détermine la position de la fréquence mqximqle de l'apparition de la dimension résultante; l'écart type s définit "l'allongement" de la courbe.
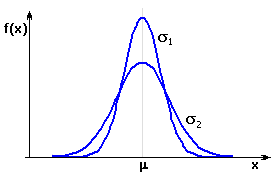
L'aire définie par l'intersection de la courbe de Gauss avec les dimensions limites requises de la composante de fermeture représente le rendement supposé du processus. Les parties de la courbe en dehors de l'intervalle de tolérance définissent la zone qui représente le rebutage dans le processus.
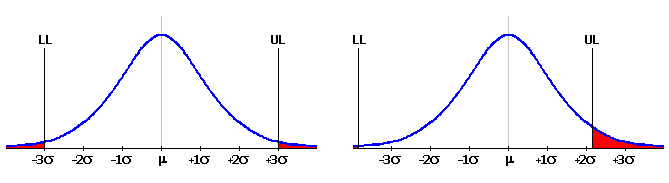
En construction mécanique, le processus de production est souvent considéré comme suffisamment satisfaisant au niveau 3s. Ce qui signifie que la limite supérieure UL et la limite inférieure LL de la dimension résultante sont à une distance de 3s de la valeur moyenne m. L'aire de la courbe de Gauss entre les deux limites est égale à 99.73% de l'aire totale et représente la portion des produits qui remplissent les critères de la spécification. La surface en dehors de ces limites est égale à 0.27% et représente les produits non satisfaisants.
| Dimensions limites | Rendement du processus [%] | Nombre de rebuts par millions de pièces produites |
| m ± 1s | 68.2 | 317310 |
| m ± 2s | 95.4 | 45500 |
| m ± 3s | 99.73 | 2700 |
| m ± 3.5s | 99.95 | 465 |
| m ± 4s | 99.994 | 63 |
| m ± 4.5s | 99.9993 | 6.8 |
| m ± 5s | 99.99994 | 0.6 |
| m ± 6s | 99.9999998 | 0.002 |
Cette méthode de calcul est traditionnelle et également la méthode de calcul statistique la plus répandue des chaînes dimensionnelles. La méthode de RSS est basée sur la supposition selon laquelle les différentes composantes sont produites avec un niveau de capacité de processus (qualité) de 3s.
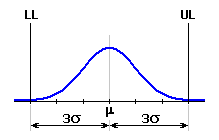
Leur valeurs limites correspondent donc à l'intervalle de la tolérance m ± 3s, et son écart type est donné par la relation:
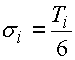
Les dimensions de la composante de fermeture sont déterminées par sa valeur moyenne:
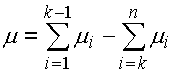
et son écart type:
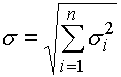
où:
si - écart type
de la ième composante
mi - dimension moyenne de la ième
composante
Ti - tolérance de la ième
composante
n - nombre total des composantes partielles
i=1,..,k - nombre de composantes croissantes
i=k,..,n - nombre de composantes décroissantes
En construction mécanique, le processus de production est souvent considéré comme suffisamment satisfaisant au niveau 3s. Ce qui représente une estimation de 2700 produits défectueux pour un million de pièces produites. Bien qu'une telle portion de produits défectueux parait très bonne, elle est souvent considérée comme insuffisante dans certains domaines de production. En plus, il est pratiquement impossible de maintenir la valeur moyenne de la courbe caractéristique du processus exactement au milieu de la zone de tolérance à long terme. Pour des productions de grands volumes, la valeur moyenne de la caractéristique du processus décale avec le temps dû à l'influence de différents facteurs (réglage erroné, usure des outils et des produits, variations de la température, etc.). Le décalage typique est de 1.5s de la valeur idéale. Pour les processus traditionnels avec un niveau de capacité de 3s, cela représente une hausse de la portion des produits défectueux à approx. 67000 par million de pièces produites.
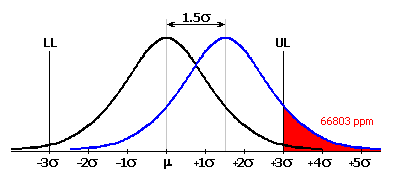
Il est évident que le processus de production avec un tel niveau de rebuts est inadmissible. Actuellement, la méthode de "6 Sigma" qui est plus moderne est utilisée pour évaluer la qualité du processus de production. Le concept de cette méthode est d'atteindre un but, tel que la valeur moyenne de la caractéristique du processus est à une distance de 6s des deux limites de la tolérance. Pour un processus de production aussi efficace, le rapport de 3,4 des produits défectueux par million de pièces produites est atteint avec un décalage moyen supposé de 1,5s.
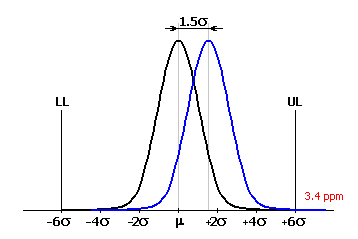
La méthode "6 Sigma" est relativement récente; elle est devenue plus populaire seulement vers la fin des années 1980. Elle a été mise en pratique pour la première fois par la compagnie Motorola et est considérablement utilisée principalement aux États Unis. Son usage est adéquat pour les processus de production où une qualité de production élevée est nécessaire et pour les productions de grands volumes où il y a possibilité de décalage de la valeur moyenne de la caractéristique du processus.
La méthode de "6 Sigma" est une modification de la méthode standard de "RSS" et introduit deux nouveaux paramètres, (Cp, Cpk), nommés Index de capacité du processus dans la problématique des solutions des chaînes dimensionnelles. Ces index de capacité sont utilisés pour évaluer la qualité du processus de production.
L'index de capacité Cp évalue la qualité du processus de production par la comparaison des limites de la tolérance spécifiées avec le niveau traditionnel de la capacité 3s.
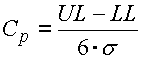
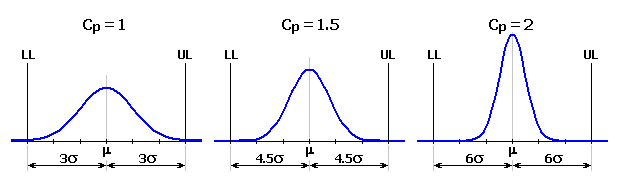
Pour le processus avec un intervalle de tolérance m ± 3s, Cp sera égal à 1. Pour les processus de haute qualité où les limites de tolérance sont à une distance de ±6s de la valeur moyenne, l'index de capacité sera Cp=2.
L'index Cpk est l'index Cp modifié pour un décalage moyen de la caractéristique du processus.
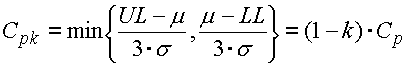
où le facteur du décalage k varie dans l'intervalle <0..1> et détermine la valeur relative du décalage de la valeur moyenne qui se rapporte à la moitié de l'intervalle de tolérance. Pour un décalage typique de la valeur moyenne de la caractéristique du processus de 1,5s, le facteur de décalage sera k=0.25 et l'index de capacité sera Cpk=1.5 pour un processus de qualité "6 Sigma".
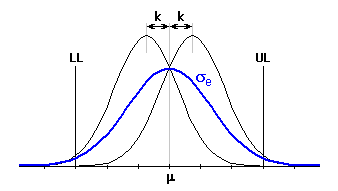
L'écart type effectif du processus peut ainsi être estimé comme:
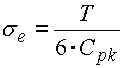
Dans l'application de l'index de capacité sur toutes les composantes partielles de la chaîne dimensionnelle, les dimensions de la composante de fermeture peuvent être exprimées de façon similaire à la méthode de "RSS" par sa valeur moyenne m et son écart type:
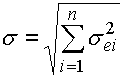
où:
sei - l'écart type effectif de la ième
composante
Pour la méthode de "6 Sigma", un processus de production avec un rapport de capacité de 4,5s est souvent considéré comme satisfaisant.
La méthode de montage sélectif s'utilise dans la production en masse et en grandes séries des pièces précises qui ne nécessitent pas d'interchangeabilité des composantes dans une pièce. Le montage du produit est précédé par la classification de différentes composantes en sous groupes de tolérance. Les dimensions de production des pièces peuvent être prescrites avec une plus large tolérance. La tolérance resserrée de la dimension résultante est atteinte par la combinaison fonctionnelle des sous groupes classifiés. Pour déterminer la dimension résultante de la composante de fermeture, la méthode de "WC" mentionnée ci-dessus est utilisée sauf que la calcul n'inclut pas toutes les tolérances de production des composantes partielles, mais seulement les tolérances resserrées, applicables pour le sous groupe de tolérance choisi.
La méthode de montage sélectif est une méthode très efficace pour la solution des chaînes dimensionnelles, permettant de sensiblement accroître les tolérances de production des composantes partielles et donc une réduction sensible des coûts de production. D'autre part, l'application de cette méthode est très exigeante du point de vue assemblage. Les coûts d'exploitation vont également accroître, du fait qu'il est souvent nécessaire de remplacer la pièce entière en cas d'usure ou d'endommagement d'une composante partielle.
Pour que la méthode de montage sélectif soit effective, il est nécessaire de résoudre le problème du choix optimal (combinaison) des composantes. Les composantes doivent être montées de sorte qu'il soit possible d'assembler le maximum de pièces possible qui remplissent les conditions de fonctionnement avec le nombre donné de composantes produites. Cette tâche peut être divisée en deux étapes:
Consiste à trouver toutes les combinaisons de différents sous groupes des composantes partielles pour lesquels les conditions de fonctionnement sont remplies par la composante de fermeture.
Cette tâche doit être résolue bien avant le début de la production, dans le processus de la conception de la chaîne dimensionnelle. Le nombre de combinaisons convenables dépend de la tolérance totale des composantes partielles tout comme le nombre de sous intervalles de tolérance. La chaîne dimensionnelle devrait être conçue de sorte que le nombre de combinaisons d'assemblages admissibles varie dans des limites raisonnables.
Pour les petits nombres de combinaisons convenables, il ne sera probablement pas possible d'utiliser toutes les pièces produites pendant le montage. C'est pourquoi le rendement de l'assemblage baisse et la production devient plus coûteuse. L'index critique est représenté par l'état où certains sous ensembles apparaissent déjà comme étant inadmissibles à l'étape de la conception.
D'autre part, un grand nombre de combinaisons convenables signifie une conception moins effective. La chaîne de tolérance pourrait être conçue d'une manière plus optimale, avec une plus large tolérance des composantes partielles ou avec un plus nombre de sous intervalles de tolérance.
Optimisation du nombre des pièces montées pour les nombres donnés de composantes produites dans les différents sous intervalles de tolérance.
Il est nécessaire de résoudre cette tâche de façon répétée pendant la production et cela toujours pendant le remplissage du stock avant le début du montage en soi. Le but principal de cette tâche est de déterminer la procédure de montage optimale de sorte que le nombre de pièces montées soit le plus grand possible. Pendant la solution de cette tâche, il est nécessaire de choisir le groupe de combinaisons optimal à partir des sous groupes de combinaisons acceptables utilisés dans l'assemblage et en même temps déterminer le nombre de pièces montées pour chaque combinaison utilisée.
L'algorithme de l'optimisation est basé sur le montage graduel de différentes pièces en retirant les composantes des sous groupes choisis. Dans la première étape, le programme de calcul estimera le nombre minimum et maximum possible de pièces montées. Dans les étapes suivantes il retire les pièces des sous groupes choisis selon un schéma choisi au préalable de sorte que la plus petite estimation du nombre de pièces montées accroît le rapidement possible et la plus grande estimation décroît le moins possible.
La solution à cette tâche n'est souvent pas claire. Il est souvent possible de trouver de différentes procédures de montage qui mènent à un nombre identique de pièces montées. C'est la raison pour laquelle le nombre de combinaisons de montage est utilisé comme un autre critère d'optimisation. Minimiser le nombre de combinaisons utilisées a comme résultat la simplification et l'accélération du montage, c.à.d la réduction des coûts de production. Dans certaines applications pratiques, les deux critères ont la même importance.
Cette rangée sert à la conversion des systèmes d'unités de calcul et à choisir les tolérances normalisées.
Choisissez le système d'unités requis pour le calcul sur la liste. Après conversion d'unités, toutes les valeurs seront automatiquement recalculées.
Pendant la définition de la chaîne dimensionnelle dans les paragraphes [1.1, 3.2, 5.1, 7.1], la tolérance est également déterminée pour chaque dimension. Pour simplifier le travail, ce programme contient un outil pour le choix automatique des tolérances normalisées.
Le programme contient un groupe des tolérances des dimensions de base selon OIN ou ANSI. En rapport avec le type de déviation et la norme appliquée, les tolérances sont reparties en 5 groupes:
Chaque groupe contient un lot des listes et des boutons dans l'entête du cahier de travail. Déterminer les paramètres de tolérance ou respectivement d'ajustement requis (degré de précision, zone de tolérance, ..) sur les listes. A l'aide des boutons, entrez les dimensions de la tolérance choisie dans la cellule appropriée du tableau d'insertion - dans la rangée avec la cellule active.
Les tolérances selon les normes OIN sont définies en [mm] et sont destinées au calcul dans les unités de SI. Les tolérances selon ANSI sont définies en [in] et sont destinées au calcul dans les unités Impériales. En cas d'usage des tolérances normalisées définies dans les unités autres que celles déterminées dans le calcul, les déviations des dimensions seront automatiquement recalculées et arrondies.
Ce chapitre permet d'effectuer l'analyse, la synthèse et l'optimisation de la chaîne dimensionnelle à l'aide de la méthode arithmétique "WC", ou éventuellement de la méthode statistique "RSS".
La méthode de "Worst Case" s'utilise au cas où le montage total et l'interchangeabilité des composantes sont requis et est appropriée pour la solution des circuits des dimensions avec un petit nombre de composantes ou si une tolérance plus brute de la dimension finale est acceptable. La méthode statistique de "Root Sum Squares" garantie seulement une partielle interchangeabilité de montage et est utilisée pour diminuer les coûts de production dans les productions en masse ou en grandes séries.
La conception et l'optimisation d'une chaîne dimensionnelle consistent aux étapes suivantes:
Ce paragraphe sert à la conception d'une chaîne dimensionnelle et à l'optimisation des tolérances des composantes partielles choisies.
Ce tableau sert à définir les dimensions de différents composantes partielles d'une chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. Le sens du tableau est évident dans la description suivante:
Colonne 1 - Le nom de la
composante est un paramètre facultatif.
Colonne 2 - Déterminez la dimension
nominale de la composante partielle. Les
composantes "croissantes"
sont positives, les composantes "décroissantes"
sont inscrites avec un signe négatif.
Colonne 3 - Déterminez les
déviations supérieure et inférieure de la dimension.
Appuyez sur le bouton choisi dans l'entête du cahier de travail pour insérer les
déviations correspondant aux tolérances choisies dans le tableau.
Colonne
4..7 - Ces colonnes contiennent le calcul des dimensions
limites, des dimensions moyennes et de l'écart type de toutes les composantes
partielles.
Colonne
8 - Par le réglage du commutateur, marquez toutes les
composantes partielles dont les tolérances doivent être optimisées.
En cochant les cases, vous déterminez les tolérances fixes, qui
resteront inchangées après optimisation.
Colonne
9,10 - Après optimisation, ces colonnes contiennent les
déviations conçues (optimisées). La colonne gauche
contient les résultats de l'optimisation à l'aide de la méthode de "WC";
la colonne droite contient les résultats obtenus à l'aide de la
méthode de "RSS". Appuyer sur le bouton dans la
rangée au bas du tableau pour transférer les déviations conçues dans la colonne
d'insertion.
Ce paragraphe sert à optimiser les tolérances des composantes partielles choisies de la chaîne dimensionnelle définie dans le tableau [1.1]. Avant le démarrage de l'optimisation, déterminez les dimensions limites requises de la composante de fermeture [1.3] et les paramètres d'optimisation [1.6]. Démarrez l'optimisation en appuyant sur le bouton dans la rangée [1.11].
L'optimisation s'effectue simultanément pour les deux méthodes de calcul (WC, RSS). Les conceptions désirées sont affichées dans le tableau [1.1], voir le paragraphe [2] pour les dimensions résultantes de la composante de fermeture.
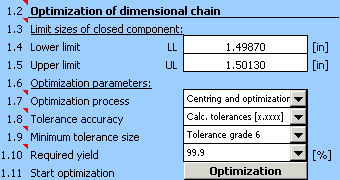
Ce paragraphe définit les dimensions limites requises de la composante de fermeture déterminées par les critères de fonctionnement de la pièce.
Choisissez l'un des modes d'optimisation sur la liste:
1. Centrage de la conception
Tout en maintenant la grandeur de la tolérance, le calcul
ajustera les déviations limites des composantes partielles choisies de sorte que
la dimension moyenne de la composante de fermeture soit le plus proche possible
du centre de l'intervalle de tolérance déterminé par les limites [1.3].
Selon le réglage de la précision de la tolérance [1.8],
le calcule travaille en deux modes:
2. Optimisation des tolérances
Tout en maintenant la valeur moyenne de l'intervalle de
tolérance, le calcule ajustera la tolérance des composantes partielles choisies
de sorte que les dimensions résultantes de la composante de fermeture
satisfassent aux critères de la spécification donnée par les limites [1.3].
3. Centrage et optimisation
Combinaison des deux processus précédents
Choisissez le type et le niveau de la précision des tolérances utilisées dans l'optimisation.
Au cas où l'un des 5 premiers éléments serait choisi, la grandeur de la tolérance optimisée sera déterminée par le calcul, avec un niveau de précision prédéfini (nombre de chiffres dans la partie décimale). Le rapport mutuel des dimensions des tolérances optimisées sera maintenu.
Si les deux autres éléments sur la liste sont choisis, la grandeur des tolérances optimisées correspondra aux valeurs normalisées. Pour le calcul dans les unités SI, les tolérances normalisées selon OIN ISO 286 sont utilisées et pour le calcul dans les unités Impériales, les tolérances selon ANSI B4.1 sont utilisées. Si l'élément "classe de tolérance identique" est choisi, les tolérances normalisées de la même classe de tolérance seront utilisées pour toutes les dimensions optimisées.
Déterminez la valeur minimale (niveau de précision) des tolérances qui peuvent être utilisées dans l'optimisation.
Choisissez le minimum de rendement requis du processus de production sur la liste.
Ce paragraphe présente d'une façon très claire les paramètres détaillés de la composante de fermeture pour la chaîne dimensionnelle définie dans le paragraphe [1]. Pour comparaison, les dimensions des composantes de fermeture des tolérances optimisées tout comme celles des tolérances originales des composantes partielles sont données dans ce paragraphe.
Dans ce paragraphe, définissez les dimensions limites requises de la composante de fermeture données par les critères de fonctionnement du produit.
Ce paragraphe donne les dimensions résultantes de la composante de fermeture au cas où la méthode de "Worst Case" serait utilisée.
Ce paragraphe donne les paramètres de la composante de fermeture au cas où la méthode de "Root Sum Squares" serait utilisée.
Le rendement de production [2.13] donne le rapport supposé des produits qui remplissent les critères spécifiés, c.à.d. les produits dont la dimension de la composante de fermeture est dans l'intervalle spécifié par les dimensions limites [2.1]. Le rebut du processus de production [2.14] représente le nombre estimé des produits défectueux par millions de pièces produites.
Ce paragraphe contient le calcul des dimensions limites de la composante de fermeture pour le rendement choisi du processus de production.
Le calcul utilisé dans le chapitre [A] est basé sur la supposition comme quoi la composante conçue fonctionnera aux températures proches de la température de base de 20°C (68°F) à laquelle les dimensions et les tolérances des composantes partielles étaient déterminées. Si les composantes fonctionnent de façon permanente aux températures élevées, leurs dimensions seront déformées pendant le fonctionnement. Ce chapitre est ainsi destiné à l'analyse de la chaîne dimensionnelle linéaire déformée sous l'effet du changement de la température de fonctionnement. Pour contrôler la dimension de la composante de fermeture, vous pouvez utiliser la méthode arithmétique "WC" ou statistique "RSS".
Dans ce paragraphe, définissez la chaîne dimensionnelle et la température de fonctionnement pour la composante conçue.
Déterminez la température supposée à laquelle la composante conçue fonctionnera.
Ce tableau sert à définir les dimensions de différentes composantes partielles de la chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. Le sens du tableau est évident dans la description suivante:
Colonne 1 - Le nom de la
composante est un paramètre facultatif.
Colonne 2 - Déterminez la dimension
nominale de la composante partielle. Les
composantes "croissantes"
sont positives, les composantes "décroissantes"
sont inscrites avec un signe négatif.
Colonne 3 - Déterminez les
déviations supérieure et inférieure de la dimension.
Appuyez sur le bouton choisi dans l'entête du cahier de travail pour insérer les
déviations correspondant aux tolérances choisies dans le tableau.
Colonne
4,5 - Les dimensions de production
(de montage) des composantes partielles sont calculées dans ces colonnes.
Colonne 6
- Choisissez le matériel de la composante sur la liste.
Colonne 7
- Déterminez le coefficient de dilatation thermique. Si la case
de contrôle à l'entête du tableau est cochée, les valeurs seront déterminées
automatiquement selon le matériel choisi et la température de fonctionnement [3.1].
Colonne 8,9 - Les
dimensions des composantes partielles à la température de fonctionnement sont
calculées dans ces colonnes.
Ce paragraphe présente d'une façon très claire les paramètres détaillés de la composante de fermeture pour la chaîne dimensionnelle définie dans le paragraphe [3]. Pour comparaison, les dimensions résultantes de la composante de fermeture pendant le montage et à la température de fonctionnement (20° C) sont données dans ce paragraphe.
Déterminez la coefficient de dilatation thermique du matériel de la composante de fermeture.
Définissez les dimension de montage requises de la composante de fermeture dans ce paragraphe. Les dimensions limites de la composante de fermeture à la température de fonctionnement sont calculées automatiquement selon le coefficient de dilatation thermique choisi [4.1].
Ce paragraphe donne les dimensions résultantes de la composante de fermeture au cas où la méthode de "Worst Case" serait utilisée.
Ce paragraphe donne les paramètres de la composante de fermeture au cas où la méthode de "Root Sum Squares" serait utilisée.
Le rendement de production [4.15] donne le rapport supposé des produits qui remplissent les critères spécifiés, c.à.d. les produits dont la dimension de la composante de fermeture est dans l'intervalle spécifié par les dimensions limites [4.3]. Le rebut du processus de production [4.16] représente le nombre estimé des produits défectueux par millions de pièces produites.
Ce paragraphe contient le calcul des dimensions limites de la composante de fermeture pour le rendement choisi du processus de production.
Ce chapitre permet d'effectuer l'analyse de la tolérance d'une chaîne dimensionnelle linéaire à l'aide de la méthode de "6 Sigma".
La méthode de "6 Sigma" est une méthode statistique moderne qui est utilisée pour évaluer la qualité du processus de production. Son usage est spécialement adéquat dans les processus de production où une qualité de production élevée est nécessaire et pour les productions de grands volumes où il y a possibilité de décalage de la valeur moyenne de la caractéristique du processus.
Le concept de cette méthode est d'atteindre un but, tel que la valeur moyenne de la caractéristique du processus est à une distance de 6s des deux limites de la tolérance. Pour un processus de production aussi efficace, le rapport de 3,4 des produits défectueux par million de pièces produites est atteint même avec un décalage moyen supposé de 1,5s.

Ce paragraphe sert à concevoir une chaîne dimensionnelle.
Ce tableau sert à définir les dimensions de différentes composantes partielles de la chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. Le sens du tableau est évident dans la description suivante:
Colonne 1 - Le nom de la
composante est un paramètre facultatif.
Colonne 2 - Déterminez la dimension
nominale de la composante partielle. Les
composantes "croissantes"
sont positives, les composantes "décroissantes"
sont inscrites avec un signe négatif.
Colonne 3 - Déterminez les
déviations supérieure et inférieure de la dimension.
Appuyez sur le bouton choisi dans l'entête du cahier de travail pour insérer les
déviations correspondant aux tolérances choisies dans le tableau.
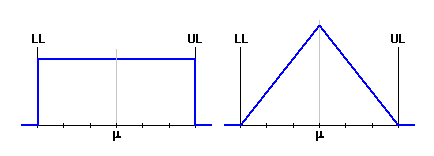
Colonne 4 - Choisissez le
type de répartition de la fréquence théorique.
D'habitude, la répartition
normale, qui correspond le mieux à la répartition
réelle des grandeurs occasionnelles du processus est utilisée pour décrire les
processus de production.
Colonne 5 - déterminez
l'index de capacité du processus de production. Si la
case de contrôle à l'entête du tableau est cochée, les valeurs appropriées au
type de répartition de la fréquence choisi seront automatiquement utilisées.
Colonne 6 - Déterminez le
facteur de décalage de la valeur moyenne de la caractéristique du processus.
Ce facteur détermine la valeur relative du décalage de la valeur
moyenne correspondant à la moitié de l'intervalle de tolérance.
Pour un processus de production avec una qualité "6 Sigma",
le facteur de décalage est souvent k=0.25.
Colonne 7 - L'index de
capacité modifié est calculé pour le décalage de la valeur moyenne de la
caractéristique du processus dans cette colonne.
Colonne 8,9 - La valeur
moyenne et l'écart type effectif du processus sont calculés dans ces colonnes.
Dans ce paragraphe, les paramètres détaillés de la composante d'entrée choisie sont présentés numériquement et graphiquement tels que définis dans la tableau [1.1].
Ce paragraphe présente d'une façon très claire les paramètres détaillés de la composante de fermeture pour la chaîne dimensionnelle définie dans le paragraphe [5].
Dans ce paragraphe, définissez les dimensions limites requises de la composante de fermeture données par les critères de fonctionnement du produit.
Ce paragraphe donne les paramètres de la composante de fermeture au cas où la méthode de "6 Sigma" serait utilisée.
Le rendement de production [6.11] donne le rapport supposé des produits qui remplissent les critères spécifiés, c.à.d. les produits dont la dimension de la composante de fermeture est dans l'intervalle spécifié par les dimensions limites [6.1]. Le rebut du processus de production [4.16] représente le nombre estimé des produits défectueux par millions de pièces produites.
Ce paragraphe contient le calcul des dimensions limites de la composante de fermeture pour le rendement choisi du processus de production.
Ce chapitre permet d'effectuer l'analyse de la tolérance d'une chaîne dimensionnelle linéaire à l'aide de la méthode de l'interchangeabilité du groupe (montage sélectif).
La méthode de montage sélectif s'utilise dans la production en masse et en grandes séries des pièces précises qui ne nécessitent pas d'interchangeabilité des composantes dans une pièce. Le montage du produit est précédé par la classification de différentes composantes en sous groupes de tolérance. Les dimensions de production des pièces peuvent être prescrites avec une plus large tolérance. La tolérance resserrée de la dimension résultante est atteinte par la combinaison fonctionnelle des sous groupes classifiés.
La conception d'une chaîne dimensionnelle consiste aux étapes suivantes:
A part la conception de la chaîne dimensionnelle, l'optimisation du nombre des pièces montées pour un nombre spécifié des composantes produites [9] est souvent une partie de la solution. Cette tâche doit être résolue à plusieures reprises pendant la production, chaque fois que le stock est complété avant le début du montage.
Ce paragraphe est destiné à la conception et au contrôle de la chaîne dimensionnelle.
Dans le tableau [7.1] définissez le nombre, les dimensions et les tolérances de toutes les composantes dont la pièce finale sera montée. Choisissez ensuite pour chaque composante, le nombre des sous groupes (sous intervalles) de tolérance, dans lesquels les composantes seront classifiées avant le montage. Dans le paragraphe [7.2] vous trouverez les dimensions limites de la composante de fermeture pour n'importe quelle combinaison des sous groupes des composantes.
Ce tableau sert à définir les dimensions de différentes composantes partielles de la chaîne dimensionnelle. Chaque rangée du tableau correspond à une composante partielle. La signification des colonnes du tableau est évidente dans la description suivante:
Colonne 1 - Déterminez
le nombre des composantes identiques de la chaîne dimensionnelle.
Colonne 2 - Le nom de la
composante est un paramètre facultatif.
Colonne 3 - Déterminez la dimension
nominale de la composante partielle. Les
composantes "croissantes"
sont positives, les composantes "décroissantes"
sont inscrites avec un signe négatif.
Colonne 4 - Déterminez les
déviations supérieure et inférieure de la dimension.
Appuyez sur le bouton choisi dans l'entête du cahier de travail pour insérer les
déviations correspondant aux tolérances choisies dans le tableau.
Colonne 5 - Déterminez le
nombre de sous groupes de tolérance (sous intervalles)
dans lesquels les composantes seront classifiées.
Vous déterminerez le nombre identique de sous groupes pour
toutes les composantes à l'aide du choix sur la liste à l'entête du tableau.
Colonne 6..11 - Les
dimensions limites de tous les sous intervalles de tolérance sont calculées dans
ces colonnes. Les différents sous groupes sont marqués
par les index numériques à l'entête du tableau. Ensemble
avec le marquage de la composante, l'index sert à identifier clairement le sous
groupe de montage choisi (A1, A2, B1, B2, B3,
...).
Les dimensions limites de la composante de fermeture déterminées par la méthode de "Worst Case" pour les tolérances complètes des composantes partielles sont données dans la première rangée du tableau. Cette donnée est à titre informatif seulement et est importante surtout pour le centrage de la conception. Pour une conception de haute qualité, la dimension moyenne donnée dans ce paragraphe devrait être aussi proche de la dimension requise que possible [8.7].
Dans la deuxième rangée, vous trouverez les dimensions limites de la composante de fermeture pour toute combinaison des sous groupes des composantes. Vous pouvez déterminer la combinaison de montage requise à l'aide des sous groupes de tolérance appropriés sur les listes.
Le couplage correct d'une composante est une partie intégrale de la conception de la chaîne dimensionnelle. le but de cette tâche est de trouver les combinaisons de différents sous groupes des composantes pour lesquelles la composante de fermeture remplit les conditions de fonctionnement de la pièce. Le nombre total des combinaisons trouvées est le critère pour l'évaluation de la qualité de la conception. La chaîne dimensionnelle devrait être conçue de sorte que le nombre des combinaisons de montages convenables varie dans des limites raisonnables.
Pour de petits nombres de combinaisons convenables, il ne sera probablement pas possible d'utiliser toutes les pièces produites dans le montage. De cette façon, le rendement de montage du processus baisse et la production devient plus coûteuse. L'index critique est l'état où certains sous groupes paraissent déjà inacceptable à l'étape de la conception.
D'autre part, un grand nombre de combinaisons convenables signifie que la conception est moins effective. La chaîne de tolérance pourrait probablement être conçue d'une manière plus effective, avec de plus larges tolérances des composantes partielles ou avec un nombre réduit des sous intervalles de tolérance.
La méthode de montage sélectif garantit seulement une interchangeabilité de montage partielle dans les combinaisons de montage choisies. En cas d'usure ou d'endommagement de la composante partielle pendant le service, il est nécessaire nécessaire de remplacer la pièce du montage tout entier. C'est pourquoi la méthode de montage sélectif s'utilise spécialement dans la production des pièces précises, quand l'interchangeabilité de fonctionnement des composantes dans la pièce est requise.
Bien que cela a comme conséquence la hausse des coûts de production, il peut toujours être économiquement plus avantageux pour certains produits d'assurer l'interchangeabilité complète d'au moins une composante. Pour une pareille condition, deux différentes solutions peuvent être appliquées pour le montage sélectif:
Dans ce paragraphe, définissez les dimensions limites requises de la composante de fermeture déterminées par les conditions de fonctionnement de la pièce. La première colonne contient les dimensions limites de la composante de fermeture pendant le montage de la pièce. La seconde colonne contient les dimensions limites après le rechange de la composante choisie.
Ce paragraphe sert à rechercher toutes les combinaisons de montage pour lesquelles la composante de fermeture remplit les conditions de fonctionnement de la pièce telles que spécifiées dans les paragraphes [8.1, 8.4]. Le programma travaille dans deux régimes:
Déterminez le régime de recherche sur la liste dans la case [8.9]. Démarrez la recherche à l'aide du bouton dans la rangée [8.10], les résultats sont donnés dans le paragraphe [8.11].
Ce paramètre donne le nombre total de toutes les combinaisons de montage qui peuvent être utilisées dans le montage de la pièce.
Ce paramètre donne le nombre de toutes les combinaisons de montage trouvées pour lesquelles la composante de fermeture remplit les conditions de fonctionnement de la pièce telles que spécifiées dans les paragraphes [8.1, 8.4]. Le nombre total des combinaisons trouvées est le critère pour l'évaluation de la qualité de la conception. La chaîne dimensionnelle devrait être conçue de sorte que le nombre des combinaisons de montages convenables varie dans des limites raisonnables.
Pour de petits nombres de combinaisons convenables, il ne sera probablement pas possible d'utiliser toutes les pièces produites dans le montage. De cette façon, le rendement de montage du processus baisse et la production devient plus coûteuse.
D'autre part, un grand nombre de combinaisons convenables signifie que la conception est moins effective. La chaîne de tolérance pourrait probablement être conçue d'une manière plus effective, avec de plus larges tolérances des composantes partielles ou avec un nombre réduit des sous intervalles de tolérance.
Le tableau des combinaisons convenables contient les combinaisons de montage où la composante de fermeture remplit les conditions de fonctionnement de la pièce telles que spécifiées dans les paragraphes [8.1, 8.4]. Les dimensions résultantes de la composante de fermeture pour la combinaison choisie sont données dans le paragraphe [8.15].
Le tableau des sous-groupes non utilisés contient tous les sous-groupes de tolérance (sous-intervalles) pour lesquels aucune combinaison de montage acceptable ne peut être trouvée. Les pièces classifiées dans ces sous-groupes ne peuvent pas être utilisées pendant le montage. Le rendement de montage du processus baisse et la production devient ainsi plus coûteuse. Pour une chaîne dimensionnelle correctement conçue, ce tableau devrait rester vide.
Ce paragraphe présente numériquement et graphiquement les dimensions résultantes de la composante de fermeture pour la combinaison de montage choisie dans le tableau [8.14]. La première colonne contient les dimensions limites de la composante de fermeture pendant le montage de la pièce. La seconde colonne contient les dimensions limites après le rechange de la composante choisie.
Pour que la méthode de montage sélectif soit effectif, il est nécessaire de résoudre le problème du choix optimal (combinaison)des composantes. Les composantes doivent être combinées de sorte qu'il soit possible d'assembler le plus grand nombre de pièces possible qui remplissent les conditions de fonctionnement en utilisant le nombre donné des pièces produites.
Il est nécessaire de résoudre cette tâche de façon répétée pendant la production et cela toujours pendant le remplissage du stock avant le début du montage en soi. Le but principal de cette tâche est de déterminer la procédure de montage optimale de sorte que le nombre de pièces montées soit le plus grand possible. Pendant la solution de cette tâche, il est nécessaire de choisir le groupe de combinaisons optimal à partir des sous groupes de combinaisons acceptables [8.14] utilisés dans l'assemblage et en même temps déterminer le nombre de pièces montées pour chaque combinaison utilisée.
La solution à cette tâche n'est souvent pas claire. Il est souvent possible de trouver de différentes procédures de montage qui mènent à un nombre identique de pièces montées. C'est la raison pour laquelle le nombre de combinaisons de montage est utilisé comme un autre critère d'optimisation. Minimaliser le nombre de combinaisons utilisées a comme résultat la simplification et l'accélération du montage, c.à.d la réduction des coûts de production. Dans certaines applications pratiques, les deux critères ont la même importance.
Déterminez le nombre de pièces produites dans les différents sous-intervalles dans le tableau.
Choisissez la méthode d'optimisation requise sur la liste.
A part la demande d'assemblage du maximum de pièces, la demande de la minimisation du nombre de combinaisons de montage qui seront utilisées pour le montage de la pièces est fréquente en pratique. Avec la croissance du nombre de combinaisons utilisées, le nombre total de pièces montées baisse également. Il est évident que ces deux demandes sont mutuellement contradictoires. Ainsi, le paramètre qui donne le poids (l'importance) de différents critères doit être spécifié pendant l'optimisation. Déterminer le niveau d'importance des deux critères à l'aide du bouton roulant.
La solution à cette tâche n'est souvent pas claire. Il est souvent possible de trouver de différentes procédures de montage qui mènent à un même nombre de pièces montées. Le calcul offre ainsi la possibilité de choisir à partir de différentes solutions à l'aide de différents schémas (algorithmes). Choisissez la solution sur la liste avant de démarrer l'optimisation.
Dans ce paragraphe vous pouvez trouver les paramètres de base de qualité du processus de montage conçu. Les détails sur le processus de montage optimisé peuvent être trouvés dans la tableau [9.12].
Ce tableau contient les spécifications détaillées d'un processus de montage optimisé. La colonne gauche contient toutes les combinaisons utilisées pour le montage de la pièce. La colonne droite contient le nombre de pièces montées dans chaque combinaison.
Ce tableau contient les nombres de composantes non utilisées, qui n'ont pas pu être utilisées dans le montage de la pièce.
Comme illustration des problèmes de l'analyse de la tolérance des chaînes dimensionnelles linéaires, le manuel de l'utilisateur (l'aide) contient quelques exemples pratiques sur l'usage de ce calcul:
Pour l'exemple de l'ajustement de l'arbre dans la boîte (voir l'image), concevez les tolérances de production de différentes composantes de sorte qu'un jeu de 0.05 - 0.80 mm soit assuré. Les tolérances conçues doivent remplir les critères technologiques suivants:
- les surfaces de contact de la boîte seront fraisées
- l'arbre et le coussinet seront usinés au tour
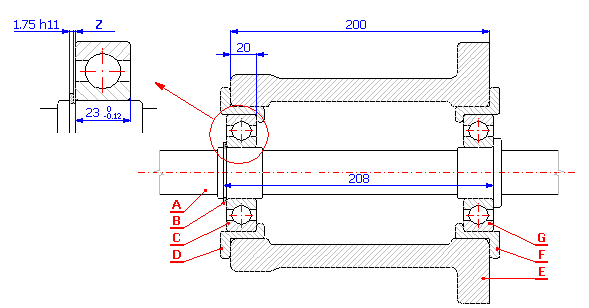
où:
A ....... Arbre
B ....... Anneau de sûreté 40 DIN 471
C,G .... Roulement 6308 DIN 625 SKF
D,F .... Coussinet
E ....... Boîte
Z ....... Jeu dans l'ajustement <0.05 to 0.80> mm
A partir du diagramme de la chaîne dimensionnelle
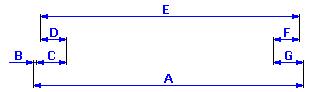
nous pouvons décrire le jeu dans l'ajustement pour le problème donné à l'aide de la relation Z = A - B - C + D - E + F - G
Dans la conception des tolérances de production, nous devons procéder sur base des conditions technologiques de la production. La valeur des tolérances conçues de différentes composantes doit se trouver dans la marge de la précision de production qui est réalisable avec le type d'usinage choisi. Pour le fraisage, la précision habituelle dans l'usinage varie entre les niveaux de tolérance 9 et 13, pour l'usinage au tour entre 6 et 12.
Nous pouvons répartir la conception et l'optimisation de la chaîne dimensionnelle aux étapes suivantes:
1) A l'aide de la relation donnée ci-dessus, nous définirons la chaîne dimensionnelle dans le tableau [1.1]. Les composantes partielles de la chaîne forment les différentes pièces; le jeu requis dans l'ajustement est la composante de fermeture de la chaîne dimensionnelle.
2) Pour les pièces avec une tolérance fixe prescrite par le producteur (roulement, anneau de sûreté), nous déterminerons la déviation dimensionnelle appropriée dans le tableau d'insertion.
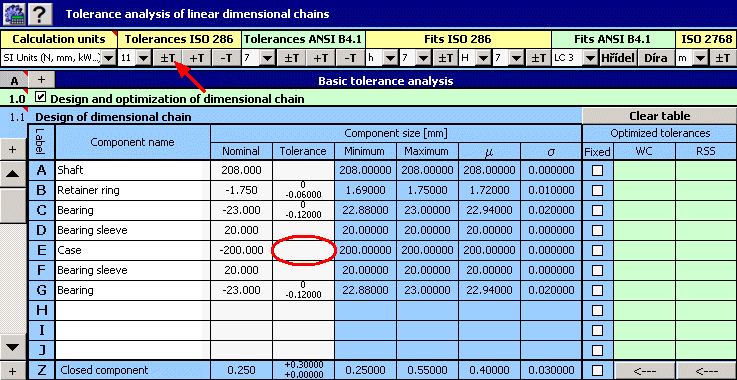
3) Les surfaces de contact de la boîte seront fraisées; dans la première conception, nous choisirons ainsi la valeur de la tolérance au niveau de précision 11 pour la largeur de la boîte.
4) En cochant les cases appropriées dans la colonne 8 du tableau, nous marquerons toutes les pièces avec une tolérance fixée.
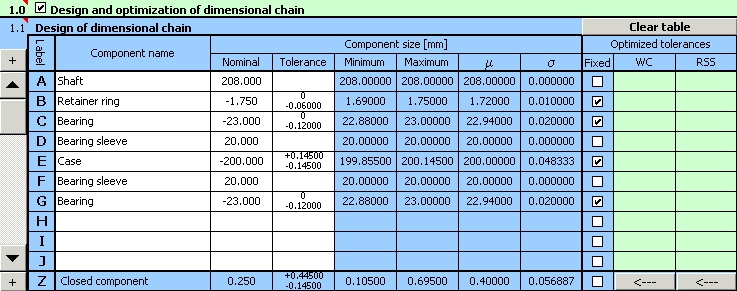
5) Dans le paragraphe [1.3] nous déterminerons les valeurs limites du jeu requis dans l'ajustement.
6) Sur la liste dans la case [1.7] choisissez la méthode de "centrage et optimisation", sur la liste [1.8] choisissez les "tolérances normalisées".
7) Toutes les pièces pour lesquelles nous voulons concevoir les tolérances dans l'étape suivante seront usinées au tour. Sur la liste dans la case [1.9] nous déterminerons ainsi le nombre minimum permis de la tolérance au niveau de précision 6.
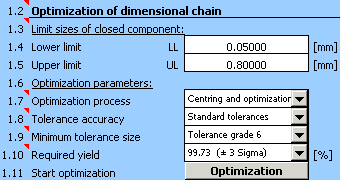
8) A l'aide du bouton dans la rangée [1.11] nous lancerons l'optimisation de la chaîne dimensionnelle.
9) Les paramètres du jeu résultant réalisé pour la conception des tolérances optimisée se trouvent dans le paragraphe [2.5],
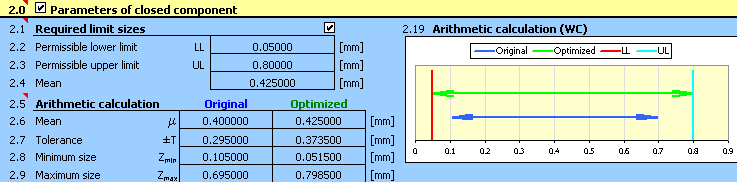
les déviations optimisées des dimensions de production sont données dans la colonne 9 du tableau [1.1].
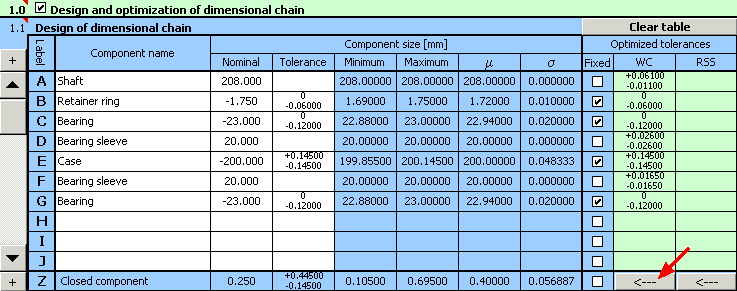
10) Pour l'exemple donné ici, une solution convenables du point de vue du fonctionnement a été trouvée pendant l'optimisation; cependant, en pratique une telle conception n'est pas du tout convenable. Le programme a conçu la largeur des coussinets dans les rangées D et F avec des tolérances différentes. Pour une production et un montage efficaces, il est nécessaire d'assurer l'interchangeabilité de tous les deux coussinets. La prochaine étape de la conception consiste à éliminer ce problème.
11) Utilisez le bouton dans la dernière rangée du tableau pour transférer les tolérances conçues à la section d'insertion du tableau, unifiez ensuite la tolérance des deux coussinets en utilisant la plus grande des valeurs conçues.
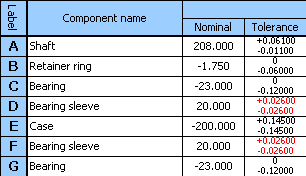
12) Dans la colonne 8 du tableau, cochez les cases dans les rangées D et F, et répétez l'optimisation à l'aide du bouton dans la rangée [1.11].
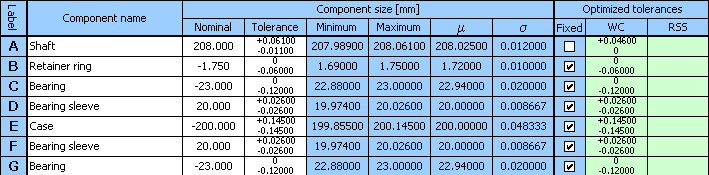
13) Cette fois-ci la conception donne une solution complètement satisfaisante avec le niveau de précision 9 de la tolérance du coussinet et 7 pour la tolérance de l'arbre.
La solution conçue ici ne sera évidemment pas l'unique solution satisfaisante du problème et ne doit pas non plus être nécessairement la solution idéale. Il est donc préférable de concevoir plusieures solutions différentes (surtout pour les productions en masse) avec de différents niveaux de précision de la production de différentes pièces.
Nous obtiendrons une autre solution au problème si nous choisissons la plus petite des valeurs originalement conçues pour la tolérance du coussinet à l'étape 11).
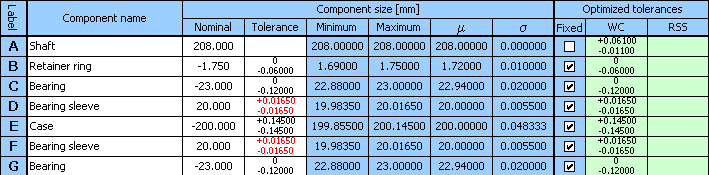
nous obtiendrons encore d'autres solutions satisfaisantes si nous choisissons une autre largeur de la boîte à l'étape 3). Le tableau suivant donne une comparaison de quelques conceptions convenables:
| Solution 1 | Solution 2 | Solution 3 | Solution 4 | |
| Degré de la tolérance | ||||
| Boîte | 11 | 11 | 10 | 10 |
| Coussinets | 9 | 8 | 10 | 9 |
| Arbre | 7 | 8 | 8 | 9 |
| Jeu dans l'ajustement [mm] | 0.053 - 0.793 | 0.061 - 0.789 | 0.062 - 0.788 | 0.073 - 0.777 |
La solution finale doit être choisie de sorte que les coûts de production soient les plus bas possibles.
Pour la pièce (voir l'image), concevez les tolérances de production des dimensions, de sorte que la déviation permise ±0.0013 pouces ne soit pas dépassée pour la dimension résultante du point de vue technologique.
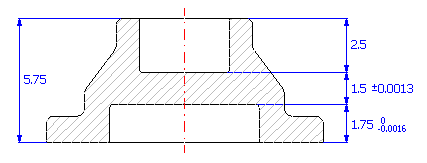
A partir du diagramme de la chaîne dimensionnelle
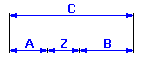
nous pouvons décrire le jeu dans l'ajustement pour le problème donné à l'aide de la relation Z = C - A - B.
Si le problème était résolu à l'aide de la méthode de "Worst Case" ordinaire, il aurait été nécessaire d'utiliser la tolérance à un niveau de précision 4 pour les dimensions B et C pour maintenir la tolérance requise de la dimension résultante. Il est évident qu'une production avec un tel niveau de précision serait trop coûteuse. Dans ce cas il sera préférable et plus avantageux d'utiliser la méthode de calcul statistique. Cette méthode permet la production d'une pièce avec des tolérances sensiblement plus grandes, avec un pourcentage de rebut (choisi au préalable) réduit.
Nous pouvons répartir la conception et l'optimisation de la chaîne dimensionnelle aux étapes suivantes:
1) A l'aide de la relation donnée ci-dessus, nous définirons la chaîne dimensionnelle dans le tableau [1.1].
2) Nous déterminerons ensuite les tolérances de production requises pour les différentes dimensions. Nous déterminerons les déviations appropriées pour la dimension A telles que indiquées par la tâche.
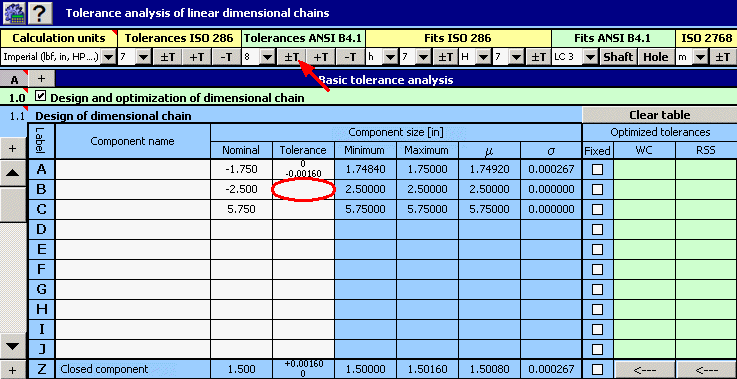
Pour le reste des dimensions, nous choisirons une tolérance symétrique au niveau 8 de précision de la tolérance.
3) Dans la colonne 8 du tableau, cochez la case de la A, dont la tolérance est fixée.
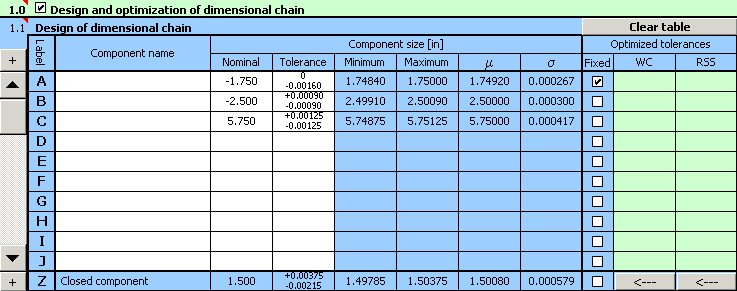
4) Dans le paragraphe [1.3] déterminez les valeurs limites de la dimension résultante.
5) Sur la liste dans la case [1.7] choisissez la méthode "Centrage et optimisation", sur la liste [1.8] déterminez la niveau de précision requis (nombre de chiffres dans la partie décimale) des tolérances conçues.
6) En rapport avec les différentes méthodes d'usinage applicables dans la production de la pièce, déterminez la tolérance minimale permise au niveau de précision 6 sur la liste [1.9].
7) Sur la liste dans la case [1.10] choisissez le rendement de production requis 99.9%, c.à.d. un processus de production avec un maximum de 1000 pièces défectueuses par million de pièces produites.
8) A l'aide du bouton dans la rangée [1.11] nous lancerons l'optimisation de la chaîne dimensionnelle.
9) Les paramètres résultants de la conception sont sont donnés dans le paragraphe [2.10],
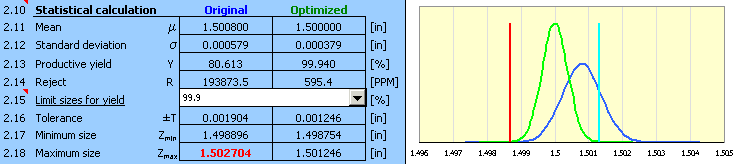
les déviations optimisées des processus de production sont données dans la colonne 10 du tableau [1.1].
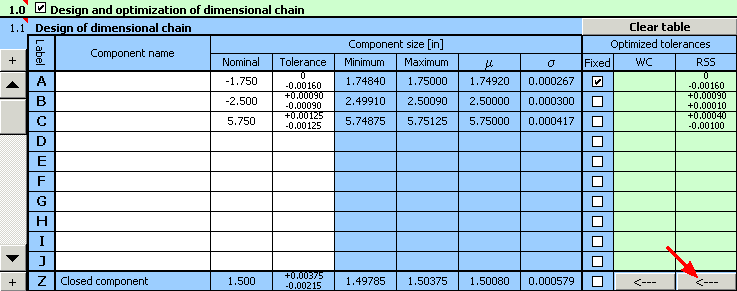
10) Les tolérances conçues peuvent toujours être ajustées. A l'aide du bouton dans la dernière rangée du tableau, transférez les tolérances conçues à la section d'insertion du tableau. Tout en concevant la valeur de la tolérance, nous pouvons par exemple accorder les déviations conçues à une forme plus appropriée.

Les résultats du calcul pour cet ajustage seront les mêmes que les résultats obtenus pour les tolérances optimisées.
La solution conçue ici ne sera évidemment pas l'unique solution satisfaisante du problème et ne doit pas non plus être nécessairement la solution idéale. En choisissant la solution adéquate, il est nécessaire d'évaluer la relation entre les dimensions choisies des tolérances de production et le rendement du processus de production prévu. En L'agrandissement des tolérances appliquées a comme effet la baisse des coûts directement reliés à l'usinage des pièces, mais cause la hausse des pertes dues à un nombre plus élevé de pièces défectueuses. La solution finale doit être choisie de sorte que les coûts de production soient les plus bas possibles.
Pour une comparaison, le tableau suivant nous donne les valeurs du rendement de production prévu pour les tolérances normalisées des dimensions B et C.
|
Classe de tolérance |
Rendement de production prévu [%] |
Nombre de rebuts par million de pièces produites |
|
6 |
99.99 |
125 |
|
7 |
99.77 |
2324 |
|
8 |
97.54 |
24640 |
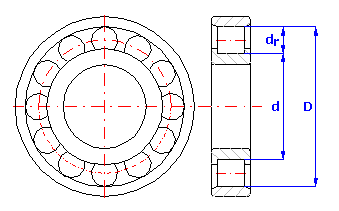
Pour un roulement à rouleaux monté de trois pièces de dimensions:
1. Anneau externe - diamètre D=160 mm
2. Anneau interne - diamètre d=120 mm
3. Rouleaux - diamètre dr=20 mm
Concevez les tolérances de production de toutes les pièces et les paramètres de montage sélectif de sorte le jeu radial soit maintenu dans l'intervalle de 60 mm à 90 mm pendant l'assemblage du roulement. Le roulement nécessite en plus l'interchangeabilité de l'anneau interne de sorte qu'un jeu radial dans l'intervalle de 40 mm à 105 mm soit garanti pendant le rechange de l'anneau en cas de réparation du roulement.
La production des roulements à rouleaux est un exemple typique pour l'usage de la méthode de montage sélectif . L'usage traditionnel de la méthode de "Worst Case" pour la solution de cet exemple assurera une totale interchangeabilité de montage et de fonctionnement de toutes les pièces, bien qu'il serait ainsi nécessaire de produire les composantes du roulement avec le degré de précision 3 pour maintenir le jeu radial requis. Il est claire qu'une production avec une telle précision serait inutilement coûteuse. Avec la méthode de montage sélectif, les pièces peuvent être produites avec un niveau de précision sensiblement inférieur. La solution au problème de montage sélectif en soi comprend deux parties:
La valeur du jeu radial pour les roulements à rouleaux est donnée par la relation c = D - d - 2*dr.
Nous pouvons répartir la conception et l'optimisation de la chaîne dimensionnelle aux étapes suivantes:
1) A l'aide de la relation donnée ci-dessus, nous définirons la chaîne dimensionnelle dans le tableau [7.1]. Les composantes partielles de la chaîne forment les différentes pièces utilisées dans l'assemblage du roulement. Le jeu radial requis est ainsi la composante de fermeture de la chaîne dimensionnelle.
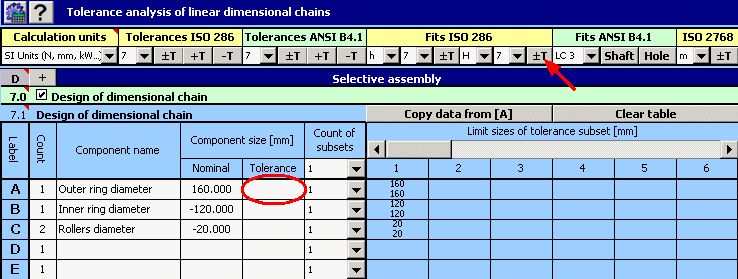
2) Déterminez ensuite les tolérances de production requises pour les différentes dimensions. Dans la première conception, utilisez les tolérances avec un niveau de précision 7 pour toutes les pièces. Pour le diamètre des rouleaux, choisissez une tolérance symétrique, H7 pour les tolérances du diamètre de l'anneau externe et h7 pour l'anneau interne.
3) Pour toutes les pièces, déterminez 10 sous-groupes de tolérance dans lesquels les pièces produites seront classifiées.
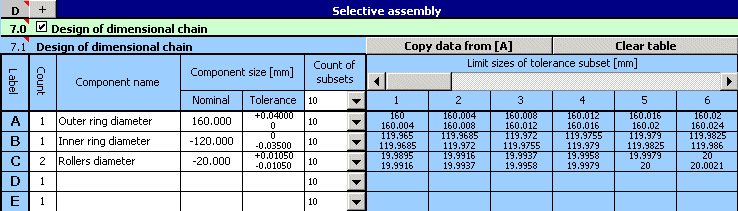
4) Dans le paragraphe [8.1] déterminez la condition de l'interchangeabilité de fonctionnement de l'anneau interne du roulement.
5) Dans le paragraphe [8.4] déterminez les dimensions limites du jeu radial requis pendant l'assemblage du roulement et le rechange de l'anneau interne.
6) Sur la liste dans la case [8.9] choisissez la recherche de toutes les combinaisons de montage. Démarrez la recherche des combinaisons à l'aide du bouton dans la rangée [8.10].
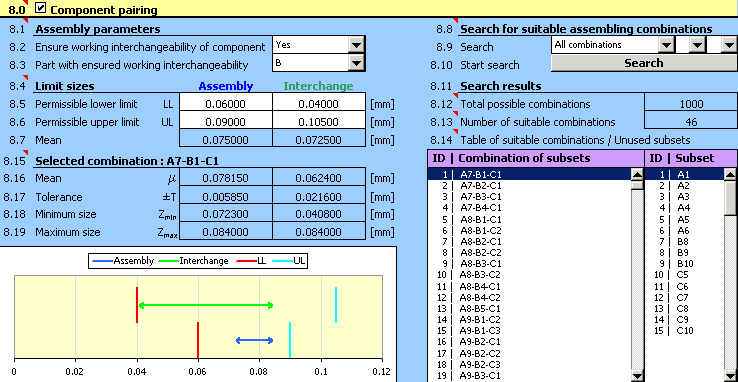
7) La qualité de la conception peut être évaluée à partir des résultats dans le paragraphe [8.11]. Il est claire que la conception n'est pas convenable dans ce cas-ci. Dans le tableau des "sous-groupes non utilisés" dans la rangée [8.14] il est claire qu'il n'était pas possible d'utiliser plus que la moitié des anneaux externes et des rouleaux produits pour l'assemblage du roulement.
8) Pour une conception inappropriée, l'étape logique suivante pourrait être la réduction des valeurs des tolérances de production utilisées. Après une évaluation plus détaillée de la conception, nous découvrirons que le problème principal ne se pose pas au niveau de la valeur des tolérances choisie, mais plutôt du mauvais centrage de la conception. La dimension moyenne de la composante de fermeture calculée dans le paragraphe [7.2] sert d'indice pour une meilleure évaluation de cet aspect de la conception.

Pour une conception optimale de la chaîne de tolérance, la dimension spécifiée devrait être aussi proche de la valeur requise que possible [8.7].
9) Dans la conception répétée, ajustez la position de la zone de tolérance de toutes les pièces tout en conservant les valeurs des tolérances. Pour le diamètre de l'anneau externe, utilisez la tolérance G7, et g7 pour le diamètre de l'anneau interne.
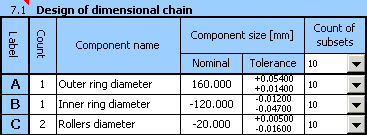
Ajustez ensuite les déviations supérieure et inférieure du diamètre des rouleaux de sorte que la conception résultante soit centrée le mieux possible.

10) Pour une telle conception ajustée de la chaîne dimensionnelle, répétez la recherche de toutes les combinaisons de montage.
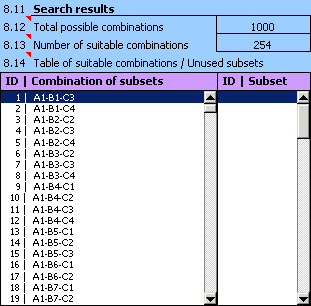
11) Dans les résultats de la recherche il est claire que toutes les pièces produites seront utilisables dans l'assemblage du roulement. Toutefois, la conception n'est pas aussi efficace du fait que le nombre de combinaisons convenables est inutilement trop élevé. Nous pouvons réduire le nombre de combinaisons convenables par exemple en réduisant le nombre de sous-groupes de tolérance dans lesquels les pièces produites seront classifiées.
12) En réduisant graduellement le nombre de sous-groupes, nous arriverons à une conception résultante de la chaîne dimensionnelle,
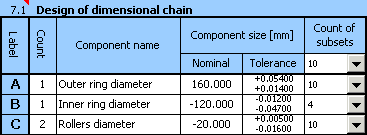
qui semble optimale pour l'exemple choisi.

Les 75 combinaisons de montage résultantes sont acceptable pour le montage sélectif.
Dans la partie précédente de ce problème, nous avons conçu les tolérances de production des pièces et procédé à la recherche de toutes les combinaisons de montage convenables qui peuvent être utilisées dans l'assemblage du roulement avec des paramètres appropriés. Toutefois, pendant l'assemblage il n'est pas pratique de monter les roulements par le choix au hasard des pièces selon les combinaisons de montages admissibles. Pour que la méthode de montage sélectif soit effectif, il est nécessaire de résoudre le problème du choix optimal (combinaison) des pièces. Les pièces doivent être montées de sorte qu'il soit possible de monter le plus grand nombre de pièces possible, qui remplissent les conditions de fonctionnement avec le nombre donné de pièces produites.
Cette tâche doit être résolue à plusieures reprises pendant la production, chaque fois que le stock est complété avant le début du montage. La partie principale du problème est de déterminer la procédure de montage optimale pour atteindre le plus grand nombre possible de pièces montées. Pendant la solution du problème, nous devons choisir le groupe de combinaisons optimal à partir des sous-groupes de combinaisons acceptables trouvées plus tôt et utilisés dans le montage et déterminer en même temps le nombre de pièces montées dans chaque combinaison.
L'optimisation du nombre de pièces montées s'effectue dans les étapes suivantes:
1) Dans le tableau [9.1] déterminez le nombre de pièces produites dans chaque sous-groupe de tolérance.

2) Sur la liste dans la case [9.3] choisissez la méthode d'optimisation adéquate. Pour l'exemple donné, choisissez la "Méthode de base", qui donne les meilleurs résultats. Malgré que cette méthode est plus lente que les autres méthodes pour les petits nombres de pièces dont le roulement sera monté dans l'exemple donné, nous pouvons l'utiliser même dans des ordinateurs moins performants.
3) Choisissez "traitement en masse" sur la liste [9.5]. Après le choix de cet élément, le programme effectuera graduellement l'optimisation pour toutes les 10 solutions de base. La meilleure solution sera ainsi choisie en rapport avec le nombre maximum de pièces montées et le minimum de combinaisons de montage utilisées.

4) Appuyez sur le bouton dans la rangée [9.5] pour démarrer l'optimisation.
5) Les paramètres de base de la qualité du processus de la conception sont donnés dans le paragraphe [9.6]

Une spécification détaillée du processus de montage optimisé est donnée dans le tableau [9.12].
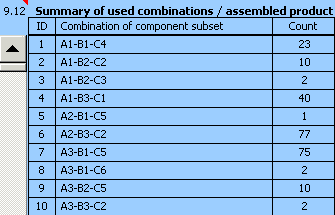
La colonne gauche du tableau donne toutes les combinaisons de montage utilisées pour le montage de la pièce. La colonne droite donne le nombre de pièces montées dans chaque combinaison.
|
Méthode d'optimisation |
Nombre de roulements montés |
Nombre de combinaisons de montage utilisées |
Vitesse de calcul |
|
A. Méthode de base |
762 |
29 |
6 min 20 s |
|
B. Méthode modifiée |
760 |
34 |
1 min 30 s |
|
C. Méthode simplifiée |
759 |
32 |
55 s |
L'information sur le réglage des paramètres de calcul et le choix de la langue peut être trouvée dans le document "Réglage des calculs, changement de langue".
Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".
^