Production et assemblage des roulements à rouleaux à l'aide de la méthode de montage sélectif.

Données du problème.

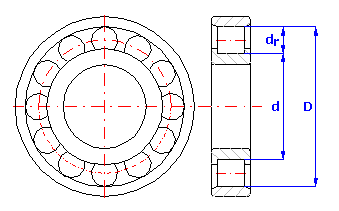
Pour un roulement à rouleaux monté de trois pièces de dimensions: 

1. Anneau externe - diamètre D=160 mm 
2. Anneau interne - diamètre d=120 mm 
3. Rouleaux - diamètre dr=20 mm 

Concevez les tolérances de production de toutes les pièces et les paramètres de montage sélectif de sorte le jeu radial soit maintenu dans l'intervalle de 60 mm à 90 mm pendant l'assemblage du roulement. Le roulement nécessite en plus l'interchangeabilité de l'anneau interne de sorte qu'un jeu radial dans l'intervalle de 40 mm à 105 mm soit garanti pendant le rechange de l'anneau en cas de réparation du roulement. 

Note: En réalité, la méthode de montage sélectif est normalement utilisée seulement dans la production des pièces qui ne nécessitent pas d'interchangeabilité des composantes internes. La nécessité d'assurer l'interchangeabilité de n'importe quelle pièce réduit les avantages de la méthode de montage sélectif de façon significative. Le problème décrit ici est à caractère purement théorique et est destiné à démontrer les diverses possibilités d'usage de ce programme.

Solution du problème.

La production des roulements à rouleaux est un exemple typique pour l'usage de la méthode de montage sélectif . L'usage traditionnel de la méthode de "Worst Case" pour la solution de cet exemple assurera une totale interchangeabilité de montage et de fonctionnement de toutes les pièces, bien qu'il serait ainsi nécessaire de produire les composantes du roulement avec le degré de précision 3 pour maintenir le jeu radial requis. Il est claire qu'une production avec une telle précision serait inutilement coûteuse. Avec la méthode de montage sélectif, les pièces peuvent être produites avec un niveau de précision sensiblement inférieur. La solution au problème de montage sélectif en soi comprend deux parties:

Conception de la chaîne dimensionnelle.

La valeur du jeu radial pour les roulements à rouleaux est donnée par la relation c = D - d - 2*dr.

Nous pouvons répartir la conception et l'optimisation de la chaîne dimensionnelle aux étapes suivantes:

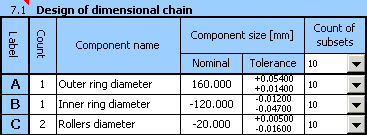
1) A l'aide de la relation donnée ci-dessus, nous définirons la chaîne dimensionnelle dans le tableau [7.1]. Les composantes partielles de la chaîne forment les différentes pièces utilisées dans l'assemblage du roulement. Le jeu radial requis est ainsi la composante de fermeture de la chaîne dimensionnelle.

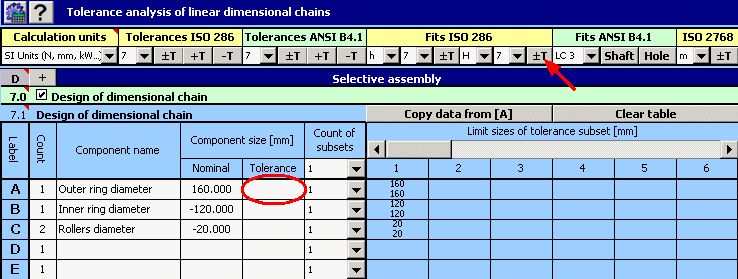
2) Déterminez ensuite les tolérances de production requises pour les différentes dimensions. Dans la première conception, utilisez les tolérances avec un niveau de précision 7 pour toutes les pièces. Pour le diamètre des rouleaux, choisissez une tolérance symétrique, H7 pour les tolérances du diamètre de l'anneau externe et h7 pour l'anneau interne.

3) Pour toutes les pièces, déterminez 10 sous-groupes de tolérance dans lesquels les pièces produites seront classifiées.

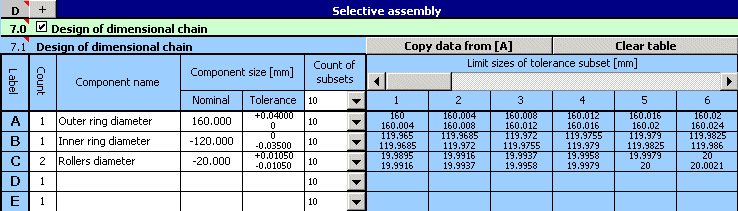
4) Dans le paragraphe [8.1] déterminez la condition de l'interchangeabilité de fonctionnement de l'anneau interne du roulement.

5) Dans le paragraphe [8.4] déterminez les dimensions limites du jeu radial requis pendant l'assemblage du roulement et le rechange de l'anneau interne.

6) Sur la liste dans la case [8.9] choisissez la recherche de toutes les combinaisons de montage. Démarrez la recherche des combinaisons à l'aide du bouton dans la rangée [8.10].

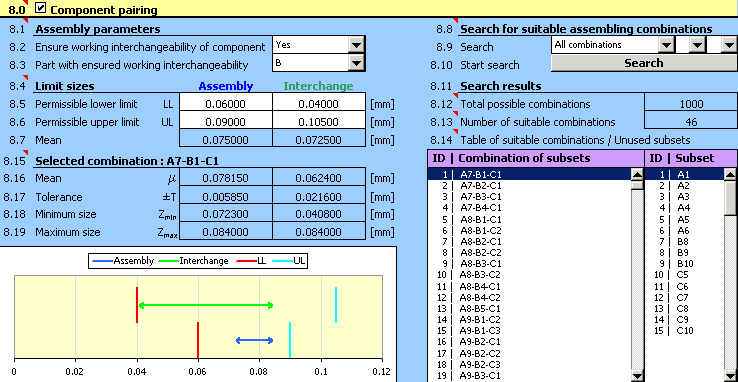
7) La qualité de la conception peut être évaluée à partir des résultats dans le paragraphe [8.11]. Il est claire que la conception n'est pas convenable dans ce cas-ci. Dans le tableau des "sous-groupes non utilisés" dans la rangée [8.14] il est claire qu'il n'était pas possible d'utiliser plus que la moitié des anneaux externes et des rouleaux produits pour l'assemblage du roulement.

8) Pour une conception inappropriée, l'étape logique suivante pourrait être la réduction des valeurs des tolérances de production utilisées. Après une évaluation plus détaillée de la conception, nous découvrirons que le problème principal ne se pose pas au niveau de la valeur des tolérances choisie, mais plutôt du mauvais centrage de la conception. La dimension moyenne de la composante de fermeture calculée dans le paragraphe [7.2] sert d'indice pour une meilleure évaluation de cet aspect de la conception.

Pour une conception optimale de la chaîne de tolérance, la dimension spécifiée devrait être aussi proche de la valeur requise que possible [8.7].

9) Dans la conception répétée, ajustez la position de la zone de tolérance de toutes les pièces tout en conservant les valeurs des tolérances. Pour le diamètre de l'anneau externe, utilisez la tolérance G7, et g7 pour le diamètre de l'anneau interne. 

Ajustez ensuite les déviations supérieure et inférieure du diamètre des rouleaux de sorte que la conception résultante soit centrée le mieux possible.

10) Pour une telle conception ajustée de la chaîne dimensionnelle, répétez la recherche de toutes les combinaisons de montage.

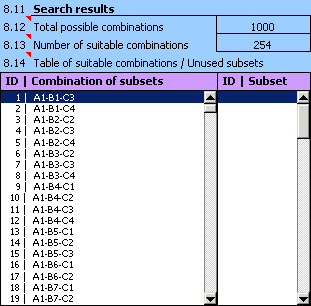
11) Dans les résultats de la recherche il est claire que toutes les pièces produites seront utilisables dans l'assemblage du roulement. Toutefois, la conception n'est pas aussi efficace du fait que le nombre de combinaisons convenables est inutilement trop élevé. Nous pouvons réduire le nombre de combinaisons convenables par exemple en réduisant le nombre de sous-groupes de tolérance dans lesquels les pièces produites seront classifiées.

12) En réduisant graduellement le nombre de sous-groupes, nous arriverons à une conception résultante de la chaîne dimensionnelle,

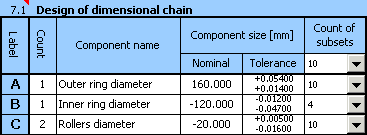
qui semble optimale pour l'exemple choisi.

Les 75 combinaisons de montage résultantes sont acceptable pour le montage sélectif.

Optimisation du nombre de pièces montées.

Dans la partie précédente de ce problème, nous avons conçu les tolérances de production des pièces et procédé à la recherche de toutes les combinaisons de montage convenables qui peuvent être utilisées dans l'assemblage du roulement avec des paramètres appropriés. Toutefois, pendant l'assemblage il n'est pas pratique de monter les roulements par le choix au hasard des pièces selon les combinaisons de montages admissibles. Pour que la méthode de montage sélectif soit effectif, il est nécessaire de résoudre le problème du choix optimal (combinaison) des pièces. Les pièces doivent être montées de sorte qu'il soit possible de monter le plus grand nombre de pièces possible, qui remplissent les conditions de fonctionnement avec le nombre donné de pièces produites.

Cette tâche doit être résolue à plusieures reprises pendant la production, chaque fois que le stock est complété avant le début du montage. La partie principale du problème est de déterminer la procédure de montage optimale pour atteindre le plus grand nombre possible de pièces montées. Pendant la solution du problème, nous devons choisir le groupe de combinaisons optimal à partir des sous-groupes de combinaisons acceptables trouvées plus tôt et utilisés dans le montage et déterminer en même temps le nombre de pièces montées dans chaque combinaison.

L'optimisation du nombre de pièces montées s'effectue dans les étapes suivantes:

1) Dans le tableau [9.1] déterminez le nombre de pièces produites dans chaque sous-groupe de tolérance.

Note: Les dimensions limites de tous les sous-intervalles de tolérance sont données dans le tableau [7.1].

2) Sur la liste dans la case [9.3] choisissez la méthode d'optimisation adéquate. Pour l'exemple donné, choisissez la "Méthode de base", qui donne les meilleurs résultats. Malgré que cette méthode est plus lente que les autres méthodes pour les petits nombres de pièces dont le roulement sera monté dans l'exemple donné, nous pouvons l'utiliser même dans des ordinateurs moins performants.

Note: La comparaison des résultats et de la vitesse de calcul réalisés pour l'exemple donné en utilisant les diverses méthodes d'optimisation est donnée à la fin de l'exemple.

3) Choisissez "traitement en masse" sur la liste [9.5]. Après le choix de cet élément, le programme effectuera graduellement l'optimisation pour toutes les 10 solutions de base. La meilleure solution sera ainsi choisie en rapport avec le nombre maximum de pièces montées et le minimum de combinaisons de montage utilisées.

4) Appuyez sur le bouton dans la rangée [9.5] pour démarrer l'optimisation.

5) Les paramètres de base de la qualité du processus de la conception sont donnés dans le paragraphe [9.6]

Une spécification détaillée du processus de montage optimisé est donnée dans le tableau [9.12].

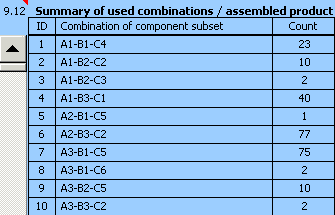
La colonne gauche du tableau donne toutes les combinaisons de montage utilisées pour le montage de la pièce. La colonne droite donne le nombre de pièces montées dans chaque combinaison.

Comparaison des résultats de l'optimisation et de la vitesse de calcul réalisés avec l'exemple donné en utilisant les diverses méthodes d'optimisation:

Note: Le "Traitement en masse" est utilisé dans toutes les méthodes d'optimisation. Le calcul est effectué dans un ordinateur avec un processeur x86, 1800 MHz, 256MB.