Program je určen pro toleranční analýzu lineárních (1D) rozměrových řetězců. Program řeší následující úlohy:
Toleranční analýza, syntéza a optimalizace rozměrového řetězce pomocí aritmetické metody "WC" (Worst case) resp. statistické metody "RSS" (Root Sum Squares).
Rozšířená statistická analýza rozměrového řetězce metodou "6 Sigma".
Toleranční analýza rozměrového řetězce při selektivní montáži včetně optimalizace počtu sestavených výrobků.
Všechny řešené úlohy umožňují pracovat s normalizovanými hodnotami tolerancí a to jak při návrhu, tak i při optimalizaci rozměrového řetězce.
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné
literatury a norem ANSI, ISO, DIN a dalších.
Seznam norem: ANSI B4.1, ISO 286, ISO 2768, DIN 7186
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
Lineární rozměrový řetězec je soubor závislých rovnoběžných rozměrů, které na sebe navazují tak, že tvoří geometricky uzavřený obvod. Mohou to být rozměry určující vzájemnou polohu prvků na jedné součásti (obr. A) nebo rozměry několika součástí v montážní jednotce (obr. B).
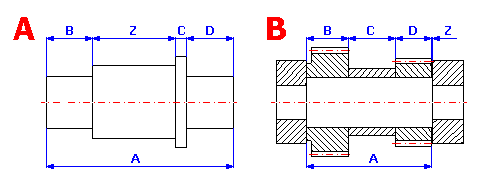
Rozměrový řetězec je sestaven z jednotlivých dílčích členů
(vstupních rozměrů) a ukončen uzavíracím členem (výsledným
rozměrem). Dílčí členy (A,B,C,..) jsou rozměry, které jsou na výkrese přímo
zakótovány nebo vyplývají z předcházejících výrobních popř. montážních
operací. Uzavírací člen (Z) představuje v daném řetězci výsledný výrobní
nebo montážní rozměr, který vyjde skládáním dílčích rozměrů jako
nekótovaný výrobní rozměr součásti, resp. jako montážní vůle nebo přesah.
Velikost, tolerance a mezní úchylky výsledného rozměru pak přímo závisí
na velikosti a toleranci dílčích rozměrů. Podle toho, jaký vliv má změna
dílčího členu na změnu členu uzavíracího, se v rozměrových řetězcích
rozlišují dva typy členů:
- členy zvětšující - dílčí členy, jejichž zvětšováním
se uzavírací člen zvětšuje
- členy zmenšující - dílčí členy, jejichž zvětšováním
se uzavírací člen zmenšuje
Při řešení tolerančních vztahů v rozměrových řetězcích se vyskytují úlohy dvojího typu:
Volba způsobu výpočtu tolerancí a mezních úchylek členů rozměrového řetězce má vliv na výrobní přesnost a montážní zaměnitelnost součástí. Závisí na něm proto hospodárnost výroby a provozu. Pro řešení tolerančních vztahů v rozměrových řetězcích se v technické praxi používají tři základní metody:
Nejčastěji používaná metoda, někdy též označovaná jako metoda výpočtu na maximum - minimum. Vychází z podmínky dodržení požadované mezní úchylky uzavíracího členu pro jakoukoliv kombinaci skutečných rozměrů dílčích členů, tedy i horních a dolních mezních rozměrů. Tato metoda zaručuje úplnou montážní a provozní zaměnitelnost součástí. Při požadavku větší přesnosti uzavíracího členu však vede na příliš úzké tolerance dílčích členů, tedy i k vysokým výrobním nákladům. Metoda WC je proto vhodná k řešení rozměrových obvodů s malým počtem členů nebo tehdy, je-li přípustná hrubší tolerance výsledného rozměru. Nejčastěji je používána v kusové nebo malosériové výrobě.
Metoda WC počítá toleranci výsledného rozměru jako aritmetický součet tolerancí všech dílčích rozměrů. Rozměry uzavíracího členu jsou tedy určeny jeho střední hodnotou:
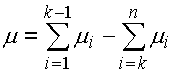
a celkovou tolerancí:
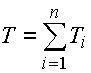
Krajní rozměry uzavíracího členu jsou pak dány vztahy:
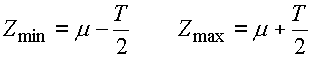
kde:
mi - střední rozměr i-tého členu
Ti - tolerance i-tého členu
n - celkový počet dílčích členů
i=1,..,k - počet zvětšujících členů
i=k,..,n - počet zmenšujících členů
Statistické metody výpočtu rozměrových řetězců se zakládají na počtu pravděpodobností. Tyto metody předpokládají, že se při při náhodném výběru součástí během montáže vyskytují krajní hodnoty úchylek jen zřídka u více dílčích členů najednou, neboť jde o složenou pravděpodobnost. Stejně tak málo pravděpodobný bude výskyt krajní hodnoty úchylek při výrobě jednotlivých rozměrů na jedné součásti. S určitým, předem zvoleným rizikem vyřazení některých součástí lze tedy tolerance dílčích členů v rozměrovém řetězci zvětšit.
Statistická metoda zaručuje pouze částečnou montážní zaměnitelnost, s malým procentem nepříznivých případů (zmetků). Vzhledem k větším tolerancím dílčích rozměrů však vede ke snížení výrobních nákladů. Užívá se především v hromadné a velkosériové výrobě, kde úspory výrobních nákladů převáží zvýšené montážní a provozní náklady, vznikající v důsledku neúplné montážní zaměnitelností součástí.
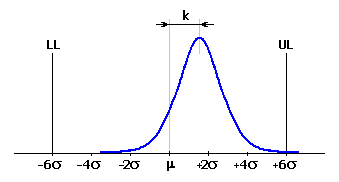
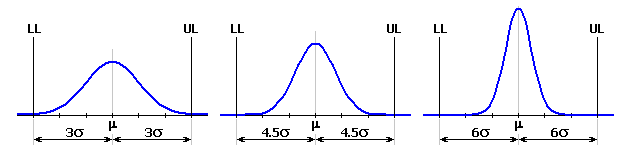
Rozměry uzavíracího členu vykazují jistý rozptyl od středu tolerančního pole. Četnost výskytu jednotlivých rozměrů se přitom řídí zákony matematické statistiky a v naprosté většině případů odpovídá normálnímu rozdělení . Toto rozdělení je popsáno Gaussovou křivkou hustoty pravděpodobnosti, pro kterou je četnost výskytu daného rozměru "x" dána vztahem:
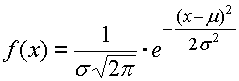
Tvar Gaussovy křivky je charakterizován dvěma parametry. Střední hodnota m určuje polohu maximální četnosti výskytu výsledného rozměru, směrodatná odchylka s definuje "štíhlost" křivky.
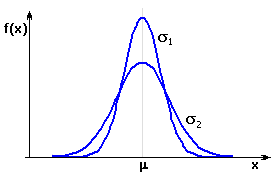
Plocha vymezená průnikem Gaussovy křivky s požadovanými mezními rozměry uzavíracího členu pak představuje předpokládanou výtěžnost procesu. Části křivky ležící vně tolerančního intervalu vymezují oblast, která představuje zmetkovost procesu.
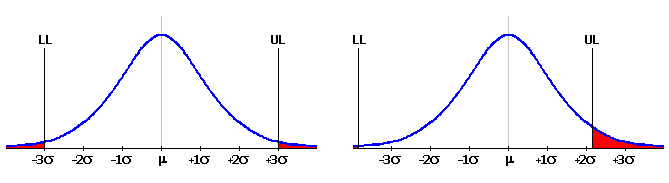
V běžném strojírenství se obvykle považuje výrobní proces za uspokojivě způsobilý na úrovni 3s. To znamená, že horní mez UL a spodní mez LL výsledného rozměru je vzdálena 3s od střední hodnoty m. Plocha Gaussovy křivky mezi oběma mezemi je pak rovna 99,73% celkové plochy a představuje podíl výrobků vyhovujícím požadavkům specifikace. Plocha mimo tyto meze je rovna 0,27% a představuje nevyhovující výrobky.
| Krajní rozměry | Výtěžnost procesu [%] | Počet zmetků na milion vyrobených součásti |
| m ± 1s | 68.2 | 317310 |
| m ± 2s | 95.4 | 45500 |
| m ± 3s | 99.73 | 2700 |
| m ± 3.5s | 99.95 | 465 |
| m ± 4s | 99.994 | 63 |
| m ± 4.5s | 99.9993 | 6.8 |
| m ± 5s | 99.99994 | 0.6 |
| m ± 6s | 99.9999998 | 0.002 |
Tato metoda výpočtu je tradiční a zároveň nejrozšířenější metodou statistického výpočtu rozměrových řetězců. Metoda RSS vychází z předpokladu, že jednotlivé dílčí členy jsou vyráběny s úrovní způsobilosti (kvality) procesu 3s.
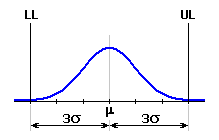
Jejich mezní hodnoty tedy korespondují s tolerančním intervalem m ± 3s, a směrodatná odchylka je dána vztahem:
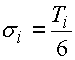
Rozměry uzavíracího členu jsou pak určeny jeho střední hodnotou:
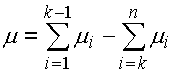
a směrodatnou odchylkou:
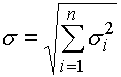
kde:
si - směrodatná odchylka i-tého členu
mi - střední rozměr i-tého členu
Ti - tolerance i-tého členu
n - celkový počet dílčích členů
i=1,..,k - počet zvětšujících členů
i=k,..,n - počet zmenšujících členů
V běžném strojírenství se tradičně považoval výrobní proces za uspokojivě způsobilý na úrovni 3s. To představuje předpokládaných 2700 vadných výrobků na milion vyrobených. Ačkoliv se takovýto podíl nevyhovujících výrobků jeví na první pohled velmi dobrý, ukazuje se v některých oblastech výroby stále častěji jako nedostatečný. Navíc je téměř nemožné udržet dlouhodobě střední hodnotu charakteristiky procesu přesně ve středu tolerančního pole. Vlivem různých faktorů (chybné nastavení, opotřebení nástrojů a přípravků, teplotních změny, atd.) dochází u velkých objemů výroby v průběhu času k posunu střední hodnoty charakteristiky procesu. Běžný je její posuv o 1.5s od ideální hodnoty. To u tradičně pojatých procesů s úrovní způsobilosti 3s představuje zvýšení podílu nevyhovujících výrobků na cca. 67000 z milionu vyrobených.
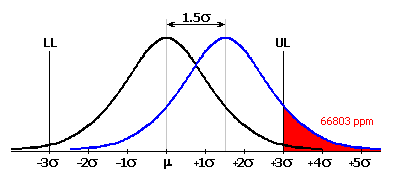
Je jasné, že výrobní proces s takovou úrovní zmetků je již nepřijatelný. V poslední době se proto stále častěji používá pro posuzování kvality výrobních procesů moderní metoda "6 Sigma". Koncepcí této metody je dosáhnout takového cíle, že střední hodnota charakteristiky procesu je vzdálena 6s od obou tolerančních mezí. Pro takto způsobilý výrobní proces je i při předpokládaném posunu střední hodnoty o 1.5s dosaženo poměru 3.4 nevyhovujících výrobků na milion vyrobených.
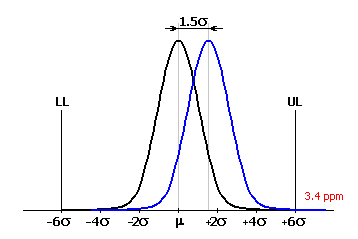
Metoda "6 Sigma" je poměrně mladá metoda, která se dočkala širšího uplatnění na přelomu 80-tých a 90-tých let minulého století. Do praxe byla uvedena poprvé firmou Motorola a je značně rozšířena zejména v USA. Její použití je vhodné při požadavku vyšší kvality výrobních procesů a pro velké objemy výroby, kde může docházet k posunu střední hodnoty charakteristiky procesu.
Metoda "6 Sigma" je modifikací standardní metody "RSS" a do problematiky řešení rozměrových řetězců zavádí dva nové parametry (Cp, Cpk) označované jako indexy způsobilosti procesu. Tyto ukazatele způsobilosti pak slouží k posouzení kvality výrobního procesu.
Ukazatel způsobilosti Cp posuzuje kvalitu výrobního procesu srovnáním specifikovaných tolerančních mezí s tradiční úrovní způsobilostí 3s.
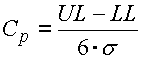
Pro proces s tolerančním intervalem m ± 3s bude tedy Cp=1. U procesů s vysokou kvalitou, kde jsou toleranční meze vzdáleny ±6s od střední hodnoty bude ukazatel způsobilosti Cp=2.
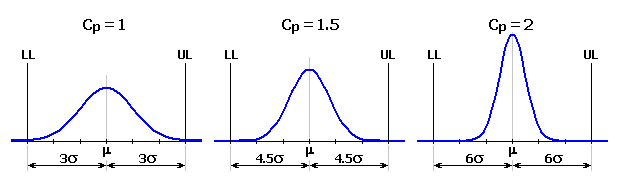
Ukazatel Cpk je modifikovaný ukazatel Cp pro posunutou střední hodnotu charakteristiky procesu.
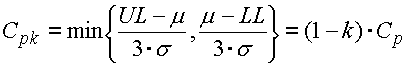
kde faktor posunutí k se pohybuje v mezích <0..1> a udává poměrnou hodnotu posunutí střední hodnoty vztaženou k polovině tolerančního intervalu. Při obvyklém posunu střední hodnoty charakteristiky procesu o 1.5s pak pro proces s kvalitou "6 Sigma" bude faktor posunutí k=0.25 a index způsobilosti Cpk=1.5.
Efektivní směrodatnou odchylku procesu pak můžeme odhadnout jako:
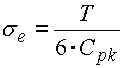
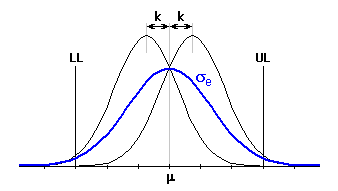
Při aplikaci ukazatelů způsobilosti na všechny dílčí členy rozměrového řetězce, pak můžeme obdobně jako u metody "RSS" popsat rozměry uzavíracího členu jeho střední hodnotou m a směrodatnou odchylkou:
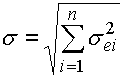
kde:
sei - efektivní směrodatná odchylka i-tého členu
Za uspokojivý se u metody "6 Sigma" obvykle považuje výrobní proces s výslednou mírou způsobilosti 4.5s.
Metoda selektivní montáže se používá v hromadné a velkosériové výrobě přesných výrobků, u nichž se nevyžaduje provozní zaměnitelnost součástí uvnitř výrobku. Montáži výrobku předchází třídění jednotlivých součástí do tolerančních podskupin. Výrobní rozměry součástí je možné předepsat s větší tolerancí. Zúžené tolerance výsledného rozměru se pak dosáhne účelným sdružováním (kombinací) roztříděných podskupin. K určení výsledného rozměru uzavíracího členu se používá výše popsaná metoda "WC" s tím rozdílem, že do výpočtu nevstupují celé výrobní tolerance dílčích členů, ale pouze zúžené tolerance platné pro zvolenou toleranční podskupinu.
Metoda selektivní montáže je velmi efektivní metodou řešení rozměrových řetězců, umožňující podstatné zvětšení výrobních tolerancí dílčích členů a tedy výrazné snížení výrobních nákladů. Na druhou stranu však použití této metody klade zvýšené nároky na montáž výrobku. Vzrostou také provozní náklady, jelikož je při opotřebení nebo poškození dílčí části obvykle nutné vyměnit celou sestavenou součástku.
Má-li být metoda selektivní montáže efektivní, je nutné vyřešit úlohu optimálního výběru (kombinace) součástek. Součástky musí být sdružovány tak, aby s daným počtem vyrobených součástek bylo možno sestavit maximální možný počet výrobků, které splňují funkční požadavky. Tuto úlohu je možné rozdělit do dvou částí:
Nalezení všech kombinací jednotlivých podskupin dílčích členů, pro které uzavírací člen splňuje funkční požadavky.
Tuto úlohu je nutné vyřešit před započetím výroby, v procesu návrhu rozměrového řetězce. Počet vyhovujících kombinací bude záviset jak na celkové výrobní toleranci dílčích členů, tak i na zvoleném počtu tolerančních subintervalů. Rozměrový řetězec by měl být navržen tak, aby se počet přijatelných montážních kombinací pohyboval v rozumných mezích.
Pro malé počty vyhovujících kombinací nebude pravděpodobně možné použít při montáži výrobku všechny vyrobené součásti. Klesá tak montážní výtěžnost procesu a výroba se prodražuje. Kritickým ukazatelem je pak stav, kdy již při konstrukčním návrhu vychází některá z podskupin jako nepoužitelná.
Vysoký počet vyhovujících kombinací naopak signalizuje neefektivní návrh. Toleranční řetězec by pravděpodobně bylo možné navrhnout optimálněji, s většími tolerancemi dílčích členů nebo menším počtem tolerančních subintervalů.
Optimalizace počtu sestavených výrobků pro dané počty vyrobených součástek v jednotlivých tolerančních subintervalech.
Tuto úlohu je nutné řešit opakovaně v průběhu výroby a to vždy při doplnění skladů před započetím vlastní montáže. Podstatou úlohy je stanovení optimálního postupu montáže tak, aby počet sestavených výrobků byl co nejvyšší. Při řešení úlohy tedy musíme z množiny přijatelných kombinací vybrat optimální sadu kombinací použitých při montáži a zároveň stanovit počet výrobků sestavených v rámci každé použité kombinace.
Algoritmus optimalizace je založen na postupném skládání jednotlivých výrobků odebíráním součástek z vybraných podskupin. V prvním kroku výpočet odhadne minimální a maximální možný počet sestavených výrobků. V dalších krocích pak podle předem zvoleného schématu odebírá součástky z vybraných podskupin tak, aby dolní odhad počtu sestavených výrobků rostl co nejrychleji a horní odhad klesal co nejméně.
Řešení této úlohy obvykle nebývá jednoznačné. Často lze nalézt i několik různých montážních postupů vedoucích ke shodnému počtu sestavených výrobků. Proto se jako další optimalizační kritérium používá počet použitých montážních kombinací. Minimalizace počtu použitých kombinací vede ke zjednodušení a urychlení montáže a tedy ke zlevnění výroby. V některých praktických aplikacích pak bývají obě kritéria stejně důležitá.
Tato řádka slouží k přepínání soustavy jednotek výpočtu a volbě normalizovaných tolerancí.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě přepočítány všechny hodnoty.
Při definici rozměrového řetězce v odstavcích [1.1, 3.2, 5.1, 7.1] se zadává pro každý rozměr také jeho tolerance. Pro usnadnění práce je program vybaven nástrojem pro automatickou volbu normalizovaných tolerancí.
Program obsahuje sadu základních rozměrových tolerancí dle ISO resp. ANSI. S ohledem na typ úchylky a použitou normu jsou tolerance rozděleny do 5 skupin:
Každá skupina obsahuje v hlavičce sešitu sadu výběrových seznamů a tlačítek. V seznamech nastavte požadované parametry tolerance resp. uložení (stupeň přesnosti, toleranční pole, ..). Pomocí tlačítek pak vložíte rozměry zvolené tolerance na příslušné místo vstupní tabulky - do řádku s aktivní buňkou.
Tolerance dle ISO jsou normou definovány v [mm] a jsou určeny pro výpočet v SI jednotkách. Tolerance dle ANSI jsou definovány v [in] a určeny pro výpočet v jednotkách "Imperial". Při použití normalizovaných tolerancí definovaných v jiných jednotkách, než je nastaveno ve výpočtu, budou úchylky rozměru automaticky přepočteny a zaokrouhleny.
Tato kapitola umožňuje provádět toleranční analýzu, syntézu a optimalizaci lineárního rozměrového řetězce pomocí aritmetické metody "WC" resp. statistické metody "RSS".
Metoda "Worst Case" je používána při požadavku úplné montážní a provozní zaměnitelnosti součástí a je vhodná k řešení rozměrových obvodů s malým počtem členů nebo tehdy, je-li přípustná hrubší tolerance výsledného rozměru. Statistická metoda "Root Sum Squares" zaručuje pouze částečnou montážní zaměnitelnost a používá se pro snížení výrobních nákladů v hromadné a velkosériové výrobě.
Úloha návrhu a optimalizace rozměrového řetězce se skládá z následujících kroků:
Tento odstavec je určen k návrhu rozměrového řetězce a optimalizaci tolerancí vybraných dílčích členů.
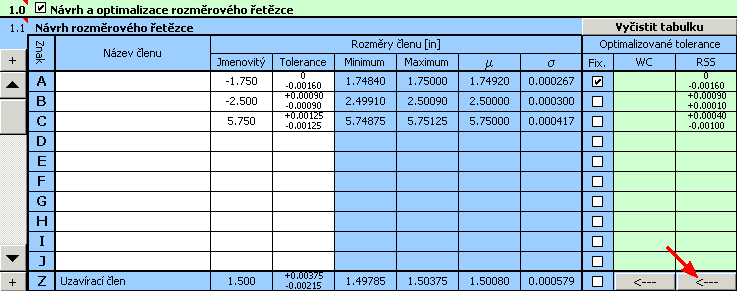
Tato tabulka slouží k definici rozměrů jednotlivých dílčích členů rozměrového řetězce. Každému dílčímu členu přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Název členu je nepovinný parametr.
Sloupec 2 - Zadejte nominální rozměr dílčího členu. Členy
"zvětšující" jsou kladné, členy "zmenšující"
zadejte se zápornou hodnotou.
Sloupec 3 - Zadejte horní a dolní úchylku rozměru. Stisknutím vybraného
tlačítka v hlavičce sešitu vložíte do tabulky úchylky příslušející
zvolené toleranci.
Sloupec 4..7 - V těchto sloupcích jsou dopočteny mezní rozměry, střední
rozměr a směrodatná odchylka všech dílčích
členů.
Sloupec 8 - Nastavením přepínačů označte všechny dílčí členy,
jejichž tolerance mají být optimalizovány. Zaškrtnutí tlačítka označuje
pevnou (fixovanou) toleranci, která zůstane při optimalizaci beze změny.
Sloupec 9,10 - Po provedení optimalizace obsahují tyto sloupce navržené
(optimalizované) úchylky. V levém sloupci jsou výsledky optimalizace při
použití aritmetické metody "WC", v pravém pak pro statistickou
metodu "RSS". Stisknutím tlačítka umístěného ve spodním řádku tabulky
přenesete navržené úchylky do vstupního sloupce.
Tento odstavec slouží k optimalizaci tolerancí vybraných dílčích členů rozměrového řetězce definovaného v tabulce [1.1]. Před spuštěním optimalizace zadejte požadované mezní rozměry uzavíracího členu [1.3] a nastavte optimalizační parametry [1.6]. Optimalizaci spustíte tlačítkem v řádku [1.11].
Optimalizace je prováděna současně pro obě výpočtové metody (WC, RSS). Navržené úchylky jsou vypsány v tabulce [1.1], výsledné rozměry uzavíracího členu naleznete v odstavci [2].
V tomto odstavci definujte požadované mezní rozměry uzavíracího členu dané funkčními požadavky výrobku.
Ve výběrovém seznamu vyberte jeden z následujících režimů optimalizace:
Při zachování velikosti tolerance upraví výpočet mezní úchylky vybraných dílčích členů tak, aby střední rozměr uzavíracího členu byl co možná nejblíže středu požadovaného tolerančního intervalu daného mezemi [1.3]. V závislosti na nastavení přesnosti tolerance [1.8] pracuje výpočet ve dvou režimech:
Při zachování střední hodnoty tolerančního intervalu upraví výpočet velikost tolerance vybraných dílčích členů tak, aby výsledné rozměry uzavíracího členu splňovaly požadavky specifikace dané mezemi [1.3].
Kombinace obou předchozích procesů.
Ve výběrovém seznamu zvolte typ a přesnost tolerancí použitých při optimalizaci.
Při výběru některé z prvních pěti položek seznamu bude velikost optimalizované tolerance dána výpočtem, s předem daným stupněm přesnosti (počtem desetinných míst). U optimalizovaných tolerancí je přitom zachován vzájemný poměr jejich velikosti.
Při výběru zbylých dvou položek seznamu bude velikost optimalizovaných tolerancí odpovídat normalizovaným hodnotám. Pro výpočet v SI jednotkách jsou přitom použity normalizované tolerance dle ISO 286, pro výpočet v jednotkách "Imperial" dle ANSI B4.1. Při výběru položky "Shodná toleranční třída" bude u všech optimalizovaných rozměrů použito normalizovaných tolerancí ze stejné toleranční třídy.
Nastavte minimální velikost (třídu přesnosti) tolerancí, jež může být při optimalizaci použita.
Ve výběrovém seznamu zvolte minimální požadovanou výtěžnost výrobního procesu.
V tomto odstavci jsou v přehledné formě prezentovány detailní parametry uzavíracího členu pro rozměrový řetězec definovaný v odstavci [1]. Pro srovnání jsou zde uvedeny výsledné rozměry uzavíracího členu jak pro originální, tak i optimalizované tolerance dílčích členů.
V tomto odstavci definujte požadované mezní rozměry uzavíracího členu dané funkčními požadavky výrobku.
V tomto odstavci jsou uvedeny výsledné rozměry uzavíracího členu při použití aritmetické výpočtové metody "Worst Case".
V tomto odstavci jsou uvedeny parametry uzavíracího členu při použití statistické metody výpočtu "Root Sum Squares".
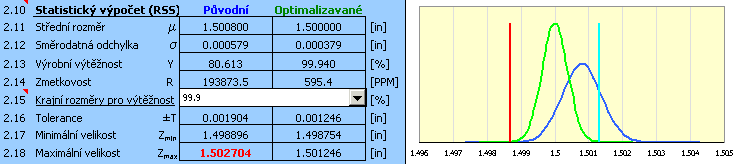
Výrobní výtěžnost [2.13] udává předpokládaný podíl výrobků vyhovujících požadavkům specifikace, to jest výrobků, u nichž bude výsledný rozměr uzavíracího členu v intervalu daném krajními mezemi [2.1]. Zmetkovost výrobního procesu [2.14] představuje předpokládaný počet nevyhovujících výrobků na milion vyrobených výrobků.
V tomto odstavci jsou dopočteny krajní rozměry uzavíracího členu pro zvolenou výtěžnost výrobního procesu.
Výpočet použitý v kapitole [A] vychází z předpokladu, že navržená součást bude pracovat za teplot blízkých základní teplotě 20°C (68°F), při níž byly stanoveny rozměry a tolerance dílčích členů. U součástí pracujících trvale za vyšších provozních teplot dochází za provozu k deformaci rozměrů součásti. Tato kapitola je pak určena k analýze lineárního rozměrového řetězce deformovaného v důsledku změny provozní teploty. Ke kontrole výsledného rozměru uzavíracího členu lze použít aritmetickou metodu "WC" nebo statistickou metodu "RSS".
V tomto odstavci definujte rozměrový řetězec a provozní teplotu, za níž bude navrhovaná součást pracovat.
Zadejte předpokládanou provozní teplotu, za níž bude navrhovaná součást pracovat.
Tato tabulka slouží k definici rozměrů jednotlivých dílčích členů rozměrového řetězce. Každému dílčímu členu přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Název členu je nepovinný parametr.
Sloupec 2 - Zadejte nominální rozměr dílčího členu. Členy
"zvětšující" jsou kladné, členy "zmenšující"
zadejte se zápornou hodnotou.
Sloupec 3 - Zadejte horní a dolní úchylku rozměru. Stisknutím vybraného
tlačítka v hlavičce sešitu vložíte do tabulky úchylky příslušející
zvolené toleranci.
Sloupec 4,5 - V těchto sloupcích jsou dopočteny výrobní (montážní)
rozměry dílčích členů.
Sloupec 6 - Ve výběrovém seznamu zvolte materiál součásti.
Sloupec 7 - Zadejte součinitel tepelné roztažnosti. Při zaškrtnutí zaškrtávacího tlačítka v
hlavičce tabulky budou hodnoty navrženy automaticky podle vybraného materiálu a provozní
teploty [3.1].
Sloupec 8,9 - V těchto sloupcích jsou dopočteny rozměry dílčích členů
za provozní teploty.
V tomto odstavci jsou v přehledné formě prezentovány detailní parametry uzavíracího členu pro rozměrový řetězec definovaný v odstavci [3]. Pro srovnání jsou zde uvedeny výsledné rozměry uzavíracího členu při montáži (20° C) a za provozní teploty.
Zadejte součinitel tepelné roztažnosti materiálu uzavíracího členu.
V tomto odstavci definujte požadované montážní rozměry uzavíracího členu. Mezní rozměry uzavíracího členu za provozní teploty jsou dopočteny automaticky v závislosti na zvoleném součiniteli tepelné roztažnosti [4.1].
V tomto odstavci jsou uvedeny výsledné rozměry uzavíracího členu při použití aritmetické výpočtové metody "Worst Case".
V tomto odstavci jsou uvedeny parametry uzavíracího členu při použití statistické metody výpočtu "Root Sum Squares".
Výrobní výtěžnost [4.15] udává předpokládaný podíl výrobků vyhovujících požadavkům specifikace, to jest výrobků, u nichž bude výsledný rozměr uzavíracího členu v intervalu daném krajními mezemi [4.3]. Zmetkovost výrobního procesu [2.16] představuje předpokládaný počet nevyhovujících výrobků na milion vyrobených výrobků.
V tomto odstavci jsou dopočteny krajní rozměry uzavíracího členu pro zvolenou výtěžnost výrobního procesu.
Tato kapitola umožňuje provádět toleranční analýzu lineárního rozměrového řetězce pomocí statistické metody "6 Sigma".
Metoda "6 Sigma" je moderní statistická metoda posuzování kvality výrobních procesů. Její použití je vhodné při požadavku vyšší kvality výrobních procesů a pro velké objemy výroby, kde může docházet k posunu střední hodnoty charakteristiky procesu. Koncepcí této metody je dosáhnout takového cíle, že střední hodnota charakteristiky procesu je vzdálena 6s od obou tolerančních mezí. Pro takto způsobilý výrobní proces je i při předpokládaném posunu střední hodnoty o 1.5s dosaženo poměru 3.4 nevyhovujících výrobků na milion vyrobených.

Tento odstavec je určen k návrhu rozměrového řetězce.
Tato tabulka slouží k definici rozměrů jednotlivých dílčích členů rozměrového řetězce. Každému dílčímu členu přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Název členu je nepovinný parametr.
Sloupec 2 - Zadejte nominální rozměr dílčího členu. Členy
"zvětšující" jsou kladné, členy "zmenšující"
zadejte jako zápornou hodnotou.
Sloupec 3 - Zadejte horní a dolní úchylku rozměru. Stisknutím vybraného
tlačítka v hlavičce sešitu vložíte do tabulky úchylky příslušející
zvolené toleranci.
Sloupec 4 - Ve výběrovém seznamu zvolte typ rozdělení hustoty pravděpodobnosti. Standardně
se k popisu výrobních procesů používá normální rozdělení,
které v naprosté většině případů nejlépe odpovídá skutečnému rozdělení
náhodných veličin procesu.
Sloupec 5 - Zadejte index způsobilosti výrobního procesu. Při zaškrtnutí zaškrtávacího tlačítka v
hlavičce tabulky budou automaticky použity hodnoty odpovídající zvolenému
typu rozdělení pravděpodobnosti.
Sloupec 6 - Zadejte faktor posunutí střední hodnoty charakteristiky
procesu. Tento faktor udává poměrnou hodnotu posunutí střední hodnoty vztaženou
k polovině tolerančního intervalu. Pro výrobní proces s kvalitou
"6 Sigma" se obvykle počítá s faktorem posunutí k=0.25.
Sloupec 7 - V tomto sloupci je dopočten modifikovaný index způsobilosti pro posunutou střední
hodnotu charakteristiky procesu.
Sloupec 8,9 - V těchto sloupcích je dopočten střední rozměr a
efektivní směrodatná odchylka procesu.
V tomto odstavci jsou v numerické a grafické formě prezentovány detailní parametry vybraného dílčího členu tak, jak byl definován v tabulce [1.1].
V tomto odstavci jsou v přehledné formě prezentovány detailní parametry uzavíracího členu pro rozměrový řetězec definovaný v odstavci [5].
V tomto odstavci definujte požadované mezní rozměry uzavíracího členu dané funkčními požadavky výrobku.
V tomto odstavci jsou uvedeny parametry uzavíracího členu při použití statistické metody výpočtu "6 Sigma".
Výrobní výtěžnost [6.11] udává předpokládaný podíl výrobků vyhovujících požadavkům specifikace, to jest výrobků u nichž bude výsledný rozměr uzavíracího členu v intervalu daném krajními mezemi [6.1]. Zmetkovost výrobního procesu [6.12] představuje předpokládaný počet nevyhovujících výrobků na milion vyrobených výrobků.
V tomto odstavci jsou dopočteny krajní rozměry uzavíracího členu pro zvolenou výtěžnost výrobního procesu.
Tato kapitola umožňuje provádět toleranční analýzu lineárního rozměrového řetězce při použití metody skupinové zaměnitelnosti (selektivní montáže).
Metoda selektivní montáže se používá v hromadné a velkosériové výrobě přesných výrobků, u nichž se nevyžaduje provozní zaměnitelnost součástí uvnitř výrobku. Montáži výrobku předchází třídění jednotlivých součástí do tolerančních podskupin. Výrobní rozměry součástí je možné předepsat s větší tolerancí. Zúžené tolerance výsledného rozměru se pak dosáhne účelným sdružováním (kombinací) roztříděných podskupin.
Úloha návrhu rozměrového řetězce se skládá z následujících kroků:
Kromě vlastního návrhu rozměrového řetězce bývá obvykle součástí řešení také optimalizace počtu sestavených výrobků pro dané počty vyrobených součástek [9]. Tuto úlohu je nutné řešit opakovaně v průběhu výroby a to vždy při doplnění skladů před započetím vlastní montáže.
Tento odstavec je určen pro návrh a kontrolu rozměrového řetězce.
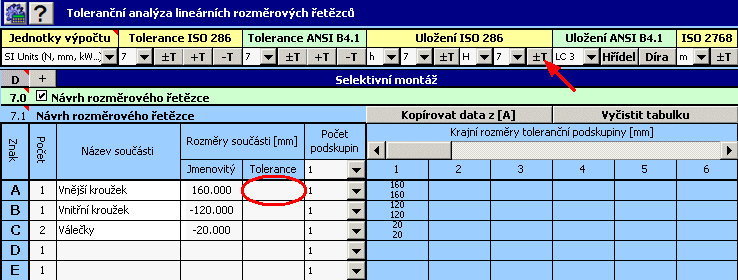
V tabulce [7.1] definujte počet, rozměry a tolerance všech součástí, z nichž bude výsledný výrobek sestaven. Dále zde pro každou součástku zvolte počet tolerančních podskupin (subintervalů), do kterých bude před montáží součástka roztříděna. V odstavci [7.2] pak zjistíte mezní rozměry uzavíracího členu pro libovolnou montážní kombinaci roztříděných podskupin součástí.
Tato tabulka slouží k definici rozměrů jednotlivých dílčích členů (součástí) rozměrového řetězce. Každé součásti přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Zadejte počet shodných součástí vstupujících do
rozměrového řetězce.
Sloupec 2 - Název součásti je nepovinný parametr.
Sloupec 3 - Zadejte nominální rozměr dílčího členu. Členy
"zvětšující" jsou kladné, členy "zmenšující"
zadejte jako zápornou hodnotou.
Sloupec 4 - Zadejte horní a dolní úchylku rozměru. Stisknutím vybraného
tlačítka v hlavičce sešitu vložíte do tabulky úchylky příslušející
zvolené toleranci.
Sloupec 5 - Nastavte počet tolerančních podskupin (subintervalů), do
kterých bude součástka roztříděna. Volbou z výběrového seznamu v hlavičce
tabulky, nastavíte shodný počet podskupin pro všechny součásti.
Sloupec 6..11 - V těchto sloupcích jsou dopočteny krajní rozměry
všech tolerančních subintervalů. Jednotlivé podskupiny jsou v hlavičce
tabulky označeny číselným indexem. Spolu s označením součástky pak tento
index slouží k jednoznačnému popisu zvolené montážní podskupiny (A1,
A2, B1, B2, B3, ...).
V prvním řádku tabulky jsou uvedeny mezní rozměry uzavíracího členu určené metodou "Worst Case" pro plné tolerance dílčích součástí. Tento údaj je pouze orientační a má význam především pro centrování návrhu. Pro dobře a efektivně provedený návrh tolerančního řetězce by se zde uvedený střední rozměr měl co nejvíce blížit požadovanému rozměru [8.7].
Ve druhém řádku pak zjistíte mezní rozměry uzavíracího členu pro libovolnou montážní kombinaci roztříděných podskupin součástí. Požadovanou montážní kombinaci nastavíte volbou příslušných tolerančních podskupin ve výběrových seznamech.
Nedílnou součástí návrhu rozměrového řetězce je vyřešení úlohy správného párování součástí. V této úloze jde o nalezení takových montážních kombinací jednotlivých podskupin součástí, pro které uzavírací člen splňuje funkční požadavky výrobku. Celkový počet nalezených kombinací je pak měřítkem pro posouzení kvality návrhu. Rozměrový řetězec by měl být navržen tak, aby se počet přijatelných montážních kombinací pohyboval v rozumných mezích.
Pro malé počty vyhovujících kombinací nebude pravděpodobně možné použít při montáži výrobku všechny vyrobené součásti. Klesá tak montážní výtěžnost procesu a výroba se prodražuje. Kritickým ukazatelem je pak stav, kdy již při konstrukčním návrhu vychází některá z podskupin jako nepoužitelná.
Vysoký počet vyhovujících kombinací naopak signalizuje neefektivní návrh. Toleranční řetězec by pravděpodobně bylo možné navrhnout optimálněji, s většími tolerancemi dílčích členů nebo menším počtem tolerančních subintervalů.
Metoda selektivní montáže zaručuje pouze částečnou (skupinovou) montážní zaměnitelnost v rámci vybraných montážních kombinací. Při opotřebení nebo poškození dílčí části za provozu je tedy nutné vyměnit celou sestavenou součástku. Metoda selektivní montáže se proto používá především k výrobě přesných výrobků, u nichž se nevyžaduje provozní zaměnitelnost součástí uvnitř výrobku.
Ačkoliv to přinese zvýšení výrobních nákladů, může být u některých výrobků přesto ekonomicky výhodnější zajistit alespoň u jedné součásti její úplnou provozní zaměnitelnost. Pro takto formulovaný požadavek se při řešení úlohy selektivní montáže setkáváme se dvěma odlišnými případy (postupy) řešení:
V tomto odstavci definujte požadované mezní rozměry uzavíracího členu dané funkčními požadavky výrobku. V prvním sloupci jsou uvedeny mezní rozměry uzavíracího členu při montáži výrobku. Ve druhém sloupci pak mezní rozměry při výměně vybrané součásti.
Tento odstavec slouží k vyhledání všech montážních kombinací, pro které uzavírací člen splňuje funkční požadavky výrobku specifikované v odstavcích [8.1, 8.4]. Program pracuje ve dvou režimech:
Režim hledání nastavte ve výběrovém seznamu [8.9]. Vyhledávání spustíte tlačítkem v řádku [8.10], výsledky jsou uvedeny v odstavci [8.11].
Tento parametr udává celkový počet všech montážních kombinací, pomocí nichž lze výrobek sestavit.
Tento parametr udává počet všech nalezených montážních kombinací, pro které uzavírací člen splňuje funkční požadavky výrobku specifikované v odstavcích [8.1, 8.4]. Celkový počet nalezených kombinací je pak měřítkem pro posouzení kvality návrhu. Rozměrový řetězec by měl být navržen tak, aby se počet přijatelných montážních kombinací pohyboval v rozumných mezích.
Pro malé počty vyhovujících kombinací nebude pravděpodobně možné použít při montáži výrobku všechny vyrobené součásti. Klesá tak montážní výtěžnost procesu a výroba se prodražuje.
Vysoký počet vyhovujících kombinací naopak signalizuje neefektivní návrh. Toleranční řetězec by pravděpodobně bylo možné navrhnout optimálněji, s většími tolerancemi dílčích členů nebo menším počtem tolerančních subintervalů.
V tabulce vyhovujících kombinací jsou vypsány montážní kombinace, pro které uzavírací člen splňuje funkční požadavky výrobku specifikované v odstavcích [8.1, 8.4]. Výsledné rozměry uzavíracího členu jsou pro zvolenou kombinaci uvedeny v odstavci [8.15].
V tabulce nevyužitých podskupin jsou vypsány všechny toleranční podskupiny (subintervaly), pro které nelze nalézt žádnou přijatelnou montážní kombinaci. Výrobky zatříděné do těchto podskupin pak není možné při montáži využít. Klesá tak montážní výtěžnost procesu a výroba se prodražuje. U správně navrženého rozměrového řetězce by měla tato tabulka zůstat prázdná.
V tomto odstavci jsou v numerické a grafické formě prezentovány výsledné rozměry uzavíracího členu pro montážní kombinaci vybranou v tabulce [8.14]. V prvním sloupci jsou uvedeny mezní rozměry uzavíracího členu při montáži výrobku. Ve druhém sloupci pak mezní rozměry při výměně vybrané součásti.
Má-li být metoda selektivní montáže efektivní, je nutné vyřešit úlohu optimálního výběru (kombinace) součástek. Součástky musí být sdružovány tak, aby s daným počtem vyrobených součástek bylo možno sestavit maximální možný počet výrobků, které splňují funkční požadavky.
Tuto úlohu je nutné řešit opakovaně v průběhu výroby a to vždy při doplnění skladů před započetím vlastní montáže. Podstatou úlohy je stanovení optimálního postupu montáže tak, aby počet sestavených výrobků byl co nejvyšší. Při řešení úlohy tedy musíme z množiny přijatelných kombinací [8.14] vybrat optimální sadu kombinací použitých při montáži a zároveň stanovit počet výrobků sestavených v rámci každé použité kombinace.
Řešení této úlohy obvykle nebývá jednoznačné. Často lze nalézt i několik různých montážních postupů vedoucích ke shodnému počtu sestavených výrobků. Proto se jako další optimalizační kritérium používá počet použitých montážních kombinací. Minimalizace počtu použitých kombinací vede ke zjednodušení a urychlení montáže a tedy ke zlevnění výroby. V některých praktických aplikacích pak bývají obě kritéria stejně důležitá.
V tabulce zadejte počty vyrobených součástek v jednotlivých tolerančních subintervalech.
Požadovanou optimalizační metodu zvolte ve výběrovém seznamu.
Kromě požadavku na sestavení maximálního počtu výrobků se v praxi často vyskytuje i požadavek na minimalizaci počtu montážních kombinací, které budou pro sestavení výrobku použity. S klesajícím počtem použitých kombinací však klesá i celkový počet sestavených výrobků. Je zřejmé, že oba tyto požadavky jsou vzájemně protichůdné. Proto musí být při optimalizaci definován parametr vyjadřující váhu (důležitost) jednotlivých kritérií. Vzájemný poměr důležitosti obou kritérií nastavte pomocí posuvníku.
Řešení úlohy optimalizace počtu sestavených výrobků obvykle nebývá jednoznačné. Často lze nalézt i několik různých montážních postupů vedoucích ke shodnému počtu sestavených výrobků. Výpočet proto nabízí možnost výběru z několika různých řešení sestavených při použití odlišných schémat (algoritmů) optimalizace. Volbu řešení proveďte ve výběrovém seznamu před spuštěním optimalizace.
V tomto odstavci naleznete základní kvalitativní parametry navrženého postupu montáže. Detailní rozpis optimalizovaného montážního postupu je uveden v tabulce [9.12].
V této tabulce je uveden detailní rozpis optimalizovaného montážního postupu. V levém sloupci jsou vypsány všechny montážní kombinace použité pro sestavení výrobku. V pravém sloupci pak počet výrobků sestavených v rámci každé kombinace.
V této tabulce jsou uvedeny počty zbylých (nevyužitých) součástí, které nebylo možné upotřebit při montáži výrobku.
Pro ilustraci problematiky toleranční analýzy lineárních rozměrových řetězců je nápověda doplněna několika praktickými ukázkami použití tohoto výpočtu:
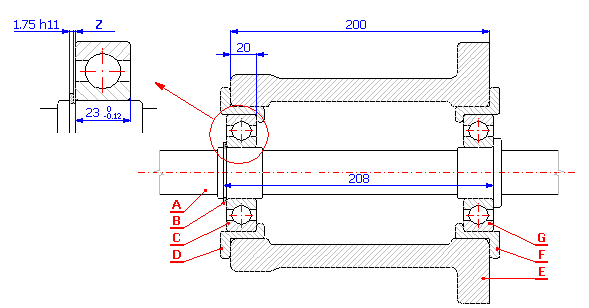
Pro příklad uložení hřídele ve skříni (viz. obrázek) navrhněte výrobní tolerance jednotlivých součástí tak, aby při montáži byla zajištěna vůle v uložení v rozsahu 0.05 až 0.80 mm. Navržené tolerance přitom musí odpovídat následujícím technologickým požadavkům výroby:
- stykové plochy skříně budou obráběny frézováním
- pro obrábění hřídele a ložiskových pouzder bude použito soustružení
kde:
A ....... Hřídel
B ....... Pojistný kroužek 40 DIN 471
C,G .... Ložisko 6308 DIN 625 SKF
D,F .... Ložiskové pouzdro
E ....... Skříň
Z ....... Vůle v uložení <0.05 až 0.80> mm
Vyjdeme-li z grafického znázornění rozměrového řetězce
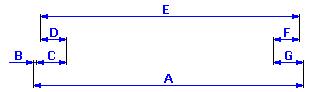
můžeme u dané úlohy popsat velikost vůle v uložení vztahem Z = A - B - C + D - E + F - G
Při vlastním návrhu výrobních tolerancí pak musíme vycházet z technologických požadavků výroby. Velikost navržených tolerancí jednotlivých součástí se musí pohybovat v rozsahu výrobní přesnosti dosažitelné u zvoleného způsobu obrábění. U frézování se běžně dosahuje přesnost výroby v rozsahu 9. až 13. tolerančního stupně, u soustružení v rozsahu 6. až 12. tolerančního stupně.
Řešení úlohy návrhu a optimalizace rozměrového řetězce můžeme rozdělit do následujících kroků:
1) Na základě výše uvedeného vztahu definujeme v tabulce [1.1] rozměrový řetězec. Dílčí členy řetězce tvoří jednotlivé součásti, uzavíracím členem rozměrového řetězce je pak požadovaná vůle v uložení.
2) U součástí s pevně danou tolerancí, předepsanou výrobcem (ložiska, pojistný kroužek) zadáme do vstupní tabulky příslušné úchylky rozměru.
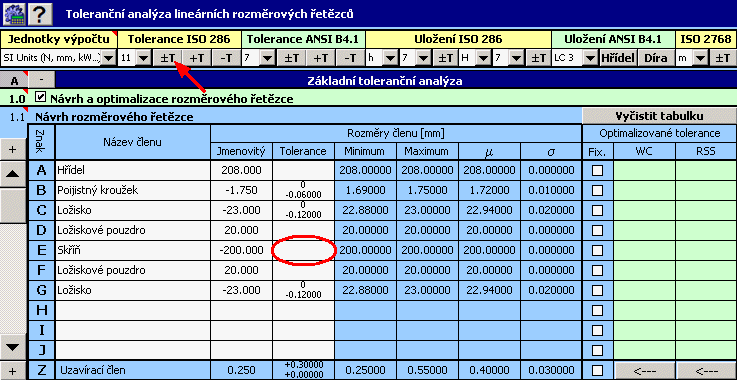
3) Stykové plochy skříně budou obráběny frézováním, v prvním návrhu proto zvolíme pro šířku skříně velikost tolerance v 11 stupni přesnosti.
4) Zaškrtnutím příslušných přepínačů v 8. sloupci tabulky označíme všechny součásti s pevnou tolerancí.
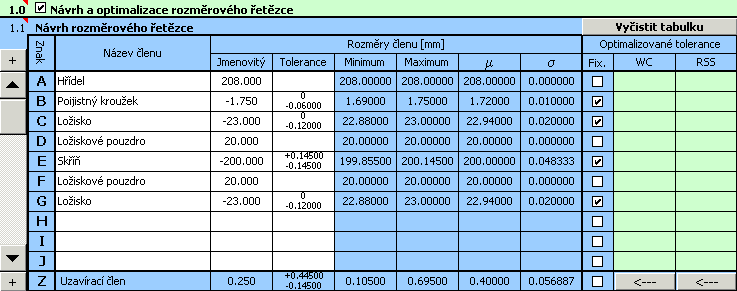
5) V odstavci [1.3] zadáme mezní hodnoty požadované vůle v uložení.
6) Ve výběrovém seznamu [1.7] zvolíme metodu "Centrování a optimalizace", v seznamu [1.8] vybereme položku "Normalizované tolerance".
7) Pro obrábění všech součástí, u nichž chceme v dalším kroku navrhnout tolerance, bude použito soustružení. Ve výběrovém seznamu [1.9] proto nastavíme minimální povolenou velikost tolerance na 6. stupeň přesnosti.

8) Tlačítkem na řádku [1.11] spustíme optimalizaci rozměrového řetězce.
9) Parametry výsledné vůle dosažené pro optimalizovaný návrh tolerancí jsou prezentovány v odstavci [2.5],
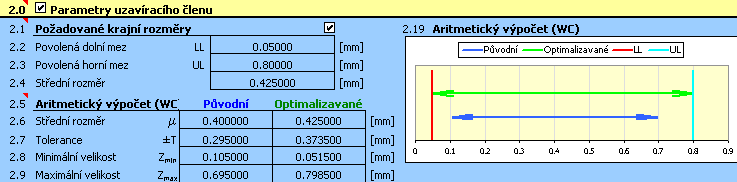
optimalizované úchylky výrobních rozměrů jsou vypsány v 9. sloupci tabulky [1.1].
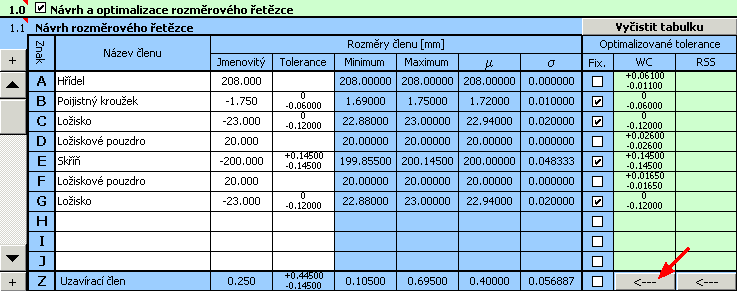
10) Pro zde uvedený příklad sice bylo při optimalizaci nalezeno funkčně vyhovující řešení, z praktického hlediska je však tento návrh nevhodný. Šířka ložiskových pouzder v řádcích D a F byla programem navržena s různými tolerancemi. Má-li být však výroba a montáž efektivní, je nutné zajistit vzájemnou zaměnitelnost obou ložiskových pouzder. Dalším krokem návrhu tedy bude odstranění tohoto nedostatku.
11) Pomocí tlačítka ve spodním řádku tabulky přeneseme navržené tolerance do vstupní části tabulky. Zde pak u obou pouzder sjednotíme tolerance při použití vyšší z navržených hodnot.
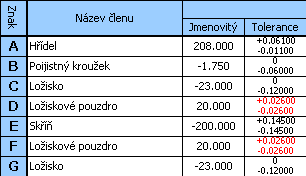
12) V 8. sloupci tabulky dále zaškrtneme přepínače v řádcích D a F, a opětovně spustíme optimalizaci pomocí tlačítka na řádku [1.11].
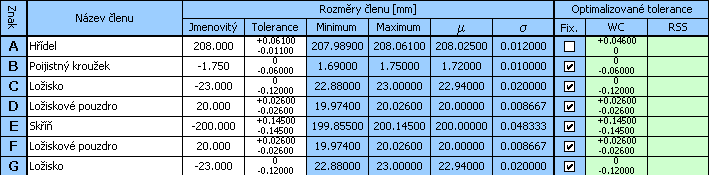
13) Výsledkem návrhu pak již bude plně vyhovující řešení úlohy, s tolerancí ložiskových pouzder v 9. stupni přesnosti a tolerancí hřídele v 7. stupni přesnosti.
Zde navržené řešení nebude samozřejmě jediným vyhovujícím řešením této úlohy, a nemusí tedy být ani řešením ideálním. Proto je vhodné (zvláště u sériové výroby) navrhnout několik různých řešení s odlišnou přesností výroby jednotlivých součástí.
Jiné řešení této úlohy získáme například tehdy, zvolíme-li pro toleranci ložiskového pouzdra v kroku 11) nižší z původně navržených hodnot.
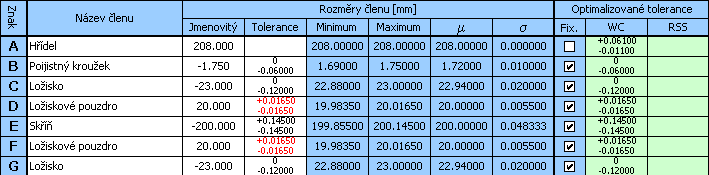
Další vhodná řešení dostaneme při volbě odlišné tolerance šířky skříně v kroku 3). Srovnání několika vyhovujících návrhů je uvedeno v následující tabulce:
| Řešení 1 | Řešení 2 | Řešení 3 | Řešení 4 | |
| Toleranční třída | ||||
| Skříň | 11 | 11 | 10 | 10 |
| Ložisková pouzdra | 9 | 8 | 10 | 9 |
| Hřídel | 7 | 8 | 8 | 9 |
| Vůle v uložení [mm] | 0.053 - 0.793 | 0.061 - 0.789 | 0.062 - 0.788 | 0.073 - 0.777 |
Výsledné řešení je pak nutné volit tak, aby celkové náklady na výrobu byly pokud možno co nejnižší.
U součástky (viz. obrázek) navrhněte výrobní tolerance rozměrů tak, aby u technologicky výsledného rozměru nebyla překročena povolená odchylka ±0.0013 in.
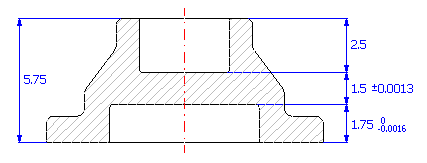
Vyjdeme-li z grafického znázornění rozměrového řetězce
můžeme u dané součásti popsat výsledný rozměr vztahem Z = C - A - B.
Při řešení této úlohy klasickou metodou "Worst Case" by pro dodržení požadované tolerance výsledného rozměru bylo nutné u rozměrů B a C použít tolerance přibližně ve 4. stupni přesnosti. Je zřejmé, že výroba s takovouto přesností by byla neúměrně nákladná. V tomto případě bude proto mnohem výhodnější použít statistickou metodu výpočtu. Tato metoda umožňuje vyrábět součástku s podstatně většími tolerancemi, při výskytu malého (předem zvoleného) procenta zmetků.
Řešení úlohy návrhu a optimalizace rozměrového řetězce můžeme rozdělit do následujících kroků:
1) Na základě výše uvedeného vztahu definujeme v tabulce [1.1] rozměrový řetězec.
2) Pro jednotlivé rozměry dále zadáme požadované výrobní tolerance. U rozměru A vyplníme příslušné odchylky, předepsané zadáním úlohy.
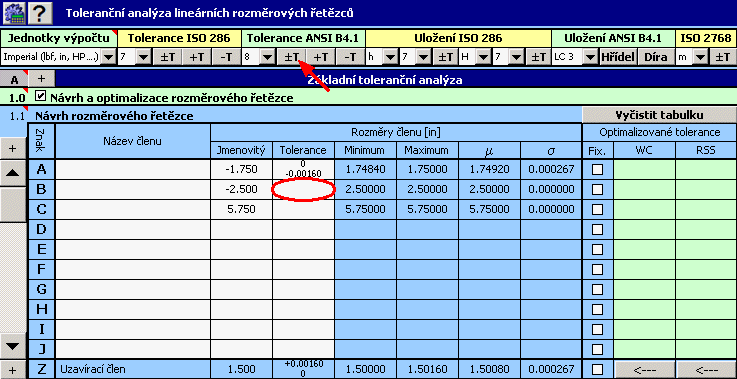
U zbylých rozměrů předběžně zvolíme symetrickou toleranci v 8. stupni přesnosti.
3) V 8. sloupci tabulky zaškrtneme přepínač u rozměru A, jehož tolerance je pevně daná.
4) V odstavci [1.3] zadáme požadované mezní hodnoty výsledného rozměru.
5) Ve výběrovém seznamu [1.7] zvolíme metodu "Centrování a optimalizace", v seznamu [1.8] nastavíme požadovanou přesnost (počet desetinných míst) navrhovaných tolerancí.
6) S ohledem na možné způsoby obrábění, použitelné při výrobě součásti, nastavíme ve výběrovém seznamu [1.9] minimální povolenou velikost tolerance na 6. stupeň přesnosti.
7) Ve výběrovém seznamu [1.10] zvolíme požadovanou výtěžnost výroby 99.9%, to jest výrobní proces s maximálním počtem 1000 zmetků na milion vyrobených součástí.

8) Tlačítkem na řádku [1.11] spustíme optimalizaci rozměrového řetězce.
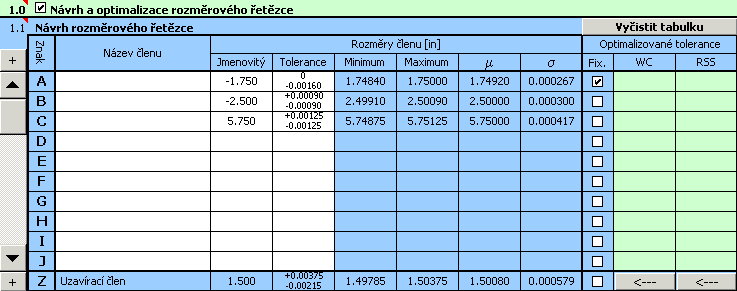
9) Výsledné parametry návrhu jsou uvedeny v odstavci [2.10],
optimalizované úchylky výrobních rozměrů jsou vypsány v 10. sloupci tabulky [1.1].
10) Navržené tolerance můžeme samozřejmě dále upravovat. Pomocí tlačítka ve spodním řádku tabulky přeneseme optimalizované hodnoty tolerancí do vstupní části tabulky. Při zachování velikosti tolerancí zde pak můžeme například jemně doladit navržené úchylky do vhodnějšího tvaru.

Výsledky výpočtu budou pro tuto úpravu shodné s výsledky dosaženými pro optimalizované tolerance.
Zde navržené řešení nebude samozřejmě jediným vyhovujícím řešením této úlohy a nemusí tedy být ani řešením ideálním. Při výběru vhodného řešení je potřeba důkladně zvážit vzájemný vztah mezi zvolenou velikostí výrobních tolerancí a předpokládanou výtěžností výrobního procesu. Zvětšením použitých tolerancí docílíme poklesu přímých nákladů spojených s obráběním součásti, vzrostou však ztráty způsobené zvýšeným výskytem vadných výrobků. Výsledné řešení je pak nutné volit tak, aby celkové náklady na výrobu byly pokud možno co nejnižší.
Pro srovnání jsou v následující tabulce uvedeny hodnoty předpokládané výtěžnosti výroby pro normalizované tolerance rozměrů B a C.
|
Toleranční třída |
Předpokládaná výrobní výtěžnost [%] |
Počet zmetků na milion vyrobených součástí |
|
6 |
99.99 |
125 |
|
7 |
99.77 |
2324 |
|
8 |
97.54 |
24640 |
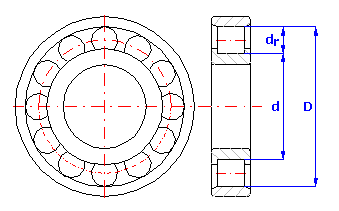
Pro válečkové ložisko sestavené ze tří součástí o rozměrech:
1. Vnější kroužek - průměr D=160 mm
2. Vnitřní kroužek - průměr d=120 mm
3. Válečky - průměr dr=20 mm
navrhněte výrobní tolerance všech součástí a parametry selektivní montáže tak, aby při montáži ložiska byla zajištěna radiální vůle v rozsahu 60 mm až 90 mm. U ložiska je dále vyžadováno zajištění zaměnitelnosti vnitřního kroužku tak, aby při výměně kroužku v případě opravy ložiska byla zaručena radiální vůle v rozsahu 40 mm až 105 mm.
Výroba valivých ložisek je typickým příkladem vhodným pro použití metody selektivní montáže. Při řešení uvedeného příkladu klasickou metodou "Worst Case" bude u ložiska sice zajištěna úplná montážní i provozní zaměnitelnost všech součástí, pro dodržení požadované radiální vůle by však bylo potřeba vyrábět součásti ložiska ve 3. stupni přesnosti. Je zřejmé že výroba s takovýmto stupněm přesnosti by byla neúměrně nákladná. Při použití metody selektivní montáže lze součásti vyrábět s podstatně nižší přesností. Vlastní řešení úlohy selektivní montáže se skládá ze dvou částí:
Velikost radiální vůle je u válečkových ložisek dána vztahem c = D - d - 2*dr.
Řešení úlohy návrhu a optimalizace rozměrového řetězce pak můžeme rozdělit do následujících kroků:
1) Na základě výše uvedeného vztahu definujeme v tabulce [7.1] rozměrový řetězec. Dílčí členy řetězce tvoří jednotlivé součásti použité při montáži ložiska. Uzavíracím členem rozměrového řetězce je pak požadovaná radiální vůle.
2) Pro jednotlivé rozměry dále zadáme požadované výrobní tolerance. V prvotním návrhu použijeme u všech součástí tolerance v 7. stupni přesnosti. Pro průměr válečků přitom zvolíme symetrickou toleranci, pro průměr vnějšího kroužku toleranci H7 a pro vnitřní kroužek h7.
3) Pro všechny součásti předběžně nastavíme 10 tolerančních podskupin, do nichž budou vyrobené součásti roztříděny.
4) V odstavci [8.1] zohledníme požadavek provozní zaměnitelnosti vnitřního kroužku ložiska.
5) V odstavci [8.4] zadáme mezní hodnoty požadované radiální vůle při montáži ložiska a při výměně vnitřního kroužku.
6) Ve výběrovém seznamu [8.9] zvolíme vyhledání všech montážních kombinací. Vlastní hledání kombinací pak spustíme tlačítkem na řádku [8.10].
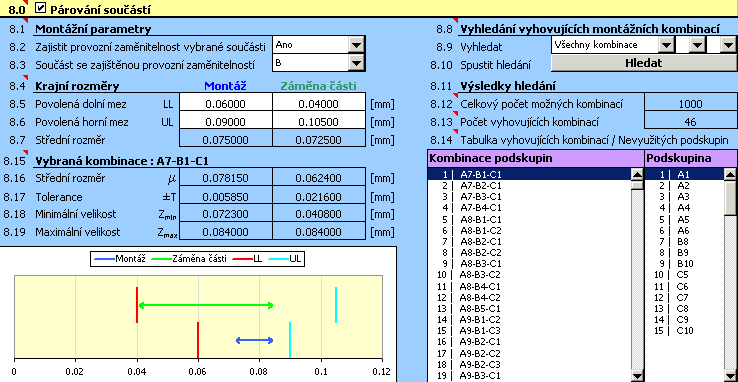
7) Kvalitu návrhu posoudíme na základě výsledků v odstavci [8.11]. Je zřejmé, že v tomto případě není návrh vyhovující. Z tabulky "Nevyužitých podskupin" v řádku [8.14] vyplývá, že pro montáž ložiska by nebylo možné použít více než polovinu vyrobených vnějších kroužků a válečků.
8) Pro nevyhovující návrh by dalším logickým krokem mohlo být zmenšení velikosti použitých výrobních tolerancí. Při bližším posouzení tohoto návrhu však zjistíme, že hlavním problémem zde nebude zvolená velikost tolerancí, ale spíše chybné vycentrování návrhu. Pro správné posouzení tohoto aspektu návrhu je směrodatným ukazatelem střední rozměr uzavíracího členu dopočtený v odstavci [7.2].

U optimálního návrhu tolerančního řetězce by se zde uvedený rozměr měl co nejvíce blížit požadované hodnotě [8.7].
9) V opakovaném návrhu tedy při zachování velikosti tolerancí upravíme pozici tolerančních polí všech součástí. Pro průměr vnějšího kroužku použijeme toleranci G7, pro průměr vnitřního kroužku toleranci g7.
Horní a dolní úchylku průměru válečků pak upravíme tak, aby výsledný návrh byl co nejlépe vycentrován.

10) Pro takto upravený návrh rozměrového řetězce opětovně vyhledáme všechny vyhovující montážní kombinace.
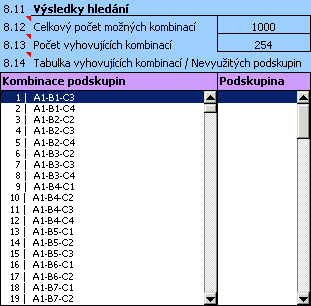
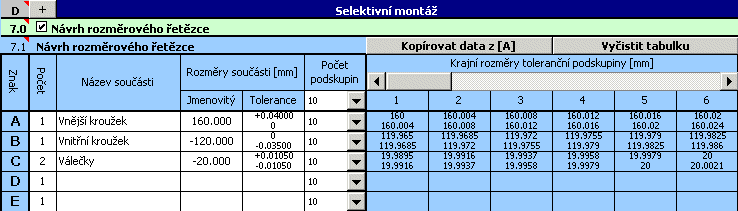
11) Z výsledků hledání je zřejmé, že při montáži ložiska budou nyní použitelné všechny vyrobené součásti. Návrh však není příliš efektivní, jelikož počet vyhovujících montážních kombinací je zbytečně vysoký. Snížení počtu přijatelných kombinací můžeme docílit například zmenšením počtu tolerančních podskupin, do nichž budou vyrobené součásti roztříděny.
12) Postupným snižováním počtu podskupin se dopracujeme k výslednému návrhu rozměrového řetězce,
který se pro zvolený příklad jeví jako optimální.

Výsledný počet 75 vyhovujících montážních kombinací je již pro účely selektivní montáže přijatelný.
V předchozí části úlohy jsme navrhli výrobní tolerance součástí a vyhledali všechny přijatelné montážní kombinace, pomocí nichž lze sestavit ložisko vyhovujících parametrů. Při vlastní montáži ložiska však není účelné sestavovat ložiska pouhým náhodným výběrem součástek v rámci přípustných montážních kombinací. Má-li být metoda selektivní montáže efektivní, je nutné vyřešit úlohu optimálního výběru (kombinace) součástek. Součástky musí být sdružovány tak, aby s daným počtem vyrobených součástek bylo možno sestavit maximální možný počet výrobků, které splňují funkční požadavky.
Tuto úlohu je nutné řešit opakovaně v průběhu výroby a to vždy při doplnění skladů před započetím vlastní montáže. Podstatou úlohy je stanovení optimálního postupu montáže tak, aby počet sestavených výrobků byl co nejvyšší. Při řešení úlohy tedy musíme z dříve nalezené množiny přijatelných kombinací vybrat optimální sadu kombinací použitých při montáži a zároveň stanovit počet výrobků sestavených v rámci každé použité kombinace.
Řešení úlohy optimalizace počtu sestavených výrobků je prováděno v následujících krocích:
1) V tabulce [9.1] zadáme počty vyrobených součástek v jednotlivých tolerančních podskupinách.

2) Ve výběrovém seznamu [9.3] zvolíme vhodnou optimalizační metodu. Pro uvedený příklad vybereme "Základní metodu", která dává nejlepší výsledky. Tato metoda je sice podstatně pomalejší než ostatní metody, pro malé počty součástek, z nichž má být v daném příkladu ložisko sestaveno, ji však můžeme bez problému použít i na méně výkonných počítačích.
3) V seznamu [9.5] vybereme položku "Dávkové zpracování". Při výběru této položky program postupně provede optimalizaci pro všech 10 základních řešení. Nejvýhodnější řešení pak vybere z hlediska maximálního počtu sestavených výrobků a minimálního počtu použitých montážních kombinací.
4) Tlačítkem na řádku [9.5] spustíme optimalizaci.
5) Základní kvalitativní parametry navrženého postupu montáže jsou uvedeny v odstavci [9.6],

detailní rozpis optimalizovaného montážního postupu je rozepsán v tabulce [9.12].
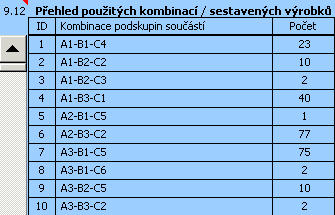
V levém sloupci tabulky jsou vypsány všechny montážní kombinace, použité pro sestavení výrobku. V pravém sloupci pak počet výrobků sestavených rámci každé kombinace.
| Optimalizační metoda | Počet sestavený ložisek | Počet použitých montážních kombinací | Rychlost výpočtu |
| A. Základní metoda | 762 | 29 | 6 min 20 s |
| B. Modifikovaná metoda | 760 | 34 | 1 min 30 s |
| C. Zjednodušená metoda | 759 | 32 | 55 s |
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
^