Návrh a optimalizace lineárního rozměrového řetězce při použití statistické metody RSS.

U součástky (viz. obrázek) navrhněte výrobní tolerance rozměrů tak, aby u technologicky výsledného rozměru nebyla překročena povolená odchylka ±0.0013 in. 

Řešení úlohy.

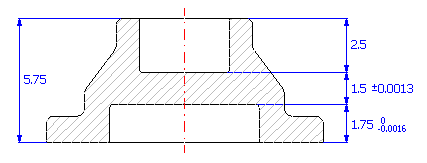
Vyjdeme-li z grafického znázornění rozměrového řetězce

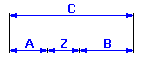
můžeme u dané součásti popsat výsledný rozměr vztahem Z = C - A - B.

Při řešení této úlohy klasickou metodou "Worst Case" by pro dodržení požadované tolerance výsledného rozměru bylo nutné u rozměrů B a C použít tolerance přibližně ve 4. stupni přesnosti. Je zřejmé, že výroba s takovouto přesností by byla neúměrně nákladná. V tomto případě bude proto mnohem výhodnější použít statistickou metodu výpočtu. Tato metoda umožňuje vyrábět součástku s podstatně většími tolerancemi, při výskytu malého (předem zvoleného) procenta zmetků.

Návrh rozměrového řetězce.

Řešení úlohy návrhu a optimalizace rozměrového řetězce můžeme rozdělit do následujících kroků:

1) Na základě výše uvedeného vztahu definujeme v tabulce [1.1] rozměrový řetězec.

2) Pro jednotlivé rozměry dále zadáme požadované výrobní tolerance. U rozměru A vyplníme příslušné odchylky, předepsané zadáním úlohy. 

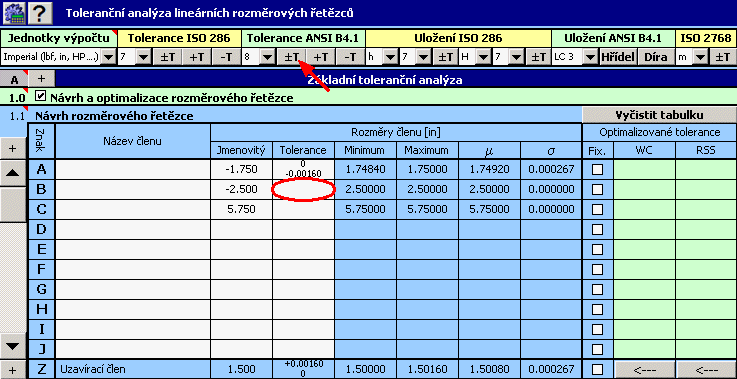
U zbylých rozměrů předběžně zvolíme symetrickou toleranci v 8. stupni přesnosti.

Poznámka: Tento krok sice není nezbytně nutný, zajistí však, aby optimalizované tolerance byly navrženy ve správném poměru. Při návrhu jednotlivých tolerancí totiž bude zachován vzájemný poměr jejich velikosti, daný hodnotami zadanými ve vstupní části tabulky.

3) V 8. sloupci tabulky zaškrtneme přepínač u rozměru A, jehož tolerance je pevně daná.

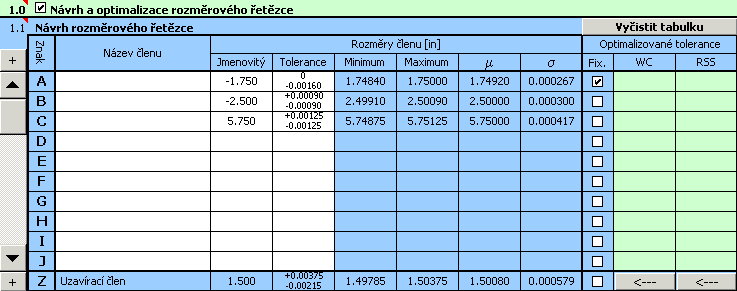
4) V odstavci [1.3] zadáme požadované mezní hodnoty výsledného rozměru.

5) Ve výběrovém seznamu [1.7] zvolíme metodu "Centrování a optimalizace", v seznamu [1.8] nastavíme požadovanou přesnost (počet desetinných míst) navrhovaných tolerancí.

6) S ohledem na možné způsoby obrábění, použitelné při výrobě součásti, nastavíme ve výběrovém seznamu [1.9] minimální povolenou velikost tolerance na 6. stupeň přesnosti.

Tip: Tabulku dosahovaných výrobních přesností pro různé způsoby obrábění naleznete v sešitu "Tolerance a úchylky".

7) Ve výběrovém seznamu [1.10] zvolíme požadovanou výtěžnost výroby 99.9%, to jest výrobní proces s maximálním počtem 1000 zmetků na milion vyrobených součástí.

8) Tlačítkem na řádku [1.11] spustíme optimalizaci rozměrového řetězce. 

9) Výsledné parametry návrhu jsou uvedeny v odstavci [2.10], 

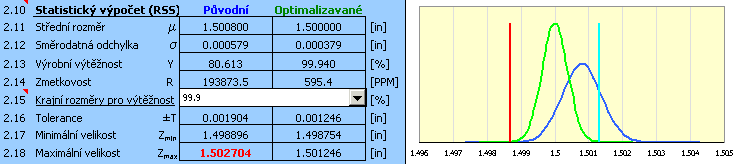
optimalizované úchylky výrobních rozměrů jsou vypsány v 10. sloupci tabulky [1.1].

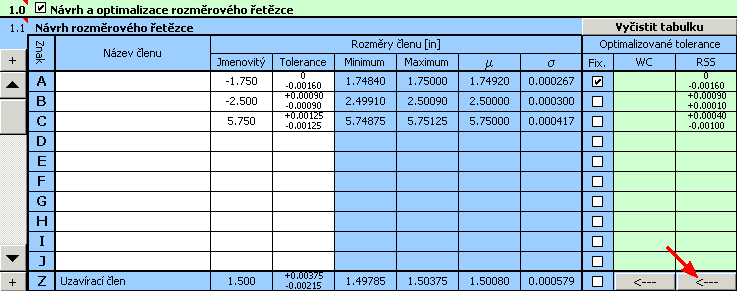
10) Navržené tolerance můžeme samozřejmě dále upravovat. Pomocí tlačítka ve spodním řádku tabulky přeneseme optimalizované hodnoty tolerancí do vstupní části tabulky. Při zachování velikosti tolerancí zde pak můžeme například jemně doladit navržené úchylky do vhodnějšího tvaru.

Výsledky výpočtu budou pro tuto úpravu shodné s výsledky dosaženými pro optimalizované tolerance.

Poznámka na závěr.

Zde navržené řešení nebude samozřejmě jediným vyhovujícím řešením této úlohy a nemusí tedy být ani řešením ideálním. Při výběru vhodného řešení je potřeba důkladně zvážit vzájemný vztah mezi zvolenou velikostí výrobních tolerancí a předpokládanou výtěžností výrobního procesu. Zvětšením použitých tolerancí docílíme poklesu přímých nákladů spojených s obráběním součásti, vzrostou však ztráty způsobené zvýšeným výskytem vadných výrobků. Výsledné řešení je pak nutné volit tak, aby celkové náklady na výrobu byly pokud možno co nejnižší.

Pro srovnání jsou v následující tabulce uvedeny hodnoty předpokládané výtěžnosti výroby pro normalizované tolerance rozměrů B a C.