Výroba a sestavení válečkových ložisek při použití metody selektivní montáže.

Zadání úlohy.

Pro válečkové ložisko sestavené ze tří součástí o rozměrech:

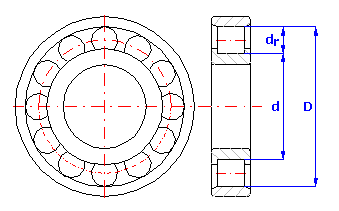
1. Vnější kroužek - průměr D=160 mm
2. Vnitřní kroužek - průměr d=120 mm
3. Válečky - průměr dr=20 mm

navrhněte výrobní tolerance všech součástí a parametry selektivní montáže tak, aby při montáži ložiska byla zajištěna radiální vůle v rozsahu 60 mm až 90 mm. U ložiska je dále vyžadováno zajištění zaměnitelnosti vnitřního kroužku tak, aby při výměně kroužku v případě opravy ložiska byla zaručena radiální vůle v rozsahu 40 mm až 105 mm.

Poznámka: V reálné praxi se metoda selektivní montáže používá obvykle pouze k výrobě výrobků, u nichž se nevyžaduje provozní zaměnitelnost součástí uvnitř výrobku. Požadavek zajištění zaměnitelnosti některé ze součástí výrazně snižuje výhody selektivní montáže. Zde uvedená úloha má tedy pouze teoretický charakter a jejím úkolem je demonstrovat širší možnosti využití programu.  

Řešení úlohy.

Výroba valivých ložisek je typickým příkladem vhodným pro použití metody selektivní montáže. Při řešení uvedeného příkladu klasickou metodou "Worst Case" bude u ložiska sice zajištěna úplná montážní i provozní zaměnitelnost všech součástí, pro dodržení požadované radiální vůle by však bylo potřeba vyrábět součásti ložiska ve 3. stupni přesnosti. Je zřejmé že výroba s takovýmto stupněm přesnosti by byla neúměrně nákladná. Při použití metody selektivní montáže lze součásti vyrábět s podstatně nižší přesností. Vlastní řešení úlohy selektivní montáže se skládá ze dvou částí:

Návrh rozměrového řetězce.

Velikost radiální vůle je u válečkových ložisek dána vztahem c = D - d - 2*dr. 

Řešení úlohy návrhu a optimalizace rozměrového řetězce pak můžeme rozdělit do následujících kroků:

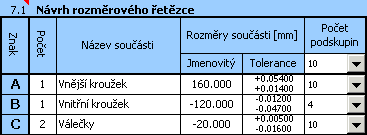
1) Na základě výše uvedeného vztahu definujeme v tabulce [7.1] rozměrový řetězec. Dílčí členy řetězce tvoří jednotlivé součásti použité při montáži ložiska. Uzavíracím členem rozměrového řetězce je pak požadovaná radiální vůle.

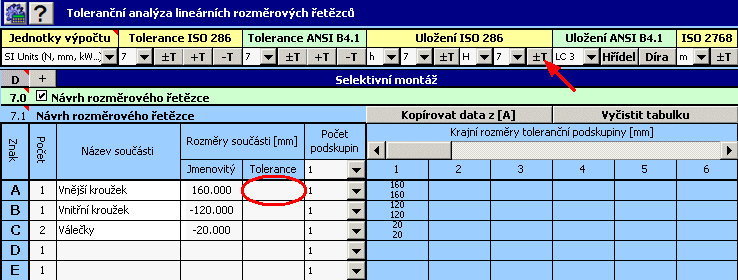
2) Pro jednotlivé rozměry dále zadáme požadované výrobní tolerance. V prvotním návrhu použijeme u všech součástí tolerance v 7. stupni přesnosti. Pro průměr válečků přitom zvolíme symetrickou toleranci, pro průměr vnějšího kroužku toleranci H7 a pro vnitřní kroužek h7.

3) Pro všechny součásti předběžně nastavíme 10 tolerančních podskupin, do nichž budou vyrobené součásti roztříděny.

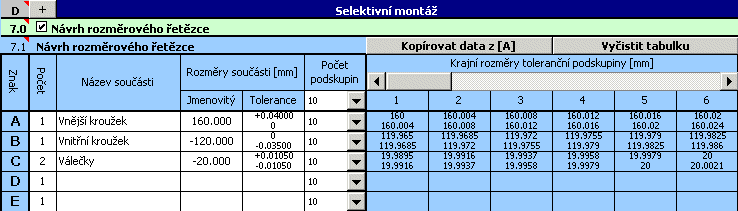
4) V odstavci [8.1] zohledníme požadavek provozní zaměnitelnosti vnitřního kroužku ložiska.

5) V odstavci [8.4] zadáme mezní hodnoty požadované radiální vůle při montáži ložiska a při výměně vnitřního kroužku.

6) Ve výběrovém seznamu [8.9] zvolíme vyhledání všech montážních kombinací. Vlastní hledání kombinací pak spustíme tlačítkem na řádku [8.10].

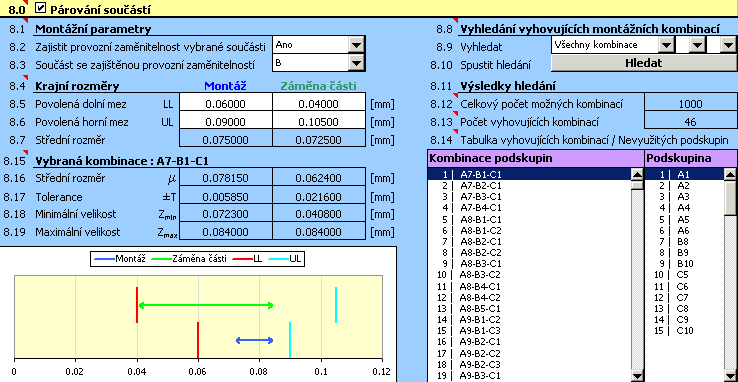
7) Kvalitu návrhu posoudíme na základě výsledků v odstavci [8.11]. Je zřejmé, že v tomto případě není návrh vyhovující. Z tabulky "Nevyužitých podskupin" v řádku [8.14] vyplývá, že pro montáž ložiska by nebylo možné použít více než polovinu vyrobených vnějších kroužků a válečků.

8) Pro nevyhovující návrh by dalším logickým krokem mohlo být zmenšení velikosti použitých výrobních tolerancí. Při bližším posouzení tohoto návrhu však zjistíme, že hlavním problémem zde nebude zvolená velikost tolerancí, ale spíše chybné vycentrování návrhu. Pro správné posouzení tohoto aspektu návrhu je směrodatným ukazatelem střední rozměr uzavíracího členu dopočtený v odstavci [7.2]. 

U optimálního návrhu tolerančního řetězce by se zde uvedený rozměr měl co nejvíce blížit požadované hodnotě [8.7]. 

9) V opakovaném návrhu tedy při zachování velikosti tolerancí upravíme pozici tolerančních polí všech součástí. Pro průměr vnějšího kroužku použijeme toleranci G7, pro průměr vnitřního kroužku toleranci g7. 

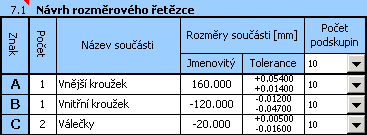
Horní a dolní úchylku průměru válečků pak upravíme tak, aby výsledný návrh byl co nejlépe vycentrován.

10) Pro takto upravený návrh rozměrového řetězce opětovně vyhledáme všechny vyhovující montážní kombinace.

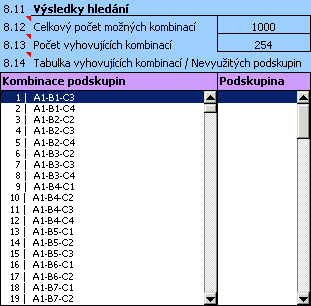
11) Z výsledků hledání je zřejmé, že při montáži ložiska budou nyní použitelné všechny vyrobené součásti. Návrh však není příliš efektivní, jelikož počet vyhovujících montážních kombinací je zbytečně vysoký. Snížení počtu přijatelných kombinací můžeme docílit například zmenšením počtu tolerančních podskupin, do nichž budou vyrobené součásti roztříděny.

12) Postupným snižováním počtu podskupin se dopracujeme k výslednému návrhu rozměrového řetězce,

který se pro zvolený příklad jeví jako optimální.

Výsledný počet 75 vyhovujících montážních kombinací je již pro účely selektivní montáže přijatelný.

Optimalizace počtu sestavených výrobků.

V předchozí části úlohy jsme navrhli výrobní tolerance součástí a vyhledali všechny přijatelné montážní kombinace, pomocí nichž lze sestavit ložisko vyhovujících parametrů. Při vlastní montáži ložiska však není účelné sestavovat ložiska pouhým náhodným výběrem součástek v rámci přípustných montážních kombinací. Má-li být metoda selektivní montáže efektivní, je nutné vyřešit úlohu optimálního výběru (kombinace) součástek. Součástky musí být sdružovány tak, aby s daným počtem vyrobených součástek bylo možno sestavit maximální možný počet výrobků, které splňují funkční požadavky.

Tuto úlohu je nutné řešit opakovaně v průběhu výroby a to vždy při doplnění skladů před započetím vlastní montáže. Podstatou úlohy je stanovení optimálního postupu montáže tak, aby počet sestavených výrobků byl co nejvyšší. Při řešení úlohy tedy musíme z dříve nalezené množiny přijatelných kombinací vybrat optimální sadu kombinací použitých při montáži a zároveň stanovit počet výrobků sestavených v rámci každé použité kombinace.

Řešení úlohy optimalizace počtu sestavených výrobků je prováděno v následujících krocích: 

1) V tabulce [9.1] zadáme počty vyrobených součástek v jednotlivých tolerančních podskupinách. 

Poznámka: Krajní rozměry všech tolerančních subintervalů jsou uvedeny v tabulce [7.1].

2) Ve výběrovém seznamu [9.3] zvolíme vhodnou optimalizační metodu. Pro uvedený příklad vybereme "Základní metodu", která dává nejlepší výsledky. Tato metoda je sice podstatně pomalejší než ostatní metody, pro malé počty součástek, z nichž má být v daném příkladu ložisko sestaveno, ji však můžeme bez problému použít i na méně výkonných počítačích.

Poznámka: Srovnání výsledků a rychlosti výpočtu, dosažené u daného příkladu při použití různých optimalizačních metod, je uvedeno na konci příkladu.

3) V seznamu [9.5] vybereme položku "Dávkové zpracování". Při výběru této položky program postupně provede optimalizaci pro všech 10 základních řešení. Nejvýhodnější řešení pak vybere z hlediska maximálního počtu sestavených výrobků a minimálního počtu použitých montážních kombinací.

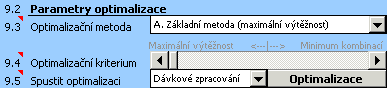
4) Tlačítkem na řádku [9.5] spustíme optimalizaci.

5) Základní kvalitativní parametry navrženého postupu montáže jsou uvedeny v odstavci [9.6],

detailní rozpis optimalizovaného montážního postupu je rozepsán v tabulce [9.12].

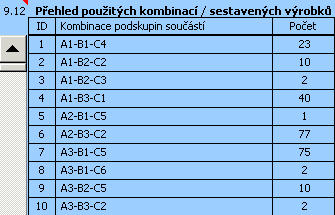
V levém sloupci tabulky jsou vypsány všechny montážní kombinace, použité pro sestavení výrobku. V pravém sloupci pak počet výrobků sestavených rámci každé kombinace.

Srovnání výsledků optimalizace a rychlosti výpočtu dosažené u daného příkladu při použití různých optimalizačních metod:

Poznámka: U všech optimalizačních metod bylo použito 'dávkové zpracování'. Výpočet byl proveden na počítači s procesorem x86, 1800Mhz, 256MB.