Das Programm ist für Toleranzanalyse ebener (2D) und räumlicher (3D) Maßketten bestimmt. Es löst folgende Aufgaben:
Beim Vorschlag der Maßkette ermöglicht das Programm das Arbeiten mit genormten Toleranzwerten.
Bei der Berechnung werden Daten, Verfahren, Algorithmen und Angaben aus der
Fachliteratur und ANSI, ISO, DIN und weiteren Normen verwendet.
Verzeichnis der Normen: ANSI B4.1, ISO 286, ISO 2768, DIN 7186
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Eine Maßkette ist ein Komplex aus voneinander abhängigen Maßen, die so aneinander anschließen, dass sie ein geometrisch geschlossenes Gebilde darstellen. Es können Abmaße sein, die die gegenseitige Lage von Elementen an einem Werkstück bestimmen, oder Abmaße mehrerer Werkstücke bei einer Montageeinheit.
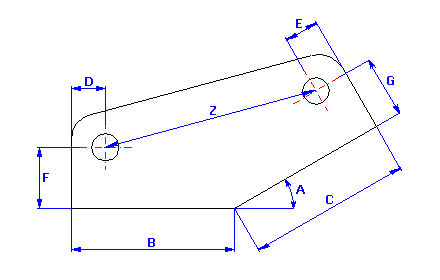
Die Maßkette setzt sich aus einzelnen Teilabmaßen
(Eingangsabmessungen) zusammen und wird mit dem Schließmaß
(resultierendes Maß) abgeschlossen. Teilabmaße (A,B,C,…) sind Abmaße, die direkt
auf der Zeichnung angegeben sind, oder sich aus den vorhergehenden produktions-
bzw. Montagevorgängen ergeben. Das Schließmaß (Z) stellt in der gegebener
Maßkette das resultierende Produktions- oder Montageabmaß dar, welches sich
durch das Zusammensetzen der Teilmaße als nicht angegebenes Abmaß des
Werkstückes, bzw. als Spiel, oder Übermaß bei der Montage ergibt. Die Größe,
Toleranz und Grenzabmaße des resultierenden Abmaßes sind direkt abhängig von der
Größe und Toleranz der Teilabmaße. Nach der gegenseitigen Lage der einzelnen
Maßglieder unterscheiden wir drei Typen von Maßketten:
- Lineare Maßketten (1D) – beinhalten nur parallele Maße
- Ebene Maßketten (2D) – die Teilabmaße sind in einer oder mehreren
parallelen Ebenen verteilt
- Räumliche Maßketten (3D) – die Teilabmaße liegen in nichtparallelen
Ebenen
Dieses Programm ist für Toleranzanalyse ebener (2D) und räumlicher (3D)
Maßketten bestimmt.
Bei der Lösung der Toleranzbeziehungen in den Maßketten kommen zwei Arten von Aufgaben vor:
Bei der Lösung der Toleranzbeziehungen in den Maßketten werden in der
Berechnung zwei Berechnungsmethoden verwendet:
- Methode "Worst Case"
- Methode "Monte Carlo"
Die Wahl der Berechnungsart der Toleranzen und Grenzabmaße der Teilmaße einer
Maßkette hat Einfluss auf die Produktionsgenauigkeit und die
Montageaustauschbarkeit von Teilen. Von ihr hängen die Produktions- und
Betriebswirtschaftlichkeit ab.
Diese Methode wird am häufigsten verwendet, sie wird auch als Maximum - Minimum Methode bezeichnet. Sie geht von der Einhaltung der geforderten Grenzmaße des Schließmaßes für eine beliebige Kombination der tatsächlichen Größen der Teilmaße aus, also auch des oberen, wie unteren Grenzmaßes. Diese Methode garantiert eine vollständige Montage- und Betriebsaustauschbarkeit der Teile. Wird eine größere Genauigkeit des Schließmaßes gefordert, führt dies aber zu einer zu engen Toleranz der Teilmaße, also auch zu hohen Herstellkosten. Die "Worst Case" Methode ist deshalb geeignet zur Lösung von Maßsystemen mit wenigen Teilmaßen, oder dann, wenn eine größere Toleranz des Schließmaßes zulässig ist. Am häufigsten wird sie in Einzel- oder Kleinserienproduktion verwendet.
Die Aufgabe der "Worst Case" Methode ist es, den minimalen und maximalen Wert zu finden, den das resultierende Abmaß für eine beliebige Kombination der tatsächlichen Eingangswerte annehmen kann. Der Algorithmus der Berechnung ist auf dem sukzessiven Durchtesten aller existierenden Kombinationen verschiedener (vorher ausgewählter) Eingangswerte aufgebaut. Bei normalen Maßketten nimmt das resultierende Abmaß seine Grenzwerte gewöhnlich nur im Rahmen bestimmter Kombinationen der Grenzwerte der Eingangswerte an. Bei der Durchführung der Toleranzanalyse können wir uns dann bei der Mehrzahl der zu lösenden Aufgaben auf das Testen der Kombinationen der minimalen und maximalen Werte der Teilabmaße der Maßkette beschränken.
In einer kleinen Anzahl von Fällen gilt aber die o.g. Voraussetzung nicht, und für die Feststellung der Grenzwerte des resultierenden Abmaßes wird es notwendig sein, die Berechnung auch für Eingangswerte durchzuführen, die innerhalb des Toleranzintervalls liegen. Das Programm berücksichtigt diese Tatsache mit der Möglichkeit, die Anzahl der zu testenden Einganzwerte auszuwählen (teilen des Toleranzintervalls).
Der gewählte Algorithmus der Berechnung garantiert zwar der Methode "Worst Case" eine hohe Erfolgsquote bei der Suche der Grenzwerte des resultierenden Abmaßes, kann aber gleichzeitig zu unangemessenen langen Berechnungszeiten führen. Die Geschwindigkeit der Berechnung hängt von der Gesamtanzahl der durchgeführten Berechnungszyklen ab, die für das Durchtesten aller Kombinationen der Eingangswerte notwendig sind. Die Anzahl dieser Zyklen hängt von der gewählten Teilung des Toleranzinterwalls ab und wächst mit einer geometrischen Progression die von der Anzahl der Teilabmaße der Maßkette abhängig ist. Mathematisch wird es mit dieser Beziehung beschrieben:
![]()
wo:
c ... Gesamtanzahl der Berechnungszyklen
n ... Anzahl der Teilmaße der Maßkette
k ... Anzahl der getesteten Werte für jedes Teilmaß
Aus dem oben Aufgeführten wird deutlich, dass die "Worst Case" Methode für die Lösung von Toleranzbeziehungen vor allem weniger komplizierter Maßketten mit einer kleinen Anzahl der Teilmaße bestimmt ist. Die praktische Verwendbarkeit dieser Methode ist begrenzt durch die Leistungsfähigkeit des PC`s, durch die Anzahl der Teilabmaße der Maßkette und durch die gewählte "Feinheit" der Teilung des Toleranzinterwalls.
Diese Methode gehört unter die statistischen Methoden bei der Berechnung von Maßketten. Die statistischen Methoden gehen von der Wahrscheinlichkeitsrechnung aus und setzen voraus, dass bei einer zufälligen Auswahl von Werkstücken während der Montage die maximalen Werte der Grenzwerte bei mehreren Teilen nur selten zusammen auftreten, weil es sich um eine zusammengesetzte Wahrscheinlichkeit handelt. Genauso wenig wahrscheinlich ist das Auftreten der maximalen Grenzwerte bei der Produktion von einzelnen Teilabmaßen an einem Werkstück. Mit einem bestimmten, vorher festgelegten Risiko der Aussonderung einiger Werkstücke kann man also die Toleranzen der Teilabmaße im Kettenmaß vergrößern.
Die "Monte Carlo" Methode garantiert nur eine teilweise Austauschbarkeit bei der Montage mit einem niedrigem prozentuellem Anteil von ungünstigen Fällen (Ausschuss). Angesichts der größeren Toleranzen bei den Teilabmaßen führt sie aber zur Senkung der Produktionskosten. Sie wird vor allem in der Massen- und Großserienproduktion verwendet, wo die Einsparungen bei der Teilefertigung, verglichen mit den Kostenerhöhungen, die durch eine nicht vollständige Austauschbarkeit bei der Montage entstehen, überwiegen.
Die Dimensionen des Schließmaßes zeigen von der Mitte des Toleranzfeldes aus eine gewisse Streuung auf. Die Häufigkeit des Auftretens der einzelnen Abmaße richtet sich hierbei nach den Gesetzen der mathematischen Statistik. Die Aufgabe der "Monte Carlo" Methode ist dann die Klärung eben dieser Häufigkeit und die Feststellung der angenommenen Prozessausbeute.
Bei der "Monte Carlo" Methode handelt es sich um eine Simulationsmethode. Ihr Algorithmus ist auf der zufälligen - im Rahmen der gewählten Toleranzfelder und nach den vorgeschriebenen Verteilungsfunktionen definierten - Generierung der Eingangswerte begründet. Für einen so generiertes Komplex von Eingangsmaßen ist weiter unten eine Berechnung der resultierenden Abmaße durchgeführt. Dieser Prozess wird für eine vorher gewählte Anzahl von Simulationen zyklisch durchgeführt. Das Ergebnis dieser Simulation ist dann ein statistischer Datenkomplex (der resultierenden Abmaße), standardmäßig als Mittelwert bezeichnet:
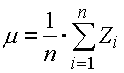
und durch die Standardabweichung:
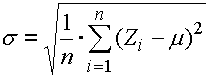
wo:
Zi ... die Größe des resultierenden Abmaßes im i-ten Zyklus der
Simulation
n ... Gesamtanzahl der Simulationszyklen
Für die Auswertung der Häufigkeit des Auftretens des resultierenden Abmaßes wird dieser statistischer Datensatz in die Form eines Histogramms umgewandelt.
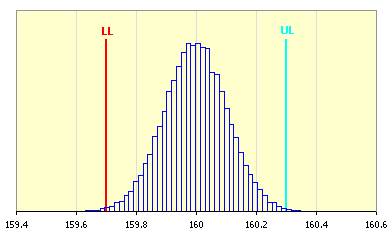
Ein maßgebliches Zeichen für die Beurteilung der Qualität des Vorschlages einer Maßkette mit der "Monte Carlo" Methode ist die vorausgesetzte Prozessausbeute. Die Produktionsausbeute gibt den angenommenen Anteil der Produkte an, die den spezifizierten Anforderungen entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes in dem durch die Randgrenzen gegebenem Intervall befindet. Im allgemeinen Maschinenbau wird meistens ein Produktionsprozess auf dem 3s Niveau, d.h. mit minimaler Prozessausbeute von 99,73% als befriedigend geeignet angesehen
Die Genauigkeit (Aussagewert) der festgestellten statistischen Ergebnisse ist von der Anzahl durchgeführter Simulationen abhängig. Es wird deutlich, dass mit steigender Anzahl der Simulationen auch die Qualität der Ergebnisse wächst. Die optimale Anzahl der Simulationen hängt von der Anzahl der Eingangswerte, der Größen ihrer Toleranzen und der Gesamtkomplexität der Maßkette ab. In der Praxis kann als eine vernünftige untere Grenze bei Endberechnungen der Wert von 30 bis 50 Tausend durchgeführter Simulationen angesehen werden.
Diese Zeile dient zum Umschalten des Einheitensystem des Rechenvorgangs und zur Wahl der genormten Toleranzen.
In der Auswahlliste das verlangte System von Berechnungsmaßeinheiten auswählen. Beim Umschalten der Einheiten werden alle Werte sofort umgerechnet.
Bei der Definition einer Maßkette im Abschnitt [1.1] ist für jede Dimension auch die dazugehörige Toleranz anzugeben. Als Arbeitserleichterung ist das Programm mit einem Tool für die automatische Wahl von genormten Toleranzen ausgestattet.
Das Programm beinhaltet ein Satz von Maßtoleranzen nach ISO bzw. ANSI. Im Hinblick auf den Typ der Abweichung und die verwendete Norm sind die Toleranzen in 5 Gruppen unterteilt:
Jede der Gruppen hat im Kopf des Mappe eine Reihe von Auswahllisten und Buttons. Stellen Sie in den Auswahllisten die erforderlichen Parameter der Toleranz bzw. Passung (Genauigkeitsgrad, Toleranzfeld,..) ein. Mit Hilfe der Buttons können Sie dann die Werte der gewählten Toleranz an die jeweilige Stelle in der Tabelle - in die Zeile mit der aktiven Zelle - einfügen.
Toleranzen nach ISO sind in der Norm in [mm] definiert und sind für die Berechnung in SI Einheiten bestimmt. Toleranzen nach ANSI sind in [in] definiert und für die Berechnung in "Imperial" Einheiten bestimmt. Bei Verwendung von genormten Toleranzen, die in anderen Einheiten definiert sind als im Programm eingestellt, werden die Maßabweichungen automatisch umgerechnet und gerundet. Für die Tolerierung der Winkelabmaße ist die Norm ISO 2768 festgelegt.
Die Aufgabe der Toleranzanalyse der Maßkette besteht aus folgenden Schritten:
Definieren Sie in diesem Abschnitt die Parameter aller Teilabmaße der Maßkette.
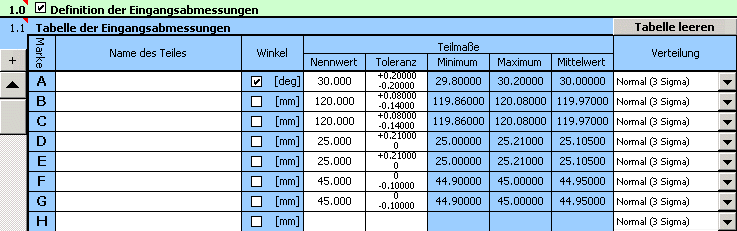
Diese Tabelle dient zur Definition der Parameter einzelner Eingangswerte (Teilabmaße) der Maßkette. Zu jedem Teilabmaß gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Benennung des Teilmaßes ist kein Pflichtparameter.
Spalte 2 – Durch Markieren der Kästchen wählen Sie den Typ des Abmaßes. Implizit ist bei allen Teilgliedern der Maßkette ein Längenmaß voreingestellt, durch die Markierung des Kästchens wählen Sie für das gewählte Glied das Winkelmaß. Hier eingestellter Typ des Abmaßes hat Einfluss auf die Funktion der automatischen Vorauswahl der genormten Toleranzen.
Spalte 3 - Geben Sie das Nominalmaß des Teilgliedes ein.
Spalte 4 - Geben Sie die obere und untere Toleranz des Abmaßes ein. Durch Drücken des ausgewählten Buttons in der Kopfzeile der Mappe fügen Sie in die Tabelle die für die gewählte Toleranz entsprechenden Abweichungen ein. Für die Tolerierung der Längenabmaße können Sie hier alle hier aufgeführten Normen verwenden, die Winkelabmaße sind nach ISO 2768 toleriert.
Spalte 5..7 – In diesen Spalten werden die minimalen, maximalen und mittleren Werte für alle Teilabmaße ausgerechnet.
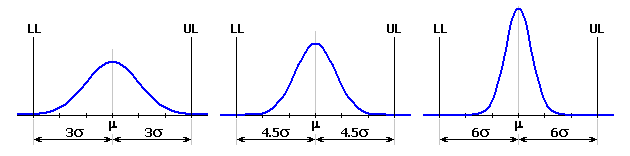
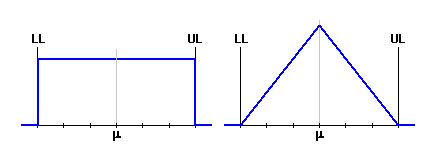
Spalte 8 - Wählen Sie aus der Liste den Typ der Verteilung der Wahrscheinlichkeitsdichte. Standardmäßig wird zur Beschreibung der Produktionsprozesse die Normalverteilung verwendet, die in der absoluten Mehrheit der Fälle am Besten der tatsächlichen Verteilung der zufälligen Prozessgrößen entspricht.
Definieren Sie in dieser Tabelle [2.1] die Parameter aller Schließmaße der Maßkette. Wählen Sie im Abschnitt [2.2] die geforderte Berechnungsmethode und stellen Sie ihre Parameter ein. Die eigentliche Berechnung starten Sie mit dem Button in der Zeile [2.7].
Diese Tabelle dient zur Definition der Parameter einzelner resultierender Abmaße (Schließmaße) der Maßkette. Zu jedem Abmaß gehört eine Zeile der Tabelle. Die Bedeutung der Spalten der Tabelle wird aus folgender Beschreibung deutlich:
Spalte 1 - Benennung des Teilmaßes ist kein Pflichtparameter.
Spalte 2 - geben Sie die Berechnungsbeziehung ein, durch die das resultierende Abmaße definiert ist. Die verwendeten Formeln (Algorithmen) müssen die Syntax von MS - Excel einhalten und können alle in Excel definierten mathematischen Formeln und Funktionen verwenden (siehe Excel-Hilfe). Kennzeichnen Sie die Eingangswerte der Teilabmaße der Maßkette in den Formeln mit der Kombination von Unterstrich und der Kennzeichnung des Abmaßes ("_A", "_B", "_C", ...). Verwenden Sie auch für die resultierenden Abmaße Symbole wie "_Z1", "_Z2", ... Ist die Berechnungsbeziehung fehlerfrei definiert, erscheint an dieser Stelle in Realzeit der ausgerechnete Nennwert des resultierenden Abmaßes. Andernfalls gibt Excel hier eine entsprechende Fehlermeldung aus.
Spalten 3,4 - Definieren Sie die geforderten Grenzdimensionen des Schließmaßes, die durch die Funktionsanforderungen an das Produkt gegeben sind. Die hier angegebenen Grenzabmaße des resultierenden Abmaßes dienen nur dem Vergleich mit den erreichten Ergebnissen. Bei der Berechnungsmethode "Monte Carlo" dienen die erlaubten Grenzwerte zur Festlegung der vorausgesetzten Produktionsausbeute und der Anzahl der Ausschussteile.
Wählen Sie in diesem Abschnitt die geforderte Berechnungsmethode aus und stellen Sie ihre Parameter ein. Die eigentliche Berechnung starten Sie mit dem Button in der Zeile [2.7]. Komplette Ergebnisse der Toleranzanalyse finden Sie im Abschnitt [3].
Die Aufgabe der "Worst Case" Methode ist es, den minimalen und maximalen Wert zu finden, den das resultierende Abmaß für eine beliebige Kombination der tatsächlichen Eingangswerte annehmen kann. Der Algorithmus der Berechnung ist auf dem sukzessiven Durchtesten aller existierenden Kombinationen verschiedener (vorher ausgewählter) Eingangswerte aufgebaut. Bei normalen Maßketten nimmt das resultierende Abmaß seine Grenzwerte gewöhnlich nur im Rahmen bestimmter Kombinationen der Grenzwerte der Eingangswerte an. Bei der Durchführung der Toleranzanalyse können wir uns dann bei der Mehrzahl der zu lösenden Aufgaben auf das Testen der Kombinationen der minimalen und maximalen Werte der Teilabmaße der Maßkette beschränken.
In einer kleinen Anzahl von Fällen gilt aber die o.g. Voraussetzung nicht, und für die Feststellung der Grenzwerte des resultierenden Abmaßes wird es notwendig sein, die Berechnung auch für Eingangswerte durchzuführen, die innerhalb des Toleranzintervalls liegen. Das Programm berücksichtigt diese Tatsache mit der Möglichkeit, die Anzahl der zu testenden Einganzwerte auszuwählen (teilen des Toleranzintervalls). Die geforderte "Feinheit" der Teilung des Toleranzinterwalls stellen Sie in der Auswahl [2.4] ein.
Der gewählte Algorithmus der Berechnung garantiert zwar der Methode "Worst Case" eine hohe Erfolgsquote bei der Suche der Grenzwerte des resultierenden Abmaßes, kann aber gleichzeitig zu unangemessenen langen Berechnungszeiten führen. Die Geschwindigkeit der Berechnung hängt von der Gesamtanzahl der durchgeführten Berechnungszyklen ab, die für das Durchtesten aller Kombinationen der Eingangswerte notwendig sind. Die Anzahl dieser Zyklen hängt von der gewählten Teilung des Toleranzinterwalls ab und wächst mit einer geometrischen Progression die von der Anzahl der Teilabmaße der Maßkette abhängig ist.
Aus dem oben Aufgeführten wird deutlich, dass die "Worst Case" Methode für die Lösung von Toleranzbeziehungen vor allem weniger komplizierter Maßketten mit einer kleinen Anzahl der Teilmaße bestimmt ist. Die praktische Verwendbarkeit dieser Methode ist begrenzt durch die Leistungsfähigkeit des PC`s, durch die Anzahl der Teilabmaße der Maßkette und durch die gewählte "Feinheit" der Teilung des Toleranzinterwalls.
Die Dimensionen des Schließmaßes zeigen von der Mitte des Toleranzfeldes aus eine gewisse Streuung auf. Die Häufigkeit des Auftretens der einzelnen Abmaße richtet sich hierbei nach den Gesetzen der mathematischen Statistik. Die Aufgabe der "Monte Carlo" Methode ist dann die Klärung eben dieser Häufigkeit und die Feststellung der angenommenen Prozessausbeute.
Die "Monte Carlo" Methode ist eine Simulationsmethode und sie gehört zu den statistischen Methoden. Ihr Algorithmus ist auf der zufälligen - im Rahmen der gewählten Toleranzfelder und nach den vorgeschriebenen Verteilungsfunktionen definierten - Generierung der Eingangswerte begründet. Für einen so generiertes Komplex von Eingangsmaßen ist weiter unten eine Berechnung der resultierenden Abmaße durchgeführt. Dieser Prozess wird für eine vorher gewählte Anzahl von Simulationen zyklisch durchgeführt. Das Ergebnis dieser Simulation ist dann ein statistischer Datenkomplex (der resultierenden Abmaße), standardmäßig als Mittelwert m und durch die Standardabweichung s bezeichnet. Ein maßgebliches Zeichen für die Beurteilung der Qualität des Vorschlages einer Maßkette mit der "Monte Carlo" Methode ist die vorausgesetzte Prozessausbeute.
Die Genauigkeit (Aussagewert) der festgestellten statistischen Ergebnisse ist von der Anzahl durchgeführter Simulationen abhängig. Es wird deutlich, dass mit steigender Anzahl der Simulationen auch die Qualität der Ergebnisse wächst. Die optimale Anzahl der Simulationen hängt von der Anzahl der Eingangswerte, der Größen ihrer Toleranzen und der Gesamtkomplexität der Maßkette ab. In der Praxis kann als eine vernünftige untere Grenze bei Endberechnungen der Wert von 30 bis 50 Tausend durchgeführter Simulationen angesehen werden. Die geforderte Anzahl der Simulationen stellen Sie in der Auswahl [2.6] ein.
Nach der Durchführung der Berechnung [2.7] werden in diesem Abschnitt die Ergebnisse der Toleranzanalyse der weiter oben definierten Maßkette dargestellt. Der Abschnitt ist in zwei Bereiche aufgeteilt. In der Tabelle [3.1] sind zusammengefasst die Grundinformationen über alle in der Tabelle [2.1] definierten Abmaße dargestellt. Im Abschnitt [3.2] sind in numerischer und grafischer Form die Detailparameter des ausgewählten resultierenden Abmaßes dargestellt.
In dieser Tabelle sind zusammengefasst die Grundinformationen über alle in der Tabelle [2.1] definierten Schließmaße der Maßkette dargestellt. Bei der Berechnung mit der "Worst Case" Methode ist das resultierende Abmaß mit dem gefundenen minimalen und maximalen Wert angegeben. Bei der Verwendung der Berechnungsmethode "Monte Carlo" ist der statistischer Datensatz, der die Häufigkeit des Auftretens der resultierenden Abmaße in der Tabelle mit dem Mittelwert, der Standardabweichung und der Anzahl der Ausschussteile pro Million gefertigter Teile angegeben.
In diesem Abschnitt werden in numerischen und graphischen Form die Detailparameter des ausgewählten resultierenden Abmaßes (Schließmaßes) der Maßkette dargestellt. Das geforderte Maß, dessen Parameter Sie darstellen wollen, wählen Sie aus dem Pull-down Menü (Pfeil neben der Tabellenüberschrift).
Im Hinblick auf die verwendete Berechnungsmethode sind die Ergebnisse der Toleranzanalyse in 2 Bereiche aufgeteilt. Für die Beurteilung der Qualität des Vorschlages der Maßkette sind bei der "Worst Case" Methode die Grenzwerte entscheidend, die das resultierende Abmaß annehmen kann [3.10, 3.11]. Bei der Methode "Monte Carlo" ist das maßgebliche Kriterium die vorausgesetzte Prozessausbeute [3.15] bzw. die Anzahl der Ausschussteile pro Million gefertigte Teil [3.16]. Die Häufigkeit des Auftretens der einzelnen Abmaße ist graphisch im beiliegendem Histogramm dargestellt.
Die Produktionsausbeute gibt den angenommenen Anteil der Produkte an, die den spezifizierten Anforderungen entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes in dem durch die Randgrenzen gegebenem Intervall befindet. Im allgemeinen Maschinenbau wird meistens ein Produktionsprozess auf dem 3s Niveau, d.h. mit minimaler Prozessausbeute von 99,73% als befriedigend geeignet angesehen.
Ausschuss gibt den vorausgesetzten Anteil der Produkte an, die den spezifizierten Anforderungen nicht entsprechen, d.h. der Produkte, bei denen sich die resultierende Dimension des Schließmaßes nicht in dem durch die Randgrenzen gegebenem Intervall befindet. Im allgemeinen Maschinenbau wird meistens ein Produktionsprozess auf dem 3s Niveau, d.h. mit maximalem Anzahl von 2700 Ausschusseile pro Million gefertigte Produkte als befriedigend geeignet angesehen.
Hier aufgeführte Grenzwerte haben nur informativen Charakter. Diese Werte bestimmen nicht die wirklichen Grenzwerte, die das resultierende Abmaß annehmen kann. Sie geben nur den minimalen und maximalen Wert an, der während der Simulationsberechnung im Rahmen der gewählten Kombinationsanzahl gefunden wurde. Damit die wirklichen Grenzwerte gefunden werden, ist es notwendig die Berechnungsmethode "Worst Case" zu verwenden.
Zur Illustration der Problematik der Toleranzanalyse von Maßketten wurde die Hilfe durch ein paar praktische Beispiele für die Verwendung des Programms ergänzt:
Untersuchen Sie für einen exzentrischen Hebelmechanismus eines Kolbenkompressors
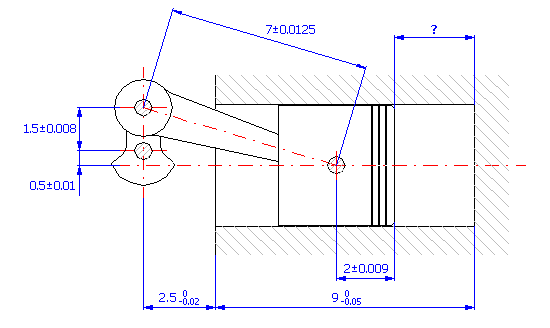
Wenn wir von der graphischen Darstellung der Maßkette ausgehen,
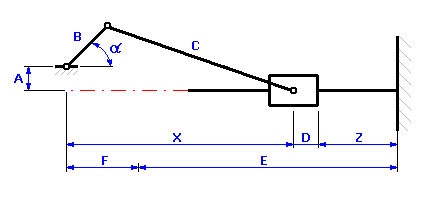
können wir bei gegebenem kinematischem Mechanismus die Größe des Zylinderhubs so beschreiben:
![]()
wo die Lage des Zylinders zu der Achse der Kurbelwelle X eine Kinematische Größe ist, die vom Drehwinkel der Kurbelwelle a abhängt. Für einen exzentrischen Kurbelmechanismus, wie er im vorhergehendem Bild dargestellt ist, können wir für die Bestimmung der Lage des Zylinders folgende Beziehung verwenden:
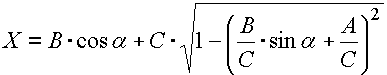
Die Grenzlagen des Zylinders auf die Achse der Kurbelwelle bezogen sind aus dem folgenden Schema deutlich
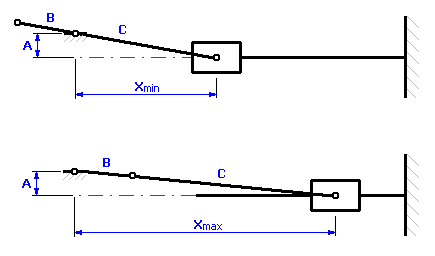
und können mit diesen Beziehungen beschrieben werden:
![]()
Die Lösung der Toleranzanalyse des kinematischen Mechanismus können wir in folgende Schritte einteilen:
1) Definieren Sie alle Eingangswerte (Teilabmaße) der Maßkette in der Tabelle [1.1].
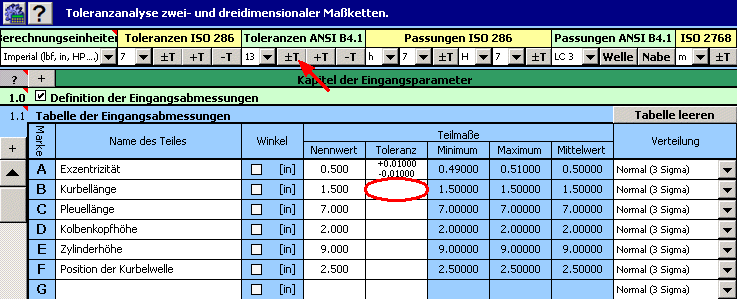
2) Für die einzelnen Abmaße geben wir dann die vorgeschriebenen Produktionstoleranzen ein. Bei den Abmaßen B,C,D sind genormte symmetrische Toleranzen nach ANSI B4.1 in der 13ten Toleranzklasse vorgeschrieben. Für ihre Eingabe in die Tabelle können wir die automatische Toleranzauswahl verwenden.
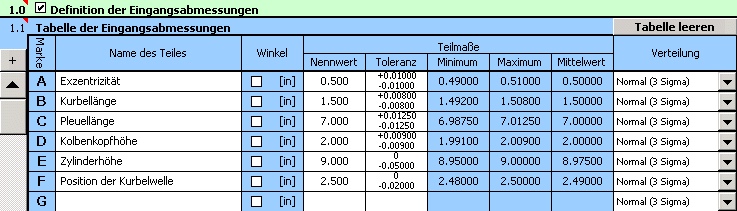
3) Definieren Sie alle Parameter der resultierenden Abmaße (Schließmaße) der Maßkette in der Tabelle [2.1]. Die Berechnungsbeziehungen für den minimalen und maximalen Zylinderhub, die im vorhergehendem Abschnitt definiert wurden, müssen an die Syntax von Excel angepasst werden. In die zweite Spalte der Tabelle geben wir für den minimalen Zylinderhub die Formel: "=_E+_F-_D-((_C+_B)^2-_A^2)^0.5" ein, für den maximalen Zylinderhub: "=_E+_F-_D-((_C-_B)^2-_A^2)^0.5".
4) In der Zeile [2.3] markieren wir das Kästchen bei der Berechnungsmethode "Worst Case". Aus der Auswahlliste [2.4] wählen wir die "gröbste" Teilung des Toleranzinterwalls (Auswahl "Min – Max"), die für die gegebene Aufgabe ausreichend ist.
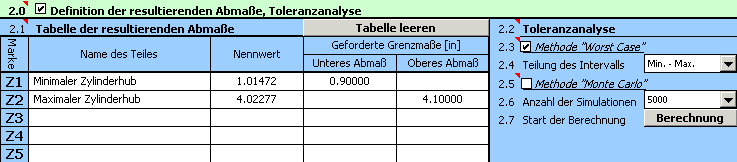
5) Mit dem Button in der Zeile [2.7] starten wir die eigentliche Berechnung (die Toleranzanalyse) der Maßkette. Die Grenzwerte des Hubes finden wir dann im Abschnitt [3].
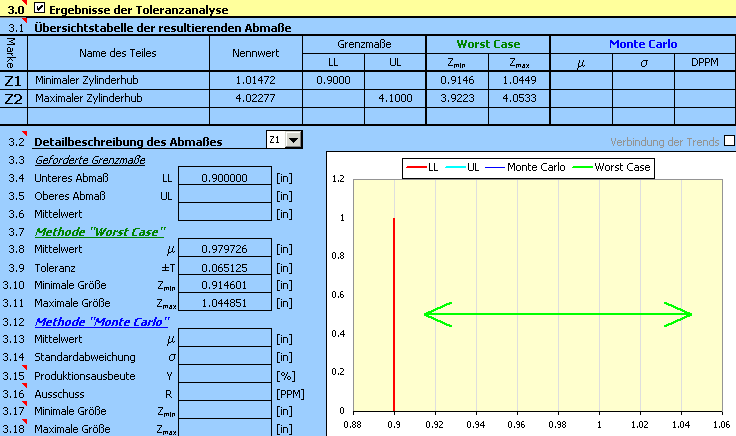
Die Berechnung dieser Aufgabe wird ähnlich der vorhergehenden und sie kann in folgende Schritte aufgeteilt werden:
1) Definieren Sie die Eingangswerte in der Tabelle [1.1], wie beim Beispiel A im Schritt 1) und 2).

2) Der Drehwinkel der Kurbelwelle für den wir den Hub des Zylinder bestimmen wollen, definieren wir in der ersten Zeile der Tabelle [2.1]als Konstante "Z1". In der zweiten Zeile der Tabelle "Z2" und dann geben wir die eigentliche Formel ein für die Hubberechnung. Die oben aufgeführte Berechnungsbeziehung muss an die Excelsyntax angepasst werden.
"=_E+_F-_D-(_B*COS(RADIANS(_Z1))+_C*(1-(_B/_C*SIN(RADIANS(_Z1))+_A/_C)^2)^0.5)"
3) In der Zeile [2.3] markieren wir das Kästchen bei der Berechnungsmethode "Worst Case". Aus der Auswahlliste [2.4] wählen wir die "gröbste" Teilung des Toleranzinterwalls (Auswahl "Min – Max").
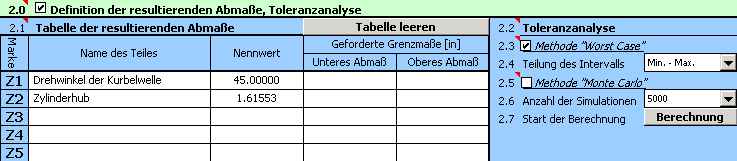
4) Mit dem Button in der Zeile [2.7] starten wir die Berechnung. Die Parameter des Hubes für den gegebenen Winkel finden wir dann im Abschnitt [3].
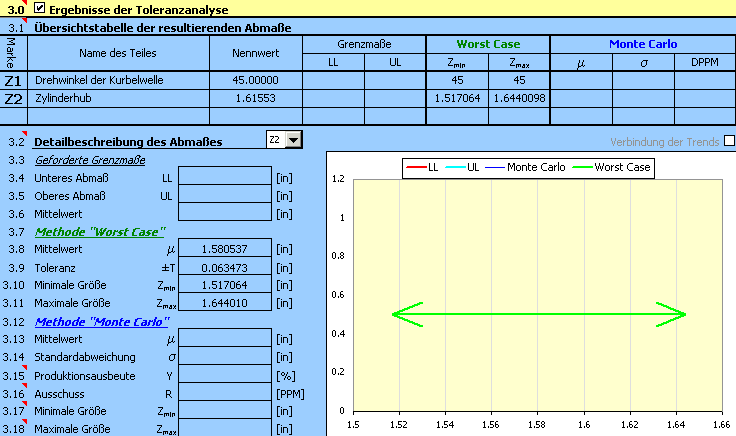
5) Für die Bestimmung des Hubes für einen anderen Wert des Drehwinkels wird es dann genügen, in der Tabelle [2.1] die Größe des Winkels zu ändern und die Berechnung mit dem Button [2.7] neu zu starten.
Schlagen Sie bei einem Einzelteil (siehe Skizze) die Produktionstoleranzen der Abmaße so vor, dass bei minimal 99.5% der gefertigten Teile der geforderte Mittenabstand von 160±0.0013“ eingehalten wird.
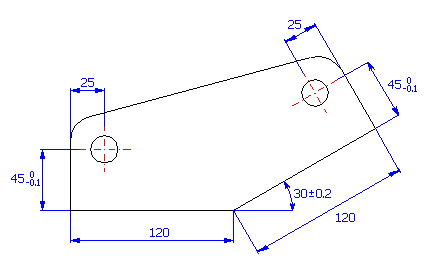
Wenn wir von der graphischen Darstellung der Maßkette ausgehen,
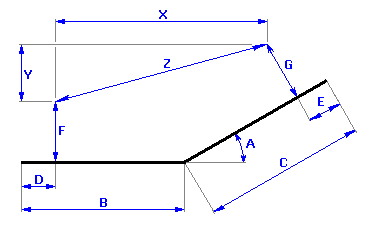
können wir beim gegebenen Einzelteil das resultierenden Abmaßes mit folgender Formel beschreiben:
![]()
wo für die Hilfsvariablen X, Y gilt:
![]()
![]()
Bei der Lösung dieser Aufgabe mit Hilfe der klassischen "Worst Case" Methode wäre es für die Einhaltung der geforderten Toleranz des resultierenden Abmaßes erforderlich bei den Abmaßen B,C,D,E die Toleranz ungefähr in der Genauigkeitsklasse 4 zu verwenden. Es wird deutlich, dass die Produktion mit dieser Genauigkeit unangemessen teuer wäre. In diesem fall wird es deshalb viel vorteilhafter sein, die statistische Methode der Berechnung zu verwenden. Diese Methoden erlauben die Fertigung dieses Teiles mit deutlich höheren Toleranzen bei kleinem (vorher festgelegten) Prozentsatz Ausschuss.
Die Lösung des Entwurfes der Maßkette können wir in folgende Schritte einteilen:
1) Definieren Sie alle Eingangswerte (Teilabmaße) der Maßkette in der Tabelle [1.1].
2) Dann geben wir für alle Abmaße die Produktionstoleranzen ein. Bei Abmaßen mit gegebenen Toleranzen stellen wir in der Eingabetabelle die vorgeschrieben Grenzwerte ein.
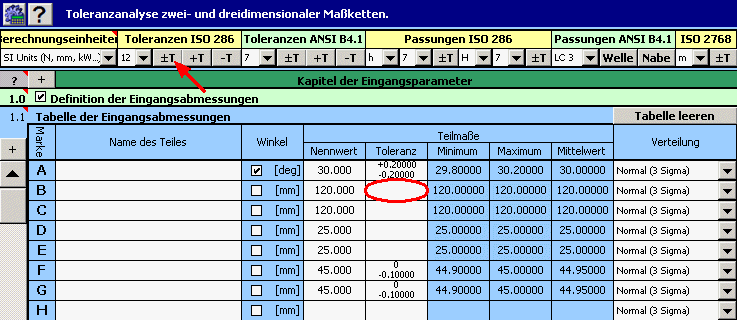
Bei den übrigen Abmaßen wählen wir vorläufig symmetrische Toleranzen im 12. Genauigkeitsgrad.
3) In den Pull-down Menüs der letzten Spalte der Tabelle wählen wir für alle Abmaße die Normalverteilung mit 3s Level der Prozesstauglichkeit.
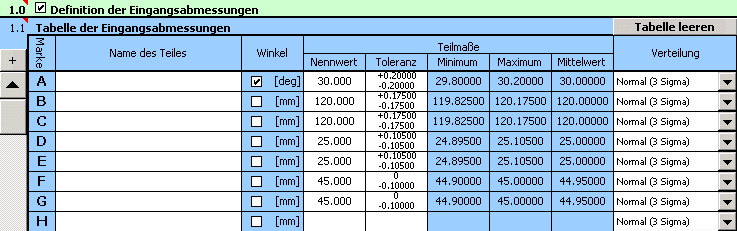
4) Definieren Sie in der Tabelle [2.1] die Parameter des resultierenden Abmaßes (Schließmaßes) der Maßkette. Aus Arbeitsersparnis- und Übersichtlichkeitsgründen teilen wir die Berechnungsformel in drei Teile (siehe oben). Die ersten beiden Zeilen der Tabelle verwenden wir für die Definition der Hilfsabmaße, die Parameter des gesuchten resultierenden Abmaßes platzieren wir in die Zeile "Z3". Die oben aufgeführten Berechnungsbeziehungen müssen an die Excelsyntax angepasst werden. In die zweite Spalte der Tabelle geben wir also in den einzelnen Zeilen folgenden Text ein:
1. Zeile "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
2. Zeile "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
3. Zeile "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) In der Zeile [2.5] markieren wir das Kästchen bei der Berechnungsmethode "Monte Carlo". Wählen Sie dann aus de Pull-down Menü [2.6] die geforderte Anzahl der Simulationen aus. Aus Gründen der Rechengeschwindigkeit wählen wir bei den Anfangsberechnungen gewöhnlich eine kleiner Anzahl Simulationen.
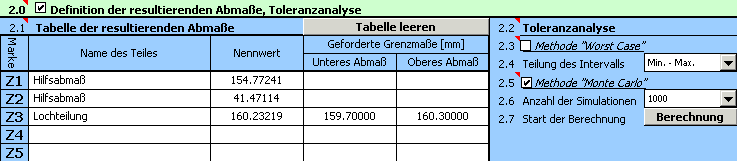
6) Mit dem Button in der Zeile [2.7] starten wir die eigentliche Berechnung (die Toleranzanalyse) der Maßkette. Die Parameter des resultierenden Abmaßes finden wir im Abschnitt [3].
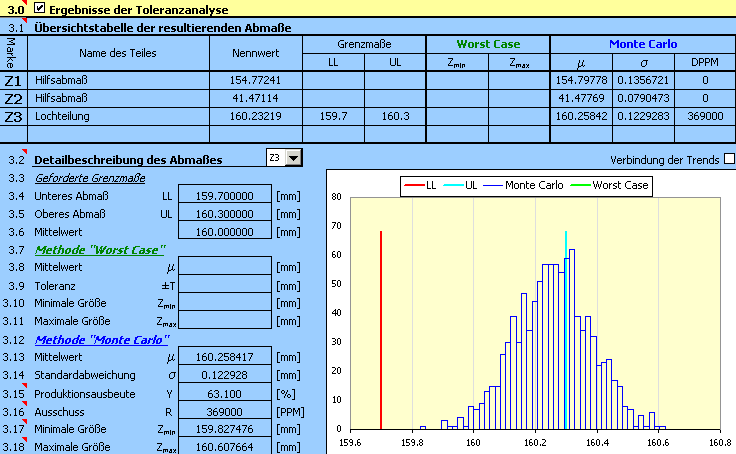
7) Das maßgebliche Kriterium für die Beurteilung der Qualität des Vorschlages wird die vorausgesetzte Prozessausbeute [3.15] bzw. die Anzahl der Ausschussteile [3.16] sein. In der Aufgabe ist die maximal erlaubte Anzahl der Ausschussteile mit 5000 pro Million gefertigter Teile angegeben. Die erreichten Zahlen sind um Größenordnungen höher, die vorgeschlagenen Toleranzen sind also ungeeignet.
Für den ungeeigneten Vorschlag könnte der nächste logische Schritt in der Verkleinerung der Größe der verwendeten Produktionstoleranzen liegen. Bei näherem Beurteilen dieses Vorschlages stellen wir aber fest, dass das Hauptproblem hier nicht die gewählte Toleranzgröße ist, aber vielmehr die falsche Zentrierung des Vorschlages. Für einen optimalen Lösungsvorschlag der Maßkette sollte sich der mittlerer Wert [3.13] so weit wie möglich der geforderten Dimension [3.6] annähern.
8) Im weiteren Schritt korrigieren wir also bei Beibehaltung der ursprünglichen Toleranzgrößen die Position der Toleranzfelder der Abmaße B,C,D,E. Mit wiederholten Korrekturen der Grenzwerte einzelner Abmaße mit darauf folgender Neuberechnung kommen wir schrittweise zu einer Lösung

für die der Vorschlag zentriert ist.

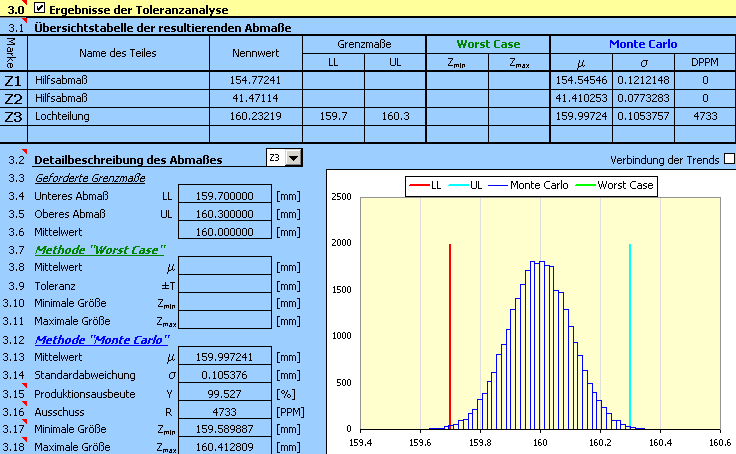
9) Auch wenn der Vorschlag nun richtig zentriert ist, gelang es nicht die geforderte Produktionsausbeute zu erreichen. Im nächsten Schritt wird es also notwendig sein zu einer Verkleinerung der Toleranzen, die im Schritt 2) vorläufig vorgeschlagen wurden, zu kommen. Bei der Wahl der Toleranzen der Abmaße B und C in der Genauigkeitsklasse 11 kommen wir nach der Zentrierung des Vorschlages zu einer ausreichenden Lösung,
die die Funktionsanforderungen der Aufgabe erfüllt.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
^