Toleranzanalyse einer 2D Maßkette mit der Methode "Monte Carlo".

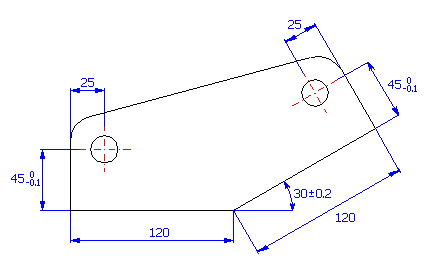
Schlagen Sie bei einem Einzelteil (siehe Skizze) die Produktionstoleranzen der Abmaße so vor, dass bei minimal 99.5% der gefertigten Teile der geforderte Mittenabstand von 160±0.0013“ eingehalten wird.

Lösung der Aufgabe.

Wenn wir von der graphischen Darstellung der Maßkette ausgehen,

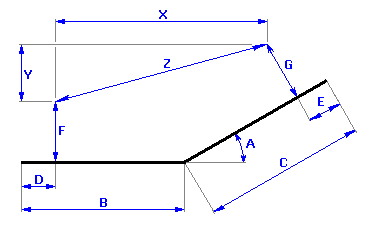
können wir beim gegebenen Einzelteil das resultierenden Abmaßes mit folgender Formel beschreiben:

wo für die Hilfsvariablen X, Y gilt:

Bei der Lösung dieser Aufgabe mit Hilfe der klassischen "Worst Case" Methode wäre es für die Einhaltung der geforderten Toleranz des resultierenden Abmaßes erforderlich bei den Abmaßen B,C,D,E die Toleranz ungefähr in der Genauigkeitsklasse 4 zu verwenden. Es wird deutlich, dass die Produktion mit dieser Genauigkeit unangemessen teuer wäre. In diesem fall wird es deshalb viel vorteilhafter sein, die statistische Methode der Berechnung zu verwenden. Diese Methoden erlauben die Fertigung dieses Teiles mit deutlich höheren Toleranzen bei kleinem (vorher festgelegten) Prozentsatz Ausschuss.

Vorschlag der Maßkette.

Die Lösung des Entwurfes der Maßkette können wir in folgende Schritte einteilen:

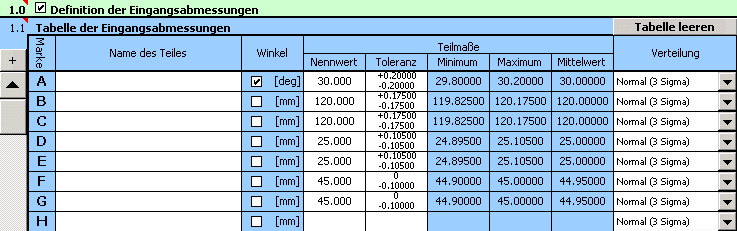
1) Definieren Sie alle Eingangswerte (Teilabmaße) der Maßkette in der Tabelle [1.1].

2) Dann geben wir für alle Abmaße die Produktionstoleranzen ein. Bei Abmaßen mit gegebenen Toleranzen stellen wir in der Eingabetabelle die vorgeschrieben Grenzwerte ein.

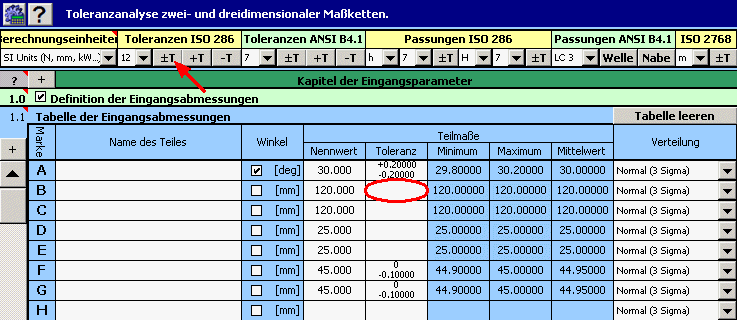
Bei den übrigen Abmaßen wählen wir vorläufig symmetrische Toleranzen im 12. Genauigkeitsgrad.

3) In den Pull-down Menüs der letzten Spalte der Tabelle wählen wir für alle Abmaße die Normalverteilung mit 3s Level der Prozesstauglichkeit.

4) Definieren Sie in der Tabelle [2.1] die Parameter des resultierenden Abmaßes (Schließmaßes) der Maßkette. Aus Arbeitsersparnis- und Übersichtlichkeitsgründen teilen wir die Berechnungsformel in drei Teile (siehe oben). Die ersten beiden Zeilen der Tabelle verwenden wir für die Definition der Hilfsabmaße, die Parameter des gesuchten resultierenden Abmaßes platzieren wir in die Zeile "Z3". Die oben aufgeführten Berechnungsbeziehungen müssen an die Excelsyntax angepasst werden. In die zweite Spalte der Tabelle geben wir also in den einzelnen Zeilen folgenden Text ein:

1. Zeile "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"

2. Zeile "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"

3. Zeile "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"

5) In der Zeile [2.5] markieren wir das Kästchen bei der Berechnungsmethode "Monte Carlo". Wählen Sie dann aus de Pull-down Menü [2.6] die geforderte Anzahl der Simulationen aus. Aus Gründen der Rechengeschwindigkeit wählen wir bei den Anfangsberechnungen gewöhnlich eine kleiner Anzahl Simulationen.

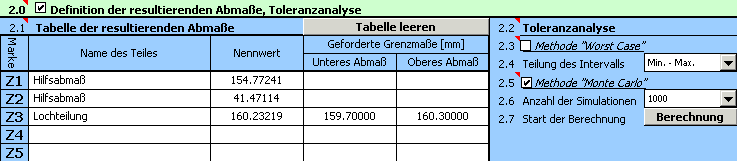
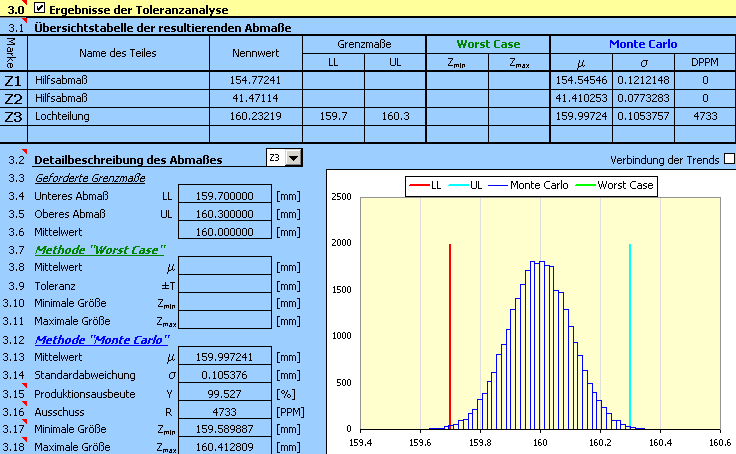
6) Mit dem Button in der Zeile [2.7] starten wir die eigentliche Berechnung (die Toleranzanalyse) der Maßkette. Die Parameter des resultierenden Abmaßes finden wir im Abschnitt [3].

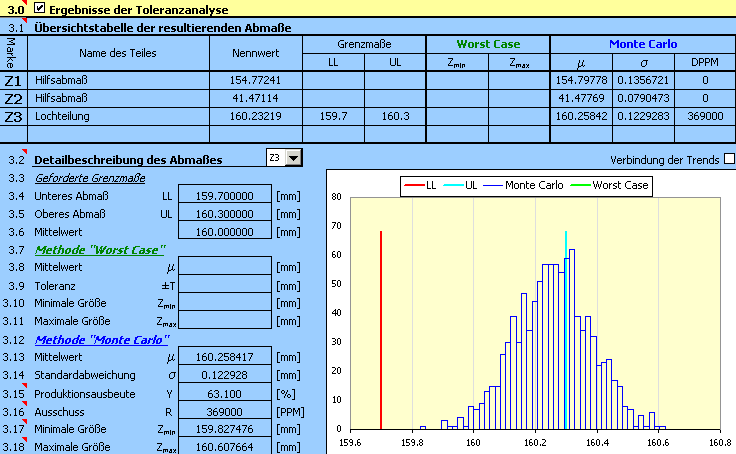
7) Das maßgebliche Kriterium für die Beurteilung der Qualität des Vorschlages wird die vorausgesetzte Prozessausbeute [3.15] bzw. die Anzahl der Ausschussteile [3.16] sein. In der Aufgabe ist die maximal erlaubte Anzahl der Ausschussteile mit 5000 pro Million gefertigter Teile angegeben. Die erreichten Zahlen sind um Größenordnungen höher, die vorgeschlagenen Toleranzen sind also ungeeignet.

Für den ungeeigneten Vorschlag könnte der nächste logische Schritt in der Verkleinerung der Größe der verwendeten Produktionstoleranzen liegen. Bei näherem Beurteilen dieses Vorschlages stellen wir aber fest, dass das Hauptproblem hier nicht die gewählte Toleranzgröße ist, aber vielmehr die falsche Zentrierung des Vorschlages. Für einen optimalen Lösungsvorschlag der Maßkette sollte sich der mittlerer Wert [3.13] so weit wie möglich der geforderten Dimension [3.6] annähern.

8) Im weiteren Schritt korrigieren wir also bei Beibehaltung der ursprünglichen Toleranzgrößen die Position der Toleranzfelder der Abmaße B,C,D,E. Mit wiederholten Korrekturen der Grenzwerte einzelner Abmaße mit darauf folgender Neuberechnung kommen wir schrittweise zu einer Lösung

für die der Vorschlag zentriert ist.

Tipp: Bei der Zentrierung eines Vorschlages kann es vorteilhafter sein die Methode "Worst Case" zu verwenden, die genauere Ergebnisse liefert und bei einer kleinen Anzahl der Eingangsabmaße auch wesentlich schneller ist.

9) Auch wenn der Vorschlag nun richtig zentriert ist, gelang es nicht die geforderte Produktionsausbeute zu erreichen. Im nächsten Schritt wird es also notwendig sein zu einer Verkleinerung der Toleranzen, die im Schritt 2) vorläufig vorgeschlagen wurden, zu kommen. Bei der Wahl der Toleranzen der Abmaße B und C in der Genauigkeitsklasse 11 kommen wir nach der Zentrierung des Vorschlages zu einer ausreichenden Lösung,

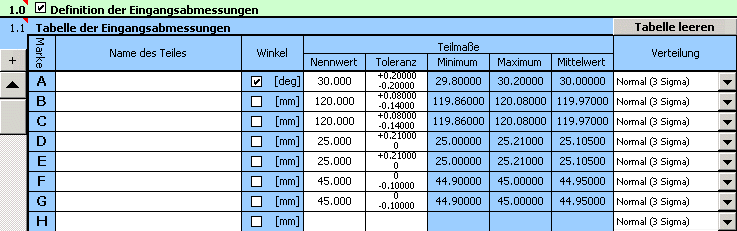
die die Funktionsanforderungen der Aufgabe erfüllt.

Hinweis: Die Methode "Monte Carlo" gehört zu den statistischen Methoden, die Qualität der erreichten Ergebnisse wird also von der Anzahl durchgeführter Simulationen abhängig sein. Mit der Schrittweisen Präzisierung des Vorschlages ist es deshalb vorteilhaft auch die Anzahl der durchzuführenden Simulationen [2.6] zu erhöhen. Bei den Endberechnungen sollte die Anzahl der Simulationen nicht kleiner als ca. 30000 sein.