Toleranzanalyse eines kinematischen Mechanismus mit der Methode
"Worst Case".Toleranzanalyse eines kinematischen Mechanismus mit der Methode
"Worst Case".Untersuchen Sie für einen exzentrischen Hebelmechanismus eines Kolbenkompressors
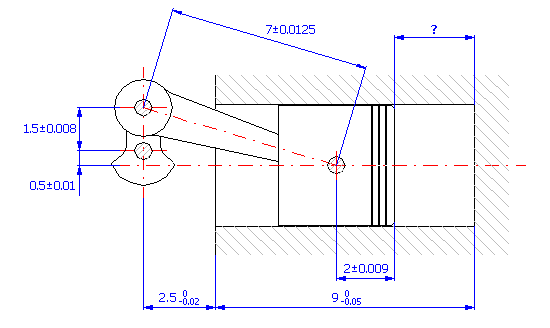
Wenn wir von der graphischen Darstellung der Maßkette ausgehen,
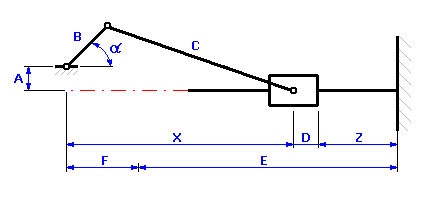
können wir bei gegebenem kinematischem Mechanismus die Größe des Zylinderhubs so beschreiben:
wo die Lage des Zylinders zu der Achse der Kurbelwelle X eine Kinematische Größe ist, die vom Drehwinkel der Kurbelwelle a abhängt. Für einen exzentrischen Kurbelmechanismus, wie er im vorhergehendem Bild dargestellt ist, können wir für die Bestimmung der Lage des Zylinders folgende Beziehung verwenden:
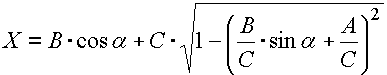
Die Grenzlagen des Zylinders auf die Achse der Kurbelwelle bezogen sind aus dem folgenden Schema deutlich
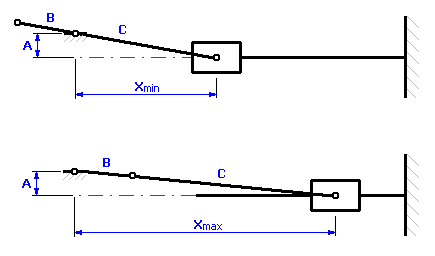
und können mit diesen Beziehungen beschrieben werden:
Die Lösung der Toleranzanalyse des kinematischen Mechanismus können wir in folgende Schritte einteilen:
1) Definieren Sie alle Eingangswerte (Teilabmaße) der Maßkette in der Tabelle [1.1].
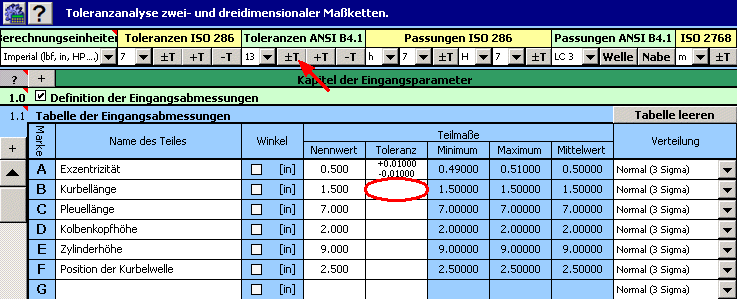
2) Für die einzelnen Abmaße geben wir dann die vorgeschriebenen Produktionstoleranzen ein. Bei den Abmaßen B,C,D sind genormte symmetrische Toleranzen nach ANSI B4.1 in der 13ten Toleranzklasse vorgeschrieben. Für ihre Eingabe in die Tabelle können wir die automatische Toleranzauswahl verwenden.
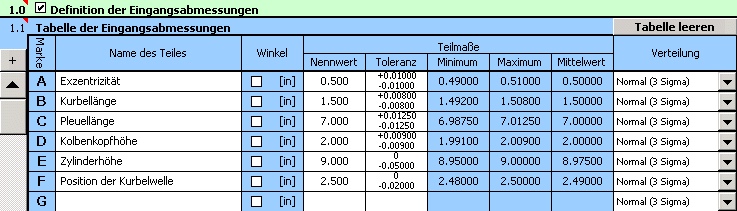
3) Definieren Sie alle Parameter der resultierenden Abmaße (Schließmaße) der Maßkette in der Tabelle [2.1]. Die Berechnungsbeziehungen für den minimalen und maximalen Zylinderhub, die im vorhergehendem Abschnitt definiert wurden, müssen an die Syntax von Excel angepasst werden. In die zweite Spalte der Tabelle geben wir für den minimalen Zylinderhub die Formel: "=_E+_F-_D-((_C+_B)^2-_A^2)^0.5" ein, für den maximalen Zylinderhub: "=_E+_F-_D-((_C-_B)^2-_A^2)^0.5".
4) In der Zeile [2.3] markieren wir das Kästchen bei der Berechnungsmethode "Worst Case". Aus der Auswahlliste [2.4] wählen wir die "gröbste" Teilung des Toleranzinterwalls (Auswahl "Min – Max"), die für die gegebene Aufgabe ausreichend ist.
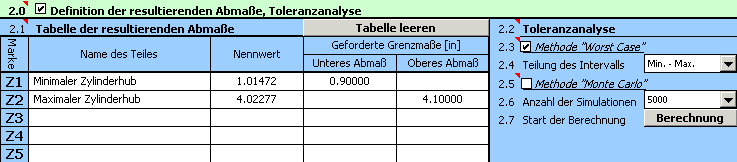
5) Mit dem Button in der Zeile [2.7] starten wir die eigentliche Berechnung (die Toleranzanalyse) der Maßkette. Die Grenzwerte des Hubes finden wir dann im Abschnitt [3].
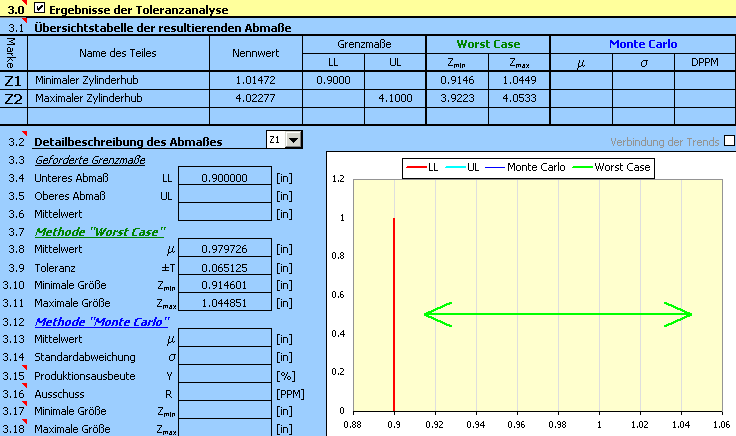
Die Berechnung dieser Aufgabe wird ähnlich der vorhergehenden und sie kann in folgende Schritte aufgeteilt werden:
1) Definieren Sie die Eingangswerte in der Tabelle [1.1], wie beim Beispiel A im Schritt 1) und 2).
2) Der Drehwinkel der Kurbelwelle für den wir den Hub des Zylinder bestimmen wollen, definieren wir in der ersten Zeile der Tabelle [2.1]als Konstante "Z1". In der zweiten Zeile der Tabelle "Z2" und dann geben wir die eigentliche Formel ein für die Hubberechnung. Die oben aufgeführte Berechnungsbeziehung muss an die Excelsyntax angepasst werden.
"=_E+_F-_D-(_B*COS(RADIANS(_Z1))+_C*(1-(_B/_C*SIN(RADIANS(_Z1))+_A/_C)^2)^0.5)"
3) In der Zeile [2.3] markieren wir das Kästchen bei der Berechnungsmethode "Worst Case". Aus der Auswahlliste [2.4] wählen wir die "gröbste" Teilung des Toleranzinterwalls (Auswahl "Min – Max").
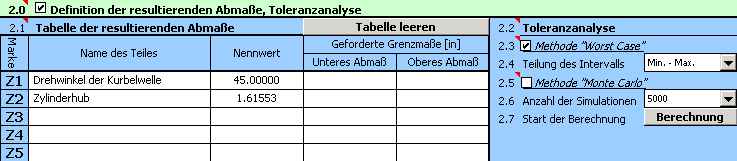
4) Mit dem Button in der Zeile [2.7] starten wir die Berechnung. Die Parameter des Hubes für den gegebenen Winkel finden wir dann im Abschnitt [3].
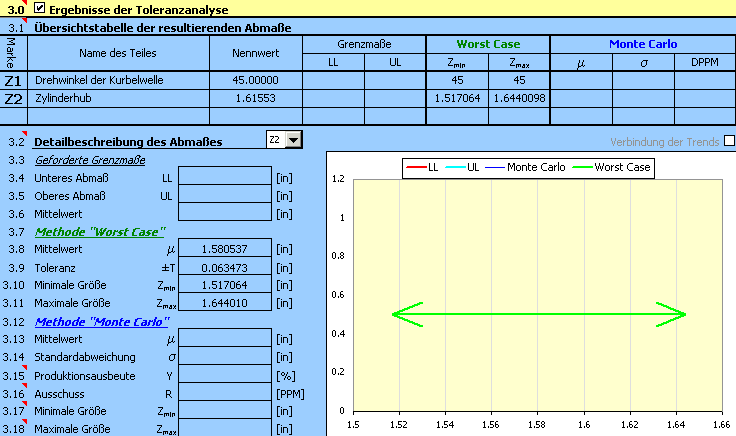
5) Für die Bestimmung des Hubes für einen anderen Wert des Drehwinkels wird es dann genügen, in der Tabelle [2.1] die Größe des Winkels zu ändern und die Berechnung mit dem Button [2.7] neu zu starten.