Program je určen pro toleranční analýzu rovinných (2D) a prostorových (3D) rozměrových řetězců. Program řeší následující úlohy:
Toleranční analýza rozměrového řetězce metodou "Worst case".
Toleranční analýza rozměrového řetězce metodou "Monte Carlo"
Při návrhu rozměrového řetězce umožňuje výpočet pracovat s normalizovanými hodnotami tolerancí.
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné
literatury a norem ANSI, ISO, DIN a dalších.
Seznam norem: ANSI B4.1, ISO 286, ISO 2768, DIN 7186
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
Rozměrový řetězec je soubor na sobě závislých rozměrů, které na sebe navazují tak, že tvoří geometricky uzavřený obvod. Mohou to být rozměry určující vzájemnou polohu prvků na jedné součásti, nebo rozměry několika součástí v montážní jednotce.
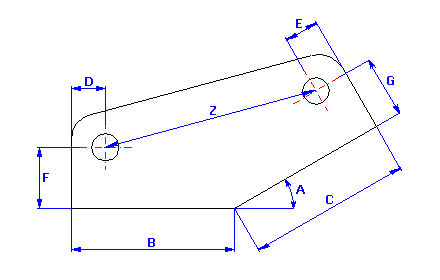
Rozměrový řetězec je sestaven z jednotlivých dílčích členů
(vstupních rozměrů) a ukončen uzavíracím členem (výsledným
rozměrem). Dílčí členy (A,B,C,..) jsou rozměry, které jsou na výkrese přímo
zakótovány nebo vyplývají z předcházejících výrobních popř. montážních
operací. Uzavírací člen (Z) představuje v daném řetězci výsledný výrobní
nebo montážní rozměr, který vyjde skládáním dílčích rozměrů jako
nekótovaný výrobní rozměr součásti, resp. jako montážní vůle nebo přesah.
Velikost, tolerance a mezní úchylky výsledného rozměru pak přímo závisí
na velikosti a toleranci dílčích rozměrů. Podle vzájemné polohy jednotlivých
členů rozlišujeme tři typy rozměrových řetězců:
- Lineární řetězce (1D) - obsahují pouze rovnoběžné rozměry
- Rovinné řetězce (2D) - rozměry jsou rozloženy v jedné nebo několika
rovnoběžných rovinách
- Prostorové řetězce (3D) - rozměry leží v nerovnoběžných rovinách
Tento výpočet je určen pro toleranční analýzu rovinných a prostorových rozměrových
řetězců.
Při řešení tolerančních vztahů v rozměrových řetězcích se vyskytují úlohy dvojího typu:
Pro řešení tolerančních
vztahů v rozměrových řetězcích jsou v tomto programu používány dvě výpočtové
metody:
- metoda "Worst Case"
- metoda "Monte Carlo"
Volba způsobu výpočtu tolerancí a mezních úchylek členů rozměrového
řetězce má vliv na výrobní přesnost a montážní zaměnitelnost součástí.
Závisí na něm proto hospodárnost výroby a provozu.
Nejčastěji používaná metoda, někdy též označovaná jako metoda výpočtu na maximum - minimum. Vychází z podmínky dodržení požadované mezní úchylky uzavíracího členu pro jakoukoliv kombinaci skutečných rozměrů dílčích členů. Tato metoda zaručuje úplnou montážní a provozní zaměnitelnost součástí. Při požadavku větší přesnosti uzavíracího členu však vede na příliš úzké tolerance dílčích členů, tedy i k vysokým výrobním nákladům. Metoda "Worst Case" je proto vhodná k řešení rozměrových obvodů s malým počtem členů nebo tehdy, je-li přípustná hrubší tolerance výsledného rozměru. Nejčastěji je používána v kusové nebo malosériové výrobě.
Úkolem metody "Worst Case" je nalezení minimální a maximální hodnoty, jichž může výsledný rozměr nabývat pro libovolnou kombinaci skutečných vstupních rozměrů. Algoritmus výpočtu je založen na postupném testování všech existujících kombinací různých (předem vybraných) hodnot vstupních rozměrů. U běžných rozměrových řetězců nabývá výsledný rozměr svých mezních hodnot obvykle pouze v rámci určité kombinace mezních hodnot vstupních rozměrů. Při provádění toleranční analýzy se pak u většiny řešených příkladů můžeme omezit pouze na testování kombinací minimálních a maximálních rozměrů dílčích členů řetězce.
V malém procentu případů však výše uvedený předpoklad platit nebude, a pro nalezení mezních hodnot výsledného rozměru bude potřeba provádět výpočet i pro hodnoty vstupních rozměrů ležící uvnitř tolerančního intervalu. V programu je tato skutečnost ošetřena možností volby počtu testovaných hodnot vstupních rozměrů (dělení tolerančního intervalu).
Zvolený algoritmus výpočtu sice zaručuje metodě "Worst Case" vysokou úspěšnost při hledání mezních hodnot výsledného rozměru, zároveň však může vést k neúměrným nárokům na délku trvání výpočtu. Rychlost výpočtu bude záviset na celkovém počtu provedených výpočetních cyklů, potřebných pro otestování všech kombinací vstupních rozměrů. Počet těchto cyklů je závislý na zvoleném dělení tolerančního intervalu a roste geometrickou řadou s rostoucím počtem dílčích členů rozměrového řetězce. Matematicky je popsán vztahem:
![]()
kde:
c ... celkový počet výpočetních cyklů
n ... počet dílčích členů rozměrového řetězce
k ... počet testovaných hodnot u každého dílčího členu
Z výše uvedeného je zřejmé, že metoda "Worst Case" je určena pro řešení tolerančních vztahů především u méně komplikovaných rozměrových řetězců s menším počtem dílčích členů. Praktická použitelnost této metody je omezena výkonem počítače, počtem dílčích členů rozměrového řetězce a zvolenou 'jemností' dělení tolerančního intervalu.
Tato metoda patří mezi statistické metody výpočtu rozměrových řetězců. Statistické metody se zakládají na počtu pravděpodobností a předpokládají, že se při při náhodném výběru součástí během montáže vyskytují krajní hodnoty úchylek jen zřídka u více dílčích členů najednou, neboť jde o složenou pravděpodobnost. Stejně tak málo pravděpodobný bude výskyt krajní hodnoty úchylek při výrobě jednotlivých rozměrů na jedné součásti. S určitým, předem zvoleným rizikem vyřazení některých součástí lze tedy tolerance dílčích členů v rozměrovém řetězci zvětšit.
Metoda "Monte Carlo" zaručuje pouze částečnou montážní zaměnitelnost, s malým procentem nepříznivých případů (zmetků). Vzhledem k větším tolerancím dílčích rozměrů však vede ke snížení výrobních nákladů. Užívá se především v hromadné a velkosériové výrobě, kde úspory výrobních nákladů převáží zvýšené montážní a provozní náklady, vznikající v důsledku neúplné montážní zaměnitelností součástí.
Rozměry uzavíracího členu vykazují jistý rozptyl od středu tolerančního pole. Četnost výskytu jednotlivých rozměrů se přitom řídí zákony matematické statistiky. Úkolem metody "Monte Carlo" pak bude vyšetření právě této četnosti a určení předpokládané výtěžnosti výrobního procesu .
Metoda "Monte Carlo" je simulační metodou. Její algoritmus je založen na náhodném generování vstupních rozměrů v rámci zvolených tolerancí podle předepsaných distribučních funkcí. Pro takto vygenerovaný soubor vstupních rozměrů je následně proveden výpočet výsledných rozměrů. Tento proces se cyklicky opakuje pro předem zvolený počet simulací. Výsledkem simulace pak bude statistický soubor dat (výsledných rozměrů) standardně popisovaný středním rozměrem:
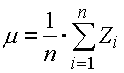
a směrodatnou odchylkou:
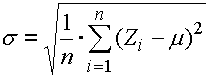
kde:
Zi ... velikost výsledného rozměru v i-tém cyklu simulace
n ... celkový počet simulačních cyklů
Pro účely zhodnocení četnosti výskytu výsledného rozměru je tento statistický soubor dále upraven do formy histogramu
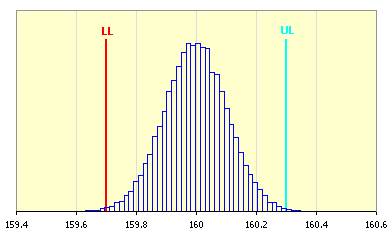
Směrodatným ukazatelem pro posouzení kvality návrhu rozměrového řetězce bude u metody "Monte Carlo" předpokládaná výrobní výtěžnost. Výrobní výtěžnost udává předpokládaný podíl výrobků vyhovujících požadavkům specifikace, to jest výrobků, u nichž bude výsledný rozměr uzavíracího členu v intervalu daném požadovanými krajními mezemi. V běžném strojírenství se obvykle považuje výrobní proces za uspokojivě způsobilý na úrovni 3s, to jest proces s minimální výtěžností 99.73%.
Přesnost (vypovídací hodnota) zjištěných statistických výsledků bude záviset na počtu provedených simulací. Je zřejmé, že s rostoucím počtem provedených simulací, roste také kvalita výsledků. Optimální počet simulací bude záviset na počtu vstupních rozměrů, velikosti jejich tolerancí a celkové složitosti rozměrového řetězce. V běžné praxi lze za rozumnou spodní hranici považovat u finálních výpočtů hodnotu cca. 30 až 50 tisíc provedených simulací.
Tato řádka slouží k přepínání soustavy jednotek výpočtu a volbě normalizovaných tolerancí.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě přepočítány všechny hodnoty.
Při definici rozměrového řetězce v odstavci [1.1] se zadává pro každý rozměr také jeho tolerance. Pro usnadnění práce je program vybaven nástrojem pro automatickou volbu normalizovaných tolerancí.
Program obsahuje sadu základních rozměrových tolerancí dle ISO resp. ANSI. S ohledem na typ úchylky a použitou normu jsou tolerance rozděleny do 5 skupin:
Každá skupina obsahuje v hlavičce sešitu sadu výběrových seznamů a tlačítek. V seznamech nastavte požadované parametry tolerance resp. uložení (stupeň přesnosti, toleranční pole, ..). Pomocí tlačítek pak vložíte rozměry zvolené tolerance na příslušné místo vstupní tabulky - do řádku s aktivní buňkou.
Tolerance dle ISO jsou normou definovány v [mm] a jsou určeny pro výpočet v SI jednotkách. Tolerance dle ANSI jsou definovány v [in] a určeny pro výpočet v jednotkách "Imperial". Při použití normalizovaných tolerancí definovaných v jiných jednotkách, než je nastaveno ve výpočtu, budou úchylky rozměru automaticky přepočteny a zaokrouhleny. Pro tolerování úhlových rozměrů je určena norma ISO 2768.
Úloha toleranční analýzy rozměrového řetězce se skládá z následujících kroků:
V tomto odstavci definujte parametry všech dílčích členů rozměrového řetězce.
Tato tabulka slouží k definici parametrů jednotlivých vstupních rozměrů (dílčích členů) rozměrového řetězce. Každému dílčímu členu přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Název členu je nepovinný parametr.
Sloupec 2 - Nastavením přepínačů zvolte typ rozměru. Implicitně je u všech členů rozměrového řetězce předpokládán délkový rozměr, zaškrtnutím tlačítka nastavíte pro zvolený dílčí člen úhlový rozměr. Zde nastavený typ rozměru má vliv na funkci automatické volby normalizovaných tolerancí.
Sloupec 3 - Zadejte nominální rozměr dílčího členu.
Sloupec 4 - Zadejte horní a dolní úchylku rozměru. Stisknutím vybraného tlačítka v hlavičce sešitu vložíte do tabulky úchylky příslušející zvolené toleranci. Pro tolerování délkových rozměrů můžete využít všechny zde uvedené normy, tolerance úhlových rozměrů jsou normalizovány v ISO 2768.
Sloupec 5..7 - V těchto sloupcích je dopočten minimální, maximální a střední rozměr všech dílčích členů.
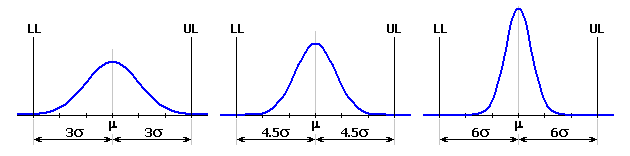
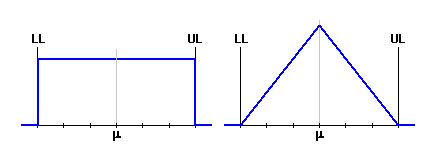
Sloupec 8 - Ve výběrovém seznamu zvolte typ rozdělení hustoty pravděpodobnosti. Standardně se k popisu výrobních procesů používá normální rozdělení, které ve většině případů nejlépe odpovídá skutečnému rozdělení náhodných veličin procesu.
V tomto odstavci definujte v tabulce [2.1] parametry všech uzavíracích členů rozměrového řetězce. V odstavci [2.2] vyberte požadovanou výpočetní metodu a nastavte její parametry. Vlastní výpočet spustíte tlačítkem na řádku [2.7].
Tato tabulka slouží k definici parametrů jednotlivých výsledných rozměrů (uzavíracích členů) rozměrového řetězce. Každému rozměru přísluší jeden řádek tabulky. Význam sloupců tabulky je zřejmý z následujícího popisu:
Sloupec 1 - Název členu je nepovinný parametr.
Sloupec 2 - Zadejte výpočetní vztah pomocí něhož je výsledný rozměr definován. Použité vzorce (algoritmy) musí dodržovat syntaxi Microsoft Excelu a mohou obsahovat všechny matematické výrazy a funkce Excelem definované (viz. nápověda Excelu). Pro označení vstupních rozměrů (dílčích členů) rozměrového řetězce používejte ve vzorcích symboly složené se znaku podtržítka a názvu rozměru ("_A", "_B", "_C", ...). Stejně tak pro názvy výsledných rozměrů používejte symboly "_Z1", "_Z2", ... Je-li výpočetní vztah definován bezchybně, bude na tomto místě v reálném čase dopočtena jmenovitá hodnota výsledného rozměru. V opačném případě zde Excel vypíše příslušnou chybovou hodnotu.
Sloupec 3, 4 - Definujte požadované mezní rozměry uzavíracího členu dané funkčními požadavky výrobku. Zde uváděné meze výsledného rozměru jsou nepovinné a slouží pouze k porovnání dosažených výsledků. U výpočtové metody "Monte Carlo" slouží povolené mezní hodnoty ke stanovení předpokládané výrobní výtěžnosti a počtu zmetků.
V tomto odstavci vyberte požadovanou výpočetní metodu a nastavte její parametry. Vlastní výpočet spustíte tlačítkem na řádku [2.7]. Kompletní výsledky provedené toleranční analýzy naleznete v odstavci [3].
Úkolem metody "Worst Case" je nalezení minimální a maximální hodnoty, jichž může výsledný rozměr nabývat pro libovolnou kombinaci skutečných vstupních rozměrů. Algoritmus výpočtu je založen na postupném testování všech existujících kombinací různých (předem vybraných) hodnot vstupních rozměrů. U běžných rozměrových řetězců nabývá výsledný rozměr svých mezních hodnot obvykle pouze v rámci určité kombinace mezních hodnot vstupních rozměrů. Při provádění toleranční analýzy se pak u většiny řešených příkladů můžeme omezit pouze na testování kombinací minimálních a maximálních rozměrů dílčích členů řetězce.
V malém procentu případů však výše uvedený předpoklad platit nebude, a pro nalezení mezních hodnot výsledného rozměru bude potřeba provádět výpočet i pro hodnoty vstupních rozměrů ležící uvnitř tolerančního intervalu. V programu je tato skutečnost ošetřena možností volby počtu testovaných hodnot vstupních rozměrů (dělení tolerančního intervalu). Požadovanou 'jemnost' dělení tolerančního intervalu nastavte ve výběrovém seznamu [2.4].
Zvolený algoritmus výpočtu sice zaručuje metodě "Worst Case" vysokou úspěšnost při hledání mezních hodnot výsledného rozměru, zároveň však může vézt k neúměrným nárokům na délku trvání výpočtu. Rychlost výpočtu bude záviset na celkovém počtu provedených výpočetních cyklů, potřebných pro otestování všech kombinací vstupních rozměrů. Počet těchto cyklů je závislý na zvoleném dělení tolerančního intervalu a roste geometrickou řadou s rostoucím počtem dílčích členů rozměrového řetězce.
Z výše uvedeného je zřejmé, že metoda "Worst Case" je určena pro řešení tolerančních vztahů především u méně komplikovaných rozměrových řetězců s menším počtem dílčích členů. Praktická použitelnost této metody je omezena výkonem počítače, počtem dílčích členů rozměrového řetězce a zvolenou 'jemností' dělení tolerančního intervalu.
Rozměry uzavíracího členu vykazují jistý rozptyl od středu tolerančního pole. Četnost výskytu jednotlivých rozměrů se přitom řídí zákony matematické statistiky. Úkolem metody "Monte Carlo" pak bude vyšetření právě této četnosti a určení předpokládané výtěžnosti výrobního procesu.
Metoda "Monte Carlo" je simulační metodou a patří mezi statistické metody. Její algoritmus je založen na náhodném generování vstupních rozměrů v rámci zvolených tolerancí podle předepsaných distribučních funkcí. Pro takto vygenerovaný soubor vstupních rozměrů je následně proveden výpočet výsledných rozměrů. Tento proces se cyklicky opakuje pro předem zvolený počet simulací. Výsledkem simulace pak bude statistický soubor dat (výsledných rozměrů) standardně popisovaný středním rozměrem m a směrodatnou odchylkou s. Směrodatným ukazatelem pro posouzení kvality návrhu rozměrového řetězce bude u metody "Monte Carlo" předpokládaná výrobní výtěžnost.
Přesnost (vypovídací hodnota) zjištěných statistických výsledků bude záviset na počtu provedených simulací. Je zřejmé, že s rostoucím počtem provedených simulací, roste také kvalita výsledků. Optimální počet simulací bude záviset na počtu vstupních rozměrů, velikosti jejich tolerancí a celkové složitosti rozměrového řetězce. V běžné praxi lze za rozumnou spodní hranici považovat u finálních výpočtů hodnotu cca. 30 až 50 tisíc provedených simulací. Požadovaný počet simulací nastavte ve výběrovém seznamu [2.6].
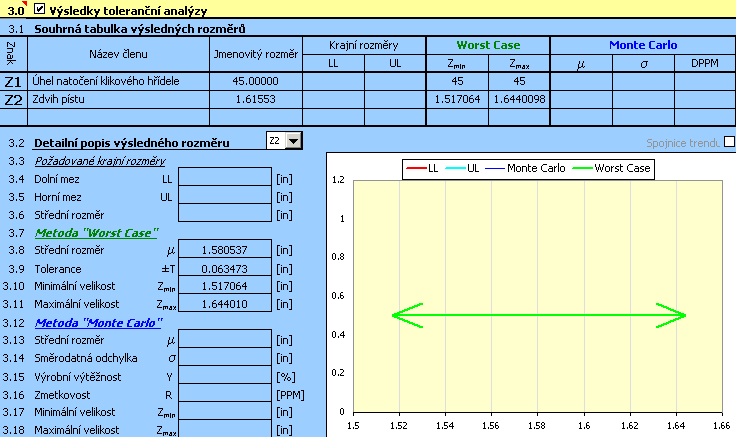
Po provedení výpočtu [2.7] jsou v tomto odstavci zobrazeny výsledky toleranční analýzy výše definovaného rozměrového řetězce. Odstavec je rozdělen do dvou částí. V tabulce [3.1] jsou v souhrnné formě vypsány základní informace o všech rozměrech definovaných v tabulce [2.1]. V odstavci [3.2] jsou v numerické a grafické formě prezentovány detailní parametry vybraného výsledného rozměru.
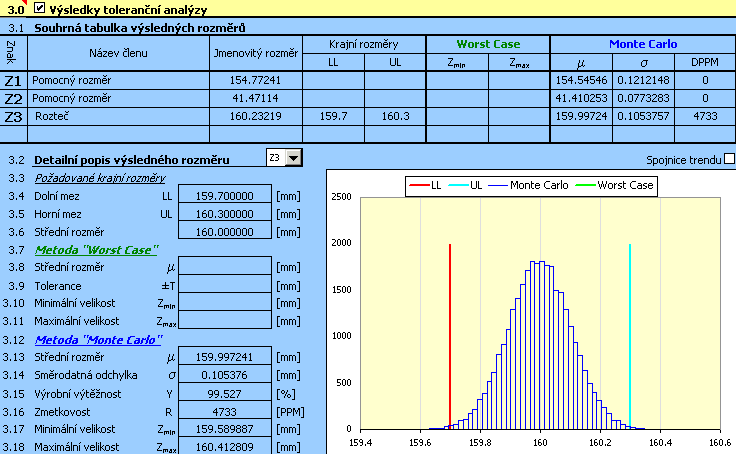
V této tabulce jsou v souhrnné formě vypsány základní informace o všech uzavíracích členech rozměrového řetězce definovaných v tabulce [2.1]. U výpočtu prováděného metodou "Worst Case" je výsledný rozměr popsán minimální a maximální nalezenou hodnotou. Při použití výpočtové metody "Monte Carlo" je statistický soubor charakterizující četnost výskytu výsledných rozměrů popsán v tabulce střední hodnotou, směrodatnou odchylkou a počtem zmetků na milion vyrobených součástí.
V tomto odstavci jsou v numerické a grafické formě prezentovány detailní parametry vybraného výsledného rozměru (uzavíracího členu) rozměrového řetězce. Požadovaný výsledný rozměr, jehož parametry chcete zobrazit, vyberte v rozbalovacím seznamu.
S ohledem na použitou výpočetní metodu jsou výsledky toleranční analýzy rozděleny do dvou částí. Pro posouzení kvality návrhu rozměrového řetězce jsou u metody "Worst Case" rozhodující mezní hodnoty, jichž může výsledný rozměr nabývat [3.10, 3.11]. U metody "Monte Carlo" je směrodatným ukazatelem předpokládaná výrobní výtěžnost [3.15] resp. počet zmetků na milion vyrobených součástí [3.16]. Četnost výskytu jednotlivých rozměrů je graficky znázorněna v přiloženém histogramu.
Výrobní výtěžnost udává předpokládaný podíl výrobků vyhovujících požadavkům specifikace, to jest výrobků, u nichž bude výsledný rozměr uzavíracího členu v intervalu daném požadovanými krajními mezemi. V běžném strojírenství se obvykle považuje výrobní proces za uspokojivě způsobilý na úrovni 3s, to jest proces s minimální výtěžností 99.73%.
Zmetkovost výrobního procesu udává předpokládaný počet nevyhovujících výrobků, to jest výrobků, u nichž bude výsledný rozměr uzavíracího členu ležet mimo interval daný požadovanými krajními mezemi. V běžném strojírenství se obvykle považuje výrobní proces za uspokojivě způsobilý na úrovni 3s, to jest proces s maximálním počtem 2700 vadných výrobků na milion vyrobených součástí.
Mezní rozměry zde uvedené mají pouze informativní charakter. Tyto meze neurčují skutečné krajní hodnoty jichž může výsledný rozměr nabývat. Udávají pouze minimální a maximální hodnotu rozměru nalezenou během simulačního výpočtu v rámci zvoleného počtu simulací. Pro nalezení skutečných mezních rozměrů je nutné použít výpočetní metodu "Worst Case".
Pro ilustraci problematiky toleranční analýzy rozměrových řetězců je nápověda doplněna praktickými ukázkami použití tohoto výpočtu:
Pro excentrický klikový mechanismus pístového kompresoru (viz. obrázek) vyšetřete
Vyjdeme-li z grafického znázornění rozměrového řetězce
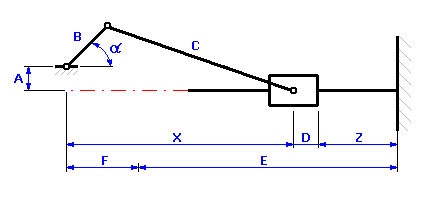
můžeme u daného kinematického mechanismu popsat velikost zdvihu pístu vztahem:
![]()
kde poloha pístu vůči ose klikového hřídele X je kinematickou veličinou, a bude závislá na úhlu natočení klikového hřídele a. Pro excentrický klikový mechanismus schématicky znázorněný na předchozím obrázku můžeme pro určení polohy pístu použít vztah:
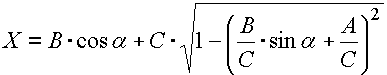
Krajní polohy pístu vůči ose klikového hřídele jsou zřejmé z následujícího schématu
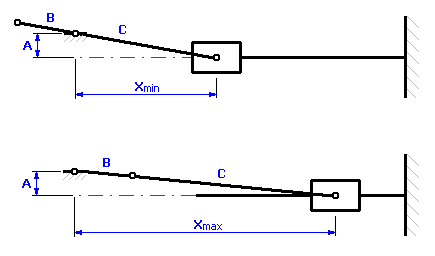
a můžeme je popsat vztahy:
![]()
Řešení úlohy toleranční analýzy kinematického mechanismu můžeme rozdělit do následujících kroků:
1) V tabulce [1.1] definujeme všechny vstupní rozměry (dílčí členy) rozměrového řetězce.
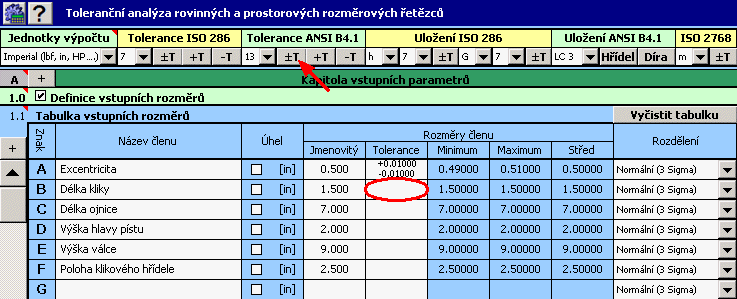
2) Pro jednotlivé rozměry dále zadáme předepsané výrobní tolerance. U rozměrů B,C,D jsou předepsány normalizované symetrické tolerance dle ANSI B4.1 ve 13-tém stupni přesnosti. Pro jejich zadání do tabulky můžeme využít funkci automatické volby tolerancí.

3) V tabulce [2.1] definujeme parametry výsledných rozměrů (uzavíracích členů) rozměrového řetězce. Výpočetní vztahy pro minimální a maximální zdvih pístu definované v předchozím odstavci je nutné upravit do tvaru (syntaxe) vyžadované Excelem. Do druhého sloupce tabulky tedy zadáme pro minimální zdvih pístu vztah "=_E+_F-_D-((_C+_B)^2-_A^2)^0.5", pro maximální zdvih pístu vztah "=_E+_F-_D-((_C-_B)^2-_A^2)^0.5"
4) V řádku [2.3] zaškrtneme přepínač u výpočetní metody "Worst Case". Ve výběrovém seznamu [2.4] dále zvolíme 'nejhrubší' dělení tolerančního intervalu (položku "Min. - Max."), které je pro danou úlohu dostačující.

5) Tlačítkem na řádku [2.7] spustíme vlastní výpočet (toleranční analýzu) rozměrového řetězce. Mezní hodnoty zdvihu pak nalezneme v odstavci [3].
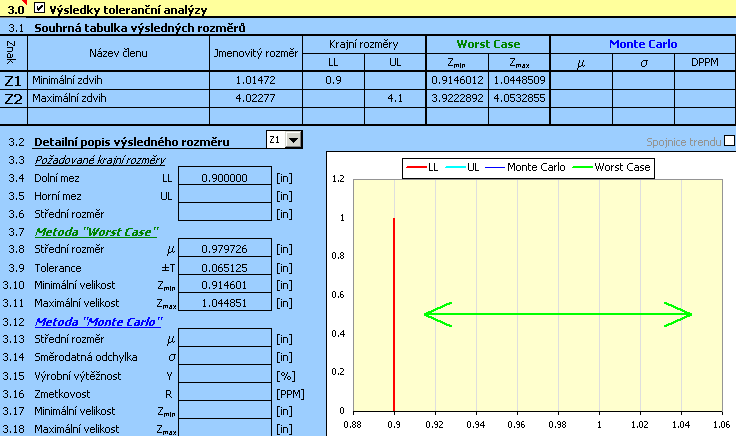
Postup řešení této úlohy bude obdobný jako u předchozí úlohy a můžeme ho rozdělit do následujících kroků:
1) Vstupní rozměry definujeme v tabulce [1.1] shodně jako u příkladu A v krocích 1) a 2).

2) Úhel natočení klikového hřídele, pro nějž chceme určit zdvih pístu, definujeme jako konstantu "Z1" v prvním řádku tabulky [2.1]. Ve druhém řádku tabulky "Z2" pak zadáme vlastní vztah pro výpočet zdvihu. Výše uvedený výpočetní vztah je nutné upravit do tvaru (syntaxe) vyžadované Excelem:
"=_E+_F-_D-(_B*COS(RADIANS(_Z1))+_C*(1-(_B/_C*SIN(RADIANS(_Z1))+_A/_C)^2)^0.5)"
3) V řádku [2.3] zaškrtneme přepínač u výpočetní metody "Worst Case". Ve výběrovém seznamu [2.4] dále zvolíme 'nejhrubší' dělení tolerančního intervalu (položku "Min. - Max.").

4) Tlačítkem na řádku [2.7] spustíme výpočet. Parametry zdvihu pro daný úhel pak nalezneme v odstavci [3].
5) K určení zdvihu pro odlišnou hodnotu úhlu natočení pak bude stačit změnit v tabulce [2.1] velikost úhlu a přepočítat úlohu tlačítkem [2.7].
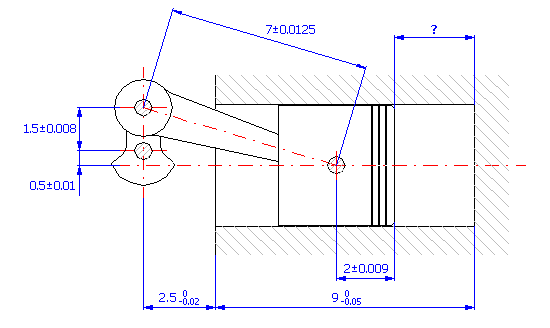
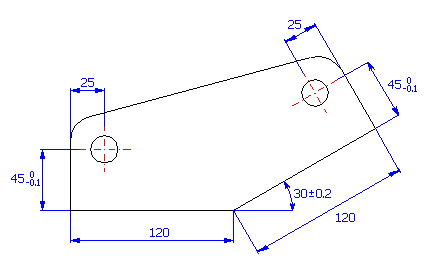
U součástky (viz. obrázek) navrhněte výrobní tolerance rozměrů tak, aby minimálně u 99.5% vyrobených součástek byla dodržena požadovaná velikost rozteče mezi středy děr 160±0.3 mm.
Vyjdeme-li z grafického znázornění rozměrového řetězce
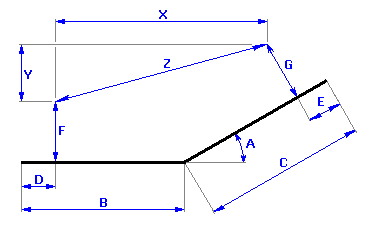
můžeme u dané součásti popsat výsledný rozměr vztahem:
![]()
kde pro pomocné proměnné X, Y bude platit:
![]()
![]()
Při řešení této úlohy klasickou metodou "Worst Case" by pro dodržení požadované tolerance výsledného rozměru bylo nutné u rozměrů B,C,D,E použít tolerance přibližně ve 4. stupni přesnosti. Je zřejmé, že výroba s takovouto přesností by byla neúměrně nákladná. V tomto případě bude proto mnohem výhodnější použít statistickou metodu výpočtu. Tyto metody umožňují vyrábět součástku s podstatně většími tolerancemi, při výskytu malého (předem zvoleného) procenta zmetků.
Řešení úlohy návrhu rozměrového řetězce můžeme rozdělit do následujících kroků:
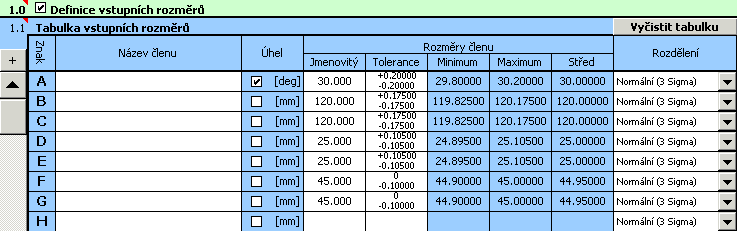
1) V tabulce [1.1] definujeme všechny vstupní rozměry (dílčí členy) rozměrového řetězce.
2) Pro všechny rozměry dále zadáme výrobní tolerance. U rozměrů s pevně danými tolerancemi nastavíme do vstupní tabulky předepsané úchylky rozměru.
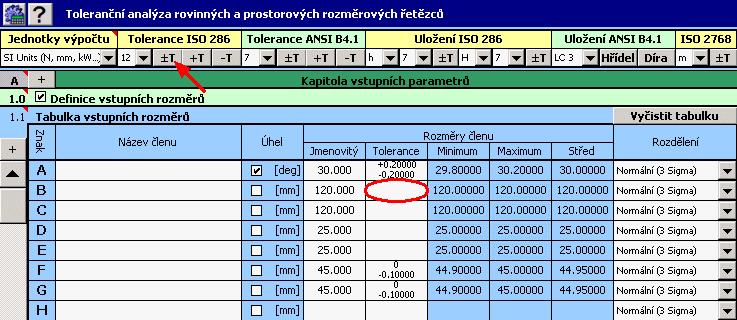
U zbylých rozměrů předběžně zvolíme symetrickou toleranci ve 12. stupni přesnosti.
3) Ve výběrových seznamech v posledním sloupci tabulky zvolíme pro všechny rozměry normální rozdělení s úrovní způsobilosti výrobního procesu 3s.
4) V tabulce [2.1] definujeme parametry výsledného rozměru (uzavíracího členu) rozměrového řetězce. Z důvodů usnadnění práce a zvýšení přehlednosti rozdělíme výpočetní vztah do tří částí (viz. výše). První dva řádky tabulky použijeme pro definici pomocných rozměrů, parametry hledaného výsledného rozměru pak umístíme do řádku "Z3". Výše uvedené výpočetní vztahy je nutné upravit do tvaru (syntaxe) vyžadované Excelem. Do druhého sloupce tabulky tedy v jednotlivých řádcích zadáme text:
1. řádek "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
2. řádek "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
3. řádek "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) V řádku [2.5] zaškrtneme přepínač u výpočetní metody "Monte Carlo". Ve výběrovém seznamu [2.6] dále nastavíme požadovaný počet simulací. Z důvodů rychlosti volíme v úvodních krocích návrhu obvykle menší počty simulací.

6) Tlačítkem na řádku [2.7] spustíme vlastní výpočet (toleranční analýzu) rozměrového řetězce. Parametry výsledného rozměru nalezneme v odstavci [3].
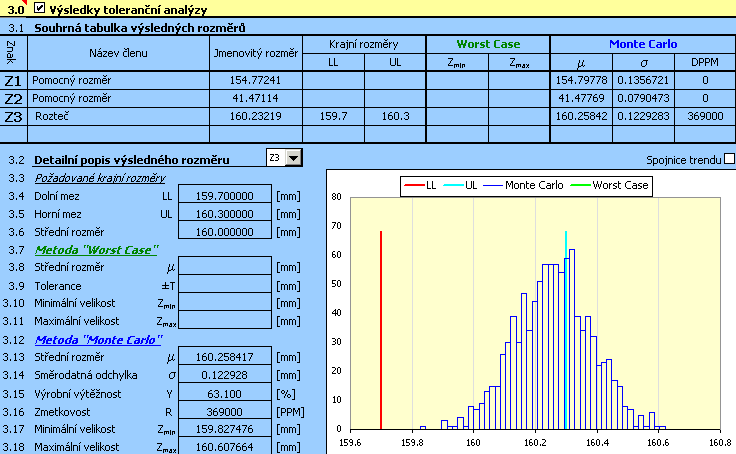
7) Směrodatným ukazatelem pro posouzení kvality návrhu bude předpokládaná výrobní výtěžnost [3.15] resp. počet zmetků [3.16]. Zadáním úlohy je předepsán maximální dovolený počet 5000 zmetků na milion vyrobených součástek. Dosažené výsledky jsou řádově vyšší, navržené tolerance tedy nevyhovují.
Pro nevyhovující návrh by dalším logickým krokem mohlo být zmenšení velikosti použitých výrobních tolerancí. Při bližším posouzení tohoto návrhu však zjistíme, že hlavním problémem zde nebude zvolená velikost tolerancí, ale spíše chybné vycentrování návrhu. U optimálně navrženého rozměrového řetězce by se měl střední rozměr [3.13] blížit požadovanému rozměru [3.6].
8) V dalším kroku tedy při zachování původně navržené velikosti tolerancí upravíme pozici tolerančních polí rozměrů B,C,D,E. Opakovanými úpravami úchylek jednotlivých rozměrů s následným přepočtením výsledků se postupně dopracujeme k řešení

pro které bude návrh vycentrován
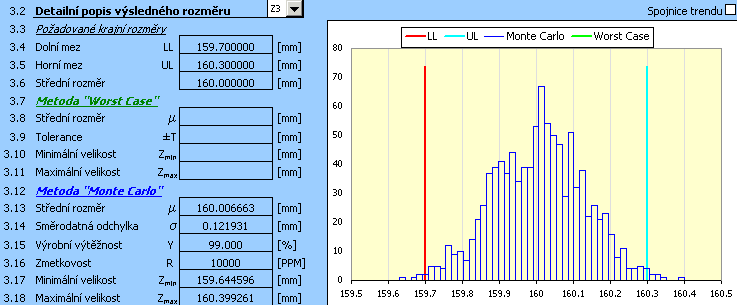
9) Přestože je nyní návrh již správně vycentrován, nepodařilo se dosáhnout požadované výrobní výtěžnosti. V dalším kroku bude proto potřeba přikročit ke zmenšení tolerancí předběžně navržených v kroku 2). Při volbě tolerance rozměrů B a C v 11. stupni přesnosti se po vycentrování návrhu dopracujeme k vyhovujícímu řešení,
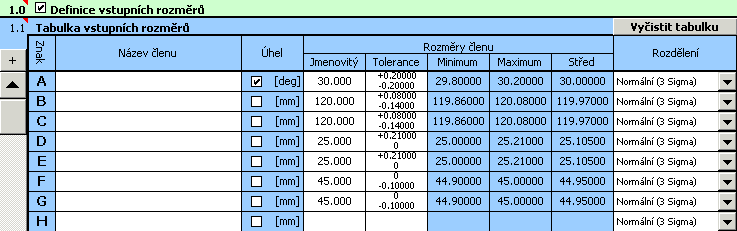
které splňuje funkční požadavky předepsané zadáním úlohy.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
^