Toleranční analýza 2D rozměrového řetězce metodou "Monte
Carlo".Toleranční analýza 2D rozměrového řetězce metodou "Monte
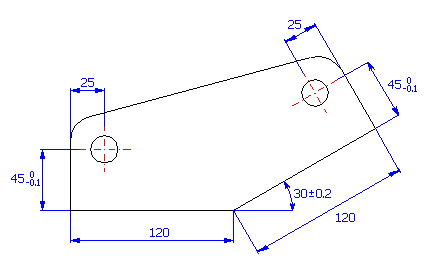
Carlo".U součástky (viz. obrázek) navrhněte výrobní tolerance rozměrů tak, aby minimálně u 99.5% vyrobených součástek byla dodržena požadovaná velikost rozteče mezi středy děr 160±0.3 mm.
Vyjdeme-li z grafického znázornění rozměrového řetězce
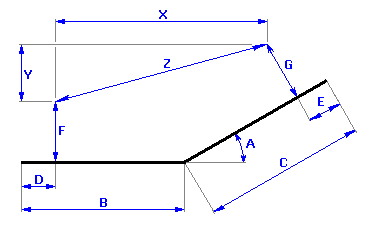
můžeme u dané součásti popsat výsledný rozměr vztahem:
kde pro pomocné proměnné X, Y bude platit:
Při řešení této úlohy klasickou metodou "Worst Case" by pro dodržení požadované tolerance výsledného rozměru bylo nutné u rozměrů B,C,D,E použít tolerance přibližně ve 4. stupni přesnosti. Je zřejmé, že výroba s takovouto přesností by byla neúměrně nákladná. V tomto případě bude proto mnohem výhodnější použít statistickou metodu výpočtu. Tyto metody umožňují vyrábět součástku s podstatně většími tolerancemi, při výskytu malého (předem zvoleného) procenta zmetků.
Řešení úlohy návrhu rozměrového řetězce můžeme rozdělit do následujících kroků:
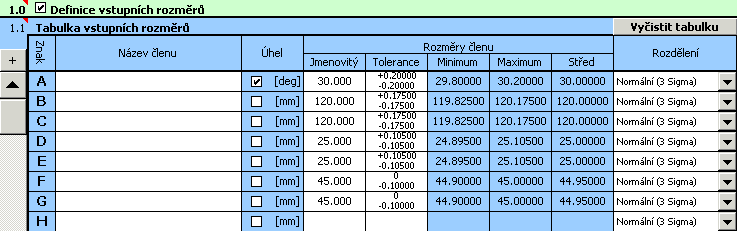
1) V tabulce [1.1] definujeme všechny vstupní rozměry (dílčí členy) rozměrového řetězce.
2) Pro všechny rozměry dále zadáme výrobní tolerance. U rozměrů s pevně danými tolerancemi nastavíme do vstupní tabulky předepsané úchylky rozměru.
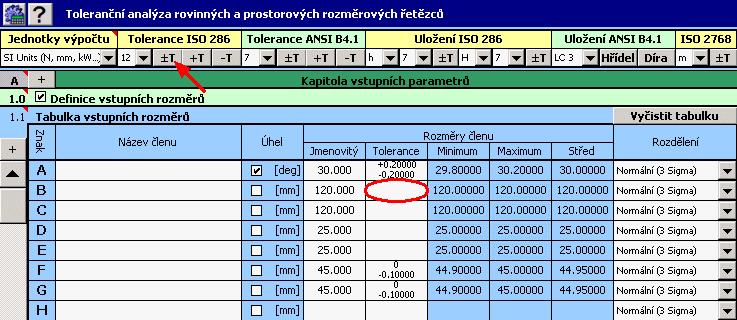
U zbylých rozměrů předběžně zvolíme symetrickou toleranci ve 12. stupni přesnosti.
3) Ve výběrových seznamech v posledním sloupci tabulky zvolíme pro všechny rozměry normální rozdělení s úrovní způsobilosti výrobního procesu 3s.
4) V tabulce [2.1] definujeme parametry výsledného rozměru (uzavíracího členu) rozměrového řetězce. Z důvodů usnadnění práce a zvýšení přehlednosti rozdělíme výpočetní vztah do tří částí (viz. výše). První dva řádky tabulky použijeme pro definici pomocných rozměrů, parametry hledaného výsledného rozměru pak umístíme do řádku "Z3". Výše uvedené výpočetní vztahy je nutné upravit do tvaru (syntaxe) vyžadované Excelem. Do druhého sloupce tabulky tedy v jednotlivých řádcích zadáme text:
1. řádek "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
2. řádek "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
3. řádek "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) V řádku [2.5] zaškrtneme přepínač u výpočetní metody "Monte Carlo". Ve výběrovém seznamu [2.6] dále nastavíme požadovaný počet simulací. Z důvodů rychlosti volíme v úvodních krocích návrhu obvykle menší počty simulací.
6) Tlačítkem na řádku [2.7] spustíme vlastní výpočet (toleranční analýzu) rozměrového řetězce. Parametry výsledného rozměru nalezneme v odstavci [3].
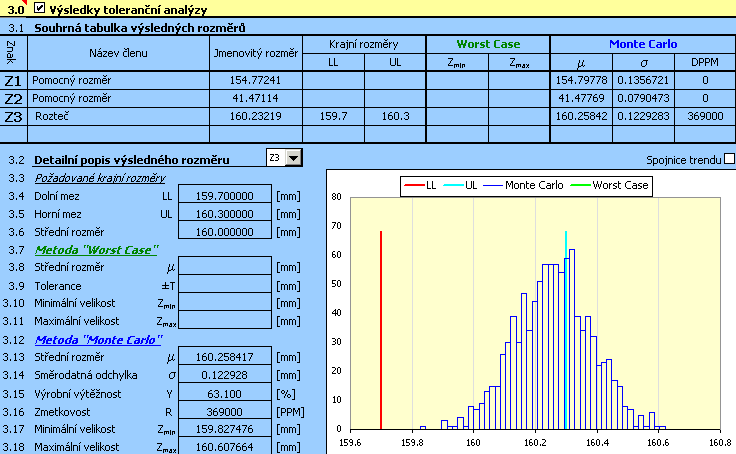
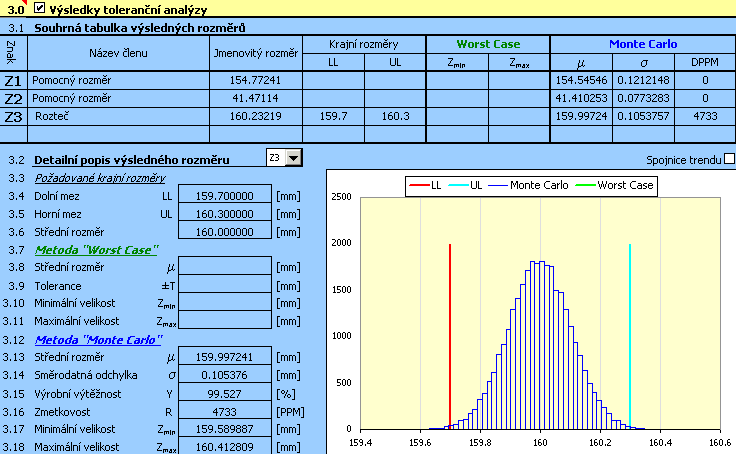
7) Směrodatným ukazatelem pro posouzení kvality návrhu bude předpokládaná výrobní výtěžnost [3.15] resp. počet zmetků [3.16]. Zadáním úlohy je předepsán maximální dovolený počet 5000 zmetků na milion vyrobených součástek. Dosažené výsledky jsou řádově vyšší, navržené tolerance tedy nevyhovují.
Pro nevyhovující návrh by dalším logickým krokem mohlo být zmenšení velikosti použitých výrobních tolerancí. Při bližším posouzení tohoto návrhu však zjistíme, že hlavním problémem zde nebude zvolená velikost tolerancí, ale spíše chybné vycentrování návrhu. U optimálně navrženého rozměrového řetězce by se měl střední rozměr [3.13] blížit požadovanému rozměru [3.6].
8) V dalším kroku tedy při zachování původně navržené velikosti tolerancí upravíme pozici tolerančních polí rozměrů B,C,D,E. Opakovanými úpravami úchylek jednotlivých rozměrů s následným přepočtením výsledků se postupně dopracujeme k řešení
pro které bude návrh vycentrován
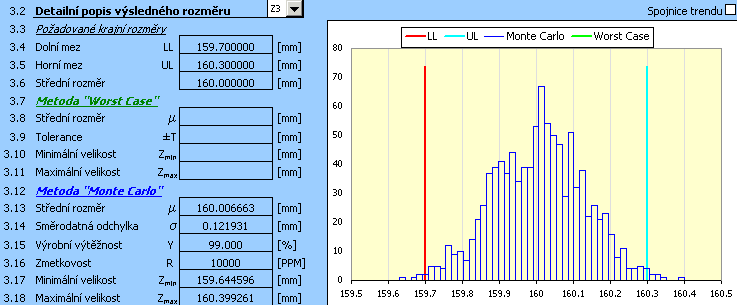
9) Přestože je nyní návrh již správně vycentrován, nepodařilo se dosáhnout požadované výrobní výtěžnosti. V dalším kroku bude proto potřeba přikročit ke zmenšení tolerancí předběžně navržených v kroku 2). Při volbě tolerance rozměrů B a C v 11. stupni přesnosti se po vycentrování návrhu dopracujeme k vyhovujícímu řešení,
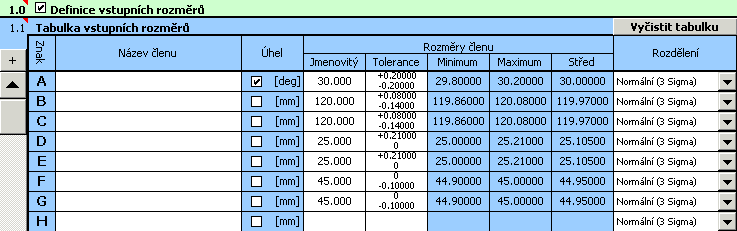
které splňuje funkční požadavky předepsané zadáním úlohy.
