Volants d'inertie

Contenu:

• Commande, structure et syntaxe des calculs.
• Information sur le projet.
• Théorie
• Procédure de calcul
• Unités de calcul, conversion d'unités [1]
• Conception et calcul du moment d'inertie et des dimensions du volant d'inertie [2]
• Analyse (calcul) du volant d'inertie [3]
• Courbes de couple des moteurs, puissances, moments d'inertie, poids, rendement [4]
• Mécanisme à manivelle [5]
• Exemple 1 - Conception du volant d'inertie d'un moteur à combustion interne monocylindre
• Exemple 2 - Conception d'un volant d'inertie pour un compresseur entraîné par un moteur électrique asynchrone
• Exemple 3 - Conception d'un volant d'inertie pour une presse à manivelle entraînée par un moteur électrique asynchrone
• Réglage des calculs, changement de langue
• Modifications du cahier de travail (calcul)
• Liste des normes, liste de la littérature

Volants d'inertie

Le programme est conçu pour la conception du volant d'inertie, son analyse et la détermination des dimensions. Dans le programme, il est également possible de résoudre le mécanisme à manivelle et de trouver les paramètres des moteurs asynchrones.

Le programme aborde les sujets suivants :

1. Calcul du moment d'inertie pour la machine sélectionnée.
2. Conception des dimensions du volant d'inertie en fonction du moment d'inertie requis.
3. Calcul du moment d'inertie à partir des dimensions du volant d'inertie.
4. Calcul du moment d'inertie de masses ayant des vitesses différentes (moment d'inertie réduit).
5. Calcul des contraintes des anneaux rotatifs.
6. Calcul du moment gyroscopique.
7. Calcul du moment d'inertie à partir du diagramme de charge et de l'irrégularité de fonctionnement requise.
8. Calcul de l'irrégularité de fonctionnement.
9. Conception du volant d'inertie en liaison avec le moteur.
10. Sélection et calcul des paramètres d'environ 1200 moteurs électriques asynchrones.
11. Solution de mécanisme à manivelle.

Les calculs utilisent des données, des procédures, des algorithmes et des informations provenant de la littérature, de normes et de catalogues d'entreprises.
[1] Strojně technická příručka (Svatopluk Černoch)
[2] Shigley’s Mechanical Engineering Design
[3] Strojírenská příručka (1992)
[4] Machinery’s Handbook (26th Edition)

Standards: EN 60034-30-1 :20 14
Rotating electrical machines — Part 30-1: Efficiency classes of line operated AC motors (IE code)
Machines Olectriques tournantes — Partie 30-1: Classes de rendement pour les moteurs a courant alternatif alimentés par le réseau (Code IE)
Drehende elektrische Maschinen — Teil 30-1: Wirkungrad-Klassifizierung von netzgespeisten Drehstrommotoren (IE-Code)

Company cataloques:Siemens, ABB Automation Products

 L’interface d’utilisateur.

 A télécharger.

 Tarif, Achat.

Commande, structure et syntaxe des calculs.

L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document "commande, structure et syntaxe des calculs".

Information sur le projet.

L'information sur le but, l'utilisation et la commande du paragraphe "information sur le projet" peut être trouvée dans le document "information sur le projet".

Théorie

Conception et calcul du moment d'inertie et des dimensions du volant d'inertie

Les formules suivantes sont utilisées dans les calculs.

Calcul approximatif du moment d'inertie du volant d'inertie

I = C * Pw / (n³ * δ)
C ... La constante de Güldner, qui détermine le type de machine
Pw ... puissance de la machine
n ... vitesse [/s]
δ ... le degré d'irrégularité de marche recommandé pour le type de machine.

Coefficient de fluctuation de la vitesse

Degré d'irrégularité de la course
δ = (ωmax - ωmin) / ωm
ωmax ... vitesse angulaire maximale
ωmin ... vitesse angulaire minimale
ωm = (ωmax - ωmin) / 2 ... vitesse angulaire moyenne

Moment d'inertie de l'anneau rotatif

I = 0.5 * Ro * Pi * b * (R⁴ - r⁴)
Ro ... densité
b ..... largeur du disque
R ..... rayon extérieur
r ...... rayon intérieur

Réduction du moment d'inertie

Si le système comporte des masses tournant à des vitesses différentes (rapport de vitesse), il est nécessaire de convertir leur moment d'inertie en moment d'inertie du volant d'inertie.
Ired = Σ I(i) * (n / n(i))².
I(i) ... moment d'inertie d'une masse tournant à une vitesse différente de celle du volant d'inertie
n ...... vitesse du volant d'inertie
n(i) ... vitesse de rotation d'une masse tournant à une vitesse différente de celle du volant d'inertie
Les moments d'inertie réduits peuvent alors être additionnés directement pour trouver le moment d'inertie total du système.

Contrainte tangentielle

σt = Ro * ω² * ((3 + ny) /8 ) * (r² + R² + r² * R² / rx² - (1 + 3 * ny) / (3 + ny) * rx²)
Ro ... densité
ω ... vitesse angulaire
ny ... constante de Poisson
R ..... rayon extérieur
r ...... rayon intérieur
rx .... le rayon auquel la contrainte est calculée

Rotation du volant d'inertie

Temps
t = (0,1047197533 * (n2 - n1) * I) / T
Énergie
E = 0,005483 * I * (n2² - n1²)
T ... Couple
I .... Moment d'inertie
n1,n2 ... vitesse

Moment gyroscopique

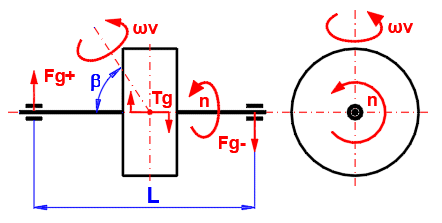
Tg = Pi * n * I * ωv / 30 * sin(β)
I .... Moment d'inertie du volant d'inertie
n ... vitesse du volant [/min]
β ... angle de l'axe de rotation du volant d'inertie
ωv ... vitesse angulaire de rotation du volant d'inertie

Analyse (calcul) du volant d'inertie

Dans les moteurs et les machines où le mouvement rotatif est converti en mouvement rectiligne et dans les machines où il n'y a pas de charge constante, des fluctuations de couple se produisent. Il n'y a pas d'équilibre constant entre les moments d'action (couple moteur, couple entraîné, forces inertielles, résistances passives). Cela modifie la vitesse angulaire pendant le cycle de travail. Pour réduire cette irrégularité, un volant d'inertie est utilisé comme accumulateur d'énergie, qu'il stocke en cas d'excès de couple et libère en cas de manque de couple.

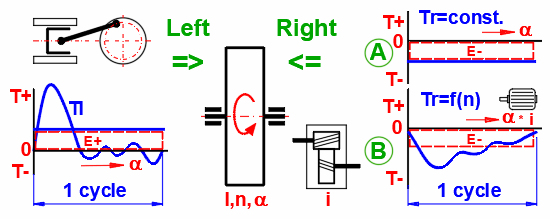
Une grande partie des machines a une allure de couple qui ne peut pas être décrite simplement de manière analytique. Par conséquent, des méthodes d'intégration numérique sont utilisées pour la solution. L'allure du couple sur le côté gauche est définie par le tableau des couples en fonction de la rotation du volant d'inertie. Le moment sur le côté droit peut être :

A. Constant
B. Dépendant de la vitesse du volant d'inertie (moteur électrique, générateur)
C. Ou bien il peut être défini par sa propre table ou fonction

Équation de base du mouvement :

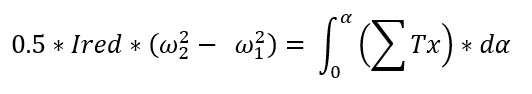
Ired … moment d'inertie réduit de toutes les masses en rotation
ω₁, ω₂ … vitesse angulaire au début et à la fin du cycle de travail
a … angle de rotation du volant d'inertie pendant le cycle de travail
da … rotation élémentaire du volant d'inertie
ΣTx ... somme de tous les moments appliqués (couple moteur, couple entraîné, forces inertielles, résistances passives)

L'objectif est de résoudre l'allure du couple du côté droit pour qu'elle satisfasse aux conditions (par exemple, caractéristique d'un moteur électrique asynchrone) et qu'en même temps la somme des énergies des côtés gauche et droit soit nulle (ω₁ = ω₂).

Un exemple peut être la dépendance du couple d'un moteur à combustion interne monocylindre à quatre temps à l'angle de rotation de la manivelle (voir la figure).

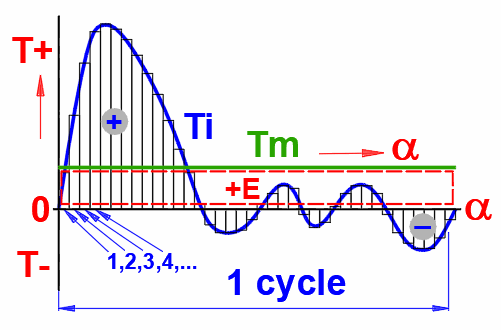
Où le calcul est effectué dans les étapes suivantes :

1) Intégration et calcul de l'énergie (division du cours Ti en n parties)

Tmid(j) = (Ti(j) + Ti(j+1)) / 2 ... <j = 1 ... n+1>
dE(j) = Tmid(j) * da ... <j = 1 ... n> ... pour chaque segment 1,2,3,4.....
da = a / n
dEsum = ΣdE(j) ... <j = 1 ... n>

2) Couple moyen

Tm = dEsum / a

3) Vitesse angulaire en chaque point

ω(j+1) = (ω(j) + 2 * dE'(j) / I)^0.5
dE'(j) = (Tmid(j) - Tm) * da
I ... le moment d'inertie du volant d'inertie et des masses en rotation qui y sont attachées.

4) Trouver les vitesses angulaires ωmin et ωmax à partir du champ ω(j) .... <j = 1 ... n+1>

ωmin = MIN (ω(j)) ... <j = 1 ... n+1>
ωmax = MAX (ω(j)) ... <j = 1 ... n+1>

5) Calcul de la vitesse angulaire moyenne

ωm = (ωmin + ωmax) / 2

6) Calcul du coefficient de fluctuation de la vitesse

δ = (ωmax - ωmin) / ωm
On peut aussi calculer le moment d'inertie à partir du coefficient de fluctuation de la vitesse
I = dEsum' / (δ * ωm^2)
dEsum' = ΣdE'(j) ... <j = 1 ... n>

Si, par exemple, on utilise un moteur asynchrone (générateur) à la place d'une valeur constante Tm dont le couple est dépendant des tours, on utilise successivement pour chaque étape la valeur de couple correspondant aux tours du volant. Chaque fois qu'une modification est apportée, l'ensemble du modèle est recalculé.

En fonction des données d'entrée (puissance du moteur, moment d'inertie, degrés d'irrégularité...), la solution converge vers l'équilibre généralement en quelques dizaines d'itérations.

L'analyse permet de résoudre/contrôler

- calcul précis du moment d'inertie pour le degré requis d'irrégularité de fonctionnement
- calcul de l'irrégularité de fonctionnement pour le moment d'inertie spécifié
- calcul de la vitesse, du couple, de l'énergie, de la puissance
- vérification de l'adéquation du moteur/générateur sélectionné (vitesse, puissance)

Exemple d'analyse d'un générateur asynchrone couplé à un moteur monocylindre à allumage par étincelle pour différentes irrégularités de fonctionnement delta.

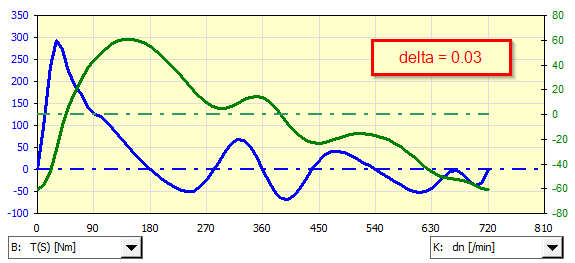
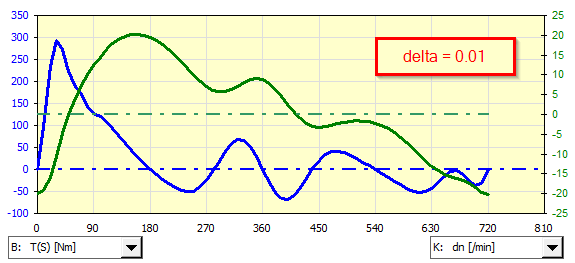
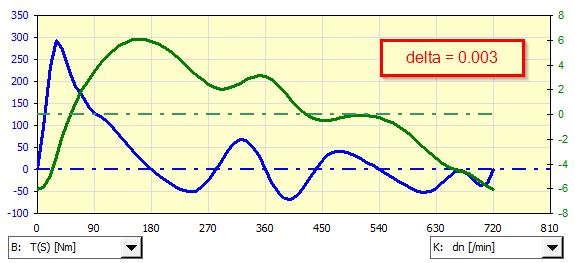
S'il est nécessaire d'utiliser un moteur asynchrone (générateur) autre que celui qui est prédéfini, ses caractéristiques peuvent être définies et utilisées dans l'itération.

Courbes de couple des moteurs

Dans le domaine des entraînements de machines et d'installations, le moteur le plus couramment utilisé est le moteur asynchrone (induction motor). Pour ce moteur, le couple varie avec la vitesse (de façon linéaire dans la plage de travail). Un tableau de paramètres pour n'importe quel moteur a été créé en comparant les catalogues de plusieurs fabricants.

Dans ce chapitre, vous trouverez les paramètres du moteur sélectionné (y compris les estimations du poids, du rendement et du moment d'inertie), la puissance et le couple pour les vitesses autres que la vitesse nominale.

Formules de base pour les moteurs à induction

Vitesse synchrone
ns = 2 * f * 60 / p
f ... fréquence du réseau électrique (60 Hz USA, Canada..., 50 Hz Europe)
p ... nombre de pôles du moteur

Vitesse nominale (vitesse asynchrone)
nr = (1 - s / 100) * ns
s ... glissement du moteur [%]

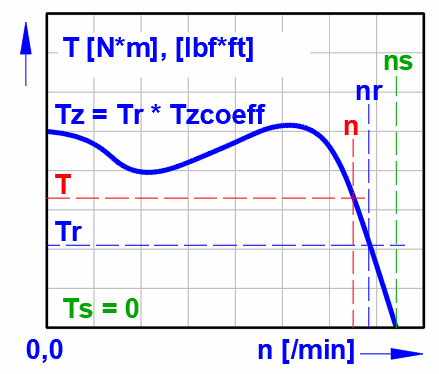
Couple nominal
Tr = Pr * 9550 / nr
Pr ... puissance nominale

Couple d'arrachement
Tz = Tr * Tzcoeff
Tzcoeff ... coefficient de couple d'arrachement
Pour les petits moteurs (≤ 30 kW), la valeur est de 2.5-3, pour les moteurs moyens 2-2.5, pour les gros moteurs 1-1.5.

Tuyau : Si vous avez besoin de la valeur du couple pour le moteur sélectionné et de la vitesse spécifiée lors de l'édition du classeur, utilisez les fonctions prédéfinies :
= linear2(n;T_4_nT) ... approxime linéairement et renvoie les valeurs de couple en fonction de la vitesse pour le moteur sélectionné au chapitre [4.0]

n ... vitesse du moteur tr/min
T_4_nT ... nom de la gamme avec la courbe T=f(n)

Mécanisme à manivelle

Pour convertir un mouvement rectiligne en mouvement rotatif (et vice versa), on utilise souvent un mécanisme à manivelle, généralement associé à un volant d'inertie. Pour la conception du volant d'inertie, il est alors nécessaire de connaître l'allure du couple. Pour calculer l'allure du couple, il est nécessaire de connaître la force de charge (Fp), les dimensions (L, R), la vitesse nombre de tours (n) et les poids des différentes parties (mp, m).

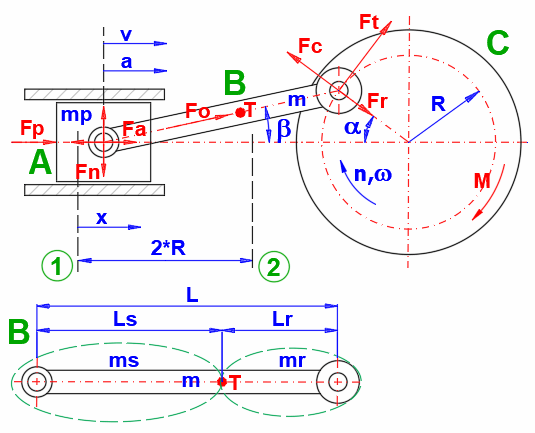
Les formules suivantes sont utilisées dans le calcul pour déterminer l'évolution du moment pendant la rotation du vilebrequin. La signification des différentes variables est indiquée sur la figure.
β = asin(R / L * sin(α))
λ = R / L
x = R * (1 - cos(α) + λ / 2 * sin(α)^2) ... distance du pivot supérieur (1)
v = R * ω * (sin(α) + λ * sin(α) * cos(α))
a = R * ω^2 * (cos(α) + λ * cos(2 * α))
ω =2 * Pi * n / 60
ms = Lr / L * m
mr = Ls / L * m
Fa = (m + ms) * a ... accélération/décélération des pièces en mouvement droit
Fn = Fp * tan(β) + Fa * tan(β)
Ft = Fp * (sin(α) + λ * sin(2 * α) + Fa * (sin(α) + λ * sin(2 * α)
Fo = Fp / cos(β)
Fr = Fo * cos(α + β)
Fc = mr * R * ω^2 ... force centrifuge de la bielle sur la manivelle
M = R * Ft ... moment de la force de charge Fp et de la force d'accélération/décélération Fa

Procédure de calcul :

Le calcul est destiné à la conception rapide du volant d'inertie et à son analyse.

Projet indicatif, paragraphe [2] :

- conception indicative du moment d'inertie du volant d'inertie en fonction du type et des paramètres de la machine
- conception des dimensions du volant d'inertie en fonction du moment d'inertie
- contrôle de la contrainte, contrôle de la vitesse maximale, contrôle du moment gyroscopique

Analyse détaillée, paragraphe [3] :

Si vous connaissez la courbe de moment de la machine pour laquelle vous voulez concevoir un volant d'inertie, définissez la courbe à l'aide d'un tableau. Vous déterminez rapidement le moment d'inertie requis pour l'irrégularité de fonctionnement requise ou l'irrégularité de fonctionnement pour le moment d'inertie spécifié (Analyse A).

Si vous devez résoudre un couple machine x moteur électrique (machine x générateur), utilisez Analyse B.

Tuyau : Essayez d'étudier les exemples à la fin de l'aide.

Unités de calcul, conversion d'unités [1]

Dans ce chapitre, vous définissez les unités de calcul.

1.1 Unités de calcul

Choisissez le système d'unités de calcul désiré sur la liste. Après changement d'unités, toutes les valeurs seront immédiatement corrigées.

1.2 Conversion d'unités

Ecrire la valeur que vous voulez convertir dans la case d'insertion du côté gauche. Choisir les unités à convertir et les unités de conversion à droite.

Conception et calcul du moment d'inertie et des dimensions du volant d'inertie [2]

- Calcul approximatif du moment d'inertie pour le type de machine sélectionné.
- Conception des dimensions du volant d'inertie en fonction du moment d'inertie.
- Calcul du moment d'inertie à partir des dimensions du volant d'inertie.
- Calcul de l'énergie du volant d'inertie en rotation, calcul de la contrainte maximale.
- Conversion des moments d'inertie de masses tournant à des vitesses différentes.
- Calcul du temps de rotation du volant d'inertie.
- Calcul du moment et des forces gyroscopiques.

2.1 Calcul approximatif du moment d'inertie du volant d'inertie

En fonction du type de machine, de la puissance et de la vitesse du volant d'inertie, il est possible d'estimer le moment d'inertie requis pour le volant d'inertie.

Sélectionnez le type de machine (et donc la constante C qui la caractérise), entrez la puissance nominale, la vitesse du volant d'inertie et le degré d'irrégularité requis.

Avertissement : Les moteurs alternatifs et les compresseurs ont des allures des diagramme de moment de charge connues. Par conséquent, il est possible de trouver un certain nombre d'études dans la littérature qui estiment la constante C de manière assez précise. Dans le cas d'autres machines, les allures du moment de charge sont essentiellement impossibles à caractériser en général. Toutefois, si vous concevez, par exemple, une version modifiée d'une machine existante, il est possible d'estimer la constante C de manière assez précise en se basant sur la solution existante.
Dans le chapitre [3.0], vous pouvez alors déterminer le moment d'inertie du volant d'inertie avec une précision suffisante.

2.6 Degré d'irrégularité de fonctionnement

Les valeurs suivantes sont recommandées pour différentes machines.

Type de machine / degré d'irrégularité de fonctionnement (δ)
Broyeurs.....0.200
Machines électriques.....0.003
Machines électriques (entraînement direct).....0.002
Moteurs à courroie.....0.030
Boîtes de vitesses avec engrenages.....0.020
Marteaux-pilons.....0.200
Machines à pomper.....0.03-0.05
Machines-outils.....0.030
Machines à papier.....0.015
Machines textiles et machines à tisser.....0.010-0.025
Machines à poinçonner, à cisailler et à presser.....0.10-0.15
Machines à filer.....0.10-0.020
Machines de laminage et d'exploitation minière.....0.025
Générateurs de courant continu.....0.006-0.013
Générateurs de courant alternatif.....0.003-0.015
Moteurs à combustion interne des véhicules.....0.003-0.006

Note : Degré d'irrégularité de la course
δ = (ωmax - ωmin) / ωm
ωmax ... vitesse angulaire maximale
ωmin ... vitesse angulaire minimale
ωm = (ωmax - ωmin) / 2 ... vitesse angulaire moyenne

2.8 Conception préliminaire des dimensions du volant d'inertie

En fonction du moment d'inertie requis, vous pouvez concevoir les dimensions de la couronne du volant d'inertie.
Entrez le moment d'inertie requis, la densité du matériau utilisé, le rapport entre la largeur et la hauteur de la couronne du volant d'inertie et le diamètre intérieur requis.

2.9 Moment d'inertie requis

Le moment d'inertie de la conception indicative est utilisé. Si vous voulez entrer sa propre valeur, cochez le bouton à droite.

2.10 Densité du matériau du volant d'inertie

Acier 7800 [kg/m³] ; 487 [lb/ft³]
Fonte 7200 [kg/m³] ; 450 [lb/ft³]
Bronze 8800 [kg/m³] ; 550 [lb/ft³]
Aluminium 2700 [kg/m³] ; 168 [lb/ft³]
Bois de feuillus 680 [kg/m³] ; 42 [lb/ft³]

2.18 Vitesse maximale, contrainte maximale

La plus grande contrainte dans un anneau en rotation est la contrainte tangentielle sur sa face interne.
Entrez la contrainte maximale admissible et la constante de Poisson du matériau.
Entrez la vitesse. Le champ vert indique la valeur de la vitesse maximale pour la contrainte maximale admissible spécifiée.
Après avoir appuyé sur le bouton "==>", les valeurs de conception calculées sont transférées dans la ligne du tableau sélectionnée.

2.19 Tension maximale admissible

Fonte ... < 8-10 MPa (1.16 - 1.45 kpsi)
Acier de fonderie ... < 100 MPa (14.5 kpsi)

2.20 Coeficiente de Poisson

Acier ... 0.27-0.30
Fonte ... 0.21-0.26
Alliages d'aluminium ... 0.33
Cuivre ... 0.33
Magnésium ... 0.35
Titane ... 0.34

2.21 Vitesse du volant d'inertie

Les vitesses préréglées sont à la ligne [2.5]. Si vous voulez entrer sa propre valeur, cochez le bouton à droite.

2.23 Contrainte tangentielle sur le diamètre intérieur

La contrainte calculée doit être inférieure au maximum autorisé [2.19]

2.25 Dimensions et calcul du volant d'inertie (masses d'inertie)

Vous pouvez définir jusqu'à 12 anneaux différents dans le tableau pour assembler une forme de volant d'inertie plus complexe ou recalculer les masses avec des taux de rotation différents.

Le bouton "Clear" efface les valeurs des dimensions dans tout le tableau, sauf dans la première ligne.
Le bouton "V" permet de transférer la valeur de la première ligne vers les autres.
Le bouton "min/max" permet de renseigner le diamètre extérieur/intérieur de l'anneau pour calculer la contrainte sur le diamètre extérieur/intérieur.

Tuyau : S'il existe d'autres masses en rotation (engrenages, poulies, etc.) reliées au volant d'inertie par un engrenage, vous pouvez les ajouter en les définissant dans le tableau et en leur attribuant la vitesse correspondante. Le moment d'inertie total réduit sera converti par le rapport de transmission à la première ligne et se trouve dans la colonne "Ired".

Marquage des colonnes
Nombre : multiplie les valeurs calculées (plusieurs masses rotatives identiques)
a : Déplacement de l'anneau (cylindre) dans le graphique selon l'axe X
D, d, b : Dimensions de l'anneau (cylindre)
Ro : Densité
ny : Constante de Poisson
n : Révolutions
ω : Vitesse angulaire
rg : Rayon d'inertie
m : Masse
I : Moment d'inertie
Ired : Moment d'inertie réduit (converti par la vitesse au premier ordre)
Ek : Énergie cinétique du disque en rotation
dx : Diamètre pour lequel la contrainte de frottement sera calculée
σt : Contrainte de traction

2.26 Faire tourner le volant d'inertie

Calcul de l'énergie et du temps nécessaires pour faire tourner le volant d'inertie avec le moment d'inertie spécifié jusqu'à la vitesse souhaitée.
Les valeurs prédéfinies sont celles du tableau ci-dessus, après avoir décoché le bouton, vous pouvez entrer vos propres valeurs.

2.33 Moment gyroscopique

Lorsque le volant d'inertie tourne autour d'un axe autre que l'axe de rotation, un moment gyroscopique est généré. Pour des moments d'inertie plus élevés et des vitesses supérieures, il peut être significatif et doit être pris en compte dans les calculs. Les valeurs prédéfinies sont celles du tableau ci-dessus, après avoir décoché le bouton, vous pouvez entrer vos propres valeurs.

2.41 Graphique

Les objets du tableau [2.25] sont reportés dans le graphique.
La coordonnée "a" dans le tableau définit le déplacement dans l'axe X.

Analyse (calcul) du volant d'inertie [3]

Dans les moteurs et les machines où le mouvement rotatif est converti en mouvement rectiligne et dans les machines où il n'y a pas de charge constante, des fluctuations de couple se produisent. Il n'y a pas d'équilibre constant entre les moments d'action (couple moteur, couple entraîné, forces inertielles, résistances passives). Cela modifie la vitesse angulaire pendant le cycle de travail. Pour réduire cette irrégularité, un volant d'inertie est utilisé comme accumulateur d'énergie, qu'il stocke en cas d'excès de couple et libère en cas de manque de couple.

Une grande partie des machines a une allure de couple qui ne peut pas être décrite simplement de manière analytique. Par conséquent, des méthodes d'intégration numérique sont utilisées pour la solution. L'allure du couple sur le côté gauche est définie par le tableau des couples en fonction de la rotation du volant d'inertie. Le moment sur le côté droit peut être :

A. Constant
B. Dépendant de la vitesse du volant d'inertie (moteur électrique, générateur)
C. Ou bien il peut être défini par sa propre table ou fonction

!!! Procédez comme suit lors de l'analyse !!!

1. Remplir le tableau [3.45] avec l'allure du couple de la machine à analyser
2. Entrer les paramètres du volant d'inertie [3.1]
3. Lancer l'analyse A ou B ou C
4. Les résultats de l'analyse sont sur les lignes [3.28-3.42], dans le tableau [3.45] et dans les graphiques

Tuyau : Pour une référence rapide, commencez toujours par l'analyse A

3.1 Paramètres requis pour le volant d'inertie

Vous pouvez soit entrer le moment d'inertie et le résultat de l'analyse sera le degré d'irrégularité de fonctionnement, soit, en cochant le bouton à droite, entrer le degré d'irrégularité de fonctionnement et le résultat sera le moment d'inertie correspondant.

Avertissement : Il est nécessaire de remplir d'abord le tableau [3.45] avec l'allure du couple de la machine analysée.

Avertissement : Bien que le volant d'inertie soit mentionné ici, il s'agit en fait de la somme des moments d'inertie de toutes les masses en rotation qui sont reliées au volant d'inertie (par exemple, le moment d'inertie du moteur électrique, du vilebrequin, des engrenages, des embrayages, etc.) Si les masses en rotation connectées ont des vitesses de rotation différentes, il est nécessaire de convertir le moment d'inertie réduit en vitesse du volant d'inertie - voir le paragraphe précédent.

Tuyau : Le moment d'inertie approximatif du moteur électrique est sur la ligne [3.21]

3.3 Degré d'irrégularité de fonctionnement

Les valeurs suivantes sont recommandées pour différentes machines.

Type de machine / degré d'irrégularité de fonctionnement (δ)
Broyeurs.....0.200
Machines électriques.....0.003
Machines électriques (entraînement direct).....0.002
Moteurs à courroie.....0.030
Boîtes de vitesses avec engrenages.....0.020
Marteaux-pilons.....0.200
Machines à pomper.....0.03-0.05
Machines-outils.....0.030
Machines à papier.....0.015
Machines textiles et machines à tisser.....0.010-0.025
Machines à poinçonner, à cisailler et à presser.....0.10-0.15
Machines à filer.....0.10-0.020
Machines de laminage et d'exploitation minière.....0.025
Générateurs de courant continu.....0.006-0.013
Générateurs de courant alternatif.....0.003-0.015
Moteurs à combustion interne des véhicules.....0.003-0.006

Note : Degré d'irrégularité de la course
δ = (ωmax - ωmin) / ωm
ωmax ... vitesse angulaire maximale
ωmin ... vitesse angulaire minimale
ωm = (ωmax - ωmin) / 2 ... vitesse angulaire moyenne

3.4 Vitesse moyenne requise du volant d'inertie

Entrez la vitesse du volant d'inertie souhaitée.

3.7 A. Analyse - moment constant (côté droit)

Analyse de base, applicable dans tous les cas.

Dans ce calcul, le gain (la perte) d'énergie est calculé à partir de la courbe de moment sur le côté gauche. Cela détermine le moment constant qui doit agir sur le côté droit pour que la somme des énergies soit nulle.

Sur la base des moments appliqués (côté gauche + côté droit), on obtient l'allure de la vitesse angulaire (vitesse) et donc l'irrégularité du fonctionnement pour le moment d'inertie spécifié du volant d'inertie. Ou bien le moment d'inertie du volant d'inertie est déterminé pour un degré d'irrégularité entré.

3.8 Puissance (puissance fournie)

Puissance + (puissance fournie -) du dispositif du côté droit, pour générer le couple constant requis (couple moyen Tm).

3.10 B. Analyse - moteur électrique/générateur (côté droit)

Un cas particulier d'analyse où un moteur asynchrone/générateur (côté droit) est connecté à l'appareil (côté gauche).

En plus de la condition selon laquelle la somme des énergies des côtés gauche et droit est égale à zéro, il est nécessaire d'observer que le couple du moteur électrique/générateur est fonction de la vitesse du volant d'inertie.

Dans ce calcul, le couple moteur est appliqué de manière répétée (voir le nombre d'étapes d'itération) en fonction de la vitesse actuelle du volant d'inertie tandis que le cycle complet est recalculé après chaque changement. Après chaque étape d'itération, la vitesse du volant d'inertie au début du cycle est ensuite ajustée en conséquence. Habituellement, l'ensemble du modèle converge assez rapidement pour des dizaines d'étapes d'itération plus petites.

Avertissement : Si le degré d'irrégularité est supérieur à environ 0.05 ou si l'on utilise un moteur dont la puissance est proche de la valeur supérieure recommandée, la solution peut devenir instable. Dans ce cas, le modèle ne converge pas. Comme c'est généralement la solution pour les valeurs élevées du degré d'irrégularité, l'analyse A peut être utilisée sans problème.

3.12 / 4.2 Type de moteur/générateur

Choisissez un moteur dans la liste.

Les moteurs sont listés sous la forme "Vitesse synchrone/nombre de pôles...fréquence du système électrique".

3.13 Puissance nominale recommandée de/à

Intervalle de puissance du moteur (générateur) recommandé, estimé à partir de l'allure du couple sur le côté gauche.

3.14 / 4.3 Puissance nominale

Entrez la puissance du moteur. En fonction de la performance, des paramètres moteur approximatifs seront proposés (nr, Tz...)

Valeurs de catalogue des fabricants de moteurs.

kW (50Hz):
0.06; 0.09; 0.12; 0.18; 0.25; 0.37; 0.55; 0.75; 1.1; 1.5; 2.2; 3; 3.7; 4; 5.5; 7.5; 9; 11; 15; 18.5; 22; 30; 37; 45; 55; 75; 90; 110; 132; 160; 200; 225; 250; 280; 315; 355; 400; 450; 500; 560; 630; 710; 800; 900; 1000

HP (60Hz):
0.25; 0.33; 0.5; 0.75; 1; 1.5; 2; 3; 4; 5; 5.5; 7.5; 10; 12; 15; 20; 25; 30; 40; 50; 60; 75; 100; 120; 150; 180; 210; 270; 300; 335; 375; 420; 475; 530; 600; 670; 750; 850; 950

3.15 / 4.4 Mode de travail

Le moteur peut également fonctionner comme un générateur d'énergie électrique. (dépassement de la vitesse synchrone et consommation d'énergie mécanique).
Sélectionnez pour définir le type de comportement.

Exemple :
En mode moteur, si la vitesse synchrone est supérieure à la vitesse de synchronisation, le couple = 0.
En mode moteur/générateur, si la vitesse synchrone est supérieure à la vitesse de synchronisation, le couple sera négatif.

3.16 / 4.5 Vitesse synchrone

Réglée en fonction du type de moteur sélectionné. À cette vitesse, le couple est nul.

3.17 / 4.6 Vitesse nominale

La vitesse nominale et le coefficient de couple de démarrage sont directement déterminés pour le moteur spécifique. Dans le champ vert figure la valeur approximative pour le type de moteur et la puissance donnés.

Après avoir coché le bouton à droite, vous pouvez entrer vos propres valeurs (nr,Tzcoeff). Il est donc possible de régler les caractéristiques du moteur exactement selon le catalogue du fabricant.

Avertissement : Dans la plupart des cas, la valeur de la vitesse nominale "nr" correspondra aux données du catalogue. Si vous définissez des valeurs personnalisées, elles doivent être très proches des valeurs suggérées.

3.19 / 4.8 Coefficient de couple de démarrage

Pour les petits moteurs (≤ 30 kW), la valeur est généralement de 2.5-3, pour les moyens 2-2.5, pour les gros 1-1.5.

Avertissement : Le couple de démarrage peut être résolu de plusieurs manières (élimination des courants élevés). Pour les gros moteurs, le coefficient peut être inférieur à 1, ce qui signifie qu'il n'est pas possible de démarrer le moteur à pleine charge. Dans ces cas, il est conseillé de consulter le fabricant.

3.21 Moment d'inertie du moteur / Ie * i

Le premier chiffre indique le moment d'inertie approximatif du moteur sélectionné. Le deuxième nombre est multiplié par le carré du rapport de transmission "i" de la ligne suivante. Il peut donc être directement comparé ou soustrait du moment d'inertie du volant d'inertie.

Tuyau : Les informations sur la façon de trouver (convertir) les moments d'inertie des masses qui ont des vitesses de rotation différentes à la vitesse de rotation du volant d'inertie se trouvent au paragraphe [2.0] (Moment d'inertie réduit).

3.22 Rapport de transmission volant d'inertie/moteur

Le rapport de transmission est réglé automatiquement. Il est estimé de manière à ce que la vitesse moyenne requise du volant d'inertie [3.4] soit proche de celle calculée.

Après avoir coché le bouton à droite, vous pouvez entrer votre propre valeur du rapport. Cela peut être utile si vous devez définir, par exemple, le rapport de transmission i = 1 (entraînement direct du volant d'inertie).

3.25 Nombre d'étapes d'itération/sensibilité

Itération

Définissez le nombre d'étapes d'itération. Après chaque étape, le tableau et le graphique sont actualisés afin que vous puissiez suivre les changements incrémentiels.

Tuyau : Chaque étape d'itération peut prendre jusqu'à plusieurs secondes. Pour une première idée du comportement du modèle, environ 5 à 10 étapes devraient suffire. Après la fin du cycle, il suffit de recommencer l'analyse, qui reprend à partir des dernières valeurs.

Sensibilité

La sensibilité détermine l'ampleur de la variation de la vitesse initiale du volant d'inertie avant chaque étape.
Plus la valeur est grande, plus le changement est important et plus la convergence est rapide. D'autre part, une valeur trop importante peut entraîner une oscillation ou une non-fonctionnalité de la solution.

Tuyau : Il est conseillé de commencer avec une valeur de 5 puis d'augmenter ou de diminuer la sensibilité en fonction du comportement du modèle (taux de convergence).

3.27 Résultats de l'analyse

Il est indiqué pour quelle analyse (A, B, C) les résultats sont donnés.

3.32 Somme de l'énergie+-/écart en pourcentage

La somme des énergies du côté gauche et du côté droit du volant d'inertie. Pour un fonctionnement en régime permanent (la vitesse du volant d'inertie au début et à la fin du cycle de travail est la même), la somme doit être proche de zéro.
Les pourcentages expriment l'écart de la somme par rapport à l'énergie d'entrée (côté gauche). Une valeur rouge signifie que l'écart est supérieur à 1 %.

3.33 Volant d'inertie

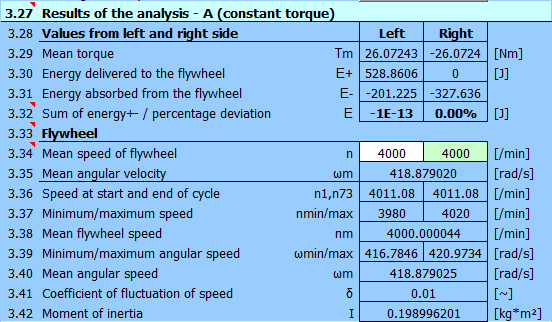
Résumé des résultats du calcul du volant d'inertie.

3.34 Vitesse moyenne du volant d'inertie

Réglage par défaut de la vitesse moyenne du volant d'inertie pour le calcul et de la vitesse angulaire calculée à partir de celle-ci.

Analyse A : La valeur de la vitesse souhaitée [3.4] est placée dans la cellule
Analyse B, C : La valeur corrigée de l'étape précédente est déplacée dans la cellule après chaque étape d'itération (cellule verte)

Avertissement : les valeurs [3.34, 3.35] sont entrées dans la dernière étape de l'itération, les valeurs [3.36 - 3.42] sont le résultat du calcul.

Tuyau : La valeur peut être modifiée manuellement pour accélérer le processus d'itération.

3.43 Définition du tableau des moments (côté gauche)

Avant de commencer l'analyse, il est nécessaire de remplir l'allure du couple de la machine à analyser (côté gauche).

Dans le tableau, définissez la charge du volant d'inertie dans les deux premières colonnes A, B.

1) Dans la colonne A, entrez successivement les angles pour lesquels vous définirez le moment agissant sur le volant d'inertie (côté gauche)

- les valeurs doivent former une série continue sans lignes vides.
- les angles doivent être entrés dans l'ordre croissant
- la différence entre les angles successifs ne doit pas être régulière. Ceci peut être utilisé, par exemple, lors d'un changement progressif de couple (la différence entre les angles suivants est faible)

2) Dans la colonne B, entrez le moment agissant sur le volant d'inertie. Une valeur positive accélère le volant d'inertie, une valeur négative le ralentit.

3.44 Nombre de lignes valides dans le tableau

Il est nécessaire de spécifier le nombre de lignes valides du tableau (celles qui seront incluses dans l'analyse).
Si vous souhaitez entrer une valeur autre que celle suggérée (cellule verte), décochez le bouton.
La valeur proposée est régie par la première cellule vide de la colonne B.

3.45 Tableau des charges et des résultats

Dans le tableau, vous avez défini la charge de moment dans la colonne A, B (côté gauche). Les autres colonnes sont alors le résultat de l'analyse choisie.

α : Angle de rotation du volant d'inertie pour lequel le moment de la colonne B est défini. Lorsque l'on appuie sur le bouton "+Δ", toute la colonne est remplie de sorte que chaque valeur suivante est augmentée de la différence entre la deuxième et la première ligne.

Note : La différence entre les angles ne doit pas nécessairement être régulière, mais elle doit être croissante.

Tl : La forme d'onde du couple de la machine que vous voulez analyser (côté gauche).
Ti=Tl+Tr : La forme d'onde du couple qui agit sur le volant d'inertie. Somme des côtés gauche et droit.
Tr=Tm : La forme d'onde du couple qui équilibre le couple de la colonne B.
Analyse A : constante, Tr = Tm
Analyse B : itération, Tr = Te * i
Analyse C : moment défini par l'utilisateur
ne : Vitesse du moteur dépendant de la vitesse du volant d'inertie. ne = n * i
Te : Couple moteur. Il dépend de la vitesse du ne.
Pwe : Puissance du moteur.
+-dE : Énergie fournie (+) / retirée (-) au volant d'inertie entre l'angle de rotation actuel et le suivant (colonne A).
E : Valeur actuelle de l'énergie cinétique à l'angle de volant d'inertie respectif.
n : Nombre de tours pour l'angle de rotation respectif du volant d'inertie.
dn : Différence entre la vitesse actuelle et la vitesse moyenne.
ω : Vitesse angulaire à l'angle de rotation respectif.
dω : Variation de la vitesse angulaire. La différence entre la vitesse actuelle pour l'angle de rotation correspondant et la valeur moyenne.
Pw : Puissance du volant d'inertie pour l'angle de rotation donné.

3.46 Graphique 1 - Moteur

Courbe de couple et de puissance du moteur/générateur électrique
Axe : X - Vitesse, (verticale rouge = ns)
Axe : Y.
Bleu : Couple [Nm ; lbf*ft] + zone de travail
Vert : Puissance [kWh ; HP] + zone de travail

3.47 Graphique 2 - Couple, vitesse de rotation

Couple et vitesse
Axe : X - Rotation du volant d'inertie
Axe : Y
Noir fin : Moment côté gauche [Nm ; lbf*ft].
Rouge fin : Moment côté droit [Nm ; lbf*ft]
Bleu épais : Somme des moments [Nm ; lbf*ft]
Vert épais : Vitesse du volant d'inertie [/min] (échelle de droite)

3.48 Graphique 3 - Valeurs sélectionnées

Dans le graphique ci-dessous, sélectionnez les courbes que vous souhaitez afficher.
Axe : X - Rotation du volant d'inertie

3.49 C. Analyse de l'utilisateur

Trois colonnes sont laissées dans le tableau pour que l'utilisateur puisse définir le couple (côté droit), par exemple en fonction de la vitesse du volant d'inertie.

Après avoir appuyé sur le bouton "Tr=O(i)", "Tr=P(i)", "Tr=Q(i)", les valeurs de la colonne correspondante sont insérées dans la colonne D (côté droit) et le même processus que dans l'analyse B a lieu.
Le nombre d'itérations et la sensibilité de l'itération sont régis par le paramètre de la ligne [3.25].
La cellule située sous le bouton (nommée "_Const1", "_Const2",...) n'a pas de fonction et peut être utilisée, par exemple, comme constante d'entrée dans la définition du moment.

Tuyau : Après l'installation du calcul, les premières lignes contiennent des exemples qui sont décrits dans l'aide et qui peuvent bien sûr être supprimés ou modifiés et copiés dans les cellules restantes de la colonne correspondante.

Exemple 1 "O" : exemple de définition du moment en fonction de la vitesse du volant d'inertie

Cet exemple montre l'utilisation de la fonction suivante
T = Const1 * cos (n / 3360)^0,33
T ... moment (côté droit)
n ... vitesse du volant d'inertie
Const1 ... Constante (dans ce cas, elle exprime la grandeur du moment à vitesse nulle)

Exemple 2 "P" : Exemple de définition d'un couple à l'aide de la table de définition

Utilisation de l'interpolation linéaire d'une courbe de moment définie par des points individuels.
T = linear2(n;T_User_nT)
T ... moment (côté droit)
n ... vitesse du volant d'inertie
T_User_nT ... Nom du tableau dans lequel la courbe est définie par la séquence de paires de points :
vitesse / moment
Le tableau est défini sur la feuille "Tableaux".

Exemple 3 "Q" : Exemple d'utilisation du moteur sélectionné dans le paragraphe [4.0].

Cet exemple montre comment utiliser le moteur sélectionné du paragraphe 4.0
T = linear2(n * _Const3 ; T_4_nT) * _Const3
n ... vitesse du volant d'inertie
T_4_nT ... nom du tableau avec la courbe T=f(n) du paragraphe 4.0
_Const3 ... rapport de démultiplication entre le volant d'inertie et le moteur

Courbes de couple des moteurs, puissances, moments d'inertie, poids, rendement [4]

Dans le domaine des entraînements de machines et d'installations, le moteur le plus couramment utilisé est le moteur asynchrone (induction motor). Pour ce moteur, le couple varie avec la vitesse (de façon linéaire dans la plage de travail). Un tableau de paramètres pour n'importe quel moteur a été créé en comparant les catalogues de plusieurs fabricants.

Dans ce chapitre, vous trouverez les paramètres du moteur sélectionné (y compris les estimations du poids, du rendement et du moment d'inertie), la puissance et le couple pour les vitesses autres que la vitesse nominale.

4.2,4.3,4.4,4.5,4.6 a 4.8

Voir les paragraphes 3.12-3.19

4.10 Poids du moteur (environ)

Bien sûr, des moteurs tout aussi puissants diffèrent par leur conception, leurs matériaux, leur objectif et leur fabricant. Les valeurs du poids et du moment d'inertie doivent donc être prises à titre indicatif.

4.12.4.13 Rendement nominal IE1/IE2,IE3/IE4

Pour des calculs plus précis, il est utile de connaître le rendement des moteurs et les marquages correspondants.

Classes d'efficacité selon la norme IEC 60034-30-1:2014
(IE = International Efficiency) :
IE1 Rendement standard (Standard Efficiency)
IE2 Haute efficacité (High Efficiency)
IE3 Rendement élevé (Premium Efficiency)
IE4 Très haute efficacité (Super Premium Efficiency)

Comparaison avec une autre norme
IEC 60034-30-1 NEMA MG1 GB 18613-2012
===========================
IE4 Grade 1 (IE4)
IE3 Premium Efficient (60 Hz) Grade 2 (IE3)
IE2 Energy Efficient (60 Hz) Grade 3 (IE2)

4.14 Calcul du couple et de la puissance pour la vitesse spécifiée

Entrez la vitesse pour laquelle vous voulez trouver la valeur du couple.
La vitesse doit être inférieure à ns, si la vitesse synchrone est dépassée, le moteur fonctionne comme un générateur (freine et produit du courant électrique) et le couple est négatif.

4.18 Courbe de couple et de puissance

Courbe de couple et de puissance d'un moteur électrique (générateur)
Axe : X - Vitesse
Axe : Y
Bleu : Couple [Nm ; lbf*ft].
Vert : Puissance [kWh ; HP]
Rouge : Couple pour la vitesse spécifiée

Mécanisme à manivelle [5]

Pour convertir un mouvement rectiligne en mouvement rotatif (et vice versa), on utilise souvent un mécanisme à manivelle, généralement associé à un volant d'inertie. Pour la conception du volant d'inertie, il est alors nécessaire de connaître l'allure du couple. Pour calculer l'allure du couple, il est nécessaire de connaître la force de charge (Fp), les dimensions (L, R), la vitesse nombre de tours (n) et les poids des différentes parties (mp, m).

5.1 Paramètres du mécanisme à manivelle

Entrez les paramètres du mécanisme à manivelle selon la figure.

5.2 Poids de la partie coulissante

Entrez le poids de toutes les pièces qui effectuent un mouvement rectiligne (A).

5.3 Poids de la bielle (total)

Entrez le poids total de la bielle (B).

5.4 Longueur de la bielle

Entrez la distance entre les axes de la bielle (B).

5.5 Position du centre de gravité de la bielle (T)

Entrez la distance du centre de gravité de la bielle (B).

Pour les moteurs, compresseurs ~0.7*L
Pour les machines-outils ~0.5*L
Elle est nécessaire pour déterminer les poids ms et mr

5.6 Répartition du poids de la bielle

Pour calculer les forces, la bielle est remplacée par deux points de masse de poids ms (mouvement rectiligne) et mr (mouvement de rotation), qui agissent dans les axes de la bielle.

5.7 Rayon de la manivelle

Entrez le rayon de la manivelle (C).

5.11 Force centrifuge pour mr

Force centrifuge exercée par la bielle sur la manivelle.

5.14 Tableau

Dans le tableau, entrez l'angle de rotation de la manivelle [α] dans la première colonne. Vous pouvez utiliser le bouton "+Δ" pour remplir toute la colonne en une seule fois de sorte que la différence entre la première et la deuxième ligne soit utilisée pour ajouter pour chaque ligne suivante.

Dans la deuxième colonne, entrez la force de chargement [Fp] pour chaque angle de rotation respectif [α] de la manivelle. Par exemple, il peut s'agir d'une force de pression (compresseur, moteur) ou d'une force d'usinage (presse).

Les colonnes suivantes contiennent les valeurs telles qu'elles figurent dans la figure (colonne C-M).

Les 4 dernières colonnes contiennent des valeurs sélectionnées dans le graphique [5.16].

5.15 Graphiques des moments

Bleu - Moment total (M)
Noir fin - Moment dû à la force Fp
Rouge fin - Moment dû à l'accélération/décélération des pièces mobiles Fa

5.16 Graphiques des valeurs sélectionnées

Sélectionnez les valeurs que vous souhaitez afficher dans le graphique de droite.
L'axe des x représente l'angle de la manivelle.

Exemple 1 - Conception du volant d'inertie d'un moteur à combustion interne monocylindre

Moteur à combustion interne

Alésage : 72 mm=>zone du piston : 0.004072 m²=>Force Fp
Course : 62 mm=>Rayon de la manivelle : 31 mm
Longueur de la bielle : 100 mm
Position du centre de gravité de la bielle : 70 mm
Poids du piston : 0.4 kg
Poids de la bielle : 0.6 kg
Irrégularité de fonctionnement requise : 0.01
Pression mesurée dans le cylindre pour 4000 tr/min en fonction de la rotation de la manivelle.

1) Mécanisme à manivelle

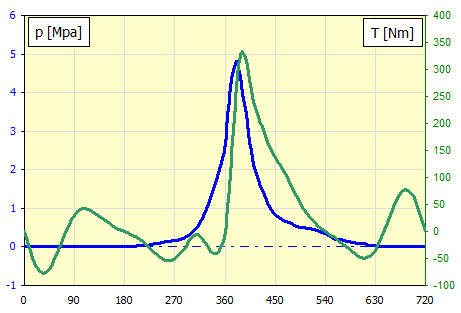
Au paragraphe [5], définissez les paramètres du mécanisme à manivelle.

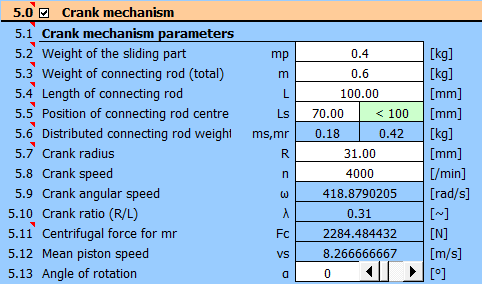
À partir de la pression et de l'alésage, on obtient la force Fp pour chaque angle de rotation de la bielle.
Remplissez le tableau avec l'angle α [°] et la force calculée.

On obtient ainsi le couple "T" pour chaque angle.

2) Volant d'inertie

Vitesse requise du volant d'inertie 4000 tr/min
Irrégularité de fonctionnement requise 0.01

Remplissez le tableau avec les valeurs de l'angle et du moment.

Remplissez le degré d'irrégularité de fonctionnement requis et la vitesse requise du volant d'inertie [3.3, 3.4].

Appuyez sur le bouton "Start A". Le moment d'inertie requis du volant d'inertie est immédiatement calculé.

Le moment moyen Tm est calculé. Celui est utilisé comme une charge constante.

Les résultats sont affichés immédiatement.

et un large éventail d'options graphiques.

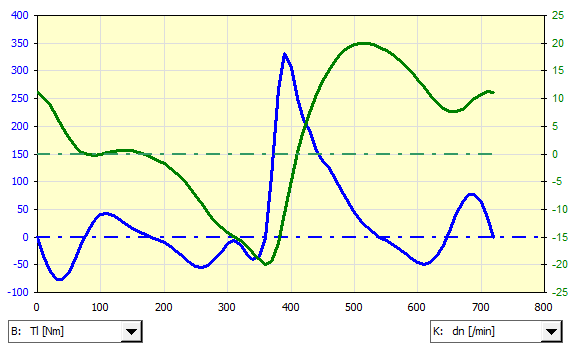
Voici, par exemple, un graphique de l'allure du couple et de la variation de la vitesse du volant d'inertie.

Exemple 2 - Conception d'un volant d'inertie pour un compresseur entraîné par un moteur électrique asynchrone

Compresseur directement relié au moteur électrique

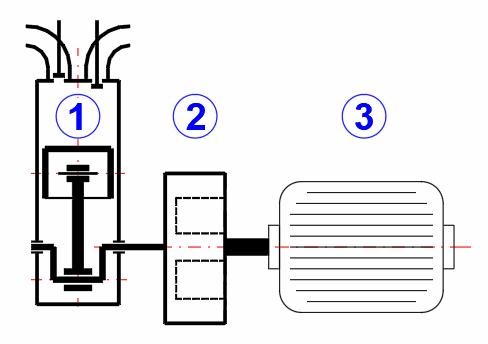
Paramètres du compresseur

Diamètre du piston : 30 mm
Rayon de la manivelle : 20 mm
Longueur de la bielle : 60 mm
Centre de gravité de la bielle : 40 mm
Poids du piston : 0.0286 kg
Poids de la bielle : 0.0572 kg
Vitesse : 3000 tr/min
Courbe de débit/pression du compresseur

À partir de la courbe de débit/pression et des paramètres du mécanisme à manivelle, nous obtenons un graphique et un tableau des moments en utilisant le calcul [5.0].

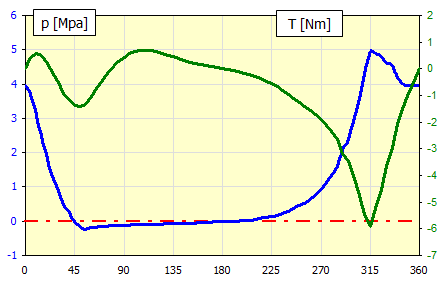
Tableau des moments.

Tout d'abord, remplissez le tableau [3.43] avec les angles α et les moments correspondants.

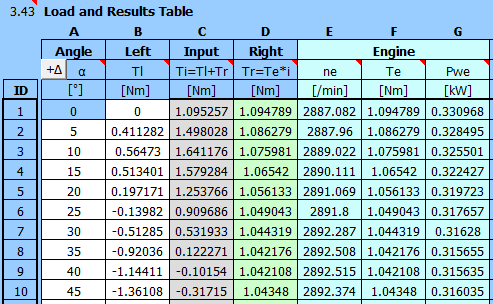
Remplissez les paramètres du volant d'inertie :
Degré d'irrégularité de fonctionnement : 0.01
Vitesse du volant d'inertie : 3000 tr/min

Paramètres du moteur :

Moteur bipolaire, ns : 3000 tr/min
Puissance du tableau d'aide : P = 0.55 kW
Réglez le rapport de transmission à : i = 1.0

Exécutez l'analyse B (plusieurs fois de suite).

Avec une connexion directe moteur-compresseur, il n'est pas possible d'atteindre une vitesse synchrone de 3000 tr/min car le moteur asynchrone a une puissance nulle à la vitesse synchrone. La vitesse est donc stabilisée à une vitesse moyenne de 2900 tr/min en raison de la charge.

Graphique de performance du moteur et de l'oscillation de la vitesse autour de la vitesse moyenne (2900 tr/min) pendant le cycle de travail.

Exemple 3 - Conception d'un volant d'inertie pour une presse à manivelle entraînée par un moteur électrique asynchrone

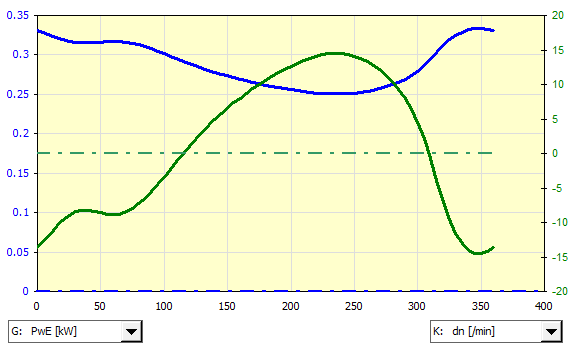
Le mécanisme à manivelle (1) est relié via un engrenage 5:1 (2) au volant d'inertie (3). Le volant d'inertie est entraîné par un moteur électrique asynchrone (5) via une transmission par courroie (4).

Tâche :
- calculer le couple de charge T1
- calculer le couple de charge T3
- déterminer le moment d'inertie du volant d'inertie pour l'irrégularité de fonctionnement spécifiée
- déterminer la puissance nécessaire du moteur électrique
- concevoir les dimensions du volant d'inertie

1) Presse à manivelle (mécanisme) :

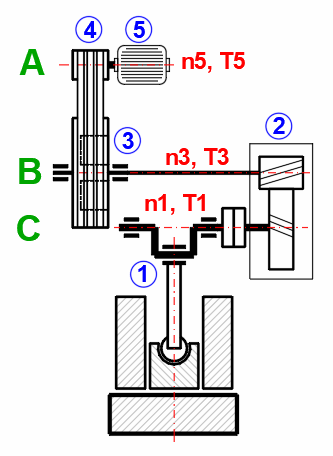
Force requise : 10 tonnes
Course de travail : 20 mm
Nombre de coups : 30 / min
Poids de la partie coulissante : 30 kg
Poids de la bielle : 30 kg
Longueur de la bielle : 400 mm
Centre de gravité de la bielle : 200 mm
Rayon de la manivelle : 100 mm
Forces de résistance : 200 N

Dans le paragraphe [5.0], définissez les paramètres du mécanisme à manivelle.

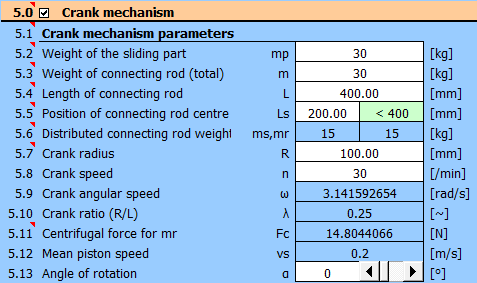
Dans le tableau, définissez le pas de 5 degrés et remplissez les valeurs de charge.
Contre la force de chargement de 10 tonnes ~ 100000 N, les forces de poids et de résistance agissent (30 kg + 30 kg + -200 N) = 800 N (400 N) tout au long de la révolution.
Une force de 100000 N agit à partir de 325 degrés (22 mm du point mort haut)

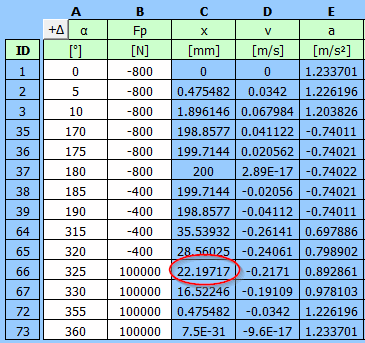
Tableau détaillé avec les données entrées pour le couple sur la manivelle T1 et le couple T3 en amont de la boîte de vitesses 5:1.
 

2) Boîte de vitesses

Le rapport de transmission est de 5:1. Les valeurs de couple figurent dans le tableau précédent. Vitesse du volant d'inertie = nombre de tours à l'entrée de la boîte de vitesses n3=30*5=150 tr/min.

3) Volant d'inertie

Irrégularité de fonctionnement requise : 0.03
Vitesse requise du volant d'inertie : 150 tr/min

Remplissez le degré d'irrégularité de fonctionnement requis et la vitesse requise du volant d'inertie [3.3, 3.4].

Remplissage du tableau des moments

Le rapport entre le mécanisme à manivelle et le volant d'inertie étant de 5:1, le volant d'inertie tourne 5 fois par tour du mécanisme à manivelle (1 cycle de travail). La division de l'angle dans le calcul du mécanisme à manivelle était de 5 °. La division dans le tableau pour l'analyse du volant d'inertie sera donc 5*5 = 25 °.

Il est alors possible de recopier les valeurs du couple T3 directement dans la deuxième colonne (B).

Données d'entrée, analyse

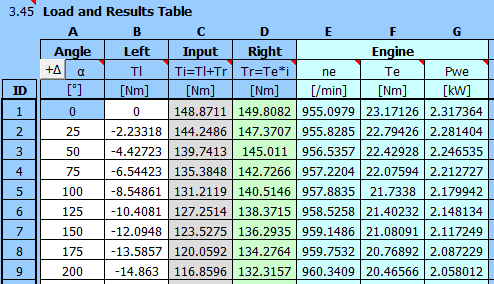
Pour sélectionner le moteur, sélectionnez le moteur 1000 tr/min. La puissance recommandée du moteur [3.13] est estimée à partir de l'allure du couple (colonne B).
Choisissez parmi une gamme de moteurs pour la puissance : 3 kW [3.14].
Le rapport de transmission volant-moteur (transmission par courroie) est réglé automatiquement [3.22] pour obtenir la vitesse de volant souhaitée.

Définissez le nombre d'étapes d'approximation à 10 et la sensibilité à 5 [3.25].

Appuyez sur le bouton "Start B". Les 10 étapes sont exécutées de manière séquentielle, pendant lesquelles le couple moteur est calculé de manière répétée à partir de la vitesse du volant d'inertie. La valeur de la somme des énergies des côtés droit et gauche [3.32] devrait diminuer (pour atteindre l'état d'équilibre). Vous pouvez appuyer sur le bouton plusieurs fois de suite pour affiner les résultats.

Dans le même temps, le moment d'inertie correspondant est calculé [3.42].

4) Conception des dimensions du volant d'inertie

Dans le paragraphe [2.0], entrez le moment d'inertie de l'étape précédente, la densité, le rapport b/h et le diamètre intérieur.

Note : Si nécessaire, il est possible d'inclure toutes les masses en rotation dans le calcul et de recalculer leurs moments d'inertie à l'aide du tableau [2.25].

Les paramètres de la couronne du volant d'inertie se trouvent sur les lignes [2.13 - 2.17].

Réglage des calculs, changement de langue.

L'information sur le réglage des paramètres de calcul et le choix de la langue peut être trouvée dans le document "Réglage des calculs, changement de langue".

Modifications du cahier de travail (calcul).

Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".

Liste des normes, liste de la littérature:

Littérature:
[1] Strojně technická příručka (Svatopluk Černoch)
[2] Shigley’s Mechanical Engineering Design
[3] Strojírenská příručka (1992)
[4] Machinery’s Handbook (26th Edition)

Normes:
ČSN EN 60034-30-1 :20 14
EN 60034-30-1 :20 14
Rotating electrical machines — Part 30-1: Efficiency classes of line operated AC motors (IE code)
Machines Olectriques tournantes — Partie 30-1: Classes de rendement pour les moteurs a courant alternatif alimentés par le réseau (Code IE)
Drehende elektrische Maschinen — Teil 30-1: Wirkungrad-Klassifizierung von netzgespeisten Drehstrommotoren (IE-Code)

Company cataloques:
Siemens
ABB Automation Products