Le programme est destiné à une résolution des tâches les plus fréquentes dans le domaine de la mécanique des fluides.
Le programme résout des tâches dans les domaines :
1. Hydrostatique
2. Décharge stationnaire d'un fluide par un orifice
3. Décharge stationnaire - déversoirs (ISO 1438, Swiss Engineers, Hansen, Bazin, Frese)
4. Flux stationnaire d'un fluide visqueux – section constante d'une tuyauterie avec jet de sortie/diffuseur
5. Flux stationnaire d'un fluide visqueux – sections diverses de tuyauterie
6. Choc hydraulique
Les calculs comportent la détermination du nombre de Reynolds, de la viscosité, des pertes pour un flux laminaire et turbulent pour divers matériaux et des dizaines de types de coefficients de perte.
Les calculs utilisent des données, des procédures, des algorithmes et des informations provenant de la littérature, de normes et de catalogues d'entreprises.
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová,
CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs a paroi mince
L’interface d’utilisateur.
A télécharger.
Tarif, Achat.
L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document "commande, structure et syntaxe des calculs".
L'information sur le but, l'utilisation et la commande du paragraphe "information sur le projet" peut être trouvée dans le document "information sur le projet".
La mécanique des fluides est un vaste domaine qui traite du mouvement et de l'action des fluides. Ces calculs comprennent certains problèmes fréquemment résolus.
La viscosité dynamique µ (µ = "mi")
est une mesure de la viscosité d'un fluide (fluide : liquide, substance qui
coule).
Plus la viscosité est élevée, plus le fluide est épais (moins liquide) ; plus la
viscosité est faible, plus il est mince (plus liquide).
Unité de viscosité dynamique dans le système SI : [µ] = Pascal-sekunda (Pa*s) =
N*s/m² = kg/m*s.
La viscosité cinématique ν (ν = "nu")
est la viscosité dynamique du milieu µ divisée par sa densité ρ (ρ = "Ro").
Équation : ν = µ / ρ
Unité SI de la viscosité cinématique : [ν] = m²/s
Les unités fréquemment utilisées sont les Stokes (St) et les Centistokes (cSt).
Conversion :
1 Stoke (St) = e-4 * m²/s = 1 cm²/s
1 cSt = e-6 m²/s = 1 mm²/s
Une formule
approximative est utilisée pour calculer la viscosité en fonction de la
température :
µ ~ µ20 * exp(C * (293 / TK - 1))
µ20 ... viscosité dynamique pour 20°C
C ... coefficient pour un liquide donné
TK ... température en Kelvin
Le paramètre de base corrélant le
comportement visqueux de tous les fluides newtoniens est le nombre de Reynolds
sans dimension.
Il dépend non seulement de la vitesse moyenne mais aussi de la dimension
caractéristique de l'écoulement du fluide (diamètre d ou dh), de la viscosité
dynamique et de la densité.
Re = v * d * r / µ, ou Re = v * dh * r / µ pour les sections non circulaires.
v ..... vitesse
d ..... diamètre
r ... densité
µ ..... viscosité dynamique
dh ... diamètre hydraulique
dh = 4 * S/O
S ... surface de la section transversale
O ... circonférence mouillée
Pour une section circulaire, d = dh.
Expression
empirique :
µ / µ20 = exp(C * (293 / T°K - 1))
µ ... viscosité dynamique
µ20 ... viscosité dynamique pour 20°C
C ... coefficient
T ... température
Différences par rapport à
l'écoulement idéal d'un fluide.
1) Des pertes se produisent lorsqu'une partie de l'énergie mécanique est
convertie en chaleur.
2) La vitesse n'est pas distribuée uniformément dans la section transversale.
3) Le mouvement du fluide peut être laminaire (Re=Re,cr<2300) ou presque
toujours turbulent (Re>3000).
Q = v1 * S1 = v2 * S2
Q ... débit
v1, v2 ... vitesse dans les sections transversales 1 et 2
S1, S2 ... surface dans les sections transversales 1 et 2
g*h1 + p1/Ro + k1*(v1^2)/2 = g*h2 +
p2/Ro + k2*(v2^2)/2 + ez(1-2)
g ... accélération de la gravité
Ro ... densité
h1, h2 ... hauteur
p1, p2 ... pression
v1, v2 ... vitesse
ez(1-2) ... énergie de perte
ez(1-2) = (Zeta + Lambda * (L/dh)) * (v^2/2)
Zeta ........ coefficient de perte locale (entrée, changement de section
transversale, valve....)
Lambda ... coefficient de perte par frottement
L ............. longueur
dh ........... diamètre
v ............. vitesse
Lambda ... coefficient de
perte par frottement
Ecoulement laminaire (Re<2300) :
Lambda = 64 / Re
Ecoulement turbulent (Re>=2300) :
Une sélection de méthodes :
Tuyau lisse :
Lambda = 0.3164 / (Re^0.25) ....... Blasius
Lambda = 1 / (2 * Log10(Re * Lambda^0.5) - 0.8)^2 ......... Nikurdas
Lambda = (1,8 * Log10(Re) - 1,5)^-2 .......... P.K.Konakov
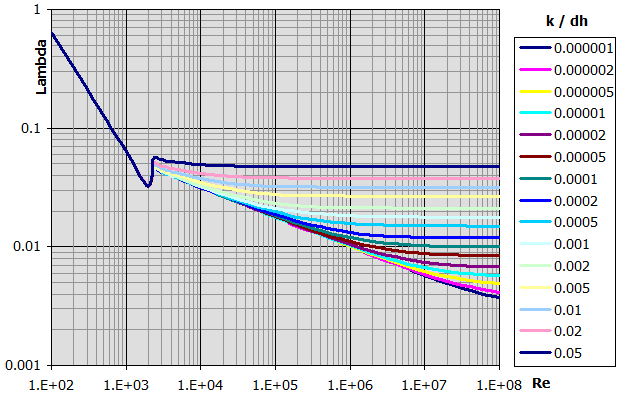
Tuyau brut :
Lambda = 0,1 * (100 / Re + kr)^0,25 ....... Altus
Lambda = 1 / (-2 * Log10(2.51 / (Re * Lambda^0.5) + 0.27 * kr))^2 ........
Colebrook - Blanc
Lambda = 8 * ((8 / Re)^12 + 1 / (a + b)^1,5)^(1/12) ....... Churchill
a = (2,457 * Log(1 / ((7 / Re)^0,9 + 0,27 * kr)))^16
b = (37530 / Re)^16
Lambda = 1 / (2 * Log10(1 / kr + 1,138))^2 ....... Formule de Gottingen
Lambda = 1 / (2 * (Log10((dh/2) / k) + 1,74)^2) ........ Formule de Karman
kr = k / dh
k ..... rugosité (hauteur de la rugosité)
dh ... diamètre (diamètre hydraulique)
Lambda = 4 * f
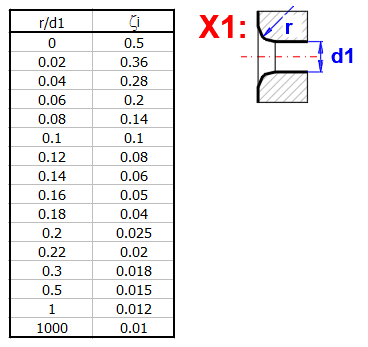
zetaI ... coefficient de perte d'entrée (arrondi)
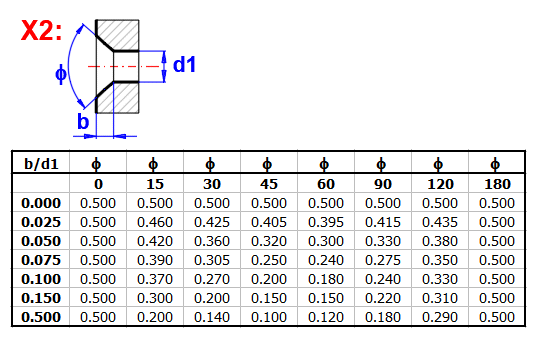
zetaI ... coefficient de perte à l'entrée (chanfrein)
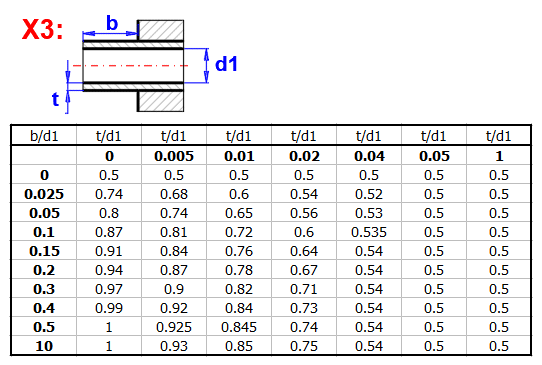
zetaI ... coefficient de perte à l'entrée (extrusion)
zetaB ... coefficient de perte (flexion)
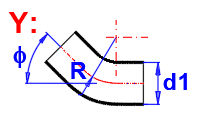
zetaB =(0.131 + 0.16 * (d1 / R)^3.5) * (Fi / 90)
zetaI ... coefficient de perte (transition)
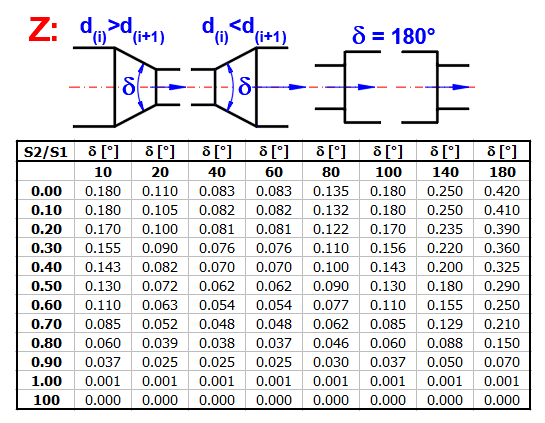
Buse, delta<10 : ZetaI = (Lambda / (8
* SIN(delta/2))) * (1 - (S2/S1)^2)
Buse, delta>=10 : ZetaI = Approximation de la table
Diffuseur : ZetaI = (S2/S1 - 1)^2 * SIN(MIN(delta;90))
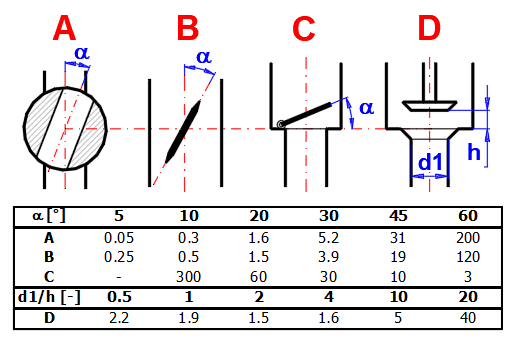
zetaV ... coefficient de perte de
charge de la vanne
Le tableau peut être utilisé pour une orientation approximative :
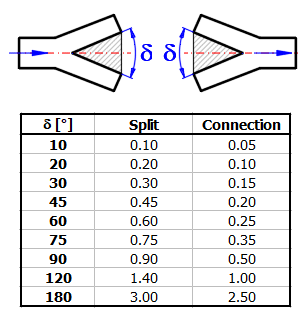
ZetaS ... Coefficient de perte pour le clivage de la tuyauterie
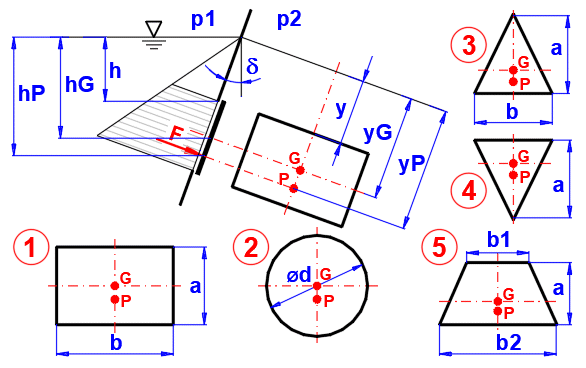
Force hydrostatique :
F = ((p1 - p2) + Ro * g * hG) * S
p1, p2 ... pression
g ... accélération de la gravité
Ro ... densité
hG ... profondeur du centre de gravité de la surface
S ... surface
Distance y du centre de pression :
1. yP = y+(2*a + 3*y)/(a + 2*y) * (a/3)
2. yP = y+(8*y + 5*a) / (2*y + a) * (a/8)
3. yP = y+(4*y + 3*a) / (3*y + 2*a) * (a/2)
4. yP = y+(2*y + a) / (3*y + a) * (a/2)
5. yP = y+(2*y*(b1 + 2*b2) + a*(b1 + 3*b2)) / (3*y*(b1 + b2) + a*(b1 + 2*b2)) * (a/2)
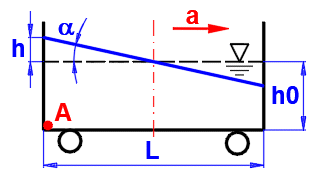
a =
atan(a / g)
a ... accélération
g ... accélération de la gravité
h = L / 2 * tan(a)
L ... longueur du vaisseau
Pression sur A :
pA = Ro * (g^2 + a^2)^0,5 * (h0 + dh) * COS (a)
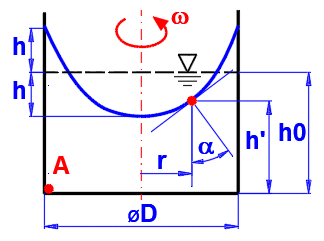
w =
2 * p
* n / 60
n ... révolution [rpm]
h = (w^2 * (D / 2)^2) / (4 * g)
w ... vitesse angulaire
D ... diamètre
g ... accélération de la gravité
Pression sur A :
pA = 0 - r * g * (-h0 +
h) + 0.5 * r * h^2 *
w^2
h' = h0 - h + r^2 * w^2 / (2 * g)
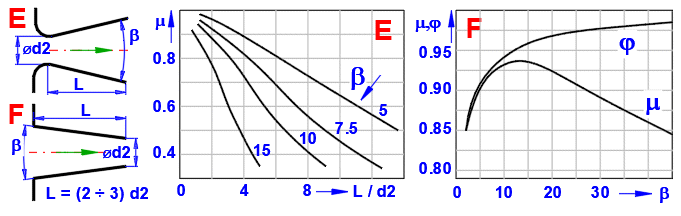
La vraie vitesse de décharge d'un fluide réel se différencie des valeurs théoriques pour les fluides idéaux. En cas de décharge d'un fluide par un orifice (ou un manchon court), le contact avec la paroi est restreint; la dissipation de l'énergie sera également restreinte. Par conséquent, il est possible de considérer le fluide comme non visqueux et les résultats théoriques peuvent être corrigés par les coefficients correcteurs suivants.
j
= v / vt
v .... vitesse réelle de l'écoulement
vt ... vitesse d'écoulement théorique
a
= S2' / S2
S' ... section réelle de l'écoulement du fluide
S .... Section transversale de l'orifice
m
= a * j = Q / Qt
Q .... débit volumétrique réel
Qt ... débit volumétrique théorique
v2t = ((2 * g * (h1 + (p1 - p2) / Ro)
/ (1 - (S2 / S1)^2))^0,5
g ... accélération de la gravité
Ro ... densité
p1, p2 ... pression
S1, S2 ... surface
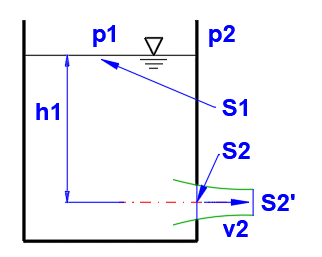
v2 = j * v2t
Qt = S2 * v2t
Q = a * S2 * j * v2t = m * Qt
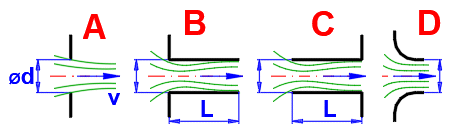
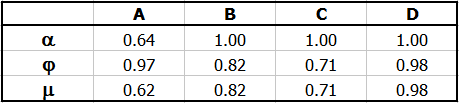
Coefficient m en fonction de Re pour une sortie de type A sans buse.
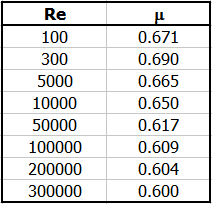
Re = v2t * d / n
n ... Viscosité cinématique
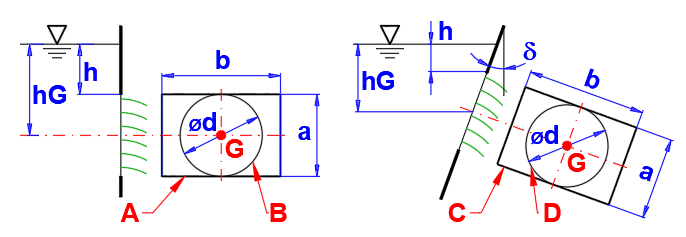
Pour les grandes ouvertures (bord supérieur proche de la surface et rapport entre la hauteur de l'ouverture et la profondeur du centre de gravité proche de un), une distribution non linéaire de la vitesse d'écoulement doit être envisagée.
Trou rectangulaire
Q = m * b * (2 * g)^0.5 * ((h + a)^(3/2) -
h^(3/2))
Trou circulaire
Q = m * p * r^2 * (2
* g * hG)^0.5 * (1 - 1/32 * (r / hG)^2 - 5/1024 * (r / hG)^4)
r = d / 2
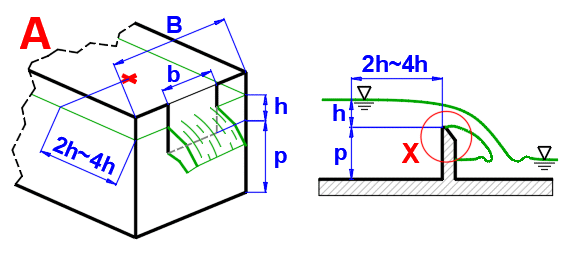
Un déversoir est du point de vue hydraulique une décharge par un grand orifice, sans paroi supérieure au-dessus du rayon (image A). Un déversoir peut être parfait si le niveau derrière le déversoir est inférieur au bord du déversoir ou imparfait (noyé) si le niveau derrière le déversoir est plus haut (image B). Les déversoirs parfaits sont utilisés pour la détermination d'une quantité de fluide s'écoulant. Les bords du déversoir peuvent être, eux, rectangulaires, triangulaires, trapézoïdaux, ronds selon la forme.
La hauteur du niveau h doit être mesurée à une distance suffisante devant le déversoir (généralement 2 h – 4 h). Le niveau au-dessus du déversoir est plus bas, parce qu'une partie de l'énergie positionnelle s'est déjà transformée en énergie cinétique.
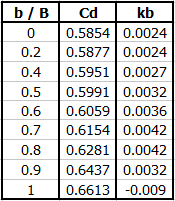
Débit volumétrique (ISO 1438)
Q = Cd * (2/3) * (2 * g)^0,5 * be * he^(3/2)
Cd ... coefficient de débit
g ... accélération de la gravité
be ... largeur effective
he ... hauteur effective de débordement
he = h + 0,001
be = b + kb
Débit volumétrique (formule
générale)
Q = 2/3 * Cd * b * h * (2 * g * h)^0.5
b ... largeur
h ... hauteur de débordement
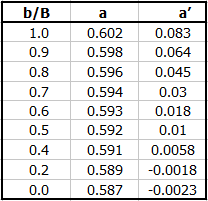
Coefficient de débit (ISO 1438)
Cd = a + a' * (h / p)
en fonction de b/B
Coefficient de débit
(Société des ingénieurs suisses)
Cd = 0.615 * (1 + (1 / (1000 * h + 1.6))) * (1 + 0.5 * (h / p)^2)
Coefficient de débit
(Hansen)
Cd = 0.61706 / (1 - 0.35815 * (h^3)^0.5)
Coefficient de débit
(Bazin)
Cd = (0.6075 + 0.045 / h) * (1 + 0.55 * (h / (h + p))^2)
Coefficient de débit
(Frese)
Cd =
(0.5755+0.017/(h+0.18)-0.075/(b+1.2))*(1+(0.25*(b/B)^2+0.025+0.0375/((h/(h+p))^2+0.02))*(h/(h+p))^2)
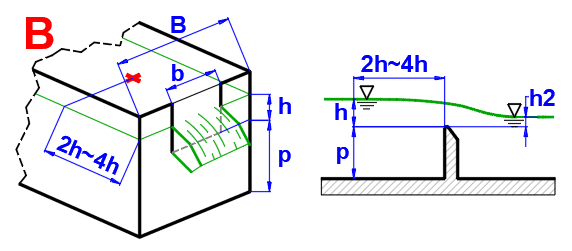
Débit volumétrique (ISO 1438)
Q = f * Cd * (2/3) * (2 * g)^0,5 * be * he^(3/2)
f ... coefficient d'inondation
pour h/p=0,5, f =1,007 * ((0,975 - h2/h)^1,45)^0,265
pour h/p=1,0, f =1,026 * ((0,960 - h2/h)^1,55)^0,242
pour h/p=1,5, f =1,098 * ((0,952 - h2/h)^1,75)^0,22
pour h/p=2.0, f =1.155 * ((0.950 - h2/h)^1.85)^0.219
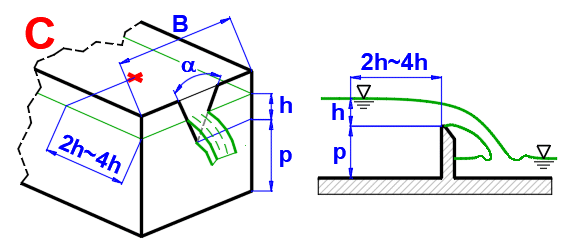
Débit volumétrique (ISO 1438)
Q = Cd * (8/15) * TAN(alfa/2) * (2 * g)^0.5 * he^(5/2)
he ... hauteur effective du déversoir
Tâche souvent résolue pour une tuyauterie à section constante, coudes, valves, etc. L'équation universelle de Bernoulli avec utilisation des coefficients de perte est utilisée pour sa résolution.
Calcul du débit, de la vitesse, des pertes, de la puissance dans une tuyauterie de section constante.
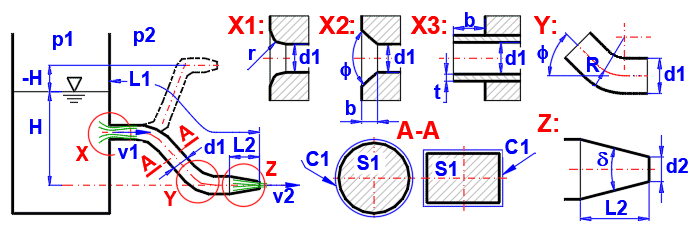
Calcul de la vitesse d'écoulement
:
v2 = ((2 * g * (H +((p1 - p2) / (Ro * g))))/((ZetaI + Lambda * ((L1-L2) / dh1) +
ZetaBV) * (dh2 / dh1)^4 + (1 + ZetaO)))^0.5
g ..... accélération de la gravité
H ..... hauteur de la surface
p1, p2 ... pression
dh1, dh2 ... diamètre hydraulique
L1,L2 ... longueur
Ro ... densité
Lambda ... coefficient de perte par frottement
ZetaI ... coefficient de perte à l'entrée
ZetaBV ... coefficient de perte des coudes+valves
ZetaO ... coefficient de perte buse/diffuseur
ZetaO ... coefficient de perte
buse/diffuseur
Intégration numérique (100 étapes), calcul séquentiel de Sx, vx, Rex, Lambdax,
hzx et, à partir de la hauteur totale de perte hz, du coefficient ZetaO lié à la
vitesse de décharge v2.
Pour un diffuseur et un angle delta > 10
ZetaO = ((S2 / S1) - 1)^2 * SIN(delta)
Pour le calcul est utilisée l'équation de Bernoulli avec utilisation des coefficients de perte pour le calcul de la vitesse de sortie vo.
Calcul du débit, de la vitesse, des pertes, de la puissance dans une tuyauterie de diverses sections et du nombre de branches.
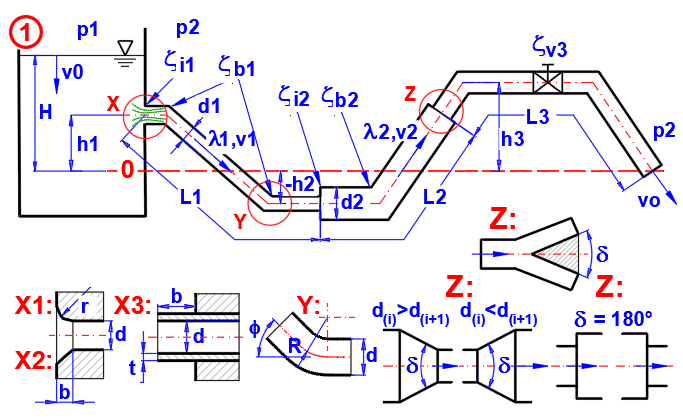
A = 2 * g * (v0^2 / (2 * g) + (p1 - p2) / (Ro * g) + H)
B(i) = (Zeta(i) + Lambda(i) * L(i) / dh(i)) * n(i) * (So / S(i))^2
vo = (A / (1 + SB(i)))^0.5
[i = 1 .... 15]
g ..... accélération de la gravité
H ..... hauteur de la surface
p1, p2 ... pression
v0 ... vitesse de la surface
dh(i) ... diamètre hydraulique
L(i) ... longueur
n(i) ... nombre de tuyaux parallèles
So ... section de sortie
S(i) ... section de la conduite i
Ro ... densité
Lambda ... coefficient de perte par frottement
Zeta ... somme des coefficients de perte zetaI, zetaB, zetaV
Le calcul des coefficients de perte est décrit ci-dessus.
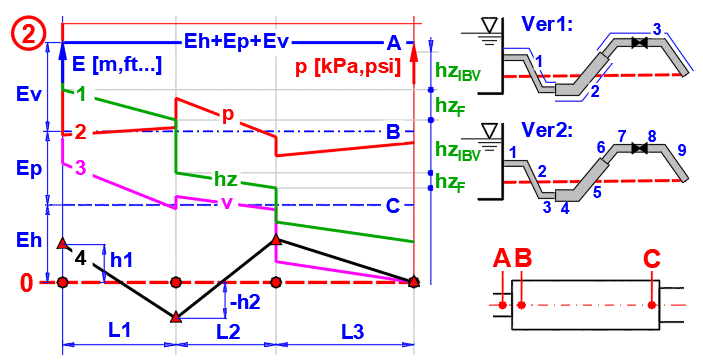
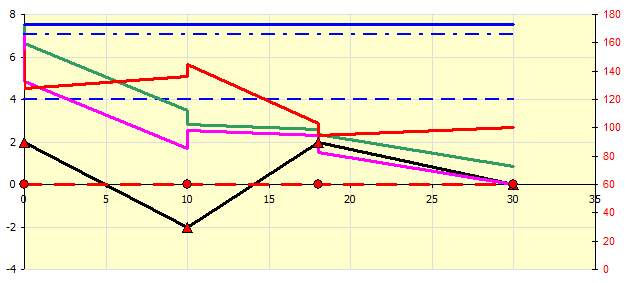
Exemple de diagramme
Lors de la régulation d'un débit de fluide par une tuyauterie naît un flux non stationnaire. Devant la valve, une pression supérieure à celle derrière la valve se forme en cas de diminution du débit. Pour les longues tuyauteries transportant un fluide, il peut y avoir une hausse de la pression pouvant endommager la tuyauterie en cas de fermeture rapide (d'urgence) de la tuyauterie.
Lors de la fermeture de la tuyauterie, l'énergie cinétique du fluide se consomme graduellement pour sa compression, le cas échéant déformation de la tuyauterie. L'onde de choc se diffuse dans la tuyauterie à la vitesse du son dans le fluide donné dans le sens B->A et retour A->B.
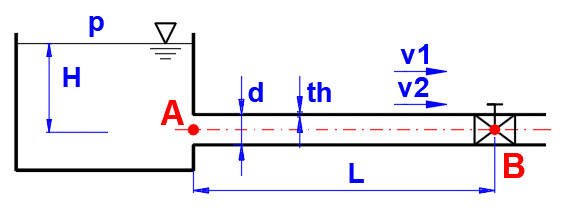
Le temps de parcours de
l'onde t
t = 2 * L / a
L ... longueur du tuyau
a ... vitesse du son
Vitesse du son
at [m/s] (théorique, pour un tuyau parfaitement rigide)
at = (K / Ro)^0.5
K ..... module de masse du fluide
Ro ... densité
Vitesse du son a [m/s]
(tuyau à paroi mince, th =< 0.1*d)
a = (K / Ro)^0.5 / (1 + (K*d) / (E*th))^0.5
E ... module d'élasticité du matériau du tuyau
d ... diamètre du tuyau
th ... épaisseur de la paroi du tuyau
Vitesse du son a [m/s]
(tuyau à paroi épaisse, th > 0.1*d)
a = (K/Ro)^0.5 / (1 + 2 * (K/E) * ((D^2 + d^2) / (D^2 -
d^2)))^0.5
E ... module d'élasticité du matériau du tuyau
d ... diamètre intérieur de la conduite
D ... diamètre extérieur de la conduite
Pour un temps de
fermeture de la conduite tc =< t
A. Tuyau parfaitement rigide
p = Ro * (v1 - v2) * at
B. Tuyau à paroi mince
p = Ro * (v1 - v2) * a
v1, v2 ... vitesse du fluide
Pour un temps de
fermeture de la conduite tc > t
p = Ro * L * (v1 - v2) / t
Les calculs couvrent certaines tâches souvent résolues dans le domaine de la mécanique des fluides. Si votre tâche tombe dans le domaine des problèmes à résoudre, procédez comme suit :
1. Dans le paragraphe [1] choisissez le fluide; le cas échéant, réglez ses
paramètres et définissez ceux de l'environnement.
2. Sélectionnez la tâche correspondante et remplissez les valeurs initiales
connues.
3. Les calculs sont sous la forme du modèle mathématique de la tâche donnée. Si,
par conséquent, le résultat d'un calcul doit être un des paramètres initiaux, il
est nécessaire de répéter graduellement ce paramètre.
Dans ce paragraphe, vous définissez les unités de calcul, sélectionnez et définissez les propriétés du fluide et de l'environnement.
Choisissez le système d'unités de calcul désiré sur la liste. Après changement d'unités, toutes les valeurs seront immédiatement corrigées.
Choisissez le fluide. Les valeurs dans la liste sont pour la pression barométrique. Si vous voulez saisir des paramètres propres d'un fluide, cochez la touche à droite.
Après avoir coché la touche à droite, vous pouvez saisir la vitesse du son et/ou le module d'élasticité volumique.
Après avoir coché la touche à droite, vous pouvez saisir la viscosité cinématique ou dynamique.
Pour la plupart des calculs, il suffit de régler une altitude nulle. Mais des tâches où il est nécessaire de prendre en compte une pression barométrique différente ou une pesanteur différente peuvent survenir.
La pesanteur standard est envisagée à la surface de la mer pour une latitude de 45°.
Le nombre de Reynolds Re est un paramètre sans dimension, déterminant la transition entre le flux laminaire et turbulent. Pour Re < 2300, il s'agit d'un flux laminaire; pour une valeur Re > 3000, le flux est presque toujours turbulent.
Le Re critique détermine donc le mode de calcul et, partant, les valeurs des coefficients de perte.
Quelques problèmes fréquemment résolus en hydrostatique.
Saisissez les valeurs demandées selon l'image.
Désignation des points :
G…Centre de gravité de la surface
P…Point d'application de la force
Après avoir coché la touche à droite, vous pouvez saisir une valeur propre de pression au-dessus de la surface et la pression à l'extérieur du récipient
Plan perpendiculaire à la surface : delta = 0
Plan parallèle à la surface : delta = 90
Force globale sur la surface S. Possède son point d'application dans le point P.
Distance du centre de gravité de la surface par rapport à la surface libre du fluide.
Distance du centre de la pression par rapport à la surface libre du liquide.
Le calcul ne résout pas une situation dans laquelle ce niveau se heurte au fond du récipient.
Le calcul ne résout pas une situation dans laquelle ce niveau se heurte au fond du récipient.
Calcul de la décharge stable d'un fluide par un orifice.
La vraie vitesse de décharge d'un fluide réel se différencie des valeurs théoriques pour les fluides idéaux. En cas de décharge d'un fluide par un orifice (ou un manchon court), le contact avec la paroi est restreint; la dissipation de l'énergie sera également restreinte. Par conséquent, il est possible de considérer le fluide comme non visqueux et les résultats théoriques peuvent être corrigés par les coefficients correcteurs suivants.
Après avoir coché la touche à droite, vous pouvez saisir une valeur propre de pression au-dessus de la surface et la pression à l'extérieur du récipient.
Si le récipient n'est pas cylindrique, il est possible de saisir directement la surface transversale après avoir coché la touche.
Si le récipient n'est pas circulaire, il est possible de saisir directement sa surface après avoir coché la touche.
Uniquement à des fins comparatives. N'inclut aucune perte.
Pour une décharge par un orifice sans manchon (A), il est possible de déterminer le coefficient de décharge en lien avec le nombre de Reynolds Re. Le Re calculé est à gauche, le coefficient de décharge, qu'il est possible d'utiliser à la place de la valeur standard 0,62, est à droite.
Choisissez les coefficients correspondants selon le type d'orifice de sortie (A-F) en fonction du tableau indiqué et des graphiques.
Cochez la touche à droite pour une saisie directe du coefficient de décharge (produit de [3.11] et [3.12]).
Pour les grands orifices (bord supérieur près de la surface et rapport entre la hauteur de l'orifice et la profondeur du centre de gravité proche de la valeur un), il faut envisager une répartition non linéaire de la vitesse de décharge.
Utilisez le coefficient de décharge de la même façon que dans le cas d'un petit orifice [3.13].
Un déversoir est du point de vue hydraulique une décharge par un grand orifice, sans paroi supérieure au-dessus du rayon (image A). Un déversoir peut être parfait si le niveau derrière le déversoir est inférieur au bord du déversoir ou imparfait (noyé) si le niveau derrière le déversoir est plus haut (image B). Les déversoirs parfaits sont utilisés pour la détermination d'une quantité de fluide s'écoulant. Les bords du déversoir peuvent être, eux, rectangulaires, triangulaires, trapézoïdaux, ronds selon la forme.
La hauteur du niveau h doit être mesurée à une distance suffisante devant le déversoir (généralement 2h – 4h). Le niveau au-dessus du déversoir est plus bas, parce qu'une partie de l'énergie positionnelle s'est déjà transformée en énergie cinétique.
Les conditions limites pour lesquelles les calculs sont définis sont ensuite inscrites dans le calcul à droite des cellules initiales.
Pour le calcul des déversoirs rectangulaires (image A) ou pour celui du coefficient de débit Cd existent de nombreuses formules et procédures indiquées dans la littérature. Nous les indiquons donc également à titre de comparaison.
La hauteur au-dessus du déversoir h se mesure généralement à une distance 2h ~ 4h du déversoir (élimination de la baisse de niveau au-dessus du déversoir).
Si la hauteur du niveau sur l'écoulement influence le débit d'eau (image B), il est possible d'utiliser ce calcul, les paramètres du déversoir étant définis dans la partie A.
La valeur du coefficient en lien avec p et le rapport h2/h sont indiqués dans la cellule verte.
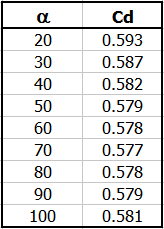
Si la surface de découpe est relativement petite par rapport à la surface de section de l'afflux, il est possible d'utiliser un Cd déterminé de manière expérimentale dépendant uniquement de l'angle de découpe.
Tâche souvent résolue pour une tuyauterie à section constante, coudes, valves, etc. L'équation universelle de Bernoulli avec utilisation des coefficients de perte est utilisée pour sa résolution.
Calcul du débit, de la vitesse, des pertes, de la puissance dans une tuyauterie de section constante.
Remplissez tous les paramètres de dimensions et de pression. Pour une estimation des coefficients de perte, vous pouvez utiliser les calculs à droite. Il est possible de sélectionner une surpression négative (p2 > p1); il est possible de sélectionner une hauteur négative (H < 0); dans chaque cas il est nécessaire de respecter le sens de flux du fluide de l'entrée vers la sortie.
La pression p1 = p2 du paragraphe [1.0] est utilisée comme valeur par défaut. Saisissez la pression à l'intérieur du récipient p1 et la pression environnante p2 après avoir coché la touche à droite.
La hauteur du niveau doit être supérieure à la valeur à droite.
Si l'orifice de sortie est supérieur au niveau de la surface, saisissez la hauteur H en tant que valeur négative (doit être équilibré par une surpression p1 > p2).
Si p1 < p2, la surpression externe doit être compensée par la hauteur de niveau H.
Si la tuyauterie n'est pas de section ronde, vous pouvez, après avoir coché la touche à droite, saisir la valeur de surface de la tuyauterie et du périmètre mouillé. Le diamètre hydrodynamique dh selon la formule dh = 4 * S / C, utilisée ensuite dans les calculs, est ensuite déterminé à partir de ces valeurs.
Indiqué dans l'image en tant que coupe A-A.
Choisissez le matériau correspondant de la tuyauterie dans la liste. La valeur présélectionnée de rugosité en [mm/in] sur la ligne suivante est la moyenne d'étendue indiquée dans la parenthèse. Vous pouvez saisir une valeur propre après avoir coché la touche.
Sur la base de la rugosité de la tuyauterie « k » et du coefficient « Re » sont indiquées dans la littérature de nombreuses formules pour le calcul du coefficient de pertes par friction pour un flux turbulent. Choisissez le calcul correspondant dans la liste.
Le calcul le plus couramment utilisé est "C. Colebrook - White", qui couvre également les tuyaux hydrauliquement lisses (k=0). Détails dans l'aide.
La proposition de coefficient de pertes par friction Lambda dépend de Re et, parallèlement, le calcul de Re dépend du coefficient de pertes par friction Lambda (calcul de vitesse de flux).
La valeur de proposition est transposée automatiquement dans la cellule initiale.
Après avoir coché la touche, vous pouvez saisir une valeur propre.
Choisissez le coefficient d'entrée selon le calcul / la recommandation à droite.
Sur l'image en tant que X1, X2, X3.
Il s'agit de la somme de tous les coefficients pour toutes les pertes possibles dans la tuyauterie (courbures, valves…).
Le coefficient de perte d'un coude de la tuyauterie peut être déterminé par le calcul à droite, les coefficients de perte des valves peuvent être en gros évalués selon l'image.
À choisir si la tuyauterie possède un jet/diffuseur à son extrémité.
Si d1>d2 (dh1>dh2) la conception des pertes est utilisée pour la buse, pour d1<d2 pour le diffuseur.
Si la tuyauterie n'est pas de section ronde, vous pouvez, après avoir coché la touche à droite, saisir la valeur de surface de la tuyauterie et du périmètre mouillé. Le diamètre hydrodynamique dh selon la formule dh = 4 * S / C, utilisée ensuite dans les calculs, est ensuite déterminé à partir de ces valeurs.
Indiqué dans l'image en tant que coupe A-A.
Saisissez la longueur du jet/diffuseur. Elle doit être inférieure à la longueur de la tuyauterie L1.
Il est calculé à partir des valeurs dh1, dh2 et L2.
Pour jet (d1 > d2) et Diffuseur (delta < 10) est utilisée une estimation sur la base d'une intégration des pertes. Pour Diffuseur et delta > 10, quand a lieu la séparation du flux du fluide de la paroi de la tuyauterie, est utilisé le rapport : zetaO = ((S2 / S1) - 1)^2 * SIN(delta).
Indique le rapport entre l'énergie de hauteur et de pression sur l'entrée et l'énergie cinétique du flux de sortie du fluide.
Les paramètres de puissance indiqués permettent une évaluation de la tuyauterie.
S'applique :
Pp + Ph = Pz + Po
respectivement.
Pp + Ph + Pv = Pz + Po pour le paragraphe [6.0].
Les débits sont souvent indiqués dans diverses unités indépendamment des unités du calcul. C'est pourquoi la conversion des plus fréquemment employées est indiquée ci-après.
Pour le calcul est utilisée l'équation de Bernoulli avec utilisation des
coefficients de perte pour le calcul de la vitesse de sortie vo.
Calcul du débit, de la vitesse, des pertes, de la puissance dans une tuyauterie
de diverses sections et du nombre de branches.
Remplissez les conditions sur l'entrée dans la tuyauterie.
Il est possible de sélectionner une surpression négative (p2 > p1), il est possible de sélectionner une hauteur négative (H < 0), dans chaque cas il est nécessaire de respecter le sens de flux du fluide de l'entrée vers la sortie.
La pression p1 = p2 du paragraphe [1.0] est utilisée comme valeur par défaut. Saisissez la pression à l'intérieur du récipient p1 et la pression environnante p2 après avoir coché la touche à droite.
Vitesse du fluide (énergie cinétique) devant l'entrée dans la tuyauterie. Dans la plupart des problèmes résolus (grand récipient par rapport au volume de la tuyauterie), il est possible de négliger la vitesse et d'utiliser une valeur nulle.
Elle sera non nulle par exemple dans le cas d'un piston refoulant un fluide par la tuyauterie.
La hauteur du niveau de surface doit être supérieure à la valeur à droite.
Si l'orifice de sortie est plus haut que le niveau de surface, saisissez la hauteur H en tant que valeur négative (doit être compensé par la surpression p1 > p2).
Si p1 < p2, la surpression extérieure doit être compensée par la hauteur de niveau H.
Sur la base de la rugosité de la tuyauterie « k » et du coefficient « Re » sont indiquées dans la littérature de nombreuses formules pour le calcul du coefficient de pertes par friction pour un flux turbulent. Choisissez le calcul correspondant dans la liste.
Le calcul le plus couramment utilisé est "C. Colebrook - White", qui couvre également les tuyaux hydrauliquement lisses (k=0). Détails dans l'aide.
Somme du potentiel énergétique de pression (p2 – p1), du potentiel de la
hauteur de pression du fluide (H) et de l'énergie cinétique du fluide (v0) sur
l'entrée dans la tuyauterie.
Généralement, le niveau énergétique est exprimé en mètres de colonne de fluide.
Sélectionnez à droite les unités dans lesquelles le niveau énergétique doit être
exprimé.
Indiqué dans le graphique ci-après par une abscisse bleue (Image 2-A).
Uniquement à des fins comparatives. N'inclut aucune perte.
Indique le rapport entre l'énergie de hauteur et de pression sur l'entrée et l'énergie cinétique du flux de sortie du fluide.
Les paramètres de puissance indiqués permettent une évaluation de la tuyauterie.
S'applique :
Pp + Ph = Pz + Po
respectivement.
Pp + Ph + Pv = Pz + Po pour le paragraphe [6.0].
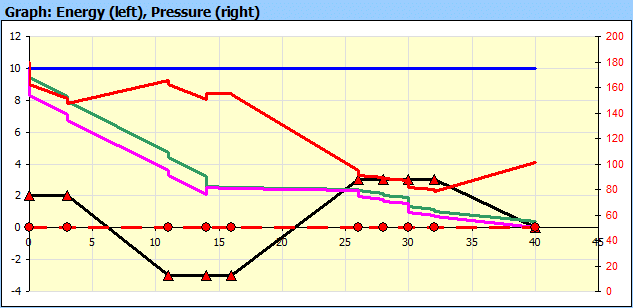
Description du graphique (Image 2) :
Ligne droite A : Ligne d'énergie totale. Indique la somme des énergies (de
hauteur-Eh, de pression-Ep et cinématique-Ev) du fluide sur l'entrée dans la
tuyauterie.
Ligne droite B : Somme de l'énergie de hauteur (Eh) et de pression (Ep)
Ligne droite C : Énergie de hauteur (Eh)
Ligne droite 0 : Ligne nulle rapportée à l'extrémité de la tuyauterie
Courbe 1 : Hauteur de perte hz (perte dans chaque partie de la tuyauterie)
Courbe 2 : Pression dans la tuyauterie (graduation à droite en kPa ou psi)
Courbe 3 : Hauteur cinématique
Courbe 4 : Points de hauteur du début de chaque section par rapport à la ligne
nulle
Remplissez graduellement les valeurs pour chaque section de la tuyauterie dans le tableau (une ligne pour chaque section).
Deux approches, le cas échéant leur combinaison, peuvent être choisies.
Simplifiée (Image2. Ver1) :
Chaque section est divisée selon le diamètre de la tuyauterie et tous les
coefficients de perte (entrée, coude, valve...) dans une section sont résumés
dans un coefficient (colonne H), appliqué au début de la section correspondante.
Détaillée (Image2. Ver2) :
La tuyauterie est divisée en sections, afin que le coefficient de perte
correspondant (colonne H) se trouve toujours au début de la section. Vous
obtenez un graphique plus détaillé [6.19]. Les résultats globaux (Q, vo...) sont
concordants.
Choisissez le nombre de sections connexes devant être résolu (1-15).
Il est possible de diviser un tube en deux tubes et plus. Le cas échéant fusion de plusieurs tubes en un (Image détail Z).
Hauteur du début de la section de la tuyauterie au-dessus (sous) le point de sortie (final) de la dernière section (ligne nulle).
Longueur de chaque section.
Saisissez le diamètre. Si le tube n'est pas rond, saisissez le diamètre
hydraulique dh (voir E).
En pressant la touche « V », la valeur de la première ligne se copie dans les
autres.
Si la touche à droite est cochée, la surface est comptée à partir de la section ronde du diamètre d de la colonne à gauche (D).
Pour une tuyauterie de section non ronde, cochez la touche à droite et saisissez la surface de section (E) et saisissez le diamètre hydraulique dh dans la cellule du diamètre d (D).
dh = 4 * S / C
S...surface de section
C...périmètre mouillé
Angle de rétrécissement/élargissement du passage entre deux sections (Image 1 Dét. Z), en cas de division de la tuyauterie en deux branches, angle entre les tubes.
Le coefficient de perte correspondant proposé ZetaI se trouve à droite (colonne G).
Sur la base de la proportion entre les surfaces (colonne E) et le biseautage (colonne F) entre deux sections est proposé un coefficient de perte au début de la section (détails dans la partie théorique de l'aide). Le coefficient de perte en cas de ramification de la tuyauterie est également proposé de manière similaire.
Avec la touche "=>" vous pouvez transférer en masse la proposition dans la colonne H, utilisée dans le calcul.
Somme de tous les coefficients de perte dans la section correspondante de la tuyauterie.
ZetaI….pertes d'entrée, pertes par modification de la section (proposition
colonne G)
ZetaB…pertes d'un coude (calcul dans le paragraphe précédent [5.0])
ZetaV…pertes de valve (tableau dans le paragraphe précédent [5.0])
Pour le calcul de la tuyauterie réelle, il faut saisir la rugosité de la tuyauterie. Pour orientation, utilisez le tableau ci-après. En pressant la touche « V », la valeur de la première ligne se copie dans les autres.
- Tuyau lisse hydraulique (0-0) mm /
(0-0) in
- Acier - Tube continu sans soudure (0.03-0.1) mm / (0.00118-0.00394) in
- Tube en acier neuf soudé (0.05-0.1) mm / (0.00197-0.00394) in
- Tubes en acier soudés corrodés (0.15-0.5) mm / (0.00591-0.01969) in
- Tôle d'acier soudée - tubes d'air (0.5-0.8) mm / (0.01969-0.0315) in
- Tôle d'acier rivetée (1-6) mm / (0.03937-0.23622) in
- Tubes en laiton et aluminium étirés à l'état pur (0.0015-0.01) mm /
(0.00006-0.00039) in
- Verre, plastique (0.0015-0.01) mm / (0.00006-0.00039) in
- Tuyau neuf en fonte (0.1-0.3) mm / (0.00394-0.01181) in
- Ancien tuyau en fonte (1-4.5) mm / (0.03937-0.17717) in
- Tuyau en caoutchouc (0.01-0.03) mm / (0.00039-0.00118) in
- Contreplaqué (0.025-0.1) mm / (0.00098-0.00394) in
- Céramique (0.45-6) mm / (0.01772-0.23622) in
- Briques avec taches de ciment (0.8-6) mm / (0.0315-0.23622) in
- Béton (0.8-9) mm / (0.0315-0.35433) in
Nombre de Reynolds Re (détails dans l'aide - Théorie)
Caractérise le flux d'un liquide visqueux, dépendant non seulement de la vitesse
moyenne, mais aussi de la dimension caractéristique de flux du fluide (diamètre
d ou dh), de la viscosité dynamique et de la densité.
Sert au calcul du coefficient des pertes par friction Lambda (colonne K).
Proposition de coefficient de pertes par friction Lambda. Dépend de Re (colonne J). Mais le calcul Re dépend rétroactivement de la vitesse de flux (pour lequel il faut connaître Lambda). Il y a donc une itération progressive des valeurs.
La valeur de proposition est automatiquement transférée dans la colonne à
droite (colonne L), qui est utilisée pour le calcul.
Après avoir coché la touche à droite, vous pouvez saisir la valeur propre du
coefficient de pertes par friction P.
Coefficient de pertes par friction Lambda. Nécessaire pour le calcul de la vitesse de flux. Si la touche à droite est cochée, c'est la valeur de proposition qui est employée (colonne K).
Si vous n'avez pas de raison impérieuse, utilisez la valeur de proposition.
En pressant la touche « V », la valeur de la première ligne se copie dans les autres lignes.
Vitesse du fluide dans la section donnée de la tuyauterie.
Sélectionnez dans la colonne N, O quelles valeurs vous voulez afficher et leurs unités. Le choix des unités est lié à la ligne [6.8].
hIBV…sommes des pertes (entrée, coude, valve) pour la section donnée
hF…...pertes par friction pour la section donnée
h-A, h-B, h-C…pertes depuis le début de la tuyauterie graduellement dans les
points A, B, C (Image 2)
v(pd)…énergie du fluide s'écoulant (pression dynamique)
p-A, p-B, p-C...pression absolue dans les points A, B, C
Lors de la régulation d'un débit de fluide par une tuyauterie naît un flux non stationnaire. Devant la valve, une pression supérieure à celle derrière la valve se forme en cas de diminution du débit. Pour les longues tuyauteries transportant un fluide, il peut y avoir une hausse de la pression pouvant endommager la tuyauterie en cas de fermeture rapide (d'urgence) de la tuyauterie.
Lors de la fermeture de la tuyauterie, l'énergie cinétique du fluide se consomme graduellement pour sa compression, le cas échéant déformation de la tuyauterie. L'onde de choc se diffuse dans la tuyauterie à la vitesse du son dans le fluide donné dans le sens B->A et retour A->B.
En pressant la touche vous lisez les paramètres du paragraphe [5.0].
Remplissez les paramètres initiaux selon l'image.
Choisissez le matériau de la tuyauterie.
Après avoir coché la touche à droite vous pouvez saisir une valeur propre.
En cas de fermeture complète de la valve v2 = 0.
Deux cas peuvent survenir.
1. Temps de fermeture de la valve t > T-temps de durée de l'onde de choc
[7.14, 7.21]
La pression s'accroît avec la réduction du temps de fermeture de la valve.
2. Temps de fermeture de la valve t < T-temps de durée de l'onde de choc
[7.14, 7.21]
La pression reste constante à son intensité maximale.
Défini dans le paragraphe [1.0]
La vitesse théorique du son [7.20] dépend de la densité du matériau et de l'élasticité volumique du fluide. Pour une tuyauterie réelle, la vitesse de diffusion du son baisse en relation avec les dimensions et le matériau de la tuyauterie.
Calcul approximatif de la viscosité et de la densité d'un fluide en relation avec la température.
Saisissez la température du fluide sélectionné. La densité et la viscosité sont proposées sur la base de la température. Le calcul est approximatif avec une précision de +- 6 % dans l'étendue des températures 0-100°C (32-212°F). .
En pressant la touche, vous transférez les valeurs de densité et de viscosité dans le paragraphe [1.0].
Paragraphe [3.0] - Calcul
du temps de diminution du niveau de h1 à h2.
Récipient défini selon la figure.
Liquide : eau, 20°C, p1=p2=pression atmosphérique (paragraphe [1.0]).
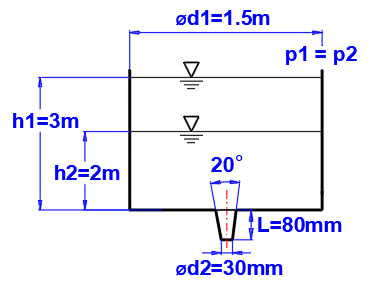
Entrez les valeurs d'entrée comme indiqué sur la figure, et obtenez les coefficients j et m à partir du graphique F. Le moment de la baisse du niveau est à [3.17].
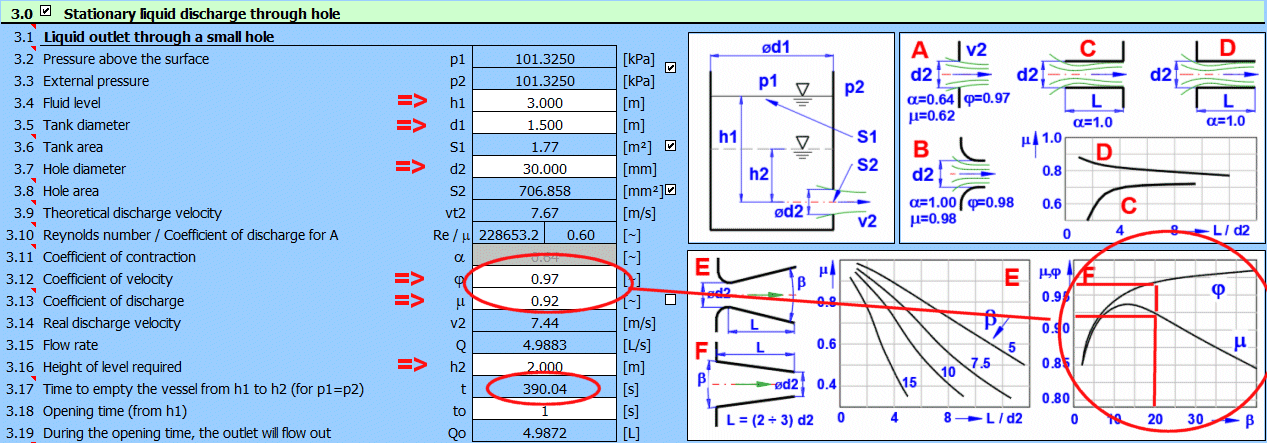
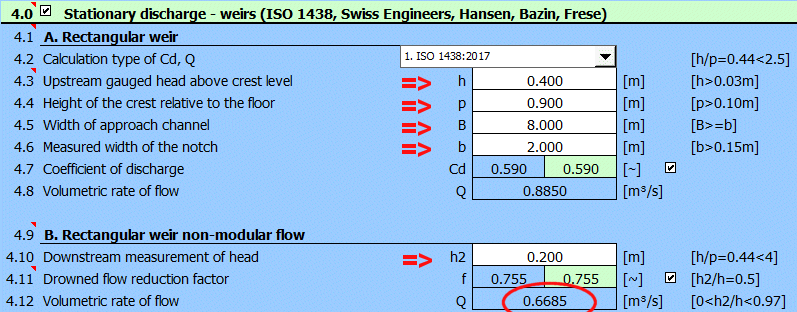
Paragraphe [4.0]. Calcul du
débit en utilisant un déversoir inondé.
Le déversoir est défini selon la figure.
Méthode de calcul selon la norme ISO 1438.
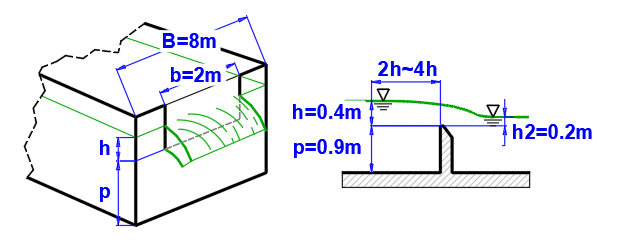
Entrez les valeurs d'entrée comme indiqué sur la figure. Le débit résultant pour le déversoir inondé est sur la ligne [4.12].
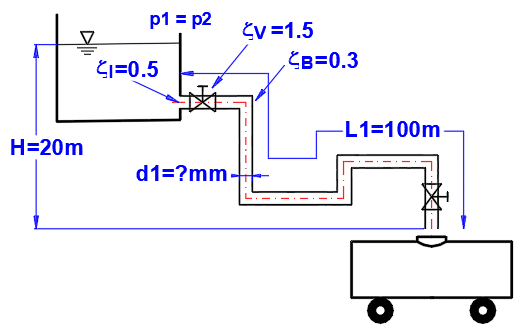
Paragraphe [5.0]. Calcul du
diamètre de la conduite pour le débit de fluide requis.
Définition des dimensions du tuyau et des coefficients de perte selon la figure.
Débit requis 100L/s = 0.1 m³/s
Pertes à l'entrée = 0,5, pertes coude+vanne = 5*0,3 + 2*1,5 = 4,5
Tuyau en fonte (neuf), rugosité k=0.2mm
Méthode de calcul du coefficient de perte Lambda : Colebrook - Blanc
Liquide : eau, 20°C, p1=p2=pression atmosphérique (Paragraphe [1.0])
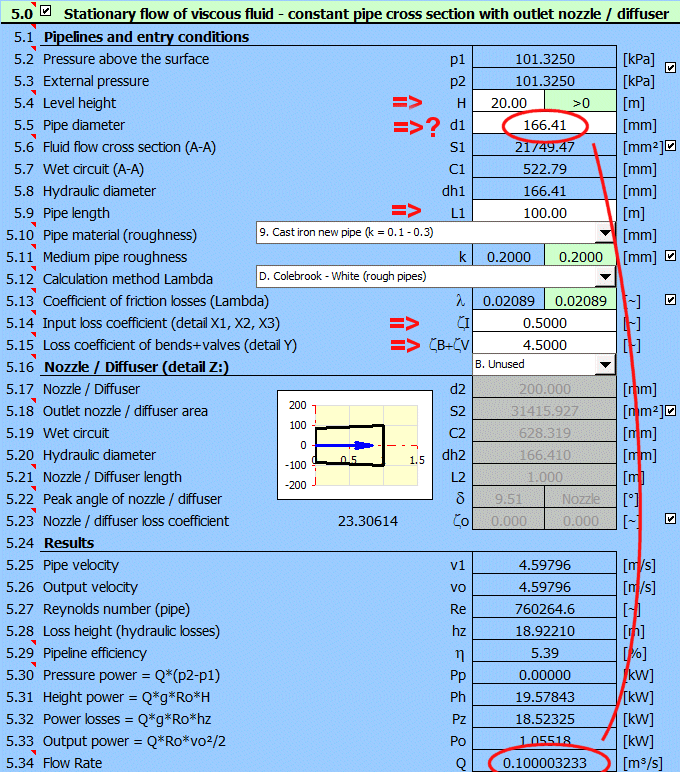
Entrer tous les paramètres connus et modifier progressivement la valeur de d1 [5.5] pour obtenir le débit souhaité Q = 0.1 m³/s.
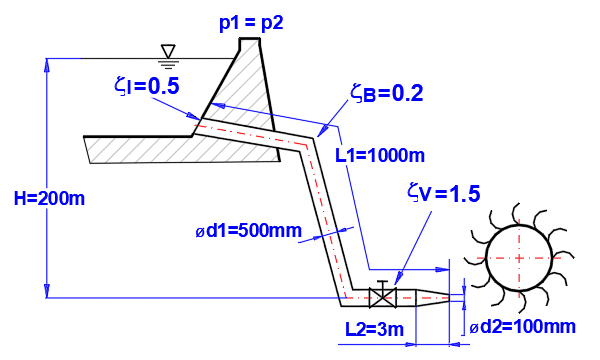
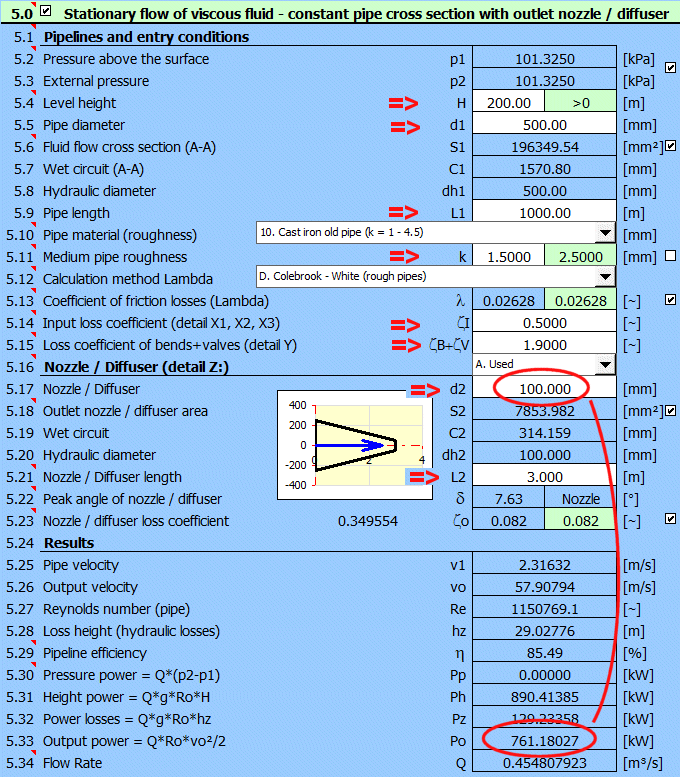
Paragraphe [5.0]. Calcul de
la puissance du courant à l'extrémité de la buse pour le diamètre spécifié.
Détermination pour quel diamètre de buse la puissance maximale est atteinte.
Définition des dimensions et des coefficients de pertes de la conduite comme
indiqué.
Pertes à l'entrée = 0.5, pertes coude+vanne = 2*0.2 + 1.5 = 1.9
Tuyau en fonte, rugosité k=1.5 mm
Méthode de calcul du coefficient de perte Lambda : Colebrook - Blanc
Liquide : eau, 20°C, p1=p2=pression atmosphérique (Paragraphe [1.0])
Entrez tous les paramètres connus. La
puissance du flux liquide en bout de tuyère est Po = 761kW [5.33].
Pour trouver la puissance maximale, on modifie progressivement le diamètre d2 de
la buse. La puissance maximale Po = 1162kW pour d2=157.6mm.
Dans le même temps, le rendement est réduit de 85.5% pour
d2=100mm à 61.8% pour d2=157.6mm.
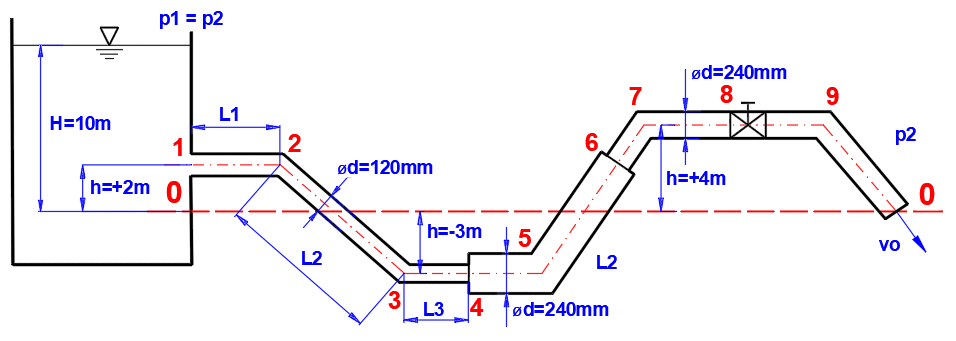
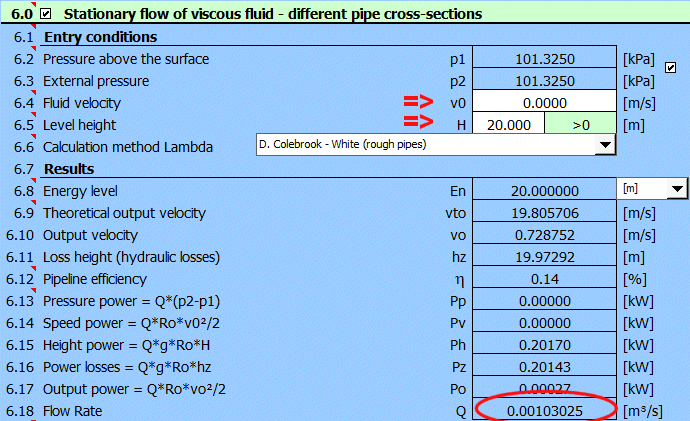
Paragraphe [6.0]. Calcul de
la progression détaillée de la pression et des pertes dans la canalisation,
calcul des vitesses et des débits des fluides.
Pipeline défini selon la figure et le tableau, où :
ID ... numéro de section (1-9)
L ... longueurs de chaque section
ZetaI, ZetaB, ZetaV ... pertes au début de la section (entrée, changement de
section, coude, vanne)
Matériau du tube : fonte, rugosité k=1.5mm
Méthode de calcul du coefficient de perte Lambda : Colebrook - Blanc
Fluide : eau, 20°C, p1=p2=pression atmosphérique (Paragraphe [1.0])
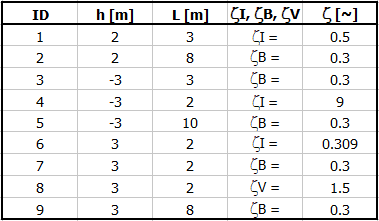
Définition des conditions :

Définir les paramètres des tuyaux (A-nombre de tuyaux, B-hauteur par rapport à la ligne zéro, C-longueur des sections, D-diamètre des tuyaux, F-angle de transition entre différents diamètres de tuyaux, H-coefficients de perte uniforme, I-rugosité des tuyaux).
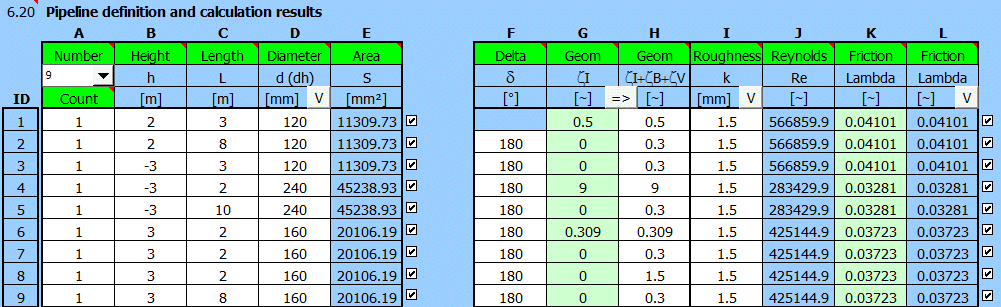
Résultats :

Détail de la pression et des pertes :
Paragraphe [6.0]. Calcul de
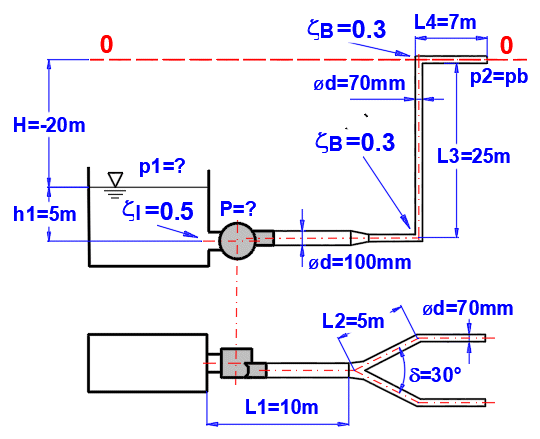
la puissance de la pompe pour pomper de l'eau jusqu'à 25m. Le débit requis est
de 10l/s.
La tuyauterie est définie comme indiqué.
L ... longueurs des sections individuelles
ZetaI, ZetaB ... pertes (entrée, changement de section, division du tuyau,
flexion).
Matériau du tube : tube en acier, rugosité k=0.1mm
Méthode de calcul du coefficient de perte Lambda : Colebrook - White
Fluide : eau, 20°C, p2=pression atmosphérique (Paragraphe [1.0])
Définir les paramètres du pipeline
(A-nombre de tuyaux, B-hauteur par rapport à la ligne zéro, C-longueur des
sections, D-diamètre des tuyaux, F-angle de séparation des tuyaux,
H-coefficients de perte individuels, I-rugosité des tuyaux).
La perte due à la séparation des tuyaux est en G2.

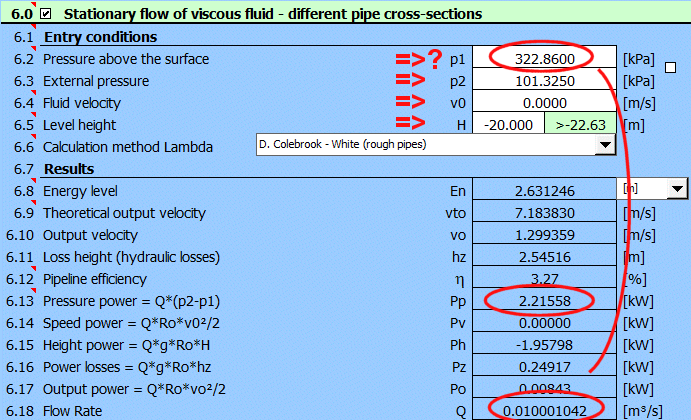
Entrez tous les paramètres connus et
modifiez progressivement la valeur de la pression p1 [6.2] pour atteindre le
débit souhaité Q = 0.01 m³/s [6.18].
La puissance nécessaire de la pompe est alors donnée par la ligne [6.13]
Pp=2.22kW.
Paragraphe [6.0]. Calcul du
débit d'eau dans la douche.
Tuyaux et douche définis selon la figure :
L ... longueurs des sections individuelles
ZetaI, ZetaV, ZetaB ... pertes (entrée, vanne, coude)
Matériau du tuyau : tuyau en acier, rugosité k=0.1mm
Méthode de calcul du coefficient de perte lambda : Colebrook - Blanc
Liquide : eau, 20°C, p1=p2=pression atmosphérique (Paragraphe [1.0])
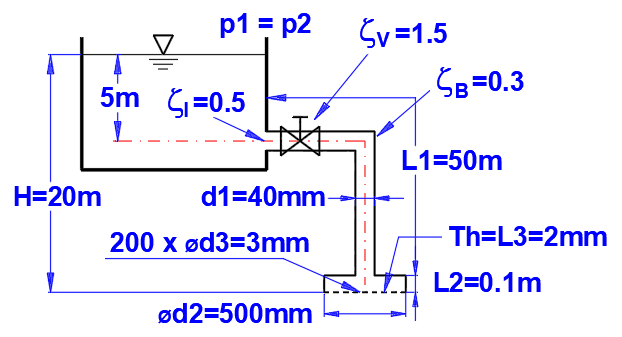
Définissez les paramètres du tuyau et de la douche avec 200 trous.

Précisez la hauteur du niveau. Le débit d'eau dans la douche Q=1L/s est sur la ligne [6.18].
Paragraphe [7.0]. Calcul du coup de bélier en cas de fermeture d'urgence de la canalisation à partir de l'exemple 4.

Vous pouvez utiliser le
bouton "[5.0] >> [7.0]" pour définir les paramètres. Ceci charge les valeurs du
paragraphe [5.0].
Ensuite, entrez le matériau, remplissez l'épaisseur de la paroi du tuyau de 20
mm et le temps de fermeture de la valve de 2 secondes.
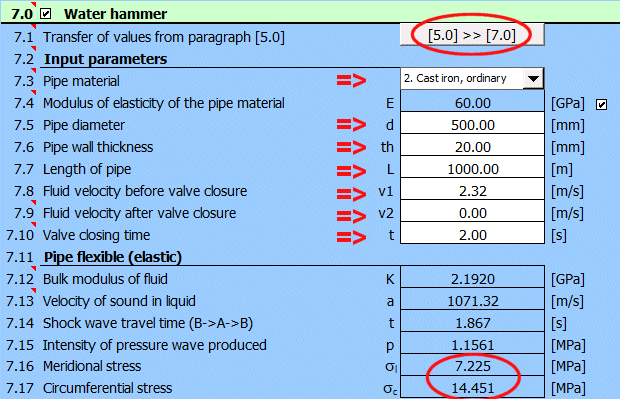
Comparez l'augmentation de la tension [7.16, 7.17] pour le temps de fermeture de la valve pour t<1.86 s.
L'information sur le réglage des paramètres de calcul et le choix de la langue peut être trouvée dans le document "Réglage des calculs, changement de langue".
Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".
Littérature:
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová, CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
Normes:
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs a paroi mince
^