Propriétés thermiques des matériaux

Contenu:

Propriétés thermiques des matériaux

Ce cahier contient des informations sur l'effet de la température sur certaines propriétés physiques et mécaniques des matériaux de l'ingénierie mécanique. Les tâches suivantes peuvent être résolues à l'aide de cet outil:

  1. Calcul du coefficient linéaire de dilatation thermique et d'allongement longitudinal d'un composant.
  2. Extension d'un groupe de composants disposés en chaîne linéaire.
  3. Calcul du module d'élasticité.

Ce calcul utilise les données, les procédures et les algorithmes de la documentation technique spécialisée et des normes.
Liste des normes: EN 1561, EN 1563, EN 16079, EN 1753, EN 10088-1, EN 10095, EN 10269, EN 10302

Note: La principale source d'informations sur un matériau spécifique devrait toujours être son fournisseur ou une base de données de matériaux vérifiée et fiable. La tâche de cet outil n'est pas de déterminer les paramètres exacts du matériau. Les valeurs calculées théoriquement ne peuvent jamais remplacer les données provenant des essais de matériaux. Le but de cette application est d'offrir à l'utilisateur une estimation qualifiée des valeurs attendues des paramètres du matériau lorsque des données précises ne sont pas disponibles pour un matériau spécifique.
Avertissement: Les résultats calculés ne sont qu’à titre indicatif et ne peuvent remplacer les données obtenues par une mesure précise d'un matériau particulier. 

L’interface d’utilisateur

 L’interface d’utilisateur.

 

A télécharger

 A télécharger.

 

Tarif, Achat

 Tarif, Achat.
 

Commande, structure et syntaxe des calculs .

L'information sur la syntaxe et la commande du calcul peut ętre trouvée dans le document " commande, structure et syntaxe des calculs ".

A. Coefficient linéaire de dilatation thermique.

Ce chapitre aborde la question de la dilatation thermique longitudinale des matériaux de l'ingénierie mécanique. Le paragraphe [1] a un caractère informatif. Le paragraphe [2] est utilisé pour le propre calcul des paramètres de matériau pertinents en fonction de la température sélectionnée.

 

Lorsqu’un corps est chauffé ou refroidi, ses dimensions changent. En cas de corps à une dimension prédominante, on parle de dilatation thermique longitudinale. La dépendance de l'allongement du type de matériau est exprimée par le coefficient de dilatation thermique longitudinale. En général, cette grandeur physique de matière est définie par le rapport:

où:
L0 ... longueur initiale d’un corps
DL ... changement de la longueur 
DT ... changement de la température

Cependant, ce coefficient n'a pas une valeur constante mais il change avec l'augmentation de la température. La description mathématique de l’évolution du coefficient de la dilatation thermique en fonction de la température est relativement compliquée. Ainsi, pour un calcul suffisamment précis de la dilatation longitudinale sur une plage de température plus large, il est généralement nécessaire d'utiliser une relation de calcul quadratique ou cubique, dans laquelle la dilatation longitudinale est décrite par deux ou plusieurs coefficients. Par exemple, la relation quadratique pour le calcul de l'allongement est donnée sous la forme:

où:
a1,a2 ... coefficient de la dilatation thermique
L ... longueur initiale
DT ... changement de la température 

Cependant, même lors de l'utilisation de ces relations plus complexes, une précision parfaite de calcul sur toute la plage de températures de fonctionnement ne peut pas être garantie.

 

Dans la pratique technique courante, l'allongement des composants est généralement calculé au moyen des coefficients "linéaires" de dilatation thermique. Ces coefficients linéaires sont définis pour le matériau échauffé d'une température initiale T0 précisément donnée à la température finale T. L'allongement du composant dû à la température dans un intervalle de température donné peut alors être déterminé à partir d'une relation linéaire:

où:
a ... coefficient linéaire de la dilatation thermique pour le échauffement depuis la température T0 jusqu’à la température T
L ... longueur initiale
DT ... changement de la température T-T0 

Il est évident que pour des calculs plus précis de dilatation longitudinale dans une plage de température plus large, il sera nécessaire de connaître plus de valeurs du coefficient linéaire de dilatation thermique pour un matériau donné. Dans les bases de données de matériaux ou les fiches de matériaux, il est généralement possible de trouver, quant à un matériau donné, une ou plusieurs valeurs de tableau du coefficient pour différents intervalles de température "T0-T". Donc, la tâche de ce calcul est de trouver une valeur approximative du coefficient linéaire de dilatation thermique pour toute combinaison des températures initiale et finale "T0-T".

Allure typique du coefficient linéaire de dilatation thermique. [1]

La figure visualise graphiquement l'évolution habituelle du coefficient de dilatation thermique en fonction de la température pour des groupes de matériaux individuels. Utilisez la liste de choix pour passer parmi différents groupes.

Note: Les courbes visualisées correspondent au changement (échauffement) à partir de la température initiale de 20°C (68°F).
Avertissement: Pour un matériau particulier du groupe sélectionné, le tracé réel de la courbe peut être légèrement différent.  

Calcul du coefficient linéaire de dilatation thermique et d'allongement longitudinal d'un composant. [2]

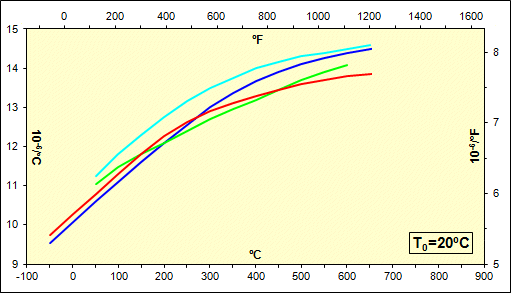
Ce paragraphe est destiné au propre calcul du coefficient linéaire de dilatation thermique et d'allongement longitudinal d’un composant.

Tout d'abord, sélectionnez un système d'unités pour le calcul [2.1] et le groupe de matériaux respectif [2.3]. Quand une valeur connue du coefficient a été définie dans les lignes [2.5 - 2.8], une courbe de l'évolution du coefficient linéaire de dilatation thermique en fonction de la température est tracée dans le graphique pour le matériau donné. Les résultats du calcul pour le changement exigé de la température [2.10, 2.11] figurent dans les lignes [2.12, 2.16].

Note: Le calcul du coefficient de dilatation thermique est effectué à l'aide d'un modèle empirique, basé sur le comportement habituel des matériaux dans un groupe donné de matériaux. Par conséquent, pour certains matériaux du groupe sélectionné, les résultats du calcul théorique peuvent différer de la réalité et il est nécessaire de les considérer comme approximatifs.
Avertissement: Les résultats calculés ne sont qu’à titre indicatif et ne peuvent remplacer les données obtenues par une mesure précise d'un matériau particulier. 

2.1 Unités de calcul.

Sélectionnez le système d’unités pour le calcul dans la liste de choix. En passant d’une unité à l’autre, toutes les valeurs seront immédiatement recalculées.

2.2 Matériel.

Dans cette partie définissez les paramètres souhaités de vos matériaux.

Conseil: Quand vous avez appuyé sur le bouton "<--", les paramètres correspondants du matériau sélectionné dans la liste [2.13] seront transférés dans le calcul. 

2.3 Groupe de matériaux.

Choisissez le groupe de matériaux correspondant à votre matériau dans la liste de choix.

2.4 Valeurs typiques du coefficient de dilatation thermique.

Cette ligne contient la plage de valeurs usuelles du coefficient linéaire de dilatation thermique pour différents matériaux du groupe de matériaux donné [2.3]. Ce coefficient est défini pour l'échauffement du matériau de 20° à 100°C (68-212°F).

2.5 - 2.7 Valeur connue du coefficient de dilatation thermique.

Dans la ligne [2.5] entrez une valeur connue du coefficient linéaire de dilatation thermique lors du échauffement du matériau à partir de la température "T0" [2.6] jusqu’à la température "T" [2.7].

Note: Les valeurs affichées en couleur rouge dans les cases d’entrée [2.6, 2.7] indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.

2.8 Coefficient linéaire de dilatation thermique.

Quand tous les paramètres de matériaux dans la partie [2.2] ont été définis, une courbe de l'évolution théorique du coefficient linéaire de dilatation thermique en fonction de la température est tracée dans cet endroit pour le matériau donné. La courbe visualisée correspond au changement de température (échauffement) à partir de la température initiale "T0" à la température indiquée. Vous pouvez sélectionner la valeur de la température initiale dans la liste située en bas à droite du graphique.

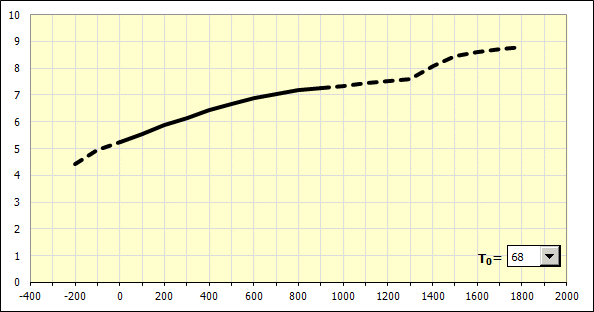
Note 1: La partie hachurée de la courbe dans le graphique ne visualise qu'une estimation de l'évolution attendue du coefficient. Il s'agit d'une plage de températures pour laquelle il n'a pas été possible d'établir un modèle empirique plus précis du comportement des matériaux en raison d’une quantité insuffisante de données ou de leurs écarts mutuels importants.

Dans la ligne [2.9] la valeur de base du coefficient linéaire de dilatation thermique pour le échauffement à partir de la température de 20° jusqu’à 100°C (68-212°F) est ajoutée.

Dans la ligne [2.12] le calcul du coefficient linéaire de dilatation thermique pour échauffer le matériau à partir de la température initiale "TI" [2.10] jusqu’à la température souhaitée "TE" [2.11] est effectué.

Note 2: Les résultats en couleur bleue du calcul indiquent la possibilité d'une imprécision de calcul accrue pour la plage de températures avec l’évolution seulement supposée de la courbe (partie hachurée du graphique).
Note 3: Les valeurs affichées en couleur rouge indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.
Avertissement: Les résultats calculés ne sont qu’à titre indicatif et ne peuvent remplacer les données obtenues par une mesure précise d'un matériau particulier. 

2.13 Tableau indicatif de valeurs.

Vous trouverez des valeurs informatives du coefficient linéaire de dilatation thermique pour les matériaux sélectionnés dans le tableau. 

Signification des paramètres:
a ... coefficient linéaire de la dilatation thermique [10-6/°C, 10-6/°F]
DT ... changement de température (échauffement) du matériau pour lequel ledit coefficient est défini [°C, °F]

Note: Les valeurs du tableau sont données dans le système d'unités défini dans la ligne [2.1].

2.14 L'allongement longitudinal d'un composant en fonction du changement de température.

Dans cette partie, l'allongement thermique d'un composant spécifique fabriqué du matériau défini ci-dessus est calculé pour le changement de température décrit dans les lignes [2.10, 2.11].

Note 1: Les résultats en couleur bleue du calcul indiquent la possibilité d'une imprécision de calcul accrue pour la plage de températures avec l’évolution seulement supposée de la courbe (voir le paragraphe [2.8]).
Note 2: Les valeurs affichées en couleur rouge indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.
Conseil: L'évolution théorique de l'allongement d'un composant dans un intervalle donné de températures est indiquée dans les graphiques correspondants. 

Extension d'un groupe de composants disposés en chaîne linéaire. [3]

Ce paragraphe est utilisé pour examiner la dilatation thermique mutuelle d'un groupe de composants constitués de différents matériaux. Les composants doivent être disposés dans une chaîne dimensionnelle linéaire. Le calcul permet de comparer l'allongement thermique de composants individuels ou de comparer deux groupes de composants.

Procédure de calcul:

1. Saisissez les températures de service dans la ligne [3.1]

2. Si les deux groupes de composants à comparer ne sont pas échauffés d’une manière uniforme, cochez le bouton à cocher dans la ligne [3.2] et saisissez la température finale différente pour les composants du groupe "B"

3. Définissez les paramètres de la chaîne dimensionnelle dans le tableau [3.3]

    Colonne 1 - choisissez le groupe à comparer dans la liste où le composant appartient

    Colonne 3 - entrez la longueur du composant

    Colonne 4 - choisissez le groupe de matériaux correspondant au matériau utilisé dans la liste de choix

    Colonne 5 - entrez la valeur de base du coefficient linéaire de dilatation thermique pour le échauffement de 20° à 100°C (68-212°F)

    Colonne 6 - si vous connaissez la valeur exacte du coefficient de dilatation thermique pour le changement de température lors du service (par exemple à partir de la fiche de matériau), cochez le bouton à cocher et entrez la valeur manuellement

4. L'allongement thermique des composants individuels est calculé dans les deux dernières colonnes du tableau

5. Vous pouvez trouver l'allongement total des deux groupes à comparer, y compris leur comparaison graphique, dans la partie [3.4]

Conseil 1: Si plusieurs composants différents fabriqués en même matériau sont utilisés dans la chaîne dimensionnelle, définissez-les dans le tableau [3.3] comme un seul composant avec leur longueur totale.
Conseil 2: Si un composé est fabriqué en un matériau qui ne correspond à aucun des groupes de matériaux proposés dans la colonne 4 du tableau, sélectionnez le dernier élément de la liste "Autres". Saisissez ensuite manuellement la valeur correspondante du coefficient de dilatation thermique dans la colonne 6 du tableau.

B. Module d'élasticité.

Ce chapitre traite de l'influence de la température sur les valeurs du module d'élasticité des matériaux de l'ingénierie mécanique. Le paragraphe [4] a un caractère informatif. Le paragraphe [5] est utilisé pour le propre calcul du module d’élasticité en fonction de la température sélectionnée.

Les données indiquées dans cet endroit concernent le module de Young. Pour vérifier le module de cisaillement il est possible d’appliquer le rapport de transfert:

où:
E ... module de Young
m ... coefficient de Poisson

Note: Le coefficient de Poisson pour les matériaux métalliques augmente, en règle générale, légèrement avec l'augmentation de la température. La diminution du module de cisaillement sera donc légèrement plus forte.

Allure typique du module d'élasticité. [4]

La figure visualise graphiquement l'évolution habituelle du module d’élasticité en fonction de la température pour des groupes de matériaux individuels. Utilisez la liste de choix pour passer parmi différents groupes.

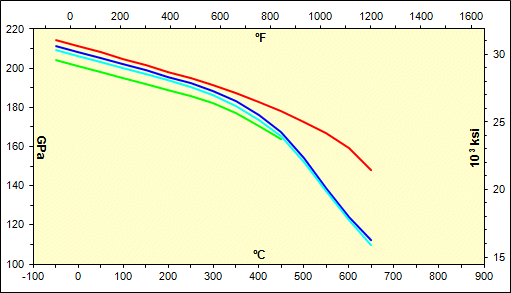
Avertissement: Pour un matériau particulier du groupe sélectionné, le tracé réel de la courbe peut être légèrement différent.  

Calcul du module d'élasticité. [5]

Ce paragraphe est destiné au calcul du module de Young.

Tout d'abord, sélectionnez un système d'unités pour le calcul [5.1] et le groupe de matériaux respectif [5.3]. Quand une valeur connue du module d’élasticité en lignes [5.5, 5.6] a été définie, une courbe de l'évolution du module d’élasticité en fonction de la température est tracée dans le graphique pour le matériau donné. La valeur résultante calculée du module d’élasticité pour la température souhaitée [5.9] figure dans la ligne [5.10].

Note: Le calcul du module d’élasticité est effectué à l'aide d'un modèle empirique basé sur le comportement habituel des matériaux dans un groupe de matériaux donné. Par conséquent, pour certains matériaux du groupe sélectionné, les résultats du calcul théorique peuvent différer de la réalité et il est nécessaire de les considérer comme approximatifs.
Avertissement: Les résultats calculés ne sont qu’à titre indicatif et ne peuvent remplacer les données obtenues par une mesure précise d'un matériau particulier. 

5.1 Unités de calcul.

Sélectionnez le système d’unités pour le calcul dans la liste de choix. En passant d’une unité à l’autre, toutes les valeurs seront immédiatement recalculées.

5.2 Matériel.

Dans cette partie définissez les paramètres souhaités de vos matériaux.

Conseil: Quand vous avez appuyé sur le bouton "<--", les paramètres correspondants du matériau sélectionné dans la liste [5.14] seront transférés dans le calcul. Quant aux matériaux avec un module d'élasticité indiqué sous la forme d'une plage de valeurs dans la liste, la valeur moyenne de cette plage sera utilisée dans le calcul.

5.3 Groupe de matériaux.

Choisissez le groupe de matériaux correspondant à votre matériau dans la liste de choix.

5.4 Valeurs typiques du module d'élasticité.

Cette ligne contient la plage de valeurs usuelles du module d’élasticité à la température de 20°C (68°F) pour différents matériaux du groupe du matériau donné [5.3].

5.5 - 5.6 Valeur connue du module d'élasticité.

Entrez une valeur connue du module d’élasticité à la température "T" [5.6] dans la ligne [5.5].

Note: Les valeurs affichées en couleur rouge dans les cases d’entrée [5.6] indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.

5.7 Module d'élasticité en traction.

Quand tous les paramètres de matériaux dans la partie [5.2] ont été définis, une courbe de l'évolution théorique du module d’élasticité en fonction de la température est tracée à cet endroit pour le matériau donné.

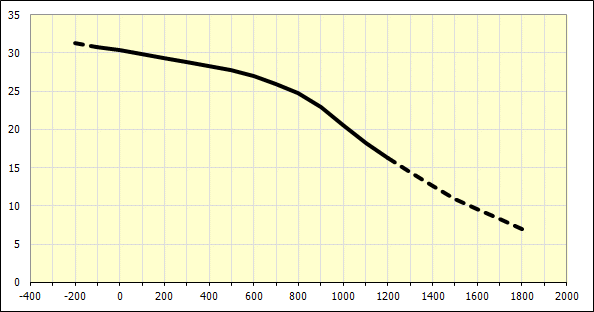
Note 1: La partie hachurée de la courbe dans le graphique ne visualise qu'une estimation de l'évolution attendue du module d’élasticité. Il s'agit d'une plage de températures pour laquelle il n'a pas été possible d'établir un modèle empirique plus précis du comportement des matériaux en raison d’une quantité insuffisante de données ou de leurs écarts mutuels importants.

La valeur de base du module d’élasticité à la température de 20°C (68°F) est calculée pour le matériau défini dans la ligne [5.8].

La valeur du module d’élasticité pour la température finale souhaitée "TE" [5.9] est calculée dans la ligne [5.10].

Note 2: Les résultats en couleur bleue du calcul indiquent la possibilité d'une imprécision de calcul accrue pour la plage de températures avec l’évolution seulement supposée de la courbe (partie hachurée du graphique).
Note 3: Les valeurs affichées en couleur rouge indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.
Avertissement: Les résultats calculés ne sont qu’à titre indicatif et ne peuvent remplacer les données obtenues par une mesure précise d'un matériau particulier. 

5.11 Module d'élasticité dans le cisaillement.

Dans cette partie, il est possible de vérifier la valeur correspondante du module de cisaillement pour la valeur calculée ci-dessus du module de Young. 

Note 1: Les résultats en couleur bleue du calcul indiquent la possibilité d'une imprécision de calcul accrue pour la plage de températures avec l’évolution seulement supposée de la courbe (voir le paragraphe [5.7]).
Note 2: Les valeurs affichées en couleur rouge indiquent le dépassement probable du point de fusion typique pour le groupe de matériaux sélectionné.
Avertissement: Le coefficient de Poisson n'a pas de valeur constante en fonction de la température. Pour les matériaux métalliques, il augmente, en règle générale, légèrement avec l'augmentation de la température.

5.14 Tableau indicatif de valeurs.

Vous trouverez des valeurs informatives du module de Young pour les matériaux sélectionnés dans le tableau.

Signification des paramètres:
E ... module de Young [GPa, 103 ksi]
T ... température du matériau pour laquelle ledit module d'élasticité est défini [°C, °F]

Note: Les valeurs du tableau sont données dans le système d'unités défini dans la ligne [5.1].

Réglage des calculs, changement de langue.

L'information sur le réglage des paramčtres de calcul et le choix de la langue peut ętre trouvée dans le document "Réglage des calculs, changement de langue".

Modifications du cahier de travail (calcul).

Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail du calcul sont mentionnées dans le document "Modifications du cahier de travail (calcul)".

Liste des normes, liste de la littérature:

EN 1561
Founding - Grey cast irons
Gießereiwesen - Gusseisen mit Lamellengraphit
Fonderie - Fontes à graphite lamellaire
Slévárenství - Litiny s lupínkovým grafitem

EN 1563
Founding - Spheroidal graphite cast irons
Gießereiwesen - Gußeisen mit Kugelgraphit
Fonderie - Fonte à graphite sphéroïdal
Slévárenství - Litina s kuličkovým grafitem

EN 16079
Founding - Compacted (vermicular) graphite cast irons
Gießereiwesen - Gusseisen mit Vermiculargraphit
Fonderie - Fontes à graphite vermiculaire (compacté)
Slévárenství - Litina s vermikulárním (kompaktním) grafitem

EN 1753
Magnesium and magnesium alloys - Magnesium alloy ingots and castings
Magnesium und Magnesiumlegierungen - Blockmetalle und Gussstücke aus Magnesiumlegierungen
Magnésium et alliages de magnésium - Lingots et pièces moulées en alliages de magnésium
Hořčík a slitiny hořčíku - Ingoty a odlitky ze slitin hořčíku

EN 10088-1
Stainless steels - Part 1: List of stainless steels
Nichtrostende Stähle - Teil 1: Verzeichnis der nichtrostenden Stähle
Aciers inoxydables - Partie 1 : liste des aciers inoxydables
Korozivzdorné oceli - Část 1: Přehled korozivzdorných ocelí

EN 10095
Heat resisting steels and nickel alloys
Hitzebeständige Stähle und Nickellegierungen
Aciers et alliages de nickel réfractaires
Oceli a niklové slitiny žáruvzdorné

EN 10269
Steels and nickel alloys for fasteners with specified elevated and/or low temperature properties
Stähle und Nickellegierungen für Befestigungselemente für den Einsatz bei erhöhten und/oder tiefen Temperaturen
Aciers et alliages de nickel pour éléments de fixation utilisés à température élevée et/ou basse température
Oceli a niklové slitiny na upevňovací prvky pro použití při zvýšených a/nebo nízkých teplotách

EN 10302
Creep resisting steels, nickel and cobalt alloys
Warmfeste Stähle, Nickel- und Cobaltlegierungen
Aciers et alliage à base de nickel et de cobalt résistant au fluage
Žáropevné oceli, niklové a kobaltové slitiny

 

ASM Handbook Volume 1: Properties and Selection: Irons, Steels, and High-Performance Alloys
ASM International, 1990

Metals Handbook Desk Edition, 2nd Edition
ASM International, 1998

ASM Ready Reference: Thermal Properties of Metals
ASM International, 2002

Materials Science and Engineering Handbook, Third Edition
CRC Press LLC, 2001

Smithells Light Metals Handbook
Butterworth-Heinemann, 1998

CRC Materials Science and Engineering Handbook, 4th Edition
CRC Press, 2015

Military Handbook - MIL-HDBK-5H: Metallic Materials and Elements for Aerospace Vehicle Structures
U.S. Department of Defense, 1998

Deutsches Kupferinstitut Berufsverband e.V,
Technische Broschüren und Datenblätter

Special Metals Corporation
High Performance Alloys Literature
 

^