Tento sešit obsahuje informace o vlivu teploty na některé fyzikální a mechanické vlastnosti strojírenských materiálů. Pomocí tohoto nástroje lze řešit následující úlohy:
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné literatury
a různých norem.
Seznam norem: EN 1561, EN 1563, EN 16079, EN 1753, EN 10088-1, EN 10095, EN
10269, EN 10302
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
V této kapitole je řešena problematika teplotní délkové roztažnosti strojírenských materiálů. Odstavec [1] má informativní charakter. Odstavec [2] pak slouží k vlastnímu výpočtu příslušných materiálových parametrů v závislosti na zvolené teplotě.
Při zahřívání nebo ochlazování tělesa dochází ke změně jeho rozměrů. U těles s jedním převažujícím rozměrem se hovoří o teplotní délkové roztažnosti. Závislost prodloužení na druhu materiálu je vyjadřována pomocí součinitele teplotní délkové roztažnosti. Obecně je tato fyzikální veličina materiálu definována vztahem:
![]()
kde:
L0 ... počáteční délka tělesa
DL ... změna délky
DT ... změna teploty
Tento součinitel však nemá konstantní velikost ale mění se s rostoucí teplotou. Matematický popis průběhu součinitele teplotní roztažnosti v závislosti na teplotě je poměrně složitý. Pro dostatečně přesný výpočet délkové roztažnosti v širším teplotním rozmezí je tak obvykle potřeba použít kvadratický nebo kubický výpočetní vztah, v němž je délková roztažnost popsána dvěma či více součiniteli. Například kvadratický vztah pro výpočet prodloužení je uváděn ve tvaru:
![]()
kde:
a1,a2 ... součinitele teplotní roztažnosti
L ... počáteční délka
DT ... změna teploty
Ani při použití těchto složitějších vztahů však nemusí být zaručena dokonalá přesnost výpočtu na celém rozsahu pracovních teplot.
V běžné technické praxi se prodloužení součásti obvykle počítá pomocí "lineárních" součinitelů teplotní roztažnosti. Tyto lineární součinitelé jsou definovány pro ohřev materiálu z přesně dané počáteční teploty T0 na koncovou teplotu T. Teplotní prodloužení součásti v daném teplotním intervalu pak můžeme určit z lineárního vztahu:
![]()
kde:
a ... lineární součinitel teplotní roztažnosti pro
ohřev z teploty T0 na teplotu T
L ... počáteční délka
DT ... změna teploty T-T0
Je zřejmé, že pro přesnější výpočty délkové roztažnosti v širším teplotním rozmezí bude potřeba znát u daného materiálu více hodnot lineárního součinitele teplotní roztažnosti. V materiálových databázích nebo materiálových listech obvykle bývá možné nalézt pro daný materiál jednu nebo několik tabulkových hodnot součinitele pro různé teplotní intervaly "T0-T". Úkolem tohoto výpočtu je pak nalezení přibližné hodnoty lineárního součinitele teplotní roztažnosti pro libovolnou kombinaci počáteční a koncové teploty "T0-T".
Na obrázku je pro jednotlivé materiálové skupiny graficky zobrazen obvyklý průběh součinitele teplotní roztažnosti v závislosti na teplotě. Pro přepínání mezi různými skupinami použijte výběrový seznam.
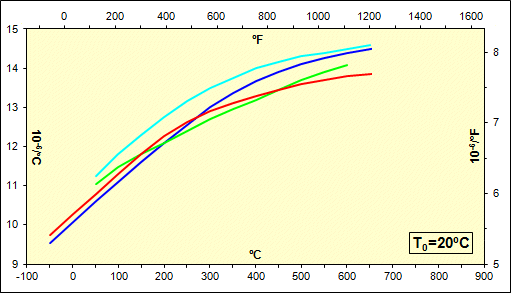
Tento odstavec je určen pro vlastní výpočet lineárního součinitele teplotní roztažnosti a délkového prodloužení součásti.
Nejprve zvolte soustavu jednotek výpočtu [2.1] a odpovídající materiálovou skupinu [2.3]. Po definování jedné známé hodnoty součinitele v řádcích [2.5 - 2.8] je v grafu pro daný materiál vykreslena křivka průběhu lineárního součinitele teplotní roztažnosti v závislosti na teplotě. Výsledky výpočtu pro požadovanou změnu teploty [2.10, 2.11] jsou uvedeny v řádcích [2.12, 2.16].
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě přepočítány všechny hodnoty.
V této části definujte požadované parametry vašeho materiálu.
Ve výběrovém seznamu vyberte materiálovou skupinu odpovídající vašemu materiálu.
V tomto řádku je pro různé materiály z dané materiálové skupiny [2.3] uveden rozsah obvyklých hodnot lineárního součinitele teplotní roztažnosti. Tento součinitel je definován pro ohřev materiálu z 20° na 100°C (68-212°F)
V řádku [2.5] zadejte jednu známou hodnotu lineárního součinitele teplotní roztažnosti při ohřevu materiálu z teploty "T0" [2.6] na teplotu "T" [2.7].
Po definování všech materiálových parametrů v části [2.2] je zde pro daný materiál vykreslena teoretická křivka průběhu lineárního součinitele teplotní roztažnosti v závislosti na teplotě. Zobrazená křivka odpovídá teplotní změně (ohřevu) z počáteční teploty "T0" na indikovanou teplotu. Velikost počáteční teploty vyberete v seznamu umístěném v pravé spodní části grafu.
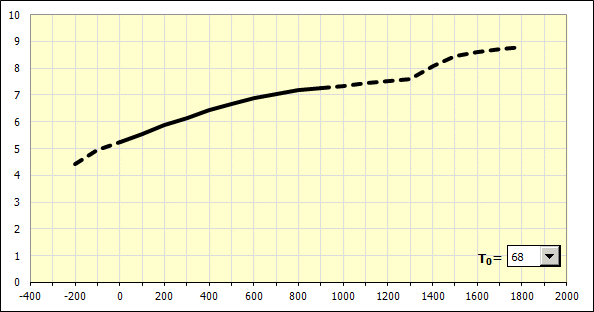
V řádku [2.9] je pro výše definovaný materiál dopočtena jeho základní hodnota lineárního součinitele teplotní roztažnosti pro ohřev z teploty 20° na 100°C (68-212°F).
V řádku [2.12] je pak proveden vlastní výpočet lineárního součinitele teplotní roztažnosti pro ohřev materiálu z počáteční teploty "TI" [2.10] na požadovanou koncovou teplotu "TE" [2.11].
V tabulce naleznete pro vybrané materiály informativní hodnoty lineárního součinitele teplotní roztažnosti.
Význam parametrů:
a ... lineární součinitel teplotní roztažnosti [10-6/°C, 10-6/°F]
DT ... změna teploty (ohřev) materiálu pro níž je
uvedený součinitel definován [°C, °F]
V této části je dopočteno teplotní prodloužení konkrétní součásti vyrobené z výše definovaného materiálu pro změnu teploty popsanou v řádcích [2.10, 2.11].
Tento odstavec slouží k vyšetření vzájemné teplotní dilatace skupiny součástí z různých materiálů. Součásti musí být seřazeny v lineárním rozměrovém řetězci. Výpočet umožňuje provádět srovnání teplotního prodloužení samostatných součástí nebo srovnání dvou skupin součástí.
Postup výpočtu:
1. V řádku [3.1] zadejte provozní teploty
2. Pokud nejsou obě srovnávané skupiny součástí zahřívány stejnoměrně, zaškrtněte v řádku [3.2] zaškrtávací tlačítko a zadejte odlišnou koncovou teplotu pro součásti ze skupiny "B"
3. V tabulce [3.3] definujte parametry rozměrového řetězce
Sloupec 1 - ze seznamu vyberte srovnávací skupinu do které součást patří
Sloupec 3 - zadejte délku součásti
Sloupec 4 - ve výběrovém seznamu vyberte materiálovou skupinu odpovídající použitému materiálu součásti
Sloupec 5 - zadejte základní hodnotu lineárního součinitele teplotní roztažnosti pro ohřev z 20° na 100°C (68-212°F)
Sloupec 6 - pokud znáte přesnou hodnotu součinitele teplotní roztažnosti pro provozní změnu teploty (např. z materiálového listu), odškrtněte zaškrtávací tlačítko a hodnotu zadejte manuálně
4. V posledních dvou sloupcích tabulky je dopočteno teplotní prodloužení jednotlivých součástí
5. Celkové prodloužení obou srovnávacích skupin včetně grafického porovnání naleznete v části [3.4]
V této kapitole je řešen vliv teploty na velikost modulu pružnosti strojírenských materiálů. Odstavec [4] má informativní charakter. Odstavec [5] slouží k vlastnímu výpočtu modulu pružnosti v závislosti na zvolené teplotě.
Údaje zde uváděné se týkají modulu pružnosti v tahu. Pro zjištění modulu pružnosti ve smyku je možné použít převodní vztah:
![]()
kde:
E ... modul pružnosti v tahu
m ... poissonovo číslo
Na obrázku je pro jednotlivé materiálové skupiny graficky zobrazen obvyklý průběh modulu pružnosti v závislosti na teplotě. Pro přepínání mezi různými skupinami použijte výběrový seznam.
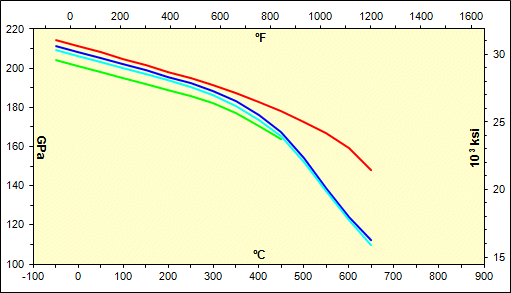
Tento odstavec je určen pro vlastní výpočet modulu pružnosti v tahu.
Nejprve zvolte soustavu jednotek výpočtu [5.1] a odpovídající materiálovou skupinu [5.3]. Po definování jedné známé hodnoty modulu pružnosti v řádcích [5.5, 5.6] je v grafu pro daný materiál vykreslena křivka průběhu modulu pružnosti v závislosti na teplotě. Výsledná dopočtená hodnota modulu pružnosti pro požadovanou teplotu [5.9] je uvedena v řádku [5.10].
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě přepočítány všechny hodnoty.
V této části definujte požadované parametry vašeho materiálu.
Ve výběrovém seznamu vyberte materiálovou skupinu odpovídající vašemu materiálu.
V tomto řádku je pro různé materiály z dané materiálové skupiny [5.3] uveden rozsah obvyklých hodnot modulu pružnosti při teplotě 20°C (68°F).
V řádku [5.5] zadejte jednu známou hodnotu modulu pružnosti při teplotě "T" [5.6].
Po definování všech materiálových parametrů v části [5.2] je zde pro daný materiál vykreslena teoretická křivka průběhu modulu pružnosti v závislosti na teplotě.
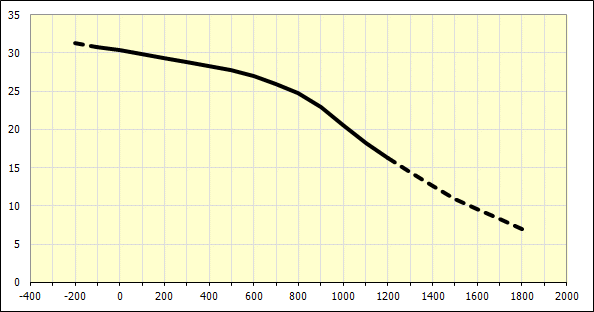
V řádku [5.8] je pro výše definovaný materiál dopočtena jeho základní hodnota modulu pružnosti při teplotě 20°C (68°F).
V řádku [5.10] je dopočtena hodnota modulu pružnosti pro požadovanou koncovou teplotu "TE" [5.9].
V této části je možné pro výše vypočtenou hodnotu modulu pružnosti v tahu zjistit odpovídající velikost modulu pružnosti ve smyku.
V tabulce naleznete pro vybrané materiály informativní hodnoty modulu pružnosti v tahu.
Význam parametrů:
E ... modul pružnosti v tahu [GPa, 103 ksi]
T ... teplota materiálu pro níž je uvedený modul pružnosti definován [°C, °F]
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
EN 1561
Founding - Grey cast irons
Gießereiwesen - Gusseisen mit Lamellengraphit
Fonderie - Fontes à graphite lamellaire
Slévárenství - Litiny s lupínkovým grafitem
EN 1563
Founding - Spheroidal graphite cast irons
Gießereiwesen - Gußeisen mit Kugelgraphit
Fonderie - Fonte à graphite sphéroïdal
Slévárenství - Litina s kuličkovým grafitem
EN 16079
Founding - Compacted (vermicular) graphite cast irons
Gießereiwesen - Gusseisen mit Vermiculargraphit
Fonderie - Fontes à graphite vermiculaire (compacté)
Slévárenství - Litina s vermikulárním (kompaktním) grafitem
EN 1753
Magnesium and magnesium alloys - Magnesium alloy ingots and castings
Magnesium und Magnesiumlegierungen - Blockmetalle und Gussstücke aus
Magnesiumlegierungen
Magnésium et alliages de magnésium - Lingots et pièces moulées en alliages de
magnésium
Hořčík a slitiny hořčíku - Ingoty a odlitky ze slitin hořčíku
EN 10088-1
Stainless steels - Part 1: List of stainless steels
Nichtrostende Stähle - Teil 1: Verzeichnis der nichtrostenden Stähle
Aciers inoxydables - Partie 1 : liste des aciers inoxydables
Korozivzdorné oceli - Část 1: Přehled korozivzdorných ocelí
EN 10095
Heat resisting steels and nickel alloys
Hitzebeständige Stähle und Nickellegierungen
Aciers et alliages de nickel réfractaires
Oceli a niklové slitiny žáruvzdorné
EN 10269
Steels and nickel alloys for fasteners with specified elevated and/or low
temperature properties
Stähle und Nickellegierungen für Befestigungselemente für den Einsatz bei
erhöhten und/oder tiefen Temperaturen
Aciers et alliages de nickel pour éléments de fixation utilisés à température
élevée et/ou basse température
Oceli a niklové slitiny na upevňovací prvky pro použití při zvýšených a/nebo
nízkých teplotách
EN 10302
Creep resisting steels, nickel and cobalt alloys
Warmfeste Stähle, Nickel- und Cobaltlegierungen
Aciers et alliage à base de nickel et de cobalt résistant au fluage
Žáropevné oceli, niklové a kobaltové slitiny
ASM Handbook Volume 1: Properties and Selection: Irons, Steels, and High-Performance
Alloys
ASM International, 1990
Metals Handbook Desk Edition, 2nd Edition
ASM International, 1998
ASM Ready Reference: Thermal Properties of Metals
ASM International, 2002
Materials Science and Engineering Handbook, Third Edition
CRC Press LLC, 2001
Smithells Light Metals Handbook
Butterworth-Heinemann, 1998
CRC Materials Science and Engineering Handbook, 4th Edition
CRC Press, 2015
Military Handbook - MIL-HDBK-5H: Metallic Materials and Elements for
Aerospace Vehicle Structures
U.S. Department of Defense, 1998
Deutsches Kupferinstitut Berufsverband e.V,
Technische Broschüren und Datenblätter
Special Metals Corporation
High Performance Alloys Literature