Die Berechnung ist für geometrischen und Entwurf und Kontrolle der
Kegel und Hypoidverzahnung mit geraden, schrägen und gekrümmten Zähnen bestimmt
- ISO 23509.
Das Programm löst folgende Aufgaben:
Vorentwurf für Verzahnungsgröße
Detailentwurf für
Verzahnungsgeometrie:
- Geradeverzahnung
- Schrägverzahnung
- Kreisbogenverzahnung
- Zerol
- Hypoid (Gleason, Oerlikon, Klingelnberg)
Automatischer Entwurf des Getriebes mit einem Minimum an Eingangsanforderungen.
Die Berechnungen verwenden Verfahren, Algorithmen und Angaben aus Norme ISO 23509 und Normen AGMA ISO 23509 : A, ANSI, ISO, DIN, BS und aus der Fachliteratur.
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Schätzung bezieht sich auf ein Getriebe mit einem Winkel der Wellenachsen von 90°. Für andere Achsenwinkel muss die Schätzung korrigiert werden.
Das Drehmoment ist das geeignete Kriterium für die Näherungsbewertung von Kegelradgetrieben, die Umrechnung der Leistung in Drehmoment erfolgt nach folgendem Verhältnis:
T1 = 9550 * P / n1
wo:
T1 ... Drehmoment - Ritzel [N*m]
P ..... Übertragene Leistung [kW]
n1 ... Drehzahl - Ritzel [/min]
Ritzeldurchmesser de1 in Abhängigkeit von Drehmoment, Übersetzung, Material, Verzahnungsart und Lasttyp:
Flankenpressung
de1 = (0 + 15 * T1^0.325) / (u^0.35) * KM * SZF * PFG [mm]
Biegungsfestigkeit
Für T1 < 5000 [N*m]
de1 = (0 + 14 * T1^0.35) / (u^0.5) *
LTF * SZF
[mm]
Für T1 >=5000 [N*m]
de1 = (0 + 14 * T1^0.35) / (u^0.5) * u^0.14 *
(T1/5000)^0.1 *
LTF * SZF
[mm]
wo:
de1 .. Teilkreisdurchmesser [mm]
T1 .... Drehmoment - Ritzel [N*m]
u ...... Übersetzungsverhältnis
KM .... Materialkoeffizient
SZF.... Koeffizient für Gerade und Zerol Verzahnung
PFG ... Präzisionsgefertigte Zahnräder
LTF ... Belastungfactor
Für Hypoidgetriebe
deplm1 = de1 - a / u
wo:
deplm1 ... Entwurf des äußeren Ritzeldurchmessers
[mm]
de1 ........ Externer Ritzeldurchmesser [mm]
(größer als die vorherige Berechnung)
a ............ Hypoid-Achsversatz [mm]
u ............ Übersetzungsverhältnis
Alle verwendeten Beziehungen zur Geometrieberechnung finden Sie in der ISO-Norm 23509. Unten finden Sie eine Geometriebeschreibung.
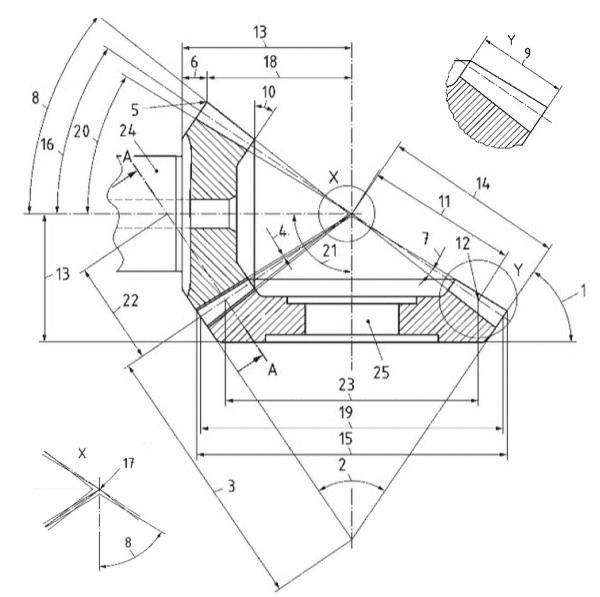
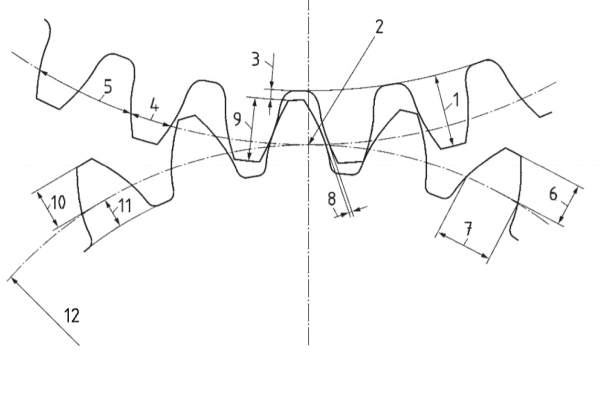
Zahnhöhe - hm
Wälzpunkt
Kopfgrundspiel - c
Zahndicke (im Bogen gemessen) - st
Kreisteilung
Zahnkopfhöhe (Sehnenmaß) - hamc
Zahndicke (Sehnenmaß) - sc
Verdrehflankenspiel
Eingriffstiefe - hmw
Zahnkopfhöhe - ham
Zahnfußhöhe - hfm
äquivalenter Teilkreisradius
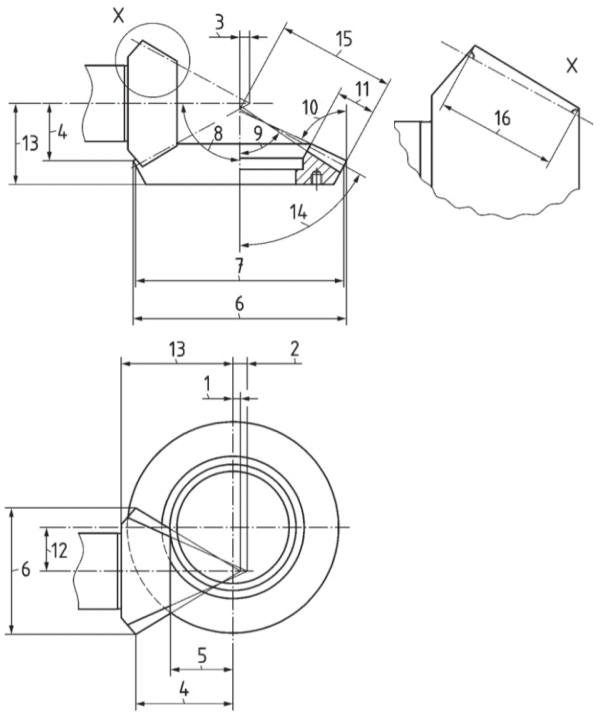
Abstand Kopfkegelspitze zum Kreuzungspunkt - tzF1
Abstand Fußkegelspitze zum Kreuzungspunkt - tzR1
Abstand Teilkegelspitze zum Kreuzungspunkt - tz1
Abstand äußere Kopfkegelkante zum Kreuzungspunkt - txo1, txo2
Abstand innere Kopfkegelkante zum Kreuzungspunkt - txi1
äußerer Durchmesser - dae1, dae2
äußerer Teilkegel-Durchmesser - de1, de2
Achswinkel - Sigma
Fußwinkel - deltaf1, deltaf2
Kopfkegelwinkel - deltaa1, deltaa2
Zahnbreite des Rades - b2
Hypoid-Achsversatz - a
Einbaumaß - tB1, tB2
Teilkegelwinkel - delta2
äußere Teilkegellänge - Re
Zahnbreite des Ritzels - b1
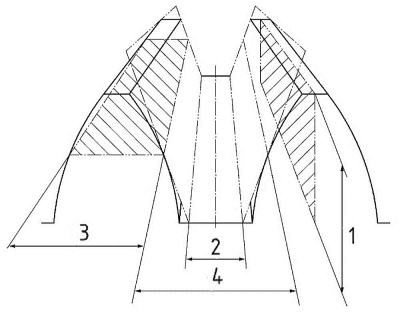
Zahnhöhe
Zahnlückenweite im Zahngrund (Planrad)
Zahndicke
Zahnlückenweite in Teilkegelebene
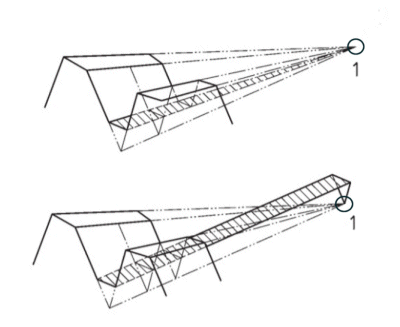
Tailkegelspitze
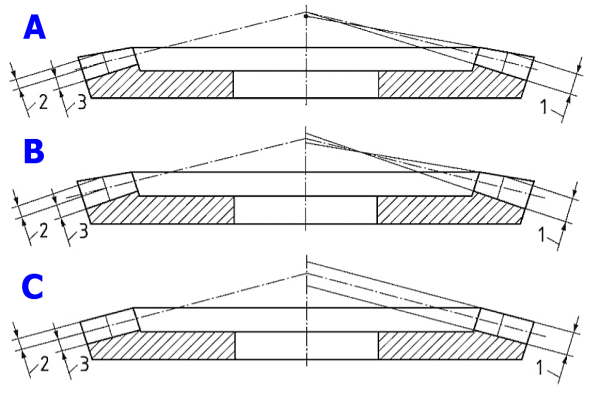
A. Standard Kegel
B. Duplex Kegel
C. Konstante Zahnhohe
Mittlere Zahnhöhe
Mittlere Zahnkopfhöhe
Mittlere Zahnfußhöhe
Überwiegend werden zwei Grundprinzipien der Bearbeitung verwendet, die auch für die Berechnung und Generierung der 3D-Modelle der Räder Anwendung finden.
Die Krümmung ist eine erweitere Epizykloide, die durch das Abwälzen des Werkzeugs über den Basiskreis der Epizykloide entsteht.
Der Radius der Krümmung ist gleich dem Radius des Werkzeugs.
|
Symbol |
Symbol |
Beschreibung |
Method 0 |
Method 1 |
Method 2 |
Method 3 |
|
Sigma |
S |
Achswinkel |
X |
X |
X |
X |
|
a |
a |
Achsversatz |
0.0 |
X |
X |
X |
|
z1, z2 |
z1, z2 |
Zähnezahl |
X |
X |
X |
X |
|
dm2 |
dm2 |
Teilkreisdurchmesser - Mitte |
- |
- |
X |
- |
|
de2 |
de2 |
Äußerer Teilkegel-Durchmesser des Tellerrades |
X |
X |
- |
X |
|
b2 |
b2 |
Zahnbreite des Tellerrades |
X |
X |
X |
X |
|
betam1 |
bm1 |
Mittlerer Spiralwinkel des Ritzels |
- |
X |
- |
- |
|
betam2 |
bm2 |
Mittlerer Spiralwinkel des Tellerrades |
X |
- |
X |
X |
|
rc0 |
rc0 |
Werkzeugradius |
X |
X |
X |
X |
|
z0 |
z0 |
Anzahl der Messergruppen (nur für kontinuierliche Fräsverfahren) |
X |
X |
X |
X |
Diese Berechnung ist vor allem für den Entwurf de Geometrie bestimmt. Die Berechnung bzw. der Entwurf der Größe der Räder ist lediglich ein Richtwert und sollte anhand der einschlägigen Norm oder gemäß jener Dokumentation kontrolliert werden, die der Hersteller der jeweiligen Bearbeitungsanlage liefert.
Entwurf der Maße der Zahnräder:
In diesem Absatz die Grundeingangsparameter der entworfenen Verzahnung eingeben.
In der Auswahlliste das gewünschte System der Berechnungseinheiten auswählen. Beim Umschalten der Einheiten werden sofort alle Werte umgerechnet.
Die Leistung für das Antriebsrad eingeben. Übliche Werte befinden sich im Bereich 2 - 500 kW / 3-700 HP, in Extremfällen bis zu 4000 kW / 6000 HP.
Die Drehzahl für das Antriebsrad eingeben. Die extreme Drehzahl kann auch bei 50 000 U/min liegen. Die Drehzahl des Antriebsrades wird aus der Anzahl der Zähne der beiden Räder berechnet.
Das ist ein Berechnungsergebnis und kann nicht eingegeben werden.
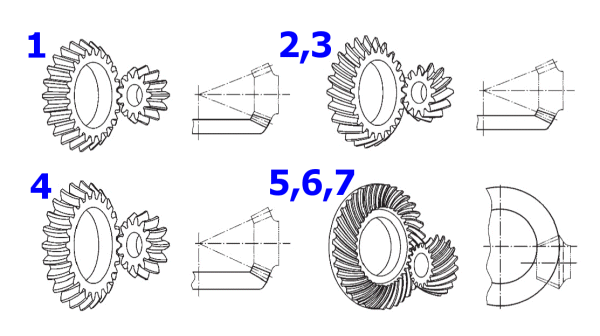
Die Berechnung ermöglicht, eine Reihe von Verzahnungsarten zu lösen. Wählen Sie die Verzahnungsart aus der Liste. Bei der Wahl wählen Sie auch eine Reihe von Koeffizienten aus, die die Schätzung der Getriebegröße und die Koeffizienten zur Geometrieberechnung beeinflussen.
Gerade Standardverzahnung - Methode 0
Gerade Standardschrägverzahnung - Methode 0
Kreisbogenverzahnung (Nicht Hypoids) - Methode 0
Zerol-Verzahnung - Methode 0
Hypoidverzahnung (Gleason) - Methode 1
Hypoidverzahnung (Oerlikon) - Methode 2
Hypoidverzahnung (Klingelnberg) - Methode 3
Für andere Werkstoffe als gehärteter Stahl mit einem Mindestwert von HRC=55 wird der errechnete Wert des Außendurchmessers des Ritzels (Diagramm B.2 ISO23509) mit dem Koeffizienten KM multipliziert.
Die „Präzisionsbearbeitung“ ist eine Nacharbeit gemeint, die Schleifen, Schleifschaben, Reibschleifen umfasst.
Statisch belastete Getriebestufen sollten eher für die Biegefestigkeit als für die Pittingbeständigkeit entworfen sein. Bei statisch belasteten Zahnrädern, die Schwingungen ausgesetzt sind, muss der Außenteilkreisdurchmesser des Ritzels gemäß B.2 ISO 23509 mit 0,70 multipliziert werden. Bei statisch belasteten Getrieben, die keinen Schwingungen ausgesetzt sind, muss der Außenteilkreisdurchmesser des Ritzels gemäß B.2, B.3 ISO 23509, mit 0,60 multipliziert werden.
Beeinflusst nur den Entwurf für das Flankenspiel der Verzahnung.
In diesem Abschnitt wählen Sie die Übersetzung, die Anzahl der Zähne, den
Achsenwinkel, die Achsverlagerung usw. So Sie erhalten einen Vorentwurf für die
Größe und Form der Verzahnung.
- Die eingegebene Anzahl der Zähne und der Achsenwinkel werden in allen Methoden
der Geometrieberechnung verwendet.
- Durchmesser, Achsverlagerungen, Zahnbreite, Verzahnungswinkel werden dann im
entsprechenden Abschnitt (Methode 0-3) als empfohlene (minimale, maximale) Werte
angeboten.
Ein optimales Übersetzungsverhältnis bewegt sich im Bereich 1-5. In Extremfällen kann es einen Wert bis zu 10 erreichen. Das Übersetzungsverhältnis geben Sie im linken Eingangsfeld aus der Tastatur ein. Im rechten Aufrollverzeichnis befinden sich die empfohlenen Werte des Übersetzungsverhältnisses und bei der Auswahl aus dieser Liste wird der ausgewählte Wert in das Feld links automatisch ergänzt.
Die empfohlene und (minimale) Anzahl der Zähne des Ritzels basiert auf ISO 23590. Die empfohlene Anzahl der Zähne des Rades wird anhand der in der vorherigen Zeile eingegebenen Übersetzung errechnet.
Geben Sie die Anzahl der Zähne des Ritzels ein. Die Anzahl der Zähne des Rades wird basierend auf der erforderlichen Übersetzung errechnet [2.1]. Nach Abstreichen der Schaltfläche rechts kann man direkt die Anzahl der Zähne des Rades eingeben.
Da das tatsächliche Übersetzungsverhältnis ein Quotient der Anzahl der Zähne der beiden Räder ist (ganze Zahlen), wird das tatsächliche Übersetzungsverhältnis meistens von dem verlangten (eingegebenen) unterschiedlich sein. Der Wert des "tatsächlichen Übersetzungsverhältnisses" ist links angeführt, rechts steht dann die prozentuale Abweichung vom verlangten Übersetzungsverhältnis. Diese Abweichung sollte für das Übersetzungsverhältnis sein im Bereich:
i = 1 - 4.5 ...........+- 2.5%
,auch größer als 4.5...+- 4.0%
Den gegenseitigen Achsenwinkel der einzelnen Räder eingeben – am häufigsten 90º. Die Berechnung erlaubt auch Verwendung von anderen Werten. Der Fall, wo der Teilkegelwinkel 90º überschreiten sollte, ist durch rote Farbe der Zelle angezeigt. (Es entsteht ein inneres Kegelgetriebe, das auf üblichen Maschinen nicht gefertigt werden kann).
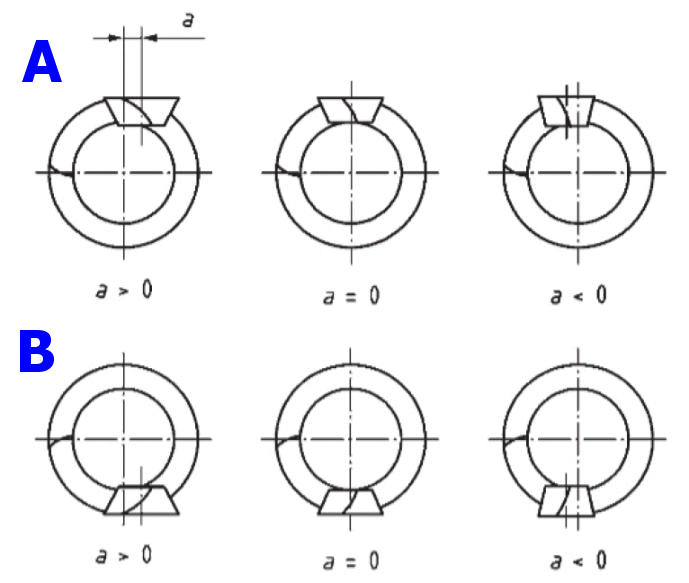
In den meisten Fällen ist die Achsverlagerung durch die Konstruktion gegeben. Die Verlagerung der Ritzelachsen ist als positiv oder negativ markiert.
Das Bild zeigt die positive und negative Verlagerung der Ritzelachsen, von der Oberseite des Rades gesehen.
A. Linksdrehendes, mit dem rechtsdrehenden Rad verbundenes Ritzel
B. Rechtsdrehendes, mit dem linksdrehenden Rad verbundenes Ritzel
Im Allgemeinen wird die positive Verlagerung der Ritzelachsen aufgrund des zunehmenden Ritzeldurchmessers, des höheren Eingriffsfaktors und der höheren Tragfähigkeit empfohlen. Darüber hinaus sollte die Achsverlagerung aufgrund des spezifischen Schlupfes von 25 % des Außenteilkreisdurchmessers des Rades nicht überschreiten (für schwere Lasten 12,5 %).
Aufgrund der Leistungs- und Geometrieunterlagen wird der Wert des Außenteilkreisdurchmessers ermittelt.
Da die Werkzeuge für die Kegelräderverzahnung nicht nach dem Modul normalisiert sind, ist es nicht notwendig, dass das Modul eine ganze Zahl ist. Es ist jedoch möglich, die Radgröße nach dem benötigten Modul in der Berechnung zu errechnen.
Nach dem Ankreuzen des Ankreuzfeldes können wir den eigenen Wert der Zahnbreite eingeben. Nach dem Ankreuzen des Feldes ist der Maximalwert automatisch gewählt.
Im Allgemeinen beträgt die Verzahnungsbreite 30% der Teilkegellänge Re2 oder 10* (kleinerer Wert). Die Konstruktionsparameter können jedoch erfordern, dass Werte größer oder kleiner sind. Bei der Zerol-Verzahnung sollte die Verzahnungsbreite mit 0.83 multipliziert werden und 25% Re2 nicht überschreiten.
Bei Wellenwinkeln weniger als 90° ist es möglich, eine größere Verzahnungsbreite als angegeben zu verwenden. Bei Wellenwinkeln größer als 90° sollte eine kleinere Verzahnungsbreite verwendet werden.
Die Verzahnungsbreite des Hypoidritzels ist allgemein größer als die Verzahnungsbreite der Räder
Die allgemeine Konstruktionspraxis empfiehlt, den Neigungswinkel der Zähne so zu wählen, dass der Eingriffsfaktor ungefähr 2.0 beträgt. Für hohe Drehungen und die Anforderungen an minimales Geräusch und Laufglätte sind die empfohlenen Werte des Eingriffsfaktors höher. Es ist jedoch möglich, den Neigungswinkel der Zähne so zu wählen, dass der Eingriffsfaktor niedriger als 2.0 ist.
Geben Sie die Zahnprofilparameter in diesem Absatz ein.
Geradverzahnung:
Verwenden Sie einen Eingriffswinkel von 20° oder höher für das Ritzel mit 14 bis
16 Zähnen und 25° für das Ritzel mit 12 oder 13 Zähnen, um ein Unterschneiden zu
verhindern.
Zerol-Verzahnung:
Bei der Zerol-Verzahnungsart wird ein Eingriffswinkel von 22,5° und 25° für
das Ritzel mit niedriger Zähnezahl und eine größere Übersetzung verwendet, um
ein Unterschneiden zu verhindern. 22,5° für Ritzel mit 14-16 Zähnen, 25° für
Ritzel mit 13 Zähnen.
Schrägverzahnug:
Ein Eingriffswinkel von 20° oder höher wird für das Ritzel mit 12 und
weniger Zähnen verwendet, um ein Unterschneiden zu verhindern.
Hypoidverzahnung:
Um die Eingriffsbedingungen auf der Eingriffs- und Nichteingriffsseite des
Zahns auszugleichen, sollte der Falfalimskoeffizient 1,0 betragen. Bei der
Nutzung von Standardwerkzeugen kann er eine Abweichung von 1.0 aufweisen. Für
weniger belastete Getriebe kann ein Nenneingriffswinkel von 18° oder 20°, für
stark belastete Getriebe zum Beispiel Winkel von 22,5° und 25° verwendet werden.
Zwei Arten von Eingabedaten sind verfügbar. Datentyp I – verwendet in europäischen Normen, Datentyp II - verwendet von American Gear Manufacturers Association AGMA.
Nach Auswahl des Typs werden die entsprechenden Werte automatisch auch für den zweiten Typ von Eingabedaten berechnet und in der rechten Spalte angezeigt. Die Daten aus der rechten Spalte werden dann für die Berechnung verwendet. In der grünen Spalte sind dann empfohlene Werte, die auf den vorherigen Daten basieren. (Verzahnungsart, Übersetzung, Anzahl der Zähne, ...)
Empfohlene Werte für Radgetriebe mit einem Achsenwinkel von 90º:
Übersetzung-sverhältnis / xhm1
1..............0.00
1.12..........0.10
1.25..........0.19
1.6............0.27
2...............0.33
2.5............0.38
3...............0.40
4...............0.43
5...............0.44
6...............0.45
In Regelfällen beträgt der entsprechende khap-Faktor 1.00 und khfp-Faktor 1.25.
In Regelfällen beträgt der entsprechende khap-Faktor 1.00 und khfp-Faktor 1.25.
Empfohlene Werte für Radgetriebe mit einem Achsenwinkel von 90º:
Übersetzung-sverhältnis / xsmn
1……………0.0
1.12………0.010
1.25………0.018
1.6…………0.024
2……………0.030
2.5…………0.039
3……………0.048
4……………0.065
5……………0.082
6……………0.100
Dieser Faktor teilt den Arbeitsbereich zwischen der Höhe des Ritzel- und Radkopfes auf. Die Höhe des Ritzelkopfes ist üblicherweise größer als die Höhe des Radkopfes, ausgenommen die gleiche Anzahl von Zähnen. Für das Ritzel wird eine größere Zahnkopfhöhe gewählt, um das Unterschneiden des Zahnes zu verhindern. Vorgeschlagene Werte für den 90° Wellenwinkel sind rechts. Andere Werte basierend auf der Schlupfrate, der Zahnbreite und der gegenseitigen Zahnbelastung können verwendet werden. Der Absatz 8 der Norm ISO 23509 zeigt die Grenzen für den mittleren Faktor der Kopfhöhe an, um das Unterschneiden des Ritzels und Rades zu verhindern.
Üblicherweise wird für die Berechnung der durchschnittliche hmw-Arbeitstiefe der Tiefenkoeffizient kd = 2.000 verwendet, er kann sich jedoch nach Konstruktions- und anderen Anforderungen unterscheiden. Der Wert rechts zeigt vorgeschlagene Tiefenkoeffizienten an, die auf der Anzahl der Ritzelzähne basiert.
Während das Einheitskopfspiel über die gesamte Zahnlänge konstant ist, erfolgt die Berechnung im Mittelpunkt. Üblicherweise wird der Wert kc = 0.125 verwendet, kann sich jedoch nach dem Entwurfszweck und anderen Anforderungen unterscheiden.
Die mittlere Umfangsdicke wird auf dem mittleren Durchmesser berechnet. Die für die Biegebeanspruchung optimierten kt-Werte sind rechts angeführt. Andere kt-Werte für eine optimale Spannungsverteilung können auch verwendet werden.
In den folgenden Abschnitten werden einzelne Rechnungsmethoden, die der gewählten Verzahnungsart [1.5] entsprechen, aufgeführt. Packen Sie die entsprechende Methode aus und präzisieren Sie die Eingabeparameter für die Verzahnung. Die empfohlenen Werte, die auf dem Vorentwurf basieren (Absätze 1.0, 2.0, 3.0), sind rechts angegeben. Bei der Methode 1,2 und 3 muss meistens die Iteration erfolgen, die die genauen geometrischen Ergebnisse ausrechnet.
Mittels der Taste „<<“, die sich zu Beginn des Absatzes rechts befindet [4.1, 5.1, 6.1, 7.1] füllen Sie die Werte aus dem vorläufigen Entwurf aus (Absatz 1.0, 2.0, 3.0).
Wählen Sie den Wert de2 (dm2). Er sollte größer als der Wert rechts sein, der das Ergebnis eines Vorentwurfs ist.
Wählen Sie den Wert de2 (dm2). Er sollte größer als der Wert rechts sein, der das Ergebnis eines Vorentwurfs ist.
Wählen Sie den Wert b2. Er sollte kleiner als der Wert rechts sein, der von den in diesem Abschnitt eingegebenen Eingabeparametern abhängig ist.
Wählen Sie den Wert betam2 (betam1). Der Wert sollte zur Erreichung eines Eingriffsfaktors eb = 2.0, Absatz [2.12] größer als der rechts in Klammern angeführte Wert sein. Der zulässige Bereich ist in spitzen Klammern „<...>“ angeführt.
Wählen Sie den Wert a. Er sollte aus dem Wertebereich rechts stammen. Der Wert ist von den eingegebenen Eingangsparametern in diesem Absatz abhängig. Siehe Absatz [2.6]
Vorgeschlagene Mindestwerte des Flankenspiels sind rechts aufgeführt. Der Wert ist proportional dem Modul. Es liegen zwei Bereiche vor: der eine für die Qualität ISO 4-7, der andere für die Qualität 8-12 nach ISO 1328-1, siehe [1.12]. In Klammern ist der empfohlene Mittelwert angeführt.
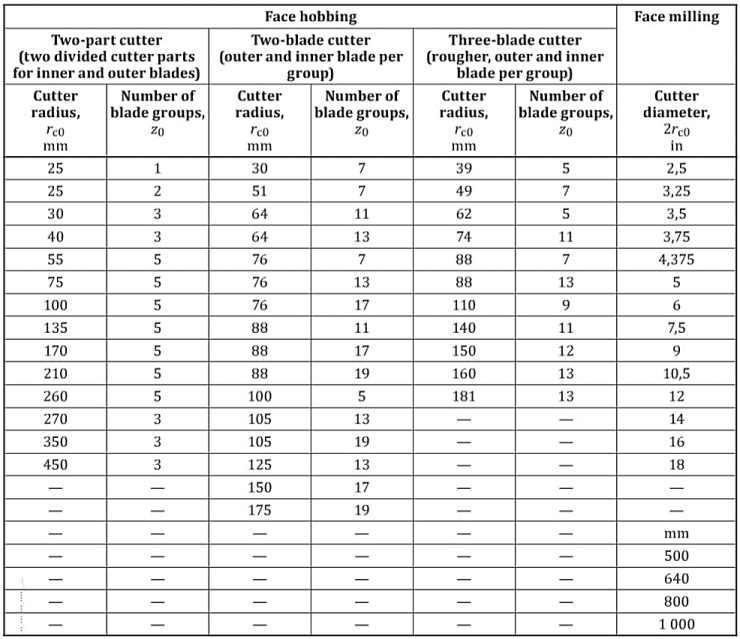
Da der Entwurf und die Herstellung von Kegelzahnrädern abhängig von dem Radius des Werkzeugs und der Anzahl der Gruppen von Schneidemessern ist, führen wir eine Liste von Standardwerkzeugen auf. Der empfohlene Bereich ist in spitzen Klammern „<...>“ angeführt.
Fräsertabelle: Fräserradius rc0 und Anzahl der Messergruppen z0.
Wählen Sie die Form des Zahnprofils, die der Verzahnungsart und Ihren Anforderungen entspricht. Nach der Wahl werden die Werte der Thetaa2- und Thetaf2-Winkel, die weiter in der Berechnung verwendet werden, entsprechend entworfen. Nach Abstreichen der Anstreich-Schaltfläche können Sie Ihre eigene Werte eingeben.
Wenn Sie das Präzisionsmodul mmn (met) erreichen möchten, geben Sie den Sollwert ein und drücken Sie die "<" Taste. Der Wert von de2 wird errechnet (dm2). Meistens ist es erforderlich, die Iteration erneut auszuführen und die Berechnung zu wiederholen (Methode 1,2,3).
In dem belasteten Getriebe entstehen Kräfte, die auf die Maschine übertragen
werden. Für die richtige Auslegung der Anlage ist die Kenntnis dieser Kräfte
überhaupt von Grundbedeutung. Die Kräfteorientierung ist in der Abbildung
dargestellt. In den Zeilen
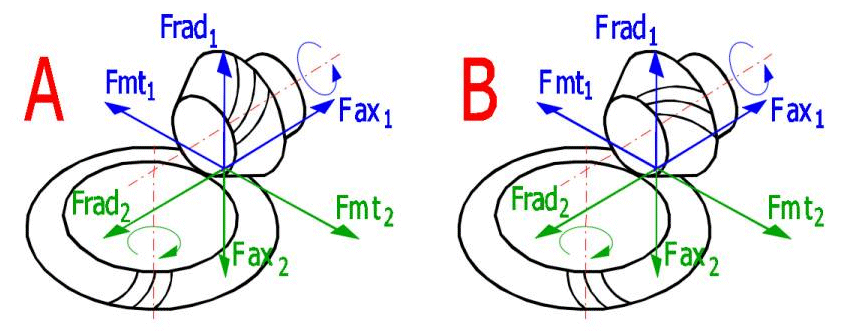
Wählen Sie für die Kraftberechnung eine Methode aus, die für die Geometrielösung angewendet wurde. Die geometrischen Werte der ausgewählten Methode und die Eingabedaten (Absätze 1–3) werden zur Kraftberechnung verwendet.
Nach Aufstiegssinn der Zähne werden Räder in rechte und linke unterschieden.
Die Zähne der Gegenräder müssen mit einer gegenseitigen Richtung der Krümmung
ausgeführt werden. Das Getriebe als Komplett ist durch Krümmung der Ritzelzähne
gekennzeichnet.
Bei Getrieben mit schrägen und gekrümmten Zähnen ist eine Drehbewegung
überwiegend in einer Richtung erforderlich. Die Richtung der Zahnkrümmung wird
dann so gewählt, dass die auf die Räder angreifenden Axialkräfte dazu tendieren,
die Räder aus dem Eingriff auszudrängen (die Zähne gehen den Eingriff mit ihren
stärkeren Enden auf der äußeren Stirnfläche der Räder ein).
In der Abbildung ist der Aufstiegssinn des Ritzels:
A – der linke
B – der rechte
Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
In dieser Berechnung sind neben dem 2D-Standard-Output für die Zeichnung auch Unterlagen für die Erstellung des exakten, für die Herstellung, den Druck bzw. das Testen geeigneten 3D-Modells der Kegel- bzw. Hypoidverzahnung vorbereitet.
1. In der Auflistung "Ausgabe der 2D - Zeichnung in" das Ziel - CAD - System (Zielprogramm) auswählen, in welches sie eine Abbildung generieren lassen wollen oder "DXF Datei" für die Herstellung der Zeichnung in die Datei des Formats DXF.
2. In der Auflistung "Maßstab der 2D - Zeichnung" den Zeichnungsmaßstab einstellen. Die Zeichnung ist immer im Maßstab 1:1 hergestellt. Durch den Maßstab stellen Sie nur bestimmte Zeichnungsparameter ein, z. B. eine Textgröße, einen Wert des Überhangs der Achsen.
3. Wenn es nötig ist, sind auch weitere Steuerungselemente einzustellen. Die meisten Berechnungen beinhalten auch weitere Einstellungsmöglichkeiten, die von der Berechnung und dem gezeichneten Objekt abhängig sind. Eine Erläuterung dieser Ergänzungsoptionen finden Sie in der Hilfe der entsprechenden Berechnung.
4. Starten Sie durch das Drücken der Schaltfläche Zeichnen mit der Ikone der verlangten Zeichnung.
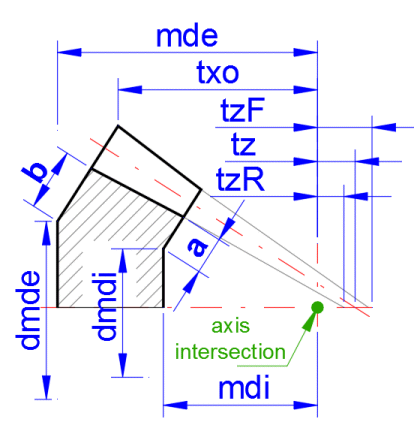
Die Funktionsmaße sind durch die Berechnung gegeben. In diesem Teil können Sie jedoch die Abmessungen der Räder so wählen, dass sie auch weiteren Anforderungen entsprechen. Es handelt sich vor allem um die Einbaumaße (mdi, mde). Nach der Kennzeichnung des Markierungsfeldes unter [9.5] können Sie die eigentlichen Maße des Versetzens a, b eingeben. Bei ihrer Änderung ändern sich die Parameter der Montagabstände (mdi, mde) bzw. der Durchmesser (dmdi, dmde). Rechts von den berechneten Werten [9.7–9.10] kann der gewünschte Wert der Abmessung eingegeben werden, und nach dem Drücken der Taste „<=1“ bzw. „<=2“ ist der Wert des Einrückens a, b für den Zahntrieb bzw. das Rad so angepasst, dass die Werte mdi, mde, dmdi, dmde dem gewünschten Wert entsprechen.
Das wechselseitige Verhältnis der eingegebenen Werte ist der Abbildung zu entnehmen.
Den Text der Beschreibung platzieren Sie in eine 2D-Zeichnung durch
Betätigung der Schaltfläche "Vykreslit – Aufzeichnen". Den Text können Sie nach
dem Ankreuzen eines Ankreuzfeldes aufbereiten.
Wenn es das entsprechende Modul für das Einfügen der Modelle in das 3D CAD
System unterstützt, ist der Inhalt der einzelnen Zeilen in die Benutzerattribute
des Modells eingefügt und kann für die Generierung der Stückliste verwendet
werden. (Einzelheiten finden Sie in der Hilfe für den
Anschluss an das zugehörige 3D CAD System.)
Eine Reihe von Berechnungen (Verzahnung, Federn…) ermöglicht es, in die Zeichnung auch eine zugehörige Tabelle mit Textinformationen über das berechnete Objekt einzufügen. Die Tabelle wählen Sie von der entsprechenden Auflistung aus (im Falle, dass die Berechnung das Einfügen von mehreren Typen ermöglicht). Die Aufzeichnung der Tabelle durch Betätigung der Schaltfläche „Tabelle zeichnen“ starten.
Die Definition eines 3D-Modells ist keinesfalls eine triviale Angelegenheit und die Definition des parametrischen Modells für ein beliebiges CAD-System ist aufwendig. Daher haben wir die Möglichkeit der Generierung der Unterlagen für die Erstellung eines nicht-parametrischen Modells im Wesentlichen für ein beliebiges 3D-CAD-System vorbereitet.
Die Erstellung eines genauen Modells besteht so aus drei einfachen Operationen.
Erstellung des Rades ohne Verzahnung (einfache Rotation eines Radprofils).
Einlesen der Profile der Lücke zwischen den Zähnen in definierten Abständen, ihre Koppelung und Abzug des entstandenen Volumens vom erstellten Rad.
Generieren des Rotationsfeldes der Lücken und hiermit Erstellung des genauen Zahnrads.
Allgemeines Verfahren:
Stellen Sie die Parameter des Outputs [9.20–9.31] der generierten, für Ihr 3D-CAD-System geeigneten Abmessungen ein (Beispiel und Details siehe Hilfe und Beispiele).
Im Punkt [9.33] stellen Sie die Drehung (Spiegelung) des Profils
des gewählten Rades auf der Abbildung so ein, dass das Profil beim Einfügen in
die von Ihnen gewählte Fläche in Ihrem CAD-System um die positive z-Halbachse
rotiert.
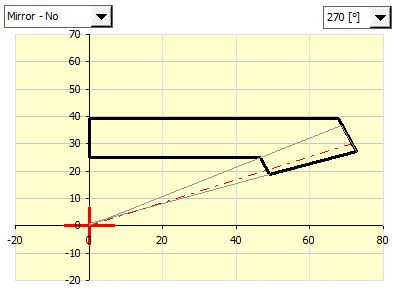
Generieren Sie das Profil des gewählten Rades (erste Taste).

Im CAD-System fügen Sie das Profil in die ausgewählte Ebene ein, wobei Sie durch Rotation um die z-Achse das Halbfabrikat des Rades erstellen.
Generieren Sie die Schnitte der Zahnlücke (zweite Taste).
Fügen Sie die generierten Schnitte schrittweise in das Modell
ein.
Für Räder mit Geradverzahnung genügen 2 Schnitte 1–9.
Für Räder mit gekrümmter Schrägverzahnung und für Hypoidräder genügt zumeist
die Verwendung der Schnitte 1–3–5–7–9.
Zur Erhöhung der Genauigkeit können ferner alle 9 Schnitte verwendet werden.
Verbinden Sie die eingefügten Schnitte durch die Operationen LOFT und ziehen Sie das entstandene Element vom Profil des Rades ab.
Erstellen Sie aus der Lücke zwischen den Zähnen ein Rotationsfeld um die z-Achse (Anzahl der Kopien = Anzahl der Zähne).
Fügen Sie das Rad in die Baugruppe ein, wobei sie für die
korrekte Positionierung die Abmessungen a, mdi oder mde aus
[9.7 oder 9.8] verwenden.
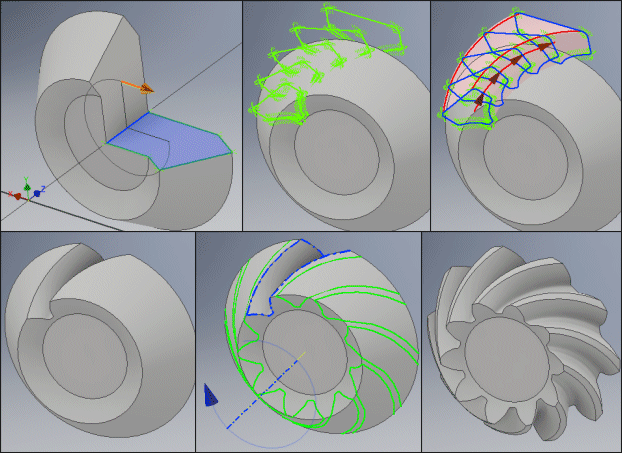
Einige CAD-Systeme können zur richtigen Verbindung der Profile
auch die Bahnen des Profils erforderlich machen (dritte Taste).

B: 1.1-1.2; C: 15-25; D: Yes; E: 5; F: No; G: XLSX; [9.22] Wheel profile rotation 270, Mirror No.
Wheel creation: 2D Sketch - XZ plane, import points from xlsx, connect points
by line, rotate profile around z-axis
Tooth creation: 3D Sketch - Import profile points from xlsx, connect points by
curve, close the open profile manually by line, repeat for profiles 1-9, join
B: 1.1-1.2; C: 15-25; D: Yes; E: 5; F: Yes; G: DXF for wheel profile, G:
SLDCRV for profiles and control curves; [9.22]
Tooth creation: 3D Sketch
a)
b) Control curve import (Profile Path) from SLDCRV. Select one or more control
curves.
c) J
B: 1.1-1.2; C: 15-25; D: Yes; E: 5; F: Yes; G: DXF for wheel profile, G: XLSX for profiles and control curves; [9.22] Wheel Profile Rotation 270, Mirror No.
Wheel creation: Open DXF from file xx_Pinion-cone.dxf (Options ...-> Import
2D geometry, Part Sketch, Right (YZ)),
Tooth creation:
a) Surfacing => Curve by table, importing profiles from XLSX (Parameters: Curve
Fit = Smoothing Off, Curve End Conditions = Closed, Natural), repeat for
sections 1-9.
b) Home => Lofted Cutout
B: 1.1-1.2; C: 15-25; D: Yes; E: 5; F: Yes; G: IBL [9.22] Wheel Profile Rotation 270, Mirror No.
Tooth creation:
a) Create a blend element from the xx_All_InOne.ibl file to create a single
dental space.
b) Creating a rotary field by multiplying the blend element.
Für das Generieren der Kurven ist ein Tool einer dritten Partei notwendig, welches die Punkte einzulesen und sie zu einer Kurve zu verbinden vermag. Catia ermöglicht nicht das direkte Einlesen der Punkte der Kurve.
Es ist selbstverständlich möglich, die einzelnen Schnitte aus den generierten Dateien manuell in die Definitionstabellen der Kurven zu kopieren.
Wählen Sie, ob Daten für das Triebrad oder für das Rad generiert werden sollen. Die Wahl des Typs der Orientierung der Verzahnung gilt für das Triebrad, das Rad hat einen entgegengesetzten Drehsinn.
Es kann der Wert 01–10 eingestellt werden. Beim Speichern der zur Erstellung des 3D-Modells notwendigen Dateien wird dann ein Name angeboten, z. B. „01_Ritzel“. Er ist unter anderem für die Erstellung verschiedener Versionen des Modells geeignet.
Sofern der Schalter der Speicherung der Anmerkungen auf Ja geschaltet ist, wird gemeinsam mit den Profilen auch eine Textdatei generiert, welche die vollständigen Eingangsparameter der Verzahnung enthält.
Stellen Sie die Drehung (Spiegelung) des Radprofils (erste Taste) ein, welches um die z-Achse rotieren wird. Durch Drehung können Sie das Radprofil im Koordinatensystem Ihres CAD-Systems korrekt positionieren. Die graphische Darstellung ist der Abb. [9.34] zu entnehmen.
Inventor - 270
Solidworks - 90
Creo - 270
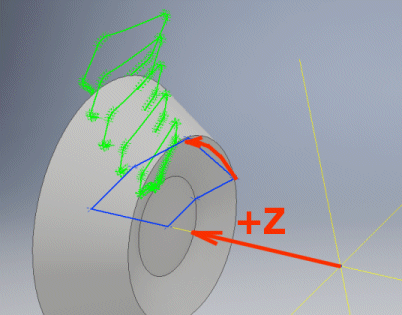
Gibt den Radius in Vielfachen des Moduls an. Für Hypoidverzahnungen und Verzahnungen mit größerem Eingriffswinkel Alpha ist es angebracht, mit dem Wert 0.1 zu beginnen und ihn nach eventueller Kontrolle des Modells je nach Bedarf zu erhöhen. Die DIN-Norm verwendet die Werte 0.25 bis 0.38, die ANSI-Norm verwendet den Wert 0.3. Im Wesentlichen kann ein beliebiger Wert im Bereich von ca. 0.02–0.4 gewählt werden.
Er gibt an, um wie viel die wechselseitige Lücke zwischen jenen Profilen vergrößert ist, welche das von der Basis des Rades in Abzug zu bringende Volumen bilden (die Breite der Verzahnung ist zu überschreiten). In üblichen Fällen ist der Wert 1.1 geeignet, für Räder eines vom Standard abweichenden Profils kann bis auf 2.0 erhöht werden.
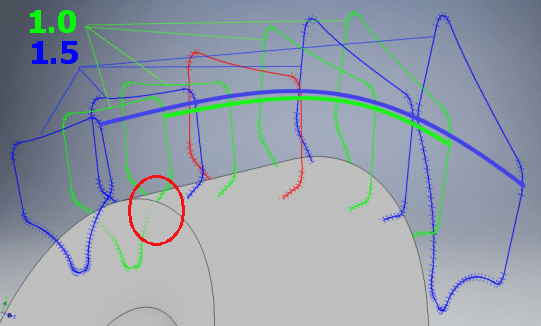
Gibt an, wie viele Punkte generiert werden, welche die Kurve der Zahnseite definieren. In der Regel ist der Wert 20 geeignet. Für spezielle Fälle (Einschränkung des CAD-Systems, Genauigkeit ...) können die Werte 12–200 verwendet werden.
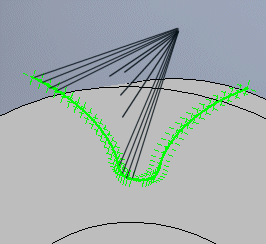
Fügt über das generierte Profil der Lücke zwischen den Zähnen hinaus ein weiteres Stück hinzu, das für die bessere Auswahl der Kurven geeignet sein kann oder dessen Existenz für die korrekte Interpretation der Kurven notwendig ist.
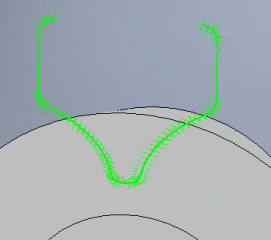
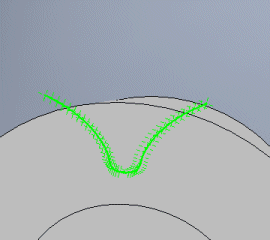
Gibt die Anzahl der Punkte an, die für die Rundung der Anbindung und des Abschlusses des Überbaus verwendet werden. In den meisten Fällen reicht der Wert 5.
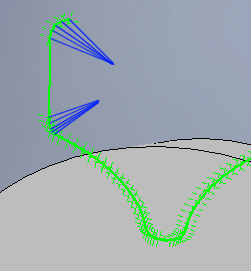
Einige CAD-Systeme erfordern ein abgeschlossenes Profil, andere erfordern ein offenes oder manuell abgeschlossenes Profil. Der Schalter verbindet / verbindet nicht den ersten und den letzten Punkt.

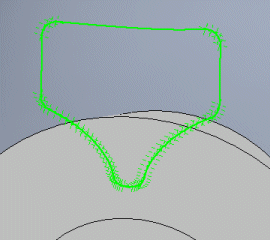
Verschiedene CAD-Systeme unterstützen den Import der die Kurven bildenden Punkte in verschiedenen Formaten. Zur Verfügung stehen die Formate:
Fügt in jeden Punkt der Kurve einen kleinen Kreis ein. Geeignet im Falle, wenn das CAD-System nur das DXF-Format einzulesen vermag und es notwendig ist, das Profil Punkt für Punkt manuell zu erstellen.
Das Programm ist in der Lage, einzelne Schnitte zu generieren, welche die Zahnzwischenlücke definieren (siehe oben). Zum Namen der Datei wird automatische auch die Nummer des Schnittes hinzugefügt. In den meisten Fällen ist es am besten, alle 9 Schnitte in einem Schritt zu generieren, und zwar mittels der Wahl: „Alle“. Die Schnitte werden in Richtung vom Außendurchmesser generiert und nummeriert.
Durch die Wahl „Alle in einem“ ist es ferner möglich, alle Schnitte in einer Datei zu generieren, und zwar im Format:
StartLoft
StartCurve
- first shape x,y,z
EndCurve
......
EndLoft
End
Arclength
Begin section
Begin curve
Begin curve
......
Einige CAD-Systeme erfordern neben den zu verbindenden Profilen auch eine Steuerkurve (Kurven). Geben Sie die laufende Nummer der Kurve ein und drücken Sie die Taste

Die Nummerierung der Kurven wird auf dem Bildschirm angezeigt und durchläuft die entsprechenden Punkte der Profile.
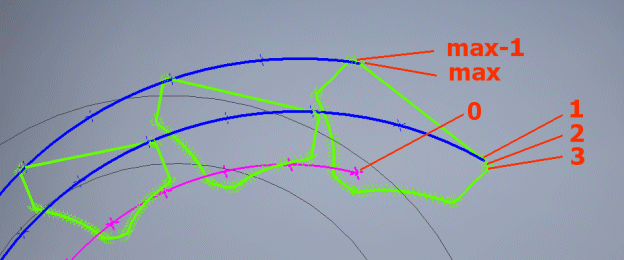
Sofern Sie die Nummer 0 eingeben, wird jene Kurve generiert, die an der Oberfläche des Teilkegels liegt und durch die Mitte eines jeden Profils verläuft.
In der Zeile sind in verkürzter Form die Parameter der Verzahnung angeführt, die vollständig die Geometrie und wichtige Abmessungen definieren.
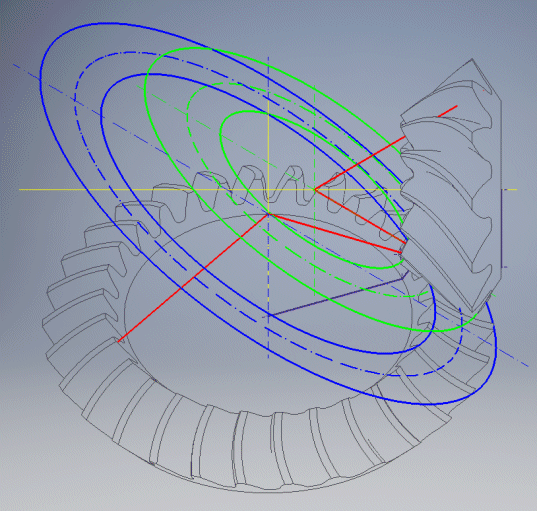
Der Graph links oben gibt an, wie das Profil des Rades generiert wird. Er kann so gedreht und gespiegelt werden, dass er (nach Eingabe in das CAD-System) der Anforderung gerecht wird, wonach das Radprofil um die positive z-Halbachse rotieren muss. Die einzelnen Profile der Zahnzwischenlücke sind in Bezug auf diese Halbachse definiert. Die Einstellung kann in Auswahllisten im Graph erfolgen.


Die Abbildung gibt die Folge der für die Generierung des Rades notwendigen Schritte an.
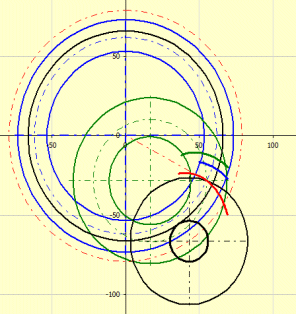
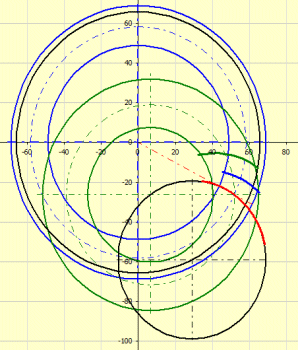
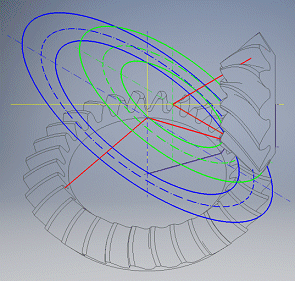
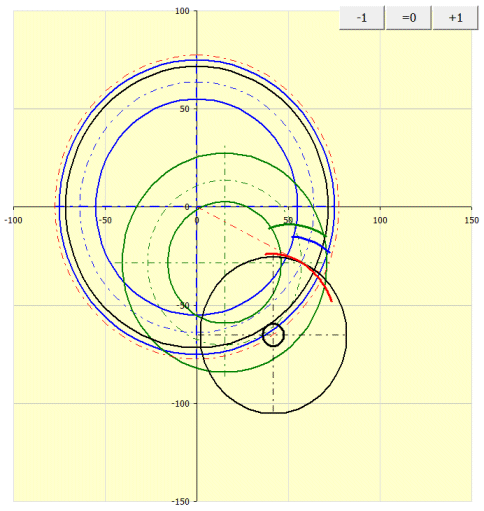
Der Graph zeigt die Geometrie der Eingriffskurven der Zähne in der Teilebene (Pitch Plane) an.
Blau ist sind das Rad und die die Zahnkurven des Rades bildende
Bahn gekennzeichnet.
Grün sind das Triebrad und die die Zahnkurven des Triebrades bildende Bahn
gekennzeichnet.
Schwarz ist das Bearbeitungswerkzeug, der Abwälzkreis gekennzeichnet.
Rot ist die Bearbeitungsbahn des Werkzeugs gemeinsam für das Triebrad und das
Rad gekennzeichnet.
Mittels der Taste „=0“ wird die Verzahnung in die Nullposition eingestellt. Mit den Tasten + und - werden das Rad und das Triebrad im Übersetzungsverhältnis gedreht.
Für das Umsetzen der Achsen a=0 (Methode 0) verfließen das Triebrad und das Rad im grünen Kreis.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
- Bevel and hypoid gear geometry
- Géométrie des engrenages coniques et hypoides
- Geometrie kuželového a hypoidního ozubení
ISO 23509:2016 specifies the geometry of bevel gears. The term bevel gears is used to mean straight, spiral, zerol bevel and hypoid gear designs. If the text pertains to one or more, but not all, of these, the specific forms are identified. ISO 23509:2016 is intended for use by an experienced gear designer capable of selecting reasonable values for the factors based on his knowledge and background. It is not intended for use by the engineering public at large.
BEVEL AND HYPOID GEAR GEOMETRY
American Gear Manufacturers Association
Equivalent Standard(s) Relationship - ISO 23509 : 2016 Identical
CALCULATION OF LOAD CAPACITY OF BEVEL GEARS - PART 1: INTRODUCTION AND GENERAL INFLUENCE FACTORS
CALCULATION OF LOAD CAPACITY OF BEVEL GEARS - PART 3: CALCULATION OF TOOTH ROOT STRENGTH
CALCULATION OF LOAD CAPACITY OF BEVEL GEARS - PART 2: CALCULATION OF SURFACE DURABILITY (PITTING)
^