Diese Arbeitsmappe enthält Informationen zum Einfluss der Temperatur auf einige physikalische und mechanische Eigenschaften der Maschinenbauwerkstoffe. Mit Hilfe dieses Werkzeuges können folgende Aufgaben gelöst werden:
In der Berechnung sind Daten, Verfahren, Algorithmen und Angaben aus der
Fachliteratur und den Normen verwendet.
Normenverzeichnis: EN 1561, EN 1563, EN 16079, EN 1753, EN 10088-1, EN 10095, EN
10269, EN 10302
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Dieses Kapitel befasst sich mit der thermischen Längenausdehnung von maschinenbaulichen Materialien. Absatz [1] dient nur zur Information. Absatz [2] dient dann zur Berechnung der relevanten Materialparameter in Abhängigkeit von der gewählten Temperatur.
Wenn ein Körper erwärmt oder abgekühlt wird, ändern sich seine Abmessungen. Bei Körpern mit einer vorherrschenden Abmessung spricht man über thermische Längenausdehnung. Die Abhängigkeit der Verlängerung von der Art des Materials wird durch den thermischen Längenausdehnungskoeffizienten ausgedrückt. Im Allgemeinen wird diese physikalische Materialgröße mit der folgenden Beziehung definiert:
![]()
wo:
L0 ... Anfangslänge des Körpers
DL ... Längenänderung
DT ... Temperaturänderung
Dieser Koeffizient ist jedoch nicht konstant, sondern ändert sich mit zunehmender Temperatur. Die mathematische Beschreibung des Verlaufs des Wärmeausdehnungskoeffizienten als Funktion der Temperatur ist relativ kompliziert. Für eine ausreichend genaue Berechnung der Längenausdehnung über einen größeren Temperaturbereich ist es daher normalerweise erforderlich, eine quadratische oder kubische Rechenbeziehung zu verwenden, in der die Längenausdehnung durch zwei oder mehr Koeffizienten beschrieben ist. Zum Beispiel wird die quadratische Beziehung zur Berechnung der Dehnung in der folgenden Form angegeben:
![]()
wo:
a1,a2 ...
Wärmeausdehnungskoeffizienten
L ... Anfangslänge
DT ... Temperaturänderung
Selbst wenn diese komplexeren Beziehungen verwendet werden, kann die perfekte Berechnungsgenauigkeit über den gesamten Betriebstemperaturbereich nicht garantiert werden.
In der üblichen technischen Praxis wird die Bauteildehnung üblicherweise unter Verwendung von "linearen" Wärmeausdehnungskoeffizienten berechnet. Diese linearen Koeffizienten werden zum Erwärmen des Materials von einer genau gegebenen Anfangstemperatur T0 auf die Endtemperatur T definiert. Die Temperaturdehnung des Bauteils in einem gegebenen Temperaturintervall kann dann aus der folgenden linearen Beziehung bestimmt werden:
![]()
wo:
a ... Linearer Wärmeausdehnungskoeffizient für die
Erwärmung von der Temperatur T0 auf die Temperatur T
L ... Anfangslänge
DT ... Temperaturänderung T-T0
Es ist offensichtlich, dass für genauere Berechnungen der Längenausdehnung in einem breiteren Temperaturbereich mehr Werte des linearen Wärmeausdehnungskoeffizienten für das jeweilige Material bekannt sein müssen. In Materialdatenbanken oder Materialmerkblättern ist es normalerweise möglich, einen oder mehrere Tabellenwerte des Koeffizienten für verschiedene Temperaturintervalle "T0-T" für das jeweilige Material zu finden. Die Aufgabe dieser Berechnung besteht dann darin, den ungefähren Wert des linearen Wärmeausdehnungskoeffizienten für jede beliebige Kombination von Anfangs- und Endtemperatur "T0-T" zu finden.
Die Abbildung zeigt grafisch den üblichen Verlauf des Wärmeausdehnungskoeffizienten in Abhängigkeit von der Temperatur für einzelne Materialgruppen. Verwenden Sie die Auswahlliste, um zwischen verschiedenen Gruppen zu wechseln.
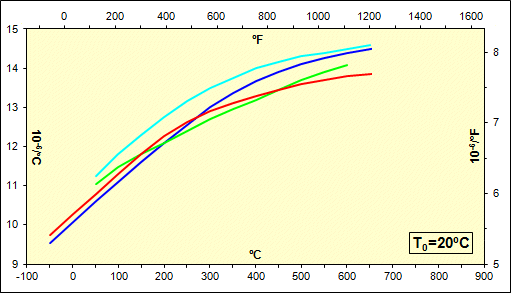
Dieser Absatz dient zur eigentlichen Berechnung des linearen Wärmeausdehnungskoeffizienten und der Längendehnung des Bauteils.
Wählen Sie zunächst das Einheitensystem der Berechnung [2.1] und die entsprechende Materialgruppe [2.3] aus. Nachdem ein bekannter Wert des Koeffizienten in den Zeilen [2.5 - 2.8] definiert wurde, wird in der Grafik für das jeweilige Material die Kurve des Verlaufs des linearen Wärmeausdehnungskoeffizienten in Abhängigkeit von der Temperatur gezeichnet. Die Ergebnisse der Berechnung für die erforderliche Temperaturänderung [2.10, 2.11] sind in den Zeilen [2.12, 2.16] angegeben.
In der Auswahlliste wählen Sie das gewünschte Einheitssystem der Berechnung. Beim Umschalten der Einheiten werden alle Werte sofort neu berechnet.
Definieren Sie in diesem Abschnitt die erforderlichen Parameter Ihres Materials.
Wählen Sie in der Auswahlliste die Materialgruppe aus, die Ihrem Material entspricht.
In dieser Zeile ist für verschiedene Materialien aus der gegebenen Materialgruppe [2.3] der Bereich der üblichen Werte des linearen Wärmeausdehnungskoeffizienten angegeben. Dieser Koeffizient ist für die Erwärmung des Materials von 20°C auf 100°C (68–212°F) definiert.
Geben Sie in Zeile [2.5] einen bekannten Wert des linearen Wärmeausdehnungskoeffizienten ein, wenn Sie das Material von der Temperatur "T0" [2.6] auf die Temperatur "T" [2.7] erwärmen.
Nachdem alle Materialparameter in Abschnitt [2.2] definiert wurden, wird für das gegebene Material eine theoretische Kurve des Verlaufs des linearen Wärmeausdehnungskoeffizienten in Abhängigkeit von der Temperatur gezeichnet. Die angezeigte Kurve entspricht der Temperaturänderung (Erwärmung) von der Anfangstemperatur "T0" auf die angezeigte Temperatur. Wählen Sie die Anfangstemperatur in der Liste unten rechts in der Grafik aus.
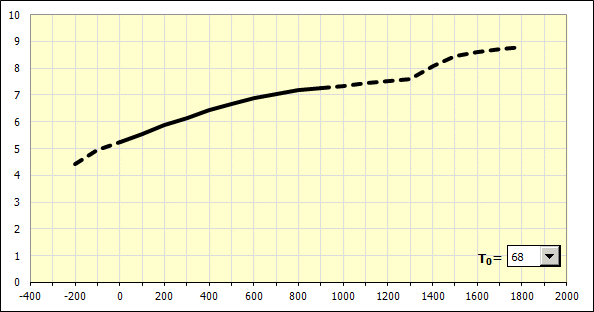
In der Zeile [2.9] wird für das oben definierte Material sein Grundwert des linearen Wärmeausdehnungskoeffizienten für die Erwärmung von 20°C auf 100°C (68–212°F) berechnet.
In der Zeile [2.12] wird die eigentliche Berechnung des linearen Wärmeausdehnungskoeffizienten zum Erwärmen des Materials von der Anfangstemperatur "TI" [2.10] auf die erforderliche Endtemperatur "TE" [2.11] durchgeführt.
In der Tabelle finden Sie informative Werte des linearen Wärmeausdehnungskoeffizienten für ausgewählte Materialien.
Bedeutung der Parameter:
a ... Linearer Wärmeausdehnungskoeffizient [10-6/°C,
10-6/°F]
DT ... Temperaturänderung (Erwärmung) des Materials,
für das der angegebene Koeffizient definiert ist [°C, °F]
In diesem Teil wird die thermische Dehnung einer bestimmten Komponente aus dem oben definierten Material für die in den Zeilen [2.10, 2.11] beschriebene Temperaturänderung berechnet.
In diesem Absatz wird die gegenseitige Wärmeausdehnung einer Gruppe von Bauteilen aus verschiedenen Materialien untersucht. Die Komponenten müssen in einer linearen Maßkette angeordnet sein. Die Berechnung ermöglicht es, die thermische Dehnung einzelner Komponenten oder zwei Gruppen von Komponenten zu vergleichen.
Berechnungsverfahren:
1. Geben Sie die Betriebstemperaturen in Zeile [3.1] ein.
2. Wenn die beiden zu vergleichenden Komponentengruppen nicht gleichmäßig erwärmt werden, aktivieren Sie das Kontrollkästchen in Zeile [3.2] und geben Sie eine andere Endtemperatur für die Komponenten aus Gruppe "B" ein.
3. Definieren Sie die Parameter der Maßkette in Tabelle [3.3].
Spalte 1 - Wählen Sie aus der Liste die Vergleichsgruppe aus, zu der die Komponente gehört.
Spalte 3 - Geben Sie die Länge des Teils ein.
Spalte 4 - Wählen Sie in der Auswahlliste die Materialgruppe aus, die dem verwendeten Teilematerial entspricht.
Spalte 5 - geben Sie den Grundwert des linearen Wärmeausdehnungskoeffizienten für die Erwärmung von 20°C auf 100°C (68–212°F) ein.
Spalte 6 - Wenn Sie den genauen Wert des Wärmeausdehnungskoeffizienten für die Betriebstemperaturänderung kennen (z. B. aus dem Materialmerkblatt), deaktivieren Sie das Kontrollkästchen und geben Sie den Wert manuell ein.
4. In den letzten beiden Spalten der Tabelle wird die thermische Dehnung der einzelnen Komponenten berechnet.
5. Die Gesamtausdehnung beider Vergleichsgruppen einschließlich eines grafischen Vergleichs finden Sie in Abschnitt [3.4].
Dieses Kapitel befasst sich mit dem Einfluss der Temperatur auf die Größe des Elastizitätsmoduls von maschinenbaulichen Materialien. Absatz [4] dient nur zur Information. Absatz [5] wird verwendet, um das Elastizitätsmodul in Abhängigkeit von der ausgewählten Temperatur zu berechnen.
Die hier angegebenen Daten beziehen sich auf das Elastizitätsmodul im Zug. Um das Elastizitätsmodul bei Schub (Schubmodul) zu bestimmen, kann die Umrechnungsbeziehung verwendet werden:
![]()
wo:
E ... Elastizitätsmodul im Zug
m ... Poissonsche Zahl
Die Abbildung zeigt grafisch den üblichen Verlauf des Elastizitätsmoduls in Abhängigkeit von der Temperatur für einzelne Materialgruppen. Verwenden Sie die Auswahlliste, um zwischen verschiedenen Gruppen zu wechseln.
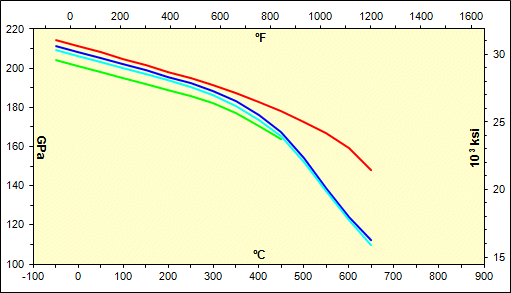
Dieser Absatz dient zur tatsächlichen Berechnung des Elastizitätsmoduls im Zug.
Wählen Sie zunächst das Einheitensystem der Berechnung [5.1] und die entsprechende Materialgruppe [5.3] aus. Nach der Definition eines bekannten Wertes des Elastizitätsmoduls in den Zeilen [5.5, 5.6] wird in der Grafik für das jeweilige Material die Kurve des Verlaufs des Elastizitätsmoduls in Abhängigkeit von der Temperatur gezeichnet. Der resultierende berechnete Wert des Elastizitätsmoduls für die erforderliche Temperatur [5.9] ist in Zeile [5.10] angegeben.
In der Auswahlliste wählen Sie das gewünschte Einheitssystem der Berechnung. Beim Umschalten der Einheiten werden alle Werte sofort neu berechnet.
Definieren Sie in diesem Abschnitt die erforderlichen Parameter Ihres Materials.
Wählen Sie in der Auswahlliste die Materialgruppe aus, die Ihrem Material entspricht.
In dieser Zeile ist der Bereich der üblichen Elastizitätsmodulwerte bei 20°C (68°F) für verschiedene Materialien aus der angegebenen Materialgruppe [5.3] angegeben.
Geben Sie in Zeile [5.5] einen bekannten Wert des Elastizitätsmoduls bei der Temperatur "T" ein [5.6].
Nach der Definition aller Materialparameter in Abschnitt [5.2] wird für das gegebene Material die theoretische Kurve des Elastizitätsmoduls in Abhängigkeit von der Temperatur gezeichnet.
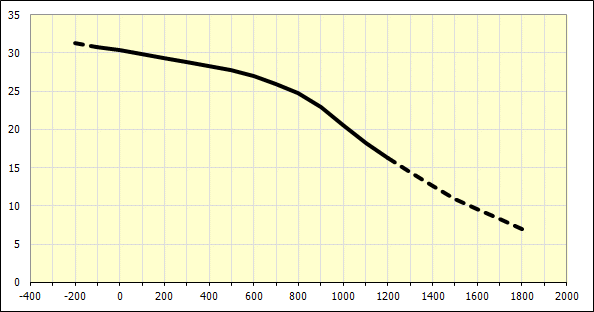
In Zeile [5.8] wird für das oben definierte Material sein Grundwert des Elastizitätsmoduls bei der Temperatur von 20°C (68°F) berechnet.
In Zeile [5.10] wird der Wert des Elastizitätsmoduls für die erforderliche Endtemperatur "TE" [5.9] berechnet.
In diesem Abschnitt ist es möglich, die entsprechende Größe des Schubmoduls für den oben berechneten Wert des Elastizitätsmoduls im Zug zu bestimmen.
In der Tabelle finden Sie informative Werte des Elastizitätsmoduls im Zug für ausgewählte Materialien.
Bedeutung der Parameter:
E ... Elastizitätsmodul im Zug [GPa, 103 ksi]
T ... Materialtemperatur, für welche das angegebene Elastizitätsmodul definiert
ist [°C, °F]
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung"
EN 1561
Founding - Grey cast irons
Gießereiwesen - Gusseisen mit Lamellengraphit
Fonderie - Fontes à graphite lamellaire
Slévárenství - Litiny s lupínkovým grafitem
EN 1563
Founding - Spheroidal graphite cast irons
Gießereiwesen - Gußeisen mit Kugelgraphit
Fonderie - Fonte à graphite sphéroïdal
Slévárenství - Litina s kulièkovým grafitem
EN 16079
Founding - Compacted (vermicular) graphite cast irons
Gießereiwesen - Gusseisen mit Vermiculargraphit
Fonderie - Fontes à graphite vermiculaire (compacté)
Slévárenství - Litina s vermikulárním (kompaktním) grafitem
EN 1753
Magnesium and magnesium alloys - Magnesium alloy ingots and castings
Magnesium und Magnesiumlegierungen - Blockmetalle und Gussstücke aus
Magnesiumlegierungen
Magnésium et alliages de magnésium - Lingots et pièces moulées en alliages de
magnésium
Hoøèík a slitiny hoøèíku - Ingoty a odlitky ze slitin hoøèíku
EN 10088-1
Stainless steels - Part 1: List of stainless steels
Nichtrostende Stähle - Teil 1: Verzeichnis der nichtrostenden Stähle
Aciers inoxydables - Partie 1 : liste des aciers inoxydables
Korozivzdorné oceli - Èást 1: Pøehled korozivzdorných ocelí
EN 10095
Heat resisting steels and nickel alloys
Hitzebeständige Stähle und Nickellegierungen
Aciers et alliages de nickel réfractaires
Oceli a niklové slitiny žáruvzdorné
EN 10269
Steels and nickel alloys for fasteners with specified elevated and/or low
temperature properties
Stähle und Nickellegierungen für Befestigungselemente für den Einsatz bei
erhöhten und/oder tiefen Temperaturen
Aciers et alliages de nickel pour éléments de fixation utilisés à température
élevée et/ou basse température
Oceli a niklové slitiny na upevòovací prvky pro použití pøi zvýšených a/nebo
nízkých teplotách
EN 10302
Creep resisting steels, nickel and cobalt alloys
Warmfeste Stähle, Nickel- und Cobaltlegierungen
Aciers et alliage à base de nickel et de cobalt résistant au fluage
Žáropevné oceli, niklové a kobaltové slitiny
ASM Handbook Volume 1: Properties and Selection: Irons, Steels, and High-Performance
Alloys
ASM International, 1990
Metals Handbook Desk Edition, 2nd Edition
ASM International, 1998
ASM Ready Reference: Thermal Properties of Metals
ASM International, 2002
Materials Science and Engineering Handbook, Third Edition
CRC Press LLC, 2001
Smithells Light Metals Handbook
Butterworth-Heinemann, 1998
CRC Materials Science and Engineering Handbook, 4th Edition
CRC Press, 2015
Military Handbook - MIL-HDBK-5H: Metallic Materials and Elements for
Aerospace Vehicle Structures
U.S. Department of Defense, 1998
Deutsches Kupferinstitut Berufsverband e.V,
Technische Broschüren und Datenblätter
Special Metals Corporation
High Performance Alloys Literature