Die Berechnung ist bestimmt für den geometrischen und Festigkeitsentwurf der metallischen Federn, verschiedener Typen und Ausführungen, mit einer statischen bzw. zyklischen Belastung. Das Programm löst folgende Aufgaben:
Den geometrischen Entwurf und die Berechnung der Parameter des Arbeitszyklus für metallische Federn folgender Typen und Ausführung:
Den automatischen Entwurf (Aufsuche) der Feder mit geeigneten Maßen.
Statische und dynamische Festigkeitskontrolle.
Das Programm enthält eine Tafel mit üblich verwendeten Federwerkstoffen nach EN, ASTM/SAE, DIN, BS, JIS, UNI, SIS, CSN und anderen.
In der Berechnung sind benutzt Daten, Verfahren, Algorithmen und Angaben aus der Fachliteratur und Normen EN 13906, DIN 2088, DIN 2089, DIN 2090, DIN 2091, DIN 2092, DIN 2093, DIN 2095, DIN 2096, DIN 2097.
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Federn sind für die Aufnahme und Speicherung der mechanischen Energie bestimmte Bauelemente, die auf dem Prinzip der elastischen Materialverformung arbeiten. Die Federn gehören zu den am meisten belasteten Maschinenelementen und werden üblich verwendet als:
Die Federfunktion wird nach Verlauf und Größe ihrer Verformung in Abhängigkeit von der einwirkenden Belastung beurteilt.
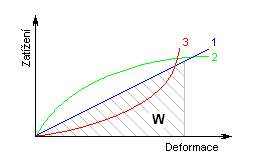
Mit Rücksicht auf den Verformungsverlauf lassen sich Federn in drei grundlegende Typen unterteilen:
Der Inhalt der Fläche W unter der Kennlinie der Feder stellt die bei der Belastung von einer Feder hergestellte Verformungsarbeit (Energie) dar. Die Verformungsenergie bei den mit Druck, Zug oder Biegung beanspruchten Federn ist mit der nachstehend aufgeführten Formel gegeben:
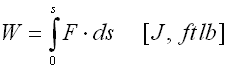
Bei den mit Verdrehung beanspruchten Federn:
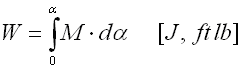
Die Grundparameter der Feder, die die Funktionalität kennzeichnet, ist ihre Härte (Federrate). Die Federrate k gibt die Belastungsgröße (Kraft bzw. Moment) an, welche die Einheitsverformung der Feder (Verschiebung bzw. Verdrehung) verursacht.
![]()
![]()
Bei Federn mit einer linearen Kennlinie ist die Federrate konstant, bei anderen Federn ist die Federrate veränderlich.
Die Federn werden mit einer Vorspannung montiert, also im Zustand, wo eine Feder der kleinsten Arbeitsbelastung unterworfen ist. In Hinsicht auf die Federfunktion werden 4 Grundzustände der Federn unterschieden und gekennzeichnet:
| Federzustand | Beschreibung des Federzustandes | Index |
| Frei | Feder ist nicht belastet | 0 |
| vorgespannt | Feder ist der kleinsten Arbeitsbelastung unterworfen | 1 |
| voll belastet | Feder ist der höchsten Arbeitsbelastung unterworfen | 8 |
| Grenzbelastung | Die Feder ist einer Grenzbelastung unterzogen – diese ist durch die Materialfestigkeit oder die konstruktiven Einschränkungen bestimmt (z. B. Einfederung einer Schraubdruckfeder auf der Berührung der Windungen) | 9 |
Die oben angeführten Indexe werden in der Berechnung zur Kennzeichnung der einzelnen dem gegebenen Federzustand angehörenden Federparameter verwendet.
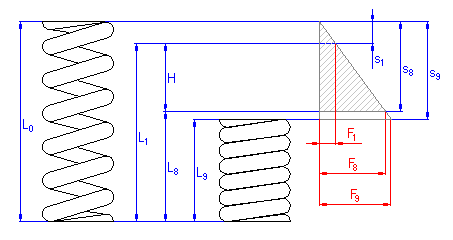
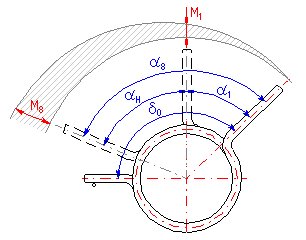
Die Differenz der Verformungen bei Federn im vollbelasteten und vorgespannten Zustand wird als der Arbeitshub der Feder H, aH bezeichnet.
Vom Gesichtspunkt der Festigkeitskontrolle und der Standzeit werden bei den metallischen Federn zwei grundlegende Arten ihrer Belastung unterschieden:
Die metallischen Federn können in Gruppen in Hinblick auf manche Aspekte unterteilt werden. Als grundlegend kann die Unterteilung nach der Belastungsart und der Bauform der Feder gehalten werden. Die üblichsten Federtypen sind detailliert nachfolgend beschrieben:
Federn für die Belastung mit Axialkräften (Druck/Zug)
- Schraubenfedern
- Tellerfedern
- Ringfedern
Federn für die Belastung mit Querkräften (Biegung)
- Blattfedern
- Formfedern
Federn für die Belastung durch Drehmomente
- Drehstabfedern
- Spiralfedern
- Schraubenfedern
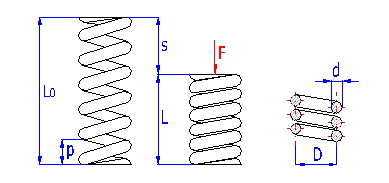
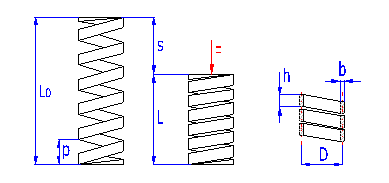
Federn in Zylinderform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt. Gewöhnlich sind die Druckfedern aus Drähten und Stäben des Kreisquerschnitts hergestellt. Die Federn mit einem Draht eines rechteckigen Querschnitts werden am häufigsten in Anwendungen benutzt, wo eine niedrige bauliche Federhöhe bei einer relativ höheren Belastung gefordert ist (Federn mit b>h).
|
Draht mit rundem Querschnitt |
Draht mit rechteckigem Querschnitt |
|
|
|
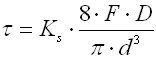 |
 |
 |
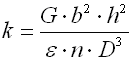 |
|
|
|
wo:
c ... Wickelverhältnis (c=D/d; c=D/b) [-]
b ... Drahtbreite [mm, in]
d ... Drahtdurchmesser [mm, in]
D ... Mittlerer Federdurchmesser [mm, in]
F ... Federbelastung [N, lb]
G ... Schubmodul [MPa, psi]
h ... Drahthöhe [mm, in]
k ... Federrate [N/mm, lb/in]
Ks ... Korrektionsfaktor einer Torsionsspannung [-]
L0 ... Länge der unbelasteten Feder [mm, in]
LS ... Blocklänge [mm, in]
n ... Anzahl der Arbeitswindungen [-]
p ... Abstand zwischen den Windungen [mm, in]
s ... Verformung (Einfederung) der Feder [mm, in]
e,y ... Formzahl [-] (siehe zum Beispiel DIN 2090)
t ... Torsionsspannung des Federmaterials [MPa,
psi]
Korrektionsfaktor einer Torsionsspannung
Durch Windungsabrundung kommt es bei gewickelten Federn zu zusätzlichen
Biegespannungen. Deshalb wird die Spannung in der Berechnung durch einen
Korrektionsfaktor korrigiert.
Bei Federn mit Draht eines Kreisquerschnitts ist der Korrektionsfaktor für das
gegebene Wickelverhältnis aus einigen diversen empirisch festgelegten Formeln
bestimmt (Wahl, Bergsträsserr, Göhner, ...). In dieser Berechnung ist folgende
Beziehung verwendet:
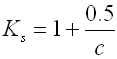
Bei Federn mit Draht eines rechteckigen Querschnitts ist der Korrektionsfaktor
für das gegebene Wickelverhältnis und das Verhältnis b/h aus einschlägigen
Nomogrammen bestimmt. In dieser Berechnung ist der Korrektionsfaktor schon in
der Formzahl y einbezogen.
| Kaltgeformte Federn | Warmgeformte Federn | |
| Wickelverhältnis c | 4 - 16 | 3 - 12 |
| Außendurchmesser De | max. 350 mm | max. 460 mm |
| Anzahl der Windungen n | min. 2 | min. 3 |
| Verhältnis b/h | 1:5 - 5:1 | |
| Freie Federlänge L0 | max. 1000 mm | |
| Schlankheitsverhältnis L0/D | 1 - 10 | |
| Abstand p | (0.3 - 0.6) D; min. 1.5 d | |
Bei den Druckfedern benutzt man einige verschiedene Weisen der Auslegung der Federenden, die sich durch die Anzahl der Schluss- und bearbeiteten Windungen der Feder und durch die Ausführung der Stützfläche der Feder unterscheiden.
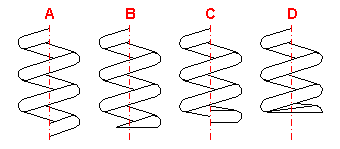
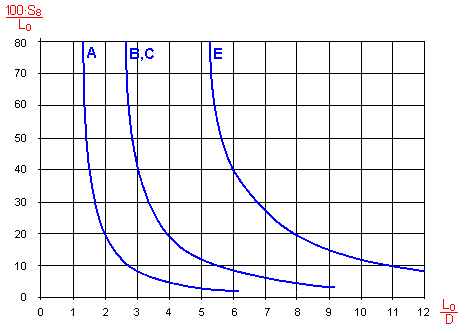
Bei einer Druckfeder ist ihre Absicherung gegen Knickung immer zu kontrollieren. Die Kontrolle ist durch einen Vergleich der maximalen Arbeitsverformung der Feder mit der zugelassenen Verformung durchgeführt. Der Wert der zugelassenen Verformung ist aus Erfahrung für das gegebene Schlankheitsverhältnis der Feder L0/D festgelegt und für den Typ der Federlagerung. Allgemein gilt, dass das Risiko einer möglichen Knickung mit dem zunehmenden Wert des Schlankheitsverhältnisses und der Arbeitseinfederung wächst. Einen schwerwiegenden Einfluss auf die mögliche Knickung hat dabei die Art der Federlagerung.
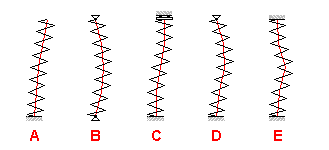
Die Feder, die nicht konstruiert werden kann als eine gegen Knickung abgesicherte, wird gewöhnlich von einem Dorn oder einer Führungsbüchse geführt. Wenn eine Gefahr dabei droht, dass es zu einer Beschädigung der Feder durch Reibung kommt, lässt sich die Feder in einige kürzere seriell angeordnete Federn teilen.
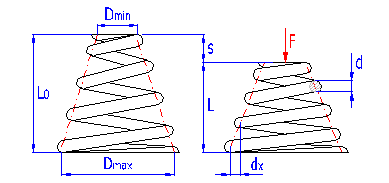
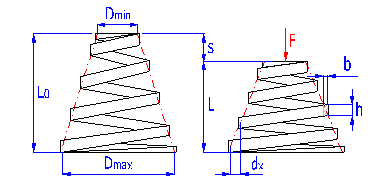
Federn in Kegelform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt. Die kegelförmigen Federn werden gewöhnlich verwendet, wenn die Federrate mit wachsender Einfederung steigen soll.
Bei der steigenden Einfederung einer kegelförmigen Feder stoßen ihre Arbeitswindungen auf die Nachbarwindungen nacheinander auf (zuerst die Windungen mit größtem Durchmesser). Diese Windungen nehmen an der weiteren Einfederung nicht mehr teil, was eine allmähliche Steigerung ihrer Federrate zur Folge hat. Die Arbeitskennlinie einer kegelförmigen Feder kann so in zwei Bereiche unterteilt werden:
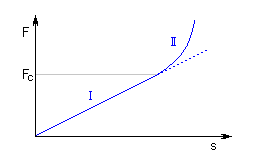
Die Größe der Grenzkraft FC ist von dem Abstand zwischen den Windungen p abhängig, also auch von der gewählten freien Federlänge L0. Mit einer steigenden Federlänge vergrößert sich auch die Grenzkraft FC und der Arbeitsbereich mit konstanter Federrate vergrößert sich.
|
Draht mit rundem Querschnitt |
Draht mit rechteckigem Querschnitt |
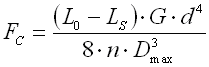 |
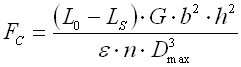 |
|
I. dem Arbeitsbereich mit einer linearen Kennlinie F≤FC |
|
|
|
|
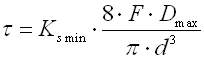 |
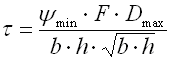 |
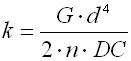 |
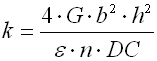 |
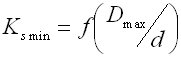 |
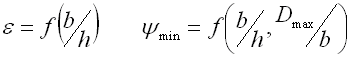 |
|
|
|
|
II. dem Arbeitsbereich mit einer progressiven Kennlinie F>FC |
|
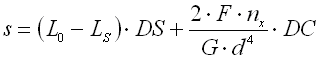 |
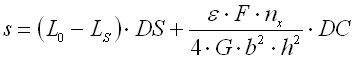 |
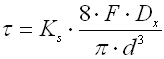 |
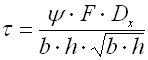 |
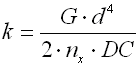 |
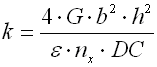 |
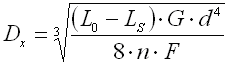 |
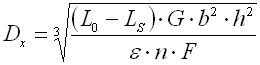 |
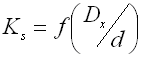 |
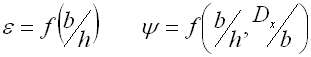 |
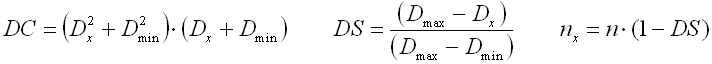 |
|
wo:
cmin ... min. Wickelverhältnis (cmin=Dmin/d; cmin=Dmin/b) [-]
cmax ... max. Wickelverhältnis (cmax=Dmax/d; cmax=Dmax/b) [-]
b ... Drahtbreite [mm, in]
d ... Drahtdurchmesser [mm, in]
dx .. Windungsdistance [mm, in]
Dmin .. min. Mittlerer Federdurchmesser [mm, in]
Dmax .. max. Mittlerer Federdurchmesser [mm, in]
F ... Federbelastung [N, lb]
G ... Schubmodul [MPa, psi]
h ... Drahthöhe [mm, in]
k ... Federrate [N/mm, lb/in]
Ks ... Korrektionsfaktor einer Torsionsspannung [-]
L0 ... Länge der unbelasteten Feder [mm, in]
LS ... Blocklänge [mm, in]
n ... Anzahl der Arbeitswindungen [-]
p ... Abstand zwischen den Windungen [mm, in]
s ... Verformung (Einfederung) der Feder [mm, in]
e,y ... Formzahl [-] (siehe zum Beispiel DIN 2090)
t ... Torsionsspannung des Federmaterials [MPa,
psi]
Korrektionsfaktor einer Torsionsspannung
Durch Windungsabrundung kommt es bei gewickelten Federn zu zusätzlichen
Biegespannungen. Deshalb wird die Spannung in der Berechnung durch einen
Korrektionsfaktor korrigiert.
Bei Federn mit Draht eines Kreisquerschnitts ist der Korrektionsfaktor für das
gegebene Wickelverhältnis aus einigen diversen empirisch festgelegten Formeln
bestimmt (Wahl, Bergsträsserr, Göhner, ...). In dieser Berechnung ist folgende
Beziehung verwendet:
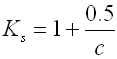
Bei Federn mit Draht eines rechteckigen Querschnitts ist der Korrektionsfaktor
für das gegebene Wickelverhältnis und das Verhältnis b/h aus einschlägigen
Nomogrammen bestimmt. In dieser Berechnung ist der Korrektionsfaktor schon in
der Formzahl y einbezogen.
| Wickelverhältnis cmin | min. 3 |
| Wickelverhältnis cmax | max. 20 |
| Durchmesser Dmax | max. 350 mm |
| Verhältnis Dmax/Dmin | min. 2 |
| Anzahl der Windungen n | min. 2 |
| Verhältnis b/h | 1:5 - 5:1 |
| Schlankheitsverhältnis L0/D | 1 - 5 |
| Abstand p | (0.4 - 0.7) D; min. 1.5 d |
Bei den Druckfedern benutzt man einige verschiedene Weisen der Auslegung der Federenden, die sich durch die Anzahl der Schluss- und bearbeiteten Windungen der Feder und durch die Ausführung der Stützfläche der Feder unterscheiden.
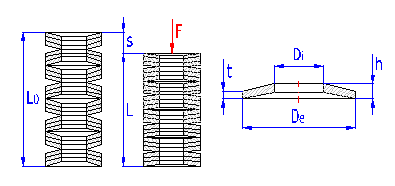
Kreisringförmige Ringe in Form eines hohlen abgestumpften Kegels, zur Aufnahme der äußeren gegenseitig in deren Achse einwirkenden Kräfte geeignet. Der Federquerschnitt ist in der Regel rechteckig. Die Federn mit größeren Maßen (t > 6 mm) werden manchmal mit bearbeiteten Auflageflächen ausgeführt.
Die Tellerfedern sind für große Belastungen bei kleinen Verformungen bestimmt. Sie werden entweder einzeln oder in Sätzen verwendet. Bei einer Verwendung der Federn im Satz ist es nötig eine Reibungseinwirkung in Betracht zu ziehen. Die Reibung im Satz beträgt etwa 3 bis 5 % der Belastung für jede Schicht. Um diese Kraft muss sich dann die Arbeitsbelastung erhöhen.
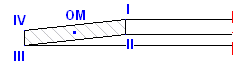
Die in einer Tellerfeder entstehende Spannung ist relativ kompliziert. Die maximale Druckspannung entsteht am inneren oberen Rand. An der äußeren unteren Kante entsteht eine Zugspannung. Die maximale Druckspannung dient dabei zur Festigkeitskontrolle der statisch belasteten Federn. Bei den zyklisch (ermüdungs-) belasteten Federn wird der Verlauf der Zugspannungen kontrolliert.
Arbeitskennlinie
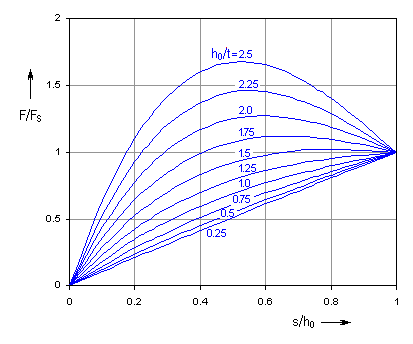
Die Form der Kennlinie einer Tellerfeder ist stark durch die relative Höhe h0/t
beeinflusst. Für kleine Werte der relativen Höhe verfügt die Feder über eine
beinahe lineare Arbeitskennlinie, mit einem steigenden Verhältnis wird die
Kennlinie deutlich degressiv.
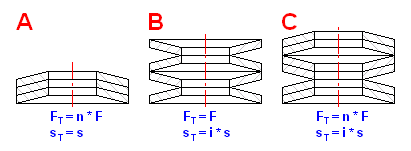
Ausführung des Satzes
Bei Tellerfedern werden drei Arten der Anordnung der Federn im Satz
unterschieden:
| Einzelfeder |
|
|
|
|
|
|
 |
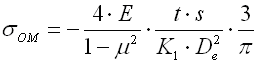 |
|
|
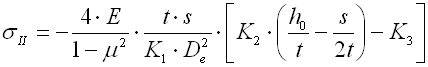 |
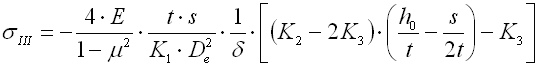 |
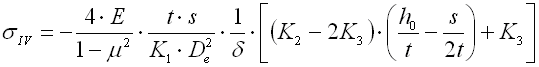 |
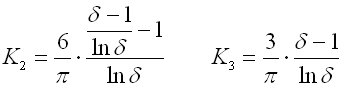 |
| Federpaket, Federsäule |
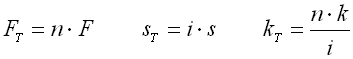 |
wo:
De .. Außendurchmesser [mm, in]
Di .. Innendurchmesser [mm, in]
E ... Elastizitätsmodul [MPa, psi]
F ... Federkraft [N, lb]
FS ... Kraft der vollgedrückten Feder [mm, in]
FT ... Gesamtkraft des Satzes [mm, in]
h ... Tellerhöhe [mm, in]
h0 ... Innere Tellerhöhe (h0=h-t) [mm, in]
i ... Anzahl der seriellen Pakete (Teller) in der Federsäule [-]
k ... Federrate [N/mm, lb/in]
kT ... Totalfederrate des Satzes [N/mm, lb/in]
K1, K2, K3 .. Formzahl [-]
L0 ... Länge der unbelasteten Feder [mm, in]
LS ... Länge der vollgedrückten Feder [mm, in]
n ... Anzahl der parallelen Teller im Federpaket [-]
s ... Verformung (Einfederung) der Feder [mm, in]
sT ... Gesamtverformung des Satzes [mm, in]
t ... Tellerdicke [mm, in]
d ... Durchmesserverhältnis (d=De/Di) [-]
m ... Poisson-Zahl [-]
sOM,
sI,
sII,
sIII,
sIV ... Spannung des Materials in
einer gegebenen Federstelle [MPa,
psi]
| Durchmesserverhältnis De/Di | 1.75 - 2.5 |
| relative Höhe h0/t | 0.4 - 1.4 |
| Verhältnis De/t | 16 - 40 |
| Anzahl der parallelen Teller n | max. 3 |
| Anzahl der seriellen Teller i | max. 20 |
| Gesamtanzahl der Teller n*i | max. 30 |
| Schlankheitsverhältnis L0/De | max. 3 |
Einen deutlichen Einfluss auf die Funktion einer Tellerfeder hat die Reibung. Bei einer Federbelastung entsteht die Reibung an der Auflagefläche (an den Rändern) der Feder. Bei einem Federpaket der parallel angeordneten Teller kommt es weiterhin zu oberflächlichen Reibung zwischen den einzelnen Scheiben. Der Reibungseinfluss äußert sich durch eine Kraftvergrößerung bei der Belastung und Kraftverminderung bei Entlastung der Feder.
| Einzelteller | ± 2...3 % |
| 2 parallel angeordnete Teller | ± 4...6 % |
| 3 parallel angeordnete Teller | ± 6...9 % |
| 4 parallel angeordnete Teller | ± 8...12 % |
| 5 parallel angeordnete Teller | ± 10...15 % |
Die Größe der Reibung ist von vielen Faktoren abhängig (Federausführung, Werkstoff, oberflächliche Behandlung, Federanzahl im Satz, Schmierstoffart, usw..). Ihr Einfluss auf die Federbelastung lässt sich theoretisch nicht genau feststellen. Für eine annähernde Feststellung der korrigierten Federkraft wir folgende Beziehung verwendet:
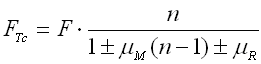
wo:
mM .. Koeffizient der
oberflächlichen Reibung [-]
mR .. Koeffizient der Reibung an
Rändern [-]
- .... bei Belastung
+ ... bei Entlastung
| Federauslegung | mM | mR |
| normal | 0.003 - 0.030 | 0.02 - 0.05 |
| mit bearbeiteten Auflageflächen | 0.002 - 0.015 | 0.01 - 0.03 |
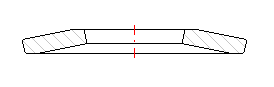
Die Federn mit größeren Maßen (t > 6 mm) werden manchmal mit bearbeiteten Auflageflächen ausgeführt. Die Beziehungen für die Berechnung dieser Federn sind leicht unterschiedlich und sind z. B. in DIN 2092 zu finden.
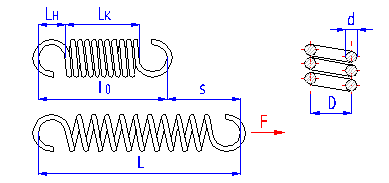
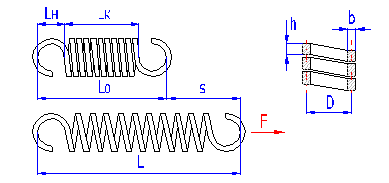
Zylindrische Federn aus schraubenförmig gewickelten Drähten hergestellt, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren voneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt. Gewöhnlich sind die Zugfedern aus Drähten und Stäben des Kreisquerschnitts hergestellt. Federn mit Draht eines rechteckigen Querschnitts werden sehr selten verwendet.
Mit Hinsicht auf einen erheblichen Einfluss der Form und Auslegung der Aufhängeösen auf Absenkung der Federstandzeit und auf Unmöglichkeit der vollkommenen Kugelstrahlung der Feder wird nicht empfohlen, zyklischer (Ermüdungs-) Belastung die Zugfedern möglichst zu verwenden. Wenn es nötig ist, eine Zugfeder bei der zyklischen Beanspruchung zu verwenden, ist es geeignet, bei der Feder keine Aufhängeösen zu verwenden, sondern eine andere Ausführung der Federhalterung auszuwählen.
Federauslegung
Die Zugfedern werden in zwei grundlegenden Ausführungen verwendet:
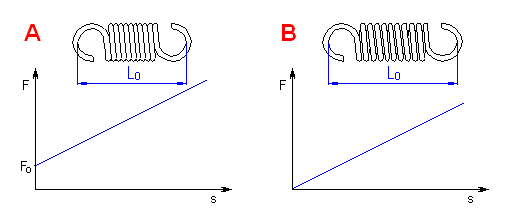
|
Draht mit rundem Querschnitt |
Draht mit rechteckigem Querschnitt |
 |
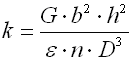 |
|
|
|
| A. Zugfeder mit Vorspannung | |
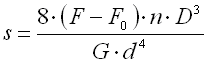 |
|
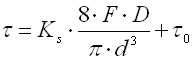 |
|
| B. Zugfeder ohne Vorspannung | |
|
|
|
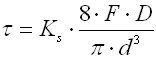 |
 |
wo:
c ... Wickelverhältnis (c=D/d; c=D/b) [-]
b ... Drahtbreite [mm, in]
d ... Drahtdurchmesser [mm, in]
D ... Mittlerer Federdurchmesser [mm, in]
F ... Federbelastung [N, lb]
F0 ... Innere Vorspannkraft [N, lb]
G ... Schubmodul [MPa, psi]
h ... Drahthöhe [mm, in]
k ... Federrate [N/mm, lb/in]
Ks ... Korrektionsfaktor einer Torsionsspannung [-]
L0 ... Länge der unbelasteten Feder [mm, in]
LH ... Höhe der Aufhängeöse [mm, in]
LK ... Länge des aktiven Federteiles [mm, in]
n ... Anzahl der Arbeitswindungen [-]
p ... Abstand zwischen den Windungen [mm, in]
s ... Verformung (Ausfederung) der Feder [mm, in]
e,y ... Formzahl [-] (siehe zum Beispiel DIN 2090)
t ... Torsionsspannung des Federmaterials [MPa,
psi]
t0 ... Innere Vorspannung [MPa,
psi]
Korrektionsfaktor einer Torsionsspannung
Durch Windungsabrundung kommt es bei gewickelten Federn zu zusätzlichen
Biegespannungen. Deshalb wird die Spannung in der Berechnung durch einen
Korrektionsfaktor korrigiert.
Bei Federn mit Draht eines Kreisquerschnitts ist der Korrektionsfaktor für das
gegebene Wickelverhältnis aus einigen diversen empirisch festgelegten Formeln
bestimmt (Wahl, Bergsträsserr, Göhner, ...). In dieser Berechnung ist folgende
Beziehung verwendet:
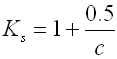
Bei Federn mit Draht eines rechteckigen Querschnitts ist der Korrektionsfaktor
für das gegebene Wickelverhältnis und das Verhältnis b/h aus einschlägigen
Nomogrammen bestimmt. In dieser Berechnung ist der Korrektionsfaktor schon in
der Formzahl y einbezogen.
Innere Federvorspannung
Eine Vorspannung entsteht bei der Aufwicklung der Feder und ihre Größe ist
von dem verwendeten Werkstoff der Feder, dem Wickelverhältnis und der
Wickelweise abhängig. Die üblichen Vorspannungswerte liegen im Bereich:
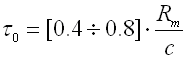
Größere Werte sind technisch schwer realisierbar, die niedrigeren lassen sich
nur sehr schwierig mit einer hinreichenden Genauigkeit messen. Die Norm DIN 2089
gibt für die Feststellung der Vorspannung, der auf einer Wickelbank gewickelten
Federn, die folgende Beziehung an:
![]()
Die innere Vorspannkraft ist gegeben als:
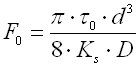
| Wickelverhältnis c | 4 - 16 |
| Außendurchmesser De | max. 350 mm |
| Anzahl der Windungen n | min. 3 |
| Verhältnis b/h | 1:5 - 5:1 |
| Freie Federlänge L0 | max. 1500 mm |
| Schlankheitsverhältnis L0/D | 1 - 15 |
| Abstand p | (0.2 - 0.4) D - Feder ohne Vorspannung |
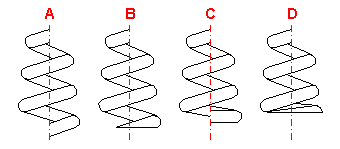
Die Zugfedern werden in vielen verschiedenen Ausführungen benutzt. Die am häufigsten verwendeten Federenden sind in der Abbildung dargestellt. Die Wahl der Ausführung der Federenden ist von der verlangten Halterung, den Maßen und dem Typ und Größe der Belastung abhängig.
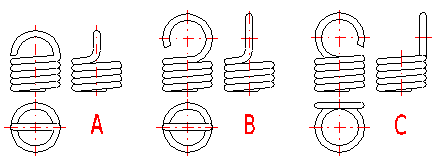
A ... Halbe deutsche Öse
B ... Ganze deutsche Öse
C ... Ganze deutsche Öse seitlich hochgestellt
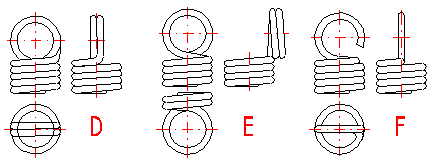
D ... Doppelte deutsche Öse
E ... Doppelte deutsche Öse seitlich hochgestellt
F ... Englische Öse
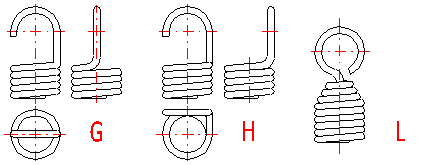
G ... Hakenöse
H ... Hakenöse deutsche Öse seitlich hochgestellt
L ... Haken eingerollt
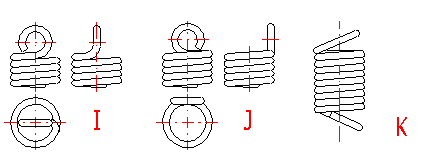
I ... Niedere Öse
J ... Niedere Öse seitlich hochgestellt
K ... Ganze deutsche Öse schräg hochgestellt
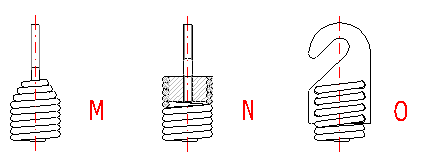
M ... Gewindebolzen eingerollt
N ... Gewindestopfen eingeschraubt
O ... Schraublasche eingeschraubt
Am häufigsten werden Aufhängeösen von einigen verschiedenen Typen als Halterung der Zugfedern verwendet (A .. J), die sich einerseits durch Höhe andererseits durch ihre Eigenschaften unterscheiden. Die Aufhängeösen sind zwar eine der vorteilhaftesten Lösungen in Hinsicht auf die Technologie, in Hinsicht auf Federtragfähigkeit bringen sie jedoch bestimmte Probleme. Bei Belastung der Feder entstehen Spannungskonzentrationen in der Aufhängeöse, die höher sein können als die berechnete Spannung in den Federwindungen. In Hinsicht auf die in der Aufhängeöse entstehenden Biegespannungen sind kleine Ösen (Typ I, J) oder Doppelösen (Typ D, E) am vorteilhaftesten. In Hinsicht auf die Konzentrationen der Verdrehungsspannung an der Übergangsstelle der Windung in die Öse sind seitlich hochgestellte Ösen am vorteilhaftesten (Typ C,E,I). Für einzelne Ausführungen der Aufhängeöse sind folgende empfohlene Werte der Höhe der Öse vorgeschrieben:
| Ausführung | A | B, C | D, E | F | G, H | I, J | K |
| Höhe der Öse | {0.55..0.8} Di | {0.8..1.1} Di | ~ Di | {1.05..1.2} Di | > 1.2 Di | < 0.6 Di | {0.35..0.9} Di |
Die warmgeformten Federn, die Federn mit Draht des rechteckigen Querschnitts und die zyklisch belasteten Federn werden gewöhnlich ohne Aufhängeösen verwendet (Ausführung M. O). Bei Ausführung ohne Aufhängeösen sind Schlusswindungen zur Befestigung der Feder verwendet, deren Steigungswinkel bei einer funktionellen Verformung nicht geändert wird.
Bei Belastung der Feder mit Aufhängeösen entstehen in der Aufhängeöse Spannungskonzentrationen, die wesentlich höher sein können als die berechnete Spannung in den Federwindungen. Deshalb ist es empfehlenswert, diese Federn auch in Hinsicht auf die Beanspruchung der Aufhängeöse zu kontrollieren.
Die Größe der möglichen Spannungskonzentrationen hängt von Typ, Ausführung und Maßen der Öse ab und es ist sehr schwierig, diese theoretisch zu berechnen. Trotzdem werden wenigstens theoretische Berechnungen verwendet, deren Aufgabe ist, Orientierungsinformationen über eventuelle Überschreitung der Festigkeitsgrenzen des gewählten Federwerkstoffes anzubieten. In Hinsicht auf die Ausführung der Aufhängeöse werden zwei grundlegende Festigkeitskontrollen durchgeführt:

Kontrolle der Aufhängeöse hinsichtlich der Biegung
Die Größe der im Bogen der Öse entstehenden Biegespannungen ist von dem Halbmesser der Rundung der Aufhängeöse rb abhängig. Mit dem zunehmenden Halbmesser nimmt auch die Größe der Spannung zu und umgekehrt. Zur Feststellung der Biegespannung kann folgende Beziehung verwendet werden:
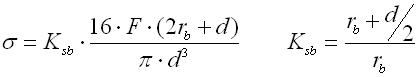
Spannungskontrolle im Übergangsbogen
Die höchsten Spannungskonzentrationen entstehen bei einer Zugfeder in der Übergangsstelle der Windung in die Aufhängeöse. Die Größe dieser Spannungen ist von dem Halbmesser des Übergangsbogens rs abhängig. Allgemein kann gesagt werden, dass der Spannungswert im Übergangsbogen mit dem zunehmenden Bogenhalbmesser abnimmt und umgekehrt. Zur Feststellung der Spannungsspitze kann diese Beziehung verwendet werden:
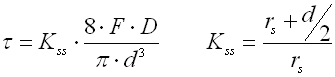
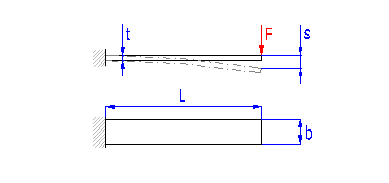
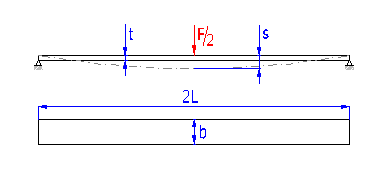
Federn auf dem Prinzip der auf Biegung belasteten langen schlanken Träger des rechteckigen Querschnitts. Sie werden entweder als einarmige (auf einem Ende eingespannte), oder als doppelarmige (beiderseits aufliegende) verwendet. Die Blattfedern können einzeln oder in Sätzen (Geschichtete Blattfedern) verwendet werden.
Einfache Blattfedern
Geschichtete Blattfedern
Ausführung der Feder
Die Blattfedern werden in vielen diversen Ausführungen und Formen verwendet.
Zwecks der Berechnung können wir sie in drei Gruppen unterteilen:
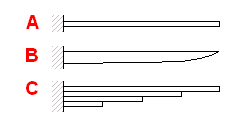
|
A. Einfache Blattfedern mit einem konstanten Profil |
||
|
|
|
|
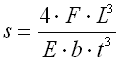 |
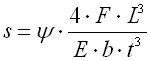 |
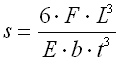 |
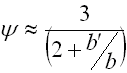 |
||
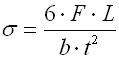 |
||
|
B. Einfache Blattfedern mit einem Parabelprofil |
|
|
|
|
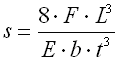 |
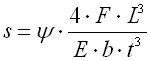 |
|
|
|
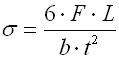 |
|
| C. Geschichtete Blattfedern | |
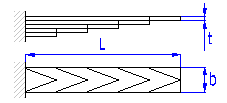 |
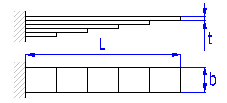 |
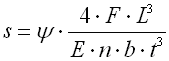 |
|
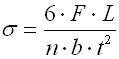 |
|
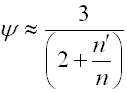 |
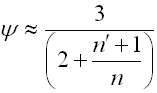 |
wo:
b ... Federblattbreite [mm, in]
b' ... Federblattbreite am Federende [mm, in]
E ... Elastizitätsmodul [MPa, psi]
F ... Federbelastung [N, lb]
k ... Federrate [N/mm, lb/in]
L ... Funktionslänge der Feder [mm, in]
L' ... Federblattlänge mit konstanter Dicke [mm, in]
n ... Gesamtzahl der Federblätter [-]
n' ... Anzahl der durchgehenden Extra-Federblätter [-]
s ... Verformung (Durchbiegung) der Feder [mm, in]
t ... Federblattdicke [mm, in]
t' ... Federblattdicke am Federende [mm, in]
y ... Formzahl [-]
s ... Biegespannung des Federmaterials [MPa,
psi]
Extra-Federblätter
Durchgehende Federblätter in voller Länge, rechteckiger Form mit
Konstantprofil. Diese Blätter werden zu einer Feder aus zwei Gründen
hinzugefügt:
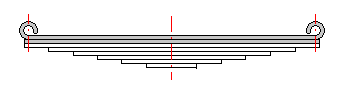
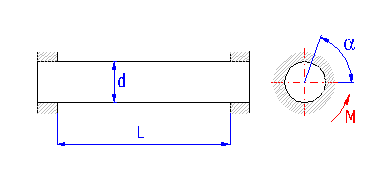
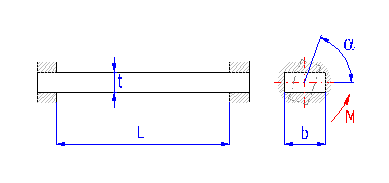
Federn nach dem Prinzip der durch Verdrehung belasteten langen schlanken Stäbe eines kreisförmigen oder rechteckigen Querschnitts. Bei den Stäben kreisförmigen Querschnitts wird am häufigsten eine Kerbverzahnung zur Befestigung der Enden verwendet. Manchmal wird eine der Seiten mit einem Prisma der leichteren Aufnahme wegen, beendet. Die Drehstabfedern müssen gegen eine Biegungsbeanspruchung gesichert sein.
|
Drehstabfedern mit rundem Querschnitt |
Drehstabfedern mit rechteckigem Querschnitt |
|
|
|
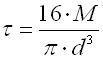 |
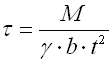 |
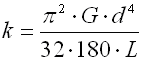 |
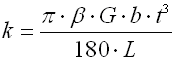 |
|
|
|
wo:
b ... Stabbreite [mm, in]
d ... Stabdurchmesser [mm, in]
M ... Federbelastung [Nmm, lb in]
G ... Schubmodul [MPa, psi]
k ... Federmomentrate [Nmm/°, lb in/°]
L ... Funktionslänge der Feder [mm, in]
t ... Stabdicke [mm, in]
a ... Drehwinkel [°]
b,g ... Formzahl [-]
t ... Torsionsspannung des Federmaterials [MPa,
psi]
Formkoeffizienten
Diese Koeffizienten berücksichtigen die Spannungsverteilung im
Stabsquerschnitt in der Abhängigkeit vom Seitenverhältnis b/t. Ihr
Wert wird in der Tabelle abgelesen:
| b/t | 1 | 1.2 | 1.5 | 2 | 3 | 4 | 5 | 6 | 8 | 10 | ∞ |
| b | 0.1406 | 0.166 | 0.196 | 0.229 | 0.263 | 0.281 | 0.291 | 0.299 | 0.307 | 0.312 | 0.333 |
| g | 0.208 | 0.219 | 0.231 | 0.246 | 0.267 | 0.282 | 0.291 | 0.299 | 0.307 | 0.312 | 0.333 |
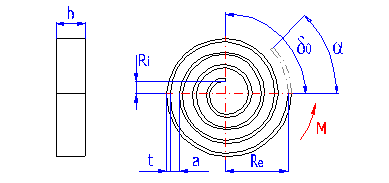
Eine Feder aus einem flachen Band rechteckigen Querschnitts, das in der Form einer Archimedischen Spirale aufgerollt ist, mit einem konstanten Spiel zwischen den aktiven Windungen, belastet mit einem Drehmoment in der Aufrollrichtung.
|
|
|
|
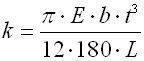 |
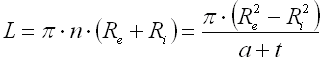 |
|
|
wo:
a ... Windungsspiel [mm,in]
b ... Federbandbreite [mm, in]
M ... Federbelastung [Nmm, lb in]
E ... Elastizitätsmodul [MPa, psi]
k ... Federmomentrate [Nmm/°, lb in/°]
Kb ... Korrektionsfaktor der Biegespannung [-]
L ... Arbeitslänge der Feder [mm, in]
n ... Anzahl der Arbeitswindungen [-]
t ... Federbanddicke [mm, in]
Re ... Außenradius [mm, in]
Ri ... Innenradius [mm, in]
a ... Drehwinkel [°]
d0 ... Schenkelwinkel im freien
Zustand [°]
s ... Biegespannung des Federmaterials [MPa,
psi]
Korrektionsfaktor der Biegespannung
Der Korrektionsfaktor drückt eine zusätzliche Beanspruchung der Feder durch
ihre Krümmung aus. Sein Wert wird im Diagramm abgelesen:
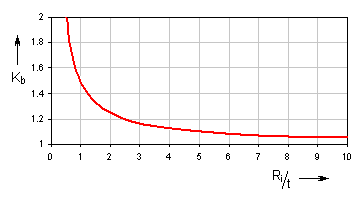
| Verhältnis Ri/t | min. 3 |
| Verhältnis b/t | 1 - 15 |
| Anzahl der Arbeitswindungen n0 | min. 2 |
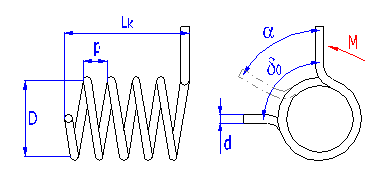
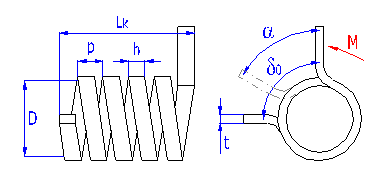
Zylindrische Federn, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren in der zur Achse senkrechten Ebenen mit einem Drehmoment im Aufroll- oder Abrollsinn einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt.
Federauslegung
Die Verdrehungsfedern werden in zwei grundlegenden Ausführungen hergestellt und
zwar entweder mit aufeinander liegenden Windungen oder mit einem Abstand unter
den Windungen. Für statisch belastete Federn werden Federn mit anliegenden
Windungen bevorzugt angewendet. Bei diesen Federn kommt es jedoch bei der
Arbeitsfunktion zur gegenseitigen Reibung unter den Windungen, was eine
Herabsetzung der Standzeit der Feder verursachen kann. Außerdem verhindern die
anliegenden Windungen in der Regel die vollkommene Kugelstrahlung der Feder.
Deshalb sind die Federn mit einem Spiel unter den Windungen für die Benutzung
bei zyklischer (Ermüdungs-) Belastung geeignet. Die Teilung zwischen den
Federwindungen ist dann gewöhnlich im Bereich 0.3*D < p < 0.5*D.
|
Draht mit rundem Querschnitt |
Draht mit rechteckigem Querschnitt |
|
|
|
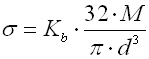 |
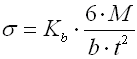 |
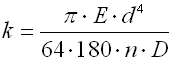 |
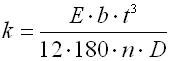 |
|
|
|
wo:
c ... Wickelverhältnis (c=D/d; c=D/t) [-]
b ... Drahtbreite [mm, in]
d ... Drahtdurchmesser [mm, in]
D ... Mittlerer Federdurchmesser [mm, in]
M ... Federbelastung [Nmm, lb in]
E ... Elastizitätsmodul [MPa, psi]
k ... Federmomentrate [Nmm/°, lb in/°]
Kb ... Korrektionsfaktor der Biegespannung [-]
LK ... Länge des Federkörpers [mm, in]
n ... Anzahl der Arbeitswindungen [-]
p ... Abstand zwischen den Windungen [mm, in]
t ... Drahtdicke [mm, in]
a ... Drehwinkel [°]
d0 ... Schenkelwinkel im freien
Zustand [°]
s ... Biegespannung des Federmaterials [MPa,
psi]
Korrektionsfaktor der Biegespannung
Der Korrektionsfaktor drückt eine zusätzliche Beanspruchung der Feder durch eine
Abrundung der Windungen aus.
Funktionelle Federmaße
Bei einer funktionellen Verformung (Schwenken des Armes) einer
Verdrehungsfeder kommt es zu einer Änderung ihrer Maße.
Bei einer im Aufrollsinn beanspruchten Feder verkleinert sich ihr Durchmesser:
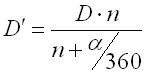
Bei einer Feder mit anliegenden Windungen kommt es zugleich zum Anwachsen ihrer Länge:

| Wickelverhältnis c | 4 - 16 |
| Außendurchmesser De | max. 350 mm |
| Anzahl der Windungen n | min. 2 |
| Verhältnis b/t | 1 - 10 |
| Länge des Federkörpers LK | max. 800 mm |
| Schlankheitsverhältnis LK/D | 1 - 10 |
Mit Hinsicht auf die Möglichkeit der Entstehung von eventuellen Spannungskonzentrationen, sollten die Arme einer Verdrehungsfeder die einfachste Form besitzen. Die Grundtypen der bei Verdrehungsfedern verwendeten Arme sind in der Abbildung aufgeführt. Die Wahl der Durchführung der Federarme ist von der verlangten Weise der Federlagerung, den Federmaßen und der verlangten Entfernung des Angriffspunktes der Belastung von der Federachse abhängig, wobei der Stütz- und Arbeitsarm der Feder nicht typgleich sein müssen.
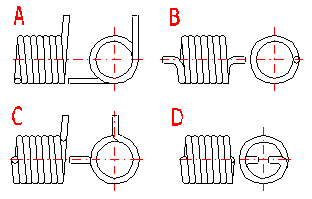
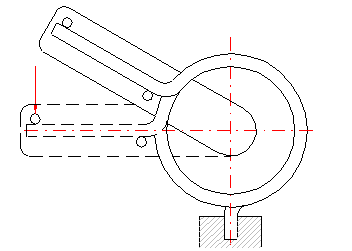
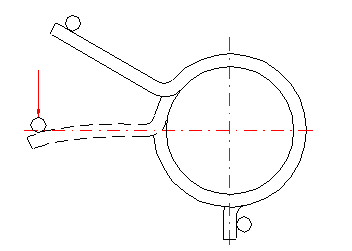
Bei einer festen Einspannung der beiden Arme der Verdrehungsfeder ist der Arbeitswinkel nur durch eine Verdrehung der Federwindungen bestimmt. Bei den frei nur in einem Punkt abgestützten (belasteten) Arme tritt eine Armverbiegung bei der Federbelastung auf. Das hat eine Vergrößerung des tatsächlichen winkeligen Arbeitsausschlages zur Folge. Der Wert der Biegung des Armes nimmt mit der zunehmenden Entfernung des Angriffspunktes der Kraft von den Federwindungen (der Armeslänge) zu. Durch die feste Einspannung der Arme wird die Genauigkeit der Berechnung erhöht und die Federfunktion verbessert.
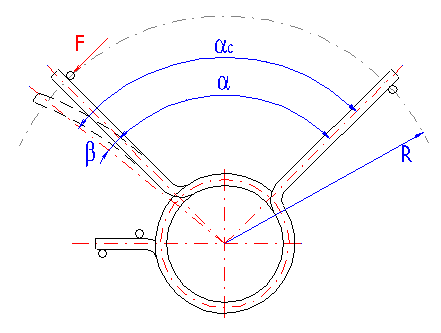
Der tatsächliche (korrigierte) Winkelausschlag bei einer Feder mit einem frei
aufgelegten Arme ist dann für:
- Radialarm
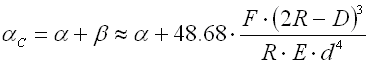
- Tangentialarm
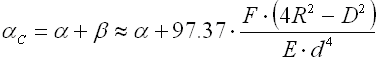
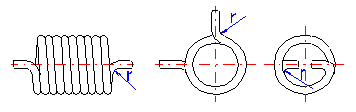
Bei den Federn mit gebogenen Arme kommt es in der Biegestelle des Armes zu Spannungskonzentrationen, die wesentlich höher sein können als die berechnete Spannung in den Federwindungen. Die Größe dieser Konzentrationen hängt vom Wert des Biegehalbmessers des Armes ab. Je kleiner der Biegehalbmesser ist, desto größer sind die Werte der Spitzenspannungen in den Federarme. Zu einer ungefähren Feststellung der Spannungsspitze kann folgende Beziehung verwendet sein:
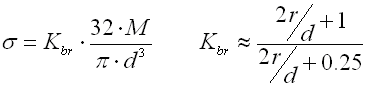
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist im Absatz "Entwurf der Feder" für jeden der Eintrittsparameter in der realen Zeit dessen, den anderen Federparametern entsprechende genaue Wert, ausgerechnet. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt.
Eine typische Berechnung / einer Federentwurf besteht in folgenden Schritten:
Dieser Absatz dient der Auswahl eines geeigneten Federwerkstoffes. Weiter sind hier die grundlegenden Betriebs- und Herstellungsparameter der Feder definiert.
Aus der Auflistung die verlangte nationale Norm zur Auswahl des Federwerkstoffs auswählen.
In Hinsicht auf die Federausführung, den in der Auflistung entsprechenden Materialtyp (Vorprodukt) auswählen, aus dem die Feder herzustellen ist.
In der Auflistung das geforderte Einheitssystem für die Berechnung wählen. Bei der Umschaltung der Einheiten werden sofort sämtliche Werte umgerechnet.
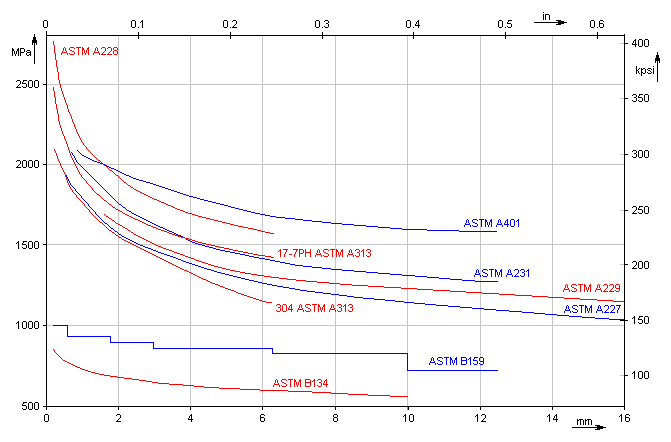
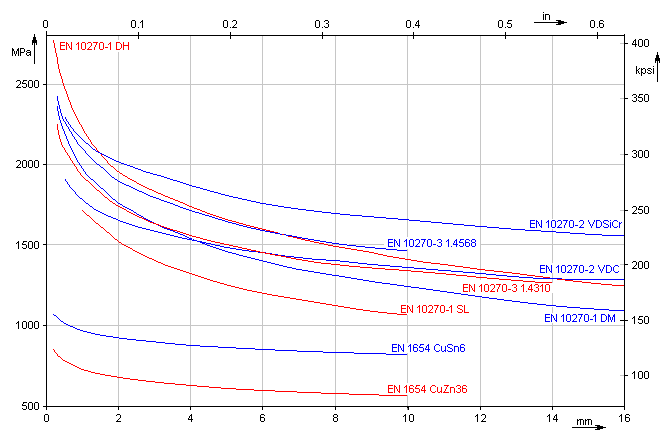
In der Auflistung den gewünschten Diagrammtyp auswählen, den Sie sich in der Federberechnung darstellen wollen.
Dieser Absatz dient der Auswahl des Federwerkstoffes.
Den Werkstoff der Feder aus der Liste [1.6] auswählen. Die ersten fünf Verzeichniszeilen sind für die vom Benutzer definierten Werkstoffe vorbehalten. Informationen über Einstellung der eigenen Werkstoffe sind dem Dokument "Benutzerspezifische Anpassungen der Berechnung" zu entnehmen. Die weiteren Verzeichniszeilen enthalten eine Auswahl der Werkstoffe für die aktuell eingestellte Norm [1.1] und Materialart [1.2].
In den Zeilen [1.7 - 1.10] sind die Informationen über eine empfohlene Verwendung des ausgewählten Werkstoffes angeführt. Der Werkstoff der Feder sollte mit Rücksicht auf den Belastungsmodus der Feder und die Betriebsbedingungen entworfen werden. Wenn Sie einen weniger geeigneten Werkstoff verwenden müssen, sollte diese Tatsache durch eine Erhöhung des Sicherheitsmaßes bei dem Federentwurf berücksichtigt werden (siehe [1.21]). Die Eigenschaften des in den Zeilen [1.7, 1.9] beschriebenen ausgewählten Werkstoffes werden in fünf Stufen bewertet (exzellent, vorzüglich, gut, schlecht, unzureichend), die relative Festigkeit des Werkstoffs in der Zeile [1.8] dann in drei Stufen (hohe, mittlere, kleine).
Bei einer Bezugstemperatur von 20°C (68°F) festgesetzter Wert.
Die Zugfestigkeit für das ausgewählte Material eingeben. Nach dem Ankreuzen des Kästchens in der Zeile [1.6] ist hier der angeführte Minimalwert der Zugfestigkeit für das ausgewählte Material automatisch eingestellt.
Dieser Absatz ist zur Einstellung der Betriebs- und Herstellungsparameter der Feder und der ihnen entsprechenden Sicherheitskoeffizienten bestimmt.
Die entsprechenden Betriebsbedingungen der Feder sind in Auswahllisten einzustellen. Rechts von jeder Auflistung ist das Eintrittsfeld für die Eingabe des entsprechenden Sicherheitskoeffizienten angebracht. Dieser Koeffizient drückt den Einfluss des gegebenen Betriebsparameters auf eventuelle Minderung der Federtragfähigkeit aus.
Die Temperatur des Arbeitsumfeldes beeinflusst die Entspannung der Feder, die sich durch eine auf Zeit abhängige Abnahme der Federkraft bei deren Verformung auf eine konstante Länge zeigt. Diese Tatsache ist bei dem Entwurf der Feder und bei einer 80°C (180°F) überschreitenden Temperatur zu berücksichtigen, und auf entsprechende Weise das Sicherheitsmaß bei der Festigkeitskontrolle der Feder zu erhöhen. Die Höhe der Betriebstemperatur ist auch bei der Auswahl des Federwerkstoffes zu berücksichtigen.
Vom Gesichtspunkt der Festigkeitskontrolle und der Standzeit werden bei den metallischen Federn zwei grundlegende Arten ihrer Belastung unterschieden:
Einen solchen Belastungsmodus auswählen, der Ihrer Eingabe am besten entspricht.
Durch Korrosionseinfluss nimmt wesentlich die Standzeit der Federn ab. Besonders bei zyklisch (ermüdungs-) belasteten Federn hat die Korrosion einen sehr bedeutenden Einfluss. Diese Tatsache ist bei dem Entwurf der Feder für ein korrosionsfördernd aggressives Umfeld zu berücksichtigen, und auf entsprechende Weise das Sicherheitsmaß bei der Festigkeitskontrolle der Feder zu erhöhen. Die Korrosionsmöglichkeit ist auch bei der Auswahl des Federwerkstoffes zu berücksichtigen.
Bei kugelgestrahlten Federn erhöht sich die Dauerfestigkeit des Federwerkstoffes um ungefähr 15 bis 25 %. Das erlaubt bei den zyklisch beanspruchten Federn den Werkstoffverbrauch für eine Feder zu vermindern, deren Maße und den Aufnahmeraum zu verringern, den Arbeitshub oder die Absicherung der Feder gegen Ermüdungsbrüche zu erhöhen. Deshalb wird empfohlen, die technische Anforderung auf kugelgestrahlte, bei allen schwingend beanspruchten, Federn durchzusetzen.
Die Federn mit einem galvanischen Überzug weisen eine erheblich größere Korrosionsbeständigkeit aus. Andererseits vermindert die Galvanisierung die Federtragfähigkeit etwa um 10 %.
Dieses gibt das minimale zulässige Verhältnis zwischen der zulässigen Grenzspannung des gewählten Federwerkstoffes und der tatsächlichen maximalen Arbeitsspannung der Feder an.
Die geforderte Sicherheitszahl wird in der Berechnung zur Festigkeitskontrolle der statisch belasteten Feder verwendet. Der hier eingegebene Wert eliminiert im Wesentlichen einen eventuellen negativen Einfluss der Betriebsbedingungen auf die Verminderung der Federtragfähigkeit. Außer den oben angeführten Tatsachen sollten sich im Wert der verlangten Sicherheitszahl auch irgendwelche weitere Einflüsse widerspiegeln (Genauigkeit und Zuverlässigkeit der Eingabeinformationen, Wichtigkeit der Anlage, Produktionsqualität, ...). Übliche Federn werden gewöhnlich mit einer Sicherheitszahl im Berech <1...2> entworfen.

Federn in Zylinderform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtdurchmesser bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [2.16] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [2.14, 2.15] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
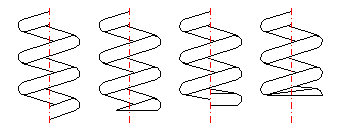
Die entsprechende Länge der unbelasteten Feder einstellen.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Einfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |

Federn in Zylinderform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem rechteckigen Drahtquerschnitt werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einer Drahtdicke von mehr als 10 mm eingesetzt.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtquerschnitt bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [3.17] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [3.15, 3.16] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
Die entsprechende Länge der unbelasteten Feder einstellen.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Einfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |

Federn in Kegelform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt.
Bei der steigenden Einfederung einer kegelförmigen Feder stoßen ihre Arbeitswindungen auf die Nachbarwindungen nacheinander auf (zuerst die Windungen mit größtem Durchmesser). Diese Windungen nehmen an der weiteren Einfederung nicht mehr teil, was eine allmähliche Steigerung ihrer Federrate zur Folge hat. Die Arbeitskennlinie einer kegelförmigen Feder kann so in zwei Bereiche unterteilt werden:

Die Größe der Grenzkraft FC ist von der gewählten freien Federlänge L0 abhängig. Mit einer steigenden Federlänge vergrößert sich auch die Grenzkraft FC und der Arbeitsbereich mit konstanter Federrate vergrößert sich.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein approximativer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die Kompliziertheit des Entwurfs der kegelförmigen Federn ermöglicht nicht alle Federparameter in der realen Zeit zu Ende zu berechnen. Deshalb ist es nötig nach jeder Änderung der Eintrittsangaben die Berechnung manuell zu starten, durch Anklicken der Schaltfläche "Berechnung".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung. Durch Bewegung irgendeiner der Laufleisten wurde der Federentwurf für die gegebenen Verhältnisse Dmax/Dmin, Dmin/d gestartet. Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtdurchmesser bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [4.19] sollte nicht den verlangten Wert [1.27] unterschreiten.
In der Zeile [4.18] ist der theoretische Wert der maximalen Arbeitsbelastung berechnet, bei dem die verlangte Sicherheitszahl der entworfenen Feder noch eingehalten wird.
Dieser Wert gibt die maximale Belastung (Grenzkraft) an, bei der die Feder noch mit der konstanten Federrate arbeiten wird. Mit einer wachsenden Belastung vergrößert sich die Federrate.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
Die entsprechende Länge der unbelasteten Feder einstellen.
Die freie Federlänge beeinflusst deutlich die Größe der Grenzkraft [4.21] und dadurch auch die Arbeitskennlinie der Feder. Mit einer steigenden Federlänge vergrößert sich auch die Grenzkraft und der Arbeitsbereich mit der konstanten Federrate vergrößert sich.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Einfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |
| k | Federrate |

Federn in Kegelform, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spielraum zwischen den Arbeitswindungen, geeignet zur Aufnahme der äußeren gegeneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem rechteckigen Drahtquerschnitt werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einer Drahtdicke von mehr als 10 mm eingesetzt.
Bei der steigenden Einfederung einer kegelförmigen Feder stoßen ihre Arbeitswindungen auf die Nachbarwindungen nacheinander auf (zuerst die Windungen mit größtem Durchmesser). Diese Windungen nehmen an der weiteren Einfederung nicht mehr teil, was eine allmähliche Steigerung ihrer Federrate zur Folge hat. Die Arbeitskennlinie einer kegelförmigen Feder kann so in zwei Bereiche unterteilt werden:

Die Größe der Grenzkraft FC ist von der gewählten freien Federlänge L0 abhängig. Mit einer steigenden Federlänge vergrößert sich auch die Grenzkraft FC und der Arbeitsbereich mit konstanter Federrate vergrößert sich.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein approximativer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die Kompliziertheit des Entwurfs der kegelförmigen Federn ermöglicht nicht alle Federparameter in der realen Zeit zu Ende zu berechnen. Deshalb ist es nötig nach jeder Änderung der Eintrittsangaben die Berechnung manuell zu starten, durch Anklicken der Schaltfläche "Berechnung".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung. Durch Bewegung irgendeiner der Laufleisten wurde der Federentwurf für die gegebenen Verhältnisse Dmax/Dmin, Dmin/b, b/h gestartet. Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtquerschnitt bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [5.20] sollte nicht den verlangten Wert [1.27] unterschreiten.
In der Zeile [5.19] ist der theoretische Wert der maximalen Arbeitsbelastung berechnet, bei dem die verlangte Sicherheitszahl der entworfenen Feder noch eingehalten wird.
Dieser Wert gibt die maximale Belastung (Grenzkraft) an, bei der die Feder noch mit der konstanten Federrate arbeiten wird. Mit einer wachsenden Belastung vergrößert sich die Federrate.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
Die entsprechende Länge der unbelasteten Feder einstellen.
Die freie Federlänge beeinflusst deutlich die Größe der Grenzkraft [5.22] und dadurch auch die Arbeitskennlinie der Feder. Mit einer steigenden Federlänge vergrößert sich auch die Grenzkraft und der Arbeitsbereich mit der konstanten Federrate vergrößert sich.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Einfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |
| k | Federrate |

Kreisringförmige Ringe in Form eines hohlen abgestumpften Kegels, zur Aufnahme der äußeren gegenseitig in deren Achse einwirkenden Kräfte geeignet. Der Federquerschnitt ist in der Regel rechteckig. Die Federn mit größeren Maßen (t > 6 mm) werden manchmal mit bearbeiteten Auflageflächen ausgeführt.
Die Tellerfedern sind für große Belastungen bei kleinen Verformungen bestimmt. Sie werden entweder einzeln oder in Sätzen verwendet. Bei einer Verwendung der Federn im Satz ist es nötig eine Reibungseinwirkung in Betracht zu ziehen. Die Reibung im Satz beträgt etwa 3 bis 5 % der Belastung für jede Schicht. Um diese Kraft muss sich dann die Arbeitsbelastung erhöhen.
Die Form der Kennlinie einer Tellerfeder ist stark durch die relative Höhe h0/t beeinflusst. Für kleine Werte der relativen Höhe verfügt die Feder über eine beinahe lineare Arbeitskennlinie, mit einem steigenden Verhältnis wird die Kennlinie deutlich degressiv.

Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier zur Erleichterung des Entwurfs, bei einigen Eintrittsparametern ihr Annäherungswert in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
In der Auswahlliste die zulässige relative Einfederung auswählen.
Bei statisch belasteten Federn sollte die Betriebseinfederung einen Wert von 75 bis 80% der maximalen (vollen) Einfederung [6.19] nicht überschreiten. Bei zyklisch belasteten Federn wird gewöhnlich ein Wert von 50% zugelassen.
Aufeinander gelegte Teller.
Teller bzw. Federpakete gegeneinander zusammengesetzt.
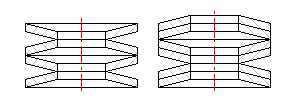
Die Kompliziertheit des Entwurfs der Tellerfedern ermöglicht nicht alle Federparameter in der realen Zeit zu Ende zu berechnen. Deshalb ist es nötig nach jeder Änderung der Eintrittsangaben die Berechnung manuell zu starten, durch Anklicken der Schaltfläche "Berechnung".
In der Auswahlliste finden Sie eine Datenbank der Tellerfedern in den üblich hergestellten Maßen. Die Federmaße sind in der Auflistung in Form "De x Di x t x h" ausgeschrieben.
Dieser Absatz dient dem automatischen Entwurf (Aufsuchen) der Tellerfeder mit passenden Maßen.
In den Auswahllisten eine zulässige Abweichung vom verlangten Arbeitshub der Feder [6.4] und die maximal zulässige Telleranzahl im Satz einstellen. Nach dem Anklicken der Schaltfläche "Aufsuchen" sucht das Programm die erste Feder in der Auflistung [6.14] aus, die bei der Einhaltung der minimalen Sicherheit die sämtlichen aufgeführten Anforderungen erfüllt. Wenn die ausgewählte Feder nicht Ihren Vorstellungen genügt, klicken Sie zwecks Auffindung einer Feder mit anderen Maßen die Schaltfläche "Weiter suchen" an.
Ein theoretisch festgelegter Wert der maximalen Arbeitsbelastung, wo bei der entworfenen Feder die maximale Druckspannung [6.31] die zulässige Grenze [6.30] nicht überschreitet und zugleich die zulässige Einfederung [6.5] bei der entworfenen Feder nicht überschritten wird.
Die in einer Tellerfeder entstehende Spannung ist relativ kompliziert. Die maximale Druckspannung entsteht am inneren oberen Rand. An der äußeren unteren Kante entsteht eine Zugspannung. Die maximale Druckspannung dient dabei zur Festigkeitskontrolle der statisch belasteten Federn. Bei den zyklisch (ermüdungs-) belasteten Federn wird der Verlauf der Zugspannungen kontrolliert.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle einer statisch belasteten Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [6.30] mit der maximalen Druckspannung der vollbelasteten Feder [6.31] durchgeführt. Die resultierende Sicherheitszahl [6.34] sollte nicht den empfohlenen Wert [6.33] unterschreiten.
Die zulässige Druckspannung des Federmaterials eingeben.
Die empfohlene Sicherheitszahl ist für das ausgewählte Material [1.6] auf Grund der im Absatz [1.21] definierten Betriebsbedingungen abgeschätzt.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung (Federkraft) |
| s | Verformung (Einfederung) der Feder |
| L | Federlänge |
| sP | Maximale Druckspannung |
| k | Federrate |

Zylindrische Federn aus schraubenförmig gewickelten Drähten hergestellt, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren voneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt.
Die Zugfedern werden in zwei grundlegenden Ausführungen verwendet:
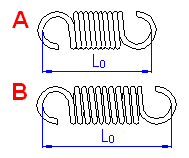
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtdurchmesser bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [7.18] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [7.16, 7.17] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
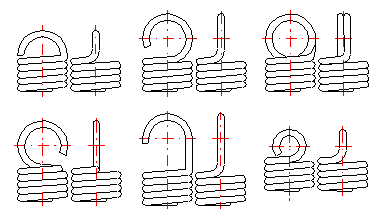
Bei Belastung der Feder mit Aufhängeösen entstehen in der Aufhängeöse Spannungskonzentrationen, die wesentlich höher sein können als die berechnete Spannung in den Federwindungen. Deshalb wird manchmal eine andere Art der Federaufnahme verwendet.
Die Höhe der Aufhängeöse ist von dem Ösentyp abhängig und für einzelne Ausführungen sind deren empfohlene Grenzen vorgeschrieben. Bei Federn mit keinen Aufhängeösen versteht sich unter diesem Begriff eine Entfernung zwischen dem Ende der Arbeitswindungen und der Stelle der Anbringung der Feder (siehe Abbildung).
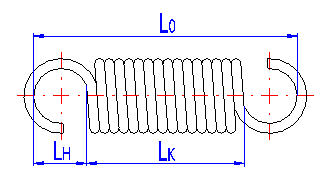
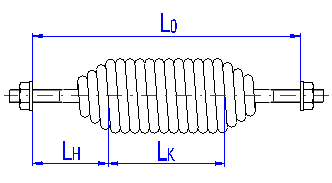
Eine Vorspannung entsteht bei der Aufwicklung der Feder und ihre Größe ist von dem verwendeten Werkstoff der Feder, dem Wickelverhältnis und der Wickelweise abhängig. Bei Federn mit einem Spiel zwischen den Windungen ist die Vorspannung gleich null.
Bei vorspannungsfreien Federn ist die entsprechende Länge der unbelasteten Feder einzustellen.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Ausfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |

Zylindrische Federn aus schraubenförmig gewickelten Drähten hergestellt, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren voneinander in deren Achse einwirkenden Kräfte. Die Federn mit einem rechteckigen Drahtquerschnitt werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einer Drahtdicke von mehr als 10 mm eingesetzt.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtquerschnitt bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [8.17] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [8.15, 8.16] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
Mit Rücksicht auf eine in der Aufhängeöse entstehende hohe Spannungskonzentration, wird üblich eine andere Art der Aufnahme bei den Federn aus Drähten mit rechteckigem Querschnitt gewählt.
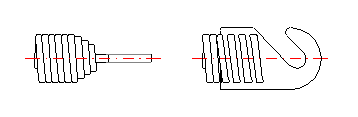
Die Höhe der Aufhängeöse ist von dem Ösentyp abhängig und für einzelne Ausführungen sind deren empfohlene Grenzen vorgeschrieben. Bei Federn mit keinen Aufhängeösen versteht sich unter diesem Begriff eine Entfernung zwischen dem Ende der Arbeitswindungen und der Stelle der Anbringung der Feder (siehe Abbildung).
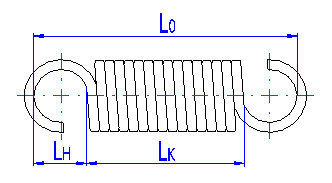
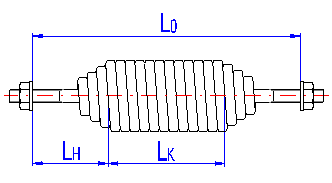
Die entsprechende Länge der unbelasteten Feder einstellen.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Ausfederung) der Feder |
| L | Federlänge |
| t | Torsionsspannung des Federmaterials |

Eine Feder aus einem flachen Band rechteckigen Querschnitts, das in der Form einer Archimedischen Spirale aufgerollt ist, mit einem konstanten Spiel zwischen den aktiven Windungen, belastet mit einem Drehmoment in der Aufrollrichtung.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung. Durch Bewegung irgendeiner der Laufleisten wurde der Federentwurf für die gegebenen Verhältnisse Ri/t, b/t, a0/t gestartet. Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Federbanddicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [9.18] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [9.16, 9.17] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| M | Federbelastung |
| n | Anzahl der Arbeitswindungen |
| a | Drehwinkel |
| d | Schenkelwinkel |
| s | Biegespannung des Federmaterials |

Zylindrische Federn, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren in der zur Achse senkrechten Ebenen mit einem Drehmoment im Aufroll- oder Abrollsinn einwirkenden Kräfte. Die Federn mit einem Drahtdurchmesser bis zu etwa 16 mm werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einem Drahtdurchmesser von mehr als 10 mm eingesetzt.
Die Verdrehungsfedern werden in zwei grundlegenden Ausführungen hergestellt und zwar entweder mit aufeinander liegenden Windungen oder mit einem Abstand unter den Windungen. Für statisch belastete Federn werden Federn mit anliegenden Windungen bevorzugt angewendet. Die Federn mit einem Spiel unter den Windungen sind für die Benutzung bei zyklischer (Ermüdungs-) Belastung geeignet.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Drahtdurchmesser bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [10.16] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [10.14, 10.15] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
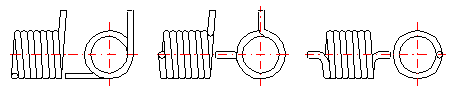
Die entsprechende Länge des Federkörpers einstellen.
Bei einer funktionellen Verformung (Schwenken des Armes) einer Verdrehungsfeder kommt es zu einer Änderung ihrer Maße. Bei einer im Aufrollsinn beanspruchten Feder verkleinert sich ihr Durchmesser. Bei einer Feder mit anliegenden Windungen kommt es zugleich zum Anwachsen ihrer Länge
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| M | Federbelastung |
| a | Drehwinkel |
| d | Schenkelwinkel |
| s | Biegespannung des Federmaterials |

Zylindrische Federn, hergestellt aus schraubenförmig gewickelten Drähten, mit einem konstanten Spiel zwischen den aktiven Windungen, geeignet zur Aufnahme der äußeren in der zur Achse senkrechten Ebenen mit einem Drehmoment im Aufroll- oder Abrollsinn einwirkenden Kräfte. Die Federn mit einem rechteckigen Drahtquerschnitt werden üblich kalt aufgewickelt. Das Warmformen wird für die Produktion hochbeanspruchter Federn größerer Abmessungen mit einer Drahtdicke von mehr als 10 mm eingesetzt.
Die Verdrehungsfedern werden in zwei grundlegenden Ausführungen hergestellt und zwar entweder mit aufeinander liegenden Windungen oder mit einem Abstand unter den Windungen. Für statisch belastete Federn werden Federn mit anliegenden Windungen bevorzugt angewendet. Die Federn mit einem Spiel unter den Windungen sind für die Benutzung bei zyklischer (Ermüdungs-) Belastung geeignet.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Drahtdicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [11.17] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [11.15, 11.16] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In der Auflistung die gewünschte Ausführung der Federenden auswählen.
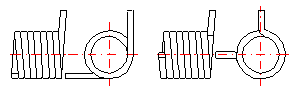
Die entsprechende Länge des Federkörpers einstellen.
Bei einer funktionellen Verformung (Schwenken des Armes) einer Verdrehungsfeder kommt es zu einer Änderung ihrer Maße. Bei einer im Aufrollsinn beanspruchten Feder verkleinert sich ihr Durchmesser. Bei einer Feder mit anliegenden Windungen kommt es zugleich zum Anwachsen ihrer Länge
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| M | Federbelastung |
| a | Drehwinkel |
| d | Schenkelwinkel |
| s | Biegespannung des Federmaterials |

Federn nach dem Prinzip der durch Verdrehung belasteten langen schlanken Stäbe eines kreisförmigen Querschnitts. Bei den Stäben wird am häufigsten eine Kerbverzahnung zur Befestigung der Enden verwendet. Manchmal wird eine der Seiten mit einem Prisma der leichteren Aufnahme wegen, beendet.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Durch Anklicken der Schaltfläche entwerfen Sie die Feder der entsprechenden Maße. Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit der Stabdurchmesser bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [12.15] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [12.13, 12.14] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| M | Federbelastung |
| a | Drehwinkel |
| t | Torsionsspannung des Federmaterials |

Federn nach dem Prinzip der durch Verdrehung belasteten langen schlanken Stäbe eines rechteckigen Querschnitts.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Stabdicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [13.16] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [13.14, 13.15] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| M | Federbelastung |
| a | Drehwinkel |
| t | Torsionsspannung des Federmaterials |

Federn auf dem Prinzip der auf Biegung belasteten langen schlanken Träger des rechteckigen Querschnitts. Sie werden entweder als einarmige (auf einem Ende eingespannte), oder als doppelarmige (beiderseits aufliegende) verwendet. Es sind die Federn mit einer rechteckigen, dreieckigen oder Trapezform zu verwenden.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Federblattdicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [14.19] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [14.17, 14.18] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Durchbiegung) der Feder |
| s | Biegespannung des Federmaterials |
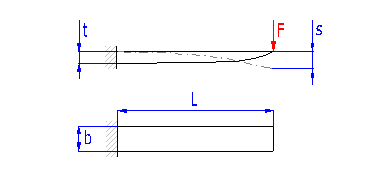
Federn auf dem Prinzip der auf Biegung belasteten langen schlanken Träger des rechteckigen Querschnitts. Sie werden entweder als einarmige (auf einem Ende eingespannte), oder als doppelarmige (beiderseits aufliegende) verwendet. Federn mit einer rechteckigen Form, manchmal werden Federn verwendet mit einer Verstärkung von Mitte und Ende des Blattes.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Federblattdicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [15.19] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [15.17, 15.18] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Durchbiegung) der Feder |
| s | Biegespannung des Federmaterials |
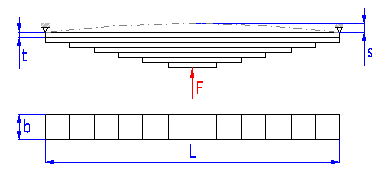
Federn auf dem Prinzip der auf Biegung belasteten langen schlanken Trägerpakete des rechteckigen Querschnitts.
Der in dieser Tabelle verwendete Entwurfsvorgang gestattet, die Federmaße mit einem bestimmten Freiheitsgrad zu definieren. Deshalb ist hier sein genauer Wert für jeden von seinen Eintrittsparametern in der realen Zeit berechnet, der den anderen Federparametern entspricht. Diese Werte sind in den grünen, rechts von den Eintrittszellen angeordneten Feldern dargestellt. Den berechneten Wert übertragen Sie in die Eintrittszelle mit Hilfe der zutreffenden Schaltfläche "<".
Durchgehende Federblätter in voller Länge, rechteckiger Form mit Konstantprofil. Diese Blätter werden zu einer Feder aus zwei Gründen hinzugefügt:

Die in diesem Absatz angebrachten Steuerelemente dienen dem Start der Entwurf- (Optimierungs-) Funktionen der Berechnung.
Beim Federentwurf bemüht sich die Berechnung die Maße so zu optimieren, damit die Federblattdicke bei Einhaltung der verlangten Sicherheit [1.27] möglichst klein ist.
In diesem Absatz sind Ergebnisse der Festigkeitskontrolle der entworfenen Feder angeführt. Die Kontrolle wird durch Vergleich der zulässigen Spannung des verwendeten Materials [1.20] mit der Spannung der vollbelasteten Feder vorgenommen. Die resultierende Sicherheitszahl [16.19] sollte nicht den verlangten Wert [1.27] unterschreiten.
In den Zeilen [16.17, 16.18] sind theoretische Werte der maximalen Arbeitsbelastung und des Arbeitshubes der Feder berechnet, bei denen die verlangte Sicherheitszahl noch eingehalten ist.
In diesem Absatz sind die grundlegenden Arbeitsparameter der entworfenen Feder im Vorspannungszustand (Index 1), im vollbelasteten (Index 8) und im Grenzzustand (Index 9) angeführt.
| F | Federbelastung |
| s | Verformung (Durchbiegung) der Feder |
| s | Biegespannung des Federmaterials |
In diesem Absatz wird die Festigkeitskontrolle der zyklisch (ermüdungs-) belasteten Federn durchgeführt, also Federn mit einer Standzeitanforderung von mehr als 105 Arbeitszyklen. Die eigentliche Kontrolle der Feder wird durch Vergleich der maximalen Ermüdungsfestigkeit des verwendeten Materials [17.8] mit der Spannung der vollbelasteten Feder [17.4] durchgeführt.
Wenn die Feder die Festigkeitskontrolle nicht besteht, ihren Entwurf bei Einhaltung der folgenden Empfehlungen wiederholen:
Bei zyklisch belasteten Federn werden zwei Bereiche der Ermüdungsbelastung der Feder unterschieden. Im ersten Bereich, mit einer begrenzten Standzeit der Feder (die Standzeit unterschreitet zirka 107 Arbeitszyklen), nimmt die Dauerfestigkeit der Feder mit der wachsenden Anzahl der Arbeitszyklen ab. Im Bereich der unbegrenzten Standzeit (die verlangte Standzeit überschreitet 107 Arbeitszyklen) bleibt schon die Dauerfestigkeit des Werkstoffes und damit auch die Festigkeit der Feder beinahe konstant.
Die maximale zulässige Spannung des Federmaterials für die schwellende Belastung und die unbegrenzte Standzeit eingeben. Wenn das Ankreuzfeld rechts vom Eintrittsfeld angekreuzt ist, ist hier der für das ausgewählte Material [1.6] und die oberflächliche Federbearbeitung [1.26] angegebene Minimalwert der Ermüdungsfestigkeit automatisch eingestellt.
Die maximale Ermüdungsfestigkeit der Feder ist auf Grund der Ermüdungsfestigkeit des gewählten Werkstoffes und des gegebenen Belastungsverlaufs der Feder aus dem zutreffenden Ermüdungsdiagramm von Goodman festgelegt.
Die empfohlene Sicherheitszahl ist für das ausgewählte Material [1.6] auf Grund der im Absatz [1.21] definierten Betriebsbedingungen abgeschätzt.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
^