Die Berechnung ist für die Lösung von Druckbehältern und deren Teile bestimmt. Die Berechnung löst die Verformungen und die Verläufe der Spannungen bei Rotationsschalen, die mit Axialkraft, Druck, Radialkraft und Biegemoment beansprucht werden. Dieses Programm ist für homogene Schalen mit der gleichen Dicke und aus einem Material bestimmt. Die Berechnung ermöglicht weiterhin die Lösung der Verbindung von zwei Schalen mit unterschiedlichen Parametern (Dicke, Material, Abmessungen...). Das Programm ermöglicht:
In der Berechnung werden Daten, Abläufe, Algorithmen und Angaben aus der Fachliteratur (Roark formulas, Machinery's Handbook 26th, Teorie desek a skořepin [doc. Ing. Ladislav Šubrt, CSc.] und weiteren) angewendet.
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Schalen sind Konstruktionselemente mit flächigem Charakter, deren Dicke
mehrfach kleiner als die zwei restlichen Maße ist. Die Mittelfläche (Fläche,
welche die Dicke der Schale halbiert) kann bei allgemeinen Schalen beliebige
Form bekommen, wobei die Schalen beliebig beansprucht werden können.
Die Schalen können je nach der Form wie folgt aufgeteilt werden:
Die Schalen können weiterhin je nach der Dicke wie folgt aufgeteilt werden:
Die Schalendicke ist mit dem minimalen Krümmungsradius vergleichbar. Bei diesen Schalen sind die zur Mittelfläche der Schale senkrechten Normalspannungen zu berücksichtigen und es ist auch die durch Schubspannung verursachte Verbiegung der Normalen zur Mittelfläche zu berücksichtigen. Dadurch kommt es zur nichtlinearen Verteilung der Spannungen in der Dicke der Schale. Daraus ergibt sich eine komplizierte analytische Lösung und deshalb wird für die Lösung dieser Schalen das Verfahren der Endelemente verwendet.
Es handelt sich um Schalen, die zwischen den dickwandigen und den dünnwandigen Schalen liegen, für welche die Theorie der dickwandigen Schalen zu kompliziert ist und bei denen die Theorie der dünnwandigen Schalen keine ausreichend genauen Ergebnisse liefert.
Bei diesen Schalen ist die Wanddicke in Bezug auf den minimalen Krümmungsradius zu klein. Bei diesen Schalen kann der Einfluss der Schubspannungen auf die Verformung der Normalen zur Mittenfläche unbeachtet bleiben. Das, zusammen mit der Möglichkeit, einige anderen Spannungen nicht zu berücksichtigen, führt zu der einfachsten analytischen Lösung dieser Schalenart. Dieser Typ der Rotationsschalen wird in dieser Berechnung gelöst.
Bei diesen sehr dünnen Schalen kommt es zur vergleichbaren oder größeren Verformung als die Wanddicke, was zur Änderung des Wirkungsbereichs der Kräfte während der Belastung führt. Die analytische Lösung ist relativ schwierig und deshalb wird für die Lösung dieser Schalen meistens die Methode der Endelemente verwendet.
Es handelt sich um Schalen, bei denen in den Wänden keine Innenmomente (Biegung, Verdrehung) auftreten. Sie werden nur mit Normal- bzw. Schubkräften beansprucht, was zur gleichmäßigen Verteilung der Spannungen auf die Wanddicke führt. Die Membranspannung ist aus der Sicht der Materialnutzung günstig und deshalb ist beim Konstruktionsentwurf wichtig zu beachten, dass dieser Status möglichst wenig durch die ungeeignete Konstruktion gestört wird.
Bei der analytischen Lösung der dünnwandigen Schalen geht man von dem aus der allgemeinen Schale entnommenen Element aus - siehe Bild.
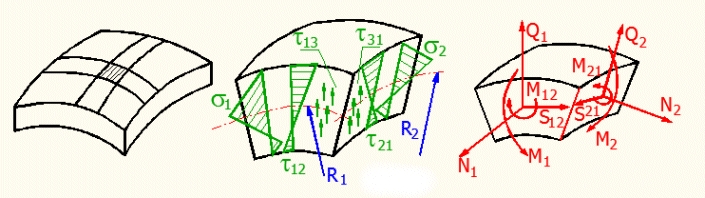
Da man mit keinen dickwandigen Schalen rechnet, können die linearen Verläufe der Normalspannungen (s1, s2) und der Schubspannungen (t12, t21) verwendet werden. Bei den Schalen sind diese Spannungen auf der mittleren Fläche nicht gleich Null, sodass es sich um die Superposition (Zusammensetzung) der Biegung und des Zugs bzw. um die Superposition der Verdrehung und der gleichmäßig verteilten Schubkraft handelt. Zum Beispiel die Spannung s1 ist damit aus der Membran- und Biegespannung zusammengesetzt.
Für dieses Element wird dann die Spannung durch die Innenkraftwirkungen nach der folgenden Tabelle ersetzt:
| Spannung | Endgültige Innenkraftwirkung |
| s1 | N1-Normalkraft |
| M1-Biegemoment | |
| s2 | N2-Normalkraft |
| M2-Biegemoment | |
| t12 | S12-Schubkraft |
| M12-Drehmoment | |
| t21 | S21-Schubkraft |
| M21-Drehmoment | |
| t13 | Q1-Querschiebekraft |
| t31 | Q2-Querschiebekraft |
Da das herausgezogene Element im Gleichgewicht sein muss, kann eine Gruppe von
Gleichgewichtsgleichungen für die Gruppe der auf das Element wirkenden Kräfte
erstellt werden. Weiterhin sind die Beziehungen für die Verformung der Schale
und die Beziehungen, welche die Abhängigkeit zwischen den Verformungen und den
inneren Krafteinwirkungen angeben, abzuleiten.
Im allgemeinen Fall führt die Lösung dieser Gleichungen zu einem komplizierten, schwierig lösbaren System von partialen Differentialgleichungen. Deshalb werden für konkrete Schalenarten verschiedene vereinfachende Bedingungen akzeptiert, was zwar zu ungefähren, jedoch ausreichend genauen Ergebnissen führt, die den praktischen Zwecken entsprechen.
Konkrete gruppen von Differentialgleichungen werden immer durch zugehörige Randbedingungen ergänzt.
In der Literatur kann man Lösungen für verschiedene Schalenarten von verschiedenen Autoren finden. Die endgültigen Gleichungsgruppen sind häufig unterschiedlich (in Abhängigkeit von den akzeptierten Vereinfachungen), die Ergebnisse der verschiedenen Gleichungen unterscheiden sich jedoch nur geringfügig (abgeschätzte Streuung bis zu 10%).
Bei der Lösung der dünnwandigen Schalen kommen folgende Voraussetzungen zum Einsatz.
In der technischen Praxis treten wahrscheinlich am häufigsten die Rotationsschalen bzw. die rotationssymmetrischen Schalen auf.
Als Rotationsschalen gelten Schalen, deren mittige Fläche die Rotationsfläche ist und bei denen keine begrenzenden Bedingungen für die Beanspruchung festgelegt sind. Allgemeine Lösung der Rotationsschalen ist wieder sehr kompliziert und ist vor allem für die Zylinderschale durchgearbeitet, was wahrscheinlich die meistverbreitete Schalenart ist.
Die rotationssymmetrischen Schalen sind die Rotationsschalen, die auf den Parallelenkreisen konstant beansprucht werden. Die Lösung dieser Schalenart ist wesentlich einfacher und von der einzigen Koordinate abhängig. In der Literatur kann man dann Lösungen für geometrische Grundformen der Schalen wie Zylinder, Kugel, Konus, Torus usw. finden.
Dieses Programm ist vor allem für die Lösung der rotationssymmetrischen Schalen bestimmt.
Als Schalenkonstruktionen werden meistens Konstruktionen bezeichnet, die durch die Verbindung von zwei oder mehreren Schalen oder als Verbindung der Schalen mit anderen Konstruktionselementen entstehen. Das typische Beispiel so einer Schalenkonstruktion kann dann ein Druckbehälter, der aus einem zylinderförmigen Behälter mit kreisförmigem Boden besteht, die Reduktion des Leitungsdurchmessers mithilfe eines kegelförmigen Übergangs oder der Flansch am Zylinderrohr sein.
Im Prinzip kann man sagen, dass diese Beispiele statisch unbestimmt sind. Das bedeutet, dass in der Verbindung von zwei Schalen Kraftwirkungen entstehen, die mithilfe der statischen Gleichgewichtsgleichungen nicht gelöst werden können. Alles kann auf folgendem Beispiel der Verbindung der mit Innenüberdruck belasteten Zylinder- und Kugelschale gezeigt werden.
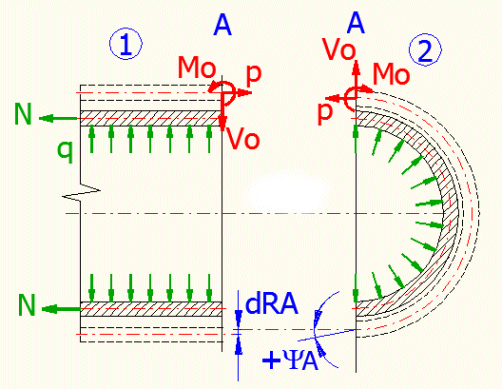
Falls die einzelnen Schalen beansprucht werden, würde in den Schalen nur eine Membranspannung entstehen und die Schalen würden sich in die (gestrichelt) gekennzeichnete Form verformen. Anstelle des Anschlusses beider Schalen würden sich die Radien um verschiedenen Wert verändern und es würde zum Drehen der Wand der Kugelschale kommen. Dieses Beispiel wird normalerweise durch Kraftmethode gelöst, bei der eine unbestimmte Kraft "Vo", der Moment "Mo" und die Kraft "p" an den Rand jeder Schale angeschlossen wird.
Damit die Schalen "verbunden" werden können, sind solche Verformungsbedingungen zu definieren, welche die Anforderuung gewährleisten, dass die Endverformung beider Schalen identisch ist. Durch die Lösung dieser Gleichungen können dann die Verformungen und Spannungen anstelle der Verbindung der Schalen gelöst werden, was meistens die Stelle mit lokaler Spitzenspannung ist, die uns interessiert.
Falls in der Schale keine Innenmomente, sondern nur die Innenkräfte auftreten, befindet sich die Schale im sogenannten Membrane-Zustand. Dieser Zustand ist günstig und gewünscht aus der Sicht der Tragfähigkeit der Schale. Ob die Schale im Membrane-Zustand ist, ist von der Form, der Lagerungsweise und der Beanspruchungsweise der Schale abhängig. Für den Entwurf der Schale, die sich im Membrane-Zustand befinden soll, gibt es deshalb folgende Grundregeln:
Falls diese Bedingungen nicht erfüllt werden, kommt es zu einer Störung des Membrane-Zustands und dadurch auch zur Erhöhung der Spannung, die durch größere Wanddicke kompensiert werden muss. Deshalb kommen häufig verschiedene Versteifungen oder Stützen zum Einsatz, welche die ungünstige Beanspruchung, die den Membrane-Zustand stört, aufnehmen.
Bei der Lösung der Verformung (Spannung) einer selbständigen Schale ist wie folgt vorzugehen.
1...Material der Schale auswählen, bzw. Materialwerte [1.0] eingeben
2...Je nach dem Typ der Schale entsprechenden Absatz der Berechnung auswählen
[2.0, 3.0, 4.0,
5.0]
3...Art der Beanspruchung auswählen [2.1, 3.1,
4.1, 5.1]
4...Abmessungen und Beanspruchung der Schale eingeben und Ergebnisse überprüfen.
Bei der Lösung der Verformung (Spannung) der Verbundschalen ist wie folgt vorzugehen.
1...Typ der Schalenverbindung [10.1] auswählen und mit Taste OK bestätigen
2...Je nach der Auswahl werden Absätze [6.0, 7.0,
8.0, 9.0] angezeigt, welche die ausgewählten
Schalen enthalten.
3...Materialwerte, Abmessungen und Beanspruchungen der Schalen eingeben
4...Im Absatz [10.0] Taste "Lösen" drücken,
dadurch wird die Iteration gestartet
5...Ergebnisse in den Absätzen mit den ausgewählten Schalen überprüfen
In diesem Absatz die Berechnungseinheiten und das Material der zu prüfenden Schale auswählen Die Materialwerte werden automatisch in Absätzen [2.0-5.0] verwendet. In Absätzen [6.0-9.0] können zu jeder Schale unterschiedliche Materialparameter zugeordnet werden.
In der Auswahlliste das gewünschte System der Berechnungseinheiten auswählen. Beim Umschalten der Einheiten werden sofort alle Werte umgerechnet.
Aus der Auswahlliste wählen Sie das geeignete Material der Schalen aus. Sofern sich die Materialkonstanten ihres Materials von den Materialkonstanten, die in den Zeilen[1.3–1.8] angeführt sind, unterscheiden, haken Sie die Abstreichtaste an der Zeile [1.3] ab und geben Sie eigene Materialkonstanten ein.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich belasteten dünnen Zylinderschale festgestellt werden. Für die Schalendicke muss t<R/10 gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein.
Wählen Sie in der Auswahlliste die Beanspruchung aus, die ihrer Aufgabe entspricht. Nach der Auswahl wird eine schematische Skizze der Beanspruchung angezeigt. Rechts von der Auswahlliste sind dann die Gültigkeitsbedingungen aufgeführt.
Hinweise zu den einzelnen Beanspruchungsfällen:
3. In einem Punkt, der von dem Rand ausreichend entfernt ist.
4. Wo "y" von dem nicht beanspruchten Ende zu messen ist.
Schalendicke, Abrundungsradius (Mittelradius) und Schalenlänge eingeben. Die Schalendicke sollte kleiner als 1/10 des Radius sein.
Sie können anwählen, ob Sie die Gesamtkraft oder die auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet.
Innenüberdruck eingeben. Beim Außenüberdruck einen negativen Wert eingeben.
Geschwindigkeit der Schalenrotation in Umdrehungen pro Minute eingeben.
In diesen Zeilen sind die Ergebnisse der Berechnung aufgeführt.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich belasteten dünnen Konusschalen festgestellt werden. Für die Schalendicke muss t<R/10, (t<r/10) gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein.
Wählen Sie in der Auswahlliste die Beanspruchung aus, die ihrer Aufgabe entspricht. Nach der Auswahl wird eine schematische Skizze der Beanspruchung angezeigt. Rechts von der Auswahlliste sind dann die Gültigkeitsbedingungen aufgeführt.
Hinweise zu den einzelnen Beanspruchungsfällen:
2...Es gibt eine Zusammenhanglosigkeit in der
Druckbeanspruchung durch die Flüssigkeit unterhalb und oberhalb des Pegels. Das
führt zur Biegungsbeanspruchung in diesem Bereich. Für "y" unter dem
Flüssigkeitspegel (y<d) ist s1max in der Höhe von
y=3*d/4 und s2max in der
Höhe von Y=d/2.
4..."r" muss ein positiver Wert und "r/t>10" sein,
damit die Bedingung des dünnwandigen Behälters erhalten bleibt
Schalendicke [3.2] eingeben. Da der Durchmesser, die Länge und der Winkel des Konus voneinander abhängige Variablen sind, stellen Sie in der Zeile [3.3] ein, welche Variablen die Eingangsvariablen sein werden. Dann diese Maßwerte eingeben.
Ist in der Zeile [3.1] die Beanspruchung durch Tangentialkraft (Anwahl -4) angewählt wird, können alle drei Werte (R,y,eingegeben werden und die abhängige Variable ist der zweite Radius "r".
Tiefe der Füllung und spezifisches Gewicht der Flüssigkeit eingeben.
Sie können anwählen, ob Sie die Gesamtkraft oder die auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet.
Innenüberdruck eingeben. Beim Außenüberdruck einen negativen Wert eingeben.
Geschwindigkeit der Schalenrotation in Umdrehungen pro Minute eingeben.
In diesen Zeilen sind die Ergebnisse der Berechnung aufgeführt.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich belasteten dünnen Kugelschale festgestellt werden. Für die Schalendicke muss t<R2/10 gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein.
Wählen Sie in der Auswahlliste die Beanspruchung aus, die ihrer Aufgabe entspricht. Nach der Auswahl wird eine schematische Skizze der Beanspruchung angezeigt. Rechts von der Auswahlliste sind dann die Gültigkeitsbedingungen aufgeführt.
Hinweise zu den einzelnen Beanspruchungsfällen:
2... Es gibt eine Zusammenhanglosigkeit in der
Druckbeanspruchung durch die Flüssigkeit unterhalb und oberhalb des Pegels. Das
führt zur Biegungsbeanspruchung in diesem Bereich. Die Berechnung gilt für "y"
unter dem Flüssigkeitsspiegel (y<d). Für y>d wird die Beanspruchung 4, bei der
die Kraft durch das Gewicht der Flüssigkeit gegeben ist.
4. Der Winkel "q0" ist der Winkel zur Unterkante des
Behälters und er muss größer als Null sein.
5. Für den Winkel "q"<=90 deg.
Dicke [4.2] und Mittenradius der Kugelschale [4.3], Winkel von der Schalenachse zur Oberkante [4.4] und eventuell auch Winkel von der Schalenachse zur Unterkante [4.5] eingeben.
Tiefe der Füllung und spezifisches Gewicht der Flüssigkeit eingeben.
Sie können anwählen, ob Sie die Gesamtkraft oder die auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet.
Innenüberdruck eingeben. Beim Außenüberdruck einen negativen Wert eingeben.
Geschwindigkeit der Schalenrotation in Umdrehungen pro Minute eingeben.
In diesen Zeilen sind die Ergebnisse der Berechnung aufgeführt.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich belasteten dicken Zylinder- oder Kugelschale festgestellt werden.
Wählen Sie in der Auswahlliste die Beanspruchung aus, die ihrer Aufgabe entspricht. Nach der Auswahl wird eine schematische Skizze der Beanspruchung angezeigt. Rechts von der Auswahlliste sind dann die Gültigkeitsbedingungen aufgeführt.
Außen- und Innenradius der Schale [5.2, 5.3] und eventuell auch die Länge der Zylinderschale [5.4] eingeben.
Belastung pro Flächeneinheit [5.5] eingeben.
In diesen Zeilen sind die Ergebnisse der Berechnung aufgeführt. In Zeile [5.15] können Sie weiterhin den Radius verändern, an dem die berechneten Spannungswerte aufgeführt werden.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich beanspruchten dünnen, langen Zylinderschale festgestellt werden. Für die Schalendicke muss t<R/10 gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein. Bei der Belastung der Schale mit dem Endmoment "Mo" und der Kraft "Vo" werden die Spannungen (Verformungen) einen schwingenden Charakter haben, der durch die Exponentiale (siehe Bild) gedämmt wird.
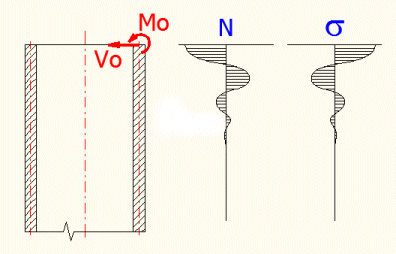
Das bedeutet, dass die Wirkungen dieser Beanspruchungen schnell ausklingen und im ausreichenden Abstand vom Rand gar nicht zum Vorschein kommen. Deshalb werden die Zylinderschalen auf sog. lange (die Beanspruchung eines Randes beeinflusst nicht die Verformungen und Spannungen des anderen Randes) und kurze Schalen (die Wirkungen der Randbeanspruchung schaffen nicht auszuklingen und beeinflussen die Verformungen und Spannungen des anderen Randes). Die Zylinderschale kann als lang angesehen werden, wenn ihre Länge größer ist als der Wert L, der in den Bedingungen in der Zeile [6.2] aufgeführt ist. Falls eine kleinere Genauigkeit in Kauf genommen wird (der Fehler der Lösung wird größer als 10% sein), kann mit dem halben L-Wert gerechnet werden.
Berechnungsformel für L:
L=6/(3*(1-ny^2)/(R^2*t^2))^(1/4); wo:
ny...Poisson-Konstante
R....Außenradius
t.....Schalendicke
Im ersten Teil der Berechnung sind Eingangsdaten, im zweiten Teil die Ergebnisse. Oben rechts finden Sie die wichtigsten Randbedingungen, unter diesen Bedingungen dann die Bilder der bemaßten Schale und deren Beanspruchung. Zwischen den Bildern schaltet man mit der Taste ">" in der rechten oberen Ecke des Bildes.
Ist das Feld rechts von dem Eingabefeld angehakt, sind die Materialkonstanten vom Absatz [1.0] übertragen. Falls Sie Ihre eigenen Werte eingeben brauchen, haken Sie bitte das Feld ab und geben Sie den Zugelastizitätsmodul [6.2] und die Poisson-Konstante [6.3] ein.
Mittenradius [6.4] und Dicke der Zylinderschale [6.5] eingeben.
Beanspruchung pro Flächeneinheit [6.6] eingeben. Falls die Schale mit
Innenüberdruck beansprucht wird, ist der Wert positiv, beim Außenüberdruck geben
Sie den negativen Wert ein. In der Zeile [6.7] ist dann die gesamte Achskraft,
die durch die Einwirkung des eingegebenen Drucks auf die Fläche des
kreisförmigen Grundfläche entsteht.
In der Zeile [6.8] geben Sie die auf die Längeneinheit bezogene Kraft "p" bzw.
die Gesamtkraft "P" ein. Sie können anwählen, ob Sie die Gesamtkraft oder die
auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option
mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert
wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet.
Wenn Sie die Taste "<-Pq" drücken, wird in dieses Eingabefeld der Wert
aus Zeile [6.7] übertragen.
In Zeile [6.9] geben Sie die Umfangskraft (senkrecht zur Schalenachse), in Zeile
[6.10] den Moment ein.
In der Zeile [6.12,6.13] ist die Verformung der Schale am Rand der Schale
(x=0) aufgeführt. In der Zeile [6.14] ist das Eingabefeld für die Koordinate "x"
(gemessen vom Rand der Schale in der Richtung der Schalenachse). Unten sind dann
die einzelnen Ergebnisse für die eingegebene "x"-Koordinate. Die "x"-Koordinate
können Sie auch durch den Schieber ändern, dessen Schiebebereich von Null bis zu
dem rechts vom Schieber angegebenen Wert reicht (voreingestellt ist die
Mindestlänge der Schale L).
Die Zeile [6.15] enthält eine Auswahlliste, über die Sie einstellen können, für
welche Eingangsbeanspruchungen (oder deren Summe) die Ergebnisse angezeigt
werden sollen.
Die Funktionalität der zweiten Berechnung ist mit der ersten Berechnung identisch.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich beanspruchten dünnen Kugelschale festgestellt werden. Für die Schalendicke muss t<R/10 gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein. Bei der Belastung der Schale mit dem Endmoment "Mo" und der Kraft "Vo" werden die Spannungen (Verformungen) einen schwingenden Charakter haben, der durch die Exponentiale (siehe Bild) gedämmt wird.
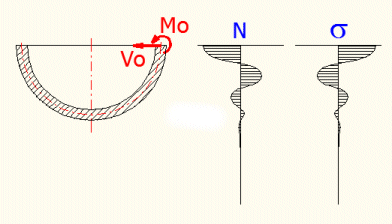
Das bedeutet, dass die Wirkungen dieser Beanspruchungen schnell ausklingen und im ausreichenden Abstand vom Rand gar nicht zum Vorschein kommen.
Im ersten Teil der Berechnung sind Eingangsdaten, im zweiten Teil die Ergebnisse. Oben rechts finden Sie die wichtigsten Randbedingungen, unter diesen Bedingungen dann die Bilder der bemaßten Schale und deren Beanspruchung. Zwischen den Bildern schaltet man mit der Taste ">" in der rechten oberen Ecke des Bildes.
Ist das Feld rechts von dem Eingabefeld angehakt, sind die Materialkonstanten vom Absatz [1.0] übertragen. Falls Sie Ihre eigenen Werte eingeben brauchen, haken Sie bitte das Feld ab und geben Sie den Zugelastizitätsmodul [7.2] und die Poisson-Konstante [7.3] ein.
Den von der Achse der Schale zum Rand der Schale gemessenen Winkel "f" [7.4] und die Schalendicke [7.5] eingeben. Ferner den Mittenradius der Kugelschale "R2" [7.6] oder den Radius "R" [7.7] (Abstand von der Achse zur Kante) eingeben. Welchen Wert Sie eingeben, stellen Sie in der Auswahlliste in Zeile [7.6] ein. Der zweite Wert wird nachberechnet.
Beanspruchung pro Flächeneinheit [7.8] eingeben. Falls die Schale mit Innenüberdruck beansprucht wird, ist der Wert positiv, beim Außenüberdruck geben Sie den negativen Wert ein. In Zeile [7.9] ist dann die gesamte Tangentialkraft, die durch die Einwirkung des eingegebenen Drucks auf die Fläche der kreisförmigen Grundfläche entsteht, und deren Verteilung in die x- und y-Komponente [7.10,7.11].
In der Zeile [7.12] geben Sie die auf die Längeneinheit bezogene Kraft "P" bzw. die Gesamtkraft "p" ein. Sie können anwählen, ob Sie die Gesamtkraft oder die auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet. Wenn Sie die Taste "<-Pq" drücken, wird in dieses Eingabefeld der Wert aus Zeile [7.9] übertragen.
In Zeile [7.13] geben Sie die Umfangskraft (senkrecht zur Schalenachse), in Zeile [7.14] den Moment ein.
In Zeile [7.16,7.17] ist die Verformung der Schale am Rand der Schale (w=0) aufgeführt. In der Zeile [7.18] ist das Eingabefeld für den Winkel w (gemessen vom Rand der Schale). Unten sind dann die einzelnen Ergebnisse für den eingegebenen Winkel w. Den Winkel w können Sie auch durch den Schieber ändern, dessen Schiebebereich von Null bis zu dem rechts vom Schieber angegebenen Wert reicht.
Die Zeile [7.19] enthält eine Auswahlliste, über die Sie einstellen können, für welche Eingangsbeanspruchungen (oder deren Summe) die Ergebnisse angezeigt werden sollen.
Die Funktionalität der zweiten Berechnung ist mit der ersten Berechnung identisch.
Den von der Achse der Schale zum Rand der Schale gemessenen Winkel "f" [7.33] und die Schalendicke [7.34] eingeben. Ferner den Mittenradius der Kugelschale "R2" [7.35] oder den Radius "R" [7.36] (Abstand von der Achse zur Kante) eingeben. Welchen Wert Sie eingeben, stellen Sie in der Auswahlliste in Zeile [7.35] ein. Der zweite Wert wird nachberechnet.
Mithilfe von zwei Tasten "<-f" rechts in der Zeile [7.33] kann derjenige Winkel "f", der einen identischen Radius "R" [7.35] mit "R" [7.6] sicherstellt. Dadurch wird eine genaue "Verbindung" mit der Kugelschale aus der ersten Berechnung ermöglicht.
Durch diese Berechnung kann die Spannung und die Verformung einer unterschiedlich beanspruchten dünnen, langen konischen Schale festgestellt werden. Für die Schalendicke muss t<R/10 gelten. Die Verformung der Schale sollte im Vergleich mit der Schalendicke klein sein. Bei der Belastung der Schale mit dem Endmoment "Mo" und der Kraft "Vo" werden die Spannungen (Verformungen) einen schwingenden Charakter haben, der durch die Exponentiale (siehe Bild) gedämmt wird.
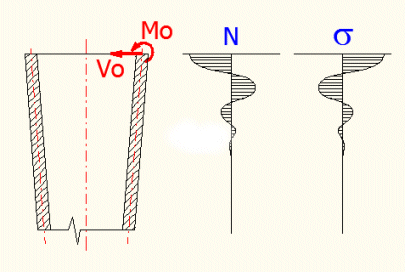
Das bedeutet, dass die Wirkungen dieser Beanspruchungen schnell ausklingen und im ausreichenden Abstand vom Rand gar nicht zum Vorschein kommen. Deshalb werden die konischen Schalen auf sog. lange (die Beanspruchung eines Randes beeinflusst nicht die Verformungen und Spannungen des anderen Randes) und kurze Schalen (die Wirkungen der Randbeanspruchung schaffen nicht auszuklingen und beeinflussen die Verformungen und Spannungen des anderen Randes). Die konische Schale kann als lang angesehen werden, wenn ihre Länge größer ist als der Wert L, der in den Bedingungen in der Zeile [8.2] aufgeführt ist.
Für die Berechnung von L (Stelle, an der die Wirkungen der Randbeanspruchung
ausreichend gedämmt werden) werden folgende Beziehungen verwendet:
1) Koeffizient k=2/sin(a)*((12*(1-ny^2)*R^2)/(t^2*(1/cos(a))^2))^(1/4)
2) Koeffizient mi=abs((kA-k)/(2^0.5))
3) R=RA-x*tan(a)
4) Die Stelle mit ausreichender Dämmung wird berücksichtigt, wenn der
Koeffizient mi=4.
wobei:
ny...Poisson-Konstante
R....Radius des Konus entlang der Konus-Achse, RA...(am Anfang)
t.....Schalendicke
a.....Halbwinkel des Konus
kA....Koeffizient k am Anfang der Schale
x......Koordinaten auf der Achse des Kegels
Die Schalendicke muss gleichzeitig die Gleichung R/(t*cos(a))>10
erfüllen, wo R der über die Länge der Schale im Intervall x<0,L> gemessene
Radius ist.
Im ersten Teil der Berechnung sind Eingangsdaten, im zweiten Teil die Ergebnisse. Oben rechts finden Sie die wichtigsten Randbedingungen, unter diesen Bedingungen dann die Bilder der bemaßten Schale und deren Beanspruchung. Zwischen den Bildern schaltet man mit der Taste ">" in der rechten oberen Ecke des Bildes.
Ist das Feld rechts von dem Eingabefeld angehakt, sind die Materialkonstanten vom Absatz [1.0] übertragen. Falls Sie Ihre eigenen Werte eingeben brauchen, haken Sie bitte das Feld ab und geben Sie den Zugelastizitätsmodul [8.2] und die Poisson-Konstante [8.3] ein.
Mittenradius der Abrundung "RA" [8.4], Schalendicke [8.5] und Halbwinkel des Konus [8.6] eingeben.
Beanspruchung pro Flächeneinheit [8.7] eingeben. Falls die Schale mit Innenüberdruck beansprucht wird, ist der Wert positiv, beim Außenüberdruck geben Sie den negativen Wert ein. In Zeile [8.8] ist dann die gesamte Tangentialkraft, die durch die Einwirkung des eingegebenen Drucks auf die Fläche der kreisförmigen Grundfläche entsteht, und deren Verteilung in die x- und y-Komponente [8.9, 8.10].
In der Zeile [8.11] geben Sie die auf die Längeneinheit bezogene Kraft "P" bzw. die Gesamtkraft "p" ein. Sie können anwählen, ob Sie die Gesamtkraft oder die auf ein Millimeter (Zoll) des Umfangs bezogene Kraft eingeben. Gewünschte Option mit dem Schalter in dieser Zeile auswählen. Der im Eingabefeld enthaltene Wert wird beim Umschalten automatisch nach dem aktuellen Durchmesser umgerechnet. Wenn Sie die Taste "<-Pq" drücken, wird in dieses Eingabefeld der Wert aus Zeile [8.8] übertragen.
In Zeile [8.12] geben Sie die Umfangskraft (senkrecht zur Schalenachse), in Zeile [8.13] den Moment ein.
In der Zeile [8.15, 8.16] ist die Verformung der Schale am Rand der Schale
(x=0) aufgeführt. In der Zeile [8.17] ist das Eingabefeld für die Koordinate "x"
(gemessen vom Rand der Schale in der Richtung der Schalenachse). Unten sind dann
die einzelnen Ergebnisse für die eingegebene "x"-Koordinate. Die "x"-Koordinate
können Sie auch durch den Schieber ändern, dessen Schiebebereich von Null bis zu
dem rechts vom Schieber angegebenen Wert reicht (voreingestellt ist die
Mindestlänge der Schale L).
Die Zeile [8.18] enthält eine Auswahlliste, über die Sie einstellen können, für
welche Eingangsbeanspruchungen (oder deren Summe) die Ergebnisse angezeigt
werden sollen.
Die Funktionalität der zweiten Berechnung ist mit der ersten Berechnung identisch.
Durch diese Berechnung kann der Verlauf der Durchbiegung, die Spannung, die Verdrehung bei den Kreisplatten der mittleren Dicke festgestellt werden, und zwar einschließlich der Höchstwerte. Da die Membranspannung bei dieser Berechnungsweise nicht berücksichtigt wird (siehe theoretischer Teil der Plattenberechnung), ist die maximale Durchbiegung zu überprüfen, die kleiner als die halbe Plattendicke sein sollte.
Ist das Feld rechts von dem Eingabefeld angehakt, sind die Materialkonstanten vom Absatz [1.0] übertragen. Falls Sie Ihre eigenen Werte eingeben brauchen, haken Sie bitte das Feld ab und geben Sie den Zugelastizitätsmodul [9.2] und die Poisson-Konstante [9.3] ein.
Außenradius [9.4] und Plattendicke [9.5] eingeben. Die Plattendicke sollte kleiner sein als 1/5 des Radius (falls höhere Genauigkeit erforderlich sein wird, 1/10 des Radius).
Geben Sie die Beanspruchung pro Flächeneinheit [9.6], die auf den Kreis mit dem Radius "ro" [9.8] wirkende Kraft "P" [9.7], die am Umfang wirkende Kraft "Vo" [9.9] und den Moment "Mo" [9.10] ein.
In Zeile [9.12, 9.13] ist die Verformung der Platte an dem Rand der Platte (R=RA) aufgeführt. In Zeile [9.14] ist das Eingabefeld für die Koordinate "R" (gemessen von der Mitte der Platte). Unten sind dann die einzelnen Ergebnisse für die eingegebene "R"-Koordinate. Die "R"-Koordinate können Sie auch durch den Schieber ändern, dessen Schiebebereich von Null bis zum "RA"-Wert reicht.
Die Zeile [9.15] enthält eine Auswahlliste, über die Sie einstellen können, für welche Eingangsbeanspruchungen (oder deren Summe) die Ergebnisse angezeigt werden sollen.
In den vorstehenden Absätzen werden selbständige Schalen gelöst. Viel häufigere Aufgabe ist in der technischen Praxis jedoch die Lösung der Verbindung der Grundformen der Schalen bzw. deren Verbindung mit einer festen Platte (das Einspannen). Diese Aufgaben sind statisch unbestimmt und analytisch schwer lösbar. In diesem Absatz können sie durch allmähliche Approximation der Beanspruchungen an den Enden einzelner Schalen so gelöst werden, dass die gleiche Randverformung bei beiden Schalen erreicht wird und die Schalen "verbunden" werden können. Man kann hier drei Parameter ändern und drei Bedingungen auswerten. Die Lösung verwendet die Excel-Funktionalität "Goal seek...", die für die Änderung einzelner geänderten Parameter [10.4, 10.5, 10.6] so zyklisch verwendet wird, dass das eingegebene Ergebnis [10.8, 10.10, 10.12] bei den eingetragenen Gleichungen [10.7, 10.9, 10.11] erreicht wird. Alle drei Felder haben einen Namen, sodass es erforderlich ist, deren Namen (z.B._Variable1,_Formula1,_dRA_06...) in den Formeln zu verwenden.
Lösungsablauf:
Allmähliche Schritte des Lösungswerkzeugs:
Alles wird auf einem Beispiel erklärt.
Ein Rohr mit sprunghafter Änderung der Wanddicke wird mit dem Innenüberdruck "q" und der Achskraft "N" beansprucht, der Mittenradius des Rohrs bleibt unverändert. Nach der Freigabe werden die Ränder beider Schalen mit der Radialkraft "Vo", der Axialkraft "p" und dem Moment "Mo" beansprucht. Die Verformungsbedingungen für diese Schale sind "dRA1=-dRA2" und "YA1+YA2=0". (siehe Bild)
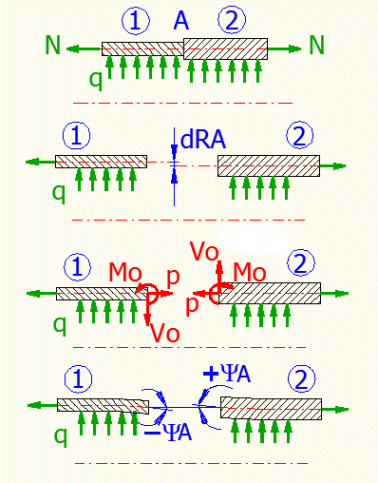
Ablauf:
Da die Definition der Schalenfreigabe und die Definition der Randbedingungen anspruchsvoller sein könnte, ist hier die Lösung der häufigsten Fälle vorbereitet. In der Auswahlliste ist der Typ der verbundenen Schalen, deren Beanspruchung und die Randbedingungen aufgeführt Nach der Auswahl wird ein Bild angezeigt. Durch Drücken der Taste "OK" werden die Absätze geöffnet, die für die Lösung der Verbindung erforderlich sind. Die einzelnen Schalen werden gleichzeitig entlastet (Definition der Beanspruchung) und es werden die Randbedingungen definiert. Das wird durch die Eintragung der entsprechenden Formel in die entsprechenden Felder gelöst.
Das Lösen der Schalen besteht in der Eintragung der entsprechenden Formeln in die Eingabeparameter einzelner Schalen (siehe [10.1]). Durch das Drücken dieser Taste werden die Formeln von allen Eingabeparametern beseitigt und durch einen Zahlenwert ersetzt. Es ist günstig, diesen Befehl zu verwenden, bevor Sie mit der Definition der eigenen Entlastung der Schale und der eigenen Randbedingungen beginnen. Sie sorgen dadurch für die Beseitigung eventueller ungewünschten Definitionen aus den vorherigen Berechnungen.
Diese Angabe definiert, wie oft hintereinander die Excel-Funktion "Goal seek..." eingeschaltet wird. . Der Bereich der Eingabewerte beträgt 1-30. Normalerweise konvergiert jedoch die Lösung sehr schnell (4-5 Schritte), sodass der voreingestellte Wert 10 ausreicht. Die im Dialogfenster angezeigten Prozentpunkte zeigen den Fortschritt der Lösung nach dem Starten der Approximation.
Die Funktion "Goal seek..." wird für die Approximation verwendet. Sie kann zwar eine geeignete Lösung finden, bei kleinen Differenzen des Ergebnisses zwischen einzelnen Schritten beendet sie jedoch die Suche nach der Lösung vorzeitig und die gefundene Lösung kann durch unnötigen Fehler belastet werden. Deshalb wird die Empfindlichkeit der Lösung in den vordefinierten Fällen durch die Multiplizierung des Ergebnisses durch diesen Koeffizient ("_Sensitivity") erhöht. Meistens ist es nicht erforderlich, diesen Parameter zu ändern, sein Wert wird automatisch bei der Auswahl von [10.1] eingestellt.
Nach der Einschaltung der Approximation werden die Werte in diesen Feldern
schrittweise so geändert, dass das Soll-Ergebnis auf [10.8-10.13] erreicht wird.
Die einzelnen Parameter (Felder) haben die Bezeichnung "_Variable1","_Variable2"
und "_Variable3". Linken Sie diese Variablen in den Eingabeparameter, den Sie im
jeweiligen Absatz [6.0,7.0,8.0,9.0] ändern möchten. Falls Sie zum Beispiel die
für die Verformung der Schale erforderliche Kraft "Vo" nicht kennen, tragen Sie
in das Feld mit dem Wert "Vo" die Formel "=_Variable1" ein.
Durch das Drücken der Taste "<=0" werden die Werte auf Null gesetzt.
Tragen Sie in dieses Feld (Felder) die Gleichung ein, die Sie lösen möchten. Nach dem Starten der Approximation wird der Parameterwert [10.5] "_Variable1" so geändert, dass das Ergebnis der in dieser Zeile eingetragenen Gleichung dem in der folgenden Zeile eingegebenen Wert entspricht. Sie wollen zum Beispiel, dass die Änderung der Zylinderschale gleich Null ist. Dann tragen Sie in dieses Feld zum Beispiel die Formel "=_dRA_06" bzw. "=_dRA_06*1000" ein, um die Empfindlichkeit zu erhöhen). Im folgenden Feld [10.9] tragen Sie das Sollergebnis "0" ein.
Tragen Sie in dieses Feld (Felder) das Sollergebnis der Gleichung von der vorstehenden Zeile ein. Wenn Sie die Taste "Lösen" drücken, wird gerade diese Gleichung ohne Rücksicht auf die anderen Gleichungen gelöst. Das kann auch in dem Fall von Vorteil sein, in dem Sie die Bedingungen bei der Entlastung der Schale falsch definieren und die Lösung nicht konvergiert.
Mithilfe der einzelnen Berechnungen können die gegenseitigen Verbindungen verschiedener Schalen gelöst werden. In diesem Fall sind die einzelnen Teile zu entlasten, die Randbedingungen zu definieren und die entsprechenden Formeln (Bedingungen) in das Lösungswerkzeug einzutragen. Im folgenden Text werden einige häufigsten Fälle der Schalenkonstruktionen detailliert beschrieben.
Dieses Beispiel der Schalenverbindung simuliert gut die Verbindung des Rohrs mit dem Flansch, was eine sehr häufig gelöste Aufgabe ist. Man kann zum Beispiel auch ein Rohr mit der Rippe simulieren.
Schalenmaße [6.4, 6.5] und Beanspruchung der Schale mit dem Überdruck "q" [6.6] definieren. Die axiale Beanspruchung "p" [6.8] wird gleich Null sein.
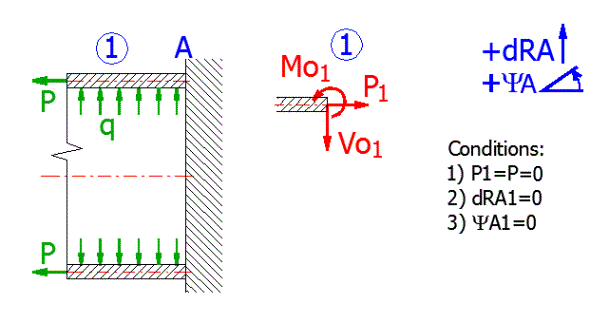
Entlastung der Schale:
Die Schale wird mit einer Randkraft und einem Randmoment belastet.
Randbedingungen:
Schalenmaße [6.4, 6.5] eintragen, die Beanspruchung mit Überdruck "q" [6.6] wird gleich Null sein, die Axialbelastung "p" [6.8] wird gleich Null sein, die Umfangskraft "Vo" [6.9] wird die halbe Umfangskraft (F/2) sein.
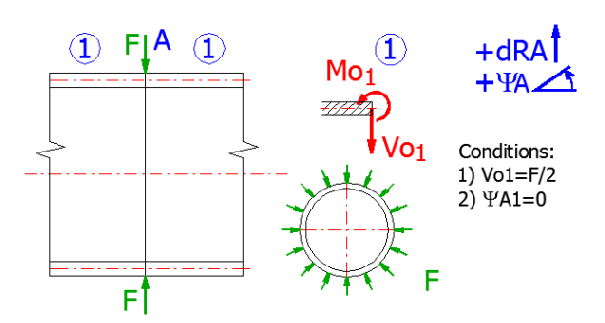
Entlastung der Schale:
Die Schale ist an der Stelle, an der die Umfangskraft wirkt, auf zwei Teile
aufzuteilen und zu lösen ist die Hälfte der Schale. Die Hälfte der Schale wird
also mit der Hälfte der ursprünglichen Umfangskraft beansprucht und anstelle der
Einwirkung wird die Verdrehung gleich Null sein.
Linken Sie in das Feld für den Moment "Mo" [6.9] den "Zu verändernden Parameter
1", sodass das Feld folgendes enthält: "=_Variable1"
Randbedingungen:
Verdrehung in Punkt A=0. Die Formel im Feld "Gleichung" 1
[10.8] ist: "=_Psi_06a*_Sensitivity". Das Sollergebnis 1 im Feld [10.9]
wird 0 sein.
Maße der Zylinderschale [6.4, 6.5] und Maße der
Konusschale [8.4, 8.5, 8.6]
(Radius RA=R) ausfüllen. Überdruckbeanspruchung "q"
[6.6, 8.7] und axiale Beanspruchung "p"
[6.8] eingeben.
Die axiale Beanspruchung bei dem konusförmigen Teil wird auf einen mit der
Oberfläche parallelen Teil und die auf den Rand der Schale wirkende Radialkraft
aufgeteilt.
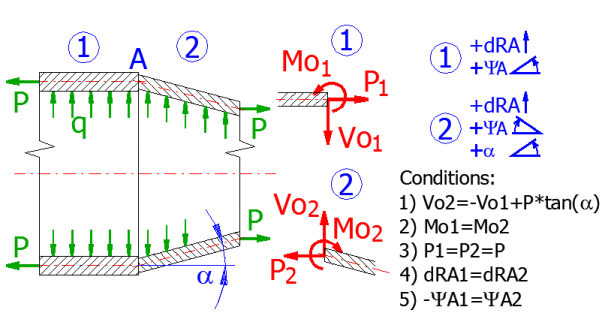
Entlastung der Schalen:
Die einzelnen Schalen werden entlastet und ihre Enden mit der Randkraft "Vo",
dem Moment "Mo" und der Axialkraft "P" beansprucht (bei der konischen Schale
wird die Randkraft Vo um die radiale Komponente erhöht, die durch die Verteilung
der mit der Konus-Oberfläche parallelen Kraft entsteht).
Zylinderschale:
Konische Schale:
Randbedingungen:
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
^