Das Programm ist für den Entwurf und die Kontrolle der Bewegungsschrauben bestimmt. Das Programm löst die nachstehenden Aufgaben:
1. Berechnung der kinematischen Parameter (Geschwindigkeit, Drehmoment, Drehzahl und Leistung ...)
2. Einfache Auswahl/Definition der Bewegungsschraube (metrisch, quadratisch, trapezförmig ...)
3. Prüfung der Schraube auf Zug/Druck, Verdrückung, Biegung, Knick und kritische Drehzahl.
4. Das Programm enthält Tabellen mit Materialien und Gewinden sowie Tabellen mit Reibungskoeffizienten.
5. Unterstützung der 2D CAD-Systeme.
In der Berechnung sind Daten, Verfahren, Algorithmen und Fachliteraturangaben und Angaben aus Normen AISC, ISO, DIN und BS verwendet.
Normenverzeichnis: ISO 68-1, 68-2, ISO 724, ISO 965, ISO 2904: 1977, DIN 513, CSN 01 4050, CSN 01 4052, ANSI/ASME B1.5-1977, ANSI/ASME B1.9-1973, ASME B1.1-2003, IS 4694-1968....
Die Literatur: Mechanical engineering design (Konstruování strojních součástí), Textbook of Machine Design, Machinery’s Handbook 26th Edition, Části a mechanismy strojů
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Bewegungsschrauben werden verwendet, um die Drehbewegung in eine geradlinige Bewegung umzuwandeln (ausnahmsweise auch in die umgekehrte Richtung). Verwendung bei Führungsschrauben von Drehbänken, Klemmen, Pressen, Hubvorrichtungen usw.
Bei Schrauben kommen mehrere Typen von Gewinden zum Einsatz, zum Beispiel:
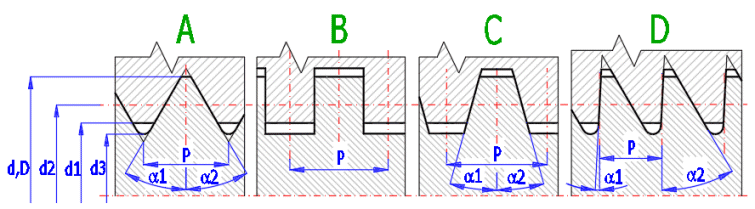
A. Metrisch / UNC, UNF, UNEF - kommt am häufigsten zum Einsatz. Es wird in zwei/drei maßtechnisch standardisierten Serien hergestellt. Sie sind mit dem Buchstaben M und dem großen Gewindedurchmesser gekennzeichnet – z. B.: M24 (bzw. Abmessung – UNC-x, wobei x die Anzahl der Gewinde pro Zoll bedeutet). Aufgrund des großen Scheitelwinkels wird es für Bewegungsschrauben nur begrenzt eingesetzt. Es eignet sich für Positionierungsmechanismen oder für gering belastete Mechanismen.
B. Flachgewinde - Es ist nicht standardisiert, hat keine festgelegte Bezeichnung und die Abmessungen seines Profils müssen detailliert bemessen werden. Höhere Anforderungen an Produktion, Präzision ... Verwendung für gering beanspruchte manuelle Mechanismen.
C. Trapezgewinde - Es hat ein Profil in Form eines gleichschenkligen Trapezes und wird für Vorschübe von Maschinenteilen, Supports, Wagenhebern usw. verwendet. Es wird mit den Buchstaben Tr, dem Außendurchmesser und der Steigung bezeichnet (Tr 22 x 8). Zollgewinde werden durch den Außendurchmesser (Nenndurchmesser), die Anzahl der Gewinde pro Zoll und das Profil bezeichnet (1.750-4-ACME-...). Das am häufigsten verwendete Gewinde für Bewegungsschrauben. Vorteil bei beidseitiger Verwendung der Druckkraft.
D. Sägegewinde - Die gleiche Verwendung, wie gleichschenkliges Gewinde. Nur sein Profil hat die Form eines ungleichschenkligen Trapezes. Es wird mit dem Buchstaben S, Außendurchmesser und der Steigung bezeichnet. Verwendung für stark (in einer Richtung) belastete Schrauben (Stanzen, Pressen, Wagenheber ...)
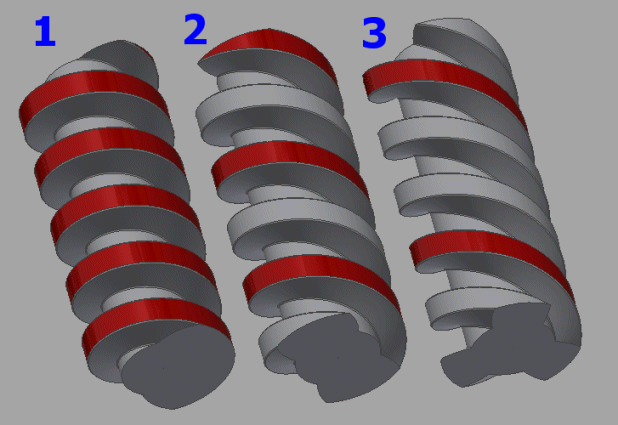
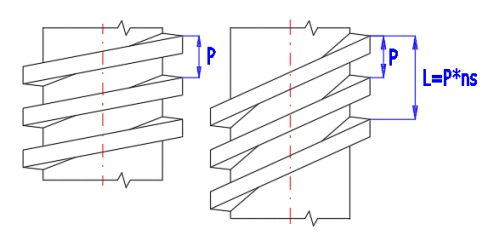
Herkömmliche Metrisch / UNC, UNF, UNEF Gewinde werden als eingängige Gewinde hergestellt. Die Bewegungsschrauben werden auch als mehrgängige Schrauben verwendet. Mehrgängige Gewinde haben eine höhere Effizienz, einen schnelleren Vorschub, im Gegenteil verlieren sie die Fähigkeit der Selbstsperrung. Siehe Abbildung für Ein-, Zwei- und Dreiganggewinde mit derselben P-Teilung.
Eingängige, quadratförmige Schraube, belastet mit Kraft Q.
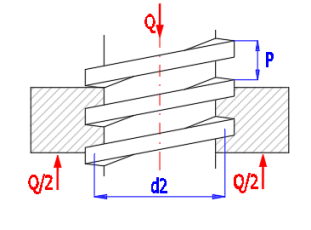
Verteilung der in einer Schraubverbindung wirkenden Kräfte bis zur Länge eines Gewindes:
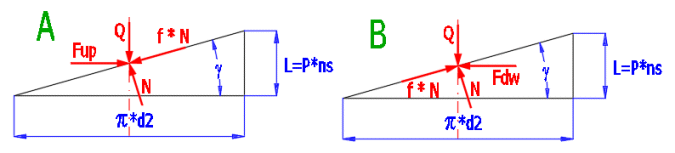
Einbeziehung der Wirkung des Gewindeflächenwinkels a1 (a2)
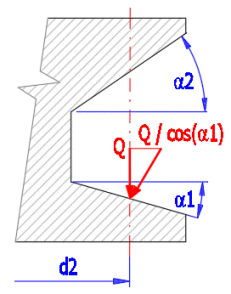
Beziehungen für die Drehmomentberechnung.
Für Heben (Abb. A):
Mkup [Nm] = Q * d2/2 * ((L * COS(a1) + p * f * d2) / (p * d2 * COS(a1) - f * L)) / 1000 + Mkj
Für Lösen (Abb. B):
Mkdw [Nm] = Q * d2/2 * ((p * f * d2 - L * COS(a1)) / (p * d2 * COS(a1) + f * L)) / 1000 + Mkj
wo:
Q.......Belastungskraft [N]
d2......Teilkreisdurchmesser der Schraube [mm]
a1,(a2).....Scheitelwinkel des Gewindeprofils [º]
f.........Reibungskoeffizient [~]
L....... Gewindesteigung [mm]
Mkj.....zusätzlicher Moment der Zapfenreibung [Nm]
Steigung des Gewindes L
Für Bewegungsschrauben kommen die mehrgängigen Gewinde häufig zum Einsatz. Die Steigung des Gewindes L ist dann ein Vielfaches des Teilkreises und der Anzahl der Gewindegänge.
L [mm] = P * ns
wo:
P.......Gewindeteilkreis [mm]
ns.....Anzahl der Gewindegänge [~]
Reibungskoeffizient f
Werte für geschmiertes
Gewinde.
0.06 - 0.09 ... Gehärteter Stahl /
Bronze
0.08 - 0.09 ... Stahl / Bronze
0.11 - 0.17 ... Stahl / Stahl
0.11 - 0.17 ... Stahl / Gusseisen
Oft wird ein mit einer Schraube (Mutter) verbundener Flansch verwendet, um die Achskraft (Wagenheber, Schraubstöcke ...) aufzunehmen, die ein zusätzliches Reibungsdrehmoment verursacht, das bei der Überprüfung der Festigkeit der Schraube berücksichtigt werden muss. Bei hohen Beanspruchungen wird die konstruktive Lösung mit Wälzlagern gewählt, bei denen das zusätzliche Drehmoment minimal ist und bei der Prüfung vernachlässigt werden kann.
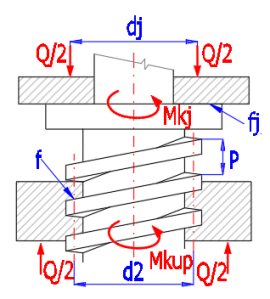
Mkj [Nm] = Q * fj * (dj / 1000) / 2)
wo:
Q......Belastungskraft [N]
dj......mittlerer Zapfendurchmesser [mm]
fj.......Reibungskoeffizient [~]
Reibungskoeffizient fj
Werte für die geschmierte
Reibung
0.06 ............ Gehärteter Stahl / Bronze
0.08 ............ Stahl / Bronze
0.09 ............ Gehärteter Stahl / Gusseisen
0.12
............ Stahl / Gusseisen
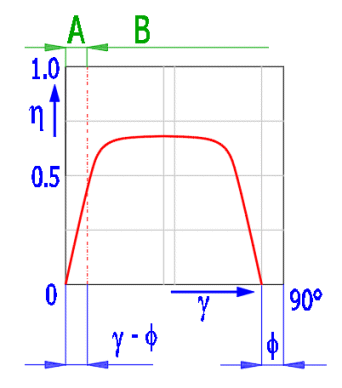
Der Wirkungsgrad wird berechnet als das Verhältnis der durch das Heben der Last geleisteten Arbeit und der Arbeit vom zugeführten Drehmoment.
h = Q * (L / 1000) / (2 * p * Mkup)
Der Wirkungsgrad steigt mit zunehmendem Steigungswinkel an g. Die theoretische Grafik ist weiter unten dargestellt und enthält nicht den Einfluss der Zapfenreibung, des Gewindenutwinkels und anderer Einwirkungen. Bereich A ist der selbstsperrende Bereich der Schraube. Reibungswinkel f = atan (Reibungskoeffizient).
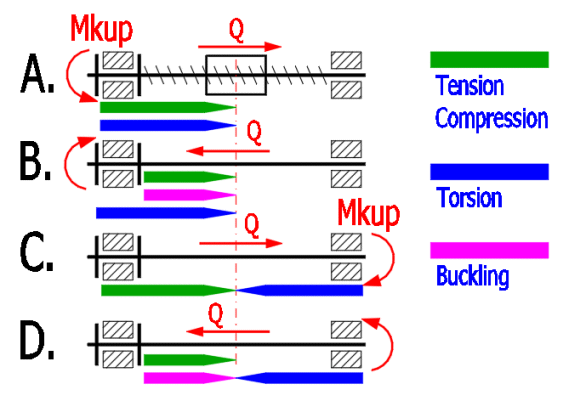
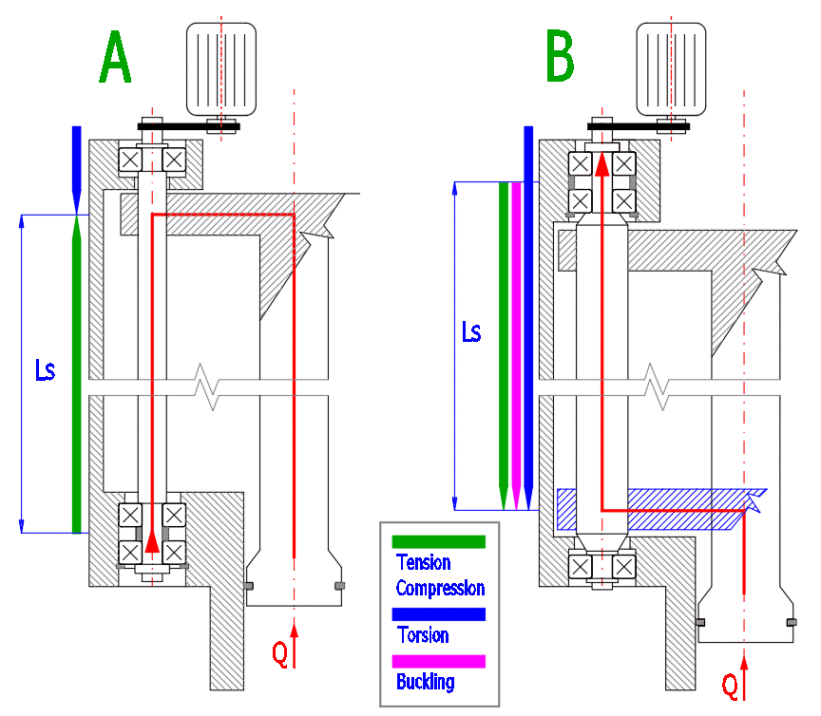
Mit der Wahl der konstruktiven Lösung kann man beispielsweise die Knickbeanspruchung der Schraube eliminieren, man kann die Zapfenreibung eliminieren, die kombinierte Beanspruchung beseitigen usw. Die Beispiele in der Abbildung zeigen, wie man durch die Wahl der Konstruktion die am wenigsten günstige Kombination der Beanspruchung – Variante B. (Druck + Torsion, Knicken) in eine wesentlich günstigere Variante C. (einfacher Zug, Torsion) ändern kann. Die Berechnung enthält alle üblich durchgeführten Kontrollen und die Art der Konstruktion bestimmt deren Bewertung.
t [MPa] = 16 * Mkup / (p * (d3 / 1000)3) / 1000000
wo:
Mkup.....Drehmoment für das Heben [Nm]
d3.........Durchmesser des Schraubenkerns [mm]
s [MPa] = 4 * Q / (p *(d3 / 1000)2) / 1000000
wo:
Q..........Belastungskraft [N]
d3.........Durchmesser des Schraubenkerns [mm]
sred [MPa] = (s2 + 3 *
t2)0.5
Sicherheitskoeffizienten SF = Rp(0.2) /
sred
Durch Axialkraft belastete Schrauben sind in drei Grundgruppen eingeteilt.
A. Kurze Schrauben
- eine Störung/Verformung tritt nach dem Erreichen der Quetschgrenze ein.
B. Schrauben mittlerer Länge
- werden im Bereich der unelastischen Knickung nach relativ komplizierten
Beziehungen und Gesetzmäßigkeiten verformt. Für die Berechnung der kritischen
Kraft gibt es eine Reihe von Theorien und Erfahrungsverfahren.
C. Lange Schrauben
- die Störung/Verformung tritt wesentlich früher ein, eher die Spannung den
zulässigen Wert der Spannung des Werkstoffes überschreitet. Die Störung tritt
als Knickung die
Schraube und dessen Verformung ein.
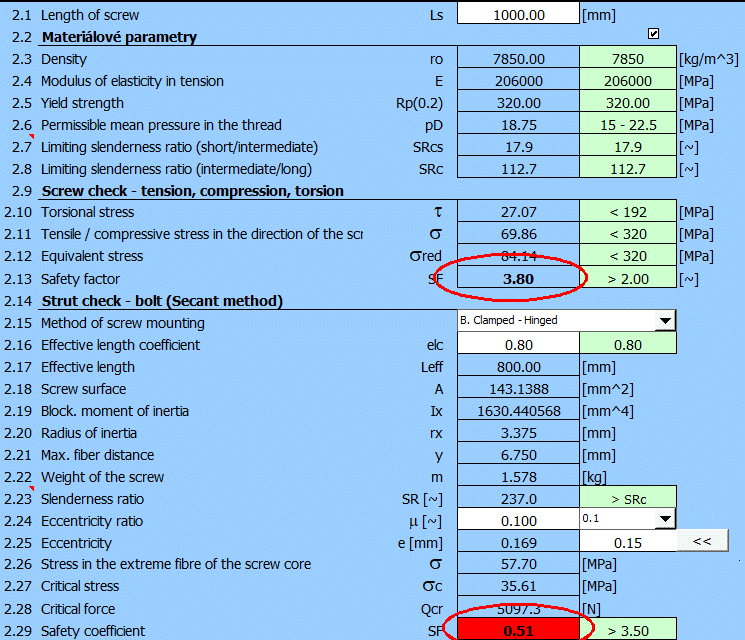
Zur Überprüfung der Knickbelastung werden verschiedene Verfahren angewendet (siehe Abbildung). In der Berechnung der Schraube wird die Secant-Methode für die Spannungsberechnung im Randfaden des Profils angewendet. Diese Methode ermöglicht es, auch Fälle zu lösen, bei denen die Kraft nicht genau in der Achse der Schraube wirkt (Unvollkommenheiten der Lagerung) oder wenn die Schraube nicht genau gerade ist (Herstellungsungenauigkeiten, Durchbiegung).
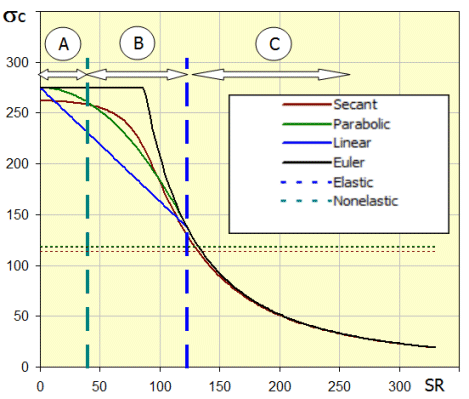
Im Graph (der kritischen, dem Schlankheitsverhältnis des Stabes SR abhängigen Spannung c )werden die Bereiche für den einfachen Druck (A), die nicht elastische Knickung (B) und die elastische Knickung (C) durch Buchstaben A,B und C gekennzeichnet.
Das Schlankheitsverhältnis der SR-Schraube ist das grundlegende geometrische Merkmal der geprüften Schraube, ausgedrückt durch die Formel:
SR [~] = Leff / (Ix / A)0.5
wo:
Reduzierte (effektive) Schraubelänge
Leff [mm] = Ls * elc
Ls......Schraubelänge [mm]
elc.....Koeffizienten für die reduzierte (effektive) Länge [~]
Ix......Quadratmoment des Profils [mm4]
A.......Profilfläche [mm2]
Secant - Formel für die
Berechnung der Spannung in der Randfaser des Profils:
s [MPa] = Q / A * (1 + (e * y / rx2)
* sec (Leff / (2 * r) * (Q / (E * A))0.5))
wo:
Q.......Kraft [N]
Leff .. Reduzierte (effektive) Schraubelänge [mm]
A.......Profilfläche [mm2]
E.......Zugelastizitätsmodul [MPa]
rx......Trägheitshalbmesser [mm]
y.......Entfernung der Randfaser [mm]
e.......Abweichung des Angriffspunktes der Kraft oder der Stabsachse [mm]
Der Klammerausdruck (e * y
/ rx2)
drückt den s. g. Exzentrizitätsgrad -
m
aus. Bei der
vorausgesetzten Kenntnis von
m
(eine Abschätzung) ist
die Secant-Formel ein sehr guter Ersatz der oben genannten Erfahrungsverfahren
und eine Grundlage einer ganzen Reihe von Entwurfvorgängen.
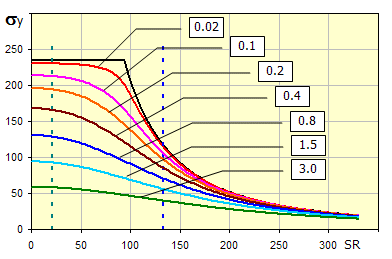
Im Graph der kritischen, dem Schlankheitsverhältnis des Stabes SR
abhängigen Spannung
sind für die verschiedenen Werte des Exzentrizitätsgrades
-
m entsprechende Kurven dargestellt.
Nach der Iteration der Formel durch Änderung von Q zum Erreichen von s = Rp(0.2) erhalten wir die kritische Kraft Qcr
Sicherheitskoeffizienten SF = Qcr / Q
In Abhängigkeit von SR werden die grundlegenden Sicherheitswerte empfohlen:
A. SR < SRcs..............Bereiche
für den einfachen Druck. Empfohlene Sicherheit SF>1.75)
B. SRcs < SR < SRc.....Bereiche für die nicht elastische Knickung. Empfohlene
Sicherheit
SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
C. SRc < SR................Bereiche für die elastische Knickung. Empfohlene
Sicherheit SF>3.5)
Aus Experimenten geht hervor, dass das erste Funktionsgewinde 38 % der Belastung überträgt, das zweite 25 %, das dritte 18% ... und das achte (in manchen Fällen sogar das fünfte) Gewinde nicht mehr beansprucht wird.
Die Gewindeprüfung auf Verdrückungen kann wie folgt durchgeführt werden. Druck p im Gewinde:
p [MPa] = 4 * Q / (p * (d2 - d12) * nz)
wo:
Q.......Kraft [N]
d ..... Außendurchmesser des Schraubengewindes [mm]
d1 ... Innendurchmesser des Muttergewindes [mm]
nz ... Anzahl der aktiven Gewinde in der Mutter.
Die Formel lautet::
ncr = 946 * K * (1 / ymax)^0.5
wo:
ymax ... Durchbiegung der Schraube [mm] vom Eigengewicht in Abhängigkeit von der Lagerung der Schraube
K ......... Koeffizient der Wellenlagerung
Bei einer großen Steigung des Gewindes L oder einer kleinen Reibung f kann sich die Schraube selbsttätig zu drehen beginnen. Es ist möglich, den Grenzwinkel für die Selbstsperrung des Gewindes zu berechnen, der jedoch keine anderen Einflüsse wie die Zapfenreibung des Stützflansches einschließt.
In diesem Fall ist der Wert des Drehmoments Mkdw (Drehmoment zum Starten, Loslassen) maßgebend. Wenn dieser Wert negativ ist, besteht eine hohe Wahrscheinlichkeit, dass sich die Schraube aufgrund der Belastungskraft Q spontan zu drehen beginnt.
Die Berechnung und Kontrolle der Bewegungsschraube setzen sich normalerweise aus den folgenden Schritten zusammen.
1. Schrauben- und Muttermaterial auswählen [1.2,1.3]
2. Schraubenbelastung und Vorschubgeschwindigkeit definieren [1.4,1.5]
3. Typ und Abmessung des Gewindes auswählen [1.8,1.9]
4. Festigkeitsüberprüfungen in [2.0] kontrollieren
5. Wenn die Prüfungen nicht genügen, ändern Sie die Abmessung der Schraube ggf. die Werkstoffe.
6. Die Arbeitsmappe mit der vorgeschlagenen Lösung unter einem neuen Namen speichern.
In diesem Abschnitt definieren Sie die Belastung, Kinematik und Kraftverhältnisse der Schraube.
In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
Wählen Sie das Material aus der Auswahlliste. Basierend auf den ausgewählten Materialien wird der Reibungskoeffizient in den Gewinden eingestellt [1.6]. Weiterhin werden der Wert der Dichte, des Elastizitätsmoduls und der Streckgrenze in den Kontrollberechnungen voreingestellt [2.0].
Geben Sie die Belastungskraft auf die Schraube / Mutter ein.
Geben Sie den gewünschten Vorschub für Schrauben / Muttern ein. Abhängig vom gewählten Typ der Schraube und von der gewählten Abmessung der Schraube wird die entsprechende Drehzahl berechnet. Wenn Sie die Drehzahl kennen, geben Sie sie in Zeile [1.28] ein und der Vorschub wird nachträglich berechnet.
Geben Sie den angenommenen Reibungskoeffizienten in Gewinden ein. Abhängig von den ausgewählten Materialien wird der entsprechende Wert für die geschmierte Verbindung voreingestellt. Die empfohlenen Werte lauten wie folgt:
Schraube / Mutter
0.11
- 0.17
... Stahl / Stahl
0.10
- 0.16
... Stahl / Bronze
0.10
- 0.15
... Stahl / Messing
0.11
- 0.17
... Stahl / Gusseisen
0.08
- 0.12
... Bronze / Stahl
0.04
- 0.06
... Bronze / Bronze
0.06
- 0.09
... Bronze / Gusseisen
Basierend auf der Belastungskraft und den ausgewählten Materialien wird der Teilkreisdurchmesser d2 geschätzt. Dies ist eine Anleitung zur Auswahl der geeigneten Schraubengröße.
Wählen Sie den Typ und die Abmessung des Gewindes in den Aufrolllisten aus.
Nach der Auswahl der Gewindegröße werden die Normparameter in die folgenden Zeilen eingetragen. Wenn Sie die Schaltfläche rechts deaktivieren, können Sie Ihre eigenen Gewindeabmessungen eingeben. Bei der Definition der Abmessungen können Sie sich nach der Abbildung rechts richten.

Für die Bewegungsschrauben wird häufig das mehrgängige Gewinde eingesetzt (schnellerer Hub, höhere Effektivität ...).
Die Steigung ist das Produkt aus der Anzahl der Gewindegänge und der Teilung. Wichtiges charakteristisches Maß der Schraube.
Der Winkel zwischen der Steigung des Gewindes und dem Umfang der Schraube am Teilkreis.
Außer dem trapezförmigen ungleichschenkligen Gewindes sind die Winkel symmetrisch. Bei einem asymmetrischen Winkel wird Winkel 1 zur Berechnung der kinematischen und Festigkeitsparameter verwendet (es sollte der kleinere Winkel sein, der auf der belasteten Seite verwendet wird).
Wenn die Axialkraft vom Reibungselement aufgenommen wird, können dessen Parameter eingegeben werden. In diesem Fall hat die Zapfenreibung einen erheblichen Einfluss auf den Wirkungsgrad, die Selbstsperrung, die Tragfähigkeit und weitere Parameter der Bewegungsschraube.
Geben Sie den Reibungskoeffizienten im Zapfen / Wälzlager ein. Die ungefähren Werte für die geschmierte Reibung sind weiter unten angegeben.
0.05-0.10 ... Gehärterer Stahl / Gehärterer Stahl
0.05-0.15 ... Gehärterer Stahl / Roheisen
0.09-0.15 ... Gehärterer Stahl / Phosphore Bronze
0.07-0.10 ... Roheisen / Roheisen
0.07-0.10 ... Roheisen / Phosphore Bronze
0.20-0.25 ... Roheisen / Holz (Eiche)
0.07-0.10 ... Phosphore Bronze / Phosphore Bronze
0.0015 … Rillenkugellager, einreihig
0.0015 … Rillenkugellager, zweireihig
0.0020 … Schrägkugellager, einreihig
0.0024 … Schrägkugellager, zweireihig
0.0010 … Pendelkugellager, mit zylindrischer Bohrung
0.0011 … Zylinderrollenlager, einreihig
0.0025 … Nadellager mit Innenring
0.0018 … Kegelrollenlager, einreihig
0.0018 … Pendelrollenlager, mit zylindrischer Bohrung
0.0013 … Axial-Rillenkugellager
0.0050 … Axial-Zylinderrollenlager
0.0050 … Axial-Nadellager
0.0018 … Axial-Pendelrollenlager
Geben Sie den mittleren Durchmesser des Zapfens oder den Innendurchmesser des Lagers ein.
Zusätzliches Moment, das die Bewegungsschraube und die gesamte Kinematik der Bewegung belastet.
Das Drehmoment, das zum Anheben der Last ggf für die Ableitung der erforderlichen Axialkraft abgeleitet werden muss.
Das Drehmoment, das abgeleitet werden muss, um die Last abzusenken bzw. die erforderliche Kraft zu lösen.
Ein wichtiger Parameter für die Beurteilung des korrekten Entwurfs einer Bewegungsschraube.
Die für das Heben einer Last oder die Ableitung der erforderlichen Kraft benötigte Antriebsleistung.
Basierend auf der eingegebenen Vorschubgeschwindigkeit und Schraubengeometrie wird die erforderliche Drehzahl berechnet. Es ist jedoch oft notwendig, das andere Problem zu lösen, wenn wir die Drehzahl der Schraube (Mutter) kennen und den Vorschub berechnen müssen. Geben Sie in diesem Fall die Drehzahl ein und berechnen Sie mit der Taste "<<" den entsprechenden Vorschub.
Geschwindigkeit am Außendurchmesser der Schraube. Sie kann ein Leitfaden für die Entwurfsbewertung sein.
Wenn Sie den Wert des Vorschubs der Mutter (Schraube) in Abhängigkeit von der Drehzahl (Schraubendrehung) bestimmen müssen, wählen Sie den entsprechenden Wert in Zeile [1.32,1.33] aus und geben Sie ihn ein.
Mit der Wahl der konstruktiven Lösung kann man beispielsweise die Knickbeanspruchung der Schraube eliminieren, man kann die Zapfenreibung eliminieren, die kombinierte Beanspruchung beseitigen usw. Die Beispiele in der Abbildung zeigen, wie man durch die Wahl der Konstruktion die am wenigsten günstige Kombination der Beanspruchung – Variante B. (Druck + Torsion, Knicken) in eine wesentlich günstigere Variante C. (einfacher Zug, Torsion) ändern kann. Die Berechnung enthält alle üblich durchgeführten Kontrollen und die Art der Konstruktion bestimmt deren Bewertung.

Geben Sie die Länge der Schraube gemäß der Konstruktionslösung ein.
Die Materialparameter werden aufgrund der Auswahl des Materials der Schraube und Mutter voreingestellt [1.2,1.3]. Die konkreten Materialwerte können jedoch geringfügig variieren. Nachdem Sie die Schaltfläche rechts deaktiviert haben, können Sie eigene Werte eingeben.
Sein Wert hängt von der Kombination der Werkstoffe, der Oberflächenbehandlung, der Schmiermethode usw. ab. Der empfohlene Wert beinhaltet die Auswirkung von Material und Geschwindigkeit für die geschmierte Verbindung.
Die folgenden Werte können verwendet werden, um die geschmierte Verbindung abzuschätzen:
Schraube / Mutter
Gehärteter Stahl / Bronze ...... 10 - 15 MPa (1.45 - 2.20 kpsi)
Stahl / Bronze ...................... 8 - 10 MPa (1.15 - 1.45 kpsi)
Stahl / Stahl ......................... 7 - 12 MPa (1.00 - 1.75 kpsi)
Stahl / Grauguss ................... 4 - 6 MPa (0.58 - 0.75 kpsi)
Bei höheren Geschwindigkeiten müssen die Werte reduziert werden. Für die Kombination von Stahl / Bronze ist beispielsweise der zulässige Druck wie folgt:
Geschwindigkeit
0.05 m/s (2.0 in/s) ................ 11-17 MPa (1.60 - 2.50 kpsi)
0.1 - 0.2 m/s (4 - 8 in/s) ......... 5-10 MPa (0.75 - 1.45 kpsi)
0.25 m/s (10 in/s) .................... 1-2 MPa (0.15 - 0.30 kpsi)
Die Grenzschlankheit SRc ist ein wichtiger Parameter eines konkreten Werkstoffes, der den Bereich der elastischen und der nicht elastischen Knickung unterscheidet und dadurch auch die Verwendung der entsprechenden Beziehungen. Es ist also empfehlenswert, diesen Parameter für einen konkreten Werkstoff zu überprüfen. Der empfohlene Wert ist also gemäß der allgemeinen Beziehung festgelegt:
SRcs = 0.5 * (E / (Rp02 * 0.5))0.5
SRc = (E *
p2
/ (Rp02 * 0.5))0.5
Je nach Bauart müssen folgende Werte überprüft werden.
Torsionsspannung im Schraubenkern. Sie sollte geringer sein als die zulässige Spannung in der grün markierten Zelle.
Zug- / Druckspannung im Schraubenkern.
Bei gleichzeitiger Einwirkung von Zug / Druck und Torsion ist es notwendig, die kombinierte Beanspruchung zu lösen. Die Vergleichsspannung sollte geringer sein als die zulässige Zugspannung.
Bezieht sich auf Vergleichsspannung.
Wenn die Schraube mit Druck belastet ist, muss die Knickprüfung für lange Schrauben vorgenommen werden. Die Notwendigkeit der Prüfung wird durch den Wert des Schlankheitsverhältnisses bestimmt [2.23]
In der Auswahlliste ist die Art der Schraubbefestigung nach der Abbildung zu wählen. Die Auswahl des Typs der Schraubbefestigung führt zur Auswahl des Koeffizienten für die reduzierte (effektive) Länge, mit dem die tatsächliche Schraubenlänge zu multiplizieren ist, um die s. g. reduzierte (effektive), in den Berechnungen verwendete Schraubenlänge, zu erreichen. In der Zeile [2.15] ist der praktische Wert, der empfohlen wird, in der Berechnung zu verwenden.
Lagerungsfälle ............ Koeffizient (theoretisch) / Koeffizient (praktisch)
A.
Einspannung - Einspannung
.................
0.50
/
0.65
B.
Einspannung - Stütze
...........................
0.70
/
0.80
C.
Einspannung - Senkrechte Führung
.......
1.00
/
1.20
D.
Stütze – Stütze
...................................
1.00
/
1.00
E.
Einspannung - Freies Trägerende
..........
2.00 2.10
F.
Einspannung - Senkrechte Führung
........
2.00 2.00
Abhängig vom Lagertyp
Gleitlager (d -
Durchmesser, l - Länge)
l / d <2 .............. Gelenk (Stütze)
2 <
l / d <3 ........
Begrenzte
Drehung
l / d> 3 .............. Einspannung
Wälzlager
Einreihiges Rillenkugellager, Pendelkugellager
..................... Gelenk
(Stütze)
Zylinderrollenlager, Rillenkugellager, zweireihig ................... Begrenzte
Drehung
Paar Kegelrollenlager, Radial + Axiallager ...........................
Einspannung
Der Wert ist in den Berechnungen verwendet. Es ist die Ist-Länge [2.1] mit dem Koeffizienten der reduzierten (effektiven) Länge [2.16] multipliziert.
Das ist die Entfernung der Randfaser von der Profilachse, die den Schwerpunkt durchgeht. Dieser Wert ist notwendig für die Berechnung mittels der „Secant“-Methode.
Der Schlankheitsgrad eines konkreten Trägers bestimmt, in welchem Bereich der Knickung sich der Träger befindet (der einfache Druck, die nicht elastische Knickung, die elastische Knickung) und dadurch wird auch die für die Bestimmung des Sicherheitskoeffizienten nötige Kontrollmethode festgesetzt.
A. SR < SRcs..............Bereiche
für den einfachen Druck. Empfohlene Sicherheit SF>1.75)
B. SRcs < SR < SRc.....Bereiche für die nicht elastische Knickung. Empfohlene
Sicherheit
SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
C. SRc < SR................Bereiche für die elastische Knickung. Empfohlene
Sicherheit SF>3.5)
Mit diesem Parameter kann ein Maßstab für die Ungenauigkeit der Konstruktion und der Belastung für einen Entwurf der Schraube von Ihnen festgesetzt werden. Im Parameter sind einbezogen:
die Abweichung der Geradlinigkeit der
Schraube
die anfängliche Durchbiegung der Schraube
den Eingriffspunkt der Kräfte außerhalb der Schraubenachse
Empfohlene Werte:
0.25 ... Stahlkonstruktionen
0.15 ... üblicher Maschinenbau
0.05 ... genaue starre Aufnahmen
Die Exzentrizität e wird anhand des Exzentrizitätsgrades berechnet [2.24]. Wenn Sie die Werte für Ausscherung, Ungenauigkeit usw. kennen, geben Sie den Wert rechts ein und nach Drücken der Taste "<<" wird der Grad der Exzentrizität berechnet.
Er drückt das Verhältnis zwischen kritischer und wirkender Kraft aus. Je nach Schlankheitsverhältnis wird der geeignete Sicherheitskoeffizient (grüne Zelle) empfohlen [2.23]
Der Wert der maximalen Durchbiegung der Schraube, die durch ihr eigenes Gewicht belastet wird, hängt von der Position der Schraube ab.
Die Anzahl der aktiven Gewinde wird aus der ausgewählten Mutterhöhe berechnet. Basierend auf der Kraft und den Abmessungen der Schraube und der Anzahl der Gewinde wird dann der Druck in den Gewinden berechnet.
Wählen Sie die Höhe der Mutter. In der grünen Zelle wird der empfohlene Wert angezeigt, der von der Erkenntnis ausgeht, dass max. 8 Gewinde an der Kraftübertragung teilnehmen.
Anzahl der Gewinde in der Mutter abhängig von der Teilung und Höhe der Mutter. Nach Eingabe der erforderlichen Anzahl von Gewinden und Drücken der Taste "<<" wird die Höhe der Mutter berechnet.
Experimente zeigen, dass das erste Funktionsgewinde 38 % der Belastung überträgt, das zweite 25 %, das dritte 18 % ... und das achte (in einigen Fällen sogar der fünfte) Gewinde nicht mehr beansprucht wird. Hier stellen Sie die maximale Anzahl aktiver Gewinde ein, die für die Berechnung angewendet werden.
Der Wert sollte unter dem zulässigen Druckwert liegen [2.6].
Belastung der Schraube Q = 10000 [N]
Vorschubgeschwindigkeit v = 50 [mm/s]
Material der Schraube =gehärteter Stahl
Material der Mutter = Bronze
Reibungskoeffizient in den Gewinden f = 0.08
Anzahl der Gewindegänge ns = 1
Hublänge Ls = 1000 [mm]
Angewendet wurde Trapezgewinde (30°,ISO2904:1997), Selbstsperrung wird nicht gefordert.

Der empfohlene Durchmesser d2prop und die entsprechende Schraube werden ausgewählt. Und selbst wenn die Schraube die Prüfung auf Zug, Druck und Verdrückung erfüllt, erfüllt sie nicht die Knickprüfung.
Daher muss ein größerer Schraubendurchmesser schrittweise gewählt werden.

Um die entsprechende Knicksicherheit zu erreichen.

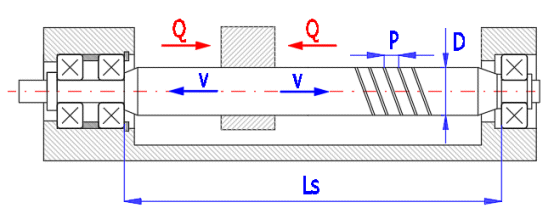
Beispiel für die Berechnung der Bewegungsschraube in einer Spritzgußvorrichtung (siehe schematisches Bild).
A. Die Bewegungsschraube ist mit Torsion oder Zug beansprucht.
B. Die Bewegungsschraube wird mit der Kombination von Torsion und Druck und Knick beansprucht.
Gesamtbelastung Q = 100000 [N]
Belastung der Schraube Q = 50000 [N]
Vorschubgeschwindigkeit v = 20 [mm/s]
Material der Schraube =gehärteter Stahl
Material der Mutter = Bronze
Reibungskoeffizient in den Gewinden f = 0.08
Anzahl der Gewindegänge ns = 1
Hublänge Ls = 3000 [mm]
Angewendet wurde Trapezgewinde (30°,ISO2904:1997), Selbstsperrung wird nicht gefordert.
Aufgrund der Empfehlung (d2prop [1.7]) wird die Schraube Tr 36 x 10ausgewählt. Alle Festigkeitsprüfungen sind zufriedenstellend, mit Ausnahme der Knickprüfung, weil die Knickbelastung nicht vorkommt (braucht nicht betrachtet zu werden).
Nach der schrittweisen Auswahl einer stärkeren Schraube (es ist erforderlich, die Knickbedingung zu erfüllen) wird eine Schraube Tr 65 x 4 ausgewählt, der auch die Knickprüfung erfüllt.
Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
Nachdem Sie die Schaltfläche rechts deaktiviert haben, können Sie die Anzahl der Gewinde eingeben, die in der Zeichnung der Schraube / Mutter dargestellt werden sollen. Vorausgefüllte Werte gehen von der Berechnung aus.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
Závity ISO pro všeobecné
použití - Základní profil - Část 1: Metrické závity
ISO general purpose screw
threads - Basic profile - Part 1: Metric screw threads
Filetages ISO pour usages généraux - Profil de base - Partie 1: Filetages
métriques
ISO-Gewinde allgemeiner Anwendung - Grundprofil - Teil 1: Metrishes Gewinde
Závity ISO pro všeobecné použití - Základní profil - Část 2: Palcové závity
ISO general purpose screw
threads - Basic profile - Part 2: Inch screw threads
Filetages ISO pour usages généraux - Profil de base - Partie 2: Filetages en
inches
ISO Gewinde allgemeiner Anwendung - Grundprofil - Teil 2: Inch-Gewinde
Metrické závity ISO pro všeobecné použití
ISO general purpose metric screw threads — General plan
Filetages metriques ISO pour usages generaux — Vue densemble
Metnsches ISO - Gewinde allgemeiner Anwendung — Ubersicht
Metrické závity ISO pro všeobecné použití - Základní rozměry
ISO general-purpose metric
screw threads - Basic dimensions
Filetages métriques ISO pour usages généraux - Dimensions de base
Metrisches ISO - Gewinde allgemeiner Anwendung - Grundmaße
Metrický lichoběžníkový ISO závit - Základní rozměry
ISO metric trapezoidal screw threads - Basic dimension
Filetagues metriques trapezoidaux ISO - Dimensions de base
Buttress Coarse Thread DIN 513
Unified Inch Screw Threads
ACME Screw Threads
Buttress Inch Screw Threads
7 / 45 Form With 0.6 Pitch Basic Height of Thread Engagement
Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas
R.S.KHURMI AND J.K.GUPTA
26th Edition
ČVUT Praha
Company catalogues: KSK, NSK, THOMSON...
^