Program je určen pro návrh a kontrolu pohybového šroubu. Program řeší následující úlohy:
Výpočet kinematických parametrů (rychlost, krouticí moment, otáčky a výkon...)
Jednoduchý výběr/definice pohybového šroubu (metrický, čtvercový, lichoběžníkový...)
Kontrola šroubu na tah/tlak, otlačení, ohyb, vzpěr a kritické otáčky.
Program obsahuje tabulky materiálů, závitů a koeficientů tření.
Podpora 2D CAD systémů.
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné literatury a norem AGMA, ISO, DIN a BS.
Seznam norem: ISO 68-1,
68-2,
ISO 261, ISO 724, ISO 965, ISO 2904: 1977, DIN 513, CSN 01 4050, CSN 01 4052, ANSI/ASME B1.5-1977, ANSI/ASME B1.9-1973, ASME B1.1-2003, IS 4694-1968....
Literatura: Mechanical engineering design (Konstruování strojních součástí), Textbook of Machine Design, Machinery’s Handbook 26th Edition, Části a mechanismy strojů
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
Pohybové šrouby slouží k transformaci rotačního pohybu na přímočarý (výjimečně i opačně). Využití u vodicích šroubů soustruhů, svěráků, lisů, zvedáků atd.
U šroubů se používá několik typů závitů, například:
A. Metrický / UNC, UNF, UNEF - je ze všech nejběžnější. Vyrábí se ve dvou/třech rozměrově normalizovaných řadách. Označují se písmenem M a velkým průměrem závitu – např.: M24 (resp. Rozměr - UNC-x, kde x počet závitů na palec). Pro pohybové šrouby se používá omezeně vzhledem k velkému vrcholovém úhlu. Použití je vhodné pro polohovací či málo zatížené mechanismy.
B. Čtvercový závit - Není normalizován, nemá žádné zavedené označení a rozměry jeho profilu musí být detailně okótovány. Náročnější na výrobu, přesnost....Použití pro málo namáhané, ruční machanismy.
C. Lichoběžníkový závit - Má profil ve tvaru rovnoramenného lichoběžníku a používá se pro posuvy strojních součástí, suportů, zvedáků apod. Označuje se písmeny Tr, vnějším průměrem a stoupáním (Tr 22 x 8). Palcové závity se označují vnějším (nominálním) průměrem, počtem závitů na palec a profilem (1.750-4-ACME-...). Nejpoužívanější závit pro silové pohybové šrouby. Výhoda při obousměrném použití tlakové síly.
D. Lichoběžníkový nerovnoramenný - Má totéž použití, jako závit rovnoramenný. Pouze jeho profil má tvar nerovnoramenného lichoběžníku. Označuje se písmenem S, vnějším průměrem a stoupáním. Použití pro silně (v jednom směru) zatížené šrouby (protlačování, lisy, zvedáky...)
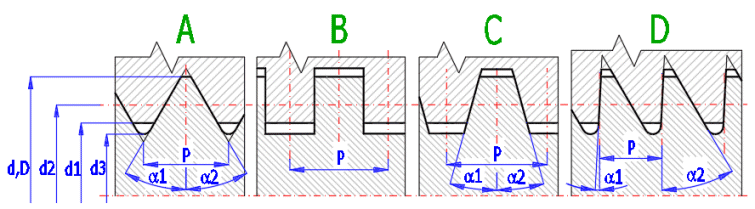
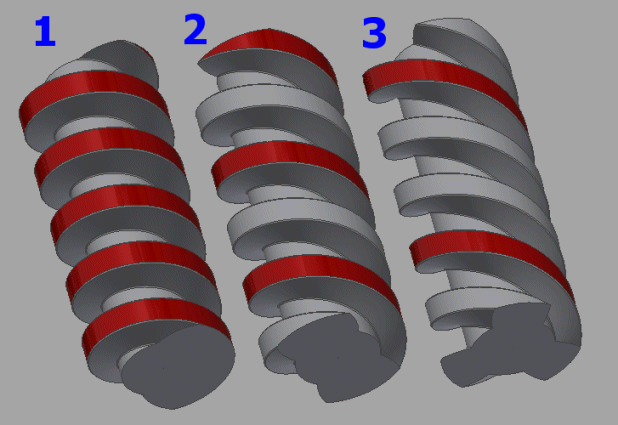
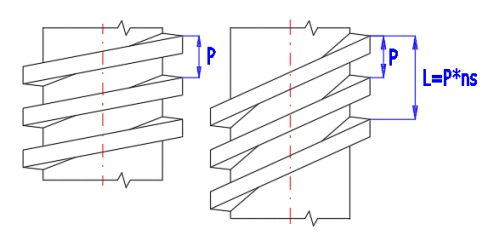
Běžné Metrické / UNC, UNF, UNEF závity se vyrábí jako jednochodé. Pohybové šrouby se používají i jako vícechodé. Vícechodé závity mají větší účinnost, rychlejší posun, naopak ztrácejí schopnost samosvornosti. Viz obrázek jednochodého, dvou a tříchodého závitu se stejnou roztečí P.
Jednochodý, čtvercový šroub zatížený silou Q.
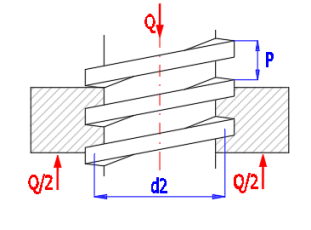
Rozložení sil, které působí ve šroubovém spojení do délky jednoho závitu:
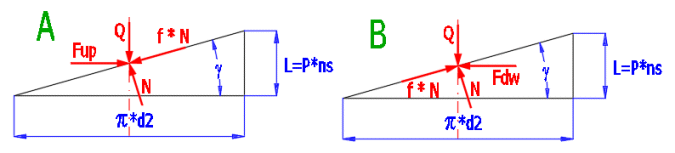
Zahrnutí vlivu úhlu plochy závitu a1 (a2)
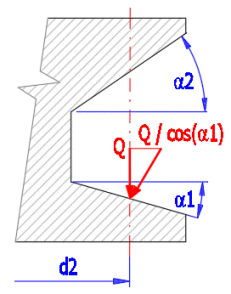
Vztahy pro výpočet krouticího momentu.
Pro zdvižení (obr. A):
Mkup [Nm] = Q * d2/2 * ((L * COS(a1) + p
* f * d2) / (p * d2 * COS(a1) - f * L)) / 1000 + Mkj
Pro uvolnění (obr. B):
Mkdw [Nm] = Q * d2/2 * ((p * f
* d2 - L * COS(a1)) / (p
* d2 * COS(a1) + f * L)) / 1000 + Mkj
Q.......zatěžovací síla[N]
d2......roztečný průměr šroubu[mm]
a1,(a2).....vrcholový úhel profilu závitu[º]
f.........součinitel tření[~]
L........stoupání závitu[mm]
Mkj.....dodatečný moment čepového tření[Nm]
Stoupání závitu L
Pro pohybové šrouby se často používá vícechodých závitů. Stoupání závitu L je pak násobkem rozteče a počtu chodů závitu.
L [mm] = P * ns
P.......rozteč závitu[mm]
ns.....počet chodů závitu[~]
Součinitel tření f
Používané hodnoty pro mazaný závit.
0.06 - 0.09.....Ocel kalená / Bronz
0.08 - 0.09.....Ocel / Bronz
0.11 - 0.17.....Ocel / Ocel
0.11 - 0.17.....Ocel / Litina
Často je pro zachycení osové síly (zvedáky, svěráky...) používána příruba spojená se šroubem (maticí), která způsobí dodatečný třecí krouticí moment, který je nutné vzít v úvahu při pevnostní kontrole šroubu. V případě velkých namáhání je voleno konstrukční řešení spíše pomocí valivých ložisek, kde je dodatečný moment minimální a je možné ho při kontrole zanedbat.
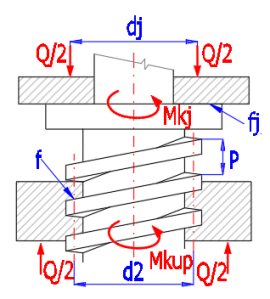
Mkj [Nm] = Q * fj * (dj / 1000) / 2)
Q......zatěžovací síla[N]
dj......střední průměr čepu[mm]
fj.......součinitel tření[~]
Součinitel tření fj
Hodnoty používané pro mazané tření
0.06..............Ocel kalená / Bronz
0.08..............Ocel / Bronz
0.09..............Ocel kalená / Litina
0.12..............Ocel / Litina
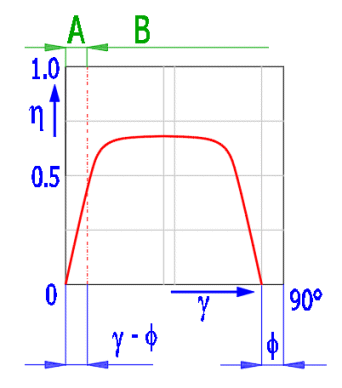
Je počítána jako poměr práce vykonané zvednutím břemene a práce od přivedeného krouticího momentu.
h = Q * (L / 1000) / (2 * p * Mkup)
Účinnost roste se zvyšujícím se úhlem stoupání g. Teoretický graf je níže a nezahrnuje vliv čepového tření, úhel drážek závitu a dalších vlivů. Oblast A je oblast samosvornosti šroubu. Třecí úhel f = atan (součinitel tření).
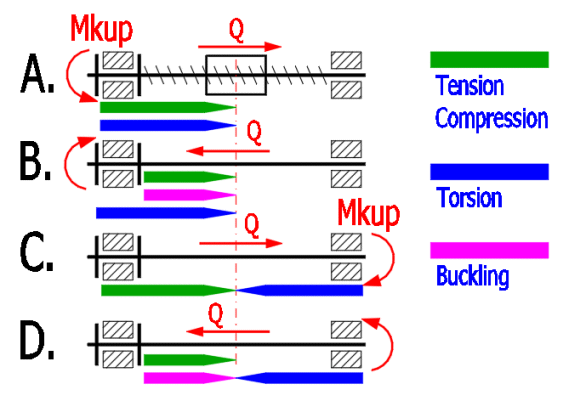
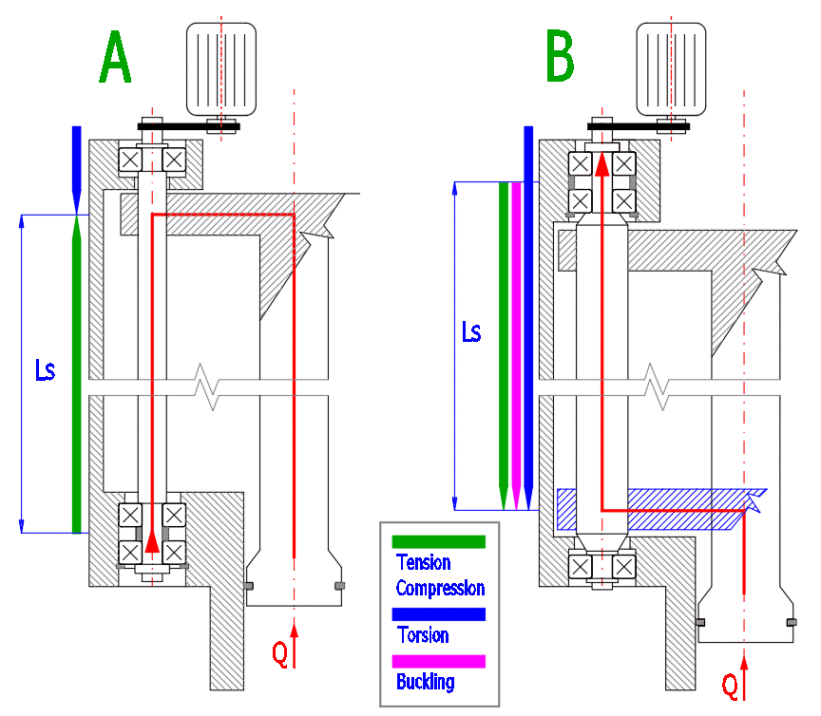
Volbou konstrukčního řešení je možné například eliminovat namáhání šroubu na vzpěr, je možné eliminovat čepové tření, je možné odstranit kombinované namáhání atd. Příklady na obrázku ukazují, jak je možné volbou konstrukce změnit nejméně příznivou kombinaci namáhání varianta B. (tlak+krut, vzpěr) na podstatně příznivější variantu C. (Prostý tah, krut). Výpočet obsahuje všechny běžně prováděné kontroly a typ konstrukce určuje jejich vyhodnocení.
t [MPa] = 16 * Mkup / (p * (d3 / 1000)3) / 1000000
Mkup.....krouticí moment pro zdvižení [Nm]
d3.........průměr jádra šroubu [mm]
s [MPa] = 4 * Q / (p *(d3 / 1000)2) / 1000000
Q..........zatěžovací síla [N]
d3.........průměr jádra šroubu [mm]
sred [MPa] = (s2 + 3 *
t2)0.5
Koeficient bezpečnosti SF = Rp(0.2) /
sred
Šrouby zatížené osovou silou je možné rozdělit do tří základních skupin.
A. Krátké šrouby - k poruše/deformaci dochází při dosažení meze kluzu v tahu/tlaku.
B. Středně dlouhé šrouby - deformují se v oblasti nepružného vzpěru podle poměrně složitých vztahů a zákonitostí. Pro výpočet kritické síly/napětí existuje řada teorií a empirických postupů.
C. Dlouhé šrouby - k poruše/deformaci dochází podstatně dříve než napětí přesáhne dovolené napětí materiálu. K poruše dochází vybočením šroubu a jeho zborcením.
Pro kontrolu vzpěru se používá řada postupů (viz obrázek). Ve výpočtu šroubu je použita Secant metoda pro výpočet napětí v krajním vlákně profilu. Tato metoda umožňuje řešit i případy, kdy síla nepůsobí přesně v ose šroubu (nedokonalosti uložení), nebo není-li šroub přesně přímý (výrobní nepřesnosti, průhyb).
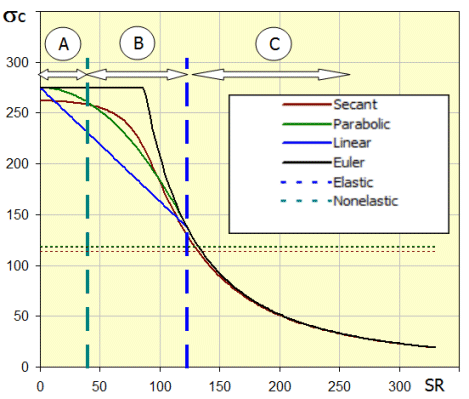
V grafu (kritické napětí sc závislé na štíhlostním poměru prutu SR) jsou písmeny A,B a C vyznačeny oblasti prostého tlaku (A), nepružného vzpěru (B) a pružného vzpěru (C).
Štíhlostní poměr šroubu SR je základní geometrická charakteristika kontrolovaného šroubu vyjádřená vzorcem:
SR [~] = Leff / (Ix / A)0.5
Redukovaná (efektivní) délka šroubu Leff [mm] = Ls * elc
Ls......délk šroubu [mm]
elc.....koeficient efektivní délky [~]
Ix......kvadratický moment setrvačnosti [mm4]
A.......plocha profilu [mm2]
Secant vzorec pro výpočet napětí v krajním vlákně profilu:
s [MPa] = Q / A * (1 + (e * y / rx2)
* sec (Leff / (2 * r) * (Q / (E * A))0.5))
Q.......síla [N]
Leff .. redukovaná
(efektivní) délka šroubu [mm]
A.......plocha profilu [mm2]
E.......modul pružnosti v tahu [MPa]
rx......poloměr setrvačnosti [mm]
y.......vzdálenost krajního vlákna [mm]
e.......odchylka působiště síly či osy prutu [mm]
Vztah v závorce (e * y / rx2) vyjadřuje takzvaný stupeň excentricity -
m. Při předpokládané znalosti
m (odhad) je Secant vzorec velmi dobrou náhradou používaných empirických postupů a je základem pro celou řadu návrhových postupů.
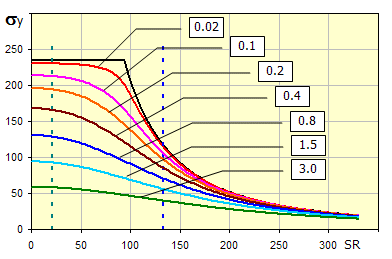
V grafu kritického napětí
sc závislého na štíhlostním poměru prutu SR jsou zobrazeny křivky pro různé hodnoty stupně excentricity.
Po iteraci vzorce změnou Q pro dosažení s = Rp(0.2) získáme kritickou sílu Qcr
Koeficient bezpečnosti SF = Qcr / Q
V závislosti na SR jsou pak doporučené základní hodnoty bezpečnosti:
A. SR < SRcs..............Oblast prostého tahu/tlaku. Doporučená bezpečnost SF>1.75)
B. SRcs < SR < SRc.....Oblast nepružného vzpěru. Doporučená bezpečnost SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
C. SRc < SR................Oblast pružného vzpěru. Doporučená bezpečnost SF>3.5)
Z experimentů vychází, že první funkční závit přenáší 38% zatížení, druhý 25%, třetí 18%......a osmý (v některých případech i pátý) závit je již nezatížený
Kontrola závitu na otlačení může být provedena následovně. Tlak p v závitu:
p [MPa] = 4 * Q / (p * (d2 - d12) * nz)
Q.......síla [N]
d.......vnější průměr závitu šroubu [mm]
d1.....vnitřní průměr závitu matice [mm]
nz......počet činných závitů v matici
Je použit vztah:
ncr = 946 * K * (1 / ymax)0.5
ymax.....průhyb šroubu v [mm] od vlastní hmotnosti v závislosti na uložení šroubu
K...........koeficient uložení hřídele
V případě velkého stoupání závitu L, popřípadě malého tření f, může dojí k samovolnému roztočení šroubu. Je možné spočítat mezní úhel pro samosvěrnost závitu, který však nezahrnuje další vlivy, jako je například čepové tření opěrné příruby.
V tomto případě je určující hodnota momentu Mkdw (moment pro spuštění, uvolnění). Pokud je jeho hodnota záporná, s vysokou pravděpodobností může dojít k samovolnému roztočení šroubu vlivem zatěžující síly Q.
Výpočet a kontrola pohybového šroubu se zpravidla skládá z následujících kroků.
V tomto odstavci definujete zatížení, kinematiku a silové poměry šroubu.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě změněny všechny hodnoty.
Ve výběrovém seznamu vyberte materiál. Na základě vybraných materiálů bude nastaven součinitel tření v závitech [1.6]. Dále pak bude přednastavena hodnota hustoty, modulu pružnosti a meze kluzu v kontrolních výpočtech [2.0]
Zadejte zatěžující sílu na šroub / matici.
Zadejte požadovanou rychlost posunu šroubu / matice. V závislosti na zvoleném typu a rozměru šroubu budou dopočtené odpovídající otáčky. Pokud znáte otáčky, zadejte je na řádku [1.28] a rychlost posuvu bude zpětně dopočítána.
Zadejte předpokládaný součinitel tření v závitech. Podle vybraných materiálů je předvolena odpovídající hodnota pro mazané spojení. Doporučené hodnoty jsou následující:
Šroub / Matice
0.11 - 0.17.....Ocel / Ocel
0.10 - 0.16.....Ocel / Bronz
0.10 - 0.15.....Ocel / Mosaz
0.11 - 0.17.....Ocel / Litina
0.08 - 0.12.....Bronz /
Ocel
0.04 - 0.06.....Bronz / Bronz
0.06 - 0.09.....Bronz / Litina
Na základě zatěžující síly a zvolených materiálů je odhadnutý roztečný průměr d2. Je to vodítko pro výběr odpovídajícího rozměru šroubu.
V rozbalovacích seznamech vyberte typ a rozměr závitu.
Po volbě rozměru závitu jsou vyplněny jeho normalizované parametry v následujících řádcích. Pokud odškrtnete tlačítko napravo, je možné vyplnit vlastní rozměry závitu. Při definici rozměrů se můžete řídit obrázkem vpravo.

Pro pohybové šrouby se používá často vícechodý závit (rychlejší zdvih, větší účinnost...).
Stoupání je součin počtu chodů závitu a rozteče. Důležitý charakteristický rozměr šroubu.
Úhel mezi stoupáním závitu a obvodem šroubu na roztečné kružnici.
Kromě lichoběžníkového nerovnoramenného závitu jsou úhly symetrické. V případě nesymetrického úhlu je pro výpočet kinematických a pevnostních parametrů použit úhel a1 (měl by to být menší úhel použitý na zatížené straně).
V případě, že je zachycení axiální síly realizováno třecím elementem je možné zadat jeho parametry. Čepové tření má v tomto případě značný vliv na účinnost, samosvornost, únosnost a další parametry pohybového šroubu.
Zadejte součinitel tření v čepu / valivého ložiska. Přibližné hodnoty pro mazané tření jsou níže.
0.05-0.10.....Kalená ocel / Kalená
ocel
0.05-0.15.....Kalená ocel / Litina
0.09-0.15.....Kalená ocel / Bronz (fosforový)
0.07-0.10.....Litina / Litina
0.07-0.10.....Litina / Bronz (fosforový)
0.20-0.25.....Litina / Dřevo (dub)
0.07-0.10.....Bronz (fosforový) / Bronz (fosforový)
0.0015 … Kuličková ložiska jednořadá
0.0015 … Kuličková ložiska dvouřadá
0.0020 … Kuličková ložiska s kosoúhlým stykem jednořadá
0.0024 … Kuličková ložiska s kosoúhlým stykem dvouřadá
0.0010 … Naklápěcí kuličková ložiska s válcovou dírou
0.0011 … Válečková ložiska jednořadá
0.0025 … Jehlová ložiska s vnitřním kroužkem
0.0018 … Kuželíková ložiska jednořadá
0.0018 … Soudečková ložiska s válcovou dírou
0.0013 … Axiální kuličková ložiska
0.0050 … Axiální válečková ložiska
0.0050 … Axiální jehlová ložiska
0.0018 … Axiální soudečková ložiska
Zadejte střední průměr čepu nebo vnitřní průměr u ložiska.
Dodatečný moment, kterým je zatížen pohybový šroub a celá kinematika pohybu.
Moment, který je nutné vyvodit pro zdvih břemene resp. pro vyvození požadované axiální síly.
Moment, který je nutné vyvodit pro spuštění břemene resp. pro uvolnění požadované síly.
Důležitý parametr pro posouzení správného návrhu pohybového šroubu.
Výkon pohonu nutný pro zdvih břemene či vyvození požadované síly.
Na základě zadané rychlosti posuvu a geometrie šroubu jsou dopočítané nutné otáčky. Často je však nutné řešit opačnou úlohu, kdy známe otáčky šroubu (matice) a je nutné dopočítat posun. V tomto případě zadejte otáčky a tlačítkem " << " dopočítejte odpovídající posun.
Rychlost na vnějším průměru šroubu. Může být vodítkem pro posouzení návrhu.
Pokud potřebujete zjistit hodnotu posunutí matice (šroubu) v závislosti na počtu otáček (pootočení šroubu) zvolte a zadejte příslušnou hodnotu na řádku [1.32,1.33].
Volbou konstrukčního řešení je možné například eliminovat namáhání šroubu na vzpěr, je možné eliminovat čepové tření, je možné odstranit kombinované namáhání atd. Příklady na obrázku ukazují, jak je možné volbou konstrukce změnit nejméně příznivou kombinaci namáhání varianta B. (tlak+krut, vzpěr) na podstatně příznivější variantu C. (Prostý tah, krut). Výpočet obsahuje všechny běžně prováděné kontroly a typ konstrukce určuje jejich vyhodnocení.

Podle konstrukčního řešení zadejte délku šroubu.
Materiálové parametry jsou přednastavené na základě volby materiálů šroubu a matice [1.2,1.3]. Konkrétní materiálové hodnoty se však mohou mírně lišit. Po odškrtnutí tlačítka vpravo, je možné vyplnit hodnoty vlastní.
Jeho hodnota je závislá na kombinaci materiálů, povrchovém zpracování, způsobu mazání atd. Doporučená hodnota zahrnuje vliv materiálu a rychlosti pro mazané spojení.
Pro odhad mazaného spojení je možné použít hodnoty:
Šroub / Matice
Kalená ocel / Bronz........10 - 16 MPa (1.45 - 2.30 kpsi)
Ocel / Bronz...................8 - 10 MPa (1.15 - 1.45 kpsi)
Ocel / Ocel.....................7 - 12 MPa (1.00 - 1.75 kpsi)
Ocel / Šedá litina..............4 - 6 MPa (0.58 - 0.75kpsi)
Při zvýšené rychlosti je třeba hodnoty snížit. Například pro kombinaci Ocel / Bronz je dovolený tlak následující:
Rychlost
0.05 m/s (2.0 in/s)..................11 - 17 MPa (1.60 - 2.50 kpsi)
0.1 - 0.2 m/s (4 - 8 in/s)...........5 - 10 MPa (0.75 - 1.45 kpsi)
0.25 m/s (10 in/s)......................1 - 2 MPa (0.15 - 0.30 kpsi)
Mezní štíhlost SRc je důležitý parametr konkrétního materiálu, rozlišující oblast pružného a nepružného vzpěru a tím i použití odpovídajících vztahů. Je proto vhodné ověřit tento parametr pro konkrétní materiál. Doporučená hodnota je určena podle obecného vztahu:
SRcs = 0.5 * (E / (Rp02 * 0.5))0.5
SRc = (E *
p2
/ (Rp02 * 0.5))0.5
Podle typu konstrukce je nutné zkontrolovat následující hodnoty.
Krutové napětí v jádře šroubu. Mělo by být menší než dovolené napětí v zeleně označené buňce.
Tahové / tlakové napětí v jádře šroubu.
V případě současného působení tahu / tlaku a krutu, je nutné řešit kombinované namáhání. Redukované napětí by mělo být menší než dovoleného napětí v tahu.
Vztahuje se k redukovanému napětí.
Pokud je šroub zatížen tlakem, je pro dlouhé šrouby nutné provádět i kontrolu na vzpěr. Nutnost kontroly určuje hodnota šťíhlostního poměru [2.23]
Ve výběrovém seznamu vyberte způsob uložení šroubu podle obrázku. Výběr typu uložení vede k výběru koeficientu redukované (efektivní) délky, kterým je násobena skutečná délka šroubu pro dosažení tzv. redukované (efektivní) délky šroubu používané ve výpočtech. V řádku [2.16] je uvedena praktická hodnota, kterou je doporučeno použít ve výpočtu.
Uložení
šroubu.................Koef.(teoret) / Koef.(prakt)
A. Vetknutí - Vetknutí........................0.50 / 0.65
B. Vetknutí - Podpora........................0.70 / 0.80
C. Vetknutí - Kolmé vedení.................1.00 / 1.20
D. Podpora - Podpora........................1.00 / 1.00
E. Vetknutí - Volný konec....................2.00 / 2.10
F. Podpora - Kolmé vedení..................2.00 / 2.00
Podle
typu ložiska
Kluzná ložiska (d - průměr, l - délka)
l / d < 2..............kloub (podpora)
2 < l / d < 3........omezené natočení
l / d > 3..............vetknutí
Valivá
ložiska
Jednořadé kuličkové ložisko, radiální ložisko naklápěcí...................kloub (podpora)
Ložisko válečkové, dvouřadé kuličkové.........................................omezené natočení
Dvojice kuželíkových ložisek, radiální+axiální ložisko.....................vetknutí
Hodnota je používána ve výpočtech. Je to skutečná délka [2.1] vynásobená koeficientem redukované (efektivní) délky [2.16].
Je to vzdálenost krajního vlákna od osy profilu, která prochází těžištěm. Tato hodnota je nutná pro výpočet pomocí "Secant" metody.
Štíhlostní poměr konkrétního šroubu určuje, v jaké oblasti vzpěru šroub je (prostý tlak, nepružný vzpěr, pružný vzpěr) a tím i kontrolní metodu použitou pro zjištění koeficientu bezpečnosti.
A. SR < SRcs [2.7]......Oblast prostého tahu / tlaku. Doporučená bezpečnost SF>1.75)
B. SRcs < SR < SRc [2.8].....Oblast nepružného vzpěru. Doporučená bezpečnost SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
C. SRc < SR.....Oblast pružného vzpěru. Doporučená bezpečnost SF>3.5)
Tímto parametrem můžete určit míru nepřesnosti konstrukce a zatížení pro návrh rozměrů šroubu. Parametr zahrnuje:
Odchylka přímosti šroubu
Počáteční průhyb šroubu
Působiště sil mimo osu šroubu
Doporučené hodnoty:
0.25...ocelové konstrukce
0.15...běžné strojírenství
0.05...přesná tuhá uložení
Excentricita e je spočítána na základě stupně excentricity [2.24]. Pokud znáte hodnoty vybočení, nepřesnosti atd. zadejte hodnotu vpravo a po stisknutí tlačítka "<<" bude dopočítán stupeň excentricity.
Vyjadřuje poměr mezi kritickou a působící silou. Vhodný koeficient bezpečnosti (zelená buňka) je doporučen v závislosti na štíhlostním poměru [2.23]
Otáčky šroubu by neměly překročit 80% kritických otáček.
Hodnota maximálního průhybu šroubu zatíženého vlastní vahou v závislosti na uložení šroubu.
Ze zvolené výšky matice je spočítán počet činných závitů. Na základě síly a rozměrů šroubu a počtu závitů je pak dopočítán tlak v závitech.
Zvolte výšku matice. V zelené buňce je doporučená hodnota vycházející z poznatku, že přenosu síly se zůčastní max. 8 závitů.
Počet závitů v matici v závislosti na rozteči a výšce matice. Po zadání požadovaného počtu závitů a stisknutí tlačítka "<<" je dopočítána výška matice.
Z experimentů vychází, že první funkční závit přenáší 38% zatížení, druhý 25%, třetí 18%......a osmý (v některých případech i pátý) závit je již nezatížený. Zde nastavte maximální počet činných závitů, které budou použity pro výpočet.
Hodnota by měla být menší než hodnota dovoleného tlaku [2.6]
Zatížení šroubu Q = 10000 [N]
Rychlost posunu v = 50 [mm/s]
Materiál šroubu = kalená ocel
Materiál matice = bronz
Součinitel tření v závitech f = 0.08
Počet chodů závitu ns = 1
Délka zdvihu Ls = 1000 [mm]
Použit lichoběžníkový závit (30°,ISO2904:1997), samosvornost není vyžadována.

Je zvolený doporučený průměr d2prop a odpovídající šroub. A i když vyhovuje šroub na kontroly tahu, tlaku, otlačení, nevyhovuje na kontrolu na vzpěr.
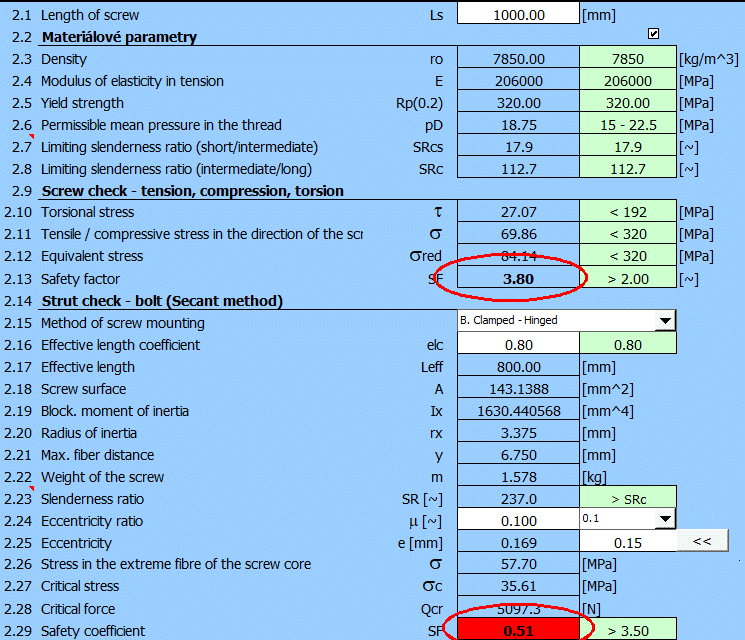
Je tedy nutné postupně volit větší průměr šroubu.

Pro dosažení odpovídající bezpečnosti ve vzpěru.

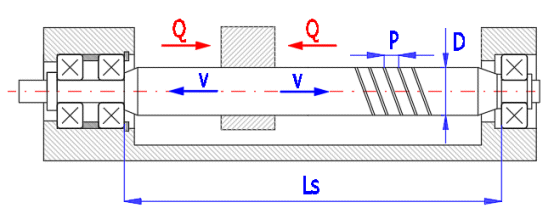
Příklad výpočtu pohybového šroubu vstřikovacího zařízení (viz. schematický obrázek).
A. Pohybový šroub je namáhán na krut a nebo tah.
B. Pohybový šroub je namáhán na kombinaci krutu a tlaku a na vzpěr.
Zatížení celkové Q = 100000 [N]
Zatížení šroubu Q = 50000 [N]
Rychlost zdvihu = 20 [mm/s]
Materiál šroubu = kalená ocel
Materiál matice = bronz
Součinitel tření v závitech f = 0.08
Počet chodů závitu ns = 1
Délka zdvihu Ls = 3000 [mm]
Použit lichoběžníkový závit (30°,ISO2904:1997), samosvornost není vyžadována.
Na základě doporučení (d2prop[1.7]) vybrán šroub Tr 36 x 10. Vyhovují všechny pevnostní kontroly, kromě kontroly na vzpěr, který se nevyskytuje (není třeba uvažovat).
Po postupné volbě silnějšího šroubu (je nutné splnit podmínku vzpěru) je vybrán šroub Tr 65 x 4, který vyhovuje i kontrole na vzpěr.
Informace o možnostech 2D a 3D grafického výstupu a informace o spolupráci se 2D a 3D CAD systémy naleznete v dokumentu "Grafický výstup, CAD systémy".
Po odškrtnutí tlačítka vpravo můžete zadat počet závitů, který má být vykreslen na výkresu šroubu / matice. Předvyplněné hodnoty vycházejí z výpočtu.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
Závity ISO pro všeobecné
použití - Základní profil - Část 1: Metrické závity
ISO general purpose screw
threads - Basic profile - Part 1: Metric screw threads
Filetages ISO pour usages généraux - Profil de base - Partie 1: Filetages
métriques
ISO-Gewinde allgemeiner Anwendung - Grundprofil - Teil 1: Metrishes Gewinde
Závity ISO pro všeobecné použití - Základní profil - Část 2: Palcové závity
ISO general purpose screw
threads - Basic profile - Part 2: Inch screw threads
Filetages ISO pour usages généraux - Profil de base - Partie 2: Filetages en
inches
ISO Gewinde allgemeiner Anwendung - Grundprofil - Teil 2: Inch-Gewinde
Metrické závity ISO pro všeobecné použití
ISO general purpose metric screw threads — General plan
Filetages metriques ISO pour usages generaux — Vue densemble
Metnsches ISO - Gewinde allgemeiner Anwendung — Ubersicht
Metrické závity ISO pro všeobecné použití - Základní rozměry
ISO general-purpose metric
screw threads - Basic dimensions
Filetages métriques ISO pour usages généraux - Dimensions de base
Metrisches ISO - Gewinde allgemeiner Anwendung - Grundmaße
Metrický lichoběžníkový ISO závit - Základní rozměry
ISO metric trapezoidal screw threads - Basic dimension
Filetagues metriques trapezoidaux ISO - Dimensions de base
Buttress Coarse Thread DIN 513
Unified Inch Screw Threads
ACME Screw Threads
Buttress Inch Screw Threads
7 / 45 Form With 0.6 Pitch Basic Height of Thread Engagement
Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas
R.S.KHURMI AND J.K.GUPTA
26th Edition
ČVUT Praha
Company catalogues: KSK, NSK, THOMSON...
^