Diese Berechnung löst die Durchbiegung, Spannung und den Kraftverlauf in den belasteten Planplatten. Die Berechnung ist für homogene Platten gleicher Stärke und aus einem Material bestimmt Die Platten können kreisförmig, kreisförmig mit einer Öffnung und rechteckig sein. Die Platten können gleichmäßig (ungleichmäßig) entlang der gesamten Fläche (oder nur deren Teil), oder mit einer am Kreis stetig wirkenden Kraft belastet werden. Das Programm ermöglicht:
In der Berechnung werden Daten, Abläufe, Algorithmen und Angaben aus der Fachliteratur (Roark formulas, Machinery's Handbook 26th, Teorie desek a skořepin [doc. Ing. Ladislav Šubrt, CSc.] und weiteren) angewendet.
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument "Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Platte ist ein Konstruktionselement von ebenem Charakter (zwei
Abmessungen sind vielfach größer als die dritte – Stärke) beansprucht vor allem
auf Biegung. Die Aufteilung der Platten nach der Form ist in kreisförmige,
rechteckige und allgemeine Formen.
Für die Vorstellung der Beanspruchung können wir aus einer kreisförmigen,
rotierenden, symmetrischen Platte ausgehen, aus der wir ein Element nehmen und
die entsprechenden Spannungen, welche auftreten können, darstellen.
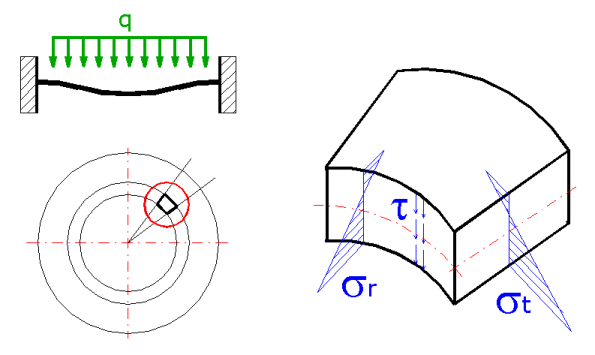
Den Verlauf der Normalspannungen sr,
st setzen wir als linear voraus, mit einer
neutralen Achse, die nicht in der Mitte der Platte ist.
Wenn wir aus dieser Voraussetzung ausgehen, können wir die Normalspannung
(radial sowie tangential) in zwei Komponenten zerlegen.
– Biegespannung (Verlauf wie bei einer einfachen Biegung) –
sr',
st'
– Membranspannung (die Spannung ist entlang der gesamten Plattenstärke konstant)
- sr'',
st''
Dann die Normalspannung sr
= sr' +
sr'' bzw.
st =
st' +
st''
und die Beanspruchung des Elementes A kann dann folgendermaßen dargestellt
werden:
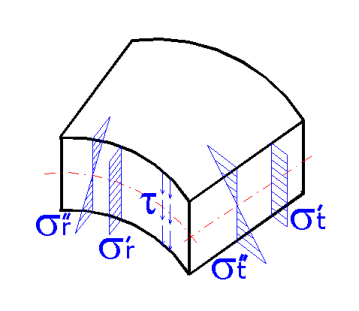
Analog ist es möglich den Spannungszustand auch in anderen, komplizierten Fällen – z.B. Platten rotierend, unsymmetrisch, rechteckig etc. zu zeichnen. Diese Fälle würden sich von diesem Fall nur dadurch unterscheiden, dass weitere Komponenten der Scherspannungen t zunehmen würden. Die einzelnen Spannungskomponenten haben dann zur Folge die Entstehung von diesen entsprechenden Verformungstypen.
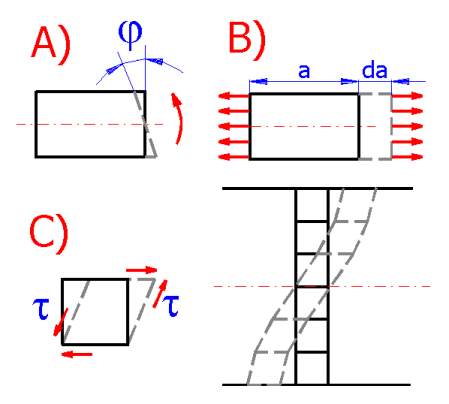
Anhand dieser Erkenntnisse ist es möglich die Platten in einzelne Gruppen
aufgrund der Beanspruchung aufzuteilen, und zwar in:
Wobei die „Plattenstärke” hier im Verhältnis zur Beanspruchung, zur überwiegenden Spannung und damit auch zum Lösungsablauf gemeint ist.
Die Durchbiegungen der starken Platte sind sehr gering und man kann deshalb die Verlängerung der Fasern nach der Verformung vernachlässigen. Da die Verlängerung der Faser durch Membranspannungen verursacht wird, können wir offensichtlich die Membranspannungen vernachlässigen. Die Biegespannungen sind aber infolge einer großen Plattenstärke auch zu gering und sind deshalb mit den Scherspannungen vergleichbar. Bei der Lösung wird also die Beanspruchung auf Biegung und Scherung überlegt. Da die Scherung eine Verbiegung der zur mittleren Fläche der Platte lotrechten Strecken hat, ist eine theoretische Lösung komplizierter. Dieser Plattentyp wird in den üblichen Maschinenkonstruktionen nicht oft eingesetzt.
Diese Platten haben bereits eine kleinere Stärke, was dazu führt, dass die Biegungsspannungen größer sind und die Scherspannung überwiegen. Man kann deshalb die Scherspannungen und deren Auswirkung, die eine Durchbiegung der ursprünglich direkten Senkrechten zur mittleren Fläche der Platte darstellt, vernachlässigen. An der zweiten Seite ist die Durchbiegung noch nicht so groß, dass sie die Fasern der mittleren Fläche (Fläche halbierend die Platte in der Mitte der Stärke) bedeutend verlängert würde. Es ist deshalb möglich auch die Membranspannungen zu vernachlässigen. Bei diesen Platten wird nur die Beanspruchung durch Biegung mit linearer Aufteilung der Biegungsspannungen entlang der Plattenstärke und mit einer Null–Biegungsspannung in der mittleren Fläche der Platte überlegt. Es ist rechnerisch der einfachste Plattentyp. Auch in der Praxis wird eine absolute Mehrheit der Platten nach den rechnerischen Abläufen gezählt, die für die Platten der mittleren Plattenstärke erstellt sind, obwohl dies nicht ganz berechtigt ist.
Bei diesen Platten ist der Einfluss der Scherung noch weniger bedeutend als bei den Platten von „mittlerer Stärke” und deshalb können wir auch ihre Auswirkungen wieder vernachlässigen. Wir müssen die Biegung überlegen und zum Schluss kommt der Einfluss der Membranspannungen hinzu, die man nicht einmal bei den dünnen Platten vernachlässigen kann. Es wird dadurch verursacht, weil hier die größten Durchbiegungen auftreten, was nicht ohne die Längenänderungen der Fasern von der mittleren Fläche auskommt. Diese Längenänderungen hängen mit der Auswirkung der Membranspannungen zusammen. Die Membranspannungen entstehen aber auch im Falle eines Schiebsitzes. Die Ränder könnten sich dann zwar annähern, aber bei der Verformung ändert sich die ursprünglich ebene Platte in eine windschiefe Rotationsfläche, was nicht ohne Längenänderungen der einzelnen Fasern der mittleren Fläche auskommt. Bei dünnen Platten überlegen wir Biegungs- und Membranspannungen auch im Falle des Schiebsitzes. Dieser Plattentyp ist nichtlinear, d.h. die Verformungen und die Spannung sind nicht proportional der Belastung und das auch wenn das lineare Hookesches Gesetz gilt. Es handelt sich um eine sog. geometrische Nichtlinearität, entstehend in Folge großer Verformungen – konkret in Folge großer Drehwinkel.
Die Membranen sind so dünne Platten, sodass deren Biegungssteifheit
vernachlässigbar ist (und auch die Biegungsspannungen) und es wird nur die
Druckbeanspruchung (z.B.: verschiedene Luftdruckmessermembranen aus Gummi)
überlegt. In Folge großer Verformungen sind diese wieder geometrisch
nichtlinear.
Diese Teilung der Platten ist selbstverständlich keineswegs fest, aber weist nur
auf bestimmte Möglichkeiten der Vereinfachung hin, welche auch eine
Vereinfachung der analytischen Lösung bei der Beibehaltung der entsprechenden
Genauigkeit in Bezug auf die anderen Ungenauigkeiten (Ungenauigkeiten der
Lagerung, Verarbeitung, Materialkonstanten etc.) ermöglicht.
In der Abbildung ist die Abhängigkeit der maßlosen Durchbiegung „y/t” und der maßlosen Belastung „q*a^4/(E*t^4)” dargestellt, wo:
y...maximale Durchbiegung
t...Plattenstärke
q...stetige Belastung
a...Plattenradius
E...Elastizitätsmodul
und die einzelnen Kurven dann folgendes darstellen:
B) Platten mittlerer Stärke (Kirchhoffs)
C) Dünne Platten (mit großen Durchbiegungen)
D) Membranen
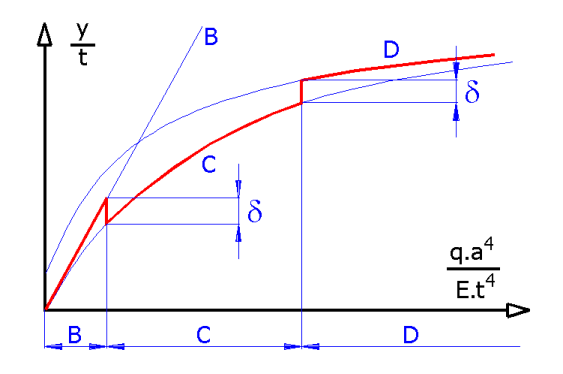
Aus der Abbildung ist zu sehen, dass es für sehr kleine dimensionslose
Durchbiegung möglich ist die, für die „Platten mittlerer Stärke” angenommenen
Vereinfachungen einzusetzen. Für eine größere dimensionslose Durchbiegung ist
dann der Berechnungstyp für „Dünne Platten” einzusetzen.
Aus der Abbildung ist auch offensichtlich, dass es nicht möglich ist eindeutig
die Grenzen der einzelnen Berechnungsmodelle zu bestimmen. Es hängt davon ab,
welch großen Fehler wir zu tolerieren bemüht sind. Wenn ein Fehler, als Delta
gekennzeichnet, zulässig ist, dann ist es möglich auch die entsprechenden
Grenzen der einzelnen Berechnungsmodelle zu bestimmen. Ähnlich wie bei der
Durchbiegung (siehe Abbildung) ist es dann möglich auch bei der Spannung so
vorzugehen.
Bei den praktischen Anwendungen sollte man mindestens die ungefähre Position der
Grenze zwischen den Berechnungsmodellen (B und C) kennen. Bei der Anforderung
des Fehlers bis zu 5 % sollte die Durchbiegung kleiner als ein Drittel der
Plattenstärke, bei einem Fehler bis zu 10 % sollte die Durchbiegung kleiner als
die Hälfte der Plattenstärke sein.
Ungefähre Schätzung des Fehlers in Abhängigkeit von der Durchbiegung, bezogen
auf die Plattenstärke:
| Durchbiegung [% Stärke] | Fehler [%] |
| 10% | 0.5% |
| 25% | 3% |
| 33% | 5% |
| 50% | 10% |
| 75% | 20% |
| 100% | 30% |
Bei der Anwendung des rechnerischen Modells B (Platten mittlerer Stärke) und bei
einer größeren dimensionslosen Durchbiegung (Durchbiegung bezogen auf die
Stärke) steigt der Fehler schlagartig an, wie aus der Abbildung ersichtlich ist.
Auch wenn der Fehler an der Seite von der Sicherheit ist, führt der Einsatz von
einer ungeeigneten Berechnung zu überflüssigerweise überdimensionierten und
schweren Konstruktionen.
Die Berechnungen und eingesetzten Formeln basieren an folgenden Voraussetzungen.
Bei der Realisierung der Durchbiegung (Spannung, Sicherheit) einer kreisförmigen oder rechteckigen Platte gehen wir wie folgt vor.
In diesem Absatz wählen Sie die Berechnungseinheiten und das Material der vorgeschlagenen/geprüften Platte.
In der Auswahlliste das gewünschte System der Berechnungseinheiten auswählen. Beim Umschalten der Einheiten werden sofort alle Werte umgerechnet.
Aus der Auswahlliste wählen Sie das geeignete Material der Platte aus. Sofern sich die Materialkonstanten ihres Materials von den Materialkonstanten, die in den Zeilen[1.3–1.8] angeführt sind, unterscheiden, haken Sie die Abstreichtaste an der Zeile [1.3] ab und geben Sie eigene Materialkonstanten ein.
Wählen Sie den Soll-Sicherheitsfaktor. Auf die eigene Berechnung der Durchbiegung oder der Spannung hat die Wahl des Sicherheitsfaktors keinen Einfluss. Der Sicherheitsfaktor hat Einfluss auf den Entwurf der maximalen Belastung [2.5,3.6,4.6] oder der minimalen Plattenstärke[2.2,3.2,4.2]. Gleichzeitig wird die Überschreitung der einzelnen Sicherheitsfaktoren in den einzelnen Absätzen geprüft.
Laut dieser Berechnung ist es möglich den Durchbiegungsverlauf, die Verdrehung an den kreisförmigen Platten der mittleren Stärke und das inkl. maximaler Werte zu ermitteln. Gleichzeitig ist es möglich die minimale Stärke bzw. maximale Belastung, die je Platte einsetzbar ist, vorzuschlagen. Da bei diesen Berechnungstyp die Membranspannung vernachlässigt wird (siehe theoretischer Teil), ist es nicht erforderlich die maximale Durchbiegung, die kleiner als die Hälfte der Plattenstärke sein sollte, zu prüfen. Für die Durchbiegung, die größer als die 1/2 der Plattenstärke ist, benutzen Sie die Berechnung im Absatz [5.0].
Im Auswahlverzeichnis wählen Sie einen solchen Plattentyp aus, der ihren Belastungs- und Randbedingungen entspricht. Nach der Auswahl wird die schematische Skizze der Platte dargestellt.
Geben Sie die Plattenstärke, den Außenradius bzw. Innenradius ein. Die Plattenstärke sollte kleiner als 1/5 vom Radius (bei größerem Anspruch auf die Genauigkeit 1/10 vom Radius) sein. Sofern Sie die Taste „<min” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei der Gleitung die entsprechende Plattenstärke ergänzt. Auf jeden Fall ist der Maximalwert der Durchbiegung zur prüfen.
Geben Sie den Belastungsradius ein. Je nach Belastungstyp wird der Belastungsradius wie folgt ausgewertet:
Stetige Belastung: Die stetige Belastung (konstant oder linear
steigend) wirkt vom Plattenrand zum eingegebenen Belastungsradius. Der
Belastungsradius kann 0, beziehungsweise bei den kreisförmigen Platten mit
Öffnungen der Innenradius sein.
Kreisförmige Belastung durch Kraft: Kraft wirkt gleichmäßig entlang des
Kreises vom eingegebenen Radius. Im Falle, dass der Belastungsradius kleiner als
die Hälfte der Plattenstärke ist, wird dieser durch einen so genannten
äquivalenten Radius ro'=(1.6*ro^2+t^2)^0.5–0.675*t ersetzt, was den Einsatz der
traditionellen Formeln für die Berechnung der Spannung ermöglicht.
Geben Sie die Größe der Kraft ein, die stetig am Belastungsradius wirkt. Bei einem anderen Belastungstyp als durch Kraft ist das Eingabefeld grau. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei Gleitung die maximale Kraft ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Die Belastung kann man auf zwei Art und Weisen eingeben. Entweder als Druck oder als Gesamtkraft, die durch Druckwirkung auf die Plattenfläche entsteht. Das Verfahren wählen Sie mit dem Schalter in dieser Zeile. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze in Gleitung der maximale Druck (die maximale Kraft) ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Geben Sie die Temperaturdifferenz zwischen der oberen und unteren Plattenseite ein.
Das Gewicht der Platte kann zum Beispiel für die Absicherung der stetigen Belastung vom eigenen Gewicht genutzt werden.
Nach der Änderung der Eingangsdaten werden die Ergebnisse umgerechnet. Das Programm rechnet stufenweise alle Werte in fünfzig Punkten von r = 0 bis r = a (bzw. von r = b bis r = a für die Platte mit Öffnung). Diese Werte werden in die Tabelle eingetragen und aus diesen wird dann der minimale bzw. maximale Wert der Durchbiegung und Spannung (siehe Ergebnisse an den folgenden Zeilen ymax, smax, SFmin) ermittelt. Diese Tabellenwerte werden auch für die Darstellung der Graphik genutzt.
Die maximale Durchbiegung der Platte sollte kleiner als die Hälfte ihrer Stärke sein. Bei größeren Werten steigt der Fehler des Ergebnisses aufgrund der Berechnungsmethode schnell an. Die Details finden Sie im Theoretischen Teil der Hilfe.
In das Eingabefeld geben Sie den Radius r ein, an welchen Sie die Werte der
Durchbiegung, Verdrehung, Spannung etc. ermitteln möchten. Die entsprechenden
Ergebnisse finden Sie in den folgenden Zeilen. Im grünen Feld ist der Bereich
vom Radius r, der eingegeben werden kann. Mit dem Schieber rechts können Sie
einfach den Wert vom Radius r ändern, die Position ist in der Graphik mit einem
senkrechten roten Strich gekennzeichnet.
Die Darstellung der Werte in der Graphik finden Sie im Verzeichnis unter dem
Schieber.
In der Zeile sind die Randbedingungen ausgeschrieben, die für den jeweiligen Typ der Platte und ihre Lagerung und Belastung gelten.
Nach dieser Berechnung ist es möglich den Durchbiegungsverlauf, die Spannung, Verdrehung an den kreisförmigen Platten mit Öffnung in der Mitte und das inkl. maximaler Werte zu ermitteln. Gleichzeitig ist es möglich die minimale Stärke bzw. maximale Belastung, die je Platte möglich einzusetzen ist vorzuschlagen. Da bei diesen Berechnungstyp die Membranspannung vernachlässigt wird (siehe theoretischer Teil), ist es nicht erforderlich die maximale Durchbiegung, die kleiner als die Hälfte der Plattenstärke sein soll, zu prüfen. Bei einer größeren Durchbiegung steigt der Berechnungsfehler schnell (siehe theoretischer Teil der Hilfe).
Im Auswahlverzeichnis wählen Sie einen solchen Plattentyp aus, der ihren Belastungs- und Randbedingungen entspricht. Nach der Auswahl wird die schematische Skizze der Platte dargestellt.
Geben Sie die Plattenstärke, den Außenradius bzw. Innenradius ein. Die Plattenstärke sollte kleiner als 1/5 vom Radius (bei größerem Anspruch auf die Genauigkeit 1/10 vom Radius) sein. Sofern Sie die Taste „<min” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei der Gleitung die entsprechende Plattenstärke ergänzt. Auf jeden Fall ist der Maximalwert der Durchbiegung zur prüfen.
Geben Sie den Belastungsradius ein. Je nach Belastungstyp wird der Belastungsradius wie folgt ausgewertet:
Stetige Belastung: Die stetige Belastung (konstant oder linear
steigend) wirkt vom Plattenrand zum eingegebenen Belastungsradius. Der
Belastungsradius kann 0, beziehungsweise bei den kreisförmigen Platten mit
Öffnungen der Innenradius sein.
Kreisförmige Belastung durch Kraft: Kraft wirkt gleichmäßig entlang des
Kreises vom eingegebenen Radius. Im Falle, dass der Belastungsradius kleiner als
die Hälfte der Plattenstärke ist, wird dieser durch einen so genannten
äquivalenten Radius ro'=(1.6*ro^2+t^2)^0.5–0.675*t ersetzt, was den Einsatz der
traditionellen Formeln für die Berechnung der Spannung ermöglicht.
Geben Sie die Größe der Kraft ein, die stetig am Belastungsradius wirkt. Bei einem anderen Belastungstyp als durch Kraft ist das Eingabefeld grau. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei Gleitung die maximale Kraft ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Die Belastung kann man auf zwei Art und Weisen eingeben. Entweder als Druck oder als Gesamtkraft, die durch Druckwirkung auf die Plattenfläche entsteht. Das Verfahren wählen Sie mit dem Schalter in dieser Zeile. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze in Gleitung der maximale Druck (die maximale Kraft) ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Geben Sie die Temperaturdifferenz zwischen der oberen und unteren Plattenseite ein.
Das Gewicht der Platte kann zum Beispiel für die Absicherung der stetigen Belastung vom eigenen Gewicht genutzt werden.
Nach der Änderung der Eingangsdaten werden die Ergebnisse umgerechnet. Das Programm rechnet stufenweise alle Werte in fünfzig Punkten von r = 0 bis r = a (bzw. von r = b bis r = a für die Platte mit Öffnung). Diese Werte werden in die Tabelle eingetragen und aus diesen wird dann der minimale bzw. maximale Wert der Durchbiegung und Spannung (siehe Ergebnisse an den folgenden Zeilen ymax, smax, SFmin) ermittelt. Diese Tabellenwerte werden auch für die Darstellung der Graphik genutzt.
Die maximale Durchbiegung der Platte sollte kleiner als die Hälfte ihrer Stärke sein. Bei größeren Werten steigt der Fehler des Ergebnisses aufgrund der Berechnungsmethode schnell an. Die Details finden Sie im Theoretischen Teil der Hilfe.
In das Eingabefeld geben Sie den Radius r ein, an welchen Sie die Werte der
Durchbiegung, Verdrehung, Spannung etc. ermitteln möchten. Die entsprechenden
Ergebnisse finden Sie in den folgenden Zeilen. Im grünen Feld ist der Bereich
vom Radius r, der eingegeben werden kann. Mit dem Schieber rechts können Sie
einfach den Wert vom Radius r ändern, die Position ist in der Graphik mit einem
senkrechten roten Strich gekennzeichnet.
Die Darstellung der Werte in der Graphik finden Sie im Verzeichnis unter dem
Schieber.
In der Zeile sind die Randbedingungen ausgeschrieben, die für den jeweiligen Typ der Platte und ihre Lagerung und Belastung gelten.
Mit dieser Berechnung ist es möglich die maximale Durchbiegung und die maximale Spannung bei den rechteckigen Platten zu ermitteln. Die Platten sind von mittlerer Stärke. Die maximale Durchbiegung der Platte sollte bis zu der Hälfte ihrer Stärke sein. Für die Durchbiegung, die größer als 1/2 der Plattenstärke beträgt, benutzen Sie die Berechnung im Absatz [6.0]. Bei einer größeren Durchbiegung steigt der Berechnungsfehler schnell (siehe theoretischer Teil der Hilfe).
Im Auswahlverzeichnis wählen Sie einen solchen Plattentyp aus, der ihren Belastungs- und Randbedingungen entspricht. Nach der Auswahl wird die schematische Skizze der Platte dargestellt.
Geben Sie die Plattenstärke, die längere und kürzere Seite ein. Die Plattenstärke sollte kleiner als 1/4 der kleinsten Querabmessung (bei größerem Anspruch auf die Genauigkeit 1/10) sein. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei Gleitung die maximale Kraft ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Die Kraft wirkt gleichmäßig entlang dem Kreis des eingegebenen Radius. Im Falle, dass der Belastungsradius kleiner als die Hälfte der Plattenstärke ist, wird dieser durch einen so genannten äquivalenten Radius ro'=(1.6*ro^2+t^2)^0.5–0.675*t ersetzt, was den Einsatz der traditionellen Formel für die Berechnung der Spannung ermöglicht.
Geben Sie die Größe der Kraft ein, die stetig am Belastungsradius wirkt. Bei einem anderen Belastungstyp als durch Kraft ist das Eingabefeld grau. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze bei Gleitung die maximale Kraft ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Die Belastung kann man auf zwei Art und Weisen eingeben. Entweder als Druck oder als Gesamtkraft, die durch Druckwirkung auf die Plattenfläche entsteht. Das Verfahren wählen Sie mit dem Schalter in dieser Zeile. Sofern Sie die Taste „<max” drücken, wird anhand des eingegebenen Soll-Sicherheitsfaktors und der Festigkeitsgrenze in Gleitung der maximale Druck (die maximale Kraft) ergänzt. Auf jeden Fall ist der Maximalwert von der Durchbiegung zur prüfen.
Das Gewicht der Platte kann zum Beispiel für die Absicherung der stetigen Belastung vom eigenen Gewicht genutzt werden.
Die maximale Durchbiegung der Platte sollte kleiner als die Hälfte ihrer Stärke sein. Bei größeren Werten steigt der Fehler des Ergebnisses aufgrund der Berechnungsmethode schnell an. Die Details finden Sie im Theoretischen Teil der Hilfe.
Sofern bei der Berechnung der kreisförmigen Platten im Absatz [2.0] eine Durchbiegung der Platte größer als 1/2 der Plattenstärke berechnet wird, wäre es angebracht die Durchbiegung der Platte in diesem Absatz zu lösen. In dieser Berechnung wird die Membranspannung berücksichtigt, was die Genauigkeit der Berechnung erhöht.
Im Auswahlverzeichnis wählen Sie einen solchen Plattentyp aus, der ihren Belastungs- und Randbedingungen entspricht. Nach der Auswahl wird die schematische Skizze der Platte dargestellt.
Geben Sie die Plattenstärke und den Außenradius ein. Die Plattenstärke sollte kleiner als 1/5 vom Radius (bei größerem Anspruch auf die Genauigkeit 1/10 vom Radius) sein.
Geben Sie die Größe der Kraft ein, die in der kleinen Kreisfläche in der Mitte wirkt. Bei einem anderen Belastungstyp als durch Kraft ist das Eingabefeld grau.
Die Belastung kann man auf zwei Arten eingeben. Entweder als Druck oder als Gesamtkraft, die durch die Druckwirkung auf die Plattenfläche entsteht. Das Verfahren wählen Sie mit dem Schalter in dieser Zeile aus.
Das Gewicht der Platte kann zum Beispiel für die Absicherung der stetigen Belastung vom eigenen Gewicht genutzt werden.
Sofern bei der Berechnung der rechteckigen Platten im Absatz [4.0] eine Durchbiegung der Platte größer als 1/2 der Plattenstärke berechnet wird, wäre es angebracht die Durchbiegung der Platte in diesem Absatz zu lösen. In dieser Berechnung wird die Membranspannung berücksichtigt, was die Genauigkeit der Berechnung erhöht.
Im Auswahlverzeichnis wählen Sie einen solchen Plattentyp aus, der ihren Belastungs- und Randbedingungen entspricht. Nach der Auswahl wird die schematische Skizze der Platte dargestellt.
Geben Sie die Plattenstärke, die längere und kürzere Seite ein. Die Plattenstärke sollte kleiner als 1/4 der kleinsten Querabmessung (bei größerem Anspruch auf die Genauigkeit 1/10) sein.
Die Belastung kann man auf zwei Arten eingeben. Entweder als Druck oder als Gesamtkraft, die durch die Druckwirkung auf die Plattenfläche entsteht. Das Verfahren wählen Sie mit dem Schalter in dieser Zeile aus.
Das Gewicht der Platte kann zum Beispiel für die Absicherung der stetigen Belastung vom eigenen Gewicht genutzt werden.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
^