Schwungräder

Inhalt:

• Steuerung, Struktur und Syntax der Berechnungen
• Projektinformationen
• Theorie
• Berechnungsverfahren
• Berechnungseinheiten, Maßeinheiten-Umwandlung [1]
• Konzept und Berechnung des Trägheitsmoments und der Abmessungen des Schwungrads [2]
• Analyse (Berechnung) des Schwungrads [3]
• Motormomentkurven, Leistungswerte, Trägheitsmomente, Gewicht, Wirkungsgrad [4]
• Kurbeltrieb [5]
• Beispiel 1 - Auslegung des Schwungrads bei einem Einzylinder-Verbrennungsmotor
• Beispiel 2 - Auslegung eines Schwungrads für einen vom Asynchronmotor angetriebenen Verdichter
• Beispiel 3 - Auslegung eines Schwungrads für eine Kurbelpresse, die von einem Asynchron-Elektromotor angetrieben wird
• Einstellung der Berechnungen, Sprachenänderung
• Benutzerspezifische Anpassungen der Berechnung
• Liste der Standards, Literaturliste

Schwungräder

Das Programm ist für die Auslegung und die Analyse des Schwungrads sowie die Festlegung der Abmessungen bestimmt. Mit dem Programm kann man auch den Kurbeltrieb gestalten und die Parameter von Asynchronmotoren ermitteln.

Das Programm behandelt Folgendes:

1. Auslegung des Trägheitsmomentes für die ausgewählte Maschine.
2. Auslegung der Abmessungen des Schwungrads anhand des Soll-Trägheitsmoments.
3. Berechnung des Trägheitsmoments anhand der Abmessungen des Schwungrads.
4. Berechnung des Trägheitsmoments von Massen mit unterschiedlichen Drehzahlen (reduziertes Trägheitsmoment).
5. Berechnung der Spannung in rotierenden Ringen.
6. Berechnung des Kreiselmoments.
7. Berechnung des Trägheitsmoments aus dem Lastdiagramm und der gewünschten Ungleichförmigkeit.
8. Berechnung der Ungleichförmigkeit.
9. Auslegung des Schwungrads in Verbindung mit dem Motor.
10. Auswahl und Berechnung der Parameter von ca. 1200 Asynchron-Elektromotoren.
11. Gestaltung des Kurbeltriebs.

Für die Berechnungen werden Daten, Verfahren, Algorithmen und Informationen aus Literatur, Normen und Firmenkatalogen verwendet.

[1] Strojně technická příručka (Svatopluk Černoch)
[2] Shigley’s Mechanical Engineering Design
[3] Strojírenská příručka (1992)
[4] Machinery’s Handbook (26th Edition)

Standards: EN 60034-30-1 :20 14
Rotating electrical machines — Part 30-1: Efficiency classes of line operated AC motors (IE code)
Machines Olectriques tournantes — Partie 30-1: Classes de rendement pour les moteurs a courant alternatif alimentés par le réseau (Code IE)
Drehende elektrische Maschinen — Teil 30-1: Wirkungrad-Klassifizierung von netzgespeisten Drehstrommotoren (IE-Code)

Company cataloques: Siemens,ABB Automation Products

 Anwenderoberfläche.

 Zum Herunterladen.

 Preisliste, Einkauf.
 

Steuerung, Struktur und Syntax der Berechnungen.

Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument"Steuerung, Struktur und Syntax der Berechnungen".

Projektinformationen.

Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".

Theorie

Auslegung und Berechnung von Trägheitsmoment und Schwungradabmessungen

Für die Berechnungen werden die folgenden Formeln verwendet.

Näherungsweise Auslegung des Trägheitsmoments des Schwungrads

I = C * Pw / (n³ * δ)
C ... Güldner-Konstante, die die Art der Maschine bestimmt
Pw ... Maschinenleistung
n ... Geschwindigkeit [/s]
δ ... der für den Maschinentyp empfohlene Grad der Laufunregelmäßigkeit

Koeffizient der Geschwindigkeitsschwankung

δ = (ωmax - ωmin) / ωm
ωmax ... maximale Winkelgeschwindigkeit
ωmin ... minimale Winkelgeschwindigkeit
ωm = (ωmax - ωmin) / 2 ... mittlere Winkelgeschwindigkeit

Trägheitsmoment des rotierenden Rings

I = 0,5 * Ro * Pi * b * (R⁴ - r⁴)
Ro ... Dichte
b ..... Scheibenbreite
R ..... Außenradius
r ...... Innenradius

Reduziertes Trägheitsmoment

Wenn es im System Massen gibt, die sich mit unterschiedlichen Geschwindigkeiten drehen (Getriebeuntersetzung), muss deren Trägheitsmoment in das Trägheitsmoment des Schwungrads umgerechnet werden.
Ired = Σ I(i) * (n / n(i))²
I(i) ... das Trägheitsmoment einer Masse, die sich mit einer anderen Geschwindigkeit als das Schwungrad dreht
n ...... Schwungraddrehzahl
n(i) ... das Rotationsmoment einer Masse, die sich mit einer anderen Geschwindigkeit als das Schwungrad dreht
Die reduzierten Trägheitsmomente können dann direkt addiert werden, um das Gesamtträgheitsmoment des Systems zu ermitteln.

Tangentiale Spannung

σt = Ro * ω² * ((3 + ny) /8 ) * (r² + R² + r² * R² / rx² - (1 + 3 * ny) / (3 + ny) * rx²)
Ro ... Dichte
ω ... Winkelgeschwindigkeit
ny ... Poissonsche Konstante
R ..... Außenradius
r ...... Innenradius
rx .... der Radius, in dem die Spannung berechnet wird

Drehung des Schwungrads

Zeit
t = (0,1047197533 * (n2 - n1) * I) / T
Energie
E = 0,005483 * I * (n2² - n1²)
T ... Drehmoment
I .... Trägheitsmoment
n1,n2 ... Geschwindigkeit

Gyroskopisches Moment

Tg = Pi * n * I * ωv / 30 * sin(β)
I .... Trägheitsmoment des Schwungrads
n ... Schwungraddrehzahl [/min]
β ... Winkel der Drehachse des Schwungrads
ωv ... Winkelgeschwindigkeit des Schwungrads

Analyse (Berechnung) des Schwungrads

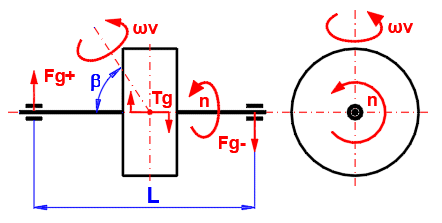
Bei Motoren und Maschinen, bei denen die Drehbewegung in eine geradlinige Bewegung umgewandelt wird, und bei Maschinen ohne konstante Last treten Momentschwankungen auf. Es gibt kein konstantes Gleichgewicht zwischen den wirkenden Momenten (Antriebsmoment, angetriebenes Moment, Trägheitskräfte, passive Widerstände). Dadurch ändert sich die Winkelgeschwindigkeit während des Arbeitszyklus. Um diese Ungleichheit zu verringern, wird ein Schwungrad als Energiespeicher verwendet, der bei überschüssigem Drehmoment Energie speichert und bei fehlendem Drehmoment wieder abgibt.

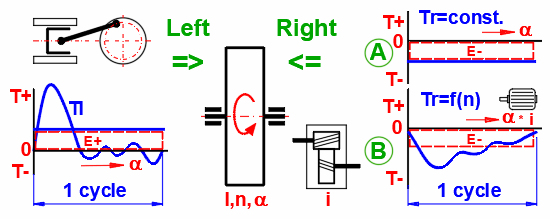
Ein großer Teil der Maschinen hat einen Momentenverlauf, der sich nicht einfach analytisch beschreiben lässt. Daher werden für die Lösung numerische Integrationsmethoden verwendet. Der Momentenverlauf auf der linken Seite ist durch die Momenten-Tabelle in Abhängigkeit von der Drehung des Schwungrades definiert. Das Moment auf der rechten Seite kann sein:

A. Konstant
B. Abhängig von der Drehzahl des Schwungrads (Elektromotor, Generator)
C. Oder kann durch eine eigene Tabelle oder Funktion definiert werden

Grundlegende Bewegungsgleichung:

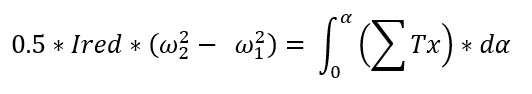
Ired ... Reduziertes Trägheitsmoment aller rotierenden Massen
ω₁, ω₂ … Winkelgeschwindigkeit am Anfang, am Ende des Arbeitszyklus
a ... Drehwinkel des Schwungrads während des Arbeitszyklus
da ... Elementardrehung des Schwungrads
ΣTx ... Summe aller einwirkenden Momente (Antriebsmoment, angetriebenes Moment, Trägheitskräfte, passive Widerstände)

Ziel ist es, den Momentenverlauf auf der rechten Seite so zu lösen, dass sie die Bedingungen erfüllt (z. B. charakteristisch für einen Asynchron-Elektromotor) und gleichzeitig die Summe der Energien der linken und rechten Seite gleich Null ist (ω₁ = ω₂).

Ein Beispiel ist die Abhängigkeit des Moments eines Einzylinder-Viertakt-Verbrennungsmotors vom Drehwinkel der Kurbel (siehe Abbildung).

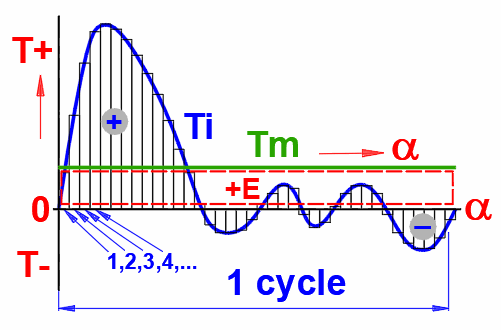
Hier läuft die Berechnung in folgenden Schritten ab:

1) Integration und Energieberechnung (Aufteilung der Strecke Ti in n Teile)

Tmid(j) = (Ti(j) + Ti(j+1)) / 2 ... <j = 1 ... n+1>
dE(j) = Tmid(j) * da ... <j = 1 ... n> ... für jedes Segment 1,2,3,4.....

wobei:
da = a / n
dEsum = ΣdE(j) ... <j = 1 ... n>

2) Mittleres Drehmoment

Tm = dEsum / a

3) Winkelgeschwindigkeit in jedem Punkt

ω(j+1) = (ω(j) + 2 * dE'(j) / I)^0.5

wobei:
dE'(j) = (Tmid(j) - Tm) * da
I ... das Trägheitsmoment des Schwungrads und der angebrachten rotierenden Massen

4) Ermitteln der Winkelgeschwindigkeiten ωmin und ωmax aus dem Feld ω(j) ... <j = 1 ... n+1>

ωmin = MIN (ω(j)) ... <j = 1 ... n+1>
ωmax = MAX (ω(j)) ... <j = 1 ... n+1>

5) Berechnung der mittleren Winkelgeschwindigkeit

ωm = (ωmin + ωmax) / 2

6) Berechnung des Koeffizienten der Geschwindigkeitsschwankung

δ = (ωmax - ωmin) / ωm

Alternativ kann man das Trägheitsmoment aus dem Geschwindigkeitsschwankungskoeffizienten berechnen
I = dEsum' / (δ * ωm^2)

wobei:
dEsum' = ΣdE'(j) ... <j = 1 ... n>

Wird anstelle eines konstanten Wertes Tm z. B. ein Asynchronmotor (Generator) verwendet, dessen Moment von der Drehzahl abhängt, wird sukzessiv der Drehmomentwert verwendet, welcher der Schwungraddrehzahl für jeden Schritt entspricht. Bei jeder Veränderung wird das gesamte Modell neu berechnet.

Je nach den Eingangsdaten (Motorleistung, Trägheitsmoment, Ungleichförmigkeitsgrad usw.) konvergiert die Lösung in der Regel in mehreren Dutzend Iterationen zum Gleichgewicht.

Durch die Analyse kann Folgendes gelöst / überprüft werden

- Genaue Berechnung des Trägheitsmomentes für die gewünschte Ungleichförmigkeit
- Berechnung der Ungleichförmigkeit für das vorgegebene Trägheitsmoment
- Berechnung von Drehzahl, Drehmoment, Energie, Leistung
- Überprüfung der Eignung des gewählten Motors/Generators (Drehzahl, Leistung)

Beispiel für die Analyse eines an einen Einzylinder-Ottomotor gekoppelten Asynchrongenerators für verschiedene Ungleichförmigkeiten im Dreiecklauf.

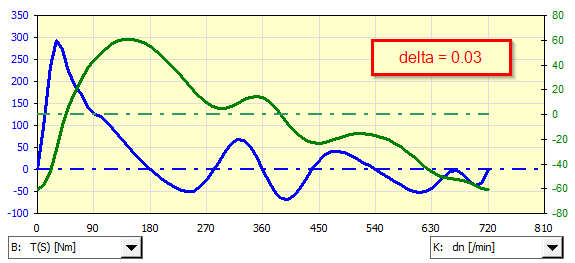
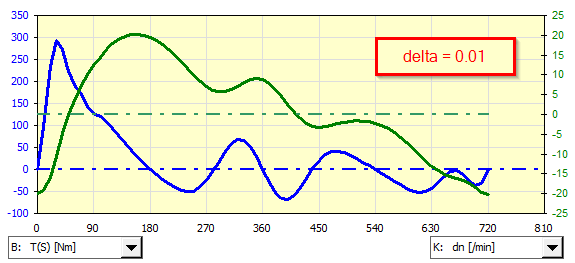
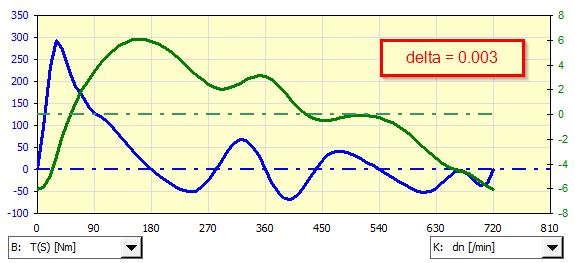
Wenn es notwendig ist, einen anderen als den vordefinierten Asynchronmotor (Generator) zu verwenden, können dessen Eigenschaften definiert und in der Iteration verwendet werden.

Motormomentkurven

Im Bereich der Maschinen- und Anlagenantriebe ist der Asynchronmotor (induction motor) der am häufigsten verwendete Motor. Bei diesem Motor ändert sich das Drehmoment mit der Drehzahl (linear im Arbeitsbereich). Durch den Vergleich der Kataloge mehrerer Hersteller wurde eine Tabelle mit Parametern für jeden beliebigen Motor erstellt.

In diesem Kapitel finden Sie daher die Parameter des ausgewählten Motors (einschließlich Gewichts-, Wirkungsgrad- und Trägheitsmomentschätzungen), Leistung und Drehmoment für andere Drehzahlen als die Nenndrehzahl.

Grundformeln für Asynchronmotoren

Synchrondrehzahl
ns = 2 * f * 60 / p
f ... Frequenz des Stromnetzes (60 Hz USA, Kanada..., 50 Hz Europa)
p ... Anzahl der Motorpole

Nenndrehzahl (Asynchrondrehzahl)
nr = (1 - s / 100) * ns
s ... Motorschlupf [%]

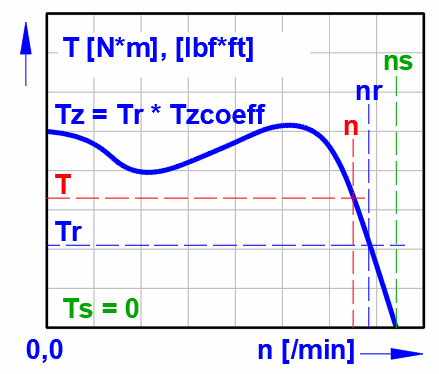
Nenndrehmoment
Tr = Pr * 9550 / nr
Pr ... Nennleistung

Anzugsmoment
Tz = Tr * Tzcoeff
Tzcoeff ... Anzugsmoment-Koeffizient
Für kleine Motoren (≤ 30 kW) beträgt der Wert 2.5-3, für mittlere Motoren 2-2.5, für große Motoren 1-1.5.

Tipp: Sollten Sie bei Bearbeitung des Arbeitshefts den Drehmomentwert für den ausgewählten Motor und die angegebene Drehzahl benötigen, verwenden Sie die vordefinierten Funktionen:
=linear2(n;T_4_nT) ... approximiert linear die Drehmomentwerte auf der Grundlage der in Kapitel [4.0] ausgewählten Motordrehzahl und bringt diese zurück.

n ... Motordrehzahl/min
T_4_nT ... Bereichsname mit Kurve T=f (n)

Kurbeltrieb

Um eine geradlinige Bewegung in eine Drehbewegung umzuwandeln (und umgekehrt), wird häufig ein Kurbeltrieb verwendet, meist in Kombination mit einem Schwungrad. Für die Auslegung des Schwungrads ist es dann notwendig, den Momentenverlauf zu kennen. Zur Berechnung des Momentenverlaufs müssen der Lastkraftverlauf (Fp), die Abmessungen (L, R), die Geschwindigkeit (n) und die Massen der einzelnen Teile (mp, m) bekannt sein.

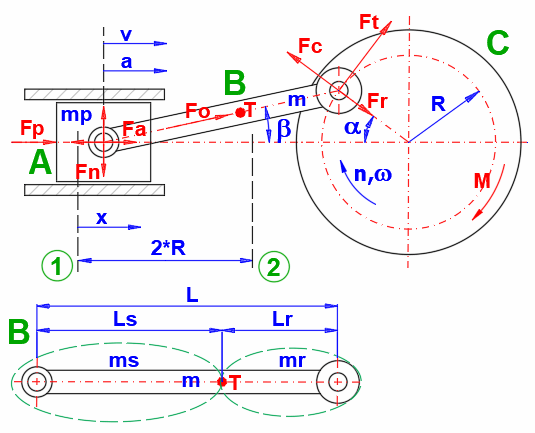
In der Berechnung werden die folgenden Formeln verwendet, um den Verlauf des Moments bei der Kurbelwellenumdrehung zu bestimmen. Die Bedeutung der einzelnen Variablen ist in der Abbildung dargestellt.
β = asin(R / L * sin(α))
λ = R / L
x = R * (1 - cos(α) + λ / 2 * sin(α)^2) ... Abstand vom oberen Drehpunkt (1)
v = R * ω * (sin(α) + λ * sin(α) * cos(α))
a = R * ω^2 * (cos(α) + λ * cos(2 * α))
ω =2 * Pi * n / 60
ms = Lr / L * m
mr = Ls / L * m
Fa = (m + ms) * a ... Beschleunigung/Verzögerung der gerade bewegten Teile
Fn = Fp * tan(β) + Fa * tan(β)
Ft = Fp * (sin(α) + λ * sin(2 * α) + Fa * (sin(α) + λ * sin(2 * α)
Fo = Fp / cos(β)
Fr = Fo * cos(α + β)
Fc = mr * R * ω^2 ... Zentrifugalkraft der Pleuelstange auf die Kurbel
M = R * Ft ... Moment aus Belastungskraft Fp und Beschleunigungs-/Verzögerungskraft Fa

Berechnungsverfahren:

Die Berechnung ist für eine schnelle Auslegung des Schwungrads und seine Analyse bestimmt.

Vorläufiges Konzept, Absatz [2]:

- Vorläufiges Konzept des Trägheitsmoments des Schwungrads je nach Typ und Maschinenparametern
- Auslegung der Schwungradabmessungen anhand des Trägheitsmoments
- Überprüfung der Spannung, Überprüfung der max. Drehzahl, Überprüfung des Kreiselmoments

Detaillierte Analyse, Absatz [3]:

Wenn Sie die Momentenkurve der Maschine kennen, für die Sie ein Schwungrad konzipieren wollen, definieren Sie die Kurve anhand einer Tabelle. So ermitteln Sie schnell das erforderliche Trägheitsmoment für die gewünschte Ungleichförmigkeit oder die Ungleichförmigkeit für das vorgegebene Trägheitsmoment (Analysis A).

Wenn Sie die Kombination Maschine x Elektromotor (Maschine x Generator) gestalten wollen, verwenden Sie Analysis B.

Tipp: Studieren Sie möglichst die Beispiele am Ende des Leitfadens.

Berechnungseinheiten, Maßeinheiten-Umwandlung [1]

In diesem Absatz werden die Einheiten der Berechnung eingestellt.

1.1 Berechnungseinheiten

In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.

1.2 Maßeinheiten-Umwandlung

In das Eingabefeld auf der linken Seite geben Sie den Wert ein, den Sie übertragen wollen. Verdoppeln Sie die Quelleneinheiten und auf der rechten Seite wählen Sie die Zieleinheiten.

Konzept und Berechnung des Trägheitsmoments und der Abmessungen des Schwungrads [2]

- Vorläufiges Konzept des Trägheitsmoments für den gewählten Maschinentyp.
- Auslegung der Abmessungen des Schwungrads anhand des Trägheitsmoments.
- Berechnung des Trägheitsmoments anhand der Abmessungen des Schwungrads.
- Berechnung der Energie des rotierenden Schwungrads, Berechnung der maximalen Spannung.
- Umrechnung der Trägheitsmomente von Massen, die mit unterschiedlichen Geschwindigkeiten rotieren.
- Berechnung der Zeit für das Ankurbeln des Schwungrads.
- Berechnung des Kreiselmoments und der Drehkräfte.

2.1 Vorläufiges Konzept des Trägheitsmoments des Schwungrads

Anhand des Maschinentyps, der Leistung und der Schwungraddrehzahl lässt sich das erforderliche Trägheitsmoment des Schwungrads abschätzen.

Wählen Sie den Maschinentyp (und damit die Konstante C, die ihn charakterisiert), geben Sie die Nennleistung, die Schwungraddrehzahl und den gewünschten Ungleichförmigkeitsgrad ein.

Hinweis: Hubkolbenmotoren und Verdichter haben bekannte Lastmomentverläufe. In der Literatur finden sich daher zahlreiche Studien, die die Konstante C ziemlich genau einschätzen. Bei anderen Maschinen lassen sich die Lastmomentverläufe in der Regel nicht allgemein charakterisieren. Wenn Sie jedoch z. B. eine modifizierte Version einer bestehenden Maschine konzipieren, ist es möglich, die Konstante C anhand der bestehenden Lösung recht genau zu schätzen.
In Kapitel [3.0] können Sie dann das Trägheitsmoment des Schwungrades mit ausreichender Genauigkeit bestimmen.

2.6 Ungleichförmigkeitsgrad

Die folgenden Werte werden für verschiedene Maschinenbereiche empfohlen.

Maschinentyp / Ungleichförmigkeitsgrad (δ)
Zerkleinerungsmaschinen.....0.200
Elektrische Maschinen.....0.003
Elektrische Maschinen (Direktantrieb).....0.002
Riemengetriebene Motoren.....0.030
Getriebe mit Zahnrädern.....0.020
Hämmer.....0.200
Pumpmaschinen.....0.03-0.05
Werkzeugmaschinen.....0.030
Papiermaschinen.....0.015
Textil- und Webmaschinen.....0.010-0.025
Stanz-, Scher- und Pressmaschinen.....0.10-0.15
Spinnmaschinen.....0.10-0.020
Walz- und Bergbaumaschinen.....0.025
Gleichstromgeneratoren.....0.006-0.013
Wechselstromgeneratoren…..0.003-0.015
Fahrzeugverbrennungsmotoren.....0.003-0.006

Anmerkung: Grad der Ungleichmäßigkeit des Laufs
δ = (ωmax - ωmin) / ωm
ωmax ... maximale Winkelgeschwindigkeit
ωmin ... minimale Winkelgeschwindigkeit
ωm = (ωmax - ωmin) / 2 ... mittlere Winkelgeschwindigkeit

2.8 Vorläufiges Konzept der Schwungradabmessungen

Anhand des Soll-Trägheitsmoments können Sie die Abmessungen des Schwungradturms festlegen.
Geben Sie das erforderliche Trägheitsmoment, die Dichte des verwendeten Materials, das Verhältnis von Breite und Höhe des Schwungradkranzes und den Soll-Innendurchmesser an.

2.9 Soll-Trägheitsmoment

Es wird das Trägheitsmoment aus dem vorläufigen Konzept angesetzt. Für die Eingabe vom eigenen Wert die Schaltfläche rechts anklicken.

2.10 Dichte des Schwungradmaterials

Stahl 7800 [kg/m³]; 487 [lb/ft³]
Gusseisen 7200 [kg/m³]; 450 [lb/ft³]
Bronze 8800 [kg/m³]; 550 [lb/ft³]
Aluminium 2700 [kg/m³]; 168 [lb/ft³]
Hartholz 680 [kg/m³]; 42 [lb/ft³]

2.18 Maximale Drehzahl, maximale Spannung

Die größte Spannung in einem rotierenden Ring ist die tangentiale Spannung auf der Innenseite des Rings.
Geben Sie die maximal zulässige Spannung und die Poisson-Konstante des Materials ein.
Geben Sie die Drehzahl ein. Das grüne Feld zeigt den maximalen Drehzahlwert für die angegebene maximal zulässige Spannung an.
Nach Betätigung der Schaltfläche "==>" werden die berechneten Bemessungswerte in die ausgewählte Tabellenzeile übernommen.

2.19 Maximal zulässige Spannung

Gusseisen ... < 8-10 MPa (1.16 - 1.45 kpsi)
Gussstahl ... < 100 MPa (14.5 kpsi)

2.20 Poissonzahl

Stahl ... 0.27-0.30
Gusseisen ... 0.21-0.26
Aluminiumlegierungen ... 0.33
Kupfer ... 0.33
Magnesium ... 0.35
Titan ... 0.34

2.21 Drehzahl des Schwungrads

Voreingestellt ist die Drehzahl von Zeile [2.5]. Für die Eingabe von eigenen Werten die Schaltfläche rechts anklicken.

2.23 Tangentiale Spannung am Innendurchmesser

Die berechnete Spannung sollte unter dem zulässigen Höchstwert liegen [2.19]

2.25 Abmessungen und Berechnung des Schwungrads (der Trägheitsmassen)

Sie können bis zu 12 verschiedene Ringe in der Tabelle definieren, um eine komplexere Schwungradform zusammenzustellen oder die Massen mit unterschiedlicher Drehgeschwindigkeit neu zu berechnen.

Die Schaltfläche "Clear" löscht die Dimensionswerte in der gesamten Tabelle mit Ausnahme der ersten Zeile.
Mit dem Drücken der Taste "V" wird der Wert aus der ersten Zeile in die übrigen Zeilen übertragen.
Die Schaltfläche "min/max" füllt den Außen-/Innendurchmesser des Rings aus, um die Spannung auf den Außen-/Innendurchmesser zu berechnen.

Tipp: Wenn es andere rotierende Massen (Zahnräder, Riemenscheiben usw.) gibt, die über ein Getriebe mit dem Schwungrad verbunden sind, können Sie diese hinzufügen, indem Sie sie in der Tabelle definieren und ihnen die entsprechende Drehzahl zuweisen. Das gesamte reduzierte Trägheitsmoment wird durch das Übersetzungsverhältnis zu der erste Zeile umgerechnet und steht in der Spalte „Ired“.

Markierung der Spalten
Anzahl: multipliziert die berechneten Werte (mehrere identische rotierende Massen)
a: Verschiebung des Rings (Zylinders) im Diagramm in der X-Achse
D, d, b: Abmessungen des Rings (Zylinders)
Ro: Dichte
ny: Poissonsche Konstante
n: Umdrehungen
ω: Winkelgeschwindigkeit
rg: Trägheitsradius
m: Masse
I: Trägheitsmoment
Ired: Reduziertes Trägheitsmoment (umgerechnet über die Geschwindigkeit erster Ordnung)
Ek: Kinetische Energie der rotierenden Scheibe
dx: Durchmesser, für den die Reibungsspannung berechnet wird
σt: Tangentiale Spannung

2.26 Ankurbeln des Schwungrads

Berechnung von Energie und Zeit, die erforderlich sind, um das Schwungrad mit dem angegebenen Trägheitsmoment auf die gewünschte Drehzahl zu bringen.
Die voreingestellten Werte stammen aus der obigen Tabelle, nach dem Anklicken der Schaltfläche können Sie Ihre eigenen Werte eingeben.

2.33 Kreiselmoment

Wenn sich das Schwungrad um eine andere Achse als die Drehachse dreht, wird ein Kreiselmoment erzeugt. Bei größeren Trägheitsmomenten und höhere Drehzahlen kann er von Bedeutung sein und sollte bei den Berechnungen berücksichtigt werden. Die voreingestellten Werte stammen aus der obigen Tabelle, nach dem Anklicken der Schaltfläche können Sie Ihre eigenen Werte eingeben.

2.41 Diagramm

Die Objekte aus Tabelle [2.25] werden in das Diagramm eingezeichnet.
Die Koordinate „a“ in der Tabelle definiert die Verschiebung in der X-Achse.

Analyse (Berechnung) des Schwungrads [3]

Bei Motoren und Maschinen, bei denen die Drehbewegung in eine geradlinige Bewegung umgewandelt wird, und bei Maschinen ohne konstante Last treten Momentschwankungen auf. Es gibt kein konstantes Gleichgewicht zwischen den wirkenden Momenten (Antriebsmoment, angetriebenes Moment, Trägheitskräfte, passive Widerstände). Dadurch ändert sich die Winkelgeschwindigkeit während des Arbeitszyklus. Um diese Ungleichheit zu verringern, wird ein Schwungrad als Energiespeicher verwendet, der bei überschüssigem Drehmoment Energie speichert und bei fehlendem Drehmoment wieder abgibt.

Ein großer Teil der Maschinen hat einen Momentenverlauf, der sich nicht einfach analytisch beschreiben lässt. Daher werden für die Lösung numerische Integrationsmethoden verwendet. Der Momentenverlauf auf der linken Seite ist durch die Momenten-Tabelle in Abhängigkeit von der Drehung des Schwungrades definiert. Das Moment auf der rechten Seite kann sein:

A. Konstant
B. Abhängig von der Drehzahl des Schwungrads (Elektromotor, Generator)
C. Oder kann durch eine eigene Tabelle oder Funktion definiert werden

!!! Bei der Analyse ist wie folgt vorzugehen !!!

1. In die Tabelle [3.45] den Momentenverlauf der zu analysierenden Maschine eintragen
2. Die Schwungradparameter [3.1] eingeben
3. Die Analyse A oder B oder C starten
4. Die Ergebnisse der Analyse finden Sie in den Zeilen [3.28-3.42], in der Tabelle [3.45] und in den Diagrammen

Tipp: Zur schnellen Orientierung beginnen Sie immer mit der Analyse A

3.1 Sollparameter Schwungrad

Sie können entweder das Trägheitsmoment eingeben und das Ergebnis der Analyse ist der Ungleichförmigkeitsgrad, oder Sie können durch Anklicken der Schaltfläche rechts Ungleichförmigkeitsgrad eingeben und das Ergebnis ist das entsprechende Trägheitsmoment.

Hinweis: Zunächst muss die Tabelle [3.45] mit dem Momentenverlauf der analysierten Maschine ausgefüllt werden.

Hinweis: Obwohl hier das Schwungrad erwähnt wird, handelt es sich in Wirklichkeit um die Summe der Trägheitsmomente aller rotierenden Massen, die mit dem Schwungrad verbunden sind (z.B. das Trägheitsmoment des Elektromotors, Kurbelwelle, Zahnräder, Kupplungen...usw.). Wenn die angeschlossenen rotierenden Massen unterschiedliche Drehzahl haben, muss das reduzierte Trägheitsmoment in Schwungraddrehzahl umgerechnet werden - siehe vorheriger Absatz.

Tipp: Das ungefähre Trägheitsmoment des Elektromotors siehe Zeile [3.21]

3.3 Ungleichförmigkeitsgrad

Die folgenden Werte werden für verschiedene Maschinenbereiche empfohlen.

Maschinentyp / Ungleichförmigkeitsgrad (δ)
Zerkleinerungsmaschinen.....0.200
Elektrische Maschinen.....0.003
Elektrische Maschinen (Direktantrieb).....0.002
Riemengetriebene Motoren.....0.030
Getriebe mit Zahnrädern.....0.020
Hämmer.....0.200
Pumpmaschinen.....0.03-0.05
Werkzeugmaschinen.....0.030
Papiermaschinen.....0.015
Textil- und Webmaschinen.....0.010-0.025
Stanz-, Scher- und Pressmaschinen.....0.10-0.15
Spinnmaschinen.....0.10-0.020
Walz- und Bergbaumaschinen.....0.025
Gleichstromgeneratoren.....0.006-0.013
Wechselstromgeneratoren…..0.003-0.015
Fahrzeugverbrennungsmotoren.....0.003-0.006

Anmerkung: Grad der Ungleichmäßigkeit des Laufs
δ = (ωmax - ωmin) / ωm
ωmax ... maximale Winkelgeschwindigkeit
ωmin ... minimale Winkelgeschwindigkeit
ωm = (ωmax - ωmin) / 2 ... mittlere Winkelgeschwindigkeit

3.4 Mittlere Soll-Drehzahl des Schwungrads

Geben Sie die gewünschte Schwungraddrehzahl ein.

3.7 A. Analyse-konstantes Moment (rechte Seite)

Grundlegende Analyse, die in allen Fällen anwendbar ist.

Bei dieser Berechnung wird der Energiegewinn (-verlust) aus der Momentenkurve auf der linken Seite berechnet. Daraus ergibt sich das konstante Moment, das auf der rechten Seite wirken muss, damit die Summe der Energien gleich Null ist.

Anhand der einwirkenden Momente (links + rechts) ergibt sich der Verlauf der Winkelgeschwindigkeit (Drehzahl) und damit die Ungleichförmigkeit für das vorgegebene Trägheitsmoment des Schwungrads. Alternativ wird das Trägheitsmoment des Schwungrads für den eingegebenen Ungleichförmigkeitsgrad bestimmt.

3.8 Leistung (Leistungsaufnahme)

Leistung + (Leistungsaufnahme -) des Geräts auf der rechten Seite, um das erforderliche konstante Drehmoment (mittleres Moment Tm) zu erzeugen.

3.10 B. Analyse-Elektromotor/Generator (rechte Seite)

Ein Sonderfall der Analyse, bei dem ein Asynchronmotor/Generator (rechts) an das Gerät (links) angeschlossen ist.

Zusätzlich zu der Bedingung, dass die Summe der Energien der linken und rechten Seite gleich Null ist, muss beachtet werden, dass das Drehmoment des Elektromotors/Generators eine Funktion der Schwungraddrehzahl ist.

Bei dieser Berechnung wird das Motordrehmoment wiederholt (siehe Anzahl der Iterationsschritte) in Abhängigkeit von der aktuellen Schwungraddrehzahl angesetzt, wobei der gesamte Zyklus nach jeder Änderung neu berechnet wird. Nach jedem Iterationsschritt wird dann die Schwungraddrehzahl zu Beginn des Zyklus entsprechend angepasst. In der Regel konvergiert das gesamte Modell schnell genug für weniger als zehn Iterationsschritte.

Hinweis: Ist der Ungleichförmigkeitsgrad größer als 0,05 oder wird ein Motor mit einer Leistung nahe dem oberen empfohlenen Wert verwendet, kann die Lösung instabil werden. In diesem Fall konvergiert das Modell nicht. Da diese Lösung in der Regel für höhere Werte des Ungleichförmigkeitsgrades gilt, kann die A-Analyse bedenkenlos verwendet werden.

3.12 / 4.2 Typ des Motors/Generators

Einen Motor aus der Liste auswählen.

Motoren werden in der Form „Synchrondrehzahl/Polzahl...Stromnetzfrequenz“ angegeben

3.13 Empfohlene Nennleistung von/bis

Empfohlenes Motor- (Generator-) Leistungsintervall, geschätzt aus dem Momentenverlauf auf der linken Seite.

3.14 / 4.3 Nennleistung

Die Motorleistung eingeben. Anhand der Leistung werden die ungefähren Motorparameter (nr, Tz...) festgelegt

Katalogwerte der Motorenhersteller.

kW (50Hz):
0.06; 0.09; 0.12; 0.18; 0.25; 0.37; 0.55; 0.75; 1.1; 1.5; 2.2; 3; 3.7; 4; 5.5; 7.5; 9; 11; 15; 18.5; 22; 30; 37; 45; 55; 75; 90; 110; 132; 160; 200; 225; 250; 280; 315; 355; 400; 450; 500; 560; 630; 710; 800; 900; 1000

HP (60Hz):
0.25; 0.33; 0.5; 0.75; 1; 1.5; 2; 3; 4; 5; 5.5; 7.5; 10; 12; 15; 20; 25; 30; 40; 50; 60; 75; 100; 120; 150; 180; 210; 270; 300; 335; 375; 420; 475; 530; 600; 670; 750; 850; 950

3.15 / 4.4 Betriebsart

Der Motor kann auch als Stromgenerator fungieren. (Überschwingen der Synchrondrehzahl und mechanische Energieaufnahme).

Über die Anwahl wird die Art des Verhaltens festgelegt.

Beispiel:
Im Motorbetrieb ist beim Überschwingen der Synchrondrehzahl das Moment=0.
Im Motor-/Generatorbetrieb ist beim Überschwingen der Synchrondrehzahl das Moment negativ.

3.16 / 4.5 Synchrondrehzahl

Je nach ausgewähltem Motorentyp eingestellt. Bei dieser Drehzahl ist das Moment gleich Null.

3.17 / 4.6 Nenndrehzahl

Die Nenndrehzahl und der Anlaufmoment-Koeffizient werden direkt für den jeweiligen Motor bestimmt. Im grünen Feld steht der ungefähre Wert für den jeweiligen Motorentyp und die jeweilige Motorleistung.

Nachdem Anklicken der Taste rechts können Sie Ihren eigenen Werte eingeben (nr,Tzcoeff). So lässt sich die Motorcharakteristik genau nach dem Herstellerkatalog einstellen.

Hinweis: In den meisten Fällen wird der Wert der Nenndrehzahl „nr“ mit den Katalogangaben übereinstimmen. Wenn Sie benutzerdefinierte Werte festlegen, sollten diese sehr nahe an den vorgeschlagenen Werten liegen.

3.19 / 4.8 Anlaufmoment-Koeffizient

Für kleine Motoren (≤30 kW) beträgt der Wert in der Regel 2.5-3, für mittlere 2-2.5, für große 1-1.5.

Hinweis: Das Anlaufmoment kann auf verschiedene Weise gestaltet werden (Eliminieren von Hochstrom). Bei großen Motoren kann der Koeffizient unter 1 liegen, was bedeutet, dass der Motor bei Volllast nicht gestartet werden kann. In diesen Fällen ist es ratsam, sich an den Hersteller zu wenden.

3.21 Trägheitsmoment des Motors / Ie * i

Die erste Zahl gibt das ungefähre Trägheitsmoment des ausgewählten Motors an. Die zweite Zahl wird mit der zweiten Potenz des Übersetzungsverhältnisses „i“ aus der nächsten Zeile multipliziert. So kann es direkt mit dem Trägheitsmoment des Schwungrads verglichen oder davon abgezogen werden.

Tipp: Informationen zur Ermittlung (Umrechnung) der Trägheitsmomente von Massen mit unterschiedlichen Drehzahlen in die Drehzahl des Schwungrads finden Sie in Abschnitt [2.0] (Reduziertes Trägheitsmoment).

3.22 Übersetzungsverhältnis Schwungrad/Motor

Das Übersetzungsverhältnis wird automatisch eingestellt. Es wird so geschätzt, dass die mittlere Soll-Drehzahl des Schwungrads [3.4] nahe an der berechneten Drehzahl liegt.

Nachdem Anklicken der Taste rechts können Sie Ihren eigenen Übersetzungswert eingeben. Dies kann nützlich sein, wenn Sie z. B. das Übersetzungsverhältnis i=1 (Direktantrieb des Schwungrads) einstellen wollen.

3.25 Anzahl der Iterationsschritte / Empfindlichkeit

Iteration

Legen Sie die Anzahl der Iterationsschritte fest. Nach jedem Schritt werden die Tabelle und das Diagramm aktualisiert, so dass Sie die schrittweisen Änderungen verfolgen können.

Tipp: Jeder Iterationsschritt dauert bis zu mehreren Sekunden. Etwa 5-10 Schritte sollten ausreichen, um eine erste Vorstellung vom Verhalten des Modells zu bekommen. Wenn der Zyklus abgeschlossen ist, starten Sie einfach die Analyse neu, die mit den letzten Werten fortgesetzt wird.

Empfindlichkeit

Die Empfindlichkeit bestimmt die Größe der Änderung der anfänglichen Schwungradgeschwindigkeit vor jedem Schritt.

Je größer der Wert, desto größer die Veränderung und desto schneller die Konvergenz. Andererseits kann ein zu großer Wert zu Oszillation oder Nichtfunktionalität der Lösung führen.

Tipp: Es ist ratsam, mit einem Wert von 5 zu beginnen und dann die Empfindlichkeit je nach Verhalten des Modells (Konvergenzrate) zu erhöhen oder zu verringern.

3.27 Analyseergebnisse

Es wird angegeben, für welche Analyse (A, B, C) die angezeigten Ergebnisse gelten.

3.32 Summe aus Energie+/Abweichung in Prozent

Die Summe der Energien auf der linken und der rechten Seite des Schwungrads. Bei stationärem Betrieb (Schwungraddrehzahl zu Beginn und am Ende des Arbeitszyklus ist gleich) muss die Summe nahe Null sein.
Die Prozentzahlen geben die Abweichung der Summe von der Eingangsenergie an (linke Seite). Ein roter Wert bedeutet, dass die Abweichung größer als 1 % ist.

3.33 Schwungrad

Zusammenfassende Ergebnisse der Schwungradberechnung.

3.34 Mittlere Schwungraddrehzahl

Voreinstellung der mittleren Schwungraddrehzahl für die Berechnung und die daraus berechneten Winkelgeschwindigkeit.

Analyse A: Der Wert aus der gewünschten Geschwindigkeit wird in die Zelle [3.4] gesetzt
Analyse B, C: Der korrigierte Wert aus dem vorherigen Schritt wird nach jedem Iterationsschritt in die Zelle verschoben (grüne Zelle)

Hinweis: Die Werte bei [3.34, 3.35] sind Eingaben für den letzten Schritt der Iteration, die Werte [3.36-3.42] sind das Ergebnis der Berechnung.

Tipp: Der Wert kann manuell geändert werden, um den Iterationsprozess zu beschleunigen.

3.43 Definition der Momenten-Tabelle (linke Seite)

Bevor Sie die Analyse starten, müssen Sie den Momentenverlauf der zu analysierenden Maschine eingeben (linke Seite).

Definieren Sie in der Tabelle die Schwungradlast in den ersten beiden Spalten A, B.

1) Geben Sie in Spalte A nacheinander die Winkel ein, für die Sie das auf das Schwungrad (linke Seite) wirkende Moment definieren wollen

- die Werte müssen in einer kontinuierlichen Reihe ohne Leerzeilen stehen.
- die Winkel müssen in aufsteigender Reihenfolge eingegeben werden
- die Differenz zwischen den nachfolgenden Winkeln muss nicht regelmäßig sein. Dies kann z. B. für eine sprunghafte Änderung des Moments verwendet werden (die Differenz zwischen den folgenden Winkeln ist klein)

2) In Spalte B geben Sie das auf das Schwungrad wirkende Moment ein. Ein positiver Wert beschleunigt das Schwungrad, ein negativer Wert bremst es ab.

3.44 Anzahl der gültigen Zeilen in der Tabelle

Es ist erforderlich, die Anzahl der gültigen Tabellenzeilen (die in die Analyse einbezogen werden) anzugeben.
Wollen Sie einen anderen Wert als den vorgeschlagenen Wert (grüne Zelle) eingeben, klicken Sie die Schaltfläche an.
Der vorgeschlagene Wert richtet sich nach der ersten leeren Zelle in Spalte B.

3.45 Last- und Ergebnistabelle

In der Tabelle haben Sie in der Spalte A, B (linke Seite) die Momentlast definiert. Die übrigen Spalten sind dann das Ergebnis der gewählten Analyse.

α: Drehwinkel des Schwungrads, für den das Moment in Spalte B definiert ist. Wenn die Taste "+Δ" gedrückt wird, wird die gesamte Spalte so ausgefüllt, dass jeder nachfolgende Wert um die Differenz zwischen der zweiten und ersten Zeile erhöht wird.

Anmerkung: Der Unterschied zwischen den Winkeln muss nicht regelmäßig sein, allerdings muss er ansteigend sein.

Tl: Die Drehmomentkurve der Maschine, die Sie analysieren möchten (linke Seite).
Ti=Tl+Tr: Die Drehmomentkurve, die auf das Schwungrad wirkt. Summe der linken und rechten Seite.
Tr=Tm: Die Drehmomentkurve, die das Drehmoment aus Spalte B ausgleicht.
Analyse A: konstant, Tr = Tm
Analyse B: Iteration, Tr = Te * i
Analyse C: Benutzerdefiniertes Moment
ne: Motordrehzahl abhängig von der Schwungraddrehzahl. ne = n * i
Te: Motordrehmoment. Es ist abhängig von der Drehzahl des ne.
Pwe: Motorleistung.
+-dE: Dem Schwungrad zugeführte (+) / entnommene (-) Energie zwischen dem aktuellen und dem nächsten Drehwinkel (Spalte A).
E: Aktueller Wert der kinetischen Energie bei dem entsprechenden Schwungradwinkel.
n: Umdrehungen für den entsprechenden Schwungradwinkel
dn: Differenz zwischen aktueller und mittlerer Drehzahl
ω: Winkelgeschwindigkeit bei dem entsprechenden Drehwinkel
dω: Variation der Winkelgeschwindigkeit. Die Differenz zwischen der aktuellen Drehzahl für den entsprechenden Drehwinkel und dem Mittelwert
Pw: Leistung des Schwungrads für den entsprechenden Drehwinkel.

3.46 Tabelle 1 - Motor

Drehmoment- und Leistungskurve von Elektromotor/Generator
Achse: X - Geschwindigkeit, (rote vertikale Linie = ns)
Achse: Y.
Blau: Drehmoment [Nm; lbf*ft] + Arbeitsbereich
Grün: Leistung [kWh; HP] + Arbeitsbereich

3.47 Tabelle 2 - Drehmoment, Drehzahl

Drehmoment und Drehzahl
Achse: X - Drehung des Schwungrads
Achse: Y
Dünn Schwarz: Moment linke Seite [Nm; lbf*ft]
Dünn Rot: Drehmoment rechte Seite [Nm; lbf*ft]
Dickes Blau: Summe der Momente [Nm; lbf*ft]
Dickes Grün: Drehzahl des Schwungrads [/min] ( Maßstab rechts)

3.48 Tabelle 3 - Ausgewählte Werte

Wählen Sie in der untenstehenden Tabelle die Kurven aus, die Sie anzeigen möchten.
X - Drehung des Schwungrads

3.49 C. Benutzeranalyse

In der Tabelle bleiben drei Spalten für die Definition des Moments durch den Benutzer (rechte Seite) belassen, zum Beispiel in Abhängigkeit von der Schwungraddrehzahl.

Nach Drücken der Schaltfläche "Tr=O(i)", "Tr=P(i)", "Tr=Q(i)" werden die Werte aus der entsprechenden Spalte in Spalte D (rechts) eingefügt und der gleiche Prozess wie in Analyse B durchgeführt. Die Anzahl der Wiederholungen und die Empfindlichkeit der Iteration richten sich nach der Einstellung in Zeile [3.25] Die Zelle unter der Schaltfläche (mit den Namen "_Const1","_Const2",...) hat keine Funktion und kann z.B. als Eingangskonstante bei der Definition des Moments verwendet werden.

Tipp: Nachdem die Berechnung installiert ist, enthalten die ersten Zeilen Beispiele, die in der Hilfe beschrieben sind und natürlich gelöscht oder geändert und in die restlichen Zellen der entsprechenden Spalte kopiert werden können.

Beispiel 1 "O": Beispiel für die Definition des Moments in Abhängigkeit von der Schwungraddrehzahl

Dieses Beispiel zeigt die Verwendung der folgenden Funktion
T = Konst1 * cos (n / 3360)^0,33
T ... Moment (rechte Seite)
n ... Schwungraddrehzahl
Const1 ... Konstante (drückt in diesem Fall die Größe des Moments bei Drehzahl Null aus)

Beispiel 2 "P": Beispiel für eine Drehmomentdefinition mit Hilfe der Definitionstabelle

Verwendung der linearen Interpolation einer durch einzelne Punkte definierten Momentenkurve.
T = linear2(n;T_User_nT)
T ... Moment (rechte Seite)
n ... Drehzahl des Schwungrads
T_User_nT ... Name der Tabelle, in der die Kurve durch die Folge der Punktepaare definiert ist:
Drehzahl / Moment
Die Tabelle ist auf dem Blatt "Tabellen" definiert.

Beispiel 3 "Q": Beispiel für die Verwendung des ausgewählten Motors aus Abschnitt [4.0].

Dieses Beispiel zeigt, wie der ausgewählte Motor aus Abschnitt 4.0 verwendet werden kann
T = linear2(n * _Const3; T_4_nT) * _Const3
n ... Schwungraddrehzahl
T_4_nT ... Name der Tabelle mit der Kurve T=f(n) aus Abschnitt 4.0
_Const3 ... Übersetzungsverhältnis zwischen Schwungrad und Motor

Motormomentkurven, Leistungswerte, Trägheitsmomente, Gewicht, Wirkungsgrad [4]

Im Bereich der Maschinen- und Anlagenantriebe ist der Asynchronmotor (induction motor) der am häufigsten verwendete Motor. Bei diesem Motor ändert sich das Drehmoment mit der Drehzahl (linear im Arbeitsbereich). Durch den Vergleich der Kataloge mehrerer Hersteller wurde eine Tabelle mit Parametern für jeden beliebigen Motor erstellt.

In diesem Kapitel finden Sie daher die Parameter des ausgewählten Motors (einschließlich Gewichts-, Wirkungsgrad- und Trägheitsmomentschätzungen), Leistung und Drehmoment für andere Drehzahlen als die Nenndrehzahl.

4.2,4.3,4.4,4.5,4.6 a 4.8

Siehe Abschnitte 3.12-3.19

4.10 Motorgewicht (ungefähr)

Gleichstarke Motoren unterscheiden sich natürlich in Konstruktion, Material, Zweckbestimmung und Hersteller. Die Werte für Gewicht und Trägheitsmoment sind daher als Richtwerte zu betrachten.

4.12.4.13 Nennwirkungsgrad IE1, IE2, IE3, IE4

Für genauere Berechnungen ist es hilfreich, den Wirkungsgrad der Motoren und die entsprechenden Kennzeichnungen zu kennen.

Wirkungsgradklassen nach IEC 60034-30-1:2014
(IE = Internationaler Wirkungsgrad):
IE1 Standard-Wirkungsgrad (Standard Efficiency)
IE2 Hoher Wirkungsgrad (High Efficiency)
IE3 Hoher Wirkungsgrad (Premium Efficiency)
IE4 Sehr hoher Wirkungsgrad (Super Premium Efficiency)

Vergleich mit einer anderen Norm
IEC 60034-30-1 NEMA MG1 GB 18613-2012
===========================
IE4 Grade 1 (IE4)
IE3 Premium Efficient (60 Hz) Grade 2 (IE3)
IE2 Energy Efficient (60 Hz) Grade 3 (IE2)

4.14 Berechnung von Moment und Leistung für die angegebene Drehzahl

Geben Sie die Drehzahl ein, für die Sie den Momentwert ermitteln möchten.

Die Drehzahl sollte niedriger als ns sein. Wird die Synchrondrehzahl überschritten, arbeitet der Motor als Generator (bremst und erzeugt elektrischen Strom) und das Moment ist negativ.

4.18 Drehmoment- und Leistungskurve

Drehmoment- und Leistungskurve eines Elektromotors (Generators)
Achse: X - Drehzahl
Achse: Y
Blau: Drehmoment [Nm; lbf*ft]
Grün: Leistung [kWh; HP]
Rot: Drehmoment für die angegebene Geschwindigkeit

Kurbeltrieb [5]

Um eine geradlinige Bewegung in eine Drehbewegung umzuwandeln (und umgekehrt), wird häufig ein Kurbeltrieb verwendet, meist in Kombination mit einem Schwungrad. Für die Auslegung des Schwungrads ist es dann notwendig, den Momentenverlauf zu kennen. Zur Berechnung des Momentenverlaufs müssen der Lastkraftverlauf (Fp), die Abmessungen (L, R), die Geschwindigkeit (n) und die Massen der einzelnen Teile (mp, m) bekannt sein.

5.1 Parameter des Kurbeltriebs

Geben Sie die Parameter des Kurbeltriebs entsprechend der Abbildung ein.

5.2 Gewicht des Gleitteils

Geben Sie die Masse aller Teile an, die eine geradlinige Bewegung ausführen (A).

5.3 Pleuelstangengewicht (gesamt)

Anzugeben ist das Gesamtgewicht der Pleuelstange (B).

5.4 Länge der Pleuelstange

Geben Sie den Achsabstand der Pleuelstange (B) an.

5.5 Schwerpunktposition (T)

Geben Sie den Abstand des Schwerpunkts der Pleuelstange (B) an.

Für Motoren, Verdichter~0,7*L
Für Werkzeugmaschinen~0,5*L
Es ist notwendig, das Gewicht von ms und mr zu bestimmen

5.6 Verteiltes Pleuelstangengewicht

Zur Berechnung der Kräfte wird die Pleuelstange durch zwei Massenpunkte mit dem Gewicht ms (geradlinige Bewegung) und mr (Drehbewegung) ersetzt, die in den Achsen der Pleuelstange wirken.

5.7 Kurbelradius

Geben Sie den Kurbelradius (C) ein.

5.11 Zentrifugalkraft für mr

Zentrifugalkraft, die von der Pleuelstange auf die Kurbel ausgeübt wird.

5.14 Tabelle

Tragen Sie in der Tabelle die Kurbeldrehung in die erste Spalte [α] ein. Sie können die Schaltfläche "+Δ" verwenden, um die gesamte Spalte auf einmal auszufüllen, so dass die Differenz zwischen der ersten und der zweiten Zeile zum Hinzuzählen für jede weitere Zeile verwendet wird.
In der zweiten Spalte geben Sie pro jeweiligen Winkel [α] der Kurbeldrehung die belastende Kraft [Fp] ein. Es kann sich zum Beispiel um eine Druckkraft (Verdichter, Motor) oder eine Bearbeitungskraft (Presse) handeln.

Die nächsten Spalten zeigen die in der Abbildung dargestellten Werte (Spalte C-M).

Die letzten 4 Spalten enthalten ausgewählte Werte aus dem Diagramm [5.16].

5.15 Momentendiagramme

Blau - Gesamtmoment (M)
Dünn schwarz - Moment aus Kraft Fp
Dünn rot - Moment aus Beschleunigung/Verzögerung der beweglichen Teile Fa

5.16 Diagramme für ausgewählte Werte

Wählen Sie die Werte aus, die Sie in der Grafik rechts anzeigen möchten.
Die x-Achse ist der Drehwinkel der Kurbel.

Beispiel 1 - Auslegung des Schwungrads bei einem Einzylinder-Verbrennungsmotor

Verbrennungsmotor:

Bohrung: 72 mm=>Kolbenfläche: 0.004072m^2=>Kraft Fp
Hub: 62 mm=>Kurbelradius: 31 mm
Pleuelstangenlänge: 100 mm
Pleuelstangen-Schwerpunktlage: 70 mm
Kolbengewicht: 0.4 kg
Pleuelstangengewicht: 0.6 kg
Erforderlicher Ungleichförmigkeitsgrad: 0.01
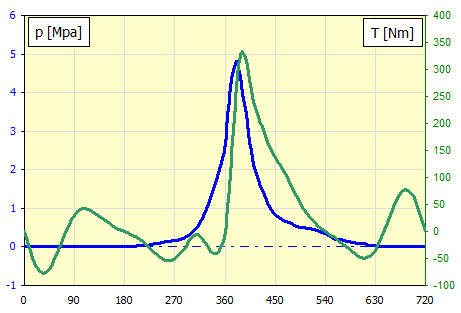
Gemessener Zylinderdruck für 4000/min in Abhängigkeit von der Kurbeldrehung.

1) Kurbeltrieb

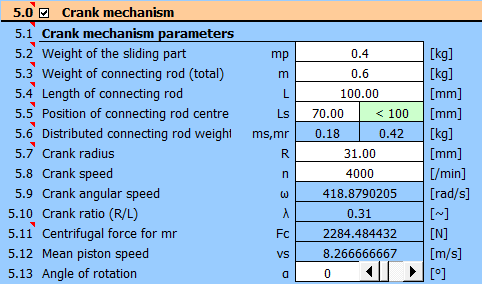
Definieren Sie in Absatz [5] die Parameter des Kurbeltriebs.

Aus dem Druck und der Bohrung erhält man die Kraft Fp für jeden Drehwinkel der Pleuelstange.
Tragen Sie in die Tabelle den Winkel α [°] und die berechnete Kraft ein.

Daraus ergibt sich das Drehmoment "T" für jeden Winkel.

2) Schwungrad

Solldrehzahl vom Schwungrad 4000/min.
Erforderliche Ungleichförmigkeit 0.01

Füllen Sie die Tabelle mit den Winkel- und Momentwerten aus.

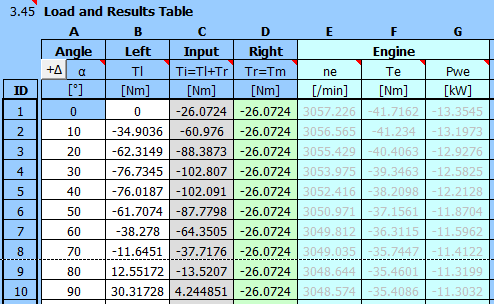
Geben Sie den gewünschten Ungleichförmigkeitsgrad und die gewünschte Drehzahl des Schwungrads ein [3.3, 3.4].

Betätigen Sie die Schaltfläche "A starten". Das erforderliche Trägheitsmoment des Schwungrads wird sofort berechnet.

Das mittlere Moment Tm wird berechnet. Dieses wird als konstante Last verwendet.

Die Ergebnisse werden sofort angezeigt.

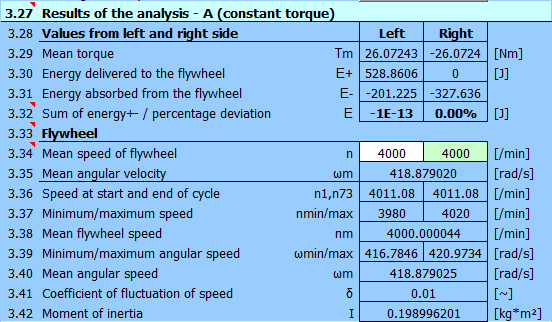
und eine breite Palette von Diagramm-Optionen.

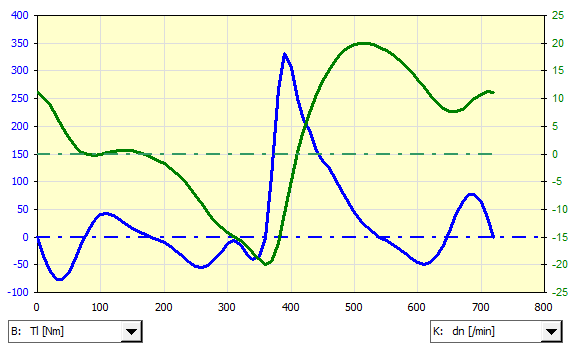
Hier zum Beispiel ein Diagramm des Momentenverlaufs beim Motor und die Schwankungen der Schwungraddrehzahl.

Beispiel 2 - Auslegung eines Schwungrads für einen vom Asynchronmotor angetriebenen Verdichter

Direkt an den Elektromotor angeschlossener Verdichter

Verdichter-Parameter

Kolbendurchmesser: 30 mm
Kurbelradius: 20 mm
Pleuelstangenlänge: 60 mm
Pleuelstangenschwerpunkt: 40 mm
Kolbengewicht: 0.0286 kg
Pleuelstangengewicht: 0.0572 kg
Drehzahl: 3000 U/min
Druckverlauf im Verdichter

Aus dem Druckverlauf und den Parametern des Kurbeltriebes erhält man mit Berechnung [5.0] ein Diagramm und eine Momenten-Tabelle.

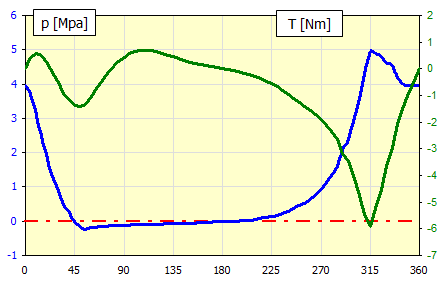
Momenten-Tabelle.

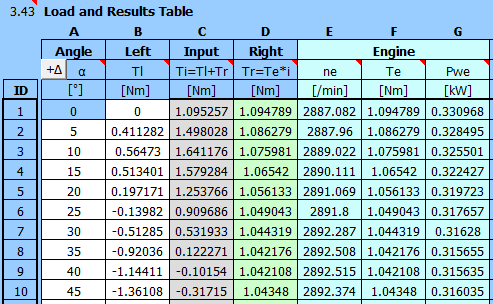
Füllen Sie zunächst die Tabelle [3.43] mit den Winkeln α und den entsprechenden Momenten aus.

Geben Sie die Parameter des Schwungrads ein:
Ungleichförmigkeitsgrad: 0,01
Schwungraddrehzahl: 3000/min

Und Motorparameter:

Zweipoliger Motor, ns: 3000/min
Leistung aus Hilfstabelle: P= 0.55 kW
Übersetzungsverhältnis einstellen auf: i=1.0

Führen Sie Analyse B durch (mehrmals hintereinander).

Bei einer direkten Motor-Verdichter-Verbindung ist es nicht möglich, eine Synchrondrehzahl von 3000/min zu erreichen, da der Asynchronmotor bei Synchrondrehzahl keine Leistung hat. Die Drehzahl stabilisiert sich somit bei einer mittleren Drehzahl von 2900/min aufgrund der Belastung.

Diagramm der Motorleistung und der Drehzahlschwankung um die mittlere Drehzahl (2900/min) während des Arbeitszyklus.

Beispiel 3 - Auslegung eines Schwungrads für eine Kurbelpresse, die von einem Asynchron-Elektromotor angetrieben wird

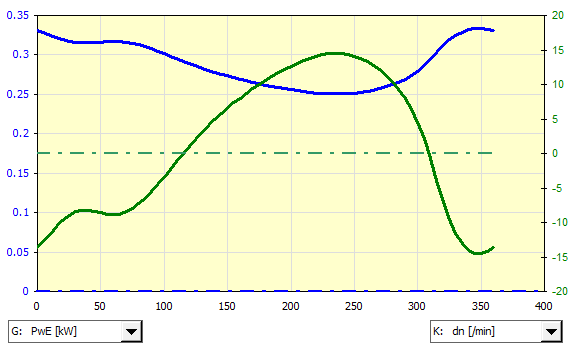
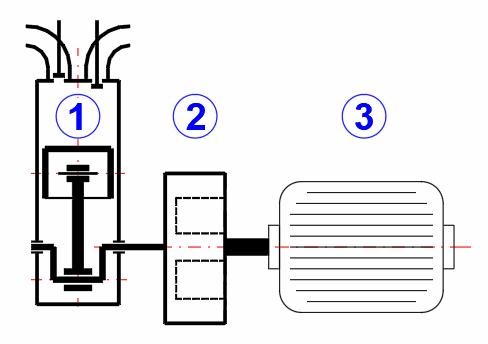
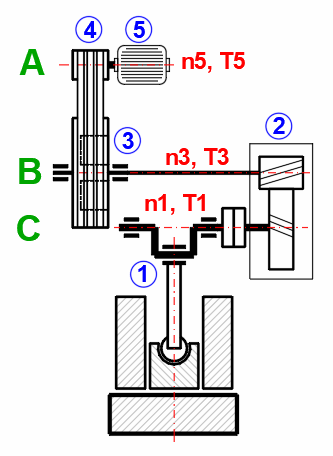
Der Kurbeltrieb (1) ist über ein 5:1-Zahnradgetriebe (2) mit dem Schwungrad (3) verbunden. Das Schwungrad wird von einem Asynchron-Elektromotor (5) über ein Riemengetriebe (4) angetrieben.

Aufgabe:
- Berechnung des Lastmoments T1
- Berechnung des Lastmoments T3
- Bestimmung des Trägheitsmoments des Schwungrads für die angegebene Ungleichförmigkeit
- Bestimmung der erforderlichen Leistung des Elektromotors
- Auslegung der Abmessungen des Schwungrads

1) Kurbelpresse (Mechanismus):

Sollkraft: 10 t
Arbeitsweg: 20 mm
Anzahl der Hübe pro Minute: 30
Gewicht des Gleitteils: 30 kg
Gewicht der Pleuelstange: 30 kg
Länge der Pleuelstange: 400 mm
Schwerpunkt der Pleuelstange: 200 mm
Kurbelradius: 100 mm
Widerstandskräfte: 200 N

Definieren Sie in Absatz [5.0] die Parameter des Kurbeltriebs.

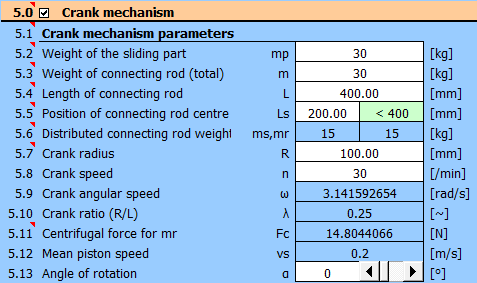
Stellen Sie in der Tabelle den Schritt von 5 Grad ein und tragen Sie die Lastwerte ein.
Gegen die Lastkraft von 10 t~100000 N wirken Kräfte von Gewicht und Widerstand (30 kg + 30 kg +-200 N) = 800 N (400N) für die gesamte Umdrehung.
Kraft 100000 N wirkt ab 325 Grad (22 mm vom oberen Totpunkt)

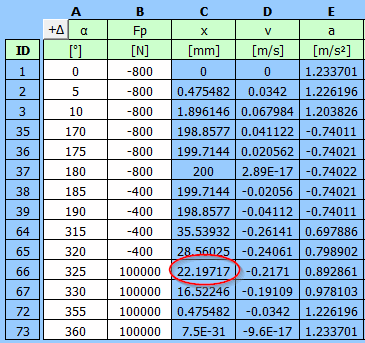
Detaillierte Tabelle mit den eingegebenen Daten für das Moment an der Kurbel T1 und das Moment vor dem 5:1-Getriebe T3.

2) Getriebe

Die Getriebeverzahnung ist 5:1. Die Momentwerte sind in der vorherigen Tabelle angegeben. Schwungraddrehzahl=Umdrehungen am Getriebeeingang n3=30*5=150/min.

3) Schwungrad

Erforderlicher Ungleichförmigkeitsgrad: 0.03
Erforderliche Schwungraddrehzahl: 150/min

Geben Sie den gewünschten Ungleichförmigkeitsgrad und die gewünschte Drehzahl des Schwungrads ein [3.3, 3.4].

Ausfüllen der Momenten-Tabelle

Da das Verhältnis zwischen Kurbeltrieb und Schwungrad 5:1 beträgt, dreht sich das Schwungrad 5 Mal pro Umdrehung des Kurbeltriebs (1 Arbeitszyklus). Die Teilung des Winkels bei der Berechnung des Kurbeltriebs war 5°, die Teilung in der Tabelle für die Schwungradanalyse ist also 5*5=25°

Die Momentwerte T3 können dann direkt in die zweite Spalte (B) kopiert werden.

Eingangsdaten, Analyse

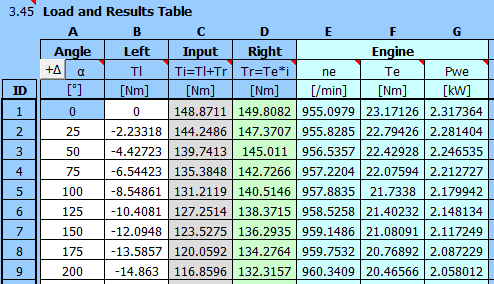
Um den Motor auszuwählen, wählen Sie den Motor 1000/min. Die empfohlene Motorleistung [3.13] wird anhand des Momentenverlaufs (Spalte B) geschätzt.
Wählen Sie aus einer Motorenreihe die Leistung: 3 kW [3.14].
Das Übersetzungsverhältnis zwischen Schwungrad und Motor (Riemenantrieb) wird automatisch eingestellt [3.22], um die gewünschte Schwungraddrehzahl zu erreichen.

Setzen Sie die Anzahl der Näherungsschritte auf 10 und die Empfindlichkeit auf 5 [3,25].

Betätigen Sie die Schaltfläche "B starten". Die 10 Schritte werden nacheinander ausgeführt, wobei das Motormoment wiederholt aus der Schwungraddrehzahl berechnet wird. Die Summe der Energien der rechten und linken Seite [3.32] sollte abnehmen (Erreichen des Gleichgewichtszustands). Sie können die Schaltfläche mehrmals hintereinander drücken, um die Ergebnisse zu präzisieren.

Gleichzeitig wird das entsprechende Trägheitsmoment nachberechnet [3.42].

4) Auslegung der Schwungradabmessungen

In Absatz [2.0] geben Sie das Trägheitsmoment aus dem vorherigen Schritt, die Dichte, das b/h-Verhältnis und den Innendurchmesser ein.

Anmerkung: Falls erforderlich, können alle umlaufenden Massen in die Berechnung einbezogen und ihre Trägheitsmomente anhand der Tabelle [2.25] neu berechnet werden.

Die Parameter des Schwungradkranzes sind in den Zeilen [2.13-2.17] angegeben.

Einstellung der Berechnungen, Sprachenänderung.

Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".

Benutzerspezifische Anpassungen der Berechnung.

Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument  "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.

Liste der Standards, Literaturliste:

Literaturliste:
[1] Strojně technická příručka (Svatopluk Černoch)
[2] Shigley’s Mechanical Engineering Design
[3] Strojírenská příručka (1992)
[4] Machinery’s Handbook (26th Edition)

Standards:
ČSN EN 60034-30-1 :20 14
EN 60034-30-1 :20 14
Rotating electrical machines — Part 30-1: Efficiency classes of line operated AC motors (IE code)
Machines Olectriques tournantes — Partie 30-1: Classes de rendement pour les moteurs a courant alternatif alimentés par le réseau (Code IE)
Drehende elektrische Maschinen — Teil 30-1: Wirkungrad-Klassifizierung von netzgespeisten Drehstrommotoren (IE-Code)

Kataloge und Firmenmaterial:
Siemens
ABB Automation Products