Das Programm ist für die Lösung der häufigsten Ausgaben aus dem Bereich der Mechanik der Flüssigkeiten bestimmt.
Das Programm löst Ausgaben aus den Bereichen:
1. Hydrostatik
2. Stationärer Austritt der Flüssigkeit durch eine Öffnung
3. Stationärer Austritt - Überläufe (ISO 1438, Swiss Engineers, Hansen, Bazin, Frese)
4. Stationäre Strömung einer zähen Flüssigkeit - konstanter Querschnitt der Rohrleitung mit Austrittsdüse/Diffusor
5. Stationäre Strömung der zähen Flüssigkeit - verschiedene Rohrleitungsquerschnitte
6. Hydraulischer Stoß
Die Berechnungen umfassen die Bestimmung der Reynolds-Zahl, der Viskosität, der Verluste für die laminare und turbulente Strömung für verschiedene Materialien und dutzende Verlustkoeffizienten.
Für die Berechnungen werden Daten, Verfahren, Algorithmen und Informationen aus Literatur, Normen und Firmenkatalogen verwendet.
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová,
CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných
přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs
a paroi mince
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument"Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Die Strömungsmechanik ist ein weites Feld, das sich mit der Bewegung und Wirkung von Flüssigkeiten befasst. Diese Berechnungen umfassen einige häufig gelöste Probleme.
Die dynamische Viskosität µ (µ =
"mi") ist ein Maß für die Viskosität eines Fluids (Fluid: Flüssigkeit,
fließender Stoff).
Je höher die Viskosität, desto dicker (weniger flüssig) ist das Fluid; je
niedriger die Viskosität, desto dünner (flüssiger) ist es.
Einheit der dynamischen Viskosität im SI-System: [µ] = Pascal-sekunda (Pa*s) =
N*s/m² = kg/m*s.
Die kinematische Viskosität ν (ν =
"nu") ist die dynamische Viskosität des Mediums µ geteilt durch seine Dichte ρ
(ρ = "Ro").
Gleichung: ν = µ / ρ
SI-Einheit der kinematischen Viskosität: [ν] = m²/s
Häufig verwendete Einheiten sind Stokes (St) und Centistokes (cSt).
Umrechnung:
1 Stoke (St) = e-4 * m²/s = 1 cm²/s
1 cSt = e-6 m²/s = 1 mm²/s
Zur Berechnung der
Viskosität in Abhängigkeit von der Temperatur wird eine ungefähre Formel
verwendet:
µ ~ µ20 * exp(C * (293 / TK - 1))
µ20 ... dynamische Viskosität für 20°C
C ... Koeffizient für eine bestimmte Flüssigkeit
TK ... Temperatur in Kelvin
Der grundlegende Parameter, der das
viskose Verhalten aller Newtonschen Flüssigkeiten bestimmt, ist die
dimensionslose Reynoldszahl.
Sie hängt nicht nur von der mittleren Geschwindigkeit, sondern auch von der
charakteristischen Abmessung der Strömung (Durchmesser d oder dh), der
dynamischen Viskosität und der Dichte ab.
Re = v * d * r / µ, oder Re = v * dh * r / µ für nicht kreisförmige Querschnitte
v ..... Geschwindigkeit
d ..... Durchmesser
r ... Dichte
µ ..... dynamische Viskosität
dh ... hydraulischer Durchmesser
dh = 4 * S/O
S ... Querschnittsfläche
O ... benetzter Umfang
Für einen kreisförmigen Querschnitt ist d = dh.
Empirischer
Ausdruck:
µ / µ20 = exp(C * (293 / T°K - 1))
µ ... dynamische Viskosität
µ20 ... dynamische Viskosität für 20°C
C ... Koeffizient
T ... Temperatur
Unterschiede zur idealen
Flüssigkeitsströmung.
1) Verluste entstehen, wenn ein Teil der mechanischen Energie in Wärme
umgewandelt wird.
2) Die Geschwindigkeit ist nicht gleichmäßig über den Querschnitt verteilt.
3) Die Fluidbewegung kann laminar (Re=Re,cr<2300) oder fast immer turbulent
(Re>3000) sein.
Q = v1 * S1 = v2 * S2
Q ... Durchflussmenge
v1, v2 ... Geschwindigkeit in den Querschnitten 1 und 2
S1, S2 ... Fläche in den Querschnitten 1 und 2
g*h1 + p1/Ro + k1*(v1^2)/2 = g*h2 +
p2/Ro + k2*(v2^2)/2 + ez(1-2)
g ... Erdbeschleunigung
Ro ... Dichte
h1, h2 ... Höhe
p1, p2 ... Druck
v1, v2 ... Geschwindigkeit
ez(1-2) ... Verlustenergie
ez(1-2) = (Zeta + Lambda * (L/dh)) * (v^2/2)
Zeta ........ lokaler Verlustkoeffizient (Eingang, Querschnittsänderung,
Ventil....)
Lambda ... Reibungsverlustkoeffizient
L ............. Länge
dh ........... Durchmesser
v ............. Geschwindigkeit
Lambda ...
Reibungsverlustkoeffizient
Laminare Strömung (Re<2300):
Lambda = 64 / Re
Turbulente Strömung (Re>=2300):
Eine Auswahl von Methoden:
Glattes Rohr:
Lambda = 0,3164 / (Re^0,25) ....... Blasius
Lambda = 1 / (2 * Log10(Re * Lambda^0.5) - 0.8)^2 ......... Nikurdas
Lambda = (1,8 * Log10(Re) - 1,5)^-2 .......... P.K.Konakov
Grobes Rohr:
Lambda = 0,1 * (100 / Re + kr)^0,25 ....... Altus
Lambda = 1 / (-2 * Log10(2,51 / (Re * Lambda^0,5) + 0,27 * kr))^2 ........
Colebrook - Weiß
Lambda = 8 * ((8 / Re)^12 + 1 / (a + b)^1,5)^(1/12) ....... Churchill
a = (2,457 * Log(1 / ((7 / Re)^0,9 + 0,27 * kr)))^16
b = (37530 / Re)^16
Lambda = 1 / (2 * Log10(1 / kr + 1,138))^2 ....... Göttinger Formel
Lambda = 1 / (2 * (Log10((dh/2) / k) + 1,74)^2) ........ Karmansche Formel
kr = k / dh
k ..... Rauhigkeit (Höhe der Rauhigkeit)
dh ... Durchmesser (hydraulischer Durchmesser)
Lambda = 4 * f
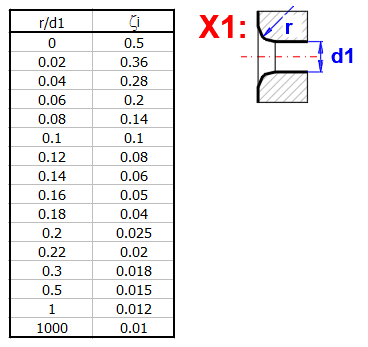
zetaI ... Eingangsverlustkoeffizient (Rundheit)
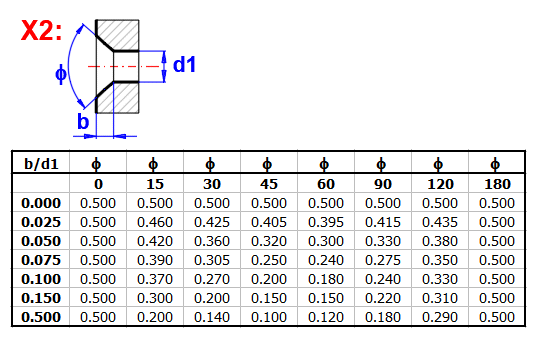
zetaI ... Eingangsverlustkoeffizient (Fase)
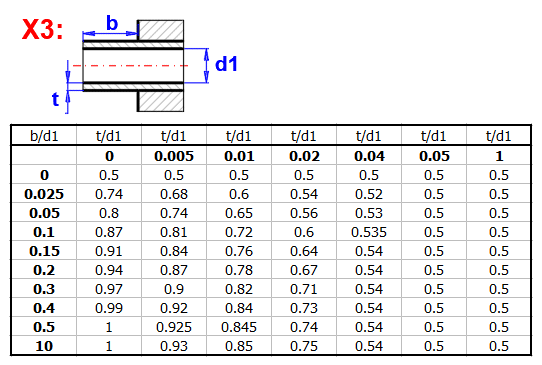
zetaI ... Eingangsverlustkoeffizient (Extrusion)
zetaB ... Verlustkoeffizient ( Biegung)
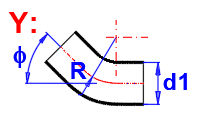
zetaB =(0.131 + 0.16 * (d1 / R)^3.5) * (Fi / 90)
zetaI ... Verlustkoeffizient (Übergang)
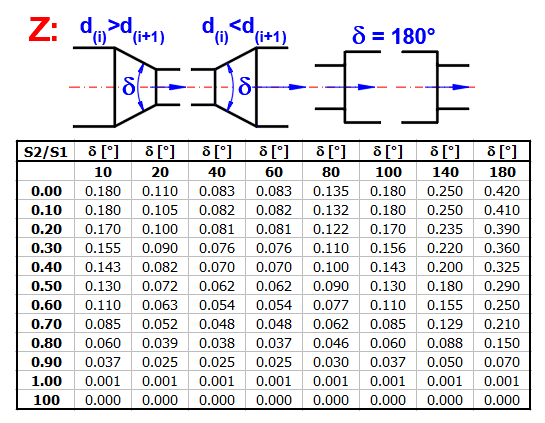
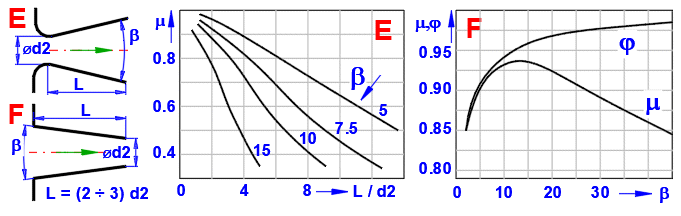
Düse, delta<10: ZetaI = (Lambda / (8
* SIN(delta/2))) * (1 - (S2/S1)^2)
Düse, delta>=10: ZetaI = Tabellenannäherung
Diffusor: ZetaI = (S2/S1 - 1)^2 * SIN(MIN(delta;90))
zetaV ... Ventilverlustkoeffizient
Die Tabelle kann für eine ungefähre Orientierung verwendet werden:
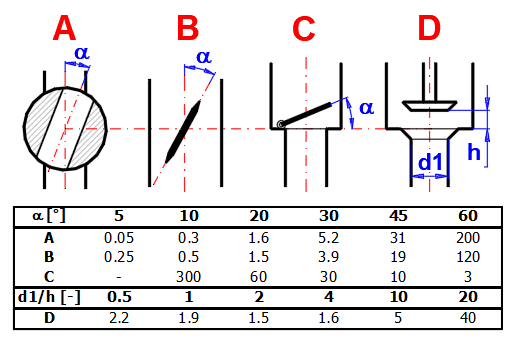
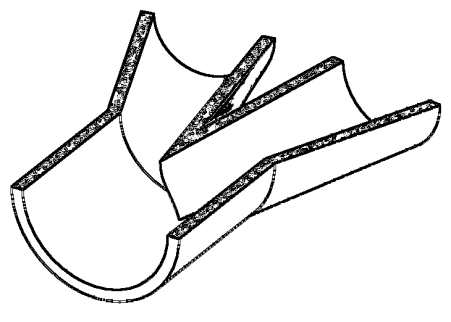
ZetaS ... Verlustkoeffizient für Rohrleitungsspaltung
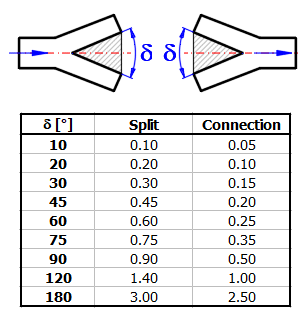
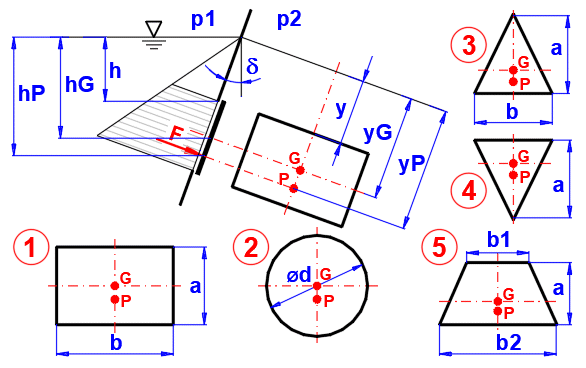
Hydrostatische Kraft:
F = ((p1 - p2) + Ro * g * hG) * S
p1, p2 ... Druck
g ... Erdbeschleunigung
Ro ... Dichte
hG ... Tiefe des Schwerpunkts der Oberfläche
S ... Oberfläche
Druckmittelpunkt y-Abstand:
1. yP = y+(2*a + 3*y)/(a + 2*y) * (a/3)
2. yP = y+(8*y + 5*a) / (2*y + a) * (a/8)
3. yP = y+(4*y + 3*a) / (3*y + 2*a) * (a/2)
4. yP = y+(2*y + a) / (3*y + a) * (a/2)
5. yP = y+(2*y*(b1 + 2*b2) + a*(b1 + 3*b2)) / (3*y*(b1 + b2) + a*(b1 + 2*b2)) * (a/2)
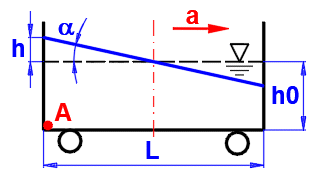
a =
atan(a / g)
a ... Beschleunigung
g ... Erdbeschleunigung
h = L / 2 * tan(a)
L ... Gefäßlänge
Druck auf A:
pA = Ro * (g^2 + a^2)^0,5 * (h0 + dh) * COS (a)
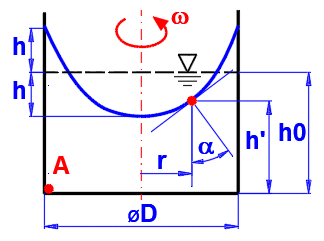
w =
2 * p
* n / 60
n ... Umdrehung
h = (w^2 * (D / 2)^2) / (4 * g)
w ... Winkeldrehzahl
D ... Durchmesser
g ... Erdbeschleunigung
Druck auf A:
pA = 0 - r * g * (-h0 +
h) + 0.5 * r * h^2 *
w^2
h' = h0 - h + r^2 * w^2 / (2 * g)
Die tatsächliche Ausflussgeschwindigkeit der realen Flüssigkeit unterscheidet sich von den theoretischen Werten für ideale Flüssigkeiten. Beim Austritt der Flüssigkeit durch die Öffnung (bzw. den kurzen Stutzen) ist die Berührung mit der Wand gering, sodass auch die Dissipation der Energie gering ausfällt. Daher kann die Flüssigkeit als nicht zäh erachtet werden, sodass die theoretischen Ergebnisse durch die folgenden Korrekturkoeffizienten berichtigt werden können.
j
= v / vt
v .... tatsächliche Austrittsgeschwindigkeit
vt ... theoretische Austrittsgeschwindigkeit
a
= S2' / S2
S' ... tatsächlicher Strömungsquerschnitt
S .... Querschnitt der Blende
m
= a * j = Q / Qt
Q .... tatsächlicher Volumendurchfluss
Qt ... theoretischer Volumendurchfluss
v2t = ((2 * g * (h1 + (p1 - p2) / Ro)
/ (1 - (S2 / S1)^2))^0,5
g ... Erdbeschleunigung
Ro ... Dichte
p1, p2 ... Druck
S1, S2 ... Fläche
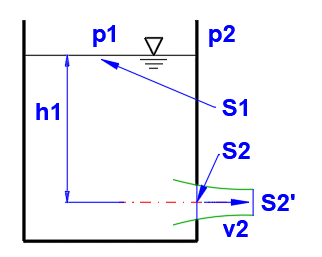
v2 = j * v2t
Qt = S2 * v2t
Q = a * S2 * j * v2t = m * Qt
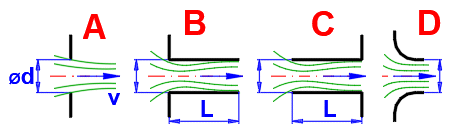
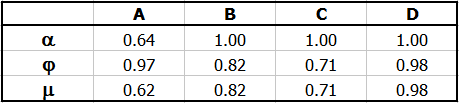
Koeffizient m vs. Re für Auslass Typ A ohne Düse.
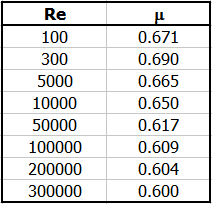
Re = v2t * d / n
n ... Kinematische Viskosität
Bei großen Öffnungen (Oberkante nahe der Oberfläche und Verhältnis von Öffnungshöhe zu Schwerpunkttiefe nahe eins) muss eine nichtlineare Verteilung der Abflussgeschwindigkeit berücksichtigt werden.
Rechteckiges Loch
Q = m * b * (2 * g)^0.5 * ((h + a)^(3/2) -
h^(3/2))
Rundes Loch
Q = m * p * r^2 * (2
* g * hG)^0.5 * (1 - 1/32 * (r / hG)^2 - 5/1024 * (r / hG)^4)
r = d / 2
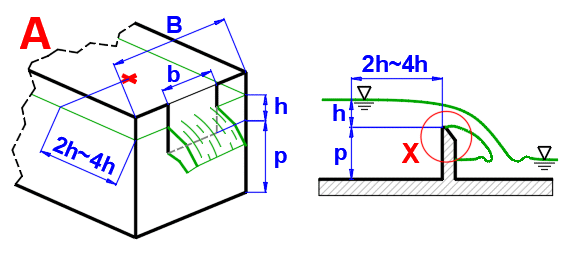
Der Überlauf ist unter dem Aspekt der Hydraulik ein Ausfluss mit großer Öffnung, ohne obere Wand über dem Strahl (Abb. A). Der Überlauf kann perfekt sein, wenn der Spiegel hinter dem Überlauf niedriger als die Überlaufkante ist, oder unvollkommen (geflutet) sein, sofern der Spiegel hinter dem Überlauf höher ist (Abb. B). Vollkommene (perfekte) Überfälle werden zur Bestimmung der Durchflussmenge der Flüssigkeit verwendet. Der Form nach können die Überläufe rechteckig, dreieckig, trapezförmig und kreisförmig sein.
Die Höhe des Spiegels h ist in ausreichendem Abstand vor dem Überlauf zu messen (in der Regel 2h - 4h). Über dem Überlauf ist der Spiegel niedriger, da sich ein Teil der potentiellen Energie bereits in kinetische Energie verwandelt hat.
Volumendurchsatz (ISO 1438)
Q = Cd * (2/3) * (2 * g)^0,5 * be * he^(3/2)
Cd ... Abflusskoeffizient
g ... Erdbeschleunigung
be ... effektive Breite
he ... effektive Überlaufhöhe
he = h + 0,001
be = b + kb
Volumendurchsatz (Allgemeine
Formel)
Q = 2/3 * Cd * b * h * (2 * g * h)^0,5
b ... Breite
h ... Überlaufhöhe
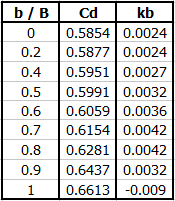
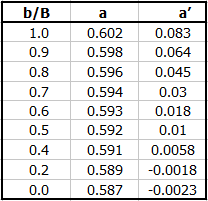
Durchflusskoeffizient (ISO 1438)
Cd = a + a' * (h / p)
abhängig von b/B
Durchflusskoeffizient
(Verein Schweizerischer Ingenieure)
Cd = 0.615 * (1 + (1 / (1000 * h + 1.6))) * (1 + 0.5 * (h / p)^2)
Durchflusskoeffizient
(Hansen)
Cd = 0.61706 / (1 - 0.35815 * (h^3)^0.5)
Durchflusskoeffizient
(Bazin)
Cd = (0.6075 + 0.045 / h) * (1 + 0.55 * (h / (h + p))^2)
Durchflusskoeffizient
(Frese)
Cd =
(0.5755+0.017/(h+0.18)-0.075/(b+1.2))*(1+(0.25*(b/B)^2+0.025+0.0375/((h/(h+p))^2+0.02))*(h/(h+p))^2)
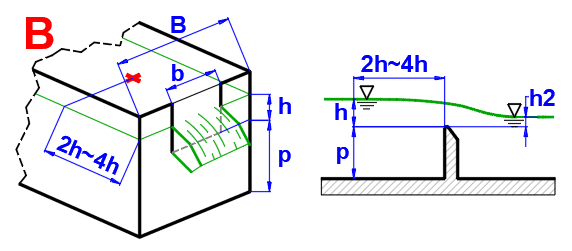
Volumendurchsatz (ISO 1438)
Q = f * Cd * (2/3) * (2 * g)^0,5 * be * he^(3/2)
f ... Durchflusskoeffizient
für h/p=0.5, f =1.007 * ((0.975 - h2/h)^1.45)^0.265
für h/p=1.0, f =1.026 * ((0.960 - h2/h)^1.55)^0.242
für h/p=1.5, f =1.098 * ((0.952 - h2/h)^1.75)^0.22
für h/p=2.0, f =1.155 * ((0.950 - h2/h)^1.85)^0.219
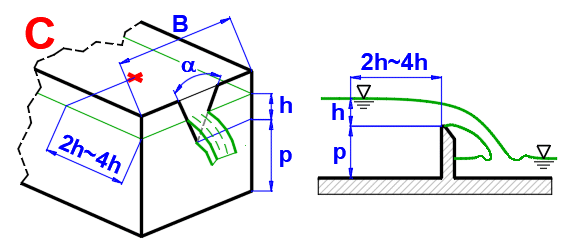
Volumendurchsatz (ISO 1438)
Q = Cd * (8/15) * TAN(alfa/2) * (2 * g)^0.5 * he^(5/2)
he ... effektive Höhe des Überlaufs
Eine häufig zu lösende Aufgabe, für Rohrleitungen mit konstantem Querschnitt, Krümmungen, Ventile etc. Zur Berechnung wird die universelle Bernoulli-Gleichung unter Verwendung der Verlustbeiwerte herangezogen.
Berechnung des Durchflusses, der Geschwindigkeiten, der Verluste, der Leistung in der Rohrleitung eines konstanten Querschnitts.
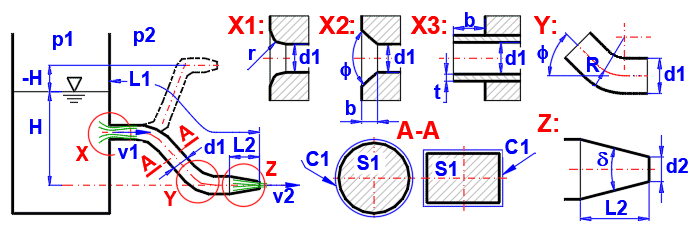
Berechnung der
Abflussgeschwindigkeit:
v2 = ((2 * g * (H +((p1 - p2) / (Ro * g))))/((ZetaI + Lambda * ((L1-L2) / dh1) +
ZetaBV) * (dh2 / dh1)^4 + (1 + ZetaO)))^0.5
g ..... Erdbeschleunigung
H ..... Höhe der Oberfläche
p1, p2 ... Druck
dh1, dh2 ... hydraulischer Durchmesser
L1,L2 ... Länge
Ro ... Dichte
Lambda ... Reibungsverlustkoeffizient
ZetaI ... Eingangsverlustkoeffizient
ZetaBV ... Verlustkoeffizient von Bögen+Ventilen
ZetaO ... Verlustkoeffizient Düse/Diffusor
ZetaO ... Verlustkoeffizient
Düse/Diffusor
Numerische Integration (100 Schritte), sequentielle Berechnung von Sx, vx, Rex,
Lambdax, hzx und aus der Gesamtverlusthöhe hz den ZetaO-Koeffizienten bezogen
auf die Ausströmgeschwindigkeit v2
Für Diffusor und Deltawinkel > 10°
ZetaO = ((S2 / S1) - 1)^2 * SIN(delta)
Für die Berechnung wird die Bernoulli-Gleichung unter Nutzung der Verlustkoeffizienten zur Berechnung der Austrittsgeschwindigkeit vo verwendet.
Berechnung des Durchflusses, der Geschwindigkeiten, der Verluste, der Leistung in der Rohrleitung verschiedener Querschnitte und der Anzahl der Zweige.
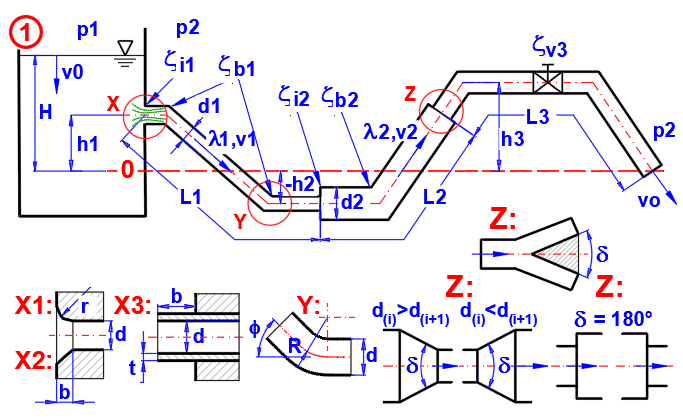
A = 2 * g * (v0^2 / (2 * g) + (p1 - p2) / (Ro * g) + H)
B(i) = (Zeta(i) + Lambda(i) * L(i) / dh(i)) * n(i) * (So / S(i))^2
vo = (A / (1 + SB(i)))^0.5
[i = 1 .... 15]
g ..... Erdbeschleunigung
H ..... Höhe der Oberfläche
p1, p2 ... Druck
v0 ... Oberflächengeschwindigkeit
dh(i) ... hydraulischer Durchmesser
L(i) ... Länge
n(i) ... Anzahl der parallelen Rohre
So ... Ausgangsquerschnitt
S(i) ... Rohrquerschnitt i
Ro ... Dichte
Lambda ... Reibungsverlustkoeffizient
Zeta ... Summe der Verlustkoeffizienten zetaI, zetaB, zetaV
Die Berechnung der Verlustkoeffizienten ist oben beschrieben.
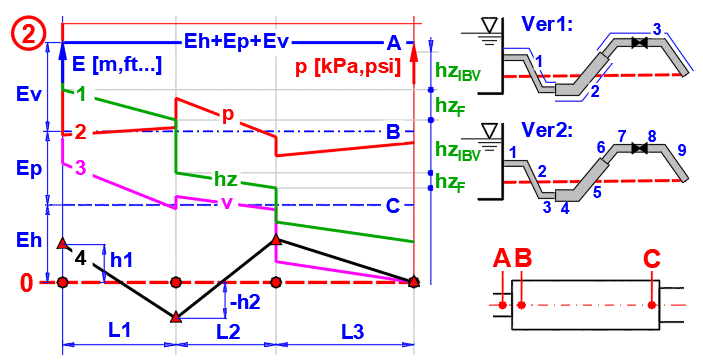
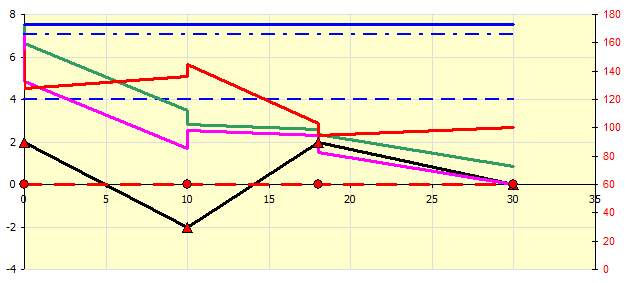
Musterdiagramm
Bei der Regelung des Durchflusses der Flüssigkeit durch die Rohrleitung entsteht eine nichtstationäre Strömung. Vor dem Ventil bildet sich bei einer Verringerung des Durchflusses ein höherer Druck als hinter ihm. Bei langen, eine Flüssigkeit transportierenden Rohrleitungen kann einem schnellen (notfallbedingten) Schließen der Rohrleitung eine derartiger Druckanstieg erfolgen, der die Rohrleitung beschädigen könnte.
Beim Schließend der Rohrleitung wird die kinetische Energie der Flüssigkeit schrittweise für ihre Kompression, ggf. für die Deformation der Rohrleitung verbraucht. Die Stoßwelle breitet sich in der Rohrleitung mit Schallgeschwindigkeit in der jeweiligen Flüssigkeit in Richtung B->A und zurück A->B aus.
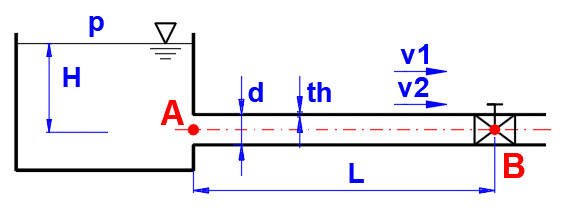
Die Laufzeit der Welle t
t = 2 * L / a
L ... Länge des Rohrs
a ... Geschwindigkeit des Schalls
Schallgeschwindigkeit at
[m/s] (theoretisch, für ein vollkommen starres Rohr)
at = (K / Ro)^0.5
K ..... Volumenmodul der Flüssigkeit
Ro ... Dichte
Schallgeschwindigkeit a
[m/s] (dünnwandiges Rohr, th =< 0.1*d)
a = (K / Ro)^0.5 / (1 + (K*d) / (E*th))^0.5
E ... Elastizitätsmodul des Rohrmaterials
d ... Durchmesser des Rohres
th ... Wanddicke des Rohres
Schallgeschwindigkeit a
[m/s] (dickwandiges Rohr, th > 0.1*d)
a = (K/Ro)^0.5 / (1 + 2 * (K/E) * ((D^2 + d^2) / (D^2 -
d^2)))^0.5
E ... Elastizitätsmodul des Rohrmaterials
d ... Innendurchmesser des Rohres
D ... Außendurchmesser des Rohres
Für eine Rohrschließzeit
tc =< t
A. Perfekt starres Rohr
p = Ro * (v1 - v2) * at
B. Dünnwandiges Rohr
p = Ro * (v1 - v2) * a
v1, v2 ... Strömungsgeschwindigkeit
Für die Rohrschließzeit
tc > t
p = Ro * L * (v1 - v2) / t
Die Berechnungen umfassen einige, häufig zu lösende Aufgaben aus dem Bereich der Mechanik der Flüssigkeiten. Sofern Ihre Ausgabe in den Kreis der zu lösenden Probleme fällt, verfahren Sie wie folgt:
1. Wählen Sie im Absatz [1] die Flüssigkeit aus, stellen Sie ggf. ihre
Parameter ein und definieren Sie die Parameter des Umfeldes.
2. Wählen Sie die entsprechende Aufgabe aus und geben Sie die bekannten
Eingangswerte ein.
3. Die Berechnungen erfolgen in Form des mathematischen Modells der jeweiligen
Aufgabe. Sofern also das Ergebnis der Berechnung einer der Eingangsparameter
sein soll, ist dieser Parameter schrittweise zu iterieren.
In diesem Abschnitt legen Sie die Berechnungseinheiten fest, wählen die Eigenschaften der Flüssigkeit und der Umgebung aus und stellen sie ein.
In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
Wählen Sie die Flüssigkeit aus. Die Werte in der Liste sind für den barometrischen Druck angeführt. Sofern Sie eigene Flüssigkeitsparameter eingeben wollen, deaktivieren Sie die Schaltfläche (Taste) rechts.
Nach der Deaktivierung der Taste rechts können Sie entweder die Schallgeschwindigkeit oder das Kompressionsmodul eingeben.
Nach der Deaktivierung der Taste rechts können Sie entweder die kinematische oder die dynamische Viskosität eingeben.
Für die meisten Berechnungen genügt die Einstellung der Null-Meereshöhe. Dennoch können Aufgaben auftreten, bei denen der abweichende, barometrische Druck bzw. die abweichende Fallbeschleunigung in Betracht zu ziehen ist.
Die Standard-Fallbeschleunigung wird auf Meeresniveau für 45° geografischer Breite erwogen.
Die Reynolds-Zahl Re ist ein dimensionsloser Parameter, der den Übergang zwischen der laminaren und der turbulenten Strömung bestimmt. Für Re<2300 handelt es sich um eine laminare Strömung, für den Wert Re>3000 ist die Strömung fast immer turbulent.
Die kritische Re bestimmt daher die Art der Berechnung und somit auch die Werte der Verlustkoeffizienten.
Einige häufig zu lösende Aufgaben aus dem Bereich der Hydrostatik.
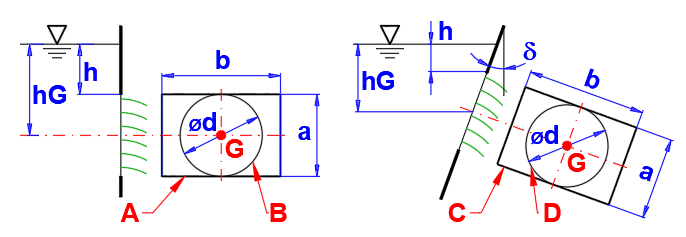
Geben Sie die gewünschten Werte anhand der Abbildung ein.
Kennzeichnung der Punkte:
G… Schwerpunkt der Fläche
P… Angriffspunkt der Kraft
Nach der Deaktivierung der Taste rechts können Sie einen eigenen Wert des Drucks über dem Spiegel und den Druck außerhalb des Gefäßes eingeben.
Fläche lotrecht zum Spiegel: Delta=0
Fläche parallel zum Spiegel: Delta=90
Die Gesamtkraft auf die Fläche S hat ihren Angriffspunkt im Punkt P.
Abstand des Schwerpunktes der Fläche von der freien Oberfläche der Flüssigkeit.
Abstand der Mitte des Drucks von der freien Oberfläche der Flüssigkeit.
Die Berechnung löst nicht jene Situation, in welcher der Spiegel auf den Boden des Gefäßes stößt.
Die Berechnung löst nicht jene Situation, in welcher der Spiegel auf den Boden des Gefäßes stößt.
Berechnung des stabilen Austritts der Flüssigkeit durch die Öffnung.
Die tatsächliche Ausflussgeschwindigkeit der realen Flüssigkeit unterscheidet sich von den theoretischen WEerten für ideale Flüssigkeiten. Beim Austritt der Flüssigkeit durch die Öffnung (bzw. den kurzen Stutzen) ist die Berührung mit der Wand gering, sodass auch die Dissipation der Energie gering ausfällt. Daher kann die Flüssigkeit als nicht zäh erachtet werden, sodass die theoretischen Ergebnisse durch die folgenden Korrekturkoeffizienten berichtigt werden können.
Nach der Deaktivierung der Taste rechts können Sie einen eigenen Wert des Drucks über dem Spiegel und den Druck außerhalb des Gefäßes eingeben.
Sofern das Gefäß nicht zylinderförmig ist, kann nach der Deaktivierung der Taste direkt die Querschnittsfläche eingegeben werden.
Sofern die Öffnung nicht kreisförmig ist, kann nach der Deaktivierung der Taste direkt die Querschnittsfläche eingegeben werden.
Nur für Vergleichszwecke. Umfasst keine Verluste.
Für den Ausfluss durch eine Öffnung ohne Stutzen (A) kann der Ausflussfaktor in Abhängigkeit von der Reynolds-Zahl Re ermittelt werden. Links ist die berechnete Re, rechts der Ausflussfaktor, der anstelle des Standardwertes 0.62 verwendet werden kann.
Wählen Sie die jeweiligen Faktoren je nach dem Typ der Austrittsöffnung (A-F) gemäß der angeführten Tabelle und anhand der Graphen aus.
Für die direkte Eingabe des Ausflussfaktors (Produkt [3.11] und [3.12]) deaktivieren Sie die Taste rechts.
Für große Öffnungen (obere Kante nahe des Spiegels und das Verhältnis der Öffnungshöhe zur Tiefe des Schwerpunktes nähert sich dem Wert 1) ist eine nichtlineare Verteilung der Ausflussgeschwindigkeit zu erwägen.
Verwenden Sie den gleichen Ausflussfaktor wie im Falle der kleinen Öffnung [3.13].
Der Überlauf ist unter dem Aspekt der Hydraulik ein Ausfluss mit großer Öffnung, ohne obere Wand über dem Strahl (Abb. A). Der Überlauf kann perfekt sein, wenn der Spiegel hinter dem Überlauf niedriger als die Überlaufkante ist, oder unvollkommen (geflutet) sein, sofern der Spiegel hinter dem Überlauf höher ist (Abb. B). Vollkommene (perfekte) Überfälle werden zur Bestimmung der Durchflussmenge der Flüssigkeit verwendet. Der Form nach können die Überläufe rechteckig, dreieckig, trapezförmig und kreisförmig sein.
Die Höhe des Spiegels h ist in ausreichendem Abstand vor dem Überlauf zu messen (in der Regel 2h - 4h). Über dem Überlauf ist der Spiegel niedriger, da sich ein Teil der potentiellen Energie bereits in kinetische Energie verwandelt hat.
In der Berechnung sind dann rechts der Eingabefelder die Randbedingungen ausgeschrieben, für welche die Berechnungen definiert sind.
Für die Berechnung der rechteckigen Überläufe (Abb. A) bzw. für die Berechnung des Strömungsbeiwertes Cd (Durchflusszahl) existieren zahlreiche Formeln und Verfahren, die in der Literatur angeführt sind. Daher führen wir Sie zum Vergleich ebenfalls an.
Die Höhe über dem Überlauf h wird in der Regel im Abstand 2h ~ 4h vom Überlauf gemessen (Eliminierung des Rückgangs des Spiegels).
Sofern die Höhe des Spiegels am Abfluss Einfluss auf den Durchfluss des Wassers hat (Abb. B), kann diese Berechnung verwendet werden, indem die Parameter des Überlaufs im Teil A definiert sind.
Der Wert des Faktors in Abhängigkeit von p und vom Verhältnis h2/h ist im grünen Feld angeführt.
Ist die Fläche des Ausschnitts relativ klein gegenüber der Fläche des Querschnitts des Zuflusses, kann der experimentell ermittelte und lediglich vom Winkel des Ausschnittes abhängige Strömungsbeiwert Cd verwendet werden.
Eine häufig zu lösende Aufgabe, für Rohrleitungen mit konstantem Querschnitt, Krümmungen, Ventile etc. Zur Berechnung wird die universelle Bernoulli-Gleichung unter Verwendung der Verlustbeiwerte herangezogen.
Berechnung des Durchflusses, der Geschwindigkeiten, der Verluste, der Leistung in der Rohrleitung eines konstanten Querschnitts.
Füllen Sie alle Abmessungs- und Druckparameter aus. Für die Schätzung der Verlustbeiwerte können Sie die Berechnungen rechts verwenden. Es kann ein negativer Überdruck (p2>p1) gewählt werden, es kann eine negative Höhe (H<0) gewählt werden, in jedem Falle ist der Sinn der Strömung der Flüssigkeit vom Eingang zum Ausgang einzuhalten.
Als voreingestellter Wert kann der Druck p1=p2 aus dem Absatz [1.0] verwendet werden. Nach der Deaktivierung der Taste rechts geben Sie den Druck im Innern des Gefäßes p1 und den Umgebungsdruck p2 an.
Die Höhe des Spiegels muss größer als der Wert rechts sein.
Sofern die Austrittsöffnung höher als das Niveau des Spiegels ist, geben Sie die Höhe H als negativen Wert ein (es muss der Überdruck p1>p2 ausgeglichen werden).
Im Falle von p1<p2 ist der äußere Überdruck durch die Höhe des Spiegels H auszugleichen.
Sofern die Rohrleitung nicht von kreisförmigem Querschnitt ist, können Sie nach der Deaktivierung der Taste rechts den Wert der Fläche der Rohrleitung und des benetzten Umfangs eingeben. Anhand dieser Werte wird dann der hydrodynamische Durchmesser dh gemäß der Formel dh=4 * S / C ermittelt werden, der anschließend in den Berechnungen verwendet wird.
In der Abbildung als Schnitt A-A angedeutet.
Wählen Sie in der Liste das entsprechende Material der Rohrleitung aus. Der vorgewählte Wert der Rauheit in [mm/in] in der weiteren Zeile ist der Durchschnitt aus dem in den Klammern angeführten Bereich. Nachdem Sie die Schaltfläche (Taste) deaktiviert haben, können Sie Ihren eigenen Wert eingeben.
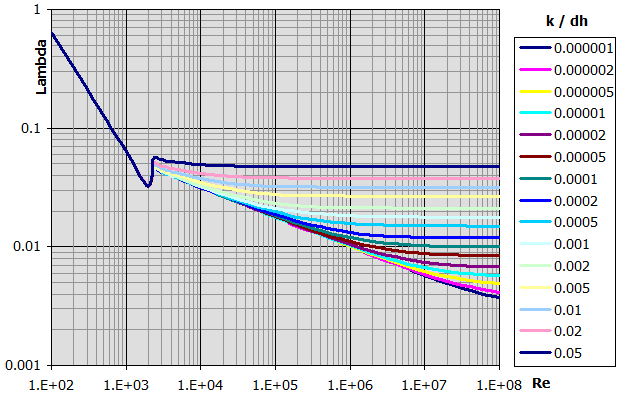
Auf der Grundlage der Rauheit der Rohrleitung „k“ und des Koeffizienten „Re“ werden in der Fachliteratur zahlreiche Formeln für die Berechnung der Rohrreibungszahl λ für turbulente Strömungen angeführt. Wählen Sie aus der Liste die entsprechende Berechnung.
Die am häufigsten verwendete Berechnung ist "C. Colebrook - White", das auch hydraulisch glatte Rohre (k=0) abdeckt. Einzelheiten in der Hilfe.
Der Vorschlag der Rohrreibungszahl Lambda hängt vom Koeffizienten Re ab, wobei die Berechnung von Re zugleich von der Rohrreibungszahl Lambda (Berechnung der Strömungsgeschwindigkeit) abhängig ist.
Der angenommene Wert wird automatisch in das Eingangsfeld übertragen.
Nachdem Sie die Schaltfläche deaktiviert haben, können Sie Ihren eigenen Wert eingeben.
Wählen Sie den Eingangskoeffizienten anhand der Berechnung/Empfehlung rechts.
Auf der Abbildung wie X1, X2, X3.
Es handelt sich um die Summe aller Koeffizienten für alle möglichen Verluste in der Rohrleitung (Krümmung, Ventile...).
Der Verlustkoeffizient der Krümmung der Rohrleitung kann durch die Berechnung rechts ermittelt werden, die Verlustkoeffizienten der Ventile können gemäß der Abbildung in etwa geschätzt werden.
Wählen Sie, sofern die Rohrleitung am Ende eine Düse/einen Diffusor hat.
Bei d1>d2 (dh1>dh2) wird die Verlustauslegung für die Düse verwendet, bei d1<d2 für den Diffusor.
Sofern die Rohrleitung nicht von kreisförmigem Querschnitt ist, können Sie nach der Deaktivierung der Taste rechts den Wert der Fläche der Rohrleitung und des benetzten Umfangs eingeben. Anhand dieser Werte wird dann der hydrodynamische Durchmesser dh gemäß der Formel dh=4 * S / C ermittelt werden, der anschließend in den Berechnungen verwendet wird.
In der Abbildung als Schnitt A-A angedeutet.
Geben Sie die Länge der Düse/des Diffusors ein. Sie muss kleiner als die Länge der Rohrleitung L1 sein.
Er wird anhand der Werte dh1, dh2 und L2 errechnet.
Für die Düse (d1>d2) und den Diffusor (Delta<10) wird die Schätzung auf der Grundlage der Integration der Verluste verwendet. Für den Diffusor und Delta>10, wo das Abreißen des Flüssigkeitsstroms von der Rohrleitungswand erfolgt, gelangt folgendes Verhältnis zur Anwendung: zetaO = ((S2 / S1) - 1)^2 * SIN(delta).
Er gibt das Verhältnis zwischen der Höhen- und Druckenergie am Eingang und der kinetischen Energie des Austrittsstroms der Flüssigkeit an.
Die angeführten Leistungsparameter ermöglichen die Auswertung der Rohrleitung.
Es gilt:
Pp + Ph = Pz + Po
beziehungsweise.
Pp + Ph + Pv = Pz + Po für Absatz [6.0]
Die Durchflüsse werden häufig in verschiedenen Einheiten, unabhängig von den Einheiten der Berechnung, angegeben. Daher ist nachstehend die Umrechnung der am häufigsten verwendeten Einheiten angeführt.
Für die Berechnung wird die Bernoulli-Gleichung unter Nutzung der
Verlustkoeffizienten zur Berechnung der Austrittsgeschwindigkeit vo
verwendet.
Berechnung des Durchflusses, der Geschwindigkeiten, der Verluste, der Leistung
in der Rohrleitung verschiedener Querschnitte und der Anzahl der Zweige.
Füllen Sie die bedingungen am Eingang in die Rohrleitung aus.
Es kann ein negativer Überdruck (p2>p1) gewählt werden, es kann eine negative Höhe (H<0) gewählt werden, in jedem Falle ist der Sinn der Strömung der Flüssigkeit vom Eingang zum Ausgang einzuhalten.
Als voreingestellter Wert kann der Druck p1=p2 aus dem Absatz [1.0] verwendet werden. Nach der Deaktivierung der Taste rechts geben Sie den Druck im Innern des Gefäßes p1 und den Umgebungsdruck p2 an.
Geschwindigkeit der Flüssigkeit (kinetische Energie) vor dem Eingang zur Rohrleitung. Bei den meisten, zu lösenden Problemen (großes Gefäß im Hinblick auf das Volumen der Rohrleitung) kann die Geschwindigkeit vernachlässigt und der Nullwert angesetzt werden.
Ungleich Null ist er beispielsweise im Falle des Kolbens, der die Flüssigkeit durch die Rohrleitung drückt.
Die Höhe des Spiegels muss größer als der Wert rechts sein.
Sofern die Austrittsöffnung höher als das Niveau des Spiegels ist, geben Sie die Höhe H als negativen Wert ein (es muss der Überdruck p1>p2 ausgeglichen werden).
Im Falle von p1<p2 ist der äußere Überdruck durch die Höhe des Spiegels H auszugleichen.
Auf der Grundlage der Rauheit der Rohrleitung „k“ und des Koeffizienten „Re“ werden in der Fachliteratur zahlreiche Formeln für die Berechnung der Rohrreibungszahl λ für turbulente Strömungen angeführt. Wählen Sie aus der Liste die entsprechende Berechnung.
Die am häufigsten verwendete Berechnung ist "C. Colebrook - White", das auch hydraulisch glatte Rohre (k=0) abdeckt. Einzelheiten in der Hilfe.
Summe des Druckenergiepotentials (p2-p1), des Potentials der Druckhöhe der
Flüssigkeit (H) und der kinetischen Energie der Flüssigkeit (v0) am Eingang in
die Rohrleitung.
Meistens wird das Energieniveau in Metern der Flüssigkeitssäule ausgedrückt. Die
Einheiten, in denen das Energieniveau ausgedrückt werden soll, wählen Sie rechts
aus.
Im nachstehend angeführten Graphen ist er durch die blaue, horizontale Strecke angedeutet (Abb. 2-A).
Nur für Vergleichszwecke. Umfasst keine Verluste.
Er gibt das Verhältnis zwischen der Höhen- und Druckenergie am Eingang und der kinetischen Energie des Austrittsstroms der Flüssigkeit an.
Die angeführten Leistungsparameter ermöglichen die Auswertung der Rohrleitung.
Es gilt:
Pp + Ph = Pz + Po
beziehungsweise.
Pp + Ph + Pv = Pz + Po für Absatz [6.0]
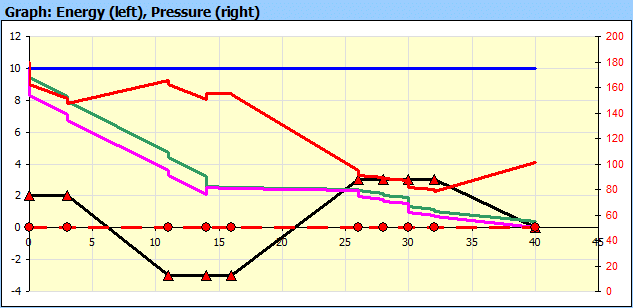
Beschreibung des Graphen (Abb. 2):
Gerade A: Linie der Gesamtenergie. Sie gibt die Summe der Energien
(Höhenenergie Eh, Druckenergie Ep und kinematische Energie Ev) der Flüssigkeit
am Eingang in die Rohrleitung an.
Gerade B: Summe der Höhenenergie (Eh) und der Druckenergie (Ep)
Gerade C: Höhenenergie (Eh)
Gerade 0: Nulllinie bezogen auf das Ende der Rohrleitung
Kurve 1: Verlusthöhe hz (Verluste in den einzelnen Teilen der Rohrleitung)
Kurve 2: Druck in der Rohrleitung (Skala rechts in kPa oder psi)
Kurve 3: Kinematische Höhe
Kurve 4: Höhenpunkte des Anfangs der einzelnen Abschnitte im Hinblick auf die
Nulllinie
Füllen Sie schrittweise die Werte für jeden Rohrleitungsabschnitt in der Tabelle aus (eine Zeile für jeden Abschnitt).
Es können zwei Verfahren, ggf. ihre Kombination, gewählt werden.
Vereinfacht (Abb. 2. Ver1):
Die einzelnen Abschnitte sind anhand des Durchmessers der Rohrleitungen
aufgeteilt, wobei alle Verlustkoeffizienten (Eingang, Krümmung, Ventil...) in
einem Abschnitt zu einem Koeffizienten (Spalte H) zusammengefasst sind, der am
Beginn des jeweiligen Abschnitts geltend gemacht wird.
Detailliert (Abb. 2. Ver2):
Die Rohrleitung ist in Abschnitte so unterteilt, dass sich der jeweilige
Verlustkoeffizient (Spalte H) stets am beginn des Abschnitts befindet. Sie
erlangen eine detaillierteren Graphen [6.19]. Die Gesamtergebnisse (Q,vo...)
sind identisch.
Wählen Sie die Anzahl der anknüpfenden Abschnitte, die zu lösen ist (1-15).
Es ist möglich, ein Rohr in zwei und mehr Rohre zu unterteilen. Gegebenenfalls können mehrere Rohre zu einem zusammengefasst werden. (Abb. Detail Z)
Höhe des Beginns des Rohrleitungsabschnitts über (unter) dem Ausgangspunkt (Endpunkt) des letzten Abschnitts (Nulllinie).
Länge des Einzelabschnitts.
Geben Sie den Durchmesser ein. Sofern das Rohr nicht kreisförmig ist, geben
Sie den hydraulischen Durchmesser dh ein (siehe E).
Mit dem Drücken der Taste „V“ wird der Wert aus der ersten Zeile in die
sonstigen kopiert.
Sofern die Taste rechts aktiviert ist, wird die Fläche aus dem kreisförmigen Querschnitt anhand des Durchmessers d aus der Spalte links (D) berechnet.
Für Rohrleitungen eines nicht kreisförmigen Querschnitts deaktivieren Sie die Taste rechts und geben Sie die Fläche des Querschnitts (E) und in das Feld des Durchmessers d (D) geben Sie den hydraulischen Durchmesser dh ein.
dh = 4 * S / C
S... Fläche des Querschnitts
C... Benetzter Umfang
Winkel der Verengung/Erweiterung des Übergangs zwischen zwei Abschnitten (Abb. 1 Detail Z), im Falle der Aufteilung in zwei Zweige, dann er Winkel zwischen den Rohren.
Der entsprechende, vorgeschlagene Verlustkoeffizient ZetaI ist rechts (Spalte G).
Auf der Grundlage des Verhältnisses der Flächen (Spalte E) und durch die Abschrägung (Spalte F) zwischen den beiden Abschnitten wird der Verlustkoeffizient am Beginn des Abschnitts vorgeschlagen (Einzelheiten im theoretischen Teil des Leitfadens). Ähnlich wird auch der Verlustkoeffizient im Falle der Verzweigung der Rohrleitung ermittelt.
Mittels der Taste "=>" können Sie den Vorschlag gesammelt in die Spalte H übertragen, der dann in der Berechnung verwendet wird.
Summe aller Verlustkoeffizienten im jeweiligen Abschnitt der Rohrleitung.
ZetaI…. Verluste des Eingangs, Verluste durch Änderung des Querschnitts
(Vorschlag Spalte G)
ZetaB… Verluste der Krümmung (Berechnung im vorherigen Absatz [5.0])
ZetaV… Verluste des Ventils (Tabelle im vorherigen Absatz [5.0])
Für die Berechnung der realen Rohrleitung ist die Rauheit der Rohrleitung einzugeben. Zur Orientierung verwenden Sie die nachstehend angeführte Tabelle. Mit dem Drücken der Taste „V“ wird der Wert aus der ersten Zeile in die sonstigen kopiert.
- Hydraulisch glattes Rohr (0-0) mm /
(0-0) in
- Stahl - Durchgehendes nahtloses Rohr (0.03-0.1) mm / (0.00118-0.00394) in
- Geschweißtes neues Stahlrohr (0.05-0.1) mm / (0.00197-0.00394)
in
- Geschweißte Stahlrohre korrodiert (0.15-0.5) mm / (0.00591-0.01969)
in
- Geschweißtes Stahlblech - Luftleitungen (0.5-0.8) mm / (0.01969-0.0315)
in
- Stahlblech genietet (1-6) mm / (0.03937-0.23622) in
- Reingezogene Messing- und Aluminiumrohre (0.0015-0.01) mm / (0.00006-0.00039)
in
- Glas, Kunststoff (0.0015-0.01) mm / (0.00006-0.00039)
in
- Gusseisen neues Rohr (0.1-0.3) mm / (0.00394-0.01181) in
- Gusseisen Altrohr (1-4.5) mm / (0.03937-0.17717) in
- Gummischlauch (0.01-0.03) mm / (0.00039-0.00118) in
- Sperrholz (0.025-0.1) mm / (0.00098-0.00394) Zoll
- Keramik (0.45-6) mm / (0.01772-0.23622) in
- Ziegel mit Zementschlieren (0.8-6) mm / (0.0315-0.23622) in
- Beton (0.8-9) mm / (0.0315-0.35433) in
Reynolds-Zahl Re (Details im Leitfaden - Theorie)
Sie charakterisiert die Strömung einer zähen Flüssigkeit, die nicht nur von der
mittleren Geschwindigkeit, sondern auch von von der charakteristischen Abmessung
des Flüssigkeitsstroms (Durchmesser d bzw. dh), der dynamischen Viskosität und
von der Dichte abhängig ist.
Sie dient zur Berechnung der Rohrreibungszahl Lambda (Spalte K).
Vorschlag der Rohrreibungszahl Lambda. Abhängig von Re (Spalte J). Jedoch ist die Berechnung von Re rückwirkend von der Geschwindigkeit der Strömung (für die Lambda bekannt sein muss) abhängig. Daher erfolgt die schrittweise Iteration der Werte.
Der Vorschlagswert wird automatisch in das Feld rechts (Spalte L) übertragen
und für die Berechnung verwendet.
Nachdem Sie die Taste rechts deaktiviert haben, können Sie Ihren eigenen Wert
der Rohrreibungszahl eingeben.
Rohrreibungszahl λ (Lambda) Sie ist für die Berechnung der Strömungsgeschwindigkeit notwendig. Sofern die Taste rechts aktiviert ist, wird der Vorschlagswert (Spalte K) verwendet.
Sofern Sie keinen triftigen Grund haben, verwenden Sie den Vorschlagswert.
Mit dem Drücken der Taste „V“ wird der Wert aus der ersten Zeile in die sonstigen Zeilen kopiert.
Geschwindigkeit der Flüssigkeit im jeweiligen Abschnitt der Rohrleitung.
Wählen Sie in der Spalte N,O aus, welche Werte Sie anzeigen wollen, sowie ihre Einheiten. Die Auswahl der Einheiten ist mit der Zeile [6.8] verbunden.
hIBV… Summe der Verluste (Eingang, Krümmung, Ventil) für den jeweiligen
Abschnitt
hF ...... Reibungsverluste für einen bestimmten Abschnitt
h-A,h-B,h-C… Verluste vom Anfang der Rohrleitung schrittweise in den Punkten A,
B, C (Abb. 2)
v(pd)… Energie der strömenden Flüssigkeit (dynamischer Druck)
p-A,p-B,p-C... Absoluter Druck in den Punkten A, B, C
Bei der Regelung des Durchflusses der Flüssigkeit durch die Rohrleitung entsteht eine nichtstationäre Strömung. Vor dem Ventil bildet sich bei einer Verringerung des Durchflusses ein höherer Druck als hinter ihm. Bei langen, eine Flüssigkeit transportierenden Rohrleitungen kann einem schnellen (notfallbedingten) Schließen der Rohrleitung eine derartiger Druckanstieg erfolgen, der die Rohrleitung beschädigen könnte.
Beim Schließend der Rohrleitung wird die kinetische Energie der Flüssigkeit schrittweise für ihre Kompression, ggf. für die Deformation der Rohrleitung verbraucht. Die Stoßwelle breitet sich in der Rohrleitung mit Schallgeschwindigkeit in der jeweiligen Flüssigkeit in Richtung B->A und zurück A->B aus.
Mit dem Drücken der Taste lesen Sie die Parameter aus Absatz [5.0] ein.
Füllen Sie die Eingangsparameter gemäß der Abbildung aus.
Wählen Sie das entsprechende Material der Rohrleitung aus.
Nachdem Sie die Taste rechts deaktiviert haben, können Sie Ihren eigenen Wert eingeben.
Bei vollständigem Schließen des Ventils v2=0.
Es können zwei Fälle auftreten:
1. Zeit des Schließens des Ventils t > T - Dauer des Laufens der Stoßwelle
[7.14,7.21]
Mit Verkürzung der Dauer des Schließens des Ventils steigt der Druck.
2. Zeit des Schließens des Ventils t < T - Dauer des Laufens der Stoßwelle
[7.14,7.21]“
Der Druck bleibt bei seiner höchsten Intensität konstant.
Dieses ist im Absatz [1.0] definiert.
Die theoretische Schallgeschwindigkeit [7.20] ist von der Dichte des Materials und von der Volumenelastizität der Flüssigkeit abhängig. Für die reale Rohrleitung verringert sich die Ausbreitung des Schalls in Abhängigkeit von den Abmessungen und vom Material der Rohrleitung.
Ungefähre Berechnung der Viskosität und der Dichte der Flüssigkeit in Abhängigkeit von der Temperatur.
Geben Sie die Temperatur der ausgewählten Flüssigkeit ein. Auf der Grundlage der Temperatur werden die Dichte und die Viskosität vorgeschlagen. Die Berechnung ist ungefähr mit einer Genauigkeit von ± 6 % im Temperaturbereich 0-100°C (32-212°F). .
Mit dem Drücken der Taste verschieben Sie die Werte der Dichte und der Viskosität in den Ansatz [1.0].
Absatz [3.0] - Berechnung
der Zeit der Füllstandsabnahme von h1 auf h2.
Das Gefäß ist gemäß der Abbildung definiert.
Flüssigkeit: Wasser, 20°C, p1=p2=atmosphärischer Druck (Absatz [1.0]).
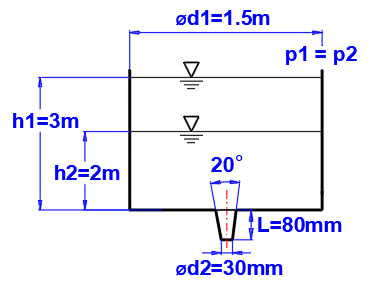
Geben Sie die in der Abbildung gezeigten Eingabewerte ein und entnehmen Sie die Koeffizienten j und m dem Diagramm F. Die Zeit für die Pegelsenkung liegt bei [3.17].
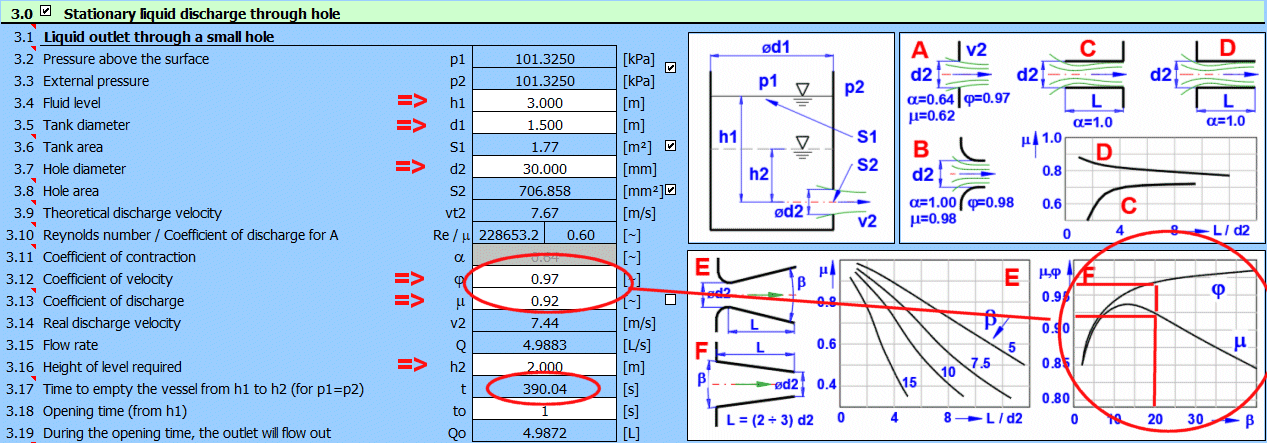
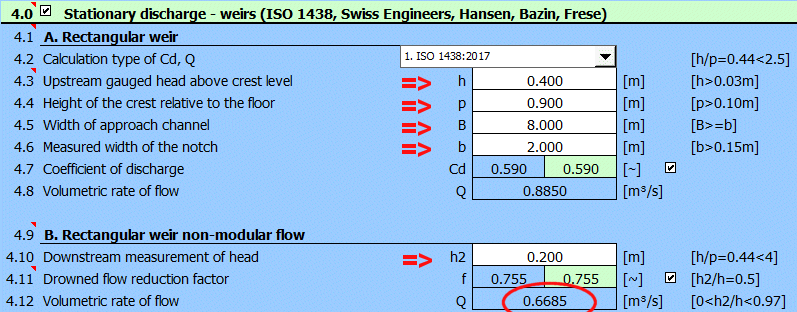
Absatz [4.0]. Berechnung
des Durchflusses mit Hilfe eines überfluteten Überlaufs.
Der Überlauf wird wie in der Abbildung gezeigt definiert.
Berechnungsmethode nach ISO 1438.
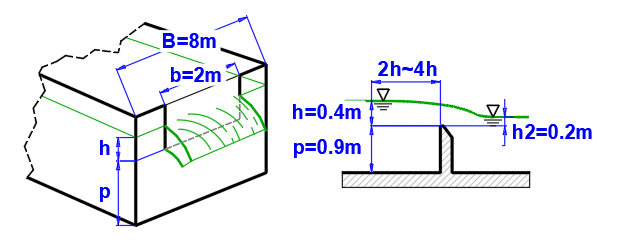
Geben Sie die Eingabewerte wie in der Abbildung gezeigt ein. Der resultierende Durchfluss für die geflutete Hochwasserentlastungsanlage steht in der Zeile [4.12].
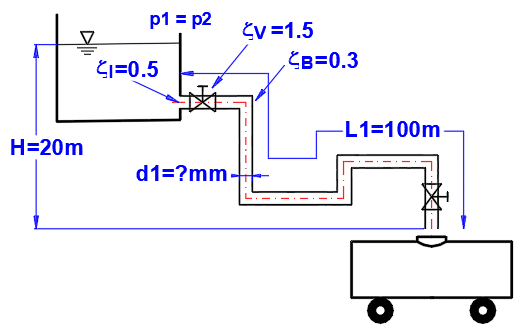
Absatz [5.0]. Berechnung
des Rohrdurchmessers für den erforderlichen Flüssigkeitsstrom.
Festlegung der Rohrdimensionen und Verlustkoeffizienten gemäß der Abbildung.
Erforderliche Durchflussmenge 100L/s = 0.1 m³/s
Eingangsverluste = 0.5, Bogen+Ventilverluste = 5*0.3 + 2*1.5 = 4.5
Gussrohr (neu), Rauheit k=0.2mm
Methode zur Berechnung des Verlustkoeffizienten Lambda: Colebrook - Weiß
Flüssigkeit: Wasser, 20°C, p1=p2=atmosphärischer Druck (Absatz [1.0])
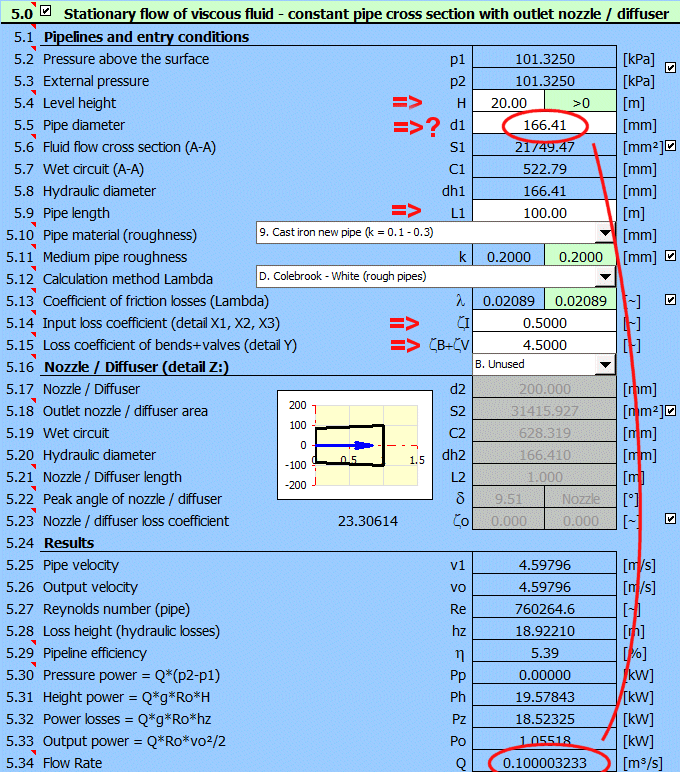
Geben Sie alle bekannten Parameter ein und ändern Sie schrittweise den Wert von d1 [5.5], um die gewünschte Durchflussmenge Q = 0.1 m³/s zu erreichen.
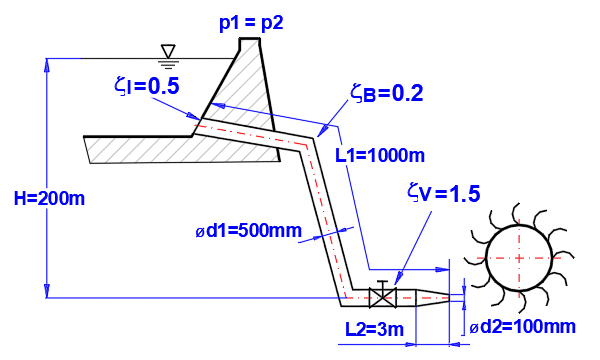
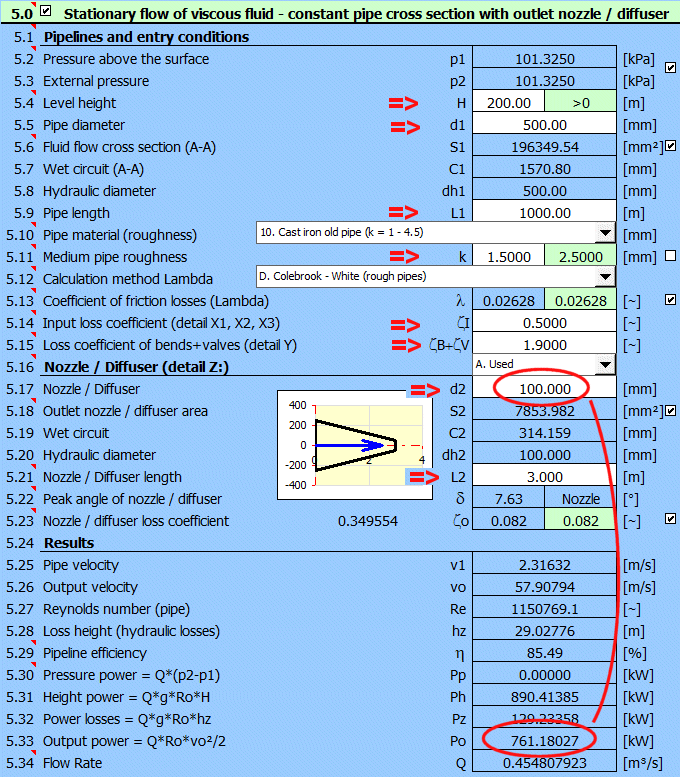
Absatz [5.0]. Berechnung
der Stromabgabe am Ende der Düse für den angegebenen Durchmesser. Bestimmung,
bei welchem Düsendurchmesser die maximale Leistung erreicht wird.
Festlegung der Abmessungen und Verlustkoeffizienten des Rohrs wie dargestellt.
Eingangsverluste = 0.5, Bögen+Ventilverluste = 2*0.2 + 1.5 = 1.9
Gussrohr, Rauheit k=1.5 mm
Methode zur Berechnung des Verlustkoeffizienten Lambda: Colebrook - Weiß
Flüssigkeit: Wasser, 20°C, p1=p2=atmosphärischer Druck (Absatz [1.0])
Geben Sie alle bekannten Parameter ein.
Die Leistung des Flüssigkeitsstroms am Ende der Düse ist Po = 761kW [5.33]
Um die maximale Leistung zu ermitteln, ändern Sie schrittweise den
Düsendurchmesser d2. Die maximale Leistung Po = 1162kW für d2=157.6mm.
Gleichzeitig sinkt der Wirkungsgrad von 85.5% für
d2=100mm auf 61.8% für d2=157.6mm.
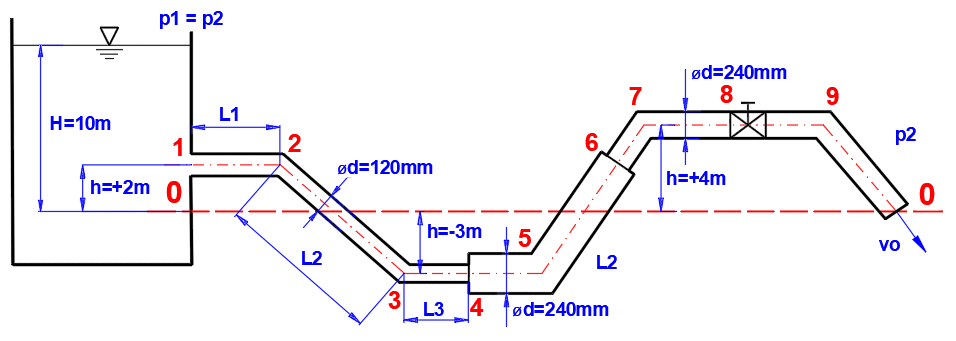
Absatz [6.0]. Berechnung
des detaillierten Verlaufs von Druck und Verlusten in der Rohrleitung,
Berechnung von Flüssigkeitsgeschwindigkeiten und Durchflussmengen.
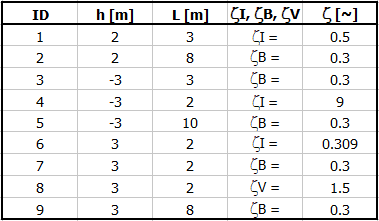
Rohrleitung gemäß Abbildung und Tabelle definiert, wobei:
ID ... Abschnittsnummer (1-9)
L ... Längen der einzelnen Abschnitte
ZetaI, ZetaB, ZetaV ... Verluste am Anfang des Abschnitts (Eingang,
Abschnittswechsel, Biegung, Ventil)
Rohrmaterial: Gusseisen, Rauheit k=1.5 mm
Methode zur Berechnung des Verlustkoeffizienten Lambda: Colebrook - Weiß
Flüssigkeit: Wasser, 20°C, p1=p2=atmosphärischer Druck (Absatz [1.0]).
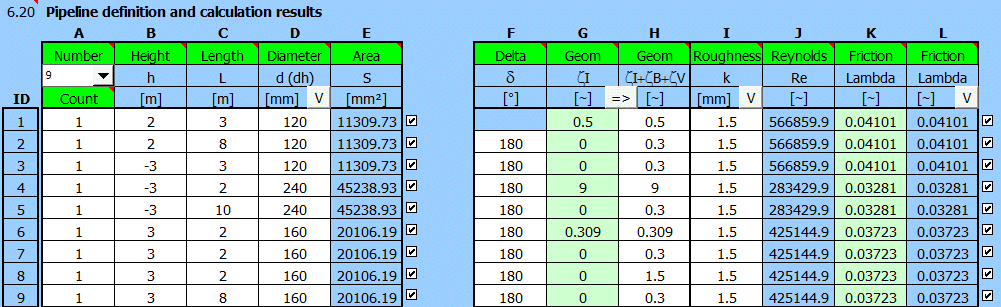
Bedingungsdefinitionen:

Definieren Sie die Rohrparameter (A-Anzahl der Rohre, B-Höhe relativ zur Nulllinie, C-Länge der Sektionen, D-Rohrdurchmesser, F-Übergangswinkel zwischen verschiedenen Rohrdurchmessern, H-gleichmäßige Verlustkoeffizienten, I-Rohrrauhigkeit)
Ergebnisse:

Druck und Verluste im Detail:
Absatz [6.0]. Berechnung
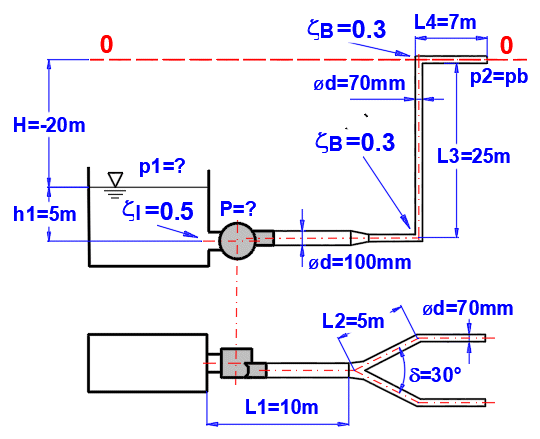
der Pumpenleistung für das Pumpen von Wasser bis zu 25 m. Die erforderliche
Durchflussmenge beträgt 10 l/s.
Die Rohrleitungen sind wie abgebildet definiert.
L ... Längen der einzelnen Abschnitte
ZetaI, ZetaB ... Verluste (Eintritt, Querschnittsveränderung, Rohrspaltung,
Biegung)
Rohrmaterial: Stahlrohr, Rauhigkeit k=0,1mm
Methode zur Berechnung des Verlustkoeffizienten Lambda: Colebrook - Weiß
Flüssigkeit: Wasser, 20°C, p2=atmosphärischer Druck (Absatz [1.0])
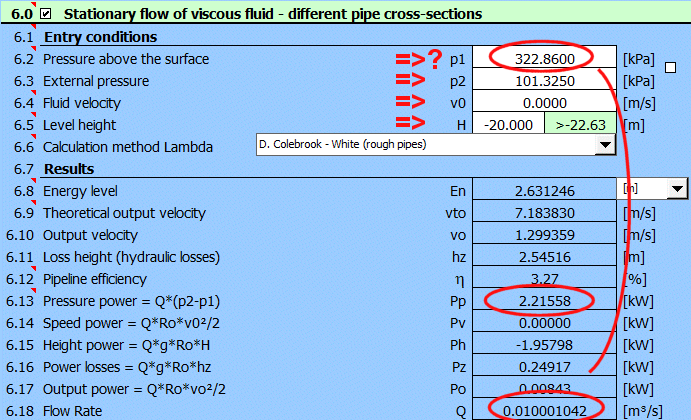
Definieren Sie die Rohrparameter
(A-Anzahl der Rohre, B-Höhe relativ zur Nulllinie, C-Länge der Abschnitte,
D-Rohrdurchmesser, F-Rohrspaltwinkel, H-Individualverlustkoeffizienten,
I-Rohrrauhigkeit)
Der Verlust für die Rohrspaltung liegt bei G2.

Geben Sie alle bekannten Parameter ein
und verändern Sie schrittweise den Druckwert p1 [6.2], um die gewünschte
Durchflussmenge Q = 0.01 m³/s [6.18] zu erreichen.
Die erforderliche Pumpenleistung ist dann in Zeile [6.13] Pp=2.22kW angegeben.
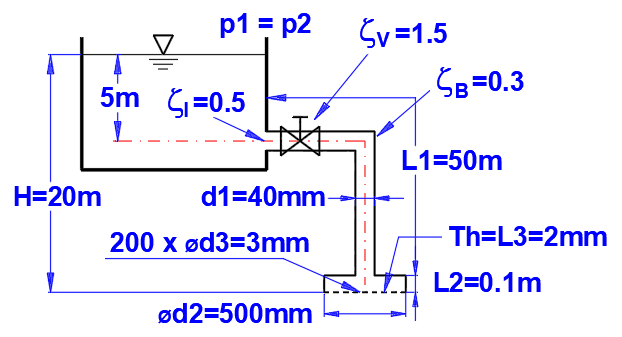
Absatz [6.0]. Berechnung des
Wasserdurchflusses in der Dusche.
Rohre und Dusche gemäß der Abbildung definiert:
L ... Längen der einzelnen Abschnitte
ZetaI, ZetaV, ZetaB ... Verluste (Eingang, Ventil, Biegung)
Rohrmaterial: Stahlrohr, Rauhigkeit k=0,1mm
Methode zur Berechnung des Lambda-Verlustkoeffizienten: Colebrook - Weiß
Flüssigkeit: Wasser, 20°C, p1=p2=Atmosphärendruck (Absatz [1.0])
Definieren Sie die Parameter des Rohrs und der Dusche mit 200 Löchern.

Geben Sie die Höhe des Niveaus an. Der Wasserdurchfluss durch die Dusche Q=1L/s steht in der Zeile [6.18].
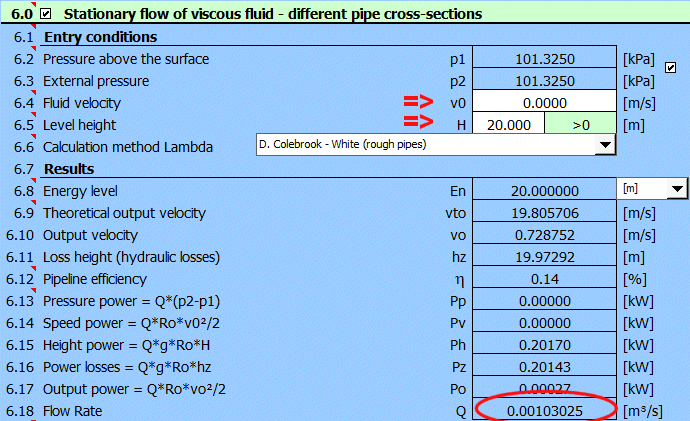
Absatz [7.0]. Berechnung des Wasserschlags im Falle einer Notschließung der Rohrleitung aus Beispiel 4.

Sie können die Schaltfläche
"[5.0] >> [7.0]" verwenden, um Parameter zu definieren. Damit werden die Werte
aus Absatz [5.0] geladen.
Als nächstes geben Sie das Material ein, die Rohrwandstärke von 20 mm und die
Ventilschließzeit von 2 Sekunden.
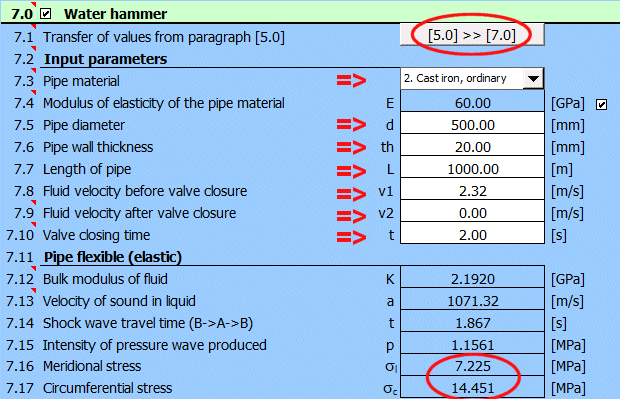
Vergleichen Sie den Spannungssprung [7.16, 7.17] für die Ventilschließzeit für t<1,86 s.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
Literaturliste:
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová, CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
Standards:
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs a paroi mince
^