Program je určen pro řešení nejčastějších úloh z oblasti mechaniky tekutin.
Program řeší úlohy z oblasti:
1. Hydrostatika
2. Stacionární výtok kapaliny otvorem
3. Stacionární výtok - přelivy (ISO 1438, Swiss Engineers, Hansen, Bazin, Frese)
4. Stacionární proudění vazké tekutiny - konstantní průřez potrubí s výstupní tryskou / difuzorem
5. Stacionární proudění vazké tekutiny - různé průřezy potrubí
6. Hydraulický ráz
Výpočty obsahují určení Reynoldsova čísla, viskozity, ztrát pro laminární a turbulentní proudění pro různé materiály a desítek typů ztrátových koeficientů.
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné literatury, norem a firemních katalogů.
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová, CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs a paroi mince
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
Mechanika tekutin je rozsáhlý obor o pohybu a působení tekutin. Tyto výpočty zahrnují některé často řešené úlohy.
Dynamická viskozita µ (µ = "mi") je mírou viskozity kapaliny (tekutiny:
kapaliny, proudící látky).
Čím je viskozita vyšší, tím je tekutina hustší (méně tekutá); čím je viskozita
nižší, tím je tekutina řidší (tekutější).
Jednotka dynamické viskozity v soustavě SI: [µ] = Pascal-sekunda (Pa*s) = N*s/m²
= kg/m*s.
Kinematická viskozita ν (ν = "nu") je dynamická viskozita prostředí µ dělená
jeho hustotou ρ (ρ = "Ro").
Rovnice: ν = µ / ρ
Jednotka SI kinematické viskozity: [ν] = m²/s
Často používané jednotky jsou Stokes (St) a Centistokes (cSt).
Přepočet:
Stokes (St) = e-4 * m²/s = 1 cm²/s.
1 cSt = e-6 m²/s = 1 mm²/s
Pro výpočet viskozity v závislosti na teplotě je použit přibližný vzorec:
µ ~
µ20 * exp(C * (293 / TK - 1))
µ20 ... dynamická viskozita pro 20°C
C ... koeficient pro danou kapalinu
TK ... teplota ve stupních Kelvina
Základním parametrem, který určuje viskózní chování všech newtonských kapalin,
je bezrozměrné Reynoldsovo číslo.
Závisí nejen na střední
rychlosti ale na charakteristickém rozměru proudu tekutiny (průměr d, resp. dh),
dynamické viskozitě a hustotě.
Re = v * d * r / µ, resp. Re = v * dh * r / µ pro nekruhové průřezy
v ..... rychlost
d ..... průměr
r ... hustota
µ ..... dynamická viskozita
dh ... hydraulický průměr
dh = 4 * S / O
S ... plocha průřezu
O ... smáčený obvod
Pro kruhový průřez d = dh.
Empirický vzorec
µ /
µ20 = exp(C * (293 / T°K - 1))
µ ... dynamická viskozita
µ20 ... dynamická viskozita pro 20°C
C ... koeficient
T ... teplota
Odlišnosti od proudění ideální tekutiny.
1) Dochází ke ztrátám, kdy se část mechanické energie přemění v teplo.
2) Rychlost v průřezu není rozložena rovnoměrně
3) Pohyb tekutiny může být laminární (Re=Re,cr<2300) a nebo téměř vždy turbulentní (Re>3000).
Q = v1 * S1 = v2 * S2
Q ... průtok
v1, v2 ... rychlost v průřezu 1 a 2
S1, S2 ... plocha v průřezu 1 a 2
g*h1 + p1/Ro + k1*(v1^2)/2 = g*h2 + p2/Ro + k2*(v2^2)/2 + ez(1-2)
g ... tíhové zrychlení
Ro ... hustota
h1, h2 ... výška
p1, p2 ... tlak
v1, v2 ... rychlost
ez(1-2) ... ztrátová energie
ez(1-2) = (Zeta + Lambda * (L / dh)) * (v^2 / 2)
Zeta ........ součinitel místních ztrát (vstup, změna průřezu, ventil....)
Lambda ... součinitel třecích ztrát
L ............. délka
dh ........... průměr
v ............. rychlost
Lambda ... součinitel třecích ztrát
Laminární proudění (Re<2300):
Lambda = 64 / Re
Turbulentní proudění (Re>=2300):
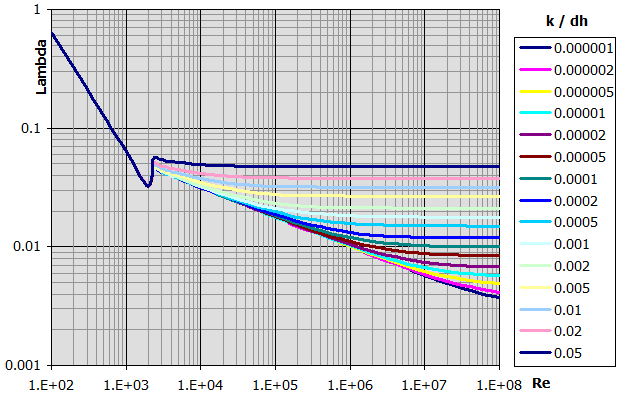
Výběr z metod:
Hladké potrubí:
Lambda = 0.3164 / (Re^0.25) ....... Blasius
Lambda = 1 / (2 * Log10(Re * Lambda^0.5) - 0.8)^2 ......... Nikurdas
Lambda = (1.8 * Log10(Re) - 1.5)^-2 .......... P.K.Konakov
Drsné potrubí:
Lambda = 0.1 * (100 / Re + kr)^0.25 ....... Altus
Lambda = 1 / (-2 * Log10(2.51 / (Re * Lambda^0.5) + 0.27 * kr))^2 ........
Colebrook - White
Lambda = 8 * ((8 / Re)^12 + 1 / (a + b)^1.5)^(1/12) ....... Churchill
a = (2.457 * Log(1 / ((7 / Re)^0.9 + 0.27 * kr)))^16
b = (37530 / Re)^16
Lambda = 1 / (2 * Log10(1 / kr + 1.138))^2 ....... Gottingen formula
Lambda = 1 / (2 * (Log10((dh / 2) / k) + 1.74)^2) ........ Karman formula
kr = k / dh
k ..... drsnost (výška nerovností)
dh ... průměr (hydraulický průměr)
Lambda = 4 * f
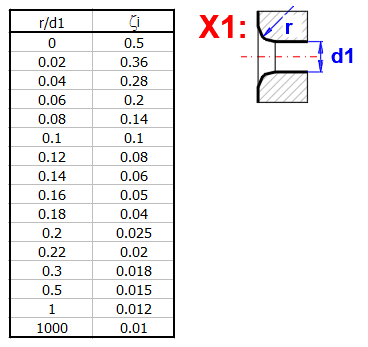
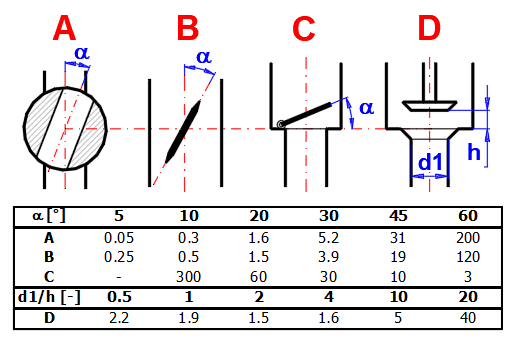
zetaI ... ztrátový součinitel vstupu (zaoblení)
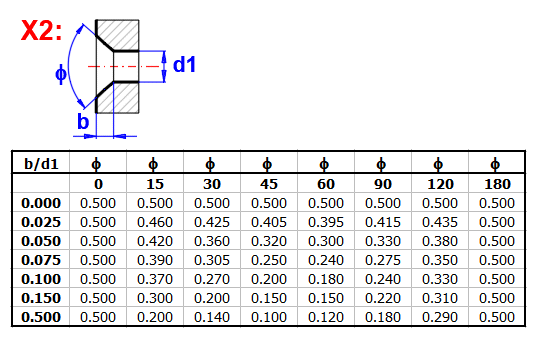
zetaI ... ztrátový součinitel vstupu (sražení)
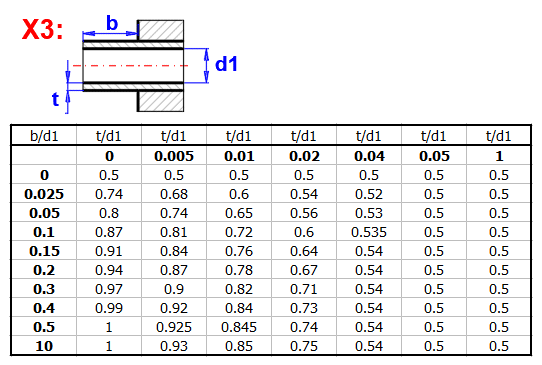
zetaI ... ztrátový součinitel vstupu (vysunutí)
zetaB ... ztrátový součinitel (ohyb)
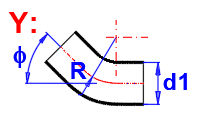
zetaB =(0.131 + 0.16 * (d1 / R)^3.5) * (Fi / 90)
zetaI ... ztrátový součinitel (přechodu)
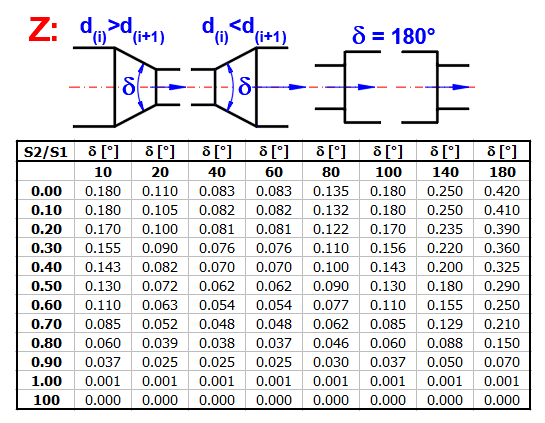
Tryska, delta<10: ZetaI = (Lambda / (8 * SIN(delta/2))) * (1
- (S2/S1)^2)
Tryska, delta>=10: ZetaI = aproximace tabulky
Difuzor: ZetaI = (S2/S1 - 1)^2 * SIN(MIN(delta;90))
zetaV ... ztrátový součinitel ventilů
Pro přibližnou orientaci je možné použít tabulku:
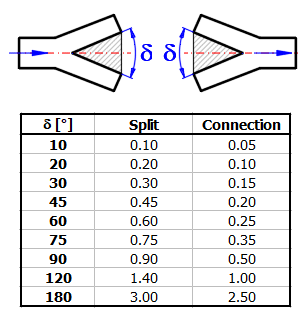
ZetaS ... ztrátový součinitel pro rozdělení potrubí
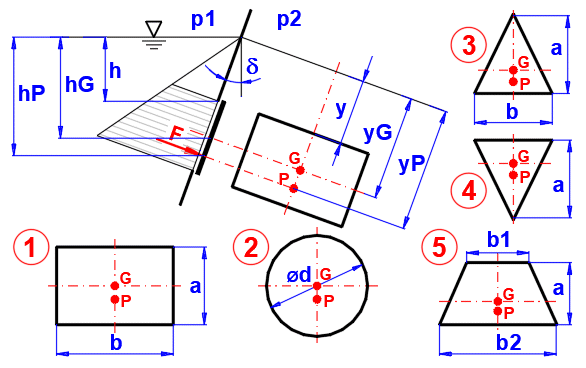
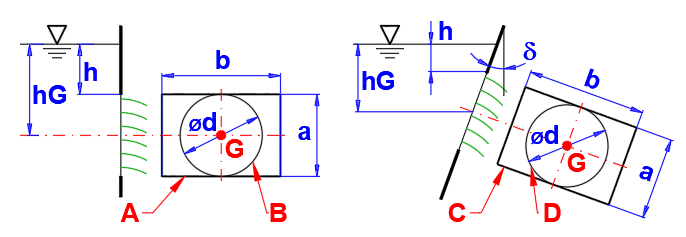
Hydrostatická síla:
F = ((p1 - p2) + Ro * g * hG) * S
p1, p2 ... tlak
g ... tíhové zrychlení
Ro ... hustota
hG ... hloubka těžiště plochy
S ... plocha
Střed tlaku y-vzdálenost:
1. yP = y+(2*a + 3*y)/(a + 2*y) * (a/3)
2. yP = y+(8*y + 5*a) / (2*y + a) * (a/8)
3. yP = y+(4*y + 3*a) / (3*y + 2*a) * (a/2)
4. yP = y+(2*y + a) / (3*y + a) * (a/2)
5. yP = y+(2*y*(b1 + 2*b2) + a*(b1 + 3*b2)) / (3*y*(b1 + b2) + a*(b1 + 2*b2)) * (a/2)
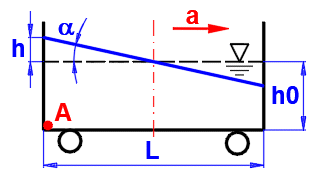
a = atan(a / g)
a ... zrychlení
g ... tíhové zrychlení
h = L / 2 * tan(a)
L ...
délka nádoby
Tlak v bodě A:
pA =
Ro * (g^2 + a^2)^0.5 * (h0 + dh) * COS (a)
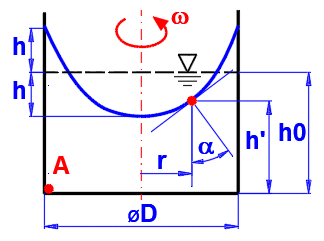
w =
2 * p
* n / 60
n ... otáčky
h = (w^2 * (D / 2)^2) / (4 * g)
w ... úhlová rychlost
D ... průměr
g ... tíhové zrychlení
Tlak v bodě A:
pA = 0 - r * g * (-h0 +
h) + 0.5 * r * h^2 *
w^2
h' = h0 - h + r^2 * w^2 / (2 * g)
Skutečná výtoková rychlost reálné tekutiny se liší od teoretických hodnot pro ideální tekutiny. Při výtoku tekutiny otvorem (resp. krátkým nátrubkem) je styk se stěnou malý, proto bude malá i disipace energie. Proto je možné považovat tekutinu za nevazkou a teoretické výsledky opravit následujícími korekčními součiniteli.
j = v / vt
v .... skutečná výtoková
rychlost
vt ... teoretická výtoková rychlost
a = S2' /
S2
S' ... skutečný průřez proudu tekutiny
S .... průřez otvoru
m = a *
j = Q / Qt
Q .... skutečný objemový tok
Qt ... teoretický objemový tok
v2t = ((2 * g * (h1 + (p1 - p2) / Ro) / (1 - (S2 /
S1)^2))^0.5
g ... tíhové zrychlení
Ro ... hustota
p1, p2 ... tlak
S1, S2 ... plocha
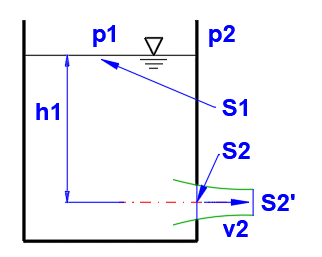
v2 = j * v2t
Qt = S2 * v2t
Q = a * S2 * j * v2t = m * Qt
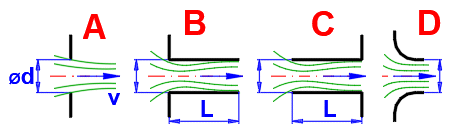
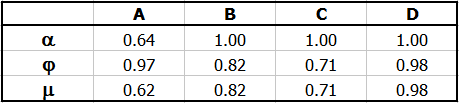
Součinitel m v závislosti na Re pro výtok typu A bez nátrubku.
Re = v2t * d / n
n ... Kinematická viskozita
Pro velké otvory (horní hrana blízko hladiny a poměr výšky otvoru k hloubce těžiště je blízko jedné) je třeba uvažovat nelineární rozložení výtokové rychlosti.
Obdélníkový otvor
Q = m * b * (2 * g)^0.5 * ((h + a)^(3/2) - h^(3/2))
Kruhový otvor
Q = m * p * r^2 * (2
* g * hG)^0.5 * (1 - 1/32 * (r / hG)^2 - 5/1024 * (r / hG)^4)
r = d / 2
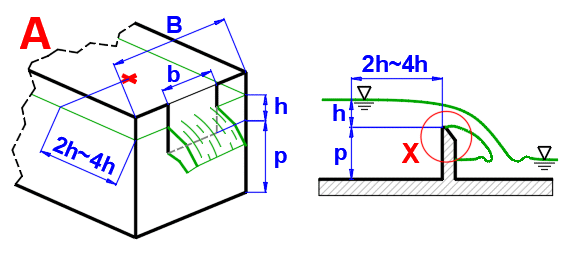
Přepad je po hydraulické stránce výtok velkým otvorem, bez horní stěny nad paprskem (obr. A). Přepad může být dokonalý, je-li hladina za přepadem níže než přepadová hrana, nebo nedokonalý (zatopený) jeli hladina za přepadem výše (obr. B). Dokonalých přepadů se používá k určení protékajícího množství tekutiny. Podle tvaru pak mohou být přepadové hrany obdélníkové, trojůhelníkové, lichoběžníkové, kruhové.
Výšku hladiny h je nutné měřit v dostatečné vzdálenosti před přepadem (obvykle 2h - 4h). Nad přepadem je hladina níže, protože se již část polohové energie změnila v kinetickou.
Objemový průtok (ISO 1438)
Q = Cd * (2/3) * (2 * g)^0.5 * be * he^(3/2)
Cd ... součinitel průtoku
g ..... tíhové zrychlení
be ... účinná šířka
he ... účinná přelivová výška
he = h + 0.001
be = b + kb
Objemový průtok (Obecný vzorec)
Q = 2/3 * Cd * b * h * (2 * g * h)^0.5
b ... šířka
h ... přelivová výška
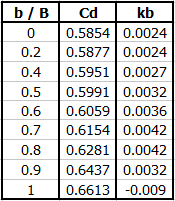
Součinitel průtoku (ISO 1438)
Cd = a + a' * (h / p)
v závislosti na b/B
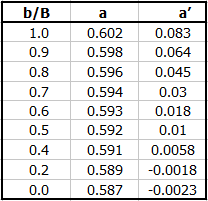
Součinitel průtoku (Spolek švýcarských inženýrů)
Cd = 0.615 * (1 + (1 / (1000 * h + 1.6))) * (1 + 0.5 * (h / p)^2)
Součinitel průtoku (Hansen)
Cd = 0.61706 / (1 - 0.35815 * (h^3)^0.5)
Součinitel průtoku (Bazin)
Cd = (0.6075 + 0.045 / h) * (1 + 0.55 * (h / (h + p))^2)
Součinitel průtoku (Frese)
Cd =
(0.5755+0.017/(h+0.18)-0.075/(b+1.2))*(1+(0.25*(b/B)^2+0.025+0.0375/((h/(h+p))^2+0.02))*(h/(h+p))^2)
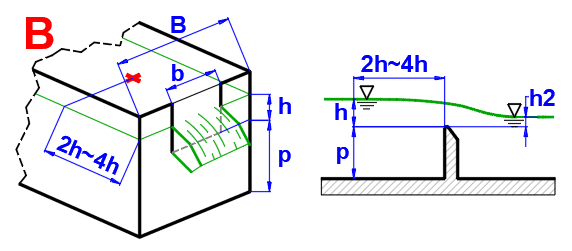
Objemový průtok (ISO 1438)
Q = f * Cd * (2/3) * (2 * g)^0.5 * be * he^(3/2)
f ... součinitel zatopení
pro h/p=0.5, f =1.007 * ((0.975 - h2/h)^1.45)^0.265
pro h/p=1.0, f =1.026 * ((0.960 - h2/h)^1.55)^0.242
pro h/p=1.5, f =1.098 * ((0.952 - h2/h)^1.75)^0.22
pro h/p=2.0, f =1.155 * ((0.950 - h2/h)^1.85)^0.219
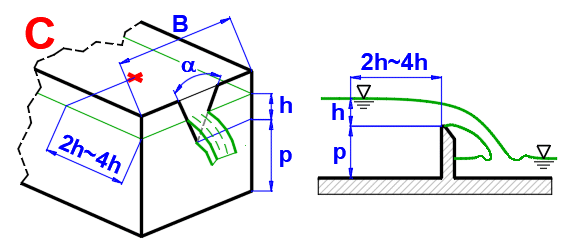
Objemový průtok (ISO 1438)
Q = Cd * (8/15) * TAN(alfa/2) * (2 * g)^0.5 * he^(5/2)
he ... účinná přelivová výška
Často řešená úloha, pro potrubí s konstantním průřezem, ohyby, ventily atd.
Pro řešení je použita univerzální Bernouliho rovnice s využitím ztrátových
součinitelů.
Výpočet průtoku, rychlostí, ztrát, výkonu v potrubí konstantního průřezu.
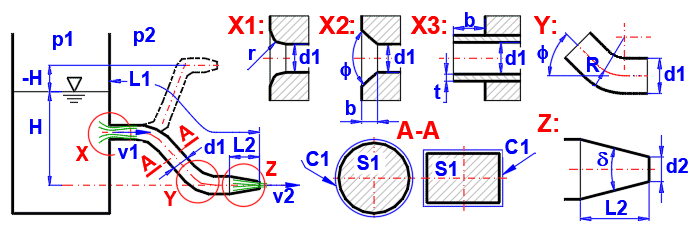
Výpočet výtokové rychlosti:
v2 = ((2 * g * (H +((p1 - p2) / (Ro * g))))/((ZetaI
+ Lambda * ((L1-L2) / dh1) + ZetaBV) * (dh2 / dh1)^4 + (1 + ZetaO)))^0.5
g ..... tíhové zrychlení
H ..... výška hladiny
p1, p2 ... tlak
dh1, dh2 ... hydraulický průměr
L1,L2 ... délka
Ro ... hustota
Lambda ... součinitel třecích ztrát
ZetaI ... ztrátový součinitel vstupu
ZetaBV ... ztrátový součinitel ohybů+ventilů
ZetaO ... ztrátový součinitel trysky / difuzoru
ZetaO ... ztrátový součinitel trysky / difuzoru
Numerická integrace (100 kroků), postupný výpočet
Sx, vx, Rex, Lambdax, hzx a z celkové ztrátové výšky hz vztažený součinitel
zetaO na výtokovou rychlost v2
Pro difuzor a úhel delta > 10°
ZetaO = ((S2 / S1) - 1)^2 * SIN(delta)
Pro výpočet je použita Bernouliho rovnice s využitím ztrátových
součinitelů pro výpočet výstupní rychlosti vo:
Výpočet průtoku, rychlostí, ztrát, výkonu v potrubí různých průřezů a počtu větví.
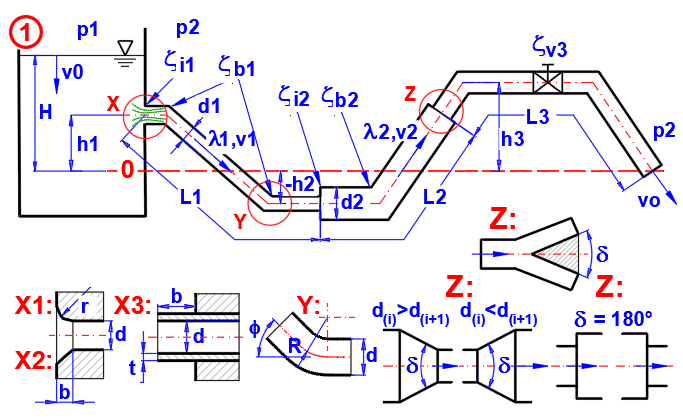
A = 2 * g * (v0^2 / (2 * g) + (p1 - p2) / (Ro * g) + H)
B(i) = (Zeta(i) + Lambda(i) * L(i) / dh(i)) * n(i) * (So / S(i))^2
vo = (A / (1 + SB(i)))^0.5
[i = 1 .... 15]
g ..... tíhové zrychlení
H ..... výška hladiny
p1, p2 ... tlak
v0 ... rychlost hladiny
dh(i) ... hydraulický průměr
L(i) ... délka
n(i) ... počet souběžných trubek
So ... průřez na výstupu
S(i) ... průřez potrubí i
Ro ... hustota
Lambda ... součinitel třecích ztrát
Zeta ... součet ztrátových součinitelů zetaI, zetaB, zetaV
Výpočet ztrátových součinitelů je popsán výše.
Ukázka grafu
Při regulaci průtoku tekutiny potrubím vzniká nestacionární proudění. Před ventilem se při zmenšování průtoku vytváří vyšší tlak než za ním. U dlouhých potrubí dopravujících kapalinu může při rychlém (havarijním) uzavření potrubí dojít k takovému nárůstu tlaku, který může potrubí porušit.
Při uzavření potrubí se kinetická energie kapaliny postupně spotřebuje na její stlačení, popř. deformaci potrubí. Rázová vlna se v potrubí šíří rychlostí zvuku v dané kapalině ve směru B->A a zpět A->B.
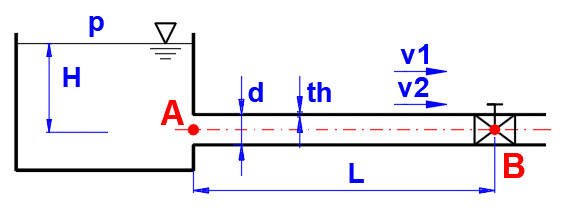
Doba běhu vlny t
t = 2 * L / a
L ... délka potrubí
a ... rychlost zvuku
Rychlost zvuku at [m/s] (teoretická, pro dokonale tuhé potrubí)
at = (K / Ro)^0.5
K ..... modul objemové pružnosti kapaliny
Ro ... hustota
Rychlost zvuku a [m/s] (tenkostěnné potrubí, th =< 0.1*d)
a = (K / Ro)^0.5 / (1 + (K * d) / (E * th))^0.5
E ... modul pružnosti materiálu
trubky
d ... průměr potrubí
th .. tloušťka stěny potrubí
Rychlost zvuku a [m/s] (tlustostěnné potrubí, th > 0.1*d)
a = (K / Ro)^0.5 / (1 + 2 * (K
/ E) * ((D^2
+ d^2) / (D^2 - d^2)))^0.5
E ... modul pružnosti materiálu
trubky
d ... vnitřní průměr potrubí
D ... vnější průměr potrubí
Pro dobu uzavírání potrubí
tc =< t
A. Dokonale tuhé potrubí
p = Ro * (v1 - v2) * at
B. Tenkostěnné potrubí
p = Ro * (v1 - v2) * a
v1, v2 ... rychlost kapaliny
Pro dobu uzavírání potrubí
tc > t
p = Ro * L * (v1 - v2) / t
Výpočty pokrývají některé často řešené úlohy z oblasti mechaniky tekutin. Pokud vaše úloha spadá do okruhu řešených problémů, postupujte následovně:
1. V odstavci [1] vyberte kapalinu, popřípadě nastavte její parametry a
definujte parametry prostředí.
2. Vyberte odpovídající úlohu a vyplňte známé vstupní hodnoty.
3. Výpočty jsou ve formě matematického modelu dané úlohy. Pokud tedy výsledkem
výpočtu má být některý ze vstupních parametrů, je nutné tento parametr postupně
iterovat.
V tomto odstavci nastavíte jednotky výpočtu, vyberete a nastavíte vlastnosti kapaliny a prostředí.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě změněny všechny hodnoty.
Vyberte kapalinu. Hodnoty v seznamu jsou pro barometrický tlak. Pokud chcete zadat vlastní parametry kapaliny, odškrtněte tlačítko vpravo.
Po odškrtnutí tlačítka vpravo můžete zadat buď rychlost zvuku a nebo modul objemové pružnosti.
Po odškrtnutí tlačítka vpravo můžete zadat buď kinematickou, nebo dynamickou viskozitu.
Pro většinu výpočtů stačí nastavení nulové nadmořské výšky. Přesto se mohou vyskytnout úlohy, kdy je nutné brát v úvahu odlišný barometrický tlak, či odlišné tíhové zrychlení.
Standardní tíhové zrychlení je uvažováno na hladině moře pro 45° zeměpisné šířky.
Reynoldsovo číslo Re je bezrozměrný parametr, určující přechod mezi prouděním laminárním a turbulentním. Pro Re < 2300 jde o proudění laminární, pro hodnotu Re > 3000 je proudění téměř vždy turbulentní.
Kritické Re tedy určuje způsob výpočtu a tím i hodnoty ztrátových součinitelů.
Některé často řešené úlohy z oblasti hydrostatiky.
Zadejte požadované hodnoty podle obrázku.
Označení bodů:
G … Těžiště plochy
P … Působiště síly
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu tlaku nad hladinou a tlak vně nádoby.
Plocha kolmá na hladinu: delta=0
Plocha rovnoběžná s hladinou: delta=90
Celková síla na plochu S. Má působiště v bodě P.
Vzdálenost těžiště plochy od volného povrchu kapaliny.
Vzdálenost středu tlaku od volného povrchu kapaliny.
Výpočet neřeší situaci, kdy hladina narazí na dno nádoby.
Výpočet neřeší situaci, kdy hladina narazí na dno nádoby.
Výpočet ustáleného výtoku kapaliny otvorem.
Skutečná výtoková rychlost reálné tekutiny se liší od teoretických hodnot pro ideální tekutiny. Při výtoku tekutiny otvorem (resp. krátkým nátrubkem) je styk se stěnou malý, proto bude malá i disipace energie. Proto je možné považovat tekutinu za nevazkou a teoretické výsledky opravit následujícími korekčními součiniteli.
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu tlaku nad hladinou a tlak vně nádoby.
V případě, že nádoba není válcová, je možné po odškrtnutí tlačítka zadat přímo příčnou plochu.
V případě, že otvor není kruhový, je možné po odškrtnutí tlačítka zadat přímo jeho plochu
Pouze pro porovnávací účely. Nezahrnuje žádné ztráty.
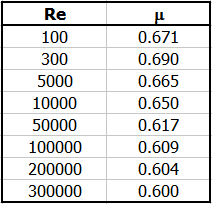
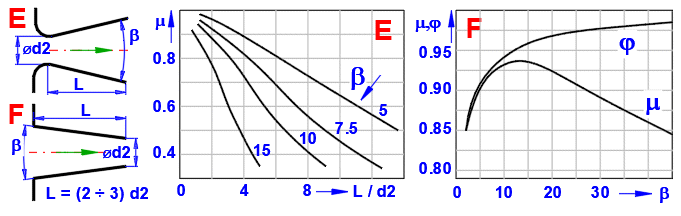
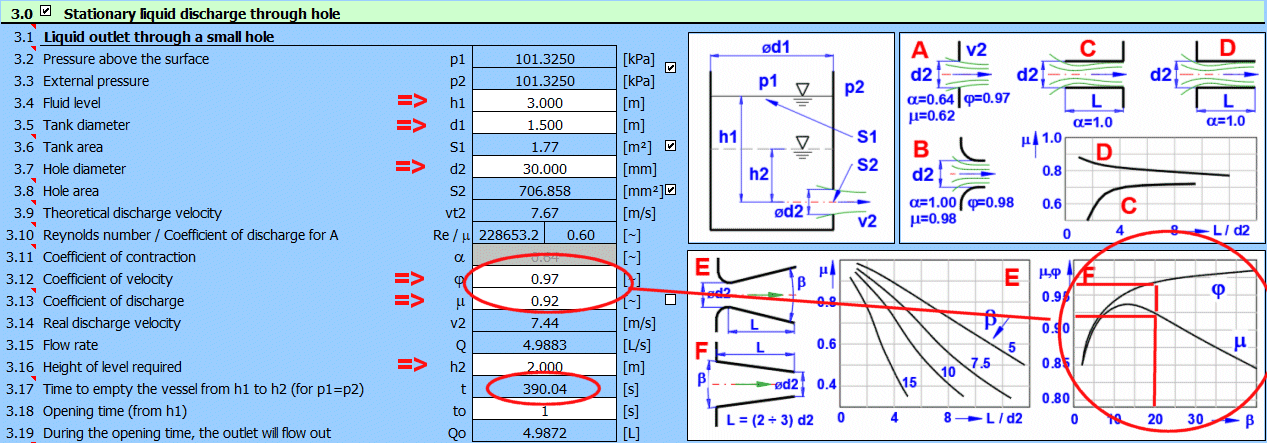
Pro výtok otvorem bez nátrubku (A) je možné určit výtokový součinitel v závislosti na Reynoldsově čísle Re. Vlevo je vypočtené Re, v pravo výtokový součinitel, který je možné použít místo standardní hodnoty 0.62
Příslušné součinitele vyberte podle typu výstupního otvoru (A-F) podle uvedené tabulky a grafů.
Pro přímé zadání součinitele výtoku (součin [3.11] a [3.12]) odškrtněte tlačítko vpravo.
Pro velké otvory (horní hrana blízko hladiny a poměr výšky otvoru k hloubce těžiště je blízko jedné) je třeba uvažovat nelineární rozložení výtokové rychlosti.
Součinitel výtoku použijte stejný jako v případě malého otvoru [3.13].
Přepad je po hydraulické stránce výtok velkým otvorem, bez horní stěny nad paprskem (obr. A). Přepad může být dokonalý, je-li hladina za přepadem níže než přepadová hrana, nebo nedokonalý (zatopený) jeli hladina za přepadem výše (obr. B). Dokonalých přepadů se používá k určení protékajícího množství tekutiny. Podle tvaru pak mohou být přepadové hrany obdélníkové, trojůhelníkové, lichoběžníkové, kruhové.
Výšku hladiny h je nutné měřit v dostatečné vzdálenosti před přepadem (obvykle 2h - 4h). Nad přepadem je hladina níže, protože se již část polohové energie změnila v kinetickou.
Ve výpočtu jsou pak napravo od vstupních buňek vypsány okrajové podmínky, pro které jsou výpočty definovány.
Pro výpočet obdélníkových přepadů (obr. A), resp. pro výpočet součinitele průtoku Cd existuje řada vzorců a postupů, které jsou v literatuře uváděné. Proto je pro srovnání uvádíme také.
Výška nad přepadem h se obvykle měří ve vzdálenosti 2h ~ 4h od přepadu (eliminace poklesu hladiny nad přepadem).
Pokud ovlivňuje výška hladiny na odtoku průtok vody (obr. B) je možné použít tento výpočet s tím, že parametry přepadu jsou definované v části A.
Hodnota součinitele v závislosti na p a poměru h2/h je uvedena v zelené buňce.
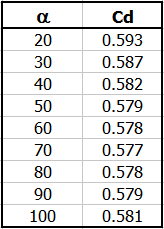
Pokud je plocha výřezu relativně malá proti ploše průřezu přítoku je možné použít experimentálně stanovené Cd závislé pouze na úhlu výřezu.
Často řešená úloha, pro potrubí s konstantním průřezem, ohyby, ventily atd.
Pro řešení je použita univerzální Bernouliho rovnice s využitím ztrátových
součinitelů.
Výpočet průtoku, rychlostí, ztrát, výkonu v potrubí konstantního průřezu.
Vyplňte všechny rozměrové a tlakové parametry. Pro odhad ztrátových koeficientů můžete využít výpočtů vpravo. Je možné volit záporný přetlak (p2>p1), je možné volit zápornou výšku (H<0), v každém případě je nutné dodržet smysl proudění tekutiny od vstupu k výstupu.
Jako přednastavená hodnota je použit tlak p1=p2 z odstavce [1.0]. Po odškrtnutí tlačítka vpravo zadejte tlak uvnitř nádoby p1 a okolní tlak p2.
Výška hladiny musí být větší, než hodnota vpravo.
Pokud je výstupní otvor výše než úroveň hladiny, zadejte výšku H jako zápornou
hodnotu (musí být vyrovnáno přetlakem p1>p2).
V případě p1<p2 musí být vnější přetlak vyrovnán výškou hladiny H.
Pokud potrubí není kruhového průřezu, můžete po odškrtnutí tlačítka vpravo zadat hodnotu plochy potrubí a smáčeného obvodu. Z těchto hodnot je pak určen hydrodynamický průměr dh podle vzorce dh = 4 * S / C, který je následně použit ve výpočtech.
V obrázku naznačeno jako řez A-A.
V seznamu vyberte odpovídající materiál potrubí. Předvolená hodnota drsnosti v [mm/in] na dalším řádku je průměr z rozsahu uvedeném v závorce. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Na základě drsnosti potrubí "k" a koeficientu "Re" je v odborné literatuře uváděna řada vzorců pro výpočet součinitele třecích ztrát pro turbulentní proudění. Zvolte příslušný výpočet ze seznamu.
Nejčasteji používaný je výpočet "C. Colebrook - White", který pokrývá i hydraulicky hladké potrubí (k=0). Detaily v nápovědě.
Návrh součinitele třecích ztrát Lambda závisí na Re a zároveň je výpočet Re závislý na součiniteli třecích ztrát
Lambda (výpočet rychlosti proudění).
Návrhová hodnota se automaticky přenáší do vstupní buňky.
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Součinitele vstupu volte dle výpočtu/doporučení vpravo.
Na obrázku jako X1, X2, X3.
Jde o součet všech koeficientů pro všechny možné ztráty v potrubí (zahnutí, ventily…).
Ztrátový součinitel ohybu potrubí je možné zjistit výpočtem vpravo, ztrátové součinitele ventilů je možné zhruba odhadnout dle obrázku.
Zvolte, pokud má potrubí na konci trysku / difuzor
Pokud je d1>d2 (dh1>dh2) je použit návrh ztrát pro trysku, pro d1<d2 pro
difuzor.
Pokud potrubí není kruhového průřezu, můžete po odškrtnutí tlačítka vpravo zadat hodnotu plochy potrubí a smáčeného obvodu. Z těchto hodnot je pak určen hydrodynamický průměr dh podle vzorce dh = 4 * S / C, který je následně použit ve výpočtech.
V obrázku naznačeno jako řez A-A.
Zadejte délku trysky / difuzoru. Musí být menší než délka potrubí L1.
Je počítán z hodnot dh1, dh2 a L2.
Pro trysku (d1>d2) a Difuzor (delta<10) je použit odhad na základě integrace ztrát. Pro Difuzor a delta>10, kdy dochází k odtržení proudu tekutiny od stěny potrubí je použit vztah: zetaO = ((S2 / S1) - 1)^2 * SIN(delta).
Udává poměr mezi výškovou a tlakovou energií na vstupu a kinetickou energií výstupního proudu tekutiny.
Uvedené výkonové parametry umožňují vyhodnocení potrubí.
Platí:
Pp + Ph = Pz + Po
resp.
Pp + Ph + Pv = Pz + Po pro odstavec [6.0]
Průtoky jsou často udávané v různých jednotkách nezávisle na jednotkách výpočtu. Proto je níže uveden přepočet těch nejčastěji používaných.
Pro výpočet je použita Bernouliho rovnice s využitím ztrátových
součinitelů pro výpočet výstupní rychlosti vo.
Výpočet průtoku, rychlostí, ztrát, výkonu v potrubí různých průřezů a počtu větví.
Vyplňte podmínky na vstupu do potrubí.
Je možné volit záporný přetlak (p2>p1), je možné volit zápornou výšku (H<0), v každém případě je nutné dodržet smysl proudění tekutiny od vstupu k výstupu.
Jako přednastavená hodnota je použit tlak p1=p2 z odstavce [1.0]. Po odškrtnutí tlačítka vpravo zadejte tlak uvnitř nádoby p1 a okolní tlak p2.
Rychlost kapaliny (kynetická energie) před vstupem do potrubí. Ve většině řešených problémů (velká nádoba vzhledem k objemu potrubí) je možné rychlost zanedbat a použít nulovou hodnotu.
Nenulová bude například v případě pístu, který vytlačuje kapalinu potrubím.
Výška hladiny musí být větší, než hodnota vpravo.
Pokud je výstupní otvor výše než úroveň hladiny, zadejte výšku H jako zápornou
hodnotu (musí být vyrovnáno přetlakem p1>p2).
V případě p1<p2 musí být vnější přetlak vyrovnán výškou hladiny H.
Na základě drsnosti potrubí "k" a koeficientu "Re" je v odborné literatuře uváděna řada vzorců pro výpočet součinitele třecích ztrát pro turbulentní proudění. Zvolte příslušný výpočet ze seznamu.
Nejčasteji používaný je výpočet "C. Colebrook - White", který pokrývá i hydraulicky hladké potrubí (k=0). Detaily v nápovědě.
Součet energetického potencionálu tlakového (p2-p1), potencionálu tlakové výšky kapaliny (H) a kinetické energie kapaliny (v0) na vstupu do potrubí.
Většinou je energetická hladina vyjadřována v metrech sloupce tekutiny.
Jednotky, ve kterých má být energetická hladina vyjádřena vyberte vpravo.
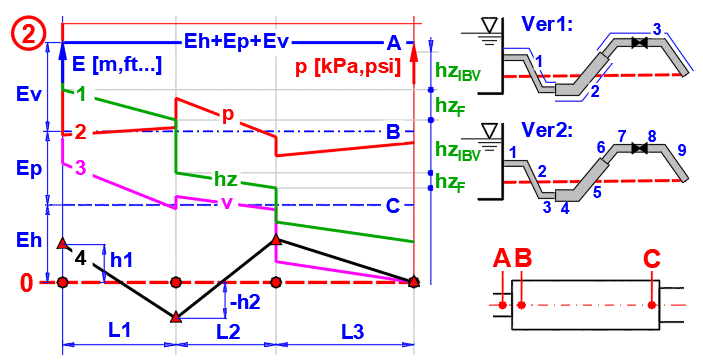
V grafu níže je naznačena modrou horizontální úsečkou (Obr2 - A).
Pouze pro porovnávací účely. Nezahrnuje žádné ztráty.
Udává poměr mezi výškovou a tlakovou energií na vstupu a kynetickou energií výstupního proudu tekutiny.
Uvedené výkonové parametry umožňují vyhodnocení potrubí.
Platí:
Pp + Ph = Pz + Po
resp.
Pp + Ph + Pv = Pz + Po pro odstavec [6.0]
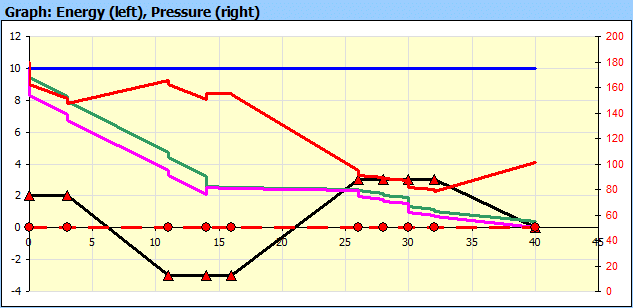
Popis grafu (Obr.2):
Přímka A: Čára celkové energie (Total Energy Line). Udává součet energií (výšková-Eh, tlaková-Ep a kinematická-Ev) kapaliny na vstupu do potrubí.
Přímka B: Součet energie výškové (Eh) a tlakové (Ep)
Přímka C: Výšková energie (Eh)
Přímka 0: Nulová čára vztažená ke konci potrubí
Křivka 1: Ztrátová výška hz (ztráty v jednotlivých částech potrubí)
Křivka 2: Tlak v potrubí (stupnice napravo v kPa nebo psi)
Křivka 3: Kinematická výška
Křivka 4: Výškové body počátku jednotlivých úseků vzhledem k nulové čáře
Postupně vyplňte hodnoty pro každý úsek potrubí v tabulce (jeden řádek pro každý úsek).
Je možné volit dva přístupy, popř. jejich kombinace.
Zjednodušený (Obr2. Ver1):
Jednotlivé úseky jsou rozdělené podle průměru potrubí a všechny ztrátové součinitele (vstup, ohyb, ventil...) v jednom úseku jsou shrnuté do jednoho součinitele (sloupec H), který je uplatněn na počátku příslušného úseku.
Detailní (Obr2. Ver2):
Potrubí je rozdělené na úseky tak, aby se příslušný ztrátový součinitel (sloupec H) nalézal vždy na začátku úseku. Získáte detailnější graf [6.19]. Celkové výsledky (Q, vo...) jsou shodné.
Zvolte počet navazujících úseků, který se bude řešit (1-15).
Je možné rozdělit jednu trubku na dvě a více trubek. Popřípadě sloučení více trubek do jedné. (Obr. detail Z)
Výška počátku úseku potrubí nad (pod) výstupním (koncovým) bodem posledního úseku (nulová čára).
Délka jednotlivého úseku.
Zadejte průměr. Pokud trubka není kruhová, zadejte hydraulický průměr dh
(viz. popis Plochy odstavec E).
Stisknutím tlačítka "V" se hodnota z prvního řádku nakopíruje do ostatních.
Pokud je zaškrtnuté tlačítko vpravo, je plocha počítána z kruhového průřezu z
průměru d ze sloupce vlevo (D).
Pro potrubí nekruhového průřezu odškrtněte tlačítko vpravo a zadejte plochu
průřezu (E) a do buňky průměru d (D) zadejte hydraulický průměr dh.
dh = 4 * S / C
kde:
S ... plocha průřezu
C ... smáčený obvod
Úhel zúžení / rozšíření přechodu mezi dvěma úseky (Obr1. Det.Z), v případě
rozdělení potrubí na dvě větve, tak úhel mezi trubkami.
Odpovídající navržený ztrátový součinitel ZetaI je v pravo (sloupec G).
Na základě poměru ploch (sloupec E) a zkosením (sloupec F) mezi dvěma úseky, je navržen ztrátový koeficient na začátku úseku (podrobnosti v teoretické části nápovědy). Podobně je navržen i ztrátový koeficient v případě rozvětvení potrubí.
Tlačítkem "=>" můžete hromadně přenést návrh do sloupce H, který je použit ve výpočtu.
Součet všech ztrátových součinitelů v příslušném úseku potrubí.
ZetaI …. ztráty vstupu, ztráty změnou průřezu (návrh sloupec G)
ZetaB … ztráty ohybu (výpočet v předchozím odstavci [5.0])
ZetaV … ztráty ventilu (tabulka v předchozím odstavci [5.0])
Pro výpočet reálného potrubí je nutné zadat drsnost potrubí. Pro orientaci použijte tabulku níže. Stisknutím tlačítka "V" se hodnota z prvního řádku nakopíruje do ostatních.
- Hydraulicky hladké potrubí (0-0) mm / (0-0) in
- Ocel - bezešvé trubky (0.03-0.1) mm / (0.00118-0.00394) in
- Ocelové trubky svařované nové (0.05-0.1) mm / (0.00197-0.00394) in
- Ocelové trubky svařované zrezivělé (0.15-0.5) mm / (0.00591-0.01969) in
- Ocelový plech svařovaný - vzduchovody (0.5-0.8) mm / (0.01969-0.0315) in
- Ocelový plech nýtovaný (1-6) mm / (0.03937-0.23622) in
- Mosazné a hliníkové trubky čistě tažené (0.0015-0.01) mm / (0.00006-0.00039)
in
- Sklo, plasty (0.0015-0.01) mm / (0.00006-0.00039) in
- Litina nové potrubí (0.1-0.3) mm / (0.00394-0.01181) in
- Litina staré potrubí (1-4.5) mm / (0.03937-0.17717) in
- Gumová hadice (0.01-0.03) mm / (0.00039-0.00118) in
- Překližka (0.025-0.1) mm / (0.00098-0.00394) in
- Keramika (0.45-6) mm / (0.01772-0.23622) in
- Cihly s cementovým výmazem (0.8-6) mm / (0.0315-0.23622) in
- Beton (0.8-9) mm / (0.0315-0.35433) in
Reynoldsovo číslo Re (detaily v nápovědě - Teorie)
Charakterizuje proudění vazké tekutiny, které závisí nejen na střední rychlosti
ale na charakteristickém rozměru proudu tekutiny (průměr d, resp. dh), dynamické
viskozitě a hustotě.
Slouží k výpočtu součinitele třecích ztrát Lambda (sloupec K).
Návrh součinitele třecích ztrát Lambda. Závisí na Re (sloupec J). Ale výpočet Re je zpětně závislý na rychlosti proudění (pro který je nutné znát Lambda). Proto dochází k postupné iteraci hodnot.
Návrhová hodnota se automaticky přenáší do buňky vpravo (sloupec L), která je
použita pro výpočet.
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu součinitele třecích
ztrát.
Součinitel třecích ztrát Lambda. Je nutný pro výpočet rychlosti proudění. Pokud je zaškrtnuté tlačítko v pravo, je použita návrhová hodnota (sloupec K).
Pokud nemáte vážný důvod, použijte návrhovou hodnotu.
Stisknutím tlačítka "V" se hodnota z prvního řádku nakopíruje do ostatních řádků.
Rychlost tekutiny v daném úseku potrubí.
Ve sloupci N,O vyberte, které hodnoty chcete zobrazit a jejich jednotky. Výběr jednotek je spojen s řádkem [6.8].
hIBV … součet ztrát (vstup, ohyb, ventil) pro daný úsek
hF …... třecí ztráty pro daný úsek
h-A, h-B, h-C … ztráty od počátku potrubí postupně v bodech A,B,C (Obr.2)
v(pd) … energie proudící tekutiny (dynamický tlak)
p-A, p-B, p-C ... absolutní tlak v bodech A,B,C
Při regulaci průtoku tekutiny potrubím vzniká nestacionární proudění. Před ventilem se při zmenšování průtoku vytváří vyšší tlak než za ním. U dlouhých potrubí dopravujících kapalinu může při rychlém (havarijním) uzavření potrubí dojít k takovému nárůstu tlaku, který může potrubí porušit.
Při uzavření potrubí se kinetická energie kapaliny postupně spotřebuje na její stlačení, popř. deformaci potrubí. Rázová vlna se v potrubí šíří rychlostí zvuku v dané kapalině ve směru B->A a zpět A->B.
Stisknutím tlačítka načtete parametry z odstavce [5.0].
Vyplňte vstupní parametry podle obrázku.
Vyberte materiál potrubí.
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Při úplném uzavření ventilu v2=0.
Mohou nastat dva případy.
1. Čas uzavření ventilu t > T-doba běhu rázové vlny [7.14,7.21]
Se zkracováním času uzavření ventilu roste tlak.
2. Čas uzavření ventilu t < T-doba běhu rázové vlny [7.14,7.21]
Tlak zůstává konstantní na své nejvyšší intenzitě.
Je definován v odstavci [1.0]
Teoretická rychlost zvuku [7.20] je závislá na hustotě materiálu a objemové pružnosti kapaliny. Pro reálné potrubí se rychlost šíření zvuku snižuje v závislosti na rozměrech a na materiálu potrubí.
Přibližný výpočet viskozity a hustoty kapaliny v závislosti na teplotě.
Zadejte teplotu vybrané kapaliny. Na základě teploty je navržena hustota a viskozita. Výpočet je přibližný s přesností +- 6% v rozsahu teplot 0-100°C (32-212°F).
Stisknutím tlačítka přesunete hodnoty hustoty a viskozity do odstavce [1.0].
Odstavec [3.0] - Výpočet doby poklesu hladiny z h1 na h2.
Nádoba definovaná dle obrázku.
Kapalina: voda, 20°C,
p1=p2=atmosférický tlak (Odstavec [1.0]).
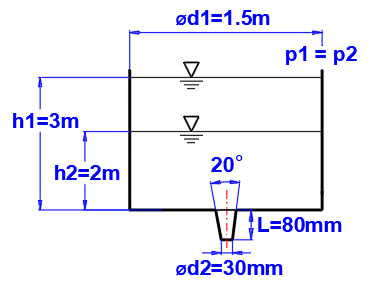
Zadejte vstupní hodnoty dle obrázku, koeficienty j a m odečtěte z grafu F. Čas pro pokles hladiny je na [3.17].
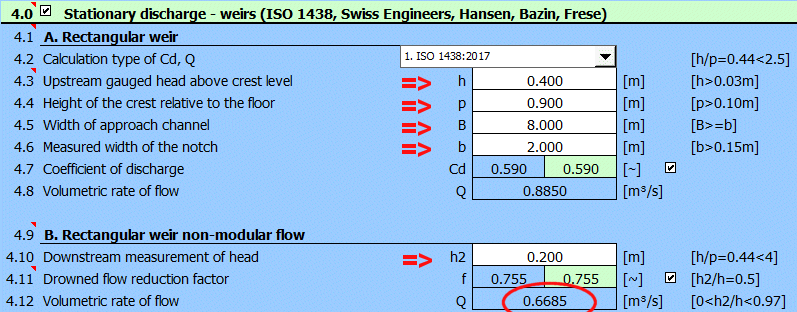
Odstavec [4.0]. Výpočet průtoku pomocí zatopeného přepadu.
Přepad je definován podle obrázku.
Způsob výpočtu dle ISO 1438.
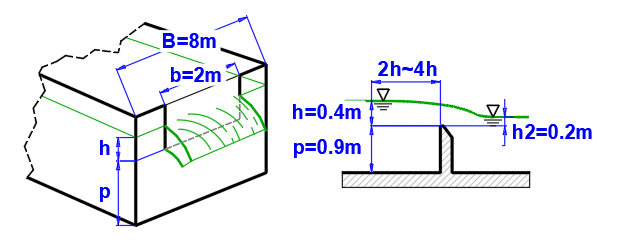
Zadejte vstupní hodnoty dle obrázku. Výsledný průtok pro zatopený přeliv je na řádku [4.12].
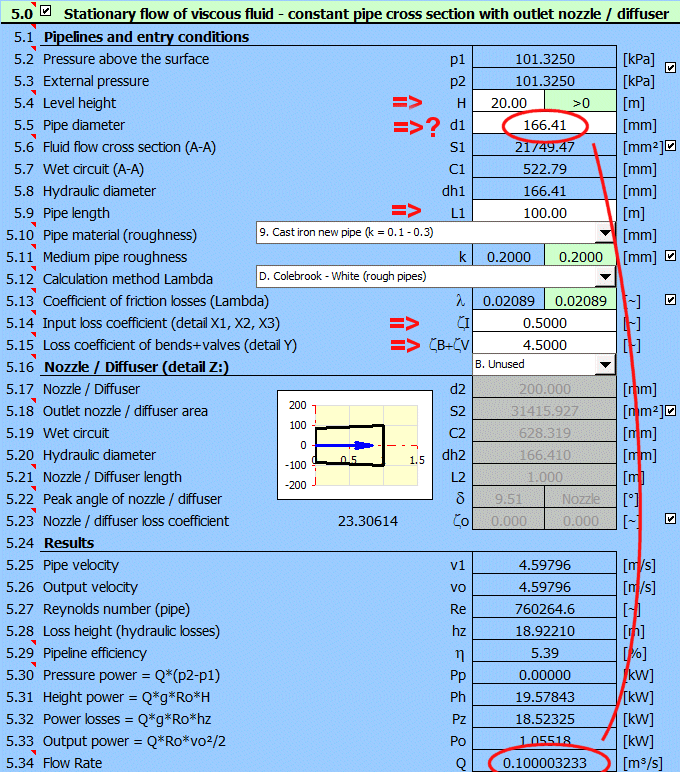
Odstavec [5.0]. Výpočet průměru potrubí pro požadovaný průtok kapaliny.
Definice rozměrů a ztrátových koeficientů potrubí dle obrázku.
Požadovaný průtok
100L/s = 0.1 m³/s
Ztráty vstup = 0.5, ztráty ohyb+ventil = 5*0.3 + 2*1.5 = 4.5
Litinové
potrubí (nové), drsnost k=0.2mm
Způsob výpočtu ztrátového koeficientu Lambda: Colebrook - White
Kapalina: voda, 20°C,
p1=p2=atmosférický tlak (Odstavec [1.0])
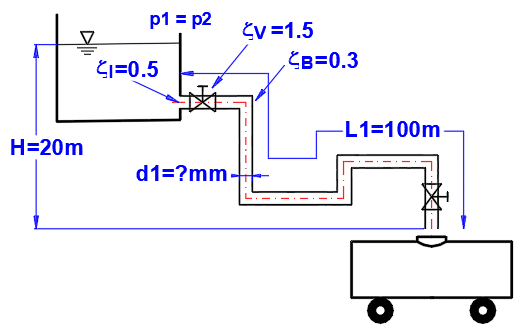
Zadejte všechny známé parametry a postupně měňte hodnotu d1 [5.5] tak, aby byl dosažen požadovaný průtok Q = 0.1 m³/s
Odstavec [5.0]. Výpočet výkonu proudu na konci trysky pro zadaný průměr. Zjištění pro jaký průměr trysky je dosažený maximální výkon.
Definice rozměrů a ztrátových koeficientů potrubí dle obrázku.
Ztráty vstup = 0.5, ztráty ohyb+ventil = 2*0.2 + 1.5 = 1.9
Litinové potrubí, drsnost k=1.5 mm
Způsob výpočtu ztrátového koeficientu Lambda: Colebrook - White
Kapalina: voda, 20°C,
p1=p2=atmosférický tlak (Odstavec [1.0])
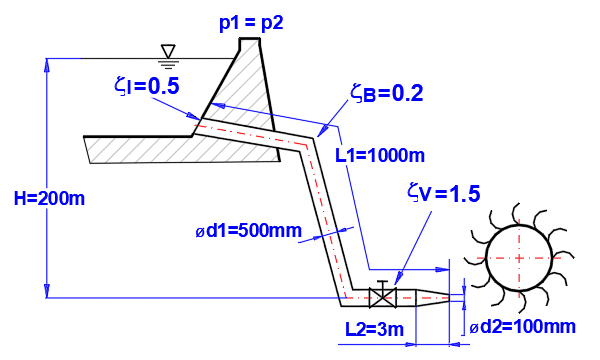
Zadejte všechny známé parametry. Výkon proudu kapaliny na konci trysky je Po = 761kW [5.33]
Pro zjištění maximálního výkonu postupně měňte průměr trysky d2. Maximální výkon
Po = 1162kW pro d2=157.6mm.
Zároveň se sníží účinnost z 85.5% pro d2=100mm na 61.8% pro d2=157.6mm.
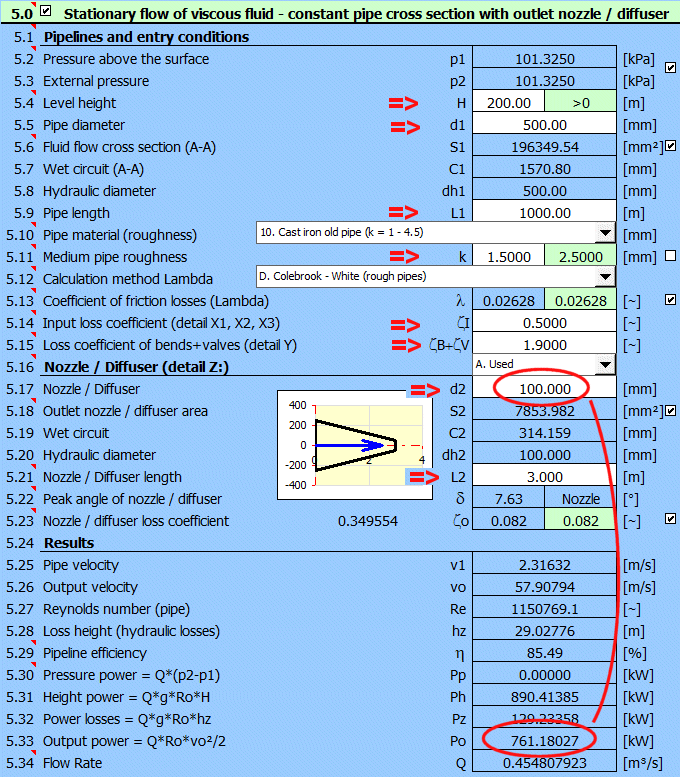
Odstavec [6.0]. Výpočet detailního průběhu tlaku a ztrát v potrubí, výpočet rychlostí kapaliny a průtoku.
Potrubí definované dle obrázku a tabulky, kde:
ID ... číslo úseku (1-9)
L ... délky jednotlivých úseků
ZetaI, ZetaB, ZetaV … ztráty na začátku úseku (vstup, změna průřezu, ohyb,
ventil)
Materiál potrubí: Litina, drsnost k=1.5mm
Způsob výpočtu ztrátového koeficientu Lambda: Colebrook - White
Kapalina: voda, 20°C,
p1=p2=atmosférický tlak (Odstavec [1.0])
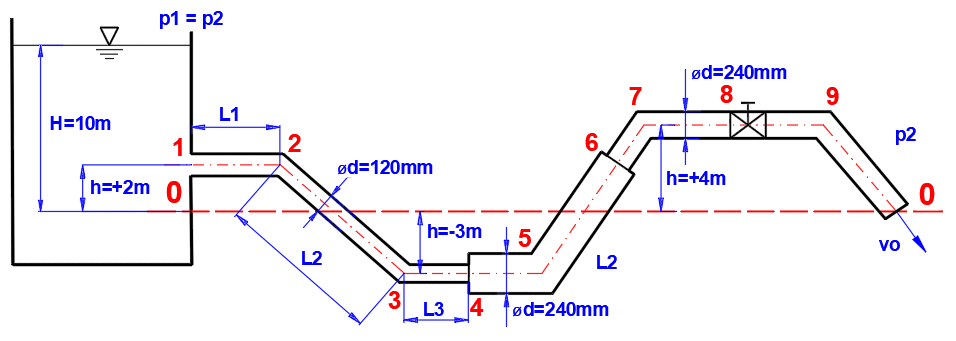
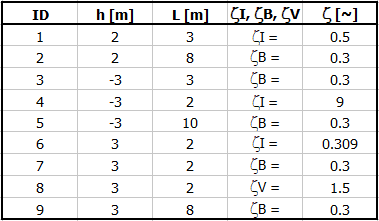
Definice podmínek:

Nadefinujte parametry potrubí (A-počet trubek, B-výška vzhledem k nulové čáře, C-délka úseků, D-průměr potrubí, F-úhel přechodu mezi různými průměry trubky, H-jednotlivé ztrátové koeficienty, I-drsnost potrubí)
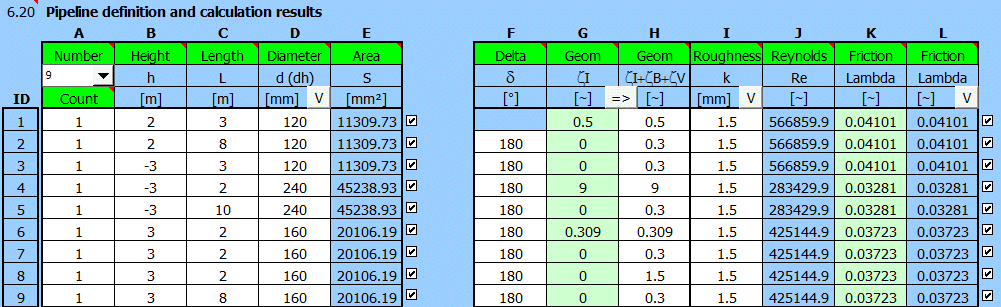
Výsledky:

Podrobný průběh tlaku a ztrát:
Odstavec [6.0]. Výpočet výkonu čerpadla pro čerpání vody do výšky 25m. Požadovaný průtok je 10l/s.
Potrubí definované dle obrázku.
L ... délky jednotlivých úseků
ZetaI, ZetaB … ztráty (vstup, změna průřezu-rozdělení
potrubí, ohyb)
Materiál potrubí: Ocelová trubka, drsnost k=0.1mm
Způsob výpočtu ztrátového koeficientu Lambda: Colebrook - White
Kapalina: voda, 20°C,
p2=atmosférický tlak (Odstavec [1.0])
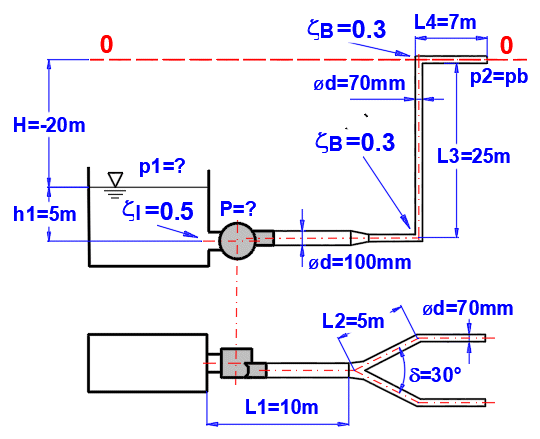
Nadefinujte parametry potrubí (A-počet trubek, B-výška vzhledem k
nulové čáře, C-délka úseků, D-průměr potrubí, F-úhel rozdvojení potrubí,
H-jednotlivé ztrátové koeficienty, I-drsnost potrubí)
Ztráta pro rozdělení potrubí je na G2.

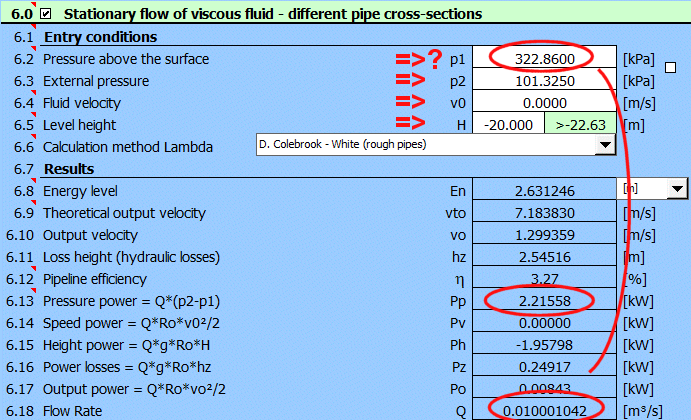
Zadejte všechny známé parametry a postupně měňte hodnotu tlaku
p1 [6.2] tak, aby byl
dosažen požadovaný průtok Q = 0.01 m³/s [6.18]
Nutný výkon čerpadla je pak uveden na řádku [6.13] Pp=2.22kW.
Odstavec [6.0]. Výpočet průtoku vody ve sprše.
Potrubí a sprcha definované dle obrázku:
L ... délky jednotlivých úseků
ZetaI, ZetaV, ZetaB … ztráty (vstup, ventil, ohyb)
Materiál potrubí: Ocelová trubka, drsnost k=0.1mm
Způsob výpočtu ztrátového koeficientu Lambda: Colebrook - White
Kapalina: voda, 20°C,
p1=p2=atmosférický tlak (Odstavec [1.0])
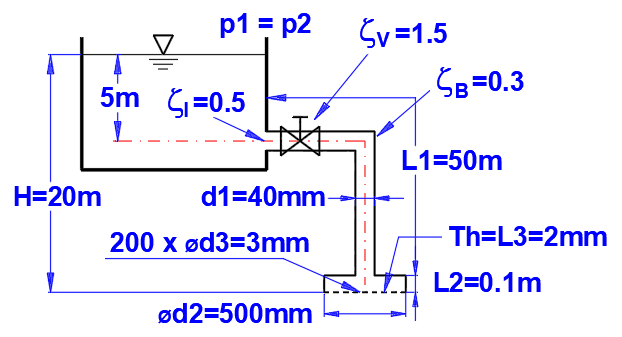
Nadefinujte parametry potrubí a sprchy s 200 otvory.

Zadejte výšku hladiny. Průtok vody sprchou Q=1l/s je na řádce [6.18].
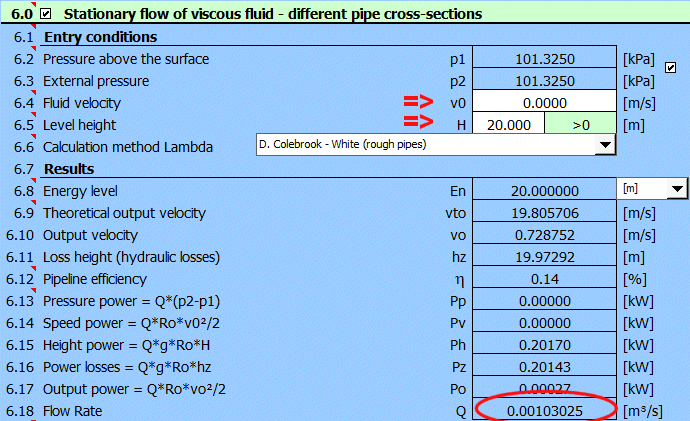
Odstavec [7.0]. Výpočet hydraulického rázu při havarijním uzavření potrubí z příkladu 4. Kontrola napětí v potrubí.

Při definici parametrů můžete použít tlačítko "[5.0] >>
[7.0]". Tím načtete hodnoty z odstavce [5.0].
Dále zadejte materiál, vyplňte tloušťku stěny potrubí 20mm a dobu
uzavírání ventilu 2 sekundy.
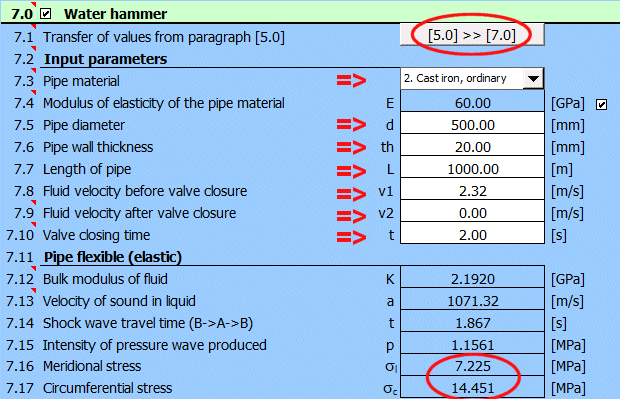
Srovnejte skokový nárůst napětí [7.16, 7.17] pro dobu uzavírání ventilu pro t<1.86 s.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
Literatura:
[1] Mechanika tekutin - ČVUT (Prof. Ing. Jan Ježek, DrSc, Ing. Blanka Váradiová, CSc., Ing Josef Adamec, CSc)
[2] Mechanika tekutin, Sbírka příkladů - ČVUT (Ing. Milan Peťa)
[3] Strojně technická příručka (Svatopluk Černoch)
[4] Mechanika tekutin, VŠB-TU Ostrava (Janalík J., Šťáva P.)
[5] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[6] A TEXTBOOK OF FLUID MECHANICS AND HYDRAULIC MACHINES (Dr. R.K. Bansal)
[7] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
[8] Fluid mechanics, seventh edition (Frank M. White)
[9] 2500 Solved problems in fluid mechanics and hydraulics (Jack Evett, Cheng Liu)
[10] Handbook of hydraulics (Brater, King, Lindell, Wei)
Normy:
ISO 1438:2017
Hydrometrie — Měření průtoku vody v otevřených korytech pomocí tenkostěných přelivů
Hydrometry — Open channel flow measurement using thin-plate weirs
Hydrometrie — Mesure de debit dans les canaux découverts au moyen de déversoirs a paroi mince
^