Das Programm ist für Entwurf, Berechnung und Prüfung von vier Grundtypen von Reibungsbremsen und Kupplungen vorgesehen. Im Programm ist es auch möglich, die kinetische Energie und die Belastungsmomente der Mechanismen zu bestimmen.
Das Programm ermöglicht:
1. Berechnung der Bremsenbelastung
2. Berechnung der Anlaufbelastung der Kupplung
3. Prüfung der belasteten Kupplung
4. Entwurf und Prüfung:
- Scheibenbremsen/Kupplungen
- Kegelbremsen/Kupplungen
- Trommelbremsen/Kupplungen
- Bandbremsen/Kupplungen
5. Berechnung und Prüfung der Erwärmung der entworfenen Bremse/Kupplung
In der Berechnung sind Daten, Verfahren, Algorithmen und Daten aus Fachliteratur, Standards und Firmenkatalogen verwendet.
[1] Clutches and Brakes Design and Selection; [2] Shigley’s Mechanical Engineering Design; [3] Textbook of Machine Design; [4] Brake Design and Safety; [5] Roloff / Matek - Maschinenelemente
VDI 2241-Blatt 1; VDI 2241-Blatt 2; SAE J866; SAE J661; Ortlinghaus, Goizper, TAROX, FERODO
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument"Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Nach dem physikalischen Prinzip unterscheiden sich Reibungsbremsen und Kupplungen nicht. Der Unterschied besteht nur in der Belastungsart der Bremse/Kupplung, deren geometrischer Lösung und Bedienung. Dem entsprechen dann auch die konkrete Lösung und die entsprechende Berechnung. Die aufgeführten Beziehungen sind universal.
The friction brakes and clutches do not differ in physical nature. The difference is only in the way the brake/clutch is loaded, their geometric design and control. The specific solution and the corresponding calculation also correspond to this. The relationships given are universal.
Die Lösung der Berechnung der Bremse/Kupplung wird gewöhnlich in zwei zusammenhängende Aufgaben geteilt.
1. Berechnung der Belastung der Bremse/Kupplung aufgrund des
gebremsten/anlaufenden Mechanismus. In der Berechnung Absatz [1].
2. Berechnung der Abmessungen der Bremse/Kupplung, die die geforderte Belastung
erfüllen. In der Berechnung Absatz [2,3,4,5,8].
Der gebremste Mechanismus weist zum Beginn des Bremszyklus die kinetische Energie Ek auf (hängt von der zweiten Potenz der Geschwindigkeit ab).
- Drehbewegung
- geradelinige Bewegung
Und gleichzeitig wirken auf ihn Kräfte und Momente, die die Belastung der Bremse reduzieren/erhöhen (sie sind während des Bremszyklus konstant).
- Reibungskräfte der Lager
- äußerer Einfluss (Bremsen auf geneigter Fläche)
- aerodynamischer Widerstand (nicht konstant) usw.
Eine weitere Variable ist die Bremszeit.
Die Lösung dieser Beziehungen ist das Drehmoment, das die Bremse entwickeln muss, und die Energie, die mit der Bremse zu absorbieren ist.
Für die Kupplung gilt ein analoges Verfahren wie bei der Bremse (Anlauf des Mechanismus – Erreichen der geforderten Ek).
Beide Aufgaben können getrennt werden und dadurch sind zum Beispiel die Unterlagen zur Auswahl der Bremse/Kupplung aus dem Herstellerkatalog zu gewinnen und aufgrund der Belastung die Bremse/Kupplung zu entwerfen.
In den folgenden Absätzen sind die für die Berechnung der Belastung und Energien für die geometrische Lösung der Reibungsbremsen und Kupplungen verwendeten Formeln, sowie die Berechnungen der Erwärmung enthalten.
Sie wird als die Summe der kinetischen Energie der geradelinigen Bewegung und der Rotationsenergie der Masse berechnet.
Ek [J]= 0.5 * m * v2 + 0.5 * I * ω2
m ... Masse der gebremsten Masse [kg]
v .... Geschwindigkeit der gebremsten Masse [m/s]
I .... Trägheitsmoment der gebremsten Masse [kg*m²]
ω ... Geschwindigkeit der gebremsten Masse mit Trägheitsmoment I [rad/s]
Beim Bremsen oder Anlaufen des Mechanismus wirken meist zusätzliche Kräfte oder Momente, die in die Berechnung einzubeziehen sind. Es kann sich um den Rollwiderstand des Rades, Wälzwiderstände der Lager, durch Masse verursachte Kräfte (Kran, Aufzug, Bewegung auf geneigter Fläche), Reibung, aerodynamischer Widerstand usw. sein.
Alle diesen nachträglichen Kräfte und Momente sind dann auf die Drehzahl der Bremse/Kupplung durch das einschlägige Übersetzungsverhältnis umzurechnen.
Sollte die Drehzahl des Fahrzeugrads zum Beispiel nw=100 [rpm] und Drehzahl der Kupplung nc=2000 [rpm] sein, dann ist das zusätzliche auf die Kupplung wirkende Moment ML:
ML = Mw * nw / nc
ML ... Zusatzlast / Entlastungsmoment
Mw ... Drehmoment, das auf das Rad des Fahrzeugs wirkt
nw ... Radgeschwindigkeit
nc .... Kupplungsgeschwindigkeit
Bei mehreren mit verschiedener Geschwindigkeit rotierenden und sich bewegenden Bauteilen ist es geeignet, deren kinetische Energien zusammenzuzählen und für weitere Berechnungen auf das reduzierte Trägheitsmoment, das auf die Drehzahl der Bremse/Kupplung bezogen ist, umzurechnen.
Ired [kg*m²] = 2 * Ek / (n / 60 * 2 * p)2
Ek ... Summe der kinetischen Energien
[J]
n ..... Brems-/Kupplungsgeschwindigkeit [/min]
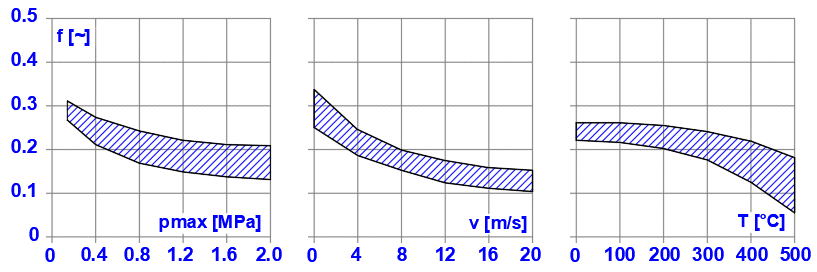
Es handelt sich um den Grundparameter, der die Abmessungen der Bremse/Kupplung meist beeinflusst. Er hängt von den eingesetzten Materialien und deren Kombinationen ab. In der Berechnung ist es möglich, aus den Grundbereichen der Reibungsmaterialien zu wählen. Wir empfehlen jedoch eindrücklich, nach den konkreten Werten des Herstellers/Lieferanten vorzugehen.
Beispiel, wie sich die Reibungszahl f [~] in Abhängigkeit von pmax [MPa], v [m/s] und T [°C] für die trockene Reibung bei der Kombination der Materialien Metallkeramik/Stahl ändern kann.
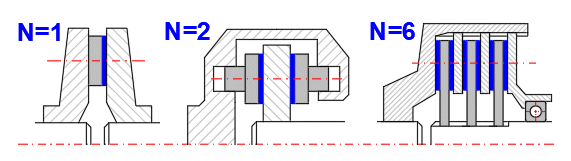
Sie gehören zu den meist benutzten Arten von Bremsen und Kupplungen. Sie weisen eine einfache Bauweise, eine große Fläche der Reibungsoberflächen sowie gute Wärmeableitung auf. Es ist möglich, Konstruktionen mit einer oder mehreren Reibungsoberflächen zu benutzen, wobei besonders die Konstruktion mit 2 Reibungsoberflächen sehr viel in der Automobilindustrie (Scheibenbremsen, Scheibenkupplungen) eingesetzt wird.
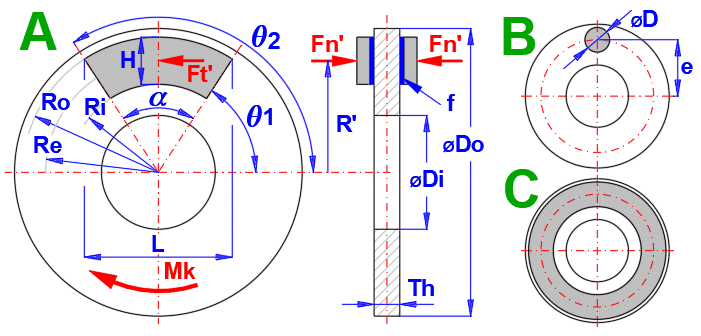
Weil sich das Prinzip von Bremsen und Kupplungen für die Berechnung nicht unterscheidet, wird die gemeinsame Vorgehensweise mit den in der Abbildung definierten Abmessungen verwendet. Die Konstruktion der Bremsen wird meist so gelöst, dass das Reibungselement die Form eines Kreisausschnittes oder des Kreises (A, B), bei der Kupplung dann des Kreisringes (C) aufweist.
Zur Lösung werden dann zwei Möglichkeiten verwendet.
A. Gleichmäßige Abnutzung (eingelaufene Bremse/Kupplung): Es wird von der Voraussetzung ausgegangen, dass die Reibungsscheiben starr sind und die größte Abnutzung zuerst auf deren Außenrand, wo die größte Arbeit der Reibkräfte entsteht, beginnt. Anschließend kommt es hier zu einer gewissen Abnutzung, die Druckverteilung ändert sich so, dass die Abnutzung der Reiboberflächen gleichmäßig ist.
B. Gleichmäßiger Druck (neue Bremse/Kupplung): Es wird vorausgesetzt, dass ein gleichmäßiger Druck auf die ganzen Reibfläche durch die Verwendung von Federn, die die Reibscheiben in die Berührung gleichmäßig andrücken, erreicht wird.
Allgemein wird die Möglichkeit A verwendet.
Maximaler Druck
pmax [MPa] =(2 * Mk) / (a *
f * Re
* (Ro^2 - Ri^2)
/ 1000000 /
FillCoeff
Äquivalenter Radius Re
Re [m] = (Ro + Ri) / 2
Reibungskraft
Ft [N] = Mk
/ Re
Normale Kraft
Fn [N] = Ft / f
Kraftangriffspunkt
R' [m] = (COS(q1) -
COS(q2)) / (q2 -
q1) * (2/3) * ((Ro^3 - Ri^3) / (Ro^2 - Ri^2))
Maximaler Druck
pmax [MPa] = (3 * Mk) / (a * f * (Ro^3 - Ri^3)) / 1000000 / FillCoeff
Äquivalenter Radius Re
Re [m] = 2 / 3 * (Ro^3 - Ri^3) / (Ro^2 - Ri^2)
Reibungskraft
Ft [N] = Mk
/ Re
Normale Kraft
Fn [N] = Ft / f
Kraftangriffspunkt
R' [m] =
(COS(q1) - COS(q2))
/ (q2 -
q1) * ((Ro
+ Ri)/2)
Mk ....................
Lastdrehmoment [Nm]
a
..................... Reibungssegmentwinkel [rad]
f ....................... Reibungskoeffizient [~]
Ro .................... Außenradius [m]
Ri ..................... Innenradius [m]
FillCoeff ............ Füllfaktor [~]
q1,q2
.............. Zusätzliche Winkel [rad]
Als Reibfläche wird die Kegelfläche verwendet. Der Vorteil dieser Konstruktion ist die kleinere Betätigungskraft Fn als bei der Scheibenbremse/Scheibenkupplung. In Abhängigkeit vom Reibmaterial wird gewöhnlich der Kegelwinkel b im Bereich von 10–15° verwendet.
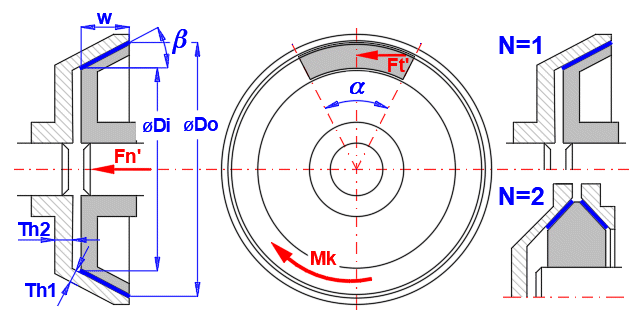
Bei der Lösung wird analog zum vorigen Fall vorgegangen; durch die Feststellung der Beziehung, die für die gleichmäßige Abnutzung des Belages und für die gleichmäßige Druckverteilung in der ganzen Reibfläche gilt.
Maximaler Druck
pmax [MPa] = (Mk / (p
* f *
Di) * (8
* SIN(b)) /
(Do^2 - Di^2))
/ 1000000 /
a
Äquivalenter Durchmesser De
De [m]=(Do +
Di) / 2
Reibungskraft
Ft [N] = Mk
/ (De / 2)
Normale Kraft
Fn [N] = Ft * SIN(b) / f
Maximaler Druck
pmax [MPa] = (Mk /(p
* f) *
(12 * SIN(b))
/ (Do^3 -
Di^3)) / 1000000
/ (a / (2 * p))
Äquivalenter Durchmesser De
De [m] = 2/3
* (Do^3 -
Di^3) / (Do^2
- Di^2)
Reibungskraft
Ft [N] = Mk
/ (De / 2)
Normale Kraft
Fn [N] = Ft * SIN(b) / f
Mk .... Lastdrehmoment [Nm]
a
..... Reibungssegmentwinkel [rad]
b
...... Kegelwinkel [rad]
f ....... Reibungskoeffizient [~]
Do .... Außendurchmesser [m]
Di ..... Innendurchmesser [m]
Trommelbremsen mit inneren Backen werden überwiegend in der Automobilindustrie eingesetzt. Bremsen mit den Außenbacken und Bremsen mit symmetrisch gelagerten Backen werden dann überwiegend in den industriellen Anwendungen eingesetzt.
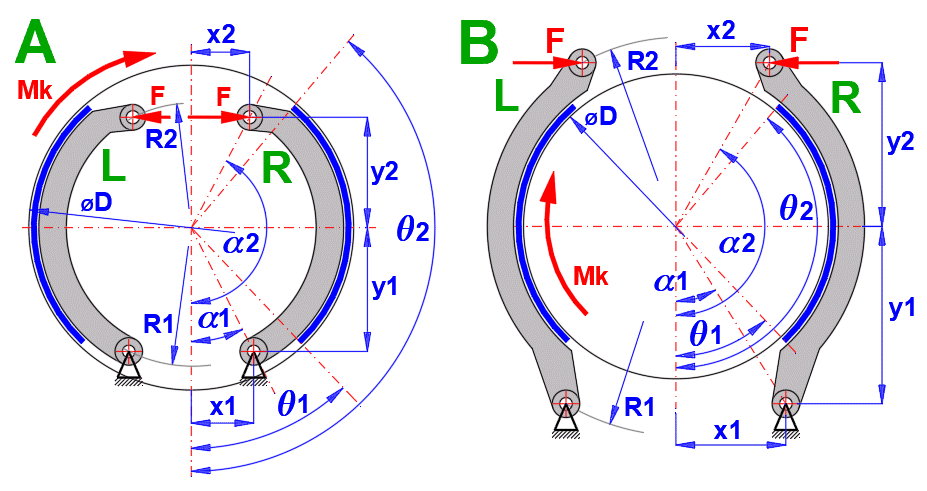
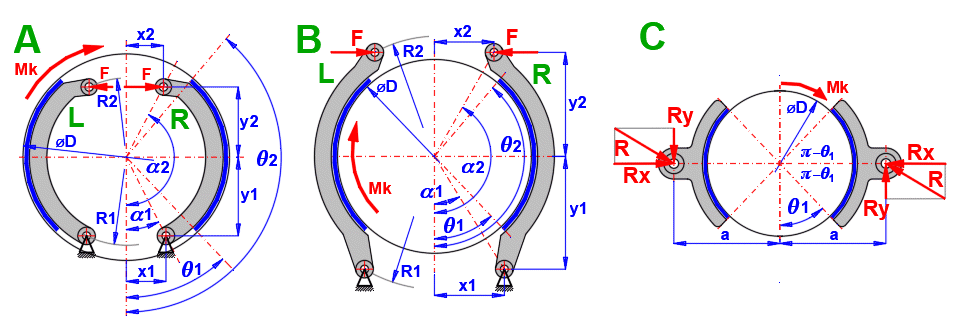
In der Trommelbremse werden prinzipiell zwei Backentypen eingesetzt. In Abhängigkeit von der Drehrichtung (Momentwirkung) werden sie als die Auflaufbacke R (Leading shoe) und Ablaufbacke L (Trailing shoe), sowie in der Abbildung L, R bezeichnet.
Für die gleiche Kraft F gelten für die Backe (L) und (R) unterschiedliche Bremsmomente, Drücke, Kräfte und Reaktionen.
Die Berechnung erfolgt deshalb prinzipiell in den folgenden Schritten
(Auflaufbacke R und Ablaufbacke L):
1. Berechnung der Kraft F' für Einheitsdruck pmaxR'=1 für Auflaufbacke (R)
2. Berechnung des Bremsmomentes MR' für Auflaufbacke (R) für Kraft F'
3. Berechnung pmaxL' für die linke Backe (L) für Kraft F'
4. Daraus Berechnung des Drehmomentes für die linke Backe (L) ML'
5. Berechnung des gesamten Bremsmomentes Msum'=MR'+ML'
6. Berechnung des Koeffizienten X=Mk/Msum'
7. Umrechnung der einzelnen Werte der Drücke, Kräfte, Momente und Reaktionen
durch den Koeffizienten X
Reibungsmoment
Mt_R [Nm] = f * pmax * w * (D/2) /
SIN(qXa) * CoefA
CoefA =(D / 2 * (-(COS(qX2) - COS(qX1))) - a * ((0.5 * SIN(qX2)^2) -
(0.5*SIN(qX1)^2)))/1000
Normales Drehmoment
Mn_R [Nm] = pmax * w * (D/2) * a /
SIN(tqXa) * CoefB / 1000
CoefB =(qX2/2 - 1/4 * SIN(2 *
qX2)) - (qX1/2 - 1/4 * SIN(2 *
qX1))
Kraft F
F [N] = (Mn_R - Mt_R) / (c / 1000)
c [mm] = ABS(y1 - y2)
Bremsmoment M_R
M_R [Nm] = f * pmax * w * (D/2)^2 *
(COS(qX1) -
COS(qX2)) / SIN(qXa) / 1000
Druck pmaxL
pmaxL [MPa] = (F * c / (Mn_R + Mt_R)) / 1000
Bremsmoment M_L
M_L [Nm] = f * pmaxL
* w * (D/2)^2 * (COS(qX1) - COS(qX2)) / SIN(qXa) / 1000
Bremsmoment Msum
Msum [Nm] = NR * M_R + NL * M_L
Koeffizient X
X = Mk / Msum
f ............. Reibungskoeffizient
[~]
pmax ...... Maximaler Druck [MPa]
w ........... Bremsbelagbreite [mm]
D ........... Trommeldurchmesser [mm]
qX1 = q1 -
a1 [rad]
qX2 = q2 -
q1 + qX1 [rad]
qXa ... a) qX2 < PI()/2 ...
qXa = qX2, b)
qX2
> PI()/2 ...
qXa = PI()/2
NR, NL ... Anzahl der Bremselemente (rechte Backe (R) und linke Backe (L))
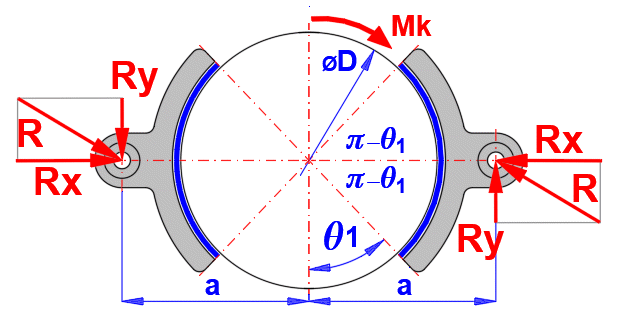
Abstand der Achse des Backenbolzens zur Trommelachse „a“, der für ein
Nulldrehmoment zur Achse des Backenbolzens sorgt. Dies stellt die gleichmäßige
Abnutzung des Belags sicher.
a = 4 * (D/2) * SIN(q1') / (2 *
q1' + SIN(2 *
q1'))
q1' = pi()/2 -
q1
Maximaler Druck
pmax [Mpa] = (Mk / (NL+NR)) / (2 * f * w * (D / 2)^2 *
SIN(q1')) / FillCoeff
Reaktion im Backenstift in x- und
y-Richtung
Rx = pmax * w * (D/4) * (2 *
q1' +
SIN(2 *
q1'))
Ry = pmax * w * f * D/4 * (2 *
q1'
+ SIN(2 *
q1'))
q1
................ Startwinkel des Bremsbelags (siehe Abbildung) [rad]
Mk ............... Lastdrehmoment [Nm]
NL, NR ......... Anzahl der Bremselemente [~]
f ................... Reibungskoeffizient [~]
w .................. Bremsbelagbreite [m]
D ................. Außendurchmesser der Trommel [m]
q1'................
halber Riemenwinkel [rad]
FillCoeff ........ Füllfaktor [~]
Die Reibfläche wird durch ein Band gebildet, das um die Bremstrommel gewickelt ist. Einsatz in industriellen Anwendungen, einfache Konstruktion. Geeignet für die manuelle Betätigung, wo es möglich ist, durch eine verhältnismäßig kleine Betätigungskraft eine hohe Bremswirkung zu erreichen.
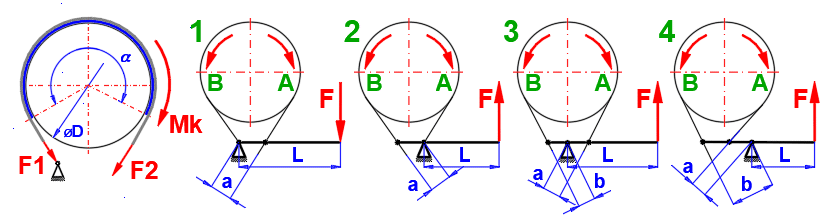
ecoef = 2.7182818 (f *a)
Ft = Mk /
((Do / 2))
F2 = Mk / (ecoef - 1) * (Do / 2))
F1 = Ft + F2
Maximaler Druck
pmax = (2 * F1 / (w * Do)) / N
Kraftberechnung F
A: in Drehrichtung:
1 ... F = (Ft * a / L) * (1 / (ecoef - 1)) / N
2 ... F = (Ft * a / L) * (ecoef / (ecoef - 1)) / N
3 ... F = (Ft / L) * ((b * ecoef - a) / (ecoef - 1)) / N
4 ... F = (Ft / L) * ((b * ecoef + a) / (ecoef - 1)) / N
B: gegen die Drehrichtung:
1 ... F = (Ft * a / L) * (ecoef / (ecoef - 1)) / N
2 ... F = (Ft * a / L) * (1 / (ecoef - 1)) / N
3 ... F = (Ft / L) * ((b - a * ecoef) / (ecoef - 1)) / N
4 ... F = (Ft / L) * ((b + a * ecoef) / (ecoef - 1)) / N
f ........... Reibungskoeffizient [~]
Ft .......... Reibungskraft [N]
Do ......... Außendurchmesser der Trommel [m]
a
.......... Trommelbandwinkel [rad]
N .......... Anzahl der Riemen [~]
a,b,L ..... Hebelabmessungen [mm]
Sowohl beim Bremsen als auch beim Anlaufen kommt es bei Berührung der Reibflächen zum Umwandlung kinetischer Energie in Wärme. In den vorhergehenden Absätzen sind die Beziehungen zur Berechnung des maximalen Momentes und des maximalen Drucks auf die Reibflächen für die angegebenen Abmessungen der Bremse/Kupplung aufgeführt. Auch wenn kein maximales Moment übertragen und der maximal zulässige Druck nicht überschritten wird, kann es zur Zerstörung der Bremse/Kupplung durch übermäßige Erwärmung kommen.
Diese Berechnung deckt selbstverständlich nicht alle Konstruktionsvarianten der Bremse/Kupplung (Ölkühlung, Sonderabmessungen, Sondermaterialien usw.) ab. Deshalb werden folgende Voraussetzungen verwendet:
-der Reibbelag weist eine niedrige Wärmeleitfähigkeit l im Vergleich zu der Wärmeleitfähigkeit der Materialien, die mit dem Belag in Berührung kommen, auf. (l des Reibbelags ~0.1, l für Stahl ~54). Deshalb wird damit gerechnet, dass sämtliche durch Reibung entstandene Wärme durch den Metallteil der Bremse/Kupplung absorbiert wird.
- Wärmeeigenschaften der Materialien sind konstant (im realen Fall ändern sie sich selbstverständlich, jedoch nicht bedeutsam)
- Die Bremszeit ist wesentlich kürzer als die Abkühlungszeit
- Gewicht der Bremse/Kupplung (nur Schätzung. Dadurch wird die ausführliche Analyse des Körpergewichtes, das die durch Reibung entstandene Wärme annimmt, nicht ersetzt)
Einige Hersteller führen für die Reibsegmente auch den maximalen Wert des Wärmflusses q auf.
q [W/mm²] = Eh / t / S''
Eh ..... Wärmeenergie, die von der
Betriebsbremse oder Kupplung während des Arbeitszyklus erzeugt wird [J]
t ........ Bremszeit / Beschleunigungszeit [s]
S'' ...... Reibungsfläche von Scheibe / Trommel [mm²]
Der Temperaturanstieg für Bremse/Kupplung ist annähernd nach der Formel zu ermitteln:
ΔT1 [°C] = Eh / (c * m)
Eh ... Wärmeenergie, die von der
Betriebsbremse oder Kupplung während des Arbeitszyklus erzeugt wird [J]
c ..... Spezifische Wärmekapazität des Materials [J/kg/K]
m .... Kupplungs- / Bremsgewicht [kg]
Weil die Formel den Zeitfaktor und die Abkühlung nicht berücksichtigt, ist sie nur zur Orientierung geeignet.
Kontaktflächenheizung
ΔT2 [°C] = (5 / 18)^0.5 * (Eh * t^0.5) / (S'' * t * (Ro * c * l)^0.5)
Eh .......... Wärmeenergie, die von
der Betriebsbremse oder Kupplung während des Arbeitszyklus erzeugt wird [J]
Ro .......... Dichte [kg/m³]
c ............ Spezifische Wärmekapazität des Materials [J/kg/K]
l ...........
Wärmeleitfähigkeit des Materials [W/m/K]
t ............ Bremszeit / Beschleunigungszeit [s]
S'' .......... Reibungsfläche von Scheibe / Trommel [mm²]
Wärmeübertragungszeit tb zum Erreichen der Trommelaußenfläche
tb [s] = Th^2 / (5 * (l / (Ro * shc)))
Th .......... Trommel- /
Scheibendicke [mm]
c ............ Spezifische Wärmekapazität des Materials [J/kg/K]
Die oben angeführte Gleichung ΔT1[°C] = Eh / (c * m) kann gemeinsam mit dem Newtonschen Abkühlungsgesetz, das die Wärmeübertragung aus der Oberfläche der Bremse/Kupplung beschreibt, angewendet werden.
Nach der einschlägigen Vereinfachung und Benutzung der vereinfachenden Voraussetzung gilt die folgende Beziehung:
(T - TA) / (T1 -TA) = exp(- (a * S) / (m * c) * t)
T ..... Körperoberflächentemperatur
zum Zeitpunkt t [°C]
TA ... Temperatur um die Oberfläche des Körpers - Lufttemperatur [°C]
T1 ... Anfängliche Körperoberflächentemperatur [°C]
a ....
Wärmeübergangskoeffizient durch Strömung und Strahlung [W*m^-2/K]
S ..... Außenfläche des Körpers [m²]
m .... Körpergewicht (Bremse, Kupplung)
c ..... Spezifische Wärmekapazität des Materials [J/kg/K]
t ..... Kühlzeit [s]
Für die wiederholte Benutzung kann der Bremsprozess danach nach der folgenden Abbildung beschrieben werden:
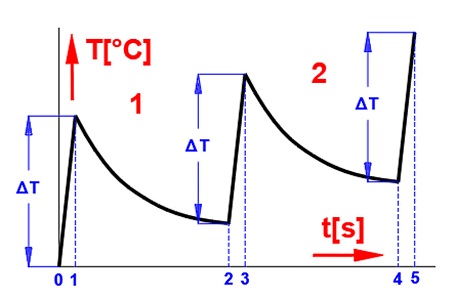
0-1...Bremsen des Mechanismus – Annahme der Reibenergie, Temperaturanstieg
1-2...Abgabe der Energie in die Umgebung (Abkühlung – Temperaturabfall)
2-3...weiterer Bremszyklus, Temperaturanstieg
3-4...Abgabe der Energie in die Umgebung (Abkühlung – Temperaturabfall)
..........................................
Die Temperaturentwicklung für einen wiederholten Zyklus kann z. B. wie folgt aussehen.
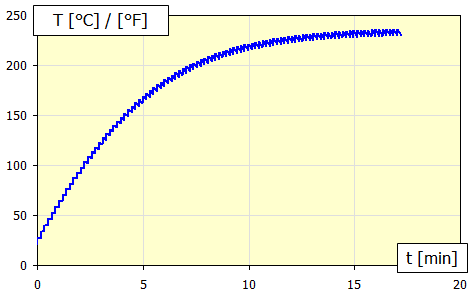
Bei steigender Temperatur der Bremse/Kupplung wird sich entsprechend auch die Wärmeübergangszahl a erhöhen, somit kommt es bei einer bestimmten Temperatur zum Ausgleich des Wertes der angenommenen Energie (Bremsprozess) und abgegebenen Energie (Abkühlung).
Die Wärmeübergangszahl a wird für den Fall dieser Berechnung durch drei Parameter beeinflusst und für ihre Berechnung wird die folgende Beziehung verwendet:
a = aR + aC * fv
aR ....
Wärmeübergangskoeffizient durch Strahlung [W*m^-2/K]
aC ....
Wärmeübergangskoeffizient durch Konvektion [W*m^-2/K]
fv ...... Luftstromkoeffizient [~]
Für die Bestimmung der Wärmeübergangszahlen aR und aC ist es möglich, den folgenden Graf zu verwenden:
dT = T - TA
T ..... Körperoberflächentemperatur
zum Zeitpunkt t [°C]
TA ... Temperatur um die Oberfläche des Körpers - Lufttemperatur [°C]
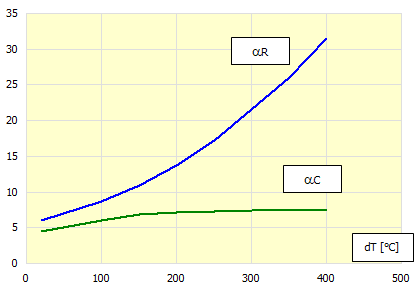
Für die Bestimmung des Koeffizienten der Luftströmung fv dann:
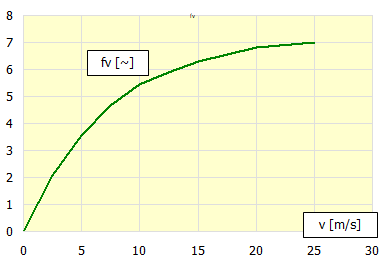
Bei dieser Berechnung werden 100 Zyklen des wiederholten Bremsens/Schaltens der Kupplung mit dem eingegebenen Zeitabstand simuliert. Für jeden Zyklus wird die entsprechende Wärmeübergangszahl Alpha berechnet, die anschließend für die Berechnung der Temperaturen im folgenden Zyklus verwendet wird. Diese Vorgehensweise genügt meist und konvergiert schnell zur konstanten Temperatur.
Bei dieser Berechnung wird der gesamte Temperaturanstieg abgeschätzt. Aus diesem Anstieg wird entsprechende Wärmeübergangszahl Alpha berechnet, die zur Berechnung der gesamten Erwärmung verwendet wird. Diese Vorgehensweise ist von der Abschätzung der Erwärmung abhängig und kann weniger genau als die vorhergehende Berechnung sein. Falls die vorgehende Vorgehensweise nicht zu einer konstanten Endtemperatur konvergiert, ist es jedoch angebracht, diese Berechnung zu verwenden.
Beispiel für die Entwicklung der Erwärmung, in dem es angebracht ist, die kumulative Berechnung zu verwenden.
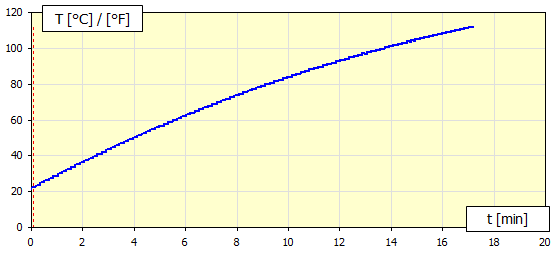
Die Lösung der Berechnung der Bremse/Kupplung wird gewöhnlich in zwei Aufgaben geteilt.
1. Berechnung der Belastung der Bremse/Kupplung aufgrund des
gebremsten/angelaufenen Mechanismus [1].
2. Berechnung der Abmessungen der Bremse/Kupplung, die die geforderte Belastung
erfüllt [2,3,4,5].
Im Absatz [1] wird die Berechnungsart der Belastung (Bremse/Kupplung) gewählt [1.3].
Füllen Sie die kinetische Energie Ek und das Moment ML aus oder berechnen Sie diese (Ergänzungsberechnungen [6,7]) und geben Sie Parameter der Geschwindigkeit, der Zeit und des Betriebs an.
Das Ergebnis ist das benötigte Moment und die zur Spezifikation der Bremse/Kupplung beim Lieferanten oder für die Abmessungsberechnungen in den Absätzen [2,3,4,5] ausreichende Energie.
Nach der Auswahl des Typs der Bremse/Kupplung [2, 3,4,5] geben Sie das Moment an, durch das die Bremse/Kupplung belastet wird.
Geben Sie die Parameter der Reibfläche und die Abmessungen des Reibelementes an.
Das Ergebnis ist der Druck auf die Reibfläche, die Geschwindigkeit und die wirkenden Kräfte.
Durch die Verbindung der Berechnung der Belastung [1] und Abmessungen [2,3,4,5] können dann auch weitere Aufgaben gelöst werden.
- Temperatur der Bremse/Kupplung beim Betrieb
- Optimierung der Abmessungen
- Optimierung der Belastung
In diesem Absatz werden die Einheiten der Berechnung eingestellt und das Belastungsmoment und die Energie berechnet, die zum richtigen Entwurf der Abmessungen der Bremse/Kupplung notwendig sind.
Hier werden auch weitere Parameter, wie die Eigenschaften des Reibmaterials, des Materials der Bremse/Kupplung und der Belastungstyp eingestellt.
In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
Zur Berechnung der Bremsen/Kupplungen ist es meist notwendig zu wissen, „was gebremst wird“, bzw. „was in Bewegung gesetzt wird“. Diese Informationen führen zu zwei Grundparametern.
1. Drehmoment, das durch die Bremse/Kupplung übertragen werden muss
2. Energie, die durch die Bremse/Kupplung absorbiert werden muss.
Zur Verfügung stehen dann die drei Grundberechnungen der Energie und der Momente.
A. Berechnung der Bremse
B. Berechnung der Anlaufkupplung
C. Prüfung der laufenden Kupplung
Die ausgewählte Berechnung ist aktiv, die übrige zwei Berechnung sind grau – inaktiv.
Die geometrische Berechnung des konkreten Typs der Bremse/Kupplung [2,3,4,5] übernimmt dann die Informationen über Belastungsmoment, Energie usw. aus der ausgewählten Berechnung der Energien und Momente. Genauso wie die Berechnung der Erwärmung der Bremse/Kupplung [8].
Die Aufgabe besteht darin, den sich bewegenden Mechanismus in den geforderten Zustand (meist bis zum Stillstand n2=0) zu bringen.
In diesem Fall wird die Aufgabe gelöst, indem die kinetische Energie Ek und die zusätzlichen Momente ML in der Reibungsbremse in Wärmeenergie überführt werden müssen.
Verwendete Voraussetzungen und Vereinfachungen:
- sämtliche gebremste Massen sind gegeneinander bei einem konstanten
Übersetzungsverhältnis verbunden
- das Belastungsmoment ML bleibt während des Bremsprozesses konstant
Kinetische Energie der sich bewegenden Massen, die abzubremsen sind. Zu deren Berechnung kann der Absatz [6] verwendet werden, zu dem mit der Taste „Ek>>“ gewechselt wird.
Belastungs-/Entlastungsmoment (+/-), auf die Drehzahl n1 umgerechnet.
Zur Lösung der gängigen Aufgaben wird die Taste „ML>>“ betätigt.
Beispiele der Belastungen (+):
- Bewegung eines Fahrzeugs bergab
- Aufzug, Kran (durch Kraft wirkendes Gewicht)
Beispiele der Entlastung (-):
- Bewegung eines Fahrzeugs bergauf
- Rollwiderstände des Mechanismus
Von allen gebremsten Massen (Dreh-, Linearbewegung – siehe Berechnung Ek) auf die Anfangsdrehzahl der gebremsten Scheibe (Trommel) n1 ungerechnetes Trägheitsmoment.
Geben Sie die Anfangsdrehzahl der Bremsscheibe oder Trommel an.
Geben Sie die Enddrehzahl der Bremsscheibe oder Trommel an. Zum völligen Stillstand des gebremsten Mechanismus n2=0.
Geforderte Bremszeit von Drehzahl n1 bis n2.
Es handelt sich um das theoretisch berechnete Bremsmoment (unter Voraussetzung der optimalen Bedingungen), das von der Bremse während des Bremszyklus sichergestellt werden muss.
Weil der gebremste Mechanismus Ungleichmäßigkeiten (Schwingungen des Drehmomentes) aufweisen kann, ist es geeignet den Koeffizienten (KA) anzuwenden, der diese Ungleichmäßigkeit berücksichtigt und die geforderte Bremszeit gewährleistet.
Der Entwurf des Koeffizienten KA geht aus praktischen Kenntnissen hervor und dessen Größe wird durch die Einstellung der Bedingungen in der Zeile [1.41] geregelt.
Nach dem Abhaken der Taste kann ein eigener Wert eingegeben werden.
Drehmoment, das von der Bremse aufgenommen werden muss. Dieses Moment wird zur Berechnung der Abmessungen der Bremse verwendet [2,3,4,5].
Energiemenge, die in der Bremse verbraucht wurde (Erwärmung der Bremse).
Die Aufgabe ist das Anlaufen des Mechanismus in den geforderten Zustand (meist aus n2=0 in n1= Solldrehzahl).
In diesem Fall wird die Aufgabe gelöst, indem in den Mechanismus eine solche Energie Ek zu liefern ist, die zum Erreichen der Sollgeschwindigkeit und Solldrehzahl bei Überwindung der zusätzlichen Momente ML notwendig ist.
Verwendete Voraussetzung und Vereinfachungen:
- Drehzahl n1 (Antrieb) bleibt während der Kupplungstätigkeit konstant
- es wird ein konstantes Moment übertragen => Beschleunigung des Mechanismus
bleibt konstant.
Kinetische Energie, auf die der Mechanismus beschleunigt werden muss. Zur Berechnung kann der Absatz [6] verwendet werden, wohin mit der Taste „Ek>>“ gewechselt wird.
Belastungs-/Entlastungsmoment (+/-) bezogen auf die Kupplungsdrehzahl n1.
Zur Berechnung der gängigen Aufgaben die Taste „ML>>“ drücken
Beispiele für Belastung (+):
- Anfahren eines Fahrzeugs bergauf
- Rollwiderstände des Mechanismus
- Aufzug, Kran (mit Kraft wirkendes Gewicht)
Beispiele für Entlastung (-):
- Anfahren eines Fahrzeugs bergab
Von allen anlaufenden Massen (Dreh-, Linearbewegung – siehe Berechnung Ek) auf die Anfangsdrehzahl der Kupplungsscheibe (Trommel) n1 umgerechnetes Trägheitsmoment.
Leistung der Antriebsmaschine, die der Kupplung geliefert wird.
Geben Sie die antriebsseitige Kupplungsdrehzahl an. Auf diese Drehzahl wird der Mechanismus beschleunigt.
In den meisten Fällen wird der Anlauf eines stillstehenden Mechanismus (n2=0) gelöst.
Falls Sie einen Mechanismus zu lösen benötigen, der schon in Bewegung ist (n2>0) und auf die Drehzahl n1 beschleunigt werden soll, geben Sie die Anfangsdrehzahl n2 an.
Durch die Antriebsmaschine geliefertes Drehmoment.
Weil der angetriebene Mechanismus sowie die Antriebsmaschine Ungleichmäßigkeit (Schwingung des Drehmomentes) aufweisen können, ist es angebracht, den Koeffizienten (KA) anzuwenden. Dieser Koeffizient berücksichtigt diese Ungleichmäßigkeit bei der Berechnung des Drehmomentes, das in der Kupplung übertragen werden muss.
Der Entwurf des Koeffizienten KA geht aus praktischen Kenntnissen hervor und
dessen Größe wird durch die Einstellung der Bedingungen in der Zeile
[1.40,1.41,1.42] geregelt.
Nach dem Abhaken der Taste kann ein eigener Wert eingegeben werden.
Drehmoment, das von der Kupplung übertragen werden muss. Dieser Momentwert wird zum Entwurf der Kupplungsabmessungen verwendet [2,3,4,5].
Der allgemein angegebene Wirkungsgrad der Reibungskupplungen beträgt annähernd 0.95.
Es handelt sich um den Teil des Drehmomentes, der durch die Antriebmaschine geliefert wird und voll zum Erreichen der geforderten Endenergie Ek des Mechanismus genutzt wird.
Der andere Momentteil wird in der Kupplung in Reibungsform verbraucht.
Das Moment Mu wird um den Wert ML [1.16] verringert/erhöht.
Aufgrund:
- der geforderten kinetischen Endenergie des Mechanismus Ek [1.15]
- des Belastungsmomentes ML [1.16]
- der Motorleistung Pw [1.18]
- des Wirkungsgrades der Kupplung h [1.24]
wird die notwendige Betriebszeit der Kupplung berechnet (Wert im grünen Feld).
Nach Abwählen der Taste kann eine eigene Zeit des Kupplungsbetriebs angegeben werden.
Der angegebenen Zeit entspricht dann dem Wert Ek' [1.27], auf den der Mechanismus beschleunigt wird.
Kinetische Energie des Mechanismus, die durch das Schalten der Kupplung in der Zeit erreicht wurde, die in der vorigen Zeile angegeben wurde.
Energie, die in der Kupplung in Wärme umgewandelt wird.
Bei der Lösung der Energieübertragung durch die Reibungskupplung ist es
angebracht, auch die Funktionsfähigkeit unter den Betriebsbedingungen zu
überprüfen.
Die Kupplung kann dem Anlauf des Mechanismus (siehe vorige Berechnung – Anlauf)
genügen, sie muss jedoch nicht der konstanten beim Erreichen der
Betriebsparameter übertragenen Energie genügen.
Beispiel:
Die Kupplung sorgt für den Anlauf des Mechanismus auf n1 bei angegebenen
Leistungen Pw.
Die Antriebsmaschine erhöht bei der geschalteten Kupplung weiterhin die Leistung
Pw und Drehzahl n auf die Betriebswerte.
Die Kupplung muss die Momentübertragung auch unter Betriebsbedingungen
sicherstellen.
Leistung der Antriebsmaschine, die der Kupplung geliefert wird.
Geben Sie die Drehzahl der Kupplung an, bei der die einschlägige Leistung abgenommen wird.
Durch die Antriebsmaschine geliefertes Drehmoment.
Weil der angetriebene Mechanismus sowie die Antriebsmaschine Ungleichmäßigkeit (Schwingung des Drehmomentes) aufweisen können, ist es angebracht, den Koeffizienten (KA) anzuwenden. Dieser Koeffizient berücksichtigt diese Ungleichmäßigkeit bei der Berechnung des Drehmomentes, das in der Kupplung übertragen werden muss.
Der Entwurf des Koeffizienten KA geht aus praktischen Kenntnissen hervor und
dessen Größe wird durch die Einstellung der Bedingungen in der Zeile
[1.40,1.41,1.42] geregelt.
Nach dem Abhaken der Taste kann ein eigener Wert eingegeben werden.
Drehmoment, das von der Kupplung übertragen werden muss. Dieser Momentwert wird zum Entwurf der Kupplungsabmessungen verwendet [2,3,4,5].
In diesem Absatz sind die Wellendurchmesser (Stahl) entworfen, die den verlangten Belastungen entsprechen (Mk). Diese Werte dienen nur als Orientierungswerte, für den Finalentwurf ist es geeignet, eine genauere Berechnung zu verwenden.
Beim Entwurf einer Bremse/Kupplung sind die genauen Verläufe der Belastungsmomente meist nicht bekannt.
Deshalb wird der KA-Koeffizient bei Berechnungen verwendet, der aufgrund der Erfahrung und Tests sagt, wie das Berechnungsmoment erhöht werden soll, damit die entworfene Bremse oder Kupplung die einschlägige Ungleichmäßigkeit der Belastung bewältigen kann.
Zur Berechnung einer Bremse wird der KA-Koeffizient vorgeschlagen, der aus dem Typ des gebremsten Mechanismus hervorgeht.
Zur Berechnung einer Kupplung wird der KA-Koeffizient vorgeschlagen, der sowohl den gebremsten Mechanismus als auch die Antriebsmaschine sowie die Betriebszeit umfasst.
Wählen Sie aus der Liste den entsprechenden Typ der Antriebsmaschine aus.
Arbeitsmaschinen
Selten Volllast
Generatoren, Kettenförderer, Kreiselverdichter, Sandstrahlgebläse,
Textilmaschinen, Transportanlagen, Ventilatoren, Zentrifugalpumpen
Volllast, stoßfrei
Aufzüge, Becherwerke, Drehöfen, Haspeln, Katzund, Kranfahrwerke,
Kühltrommeln, Winden, Rührwerke, Scheren, Schleif- und Werkzeugmaschinen,
Waschmaschinen, Webstühle, Ziegelpressen
Volllast, mäßige Stöße
Bagger, Bohranlagen, Brikettpressen, Grubenventilatoren, Gummiwalzwerke,
Hubwerke, Kollergänge, Plungerpumpen, Putztrommeln, Rüttler, Verbundmühlen
Volllast, starke Stöße
Kolbenverdichter, Gattersägen, Naßpressen, Papierkalander, Rollgänge,
Trockenzylinder, Walzwerke, Zementmühlen, Zentrifugen
In der Liste befindet sich die Grundliste der eingesetzten Reibungsmaterialien. In Klammern sind die Reibungszahl und der maximal zulässige Druck und die Verwendung aufgeführt.
Nach dem ausgewählten Material sind die Werte vorab ausgefüllt [1.45-1.49].
Wählen Sie das Material aus, das die beim Bremsen oder Anlauf des Mechanismus verbrauchte Energie absorbiert. Die Auswahl hat keinen Einfluss auf die Berechnung der Parameter der Bremse/Kupplung.
Die Materialwerte dienen zur Berechnung der Erwärmung (des Gewichtes).
Beispiele:
1. Die Bremsscheibe einer Scheibenbremse absorbiert die Energie beim Bremsen und
wird aus Stahl hergestellt.
2. Das Kupplungsgehäuse absorbiert die Verlustenergie und wird aus Aluminium
hergestellt.
Sie gehören zu den meist benutzten Arten von Bremsen und Kupplungen. Sie weisen eine einfache Bauweise, eine große Fläche der Reibungsoberflächen sowie gute Wärmeableitung auf. Es ist möglich, Konstruktionen mit einer oder mehreren Reibungsoberflächen zu benutzen, wobei besonders die Konstruktion mit 2 Reibungsoberflächen sehr viel in der Automobilindustrie (Scheibenbremsen, Scheibenkupplungen) eingesetzt wird.

Zur Berechnung und für den Entwurf der Bremse/Kupplung sind zwei Grundparameter notwendig. Drehmoment Mk und Reibungszahl f.
Diese Parameter gemeinsam mit der Definition der Abmessungen führen zur Berechnung des maximalen Drucks auf die Reibungsfläche, zur Berechnung der Betätigungskraft und bei Kenntnis der energetischen und zeitlichen Parameter aus [1] auch zur Berechnung der Erwärmung.
Im grünen Feld ist das Moment Mk aus dem Absatz [1]. Wenn nur die Geometrie für das eingegebene Drehmoment Mk gelöst werden muss, wird die Taste rechts abgewählt und das Moment Mk, das die Bremse/Kupplung übertragen soll, eingegeben. Dadurch wird die Verbindung mit dem Absatz [1] unterbrochen und es werden dadurch die Erwärmung und die Geschwindigkeit nicht mehr berechnet (die Ergebnisse sind grau).
Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Der empfohlene Wert geht aus dem gewählten Reibungsmaterial hervor [1.44].
In diesem Teil werden die Abmessungen der Reibelementes definiert. Die Abmessungen können im Bild rechts geprüft werden.
Zur Auswahl gibt es die drei meistbenutzten Formen:
A. Kreisringausschnitt – Einsatz meist für Bremsen
B. Kreis – Einsatz für weniger beanspruchte Bremsen (einfache Herstellung,
einfache Konstruktion)
C. Kreisring – Einsatz meist für Kupplungen.
Nach der Auswahl der Form werden die Anforderungen an die einschlägigen Eingangsparameter eingestellt.
Zur Lösung werden dann zwei Möglichkeiten verwendet.
A. Gleichmäßige Abnutzung (eingelaufene Bremse/Kupplung): Es wird von der Voraussetzung ausgegangen, dass die Reibungsscheiben starr sind und die größte Abnutzung zuerst auf deren Außenrand, wo die größte Arbeit der Reibkräfte entsteht, beginnt. Anschließend kommt es hier zu einer gewissen Abnutzung, die Druckverteilung ändert sich so, dass die Abnutzung der Reiboberflächen gleichmäßig ist.
B. Gleichmäßiger Druck (neue Bremse/Kupplung): Es wird vorausgesetzt, dass ein gleichmäßiger Druck auf die ganzen Reibfläche durch die Verwendung von Federn, die die Reibscheiben in die Berührung gleichmäßig andrücken, erreicht wird.
Allgemein wird die Möglichkeit A verwendet.
Geben Sie die Anzahl der Reibungsflächen nach Ihrer Konstruktion ein (siehe Abbildung).

Für die Form des Reibsegmentes [2.5] A,C geben Sie ein: Außenradius des Reibsegmentes Ro (siehe Abbildung).
Für die Form B geben Sie ein: Abstand der Kreismitte „e“ zur Achse (siehe Abbildung).
Rechts wird der optimale Wert H (bzw. D für Kreissegment) zum Erreichen des maximalen Reibmomentes aus der Beziehung Ri=Ro/1.732 vorgeschlagen.
Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Für die Form des Reibsegmentes [2.5] A geben Sie den Segmentwinkel (siehe Abbildung) ein.
Aufgrund der Flächencharakteristik des Reibsegmentes wird der äquivalente Radius Re berechnet, der zur Berechnung der Kräfte dient.
Radius, in dem die Normalkraft Fn' wirken sollte.
Der Bremsbelag (Kupplungsbelag) wird häufig mittels Nieten befestigt. Dieser
Koeffizient drückt die Reduzierung der Reibfläche des Belags um die
einschlägigen Montagebohrungen aus.
Für geklebten Belag cF=1.0, für genieteten Belag dann cF~0.90-0.95.
Fläche, mit der das Reibsegment auf der Reibfläche aufliegt. Sie ist von der Definition der Abmessung des Reibsegmentes abhängig.
Fläche der Bremse/Kupplung, die das Reibsegment berührt (mit Strichlinie gekennzeichnet, wenn sie in der Skizze zu sehen ist).
In diesem Teil werden die Werte für eine Reibfläche aufgeführt.
Gesamtmoment Mk, in die einzelnen Reibflächen aufgeteilt.
Die meisten Hersteller von Reibmaterialien führen auch den maximalen Wert der Reibgeschwindigkeit auf, die das Material aushalten kann. Der empfohlene Wert geht aus der Wahl des Materials hervor [1.43].
Der maximale Druck an der meistbelasteten Belagsstelle. Die Belagshersteller führen meist dessen maximalen Wert auf (siehe empfohlener Wert rechts). Beim Überschreiten des maximalen Wertes versuchen Sie die Geometrie bzw. den Belagtyp zu ändern.
Einige Hersteller führen für die Reibsegmente auch den maximalen empfohlenen Wert des Wärmeflusses q auf.
Der Reibbelag weist eine schlechte Wärmeleitfähigkeit Lambda im Vergleich zur Wärmeleitfähigkeit der Materialien auf, die mit dem Belag in Kontakt kommen. (Lambda des Reibbelags ~0.1, Lambda für Stahl ~54). Deshalb wird angenommen, dass sämtliche durch Reibung entstandene Wärme durch den metallenen Teil der Bremse/Kupplung absorbiert wird.
Diese Orientierungsberechnung verwendet nur das Gewicht der Scheibe (des Kegels, der Trommel) m (siehe Berechnung unten). Die Berechnung ist richtig, wenn die Scheibe der Energieempfänger ist (typisch Scheibenbremse).
Für eine andere Konstruktionsgestaltung (typisch Kupplung) wird die Reibungsenergie zum Beispiel durch das Kupplungsgehäuse absorbiert und das Ergebnis ist selbstverständlich ungültig.
Es wird vorausgesetzt, dass der Prozess Bremsen/Schalten der Kupplung kurz ist, deshalb wird nicht mit einer Abkühlung während dieses Prozess gerechnet. Aus dieser Voraussetzung geht auch die Berechnung der Erwärmung der Reibfläche hervor, wobei nur mit dem Übergang der Wärme in die Scheibe (Trommel, Gehäuse …) aufgrund der Wärmeleitfähigkeit des Materials gerechnet wird.
Aufgaben des Typs:
- wie lassen sich die Abmessungen zum Erreichen des zulässigen Drucks pmax.
ändern
- wie darf die Bremse/Kupplung zum Erreichen des zulässigen Drucks pmax belastet
werden
- wie hoch kann die maximale Kraft Fn' sein
und Weiteres können leicht mittels der Excel-Funktion „Suche nach Lösungen“ (GoalSeek) gelöst werden.
Für die häufigsten Aufgaben werden die Eingänge in dieser Funktion und deren Aufrufen vordefiniert.
Nach der Auswahl der Abfrage und Eingabe des geforderten Wertes wird das Aufrufen der Funktion mit der Taste „Finden“ gestartet.
Zum ursprünglichen Wert des zu ändernden Parameters wird es durch das Drücken der Taste „Zurück“ zurückgekehrt. (die Funktionsfähigkeit ist zeitlich begrenzt, damit es zu keinem unerwünschten Überschreiben der Werte kommt).
Beispiel:
Sie möchten den Winkel des Reibsegmentes für die Scheibenbremse, der den
geforderten maximalen Druck „pmax“ sicherstellt, berechnen. Es ist klar, dass
sich der Winkel des Reibsegmentes nur in einem bestimmten Bereich bewegen kann,
die Anforderung an pmax ist jedoch nicht begrenzt. Also kann die Anforderung an
eine große Veränderung von pmax zu einem ganz unsinnigen Segmentwinkel Alpha
führen.
Wählen Sie aus der Liste die Aufgabe, die Sie lösen wollen.
Geben Sie den Sollwert ein, der durch die Veränderung des Eingangsparameters geändert werden soll und rufen Sie die Funktion „Suche nach Lösung“ durch die Taste rechts auf.
Die Abmessungsparameter werden aufgrund der vorhergehenden Angaben abgeschätzt. Nach Abwählen der Taste rechts können eigene Abmessungen eingegeben werden (siehe Abbildung).
Der Gewichtswert wird für die Berechnung ΔT1 verwendet.
Der Flächenwert wird zur Berechnung der Abkühlung im Absatz [8] genutzt.
Der Wert der Oberfläche S' wird als voreingestellt für die Berechnung der Erwärmung im Absatz [8] verwendet und in diesem Absatz nicht genutzt.
Die Fläche S' wird nach der Abbildung berechnet.
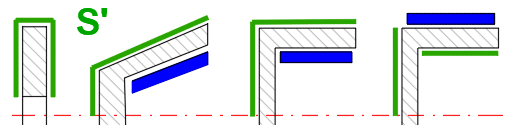
Als Reibfläche wird die Kegelfläche verwendet. Der Vorteil dieser Konstruktion ist die kleinere Betätigungskraft Fn als bei der Scheibenbremse/Scheibenkupplung. In Abhängigkeit vom Reibmaterial wird gewöhnlich der Kegelwinkel b im Bereich von 10–15° verwendet.

Zur Berechnung und für den Entwurf der Bremse/Kupplung sind zwei Grundparameter notwendig. Drehmoment Mk und Reibungszahl f.
Diese Parameter gemeinsam mit der Definition der Abmessungen führen zur Berechnung des maximalen Drucks auf die Reibungsfläche, zur Berechnung der Betätigungskraft und bei Kenntnis der energetischen und zeitlichen Parameter aus [1] auch zur Berechnung der Erwärmung.
Im grünen Feld ist das Moment Mk aus dem Absatz [1]. Wenn nur die Geometrie für das eingegebene Drehmoment Mk gelöst werden muss, wird die Taste rechts abgewählt und das Moment Mk, das die Bremse/Kupplung übertragen soll, eingegeben. Dadurch wird die Verbindung mit dem Absatz [1] unterbrochen und es werden dadurch die Erwärmung und die Geschwindigkeit nicht mehr berechnet (die Ergebnisse sind grau).
Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Der empfohlene Wert geht aus dem gewählten Reibungsmaterial hervor [1.44].
In diesem Teil werden die Abmessungen der Reibelementes definiert. Die Abmessungen können im Bild rechts geprüft werden.
Zur Auswahl gibt es zwei Möglichkeiten:
A. Ausschnitt der Kegelfläche – diese Konstruktion wird minimal verwendet
B. Komplette Kegelfläche – Verwendung für Bremsen und Kupplungen
Nach der Auswahl der Form werden die Anforderungen an die einschlägigen Eingangsparameter eingestellt.
Zur Lösung werden dann zwei Möglichkeiten verwendet.
A. Gleichmäßige Abnutzung (eingelaufene Bremse/Kupplung): Es wird von der Voraussetzung ausgegangen, dass die Reibungsscheiben starr sind und die größte Abnutzung zuerst auf deren Außenrand, wo die größte Arbeit der Reibkräfte entsteht, beginnt. Anschließend kommt es hier zu einer gewissen Abnutzung, die Druckverteilung ändert sich so, dass die Abnutzung der Reiboberflächen gleichmäßig ist.
B. Gleichmäßiger Druck (neue Bremse/Kupplung): Es wird vorausgesetzt, dass ein gleichmäßiger Druck auf die ganzen Reibfläche durch die Verwendung von Federn, die die Reibscheiben in die Berührung gleichmäßig andrücken, erreicht wird.
Allgemein wird die Möglichkeit A verwendet.
Geben Sie die Anzahl der Reibungsflächen nach Ihrer Konstruktion ein (siehe Abbildung).
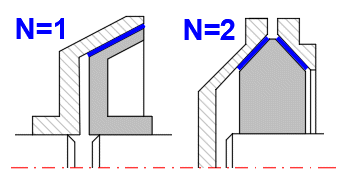
Geben Sie die Abmessungen des Reibsegmentes nach der Abbildung ein.
Sie können den Spitzenwinkel oder die Kegelbreite eingeben. Die Wahl wird mit dem Wahlschalter rechts eingestellt.
Aufgrund der Flächencharakteristik des Reibsegmentes wird der äquivalente Durchmesser De berechnet, der zur Berechnung der Kräfte dient.
Fläche, mit der das Reibsegment auf der Reibfläche aufliegt. Sie ist von der Definition der Abmessung des Reibsegmentes abhängig.
Fläche der Bremse/Kupplung, die das Reibsegment berührt (mit Strichlinie gekennzeichnet, wenn sie in der Skizze zu sehen ist).
In diesem Teil werden die Werte für eine Reibfläche aufgeführt.
Gesamtmoment Mk, in die einzelnen Reibflächen aufgeteilt.
Die meisten Hersteller von Reibmaterialien führen auch den maximalen Wert der Reibgeschwindigkeit auf, die das Material aushalten kann. Der empfohlene Wert geht aus der Wahl des Materials hervor [1.43].
Der maximale Druck an der meistbelasteten Belagsstelle. Die Belagshersteller führen meist dessen maximalen Wert auf (siehe empfohlener Wert rechts). Beim Überschreiten des maximalen Wertes versuchen Sie die Geometrie bzw. den Belagtyp zu ändern.
Einige Hersteller führen für die Reibsegmente auch den maximalen empfohlenen Wert des Wärmeflusses q auf.
Der Reibbelag weist eine schlechte Wärmeleitfähigkeit Lambda im Vergleich zur Wärmeleitfähigkeit der Materialien auf, die mit dem Belag in Kontakt kommen. (Lambda des Reibbelags ~0.1, Lambda für Stahl ~54). Deshalb wird angenommen, dass sämtliche durch Reibung entstandene Wärme durch den metallenen Teil der Bremse/Kupplung absorbiert wird.
Diese Orientierungsberechnung verwendet nur das Gewicht der Scheibe (des Kegels, der Trommel) m (siehe Berechnung unten). Die Berechnung ist richtig, wenn die Scheibe der Energieempfänger ist (typisch Scheibenbremse).
Für eine andere Konstruktionsgestaltung (typisch Kupplung) wird die Reibungsenergie zum Beispiel durch das Kupplungsgehäuse absorbiert und das Ergebnis ist selbstverständlich ungültig.
Es wird vorausgesetzt, dass der Prozess Bremsen/Schalten der Kupplung kurz ist, deshalb wird nicht mit einer Abkühlung während dieses Prozess gerechnet. Aus dieser Voraussetzung geht auch die Berechnung der Erwärmung der Reibfläche hervor, wobei nur mit dem Übergang der Wärme in die Scheibe (Trommel, Gehäuse …) aufgrund der Wärmeleitfähigkeit des Materials gerechnet wird.
Aufgaben des Typs:
- wie lassen sich die Abmessungen zum Erreichen des zulässigen Drucks pmax.
ändern
- wie darf die Bremse/Kupplung zum Erreichen des zulässigen Drucks pmax belastet
werden
- wie hoch kann die maximale Kraft Fn' sein
und Weiteres können leicht mittels der Excel-Funktion „Suche nach Lösungen“ (GoalSeek) gelöst werden.
Für die häufigsten Aufgaben werden die Eingänge in dieser Funktion und deren Aufrufen vordefiniert.
Nach der Auswahl der Abfrage und Eingabe des geforderten Wertes wird das Aufrufen der Funktion mit der Taste „Finden“ gestartet.
Zum ursprünglichen Wert des zu ändernden Parameters wird es durch das Drücken der Taste „Zurück“ zurückgekehrt. (die Funktionsfähigkeit ist zeitlich begrenzt, damit es zu keinem unerwünschten Überschreiben der Werte kommt).
Beispiel:
Sie möchten den Winkel des Reibsegmentes für die Scheibenbremse, der den
geforderten maximalen Druck „pmax“ sicherstellt, berechnen. Es ist klar, dass
sich der Winkel des Reibsegmentes nur in einem bestimmten Bereich bewegen kann,
die Anforderung an pmax ist jedoch nicht begrenzt. Also kann die Anforderung an
eine große Veränderung von pmax zu einem ganz unsinnigen Segmentwinkel Alpha
führen.
Wählen Sie aus der Liste die Aufgabe, die Sie lösen wollen.
Geben Sie den Sollwert ein, der durch die Veränderung des Eingangsparameters geändert werden soll und rufen Sie die Funktion „Suche nach Lösung“ durch die Taste rechts auf.
Die Abmessungsparameter werden aufgrund der vorhergehenden Angaben abgeschätzt. Nach Abwählen der Taste rechts können eigene Abmessungen eingegeben werden (siehe Abbildung).
Der Gewichtswert wird für die Berechnung ΔT1 verwendet.
Der Flächenwert wird zur Berechnung der Abkühlung im Absatz [8] genutzt.
Der Wert der Oberfläche S' wird als voreingestellt für die Berechnung der Erwärmung im Absatz [8] verwendet und in diesem Absatz nicht genutzt.
Die Fläche S' wird nach der Abbildung berechnet.

Trommelbremsen mit inneren Backen werden überwiegend in der Automobilindustrie eingesetzt. Bremsen mit den Außenbacken und Bremsen mit symmetrisch gelagerten Backen werden dann überwiegend in den industriellen Anwendungen eingesetzt.
Zur Berechnung und für den Entwurf der Bremse/Kupplung sind zwei Grundparameter notwendig. Drehmoment Mk und Reibungszahl f.
Diese Parameter gemeinsam mit der Definition der Abmessungen führen zur Berechnung des maximalen Drucks auf die Reibungsfläche, zur Berechnung der Betätigungskraft und bei Kenntnis der energetischen und zeitlichen Parameter aus [1] auch zur Berechnung der Erwärmung.
Im grünen Feld ist das Moment Mk aus dem Absatz [1]. Wenn nur die Geometrie für das eingegebene Drehmoment Mk gelöst werden muss, wird die Taste rechts abgewählt und das Moment Mk, das die Bremse/Kupplung übertragen soll, eingegeben. Dadurch wird die Verbindung mit dem Absatz [1] unterbrochen und es werden dadurch die Erwärmung und die Geschwindigkeit nicht mehr berechnet (die Ergebnisse sind grau).
Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Der empfohlene Wert geht aus dem gewählten Reibungsmaterial hervor [1.44].
In diesem Teil werden die Abmessungen der Reibelementes definiert. Die Abmessungen können im Bild rechts geprüft werden.
Wählen Sie aus der Liste den entsprechenden Typ.
Geben Sie die Anzahl der Ablaufbacken (L) und Auflaufbacken (R) ein.
Werden die Auflaufbacken (R) sowie Ablaufbacken (L) gleichzeitig benutzt, muss deren Anzahl gleich sein. NL/NR=1/1,2/2 ...
Es wird auch deren gleiche Größe und Betätigungskraft F angenommen.
Sollten nur die Auflaufbacke oder Ablaufbacke eingesetzt werden, ist es möglich, eine beliebige Anzahl der Backen mit gleichen Abmessungen zu wählen.
Geben Sie die Bolzenposition hinsichtlich der Trommelmitte ein. Rechts kann die Eingabeart umgeschaltet werden. Die Position kann in der Abbildung rechts überprüft werden.
Geben Sie den Angriffspunkt der Kraft zur Trommelmitte ein. <viz 4.9>Napravo můžete přepnout způsob zadání. Rechts kann die Eingabeart umgeschaltet werden. Die Position kann in der Abbildung rechts überprüft werden.
Geben Sie den Winken für den Beginn und für das Ende des Bremssegmentes ein. Die Position können Sie nach der Abbildung rechts überprüfen.
Der Abstand der Achse des Backenbolzens zur Trommelachs (Abb. C), der das Nullreibmoment zur Achse des Backenbolzens sicherstellt. Dies sorgt für die gleichmäßige Abnutzung des Belags.
Der Bremsbelag (Kupplungsbelag) wird häufig mittels Nieten befestigt. Dieser
Koeffizient drückt die Reduzierung der Reibfläche des Belags um die
einschlägigen Montagebohrungen aus.
Für geklebten Belag cF=1.0, für genieteten Belag dann cF~0.90-0.95.
Fläche, mit der das Reibsegment auf der Reibfläche aufliegt. Sie ist von der Definition der Abmessung des Reibsegmentes abhängig.
Fläche der Bremse/Kupplung, die das Reibsegment berührt (mit Strichlinie gekennzeichnet, wenn sie in der Skizze zu sehen ist).
Die Ergebnisse werden für die Auflaufbacken (R) und Ablaufbacken (L) geteilt. Bei der gleichzeitigen Benutzung R+L ist es günstig, die Konstruktion für die stärker belastete (R)-Backe auszulegen.
Die meisten Hersteller von Reibmaterialien führen auch den maximalen Wert der Reibgeschwindigkeit auf, die das Material aushalten kann. Der empfohlene Wert geht aus der Wahl des Materials hervor [1.43].
Der maximale Druck an der meistbelasteten Belagsstelle. Die Belagshersteller führen meist dessen maximalen Wert auf (siehe empfohlener Wert rechts). Beim Überschreiten des maximalen Wertes versuchen Sie die Geometrie bzw. den Belagtyp zu ändern.
Einige Hersteller führen für die Reibsegmente auch den maximalen empfohlenen Wert des Wärmeflusses q auf.
Der Reibbelag weist eine schlechte Wärmeleitfähigkeit Lambda im Vergleich zur Wärmeleitfähigkeit der Materialien auf, die mit dem Belag in Kontakt kommen. (Lambda des Reibbelags ~0.1, Lambda für Stahl ~54). Deshalb wird angenommen, dass sämtliche durch Reibung entstandene Wärme durch den metallenen Teil der Bremse/Kupplung absorbiert wird.
Diese Orientierungsberechnung verwendet nur das Gewicht der Scheibe (des Kegels, der Trommel) m (siehe Berechnung unten). Die Berechnung ist richtig, wenn die Scheibe der Energieempfänger ist (typisch Scheibenbremse).
Für eine andere Konstruktionsgestaltung (typisch Kupplung) wird die Reibungsenergie zum Beispiel durch das Kupplungsgehäuse absorbiert und das Ergebnis ist selbstverständlich ungültig.
Es wird vorausgesetzt, dass der Prozess Bremsen/Schalten der Kupplung kurz ist, deshalb wird nicht mit einer Abkühlung während dieses Prozess gerechnet. Aus dieser Voraussetzung geht auch die Berechnung der Erwärmung der Reibfläche hervor, wobei nur mit dem Übergang der Wärme in die Scheibe (Trommel, Gehäuse …) aufgrund der Wärmeleitfähigkeit des Materials gerechnet wird.
Aufgaben des Typs:
- wie lassen sich die Abmessungen zum Erreichen des zulässigen Drucks pmax.
ändern
- wie darf die Bremse/Kupplung zum Erreichen des zulässigen Drucks pmax belastet
werden
- wie hoch kann die maximale Kraft Fn' sein
und Weiteres können leicht mittels der Excel-Funktion „Suche nach Lösungen“ (GoalSeek) gelöst werden.
Für die häufigsten Aufgaben werden die Eingänge in dieser Funktion und deren Aufrufen vordefiniert.
Nach der Auswahl der Abfrage und Eingabe des geforderten Wertes wird das Aufrufen der Funktion mit der Taste „Finden“ gestartet.
Zum ursprünglichen Wert des zu ändernden Parameters wird es durch das Drücken der Taste „Zurück“ zurückgekehrt. (die Funktionsfähigkeit ist zeitlich begrenzt, damit es zu keinem unerwünschten Überschreiben der Werte kommt).
Beispiel:
Sie möchten den Winkel des Reibsegmentes für die Scheibenbremse, der den
geforderten maximalen Druck „pmax“ sicherstellt, berechnen. Es ist klar, dass
sich der Winkel des Reibsegmentes nur in einem bestimmten Bereich bewegen kann,
die Anforderung an pmax ist jedoch nicht begrenzt. Also kann die Anforderung an
eine große Veränderung von pmax zu einem ganz unsinnigen Segmentwinkel Alpha
führen.
Wählen Sie aus der Liste die Aufgabe, die Sie lösen wollen.
Geben Sie den Sollwert ein, der durch die Veränderung des Eingangsparameters geändert werden soll und rufen Sie die Funktion „Suche nach Lösung“ durch die Taste rechts auf.
Die Abmessungsparameter werden aufgrund der vorhergehenden Angaben abgeschätzt. Nach Abwählen der Taste rechts können eigene Abmessungen eingegeben werden (siehe Abbildung).
Der Gewichtswert wird für die Berechnung ΔT1 verwendet.
Der Flächenwert wird zur Berechnung der Abkühlung im Absatz [8] genutzt.
Der Wert der Oberfläche S' wird als voreingestellt für die Berechnung der Erwärmung im Absatz [8] verwendet und in diesem Absatz nicht genutzt.
Die Fläche S' wird nach der Abbildung berechnet.

Die Reibfläche wird durch ein Band gebildet, das um die Bremstrommel gewickelt ist. Einsatz in industriellen Anwendungen, einfache Konstruktion. Geeignet für die manuelle Betätigung, wo es möglich ist, durch eine verhältnismäßig kleine Betätigungskraft eine hohe Bremswirkung zu erreichen.

Zur Berechnung und für den Entwurf der Bremse/Kupplung sind zwei Grundparameter notwendig. Drehmoment Mk und Reibungszahl f.
Diese Parameter gemeinsam mit der Definition der Abmessungen führen zur Berechnung des maximalen Drucks auf die Reibungsfläche, zur Berechnung der Betätigungskraft und bei Kenntnis der energetischen und zeitlichen Parameter aus [1] auch zur Berechnung der Erwärmung.
Im grünen Feld ist das Moment Mk aus dem Absatz [1]. Wenn nur die Geometrie für das eingegebene Drehmoment Mk gelöst werden muss, wird die Taste rechts abgewählt und das Moment Mk, das die Bremse/Kupplung übertragen soll, eingegeben. Dadurch wird die Verbindung mit dem Absatz [1] unterbrochen und es werden dadurch die Erwärmung und die Geschwindigkeit nicht mehr berechnet (die Ergebnisse sind grau).
Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Der empfohlene Wert geht aus dem gewählten Reibungsmaterial hervor [1.44].
In diesem Teil werden die Abmessungen der Reibelementes definiert. Die Abmessungen können im Bild rechts geprüft werden.
Fläche, mit der das Reibsegment auf der Reibfläche aufliegt. Sie ist von der Definition der Abmessung des Reibsegmentes abhängig.
Fläche der Bremse/Kupplung, die das Reibsegment berührt (mit Strichlinie gekennzeichnet, wenn sie in der Skizze zu sehen ist).
Die Ergebnisse bestimmen die Zugkraft für ein Band F1 und F2, die zur Sicherstellung des geforderten Reibmomentes Mk notwendig ist.
Die meisten Hersteller von Reibmaterialien führen auch den maximalen Wert der Reibgeschwindigkeit auf, die das Material aushalten kann. Der empfohlene Wert geht aus der Wahl des Materials hervor [1.43].
Der maximale Druck an der meistbelasteten Belagsstelle. Die Belagshersteller führen meist dessen maximalen Wert auf (siehe empfohlener Wert rechts). Beim Überschreiten des maximalen Wertes versuchen Sie die Geometrie bzw. den Belagtyp zu ändern.
Einige Hersteller führen für die Reibsegmente auch den maximalen empfohlenen Wert des Wärmeflusses q auf.
Der Reibbelag weist eine schlechte Wärmeleitfähigkeit Lambda im Vergleich zur Wärmeleitfähigkeit der Materialien auf, die mit dem Belag in Kontakt kommen. (Lambda des Reibbelags ~0.1, Lambda für Stahl ~54). Deshalb wird angenommen, dass sämtliche durch Reibung entstandene Wärme durch den metallenen Teil der Bremse/Kupplung absorbiert wird.
Diese Orientierungsberechnung verwendet nur das Gewicht der Scheibe (des Kegels, der Trommel) m (siehe Berechnung unten). Die Berechnung ist richtig, wenn die Scheibe der Energieempfänger ist (typisch Scheibenbremse).
Für eine andere Konstruktionsgestaltung (typisch Kupplung) wird die Reibungsenergie zum Beispiel durch das Kupplungsgehäuse absorbiert und das Ergebnis ist selbstverständlich ungültig.
Es wird vorausgesetzt, dass der Prozess Bremsen/Schalten der Kupplung kurz ist, deshalb wird nicht mit einer Abkühlung während dieses Prozess gerechnet. Aus dieser Voraussetzung geht auch die Berechnung der Erwärmung der Reibfläche hervor, wobei nur mit dem Übergang der Wärme in die Scheibe (Trommel, Gehäuse …) aufgrund der Wärmeleitfähigkeit des Materials gerechnet wird.
Aufgaben des Typs:
- wie lassen sich die Abmessungen zum Erreichen des zulässigen Drucks pmax.
ändern
- wie darf die Bremse/Kupplung zum Erreichen des zulässigen Drucks pmax belastet
werden
- wie hoch kann die maximale Kraft Fn' sein
und Weiteres können leicht mittels der Excel-Funktion „Suche nach Lösungen“ (GoalSeek) gelöst werden.
Für die häufigsten Aufgaben werden die Eingänge in dieser Funktion und deren Aufrufen vordefiniert.
Nach der Auswahl der Abfrage und Eingabe des geforderten Wertes wird das Aufrufen der Funktion mit der Taste „Finden“ gestartet.
Zum ursprünglichen Wert des zu ändernden Parameters wird es durch das Drücken der Taste „Zurück“ zurückgekehrt. (die Funktionsfähigkeit ist zeitlich begrenzt, damit es zu keinem unerwünschten Überschreiben der Werte kommt).
Beispiel:
Sie möchten den Winkel des Reibsegmentes für die Scheibenbremse, der den
geforderten maximalen Druck „pmax“ sicherstellt, berechnen. Es ist klar, dass
sich der Winkel des Reibsegmentes nur in einem bestimmten Bereich bewegen kann,
die Anforderung an pmax ist jedoch nicht begrenzt. Also kann die Anforderung an
eine große Veränderung von pmax zu einem ganz unsinnigen Segmentwinkel Alpha
führen.
Wählen Sie aus der Liste die Aufgabe, die Sie lösen wollen.
Geben Sie den Sollwert ein, der durch die Veränderung des Eingangsparameters geändert werden soll und rufen Sie die Funktion „Suche nach Lösung“ durch die Taste rechts auf.
Die am häufigsten benutzte konstruktive Anordnung ist in der Abbildung zu sehen.
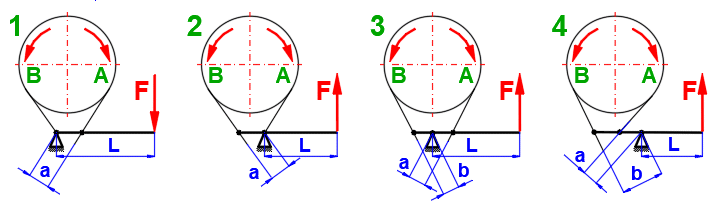
Wählen Sie den Konstruktionstyp und die Drehrichtung der Trommel aus und geben Sie die geforderten Abmessungen ein. Das Ergebnis ist die Betätigungskraft F.
Verwendung: Für eine Drehrichtung, manuelle Betätigung.
Verwendung: Für eine Drehrichtung, manuelle Betätigung
Vorteil: Durch die verhältnismäßig kleine Kraft F ist ein großes Drehmoment zu
bremsen. Für a=b*e^(f*Alpha) ist F=0. Das Bremsen wäre aber ruckartig,
ungenügend.
Deshalb wird meist a>2.5*b entworfen.
Verwendung: Für beide Drehrichtungen, für a=b ist F für beide Richtungen gleich.
Die Abmessungsparameter werden aufgrund der vorhergehenden Angaben abgeschätzt. Nach Abwählen der Taste rechts können eigene Abmessungen eingegeben werden (siehe Abbildung).
Der Gewichtswert wird für die Berechnung ΔT1 verwendet.
Der Flächenwert wird zur Berechnung der Abkühlung im Absatz [8] genutzt.
Der Wert der Oberfläche S' wird als voreingestellt für die Berechnung der Erwärmung im Absatz [8] verwendet und in diesem Absatz nicht genutzt.
Die Fläche S' wird nach der Abbildung berechnet.

In diesem Kapitel werden einige Ergänzungsberechnungen für die Bestimmung der Belastung der Bremse/Kupplung und für die Berechnung der Erwärmung aufgeführt.
Die primäre Aufgabe einer Bremse/Kupplung ist, die definierte Masse anzuhalten/in Bewegung zu setzen (kinetische Energie Ek entnehmen/zuführen). In den absolut meisten Fällen handelt es sich um zwei Grundaufgaben.
1. Rotierende Bauteile abbremsen/in Rotation versetzen
2. Sich bewegende Bauteile direkt abbremsen/in Bewegung setzen
3. Kombination der oben aufgeführten Punkte
Die Berechnungen in diesem Absatz ermöglichen, 5 Berechnungen für jede Aufgabe zu definieren. Durch das Ankreuzen/Abwählen der Taste in der Kopfzeile wird die Summe von Ek in das Schlussergebnis in der Zeile zugefügt/entnommen [6.6].
Eine häufige Aufgabe der Berechnung von Ek ist die Lösung eines rotierenden Zylinders. Geben Sie die Abmessungen und die Drehzahl nach der Abbildung ein.
Zuweilen werden das Gewicht des rotierenden Bauteils und der Trägheitsradius angegeben. Zur Berechnung von Ek kann diese Tabelle verwendet werden.
Für rotierende Bauteile wird oft das Trägheitsmoment angegeben. In diesem Fall wird diese Tabelle für die Berechnung von Ek verwendet.
Für die Berechnung von Ek wird das Gewicht und die Geschwindigkeit der sich bewegenden Teile angegeben. Wenn Sie eine geradelinige Bewegung in eine Drehzahl umrechnen müssen, geben Sie den Raddurchmesser in der als D gekennzeichneten Spalte ein.
Nach dem eingestellten Berechnungstyp [1.2] wird der Wert von Ek nach dem Drücken der Taste nach [1.4] (Bremsen) oder [1.15] (Kupplungen) übertragen.
In den meisten Fällen wird das System der Bremse/Kupplung neben der kinetischen Energie (siehe Absatz 6) auch mit dem nachträglichen Drehmoment belastet, das zum Beispiel wie folgt entsteht:
- Reibkräfte der Lager
- Reibkräfte der Mechanismen
- Bewegung auf der Neigungsebene
- aerodynamischer Widerstand
- usw.
Die aufgeführten Berechnungen umfassen die am häufigsten gelösten Aufgaben.
Der Wert des belastenden Momentes ML wird in den Absatz [1] durch das Drücken der Taste „>>ML“ übertragen.
Berechnung des belastenden/entlastenden Momentes des Fahrzeugs, das durch den Rollwiderstand und die Bewegung auf der geneigten Ebene entsteht. In der Berechnung sind die Sollparameter auszufüllen.
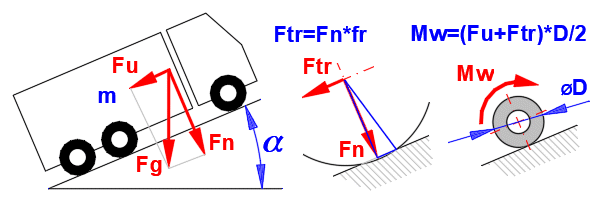
Asphalt / Reifen (LKW)…(0.006-0.010)
Asphalt / Reifen (PKW)…(0.010-0.015)
Asphalt / Reifen (Motorrad)…(0.010-0.015)
Asphalt / Reifen (Rad)…(0.002-0.005)
Pflaster / Reifen…(0.015-0.030)
Sand und Kies / Reifen…(0.040-0.080)
Schiene / Stahlfelge…(0.001-0.002)
Nach dem eingestellten Berechnungstyp [1.2] wird der Wert von ML nach dem Drücken der Taste nach [1.5] (Bremsen) oder [1.16] (Kupplungen) übertragen.
Das zusätzliche belastende/entlastende Moment ist vom Gewicht der Hebeeinrichtung abhängig. In der Berechnung sind die Sollparameter auszufüllen.
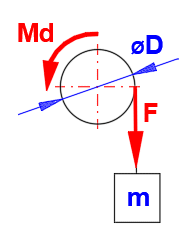
Nach dem eingestellten Berechnungstyp [1.2] wird der Wert von ML nach dem Drücken der Taste nach [1.5] (Bremsen) oder [1.16] (Kupplungen) übertragen.
Das zusätzliche belastende/entlastende Moment ist vom Gewicht, von der Reibungszahl f und vom Winkel der geneigten Ebene abhängig. In der Berechnung sind die Sollparameter auszufüllen.
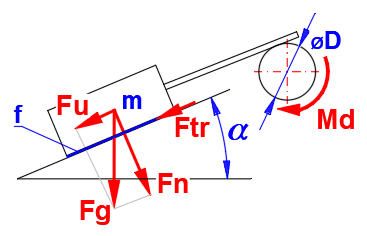
=======Dynamisch (v>0), Sauber, Trocken
========
Gehärterer Stahl - Gehärterer Stahl (0.1)
Gehärterer Stahl - Roheisen (0.13-0.27)
Gehärterer Stahl - Phosphore Bronze (0.15)
Gehärterer Stahl - Holz (Eiche) (0.4-0.5)
Roheisen - Roheisen (0.15-0.2)
Roheisen - Phosphore Bronze (0.15-0.2)
Roheisen - Holz (Eiche) (0.3-0.5)
Phosphore Bronze - Phosphore Bronze (0.2)
Leder - Roheisen (0.56)
Gummi - Roheisen (0.8)
Gummi - Betone (0.7)
Gummi - Asphaltstraße (0.7)
Asbest (Gewebe) - Stahl (0.3-0.35)
Nylon - Stahl (0.3)
Polystyrene - Stahl (0.5)
=======Dynamisch (v>0), Geschmierte ========
Gehärterer Stahl - Gehärterer Stahl (0.05-0.1)
Gehärterer Stahl - Roheisen (0.05-0.15)
Gehärterer Stahl - Phosphore Bronze (0.09-0.15)
Gehärterer Stahl - Holz (Eiche) (0.08)
Roheisen - Roheisen (0.07-0.1)
Roheisen - Phosphore Bronze (0.07-0.1)
Roheisen - Holz (Eiche) (0.2)
Phosphore Bronze - Phosphore Bronze (0.07-0.1)
Leder - Roheisen (0.15-0.35)
Gummi - Roheisen (0.5)
Gummi - Betone (0.3-0.5)
Gummi - Asphaltstraße (0.2-0.3)
Asbest (Gewebe) - Stahl (0.08-0.12)
Sowohl beim Bremsen als auch beim Anlaufen kommt es bei Berührung der Reibflächen zum Umwandlung kinetischer Energie in Wärme. In den vorhergehenden Absätzen sind die Beziehungen zur Berechnung des maximalen Momentes und des maximalen Drucks auf die Reibflächen für die angegebenen Abmessungen der Bremse/Kupplung aufgeführt. Auch wenn kein maximales Moment übertragen und der maximal zulässige Druck nicht überschritten wird, kann es zur Zerstörung der Bremse/Kupplung durch übermäßige Erwärmung kommen.
In diesem Absatz kann:
- die Erwärmung der Bremse/Kupplung beim einmaligen Abbremsen/Schalten der
Kupplung gelöst werden.
- wiederholtes Abbremsen/Schalten der Kupplung simuliert werden.
Nach der Auswahl aus der Liste [8.2] werden die Werte der Oberflächengröße und des Gewichtes aus dem einschlägigen Absatz des Typs der Bremse/Kupplung [2,3,4,5] ausgefüllt. Für die vernünftige Berechnung (Abschätzung) der Temperaturcharakteristik ist es jedoch notwendig, die Größe der Oberfläche und des Gewichtes möglichst genau im Hinblick auf die verwendete Konstruktion der Bremse/Kupplung festzulegen.
Als Beispiel wird der Unterschied zwischen einer Scheibenbremse und einer Scheibenkupplung aufgeführt.
Scheibenbremse:
Sie wird durch eine Metallscheibe gebildet, die mit Bremsklötzen gebremst
wird. Sämtliche Wärme wird in der Metallscheibe akkumuliert, die die Wärme in
die Umluft abgibt. Zur Berechnung der Wärme sind die Werte der Fläche und des
Gewichtes aus dem Absatz [2] zu verwenden.
Scheibenkupplung:
Sie besteht aus dünnen Scheiben mit Reibungsbelag, der in die metallene
Kupplungskonstruktion eingreift. Sämtliche Wärme wird in der
Kupplungskonstruktion akkumuliert. Die Parameter der Fläche und des Gewichtes
unterscheiden sich stark von den in Absatz [2] entworfenen Parametern und es
sind die eigene Werte einzugeben.
Zur Eingabe der eigenen Werte wird die Taste rechts abgewählt.
Der Wert wird aufgrund der Materialauswahl [1.54] voreingestellt.
Nach der Wahl der Berechnungstyps im Absatz [1] werden die Energiewerte übertragen. Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Zur Berechnung des Temperaturanstieges werden die Werte aus [8.4, 8.5, 8.7] verwendet.
Bei einem Zyklus Bremsen/Schalten der Kupplung kommt es zum annähernden Temperaturanstieg um die Temperatur ΔT. Der Wert ist annähernd, die ausführlichere Beschreibung ist im theoretischen Hilfeteil zu finden.
Bei dieser Berechnung werden 100 Zyklen des wiederholten Bremsens/Schaltens der Kupplung mit dem vorgegebenen Zeitabstand [8.13] simuliert. Für jeden Zyklus wird die entsprechende Wärmeübergangszahl Alpha berechnet, die dann zur Berechnung der Temperaturen des folgenden Zyklus verwendet wird. Diese Vorgehensweise ist meist genügend und konvergiert schnell zur konstanten Temperatur.
Der Temperaturverlauf ist im Graph B [8.25] dargestellt. Die X-Koordinate ist in Minuten angegeben.
Bei einer großen Wärmeträgheit der Bremse/Kupplung (großes Gewicht) können 100 Iterationszyklen ungenügend sein. Dieser Fall ist aus dem Graph B zu erkennen, wo die Kurve nicht zur konstanten Temperatur Max/Min konvergiert. In diesem Fall wird die kumulative Berechnung [8.17] verwendet.
Geben Sie die Umlufttemperatur ein.
Die Geschwindigkeit der Luftströmung um den Körper der Bremse/Kupplung beeinflusst erheblich den Wärmeübergang. Versuchen Sie, diesen Wert möglichst genau abzuschätzen.
Der Wert wird aufgrund der Berechnung aus [1] voreingestellt. Nach Abwählen der Taste rechts kann ein eigener Wert eingegeben werden.
Geben Sie den Zeitabstand zwischen der wiederholten Benutzung der Bremse/Kupplung ein.
Im Graph B kann meist die allmähliche Konvergenz zum konstanten Wert Min, Max beobachtet werden.
Der Wert Min, Max wird aus dem letzten Zyklus (100) der allmählichen Iteration genommen.
Bei dieser Berechnung wird der gesamte Temperaturanstieg abgeschätzt. Aus diesem Anstieg wird die entsprechende Wärmeübergangszahl Alpha berechnet, die zur Berechnung der gesamten Erwärmung verwendet wird.
Nach Abwählen der Taste rechts kann Ihre Abschätzung des Temperaturanstiegs eingegeben werden. In den meisten Fällen ist dies jedoch überflüssig und der empfohlene Wert im grünen Feld ist ausreichend genau.
Maximale Temperatur der Bremse/Kupplung für eine unbegrenzte Anzahl von Zyklen beim Bremsen/Schalten der Kupplung.
Die Zyklusnummer kann direkt eingegeben oder über den Reiter rechts eingestellt werden. Der Temperaturverlauf des ausgewählten Zyklus ist im Graph dargestellt.
Scheibenbremsen-Design der Vorderachse eines Autos + Temperaturanalyse.
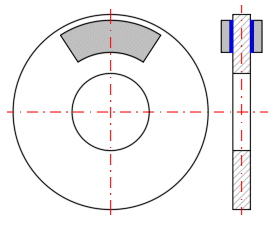
Fahrzeuggewicht: m = 1600 kg
Anfangsgeschwindigkeit v1 = 180 km/h (50 m/s)
Endgeschwindigkeit v2 = 0
Straßengefälle
a
= -5 ° (8,75%)
Durchschnittliche Verzögerung a = -7 m/s^2
Raddurchmesser = 620 mm
Verteilung der Bremskraft 70% Vorderachse 30% Hinterachse.
Wiederholtes Bremsen 180->0 km-h mit einem Zeitraum von 180s
Bremszeit:
t = v1 / a; t = 50 / 7 => t = 7,14 s
v1-Anfangsgeschwindigkeit; a-Beschleunigung/Verzögerung; t-Zeit
Berechnungsannahmen:
- Luftwiderstand ist nicht enthalten
- Keinen Radschlupf
- Linearer Verlauf
Im Absatz [1] werden die Einheiten der Berechnung [1.1] und die Berechnung der Bremse [1.2] gewählt.
Zuerst ist die Belastung der Bremse zu lösen.

Zur Berechnung der kinetischen Energie Ek wird der Absatz [6], durch das Drücken der Taste „Ek>>“ verwendet.
Berechnung von Ek für eine Bremsscheibe. Vorderachse 70 % Belastung, ein Rad => 0.7/2=0.35.
Für PKW wird der Koeffizient 1.05 (der die rotierenden gebremsten Massen, wie Räder, Wellen, Zahnräder usw. umfasst) verwendet.
Erste Spalte 0.35*1.05=0.3675.
Ergebnis Ek=735000 [J] und für Raddurchmesser 620 mm=> Drehzahl 1540 [/min].
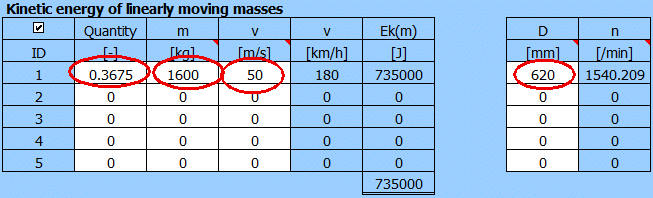
Zur Berechnung des nachträglichen Belastungsmomentes ML wird der Absatz [7], durch Drücken der Taste „ML>>“ verwendet.
Das Gesamtgewicht des Fahrzeugs wird auf ein Rad der Vorderachse nach der vorherigen Überlegung m=1600*0.35=560 [kg] aufgeteilt.
Nach Ausfüllen der übrigen Angaben wird das zusätzliche Belastungsmoment 123 [Nm] erhalten und in den Absatz [1] übertragen.
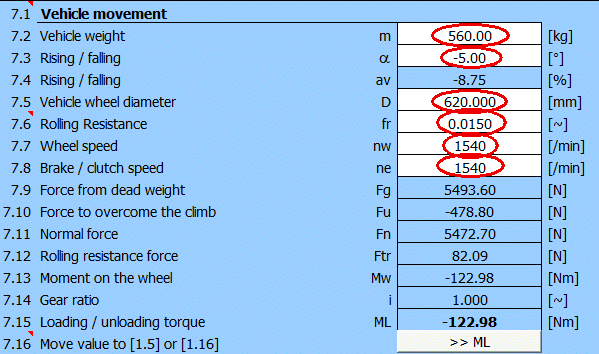
Nach Ausfüllen aller Angaben und nach der Wahl KA=1.1 werden die Parameter zur Berechnung der Abmessungen der Scheibenbremse (t,Mk,Eh) definiert.

Vorläufig ist es günstig, das Material des Bremsbelags und der Bremsscheibe im Absatz [1] zu definieren (auszuwählen).
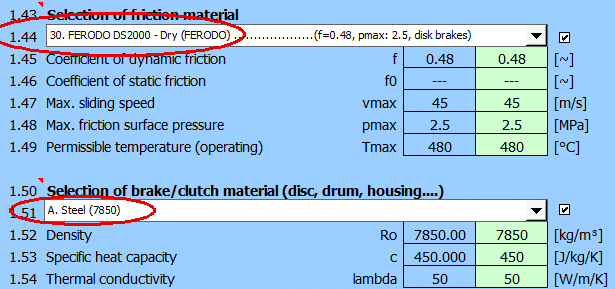
Nach Wechseln in den Absatz zur Berechnung der Scheibenbremse/Kupplung [2] werden die Anfangsparameter [2.1-2.7] eingestellt.

Es wird der Winkel des Reibsegmentes Alpha [2.11]=80° gewählt.
Es ist wahrscheinlich, dass der Wert des maximalen Drucks pmax [2.24] entweder den zulässigen Wert aus [1.48] überschreiten wird oder zu niedrig ist und das Potential der Bremse nicht genutzt wird.
Wählen Sie deshalb auf [2.29] „Suche nach Lösung“ (03.) für pmax aus, geben Sie den Sollwert 2.5[MPa] ein (siehe ausgewähltes Material) und drücken Sie die Taste „Suchen“ („Run“).
Es wird der minimale Außenradius des Reibsegmentes zum Erreichen des vorgegeben Drucks pmax=2.5[MPa] gesucht.
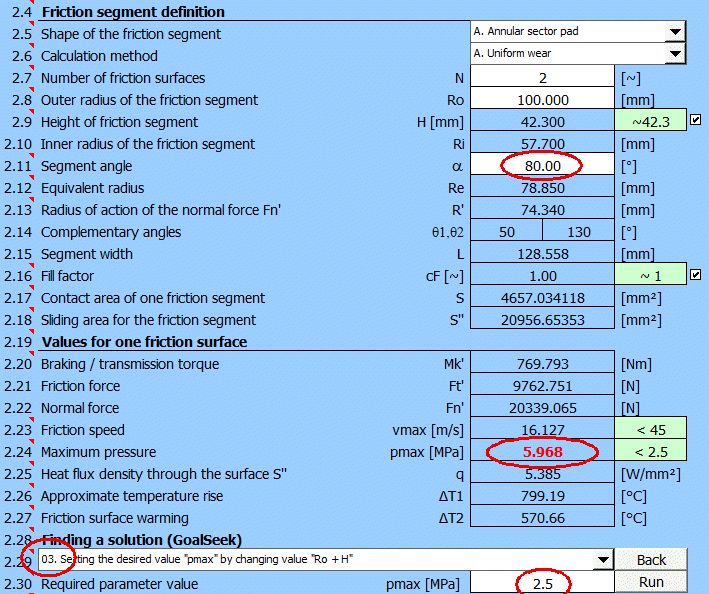
Nach Suche der Lösung erhalten Sie die Ergebnisse:

Nach der geeigneten Wahl der Werte Ro und H wird dann der Entwurf der Scheibenbremse wie folgt aussehen.
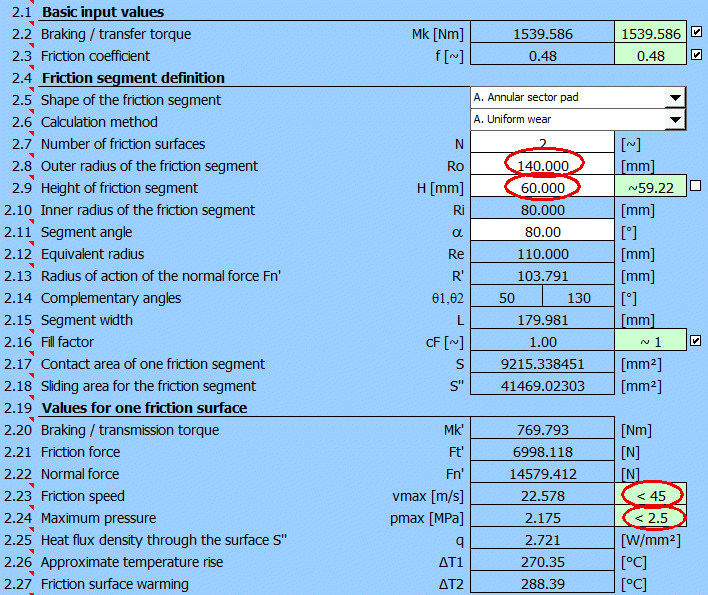
Der Entwurf erfüllt die Grundanforderungen, die an die Reibgeschwindigkeit und an den Druck auf den Belag bei Erfüllung der Anforderung an das zu bremsende Moment Mk gestellt werden.
Ein untrennbarer Bestandteil des Entwurfs einer Bremse sollte auch die
Temperaturanalyse sein. Der Absatz [2] umfasst auch den Entwurf der Abmessungen
der Bremsscheibe. Diese sind zur Analyse notwendig.
Für dieses Beispiel werden die voreingestellten (abgeschätzten) Werte verwendet.

Nach Wechseln in den Absatz [8] werden die Parameter wie folgt eingestellt.
- [8.3] Es werden die Parameter der Scheibe aus der ausgewählten Berechnung der Scheibenbremse [2] verwendet
- [8.7] Es wird die Bremsenergie aus dem Absatz [1] verwendet
Geben Sie die Lufttemperatur, die Geschwindigkeit der Luftströmung (geschätzt die halbe Fahrzeuggeschwindigkeit zu Beginn des Bremsens) und den geforderten Zeitabstand zwischen dem Bremsen ein.
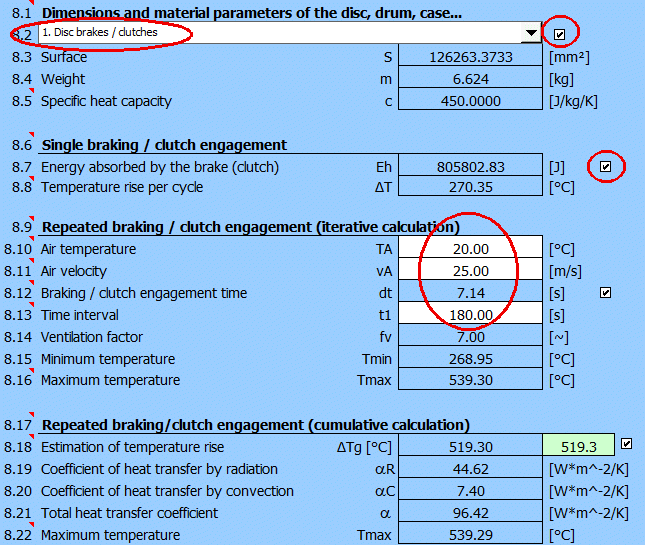
Das Ergebnis ist der Graph des Temperaturanstiegs und des Temperaturabfalls zwischen den einzelnen Bremszyklen.
Entwurf einer Scheibenkupplung eines Personenkraftwagens.
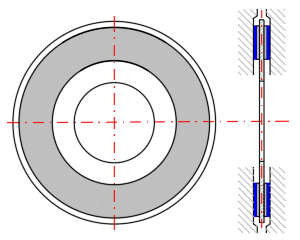
Fahrzeuggewicht: m = 1600 kg
Motor leistungsdiagramm
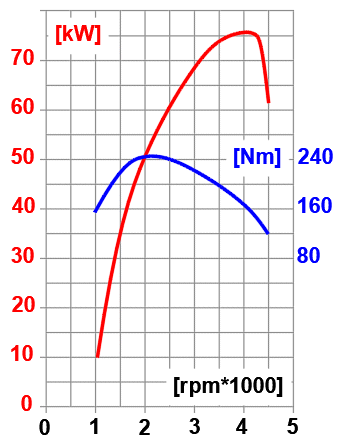
Geschätzt aus dem Leistungsdiagramm:
- gewählte Drehzahl für Start = 2500 [/min]
- Motorleistung für 2500 [/min] = 60kW
Anfangsgeschwindigkeit v1 = 0
Endgeschwindigkeit v2 = 25 km/h (7 m/s) bei Kupplungsdrehzahl 2500 /min im 1.
Gang
Straßengefälle
a
= + 5 ° (8,75%)
Raddurchmesser = 620 mm
Berechnungsannahmen und
Vereinfachungen:
- Luftwiderstand ist nicht enthalten
- Keinen Radschlupf
- Leistung und Antriebsdrehzahl werden beim Einrücken der Kupplung als konstant
angenommen
Im Absatz [1] werden die Einheiten der Berechnung [1.1] und Berechnung der Kupplung [1.2] gewählt.
Zuerst ist die Belastung der Kupplung zu lösen.
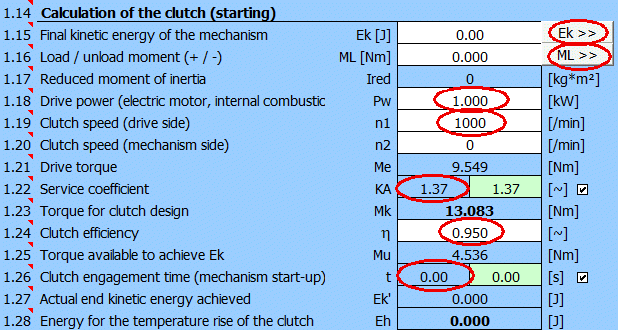
Zur Berechnung der kinetischen Energie Ek wird der Absatz [6], durch Drücken der Taste „Ek>>“ verwendet.
Berechnung der Endenergie Ek. Ergebnis Ek=39200 [J] und für Raddurchmesser 620 mm=>Drehzahl 215 [/min].
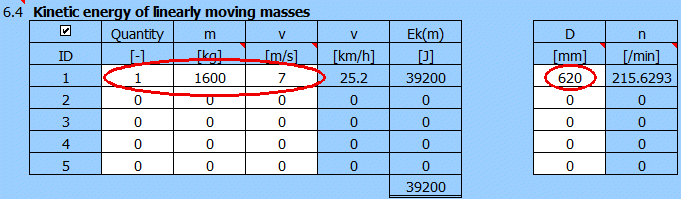
Zur Berechnung des nachträglichen Belastungsmomentes ML wird der Absatz [7], durch Drücken der Taste „ML>>“ verwendet.
Füllen Sie Gewicht, Fahrbahnsteigung, Raddurchmesser, Raddrehzahl und Kupplungsdrehzahl aus.
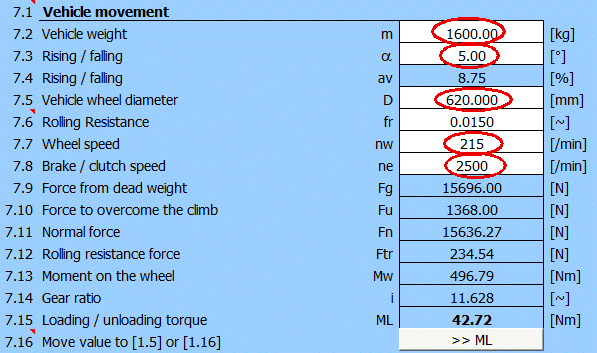
Nach Ausfüllen der Angaben wird das zusätzliche Belastungsmoment 42.7 [Nm] ausgegeben. Der Wert wird in den Absatz [1] übertragen.
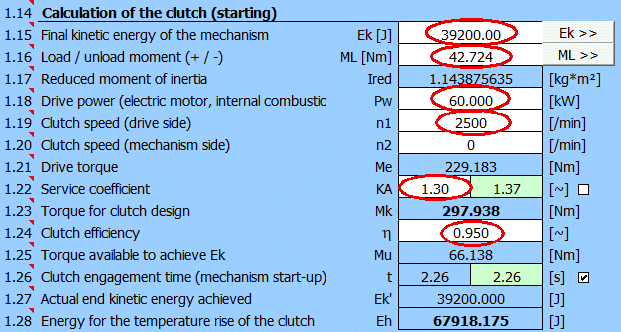
Nach Ergänzung aller Angaben und Wahl von KA=1.3 werden Parameter zur Berechnung der Abmessungen der Scheibenbremse (t,Mk,Eh) definiert.
Vorläufig ist es angebracht, das Material des Kupplungsbelags und des Kupplungsgehäuses im Absatz [1] zu definieren (auszuwählen).
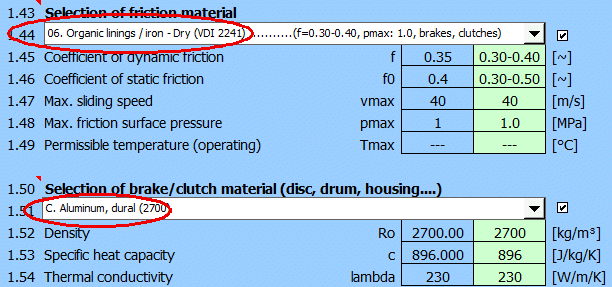
Nach Umschalten in den Absatz zur Berechnung der Scheibenbremse/Kupplung [2] werden die Anfangsparameter [2.1-2.7] eingestellt.

Es ist wahrscheinlich, dass der Wert des maximalen Drucks pmax [2.24] entweder den zulässigen Wert aus [1.48] überschreitet oder zu niedrig ist und das Potential der Kupplung nicht genutzt wird.
Wählen Sie in [2.29] „Suche nach Lösung“ (03.) für pmax, geben Sie den Wert 1.0[MPa] (siehe ausgewähltes Material) ein und drücken Sie die Taste „Suchen“ („Run“).
Es wird der minimale Außenradius des Reibsegmentes zum Erreichen des vorgegebenen Drucks pmax=1.0 [MPa] gesucht.
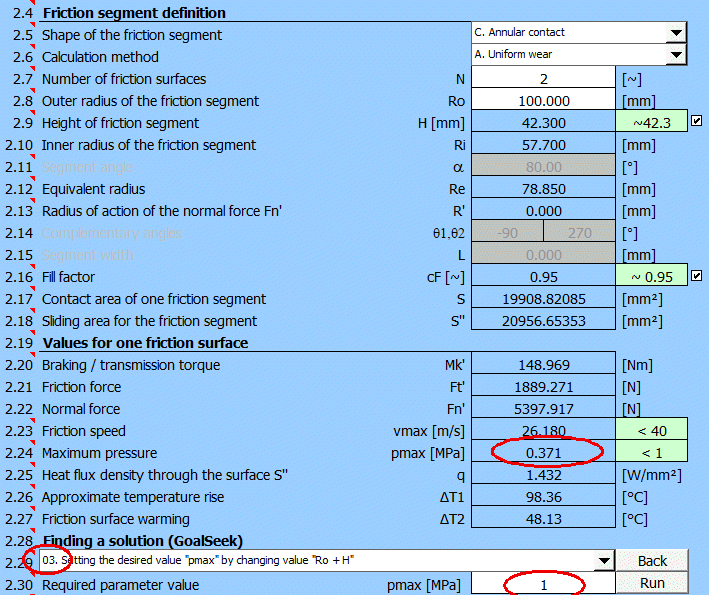
Nach Suche der Lösung erhalten Sie die Ergebnisse:

Nach der geeigneten Wahl der Werte Ro und H wird dann der Entwurf der Kupplung wie folgt aussehen.
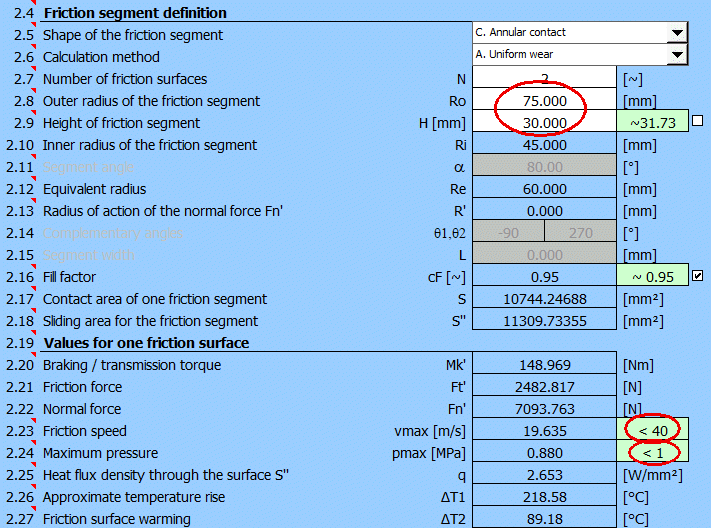
Der Entwurf erfüllt die Grundanforderungen, die an die Reibgeschwindigkeit und an den Druck auf den Belag bei Erfüllung der Anforderung an das zu bremsende Moment Mk gestellt werden.
Berechnung der Tabelle der Betätigungskraft F und des Bremsmomentes Mk für die definierte Bremse.
Abmessungen der Bremse gemäß Abbildung [mm].
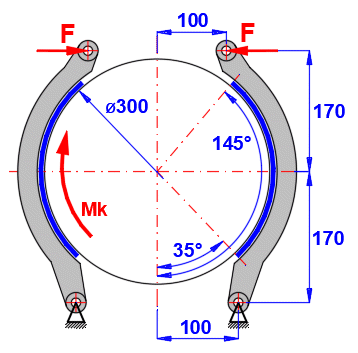
Reibungskoeffizient des Bremsbelags
............. f = 0,4 [~]
Bremsbelagbreite ....................................... w = 100 [mm]
Klebefutter => ......................................... cF = 1,0 [~]
Maximaler Druck .................................. pmax = 0,5 [MPa]
Geben Sie die eingegebenen Bremsmaße ein (deaktivieren Sie die Tasten rechts, um sie einzugeben).
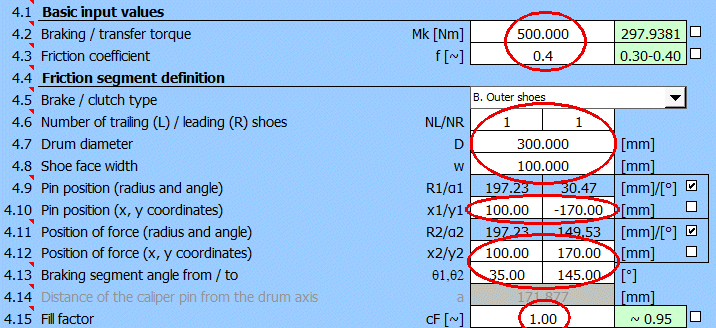
Das Drehmoment Mk[Nm] wird allmählich im Bereich von 300–1100 geändert.
Tabelle der Ergebnisse:
| ID | Mk [Nm] | F [N] | pmaxR [MPa] |
| 1 | 500 | 1932 | 0.24 |
| 2 | 600 | 2319 | 0.29 |
| 3 | 700 | 2705 | 0.34 |
| 4 | 800 | 3092 | 0.39 |
| 5 | 900 | 3478 | 0.43 |
| 6 | 1000 | 3865 | 0.48 |
| 7 | 1100 | 4251 | 0.53 |
Durch die Verwendung der Funktion „Suche nach Lösung“ in [4.24-4.26] werden dann das maximale Moment Mk und die maximale Betätigungskraft F für den maximalen zulässigen Druck pmax=0.5[MPa] gefunden.
Bandbremse mit den vorgegebenen Abmessungen, Ermittlung des max. Drehmomentes Mk und Betätigungskraft F.
Abmessungen der Bremse gemäß Abbildung [mm]. D=300mm, L=400mm, a=60mm, b=30mm
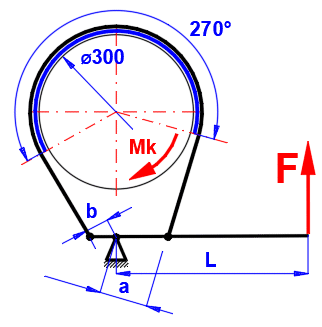
Reibungskoeffizient des Bremsbelags
............. f = 0.3 [~]
Bremsbelagbreite ....................................... w = 100 [mm]
Maximaler Druck .................................. pmax = 0.3 [MPa]
Geben Sie die eingegebenen Bremsmaße ein (deaktivieren Sie die Tasten rechts, um sie einzugeben).
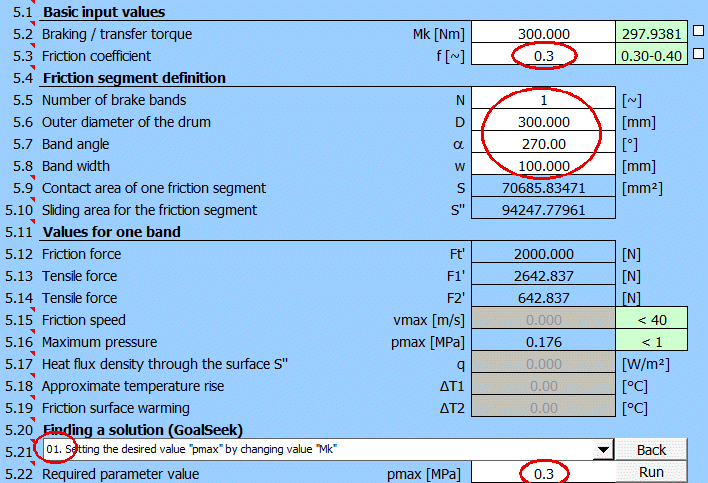
Wählen Sie in [5.21] „Suche nach Lösung“ (01.) für pmax, geben Sie den Sollwert 0.3 [MPa] ein und drücken Sie die Taste „Suchen“ („Run“).
Es wird das Moment Mk zum Erreichen des vorgegebenen Drucks pmax=0.3 [MPa] gesucht.
Nach der Wahl des Typs des Betätigungsmechanismus und Eingabe der Abmessungen erhalten Sie die Gesamtlösung. Maximales Moment Mk und Betätigungskraft F.
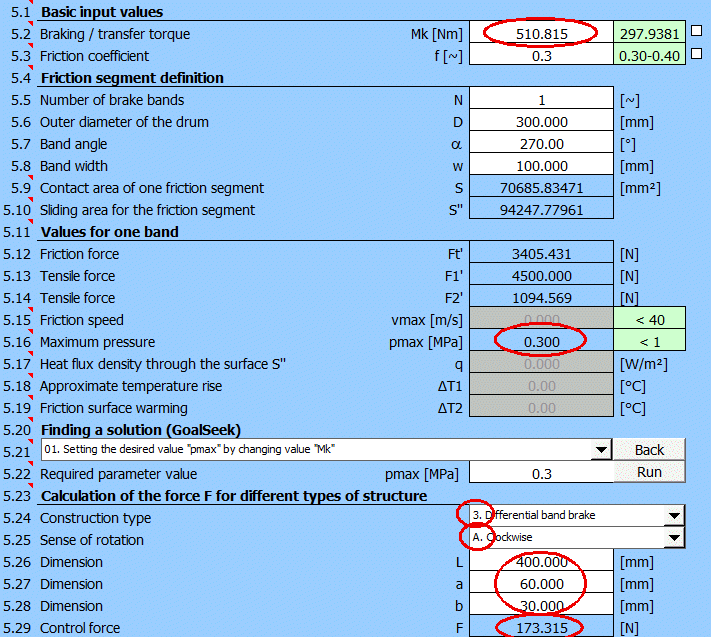
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
Litrature:
[1] Clutches and Brakes Design and Selection Second Edition (William C. Orthwein)
[2] Shigley’s Mechanical Engineering Design (Richard G. Budynas, J. Keith Nisbett)
[3] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[4] Brake Design and Safety Third Edition (Rudolf Limpert)
[5] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
Standards:
VDI 2241-Blatt 1
Schaitbare fremdbetätigte Reibkupplungen und -bremsen.
Begriffe, Bauarten, Kennwerte, Berechnungen
Friction clutches and brakes Vocabulary, types, characteristic data,
calculations
VDI 2241-Blatt 2
Schaitbare fremdbetätigte Reibkupplungen und -bremsen,
Systembezogene Eigenschatten, Auswahlkriterien, Berechnungsbeispiele
Friction clutches and brakes Typ related properties, criteria for selection,
examples of calculations
SAE J866
Friction Coefficient Identification and Environmental Marking System for Brake
Linings
SAE J661
(R) BRAKE LINING QUALITY TEST PROCEDURE
Company cataloques: Ortlinghaus, Goizper, TAROX, FERODO...
^