Program je určen pro návrh, výpočet a kontrolu čtyř základních typů třecích brzd a spojek. V programu je možné také určit kinetickou energii a zatěžovací momenty mechanismů.
Program umožňuje:
1. Výpočet zatížení brzdy
2. Výpočet rozběhového zatížení spojky
3. Kontrolu zatížené spojky
4. Návrh a kontrolu:
- Diskové brzdy/spojky
- Kuželové brzdy/spojky
- Bubnové brzdy/spojky
- Pásové brzdy/spojky
5. Výpočet a kontrolu oteplení navržené brzdy/spojky
Ve výpočtu jsou použita data, postupy, algoritmy a údaje z odborné literatury, norem a firemních katalogů.
[1] Clutches and Brakes Design and Selection; [2] Shigley’s Mechanical Engineering Design; [3] Textbook of Machine Design; [4] Brake Design and Safety; [5] Roloff / Matek - Maschinenelemente
VDI 2241-Blatt 1; VDI 2241-Blatt 2; SAE J866; SAE J661; Ortlinghaus, Goizper, TAROX, FERODO
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
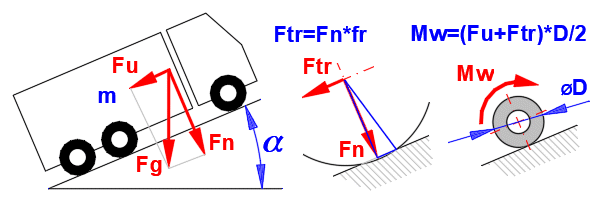
Z fyzikální podstaty se třecí brzdy a spojky neliší. Rozdíl je pouze v tom, jakým způsobem je brzda/spojka zatěžována, jejich geometrické řešení a ovládání. Tomu pak odpovídá i konkrétní řešení a příslušný výpočet. Uváděné vztahy jsou univerzální.
Řešení výpočtu brzdy/spojky se obvykle dělí na dvě
související úlohy.
1. Výpočet zatížení brzdy/spojky na základě bržděného / rozjížděného
mechanismu. Ve výpočtu odstavec [1].
2. Výpočet rozměrů brzdy/spojky splňujícího požadované zatížení. Ve výpočtu odstavec
[2,3,4,5,8].
Bržděný mechanismus má na začátku brzdícího cyklu kinetickou
energii Ek (závisí na druhé mocnině rychlosti).
- rotační pohyb
- přímočarý pohyb
A zároveň na něj působí síly a momenty, které snižují / zvyšují zatížení brzdy
(jsou v průběhu brzdícího cyklu konstantní).
- třecí síly ložisek
- vnější vliv (brždění na nakloněné rovině)
- aerodynamický odpor (není konstantní) atd.
Další proměnnou je čas brždění.
Řešením těchto vztahů je krouticí moment, který musí brzda vyvinout a energie, která musí být brzdou absorbována.
Pro spojku platí analogický posup jako pro brzdu (rozpohybování mechanismu - dosažení požadované Ek).
Obě úlohy je možné oddělit a získat například podklady pro výběr brzdy/spojky z katalogu výrobce, nebo na základě zatížení brzdu / spojku navrhnout.
V následujících odstavcích jsou obsažené vzorce pro výpočet zatížení, výpočet energií, vzorce použité pro rozměrové řešení třecích brzd a spojek a výpočty oteplení.
Vypočítá se jako součet kinetické energie přímočarého pohybu a energie rotace hmoty.
Ek [J]= 0.5 * m * v2 + 0.5 * I * ω2
m ... hmotnost bržděné hmoty [kg]
v .... rychlost bržděné hmoty [m/s]
I .... moment setrvačnosti bržděné hmoty [kg*m²]
ω ... otáčky bržděné hmoty s momentem setrvačnosti I [rad/s]
Při brždění či rozběhnutí mechanismu působí většinou dodatečné síly nebo momenty, které je nutné zahrnout do výpočtu. Může to být valivý odpor kola, valivé odpory ložisek, síly způsobené hmotností (jeřáb, výtah, pohyb po nakloněné rovině), třením, aerodynamický odpor atd.
Všechny tyto dodatečné síly a momenty je pak nutné přepočítat na otáčky brzdy/spojky příslušným převodovým poměrem.
Pokud budou například otáčky kola vozidla nw=100 [/min] a otáčky spojky nc=2000 [/min], tak dodatečný moment ML působící na spojku je:
ML = Mw * nw / nc
ML ... dodatečný zatěžovací / odlehčovací moment
Mw ... moment působící na kolo vozidla
nw ... otáčky kola
nc .... otáčky spojky
Při více rotujících a posouvajících se částí s různou rychlostí je vhodné sečíst jejich kinetické energie a pro další výpočty přepočíst na redukovaný moment setrvačnosti vztažený na otáčky brzdy/spojky.
Ired [kg*m²] = 2 * Ek / (n / 60 * 2 * p)2
Ek ... součet kinetických energií [J]
n ..... otáčky brzdy/spojky [/min]
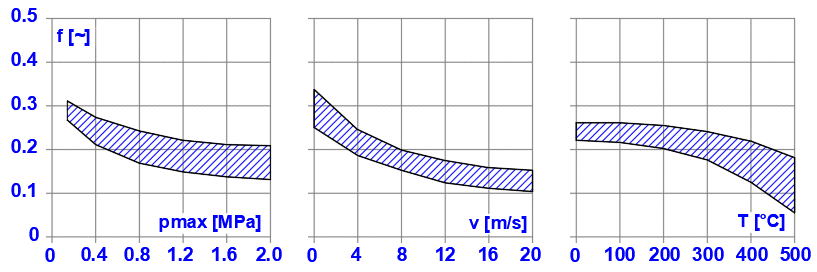
Jedná se o základní parametr, který nejvíce ovlivňuje rozměry brzdy/spojky. Závisí na použitých materiálech a jejich kombinaci. Ve výpočtu je možné vybrat ze základních oblastí třecích materiálů. Nicméně důrazně doporučujeme řídit se konkrétními hodnotami výrobce, dodavatele.
Příklad, jak se může měnit koeficient tření f [~] v závislosti na pmax [MPa], v [m/s] a T [°C] pro suché tření pro kombinaci materiálů Kovokeramika / ocel.
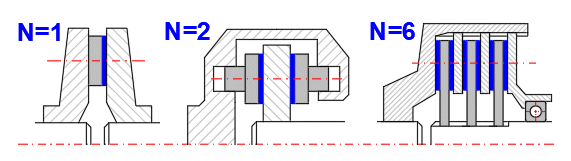
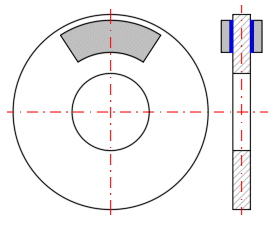
Patří mezi nejpoužívanější druhy brzd a spojek. Mají jednoduchou konstrukci, velkou plochu třecích povrchů, dobrý odvod tepla. Je možné používat konstrukce s jedním a více třecími povrchy, kdy zvláště konstrukce se 2 třecími povrchy je významě používána v automobilovém průmyslu (diskové brzdy, kotoučové spojky).
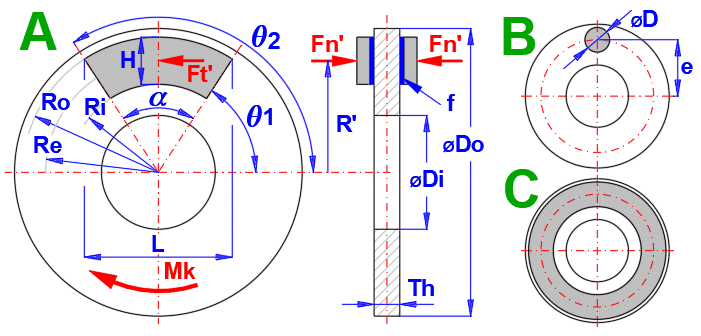
Jelikož princip brzd a spojek se pro výpočet nijak neliší, je použit společný postup s rozměry definovanými obrázkem. Brzdy bývají většinou konstrukčně řešené tak, že třecí element má tvar kruhové výseče či kružnice (A,B), u spojky pak mezikruží (C).
Pro řešení se používají dva přístupy.
A. Rovnoměrné opotřebení (zaběhnutá brzda/spojka): Vychází z předpokladu, že třecí kotouče jsou tuhé a největší opotřebení nastává nejdříve na jejich vnějším obvodě, kde je práce třecích sil největší. Poté, co zde dojde k jistému opotřebení, změní se rozložení tlaku tak, že opotřebení třecích povrchů bude rovnoměrné.
B. Rovnoměrný tlak (nová brzda/spojka): Předpokládá, že užitím pružin rovnoměrně přitlačujících třecí kotouče do styku je dosaženo rovnoměrného tlaku po celé třecí ploše.
Všeobecně se používá přístup A.
Maximální tlak
pmax [MPa] =(2 * Mk) / (a *
f * Re
* (Ro^2 - Ri^2)
/ 1000000 /
FillCoeff
Ekvivalentní poloměr Re
Re [m] = (Ro + Ri) / 2
Třecí síla
Ft [N] = Mk
/ Re
Normálová síla
Fn [N] = Ft / f
Působiště normálové síly
R' [m] = (COS(q1) -
COS(q2)) / (q2 -
q1) * (2/3) * ((Ro^3 - Ri^3) / (Ro^2 - Ri^2))
Maximální tlak
pmax [MPa] = (3 * Mk) / (a * f * (Ro^3 - Ri^3)) / 1000000 / FillCoeff
Ekvivalentní poloměr Re
Re [m] = 2 / 3 * (Ro^3 - Ri^3) / (Ro^2 - Ri^2)
Třecí síla
Ft [N] = Mk
/ Re
Normálová síla
Fn [N] = Ft / f
Působiště normálové síly
R' [m] =
(COS(q1) - COS(q2))
/ (q2 -
q1) * ((Ro
+ Ri)/2)
Mk .................... zatěžovací moment [Nm]
a ..................... úhel třecího segmentu [rad]
f ....................... koeficient tření [~]
Ro .................... vnější poloměr [m]
Ri ..................... vnitřní poloměr [m]
FillCoeff ............ koeficient vyplnění [~]
q1,q2 .............. doplňkové úhly [rad]
Jako třecí plocha je použita kuželová plocha. Výhodou této konstrukce je nižší ovládací síla Fn než u diskové brzdy/spojky. V závislosti na třecím materiálu se obvykle používá úhel kužele b v rozmezí 10 -15°.
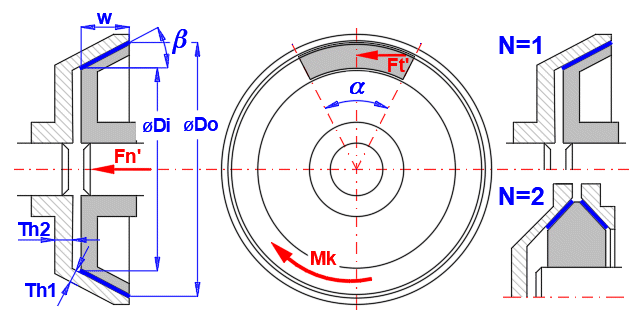
Při řešení se postupuje obdobně jako v předchozím případě, stanovením vztahů platných pro rovnoměrné opotřebení obložení a pro rovnoměrné rozložení tlaku po celé třecí ploše.
Maximální tlak
pmax [MPa] = (Mk / (p
* f *
Di) * (8
* SIN(b)) /
(Do^2 - Di^2))
/ 1000000 /
a
Ekvivalentní průměr De
De [m]=(Do +
Di) / 2
Třecí síla
Ft [N] = Mk
/ (De / 2)
Normálová síla
Fn [N] = Ft * SIN(b) / f
Maximální tlak
pmax [MPa] = (Mk /(p
* f) *
(12 * SIN(b))
/ (Do^3 -
Di^3)) / 1000000
/ (a / (2 * p))
Ekvivalentní průměr De
De [m] = 2/3
* (Do^3 -
Di^3) / (Do^2
- Di^2)
Třecí síla
Ft [N] = Mk
/ (De / 2)
Normálová síla
Fn [N] = Ft * SIN(b) / f
kde:
Mk .... zatěžovací moment [Nm]
a ..... úhel třecího segmentu [rad]
b
...... úhel kužele [rad]
f ....... koeficient tření [~]
Do .... vnější průměr [m]
Di ..... vnitřní průměr [m]
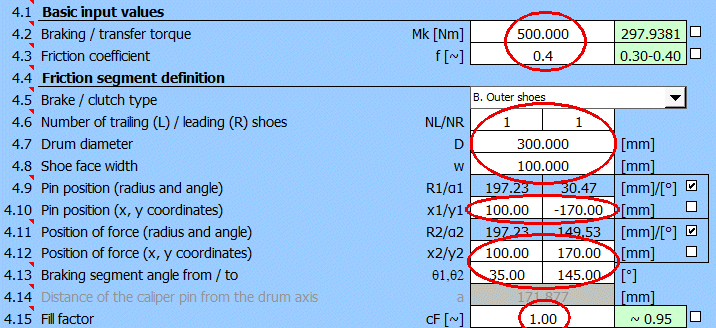
Bubnové brzdy s vnitřními čelistmi jsou používány převážně v automobilovém průmyslu. Brzdy s vnějšími čelistmi a brzdy se symetricky uloženými čelistmi jsou pak používány převážně v průmyslových aplikacích.
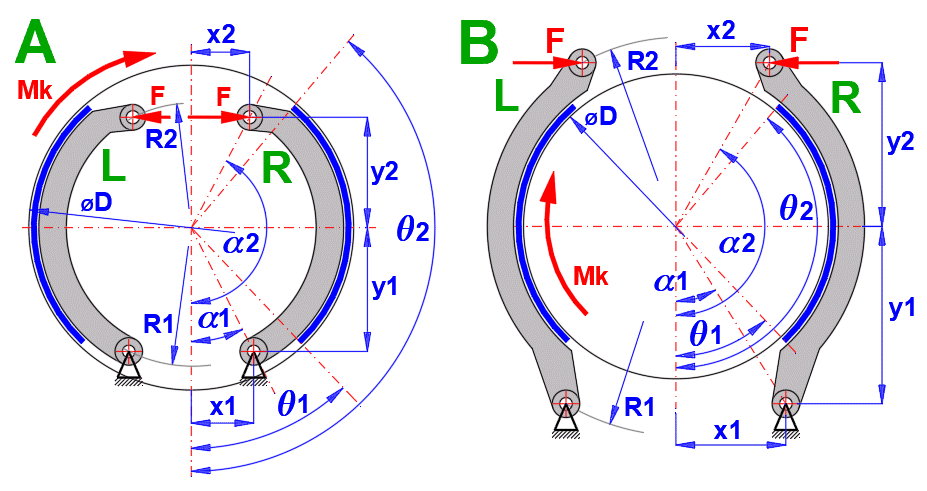
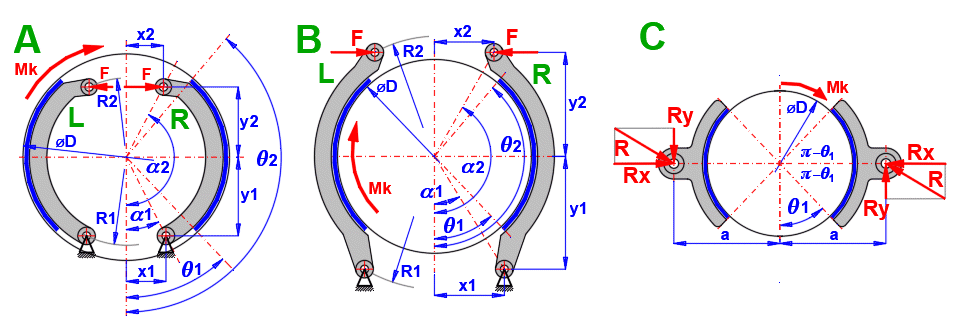
V bubnové brzdě jsou principiálně používány dva typy čelistí. V závislosti na smyslu otáčení (působení momentu) jsou označovány jako náběžná R (Leading shoe) a úbežná L (Trailing shoe) tak jak jsou označeny na obrázku L,R.
Pro shodnou sílu F jsou pro čelist (L) a (R) rozdílné brzdné momenty, tlaky ,síly a reakce.
Výpočet proto pricipiálně probíhá v následujících krocích
(náběžná (R) a úběžná (L) čelist):
1. Výpočet síly F' pro jednotkový pmaxR'=1 pro náběžnou
čelist (R)
2. Výpočet brzdného momentu MR' pro náběžnou čelist (R)
pro sílu F'
3. Výpočet pmaxL' pro levou čelist (L) pro sílu F'
4. Z toho výpočet brzdného momentu pro levou čelist (L) ML'
5. Výpočet celkového brzdného momentu Msum' = MR'+ML'
6. Výpočet koeficientu X, X = Mk / Msum'
7. Přepočtení jednotkových hodnot tlaků, sil, momentů a reakcí koeficientem X
Třecí moment
Mt_R [Nm] = f * pmax * w * (D/2) /
SIN(qXa) * CoefA
CoefA =(D / 2 * (-(COS(qX2) - COS(qX1))) - a * ((0.5 * SIN(qX2)^2) -
(0.5*SIN(qX1)^2)))/1000
Normálový moment
Mn_R [Nm] = pmax * w * (D/2) * a /
SIN(tqXa) * CoefB / 1000
CoefB =(qX2/2 - 1/4 * SIN(2 *
qX2)) - (qX1/2 - 1/4 * SIN(2 *
qX1))
Síla F
F [N] = (Mn_R - Mt_R) / (c / 1000)
c [mm] = ABS(y1 - y2)
Brzdný moment M_R
M_R [Nm] = f * pmax * w * (D/2)^2 *
(COS(qX1) -
COS(qX2)) / SIN(qXa) / 1000
Tlak pmaxL
pmaxL [MPa] = (F * c / (Mn_R + Mt_R)) / 1000
Brzdný moment M_L
M_L [Nm] = f * pmaxL
* w * (D/2)^2 * (COS(qX1) - COS(qX2)) / SIN(qXa) / 1000
Brzdný moment Msum
Msum [Nm] = NR * M_R + NL * M_L
Koeficient X
X = Mk / Msum
f ............. koeficient tření [~]
pmax ...... maximální tlak [MPa]
w ........... šířka obložení [mm]
D ........... průměr bubnu [mm]
qX1 = q1 -
a1 [rad]
qX2 = q2 -
q1 + qX1 [rad]
qXa ... a) qX2 < PI()/2 ...
qXa = qX2, b)
qX2
> PI()/2 ...
qXa = PI()/2
NR, NL ... počet brzdících elementů (náběžná (R) a úběžná (L) čelist)
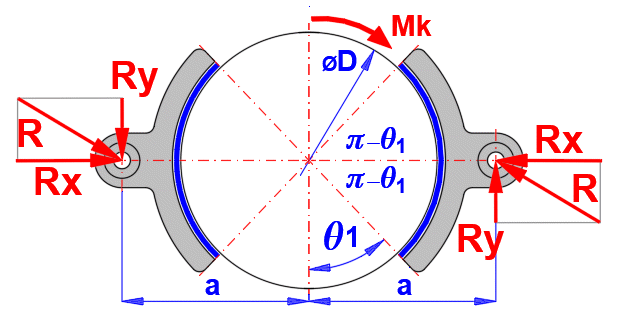
Vzdálenost osy čepu čelisti od osy bubnu "a", která zajišťuje nulový
třecí moment k ose čepu čelisti.To zajišťuje souměrné opotřebení obložení.
a = 4 * (D/2) * SIN(q1') / (2 *
q1' + SIN(2 *
q1'))
q1' = pi()/2 -
q1
Maximální tlak
pmax [Mpa] = (Mk / (NL+NR)) / (2 * f * w * (D / 2)^2 *
SIN(q1')) / FillCoeff
Reakce v čepu čelisti ve směru x a y
Rx = pmax * w * (D/4) * (2 *
q1' +
SIN(2 *
q1'))
Ry = pmax * w * f * D/4 * (2 *
q1'
+ SIN(2 *
q1'))
q1 ................ úhel počátku brzdového
obložení (viz obrázek)
[rad]
Mk ............... zatěžovací moment
[Nm]
NL, NR ......... počet brzdících elementů [~]
f ................... koeficient tření [~]
w .................. šířka brzdícího elementu
[m]
D ................. vnější průměr bubnu
[m]
q1' ................ poloviční
úhel opásání [rad]
FillCoeff ........ koeficient vyplnění
[~]
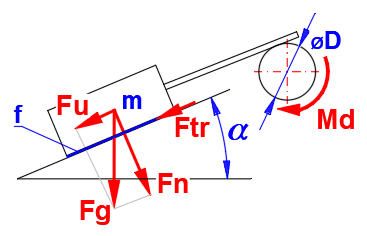
Třecí plocha je tvořena pásem, který je ovinut kolem brzdícího bubnu. Využití v průmyslových aplikacích, jednoduchá konstrukce. Vhodné pro manuální ovládání, kdy je možné poměrně malou ovládací silou dosáhnout vysokého brzdného účinku.
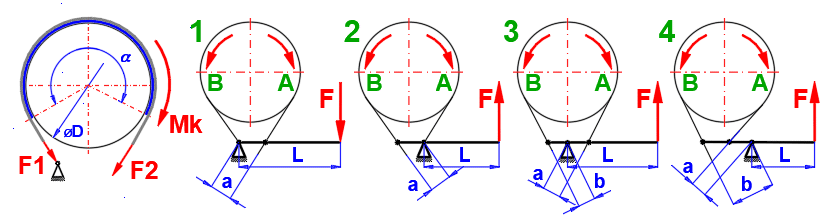
ecoef = 2.7182818 (f *a)
Ft = Mk /
((Do / 2))
F2 = Mk / (ecoef - 1) * (Do / 2))
F1 = Ft + F2
Maximální tlak
pmax = (2 * F1 / (w * Do)) / N
Výpočet síly F
A: ve směru otáčení:
1 ... F = (Ft * a / L) * (1 / (ecoef - 1)) / N
2 ... F = (Ft * a / L) * (ecoef / (ecoef - 1)) / N
3 ... F = (Ft / L) * ((b * ecoef - a) / (ecoef - 1)) / N
4 ... F = (Ft / L) * ((b * ecoef + a) / (ecoef - 1)) / N
B: proti směru otáčení:
1 ... F = (Ft * a / L) * (ecoef / (ecoef - 1)) / N
2 ... F = (Ft * a / L) * (1 / (ecoef - 1)) / N
3 ... F = (Ft / L) * ((b - a * ecoef) / (ecoef - 1)) / N
4 ... F = (Ft / L) * ((b + a * ecoef) / (ecoef - 1)) / N
f ........... koeficient tření [~]
Ft .......... třecí síla [N]
Do ......... vnější průměr bubnu
[m]
a .......... úhel
opásání bubnu [rad]
N .......... počet pásů [~]
a,b,L ..... rozměry páky [mm]
Jak při brždění, tak při rozběhu dochází při styku třecích ploch k přeměně kinetické energie v teplo. V předchozích odstavcích jsou uvedené vztahy pro výpočet maximálního momentu a maximálního tlaku na třecí plochy pro zadané rozměry brzdy/spojky. I v případě, že není přenášen maximální moment a není překročen maximální dovolený tlak, může dojít ke zničení brzdy/spojky nadměrným oteplením.
Tento výpočet samozřejmě nepokrývá všechny konstrukční varianty brzdy/spojky. (olejové chlazení, speciální geometrie, speciální materiály atd). Proto jsou použité následující předpoklady:
- Třecí obložení má nízkou
tepelnou vodivost l v porovnáním s tepelnou vodivostí materiálů které jsou
s obložením ve styku. (l třecího obložení ~ 0.1, l
pro ocel ~ 54). Proto se počítá s tím, že veškeré teplo vzniklé třením je
pohlceno kovovou částí brzdy/spojky
- Tepelné vlastnosti materiálů jsou konstantní (v reálném
případě se samozřejmě mění i když nevýrazně)
- Čas brždění je řádově kratší, než čas ochlazování
- Hmotnost brzdy/spojky (je pouze odhad. Nenahradí podrobnou analýzu hmotnosti tělesa, které
přijímá teplo vzniklé třením)
Někteří výrobci uvádějí pro třecí segmenty i maximální hodnotu tepelného toku q.
q [W/mm²] = Eh / t / S''
Eh ..... tepelná energie, vzniklá prací spojky / brzdy během pracovního cyklu [J]
t ........ čas brždění / sepnutí spojky [s]
S'' ...... třecí plocha
disku / bubnu [mm²]
Nárůst teploty pro brzdu / spojku je možné přibližně určit podle vzorce:
ΔT1 [°C] = Eh / (c * m)
Eh ... tepelná energie, vzniklá prací spojky / brzdy během pracovního cyklu [J]
c ..... měrná tepelná kapacita materiálu [J/kg/K]
m .... hmotnost spojky / brzdy [kg]
Jelikož vzorec nezohledňuje časový faktor a ochlazování, je vhodné ho brát jako orientační.
Ohřev stykové plochy
ΔT2 [°C] = (5 / 18)^0.5 * (Eh * t^0.5) / (S'' * t * (Ro * c * l)^0.5)
Eh .......... tepelná energie, vzniklá prací spojky / brzdy během pracovního cyklu [J]
Ro .......... hustota [kg/m³]
c ............ měrná tepelná kapacita materiálu [J/kg/K]
l ........... tepelná vodivost materiálu [W/m/K]
t ............ čas brždění / sepnutí spojky [s]
S'' .......... třecí plocha disku / bubnu [mm²]
Doba průniku tepla tb k dosažení vnějšího povrchu bubnu
tb [s] = Th^2 / (5 * (l / (Ro * shc)))
Th .......... tloušťka bubnu / disku [mm]
c ............ tepelná kapacita materiálu [J/kg/K]
Předchozí rovnici ΔT1[°C] = Eh / (c * m) je možné použít spolu s Newtonovým ochlazovacím zákonem, který popisuje přenos tepla z povrchu spojky / brzdy.
Po příslušném zjednodušení a použití zjednodušujících předpokladů dostaneme vztah:
(T - TA) / (T1 -TA) = exp(- (a * S) / (m * c) * t)
T ..... teplota povrchu tělesa v čase t [°C]
TA ... teplota přímého okolí povrchu tělesa - teplota vzduchu [°C]
T1 ... počáteční teplota povrchu tělesa [°C]
a .... součinitel přestupu
tepla prouděním a zářením [W*m^-2/K]
S ..... plocha vnějšího povrchu tělesa [m²]
m .... hmotnost tělesa (brzda, spojka)
c ..... měrná tepelná kapacita materiálu [J/kg/K]
t ..... čas ochlazování [s]
Pro opakované použití pak může být proces brždění popsán podle obrázku:
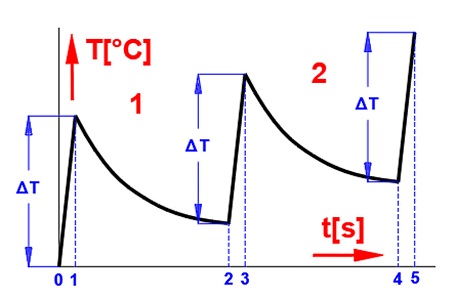
0-1 ... brždění mechanismu - příjem třecí energie, zvýšení
teploty
1-2 ... předávání energie okolnímu prostředí (ochlazování - pokles teploty)
2-3 ... další cyklus brždění, zvýšení teploty
3-4 ... předávání energie okolnímu prostředí (ochlazování - pokles teploty)
..................
Vývoj teploty pro opakovaný cyklus pak může vypadat třeba následovně.
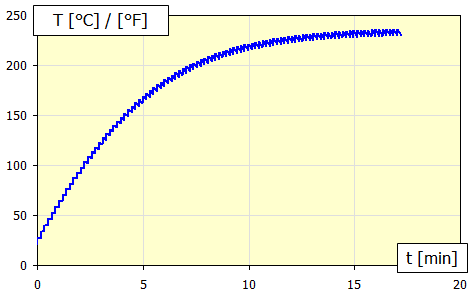
Kdy při stoupající teplotě brzdy/spojky se příslušným způsobem zvyšuje i součinitel přestupu tepla a, takže za určité teploty dochází k vyrovnání hodnoty přijaté energie (proces brždění) a vydané energie (ochlazování).
Součinitel přestupu tepla a v případě tohoto výpočtu ovlivňují 3 parametry a pro jeho výpočet je použit vztah:
a = aR + aC * fv
aR .... Součinitel přestupu tepla zářením [W*m^-2/K]
aC .... Součinitel přestupu tepla prouděním [W*m^-2/K]
fv ...... Součinitel proudění vzduchu [~]
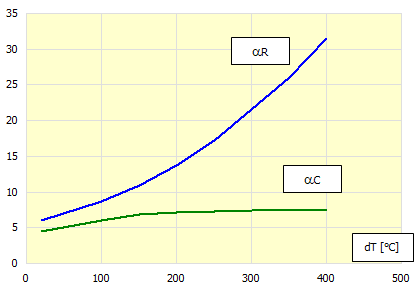
Pro určení koeficientů aR a aC je možné použít následující graf:
dT = T - TA
T ..... teplota povrchu tělesa v čase t [°C]
TA ... teplota přímého okolí povrchu tělesa - teplota vzduchu [°C]
Pro určení součinitele proudění vzduchu fv pak:
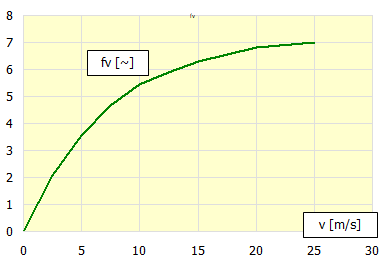
Při tomto výpočtu je simulováno 100 kroků opakovaného brždění / sepnutí spojky se zadaným časovým intervalem. Pro každý krok je spočítán odpovídající součinitel přestupu tepla alfa, který je pak použit pro výpočet teplot v následujícím kroku. Většinou je tento postup vyhovující a rychle konverguje k ustálené teplotě.
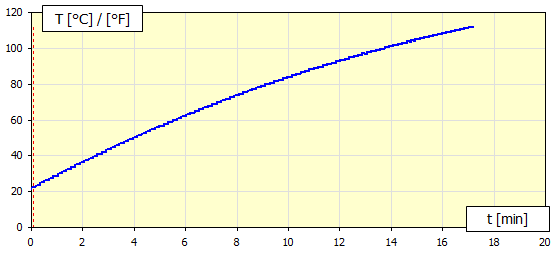
Při tomto výpočtu odhadnete celkový nárůst teploty. Z tohoto nárůstu je spočítán odpovídající součinitel přestupu tepla alfa, který je použit pro celkový výpočet oteplení. Tento postup je závislý na odhadu oteplení a může být méně přesný než výpočet předcházející. Nicméně v případě, že předchozí postup nekonverguje k ustálené koncové teplotě, je vhodné použít tento výpočet.
Příklad vývoje oteplení, kdy je vhodné použít kumulativní výpočet.
Řešení výpočtu brzdy/spojky se obvykle dělí na dvě úlohy.
1. Výpočet zatížení brzdy/spojky na základě bržděného / spouštěného mechanismu
[1].
2. Výpočet rozměrů brzdy/spojky splňujícího požadované zatížení [2,3,4,5].
V odstavci [1] zvolte způsob výpočtu zatížení (brzda / spojka) [1.3].
Vyplňte, či spočítejte kinetickou energii Ek a moment ML (doplňkové výpočty
[6,7]) a zadejte rychlostní, časové a provozní parametry.
Výsledek je potřebný moment a energie dostačující pro specifikaci brzdy/spojky
u dodavatele nebo pro rozměrové výpočty v odstavcích [2,3,4,5]
Po výběru typu brzdy/spojky [2,3,4,5] zadejte moment, kterým je brzda / spojka
zatížena.
Zadejte parametry třecí plochy a rozměry třecího elementu.
Výsledek je tlak na třecí plochu, rychlost a působící síly.
Propojením výpočtu zatížení [1] a výpočtu rozměrů [2,3,4,5] je pak možné řešit i
další úlohy.
- teplota brzdy/spojky za provozu
- optimalizace rozměrů
- optimalizace zatížení
V tomto odstavci nastavíte jednotky výpočtu a počítáte zatěžující moment a energii, které jsou nutné pro správný návrh rozměrů brzdy/spojky.
Nastavujete zde také další parametry, jako jsou vlastnosti třecího materiálu, materiálu brzdy/spojky a typ zatížení.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě změněny všechny hodnoty.
Pro výpočet brzd/spojek je většinou nutné znát "co brzdíme" resp. "co
chceme rozpohybovat". Tyto informace vedou ke dvěma základním parametrům.
1. Kroutící moment, který musí brzda/spojka přenést
2. Energie, kterou musí brzda/spojka absorbovat
K dispozici jsou tak tři základní výpočty energií a momentů.
A. Výpočet brzdy
B. Výpočet rozběhové spojky
C. Kontrola spojky za běhu
Vybraný výpočet je aktivní, zbývající dva jsou šedivé - neaktivní.
Geometrický výpočet konkrétního typu brzdy/spojky [2,3,4,5] pak přebírá
informace o zatěžujícím momentu, energii atd. ze zvoleného výpočtu energií a
momentů. Stejně tak jako výpočet oteplení brzdy/spojky
[8]
Úkolem je zabrzdit pohybující se mechanismus do požadovaného stavu (většinou
do zastavení n2=0).
V tomto případě řešíme úlohu, kdy kinetickou energii Ek a dodatečné momenty ML
je nutné převést ve třecí brzdě na tepelnou energii.
Použité předpoklady a zjednodušení:
-všechny bržděné hmoty jsou navzájem propojené při konstantním převodu
-zatěžovací moment ML je konstantní v průběhu procesu brždění
Kinetická energie pohybujících se hmot, které potřebujete zabrzdit. Pro jejich výpočet můžete použít odstavce [6.0], kam se přepnete tlačítkem "Ek>>".
Zatěžovací / odlehčovací moment (+/-) přepočítaný na otáčky brzdy n1.
Pro řešení obvyklých úloh stiskněte tlačítko "ML>>"
Příklady zatížení (+):
- Pohyb vozidla z kopce
- Výtah, jeřáb (hmotnost působící silou)
Příklady odlehčení (-):
- Pohyb vozidla do kopce
- Valivé odpory mechanismu
Moment setrvačnosti přepočtený ze všech bržděných hmot (rotační, lineární pohyb - viz Výpočet Ek) na počáteční otáčky bržděného disku (bubnu) n1.
Zadejte počáteční otáčky brzdového disku či bubnu.
Zadejte koncové otáčky brzdového disku či bubnu. Pro úplné zastavení bržděného mechanismu n2 = 0.
Požadovaný čas brždění z otáček n1 na n2.
Jedná se o teoriticky vypočtený moment (za předpokladu optimálních podmínek), který musí brzda zajistit v průběhu brzdícího cyklu.
Jelikož bržděný mechanismus může vykazovat nerovnoměrnost (oscilace
kroutícího momentu) je vhodné použít koeficient (KA), který tuto nerovnoměrnost
zohlední a zaručí vyžadovaný čas brždění.
Návrh koeficientu KA vychází z
praktických poznatků a jeho velikost se řídí nastavením podmínek na řádku
[1.41].
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Krouticí moment, který musí brzda zachytit. Tato hodnota momentu je použita pro výpočet rozměrů brzdy [2,3,4,5]
Množství energie, která musí být zmařena v brzdě (oteplení brzdy).
Úkolem je rozběhnout mechanismus do požadovaného stavu (většinou z n2=0 do
n1=požadované otáčky).
V tomto případě řešíme úlohu, kdy je nutné dodat do mechanismu takovou energii
Ek, která je nutná pro dosažení požadované rychlosti a otáček při překonávání
dodatečných momentů ML.
Použité předpoklady a zjednodušení:
- otáčky n1 (pohon) jsou v průběhu činnosti spojky konstantní
- je přenášen konstantní moment => zrychlení mechanismu je konstantní
Kinetická energie na kterou je nutné urychlit mechanismus. Pro výpočet můžete použít odstavce [6], kam se přepnete tlačítkem "Ek >>".
Zatěžovací / odlehčovací moment (+ / -) vztažený na otáčky spojky n1.
Pro výpočet obvyklých úloh stiskněte tlačítko "ML >>"
Příklady zatížení (+):
- Rozjetí vozidla do kopce
- Valivé odpory mechanismu
- Výtah, jeřáb (hmotnost působící silou)
Příklady odlehčení (-):
- Rozjetí vozidla z kopce
Moment setrvačnosti přepočtený ze všech rozbíhajících se hmot (rotační, lineární pohyb - viz Výpočet Ek) na počáteční otáčky disku spojky (bubnu) n1.
Výkon hnacího stroje, který je dodáván na spojku.
Zadejte otáčky spojky na straně pohonu. Na tyto otáčky bude urychlen mechanismus.
Ve většině případů budete řešit rozběh zastaveného mechanismu (n2=0).
Pokud potřebujete řešit mechanismus, který je již v pohybu (n2>0) a urychlit jej
na otáčky n1, zadejte počáteční otáčky n2.
Kroutící moment dodaný hnacím strojem.
Jelikož poháněný mechanismus i hnací stroj mohou vykazovat nerovnoměrnost (oscilace kroutícího momentu) je vhodné použít koeficient (KA). Tento koeficient zohlední tuto nerovnoměrnost při výpočtu krouticího momentu, který musí spojka přenést.
Návrh koeficientu KA vychází z praktických poznatků a jeho velikost se řídí nastavením podmínek na řádku [1.40,1.41,1.42]. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Kroutící moment, který musí spojka přenést. Tato hodnota momentu je použita pro návrh rozměrů spojky [2,3,4,5].
Obecně udávaná účinnost třecích spojek je přibližně 0.95.
Jde o část krouticího momentu, který je dodán hnacím strojem a je plně využit pro dosažení požadované koncové Ek mechanismu.
Druhá část momentu je ve spojce zmařena ve formě tření.
Moment Mu je snížen / zvýšen o hodnotu ML [1.16].
Na základě:
- požadované koncové kinetické energie mechanismu Ek [1.15]
- zatěžovacíího momentu ML [1.16]
- výkonu motoru Pw [1.18]
- účinnosti spojky h [1.24]
je spočítán nutný čas provozu spojky (hodnota v zeleném poli).
Po odškrtnutí tlačítka můžete zadat vlastní čas provozu spojky.
Zadanému času pak odpovídá hodnota Ek' [1.27], na kterou je mechanismus
urychlen.
Kinetická energie mechanismu, která je dosažena sepnutím spojky za čas, zadaný v předchozím řádku.
Energie, která se ve spojce přemění na teplo.
Při řešení přenosu energie třecí spojkou je vhodné zkontrolovat i funkčnost
za provozních podmínek.
Spojka může vyhovovat pro rozběh mechanismu (viz předchozí výpočet - rozběh),
ale nemusí vyhovět pro ustálený přenos energie při dosažení provozních
parametrů.
Příklad:
Spojka zajistí rozběh mechanismu na n1 při zadaném výkonu Pw.
Hnací stroj při sepnuté spojce dále zvyšuje výkon Pw a otáčky n na provozní
hodnoty.
Spojka musí zajistit přenos momentu i za provozních podmínek.
Výkon hnacího stroje, který je dodáván na spojku.
Zadejte provozní otáčky spojky, při kterých je odebírán příslušný výkon.
Kroutící moment dodaný hnacím strojem.
Jelikož poháněný mechanismus i hnací stroj mohou vykazovat nerovnoměrnost (oscilace kroutícího momentu) je vhodné použít koeficient (KA). Tento koeficient zohlední tuto nerovnoměrnost při výpočtu krouticího momentu, který musí spojka přenést.
Návrh koeficientu KA vychází z
praktických poznatků a jeho velikost se řídí nastavením podmínek na řádku [1.40,
1.41 a 1.42].
Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
Kroutící moment, který musí spojka přenést. Tato hodnota momentu je použita pro návrh rozměrových parametrů spojky [2,3,4,5]
V tomto odstavci jsou navrženy průměry hřídelí (ocel), které odpovídají požadovanému zatížení (Mk). Tyto hodnoty jsou pouze orientační, pro konečný návrh je vhodné použít přesnějšího výpočtu.
Při návrhu brzdy/spojky nejsou většinou známé přesné průběhy zatěžovacích momentů.
Proto je používán ve výpočtech koeficient KA, který na základě zkušeností a testů říká, jak navýšit výpočtový moment tak, aby navržená brzda / spojka zvládla příslušnou nerovnoměrnost zatížení.
Pro výpočet brzdy je navržen koeficient KA vycházející z typu bržděného
mechanismu.
Pro výpočet spojky je navržen koeficient KA, který zahrnuje jak bržděný
mechanismus, tak i hnací stroj a provozní dobu.
Vyberte ze seznamu odpovídající typ hnacího stroje.
Pracovní stroj
Občasné plné zatížení
Generátory, řetězové dopravníky, odstředivé, kompresory, pískovací dmychadla,
textilní stroje, dopravníky, ventilátory a odstředivá čerpadla.
Plné zatížení bez rázů
Výtahy, korečkové dopravníky, rotační pece, navíječky drátu, pojezdy jeřábů a
vozíků, navijáky, míchadla, nůžky, obráběcí stroje, pračky, tkalcovské stavy,
vytlačovací stroje na cihly
Plné zatížení, mírné rázy
Rypadla, vrtné soupravy, briketovací lisy, důlní ventilátory, válcovny pryže, kladkostroje, mlýny, pístová čerpadla,
bubnové mlýny, vibrátory,
kombinované mlýny.
Plné zatížení, silné rázy
Pístové kompresory, rámové pily, mokré lisy, papírové kalandry, válečkové
dopravníky, sušicí válce, válcovací stolice, cementárny, odstředivky
V seznamu je základní seznam používaných třecích materiálů. V závorce je
uveden koeficient tření a maximální dovolený tlak a použití.
Na základě vybraného materiálu jsou předvyplněné hodnoty [1.45-1.49].
Vyberte materiál, který absorbuje zmařenou energii při brždění nebo při
rozběhu mechanismu.
Výběr nemá žádný vliv na výpočet parametrů brzdy/spojky. Materiálové hodnoty
slouží pro výpočet oteplení (hmotnosti).
Příklady:
1. Brzdící kotouč diskové brzdy absorbuje energii brždění a je vyroben z ocele.
2. Skříň spojky absorbuje ztrátovou energii a je vyrobena z hliníku.
Patří mezi nejpoužívanější druhy brzd a spojek. Mají jednoduchou konstrukci, velkou plochu třecích povrchů, dobrý odvod tepla. Je možné používat konstrukce s jedním a více třecími povrchy, kdy zvláště konstrukce se 2 třecími povrchy je významě používána v automobilovém průmyslu (diskové brzdy, kotoučové spojky).

Pro výpočet a návrh brzdy/spojky jsou nutné dva základní parametry. Kroutící moment Mk a součinitel tření f.
Tyto parametry spolu s definicí rozměrů vedou k výpočtu maximálního tlaku na třecí plochu, výpočtu ovládací síly a při znalosti energetických a časových parametrů z [1] i k výpočtu oteplení.
V zeleném poli je moment Mk z odstavce [1]. Pokud potřebujete řešit pouze geometrii pro zadaný krouticí moment Mk, odškrtněte tlačítko vpravo a zadejte Mk, který má brzda / spojka přenést. Tím přerušíte spojení s odstavcem [1] a není tak počítáno oteplení a rychlost (výsledky jsou šedivé).
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Doporučená hodnota vychází ze zvoleného třecího materiálu [1.44].
V této části definujete rozměry třecího elementu. Rozměry můžete kontrolovat na obrázku vpravo.
Na výběr jsou tři nejpoužívanější tvary:
A. Mezikruhová výseč - použití většinou pro brzdy
B. Kružnice - použití pro méně namáhané brzdy (snadná výroba, jednoduchá
konstrukce)
C. Mezikruží - použití většinou pro spojky.
Podle výběru tvaru jsou nastavené požadavky na příslušné vstupní parametry.
Pro řešení se používají dva přístupy.
A. Rovnoměrné opotřebení (zaběhnutá brzda/spojka): Vychází z předpokladu, že třecí kotouče jsou tuhé a největší opotřebení nastává nejdříve na jejich vnějším obvodě, kde je práce třecích sil největší. Poté, co zde dojde k jistému opotřebení, změní se rozložení tlaku tak, že opotřebení třecích povrchů bude rovnoměrné.
B. Rovnoměrný tlak (nová brzda/spojka): Předpokládá, že užitím pružin rovnoměrně přitlačujících třecí kotouče do styku je dosaženo rovnoměrného tlaku po celé třecí ploše.
Všeobecně se používá přístup A.
Zadejte počet třecích ploch podle vaší konstrukce (viz. obrázek).

Pro tvar třecího segmentu [2.5] A a C zadejte: Vnější
poloměr třecího segmentu Ro (viz. obrázek).
Pro tvar B zadejte: Vzdálenost
středu kružnice "e" od osy (viz.
obrázek).
Vpravo je navržena optimální hodnota H (resp D pro kruhový
segment) pro dosažení maximálního třecího momentu ze vztahu Ri = Ro /
1.732.
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Pro tvar třecího segmentu [2.5] A zadejte úhel segmentu (viz. obrázek).
Na základě plošné charakteristiky třecího segmentu je spočítán ekvivalentní poloměr Re, který slouží k výpočtu sil.
Poloměr, na kterém by měla působit normálová síla Fn'.
Brzdové (spojkové) obložení bývá často připevněno pomocí nýtů. Tento
koeficient vyjadřuje snížení třecí plochy obložení o příslušné montážní otvory.
Pro lepené obložení cF = 1.0, pro nýtované pak cF ~ 0.90 - 0.95.
Plocha, kterou třecí segment doléhá na třecí plochu. Závislá na definici rozměrů třecího segmentu.
Plocha brzdy/spojky, se kterou je ve styku třecí segment (označena čárkovanou čarou, pokud je to na nákresu viditelné).
V této části jsou uvedené hodnoty pro jednu třecí plochu.
Celkový moment Mk rozdělený na jednotlivé třecí plochy.
Většina výrobců třecích materiálů uvádí i maximální hodnotu třecí rychlosti, kterou je schopen materiál zvládnout. Doporučená hodnota vychází z volby materiálu [1.43].
Maximální tlak na nejvíce zatíženém místě obložení. Výrobci obložení většinou uvádějí jeho maximální hodnotu (viz doporučená hodnota vpravo). V případě překročení doporučené maximální hodnoty zkuste změnit geometrii, popřípadě typ obložení.
Někteří výrobci uvádějí pro třecí segmenty i maximální doporučenou hodnotu tepelného toku q.
Třecí obložení má špatnou tepelnou vodivost lambda v porovnáním s tepelnou vodivostí materiálů které jsou s obložením ve styku. (lambda třecího obložení ~ 0.1, lambda pro ocel ~ 54). Proto se předpokládá, že veškeré teplo vzniklé třením je pohlceno kovovou částí brzdy/spojky.
Tento orientační výpočet používá pouze hmotnost kotouče (kužele, bubnu) m
(viz výpočet níže). Výpočet je správně, pokud je kotouč příjemce energie
(typicky kotoučová brzda).
Pro jiné konstrukční uspořádání (typicky spojka) je třecí energie absorbována
například skříní spojky a výsledek je samozřejmě neplatný.
Předpokládá se, že proces brždění / zapnutí spojky je krátký, tudíž není uvažováno s ochlazením v průběhu tohoto procesu. Z tohoto předpokladu vychází i výpočet oteplení povrchu třecí plochy, kde se uvažuje pouze s přestupem tepla do disku (bubnu, skříně...) na základě tepelné vodivosti materiálu.
Úlohy typu:
- jak změnit rozměry pro dosažení dovoleného pmax
- jak může být zatížená brzda / spojka pro dosažení dovoleného pmax
- jaká může být maximální síla Fn'
a další můžete snadno řešit pomocí funkce excelu "Hledání
řešení" (GoalSeek).
Pro nejčastější úlohy jsou předdefinované vstupy do této funkce a její
vyvolání.
Po výběru dotazu a zadání požadované hodnoty spustíte
vyvolání funkce tlačítkem "Najít".
K původní hodnotě měněného parametru se vrátíte stisknutím tlačítka "Zpět".
(funkčnost je časově omezena aby nedošlo k nechtěnému
přepsání hodnot).
Příklad:
Chcete spočítat úhel třecího segmentu pro diskovou brzdu,
který zajistí požadovaný maximální tlak "pmax".
Je jasné, že úhel třecího segmentu se může pohybovat pouze v nějakém rozmezí,
požadavek na pmax však není nijak omezen. Takže požadavek na velikou změnu pmax
může vést ke zcela nesmyslnému úhlu segmentu alfa.
Ze seznamu vyberte úlohu, kterou chcete řešit.
Zadejte požadovanou hodnotu, která má být dosažena změnou vstupního parametru a vyvolejte funkci "Hledání řešení" tlačítkem vpravo.
Rozměrové parametry jsou odhadnuté na základě předchozích údajů. Po odškrtnutí talčítka vpravo můžete zadat vlastní rozměry (viz. obrázek).
Hodnota hmotnosti je použita pro výpočet ΔT1.
Hodnota plochy je využitá pro výpočet ochlazení v odstavci [8].
Hodnota povrchu S' je použita jako přednastavená pro výpočet oteplení v odstavci [8] a není využita v tomto odstavci.
Plocha S' je počítána podle obrázku.
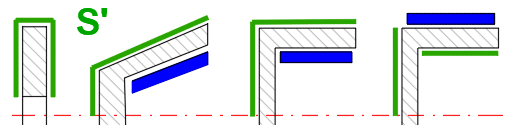
Jako třecí plocha je použita kuželová plocha. Výhodou této konstrukce je nižší ovládací síla Fn než u diskové brzdy/spojky. V závislosti na třecím materiálu se obvykle používá úhel kužele beta v rozmezí 10 -15°.

Pro výpočet a návrh brzdy/spojky jsou nutné dva základní parametry. Kroutící moment Mk a součinitel tření f.
Tyto parametry spolu s definicí rozměrů vedou k výpočtu maximálního tlaku na třecí plochu, výpočtu ovládací síly a při znalosti energetických a časových parametrů z [1] i k výpočtu oteplení.
V zeleném poli je moment Mk z odstavce [1]. Pokud potřebujete řešit pouze geometrii pro zadaný krouticí moment Mk, odškrtněte tlačítko vpravo a zadejte Mk, který má brzda / spojka přenést. Tím přerušíte spojení s odstavcem [1] a není tak počítáno oteplení a rychlost (výsledky jsou šedivé).
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Doporučená hodnota vychází ze zvoleného materiálu třecí plochy [1.44].
V této části definujete rozměry třecího elementu. Rozměry můžete kontrolovat na obrázku vpravo.
Na výběr jsou dvě možnosti:
A. Výseč kuželové plochy - tato konstrukce se používá minimálně
B. Kompletní kuželová plocha - použití pro brzdy i spojky
Podle výběru tvaru jsou nastavené požadavky na příslušné vstupní parametry.
Pro řešení se používají dva přístupy.
A. Rovnoměrné opotřebení (zaběhnutá brzda/spojka): Vychází z předpokladu, že třecí kotouče jsou tuhé a největší opotřebení nastává nejdříve na jejich vnějším obvodě, kde je práce třecích sil největší. Poté, co zde dojde k jistému opotřebení, změní se rozložení tlaku tak, že opotřebení třecích povrchů bude rovnoměrné.
B. Rovnoměrný tlak (nová brzda/spojka): Předpokládá, že užitím pružin rovnoměrně přitlačujících třecí kotouče do styku je dosaženo rovnoměrného tlaku po celé třecí ploše.
Všeobecně se používá přístup A.
Zadejte počet třecích ploch podle vaší konstrukce (viz. obrázek).
Zadejte rozměry třecího segmentu podle obrázku.
Můžete zadat vrcholový úhel, nebo šířku kužele. Volbu nastavíte přepínačem vpravo.
Na základě plošné charakteristiky třecího segmentu je spočítán ekvivalentní průměr De, který slouží k výpočtu sil.
Plocha, kterou třecí segment doléhá na třecí plochu. Závislá na definici rozměrů třecího elementu.
Plocha brzdy/spojky, se kterou je ve styku třecí segment (označena čárkovanou čarou, pokud je to na nákresu viditelné).
V této části jsou uvedené hodnoty pro jednu třecí plochu.
Celkový moment Mk rozpočtený na jednotlivé třecí plochy.
Většina výrobců třecích materiálů uvádí i maximální hodnotu třecí rychlosti, kterou je schopen materiál zvládnout. Doporučená hodnota vychází z volby materiálu [1.43]
Maximální tlak na nejvíce zatíženém místě obložení. Výrobci obložení většinou uvádějí jeho maximální hodnotu (viz doporučená hodnota vpravo). V případě překročení doporučené maximální hodnoty zkuste změnit geometrii, popřípadě typ obložení.
Někteří výrobci uvádějí pro třecí segmenty i maximální doporučenou hodnotu tepelného toku q.
Třecí obložení má špatnou tepelnou vodivost lambda v porovnáním s tepelnou vodivostí materiálů které jsou s obložením ve styku. (lambda třecího obložení ~ 0.1, lambda pro ocel ~ 54). Proto se předpokládá, že veškeré teplo vzniklé třením je pohlceno kovovou částí brzdy/spojky.
Tento orientační výpočet používá pouze hmotnost kotouče (kužele, bubnu) m
(viz výpočet níže). Výpočet je správně, pokud je kotouč příjemce energie
(typicky kotoučová brzda).
Pro jiné konstrukční uspořádání (typicky spojka) je třecí energie absorbována
například skříní spojky a výsledek je samozřejmě neplatný.
Předpokládá se, že proces brždění / zapnutí spojky je krátký, tudíž není uvažováno s ochlazením v průběhu tohoto procesu. Z tohoto předpokladu vychází i výpočet oteplení povrchu třecí plochy, kde se uvažuje pouze s přestupem tepla do disku (bubnu, skříně...) na základě tepelné vodivosti materiálu.
Úlohy typu:
- jak změnit rozměry pro dosažení dovoleného pmax
- jak může být zatížená brzda / spojka pro dosažení dovoleného pmax
- jaká může být maximální síla Fn'
a další můžete snadno řešit pomocí funkce excelu "Hledání
řešení" (GoalSeek).
Pro nejčastější úlohy jsou předdefinované vstupy do této funkce a její
vyvolání.
Po výběru dotazu a zadání požadované hodnoty spustíte vyvolání funkce tlačítkem
"Najít".
K původní hodnotě měněného parametru se vrátíte stisknutím tlačítka "Zpět".
(funkčnost je časově omezena aby nedošlo k nechtěnému
přepsání hodnot).
Příklad:
Chcete spočítat úhel třecího segmentu pro diskovou brzdu,
který zajistí požadovaný maximální tlak "pmax".
Je jasné, že úhel třecího segmentu se může pohybovat pouze v nějakém rozmezí,
požadavek na pmax však není nijak omezen. Takže požadavek na velikou změnu pmax
může vést ke zcela nesmyslnému úhlu segmentu alfa.
Ze seznamu vyberte úlohu, kterou chcete řešit.
Zadejte požadovanou hodnotu, která má být dosažena změnou vstupního parametru a vyvolejte funkci "Hledání řešení" tlačítkem vpravo.
Rozměrové parametry jsou odhadnuté na
základě předchozích údajů. Po odškrtnutí talčítka vpravo můžete zadat vlastní
rozměry (viz. obrázek).
Hodnota hmotnosti je použita pro výpočet ΔT1
Hodnota plochy je využitá pro výpočet ochlazení v odstavci [8.0].
Upozornění:
Přednastavené hodnoty jsou zaokrouhleny tak, aby hodnoty dávaly smysl jak pro
palcové, tak pro metrické jednotky. Při přepnutí jednotek tak mohou být některé
výsledky (hmotnost, plocha, oteplení) vlivem zaoukrouhlení mírně odlišné.
Hodnota povrchu S' je použita jako přednastavená pro výpočet oteplení v odstavci [8] a není využita v tomto odstavci.
Plocha S' je počítána podle obrázku.

Bubnové brzdy s vnitřními čelistmi jsou používány převážně v automobilovém průmyslu. Brzdy s vnějšími čelistmi a brzdy se symetricky uloženými čelistmi jsou pak používány převážně v průmyslových aplikacích.
Pro výpočet a návrh brzdy/spojky jsou nutné dva základní parametry. Kroutící moment Mk a součinitel tření f.
Tyto parametry spolu s definicí rozměrů vedou k výpočtu maximálního tlaku na třecí plochu, výpočtu ovládací síly a při znalosti energetických a časových parametrů z [1] i k výpočtu oteplení.
V zeleném poli je moment Mk z odstavce [1]. Pokud potřebujete řešit pouze geometrii pro zadaný krouticí moment Mk, odškrtněte tlačítko vpravo a zadejte Mk, který má brzda / spojka přenést. Tím přerušíte spojení s odstavcem [1] a není tak počítáno oteplení a rychlost (výsledky jsou šedivé).
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Doporučená hodnota vychází ze zvoleného materiálu třecí plochy [1.44].
V této části definujete rozměry třecího elementu. Rozměry můžete kontrolovat na obrázku vpravo.
Vyberte ze seznamu odpovídající typ.
Zadejte počet úběžných čelistí (L) a náběžných čelistí (R).
Pokud je použita současně náběžná (R) i úběžná čelist (L), musí být jejich počty
shodné. NL/NR = 1/1, 2/2, .....
Předpokládá se i jejich stejná velikost a stejná ovládací síla F.
Pokud je použita pouze náběžná nebo úběžná čelist je možné volit libovolné
množství čelistí stejných rozměrů.
Zadejte polohu čepu vzhledem ke středu bubnu. Napravo můžete přepnout způsob zadání. Polohu můžete kontrolovat na obrázku vpravo.
Zadejte působiště síly vzhledem ke středu bubnu. Napravo můžete přepnout způsob zadání. Polohu můžete kontrolovat na obrázku vpravo.
Zadejte úhel pro začátek a konec brzdícího segmentu. Polohu můžete kontrolovat na obrázku vpravo.
Vzdálenost osy čepu čelisti od osy bubnu (obr. C), která zajišťuje nulový třecí moment k ose čepu čelisti. To zajišťuje souměrné opotřebení obložení.
Brzdové (spojkové) obložení bývá často připevněno pomocí nýtů. Tento
koeficient vyjadřuje snížení třecí plochy obložení o příslušné montážní otvory.
Pro lepené obložení cF = 1.0, pro nýtované pak cF ~ 0.90 - 0.95.
Plocha, kterou třecí segment doléhá na třecí plochu. Závislá na definici rozměrů třecího elementu.
Plocha brzdy/spojky, se kterou je ve styku třecí segment (označena čárkovanou čarou, pokud je to na nákresu viditelné).
Výsledky jsou rozdělené pro náběžnou (R) a úběžnou (L) brzdící čelist. Při současném použití R+L je vhodné konstrukci dimenzovat na více zatíženou (R) čelist.
Většina výrobců třecích materiálů uvádí i maximální hodnotu třecí rychlosti, kterou je schopen materiál zvládnout. Doporučená hodnota vychází z volby materiálu [1.43]
Maximální tlak na nejvíce zatíženém místě obložení. Výrobci obložení většinou uvádějí jeho maximální hodnotu (viz doporučená hodnota vpravo). V případě překročení doporučené maximální hodnoty zkuste změnit geometrii, popřípadě typ obložení.
Někteří výrobci uvádějí pro třecí segmenty i maximální doporučenou hodnotu tepelného toku q.
Třecí obložení má špatnou tepelnou vodivost lambda v porovnáním s tepelnou vodivostí materiálů které jsou s obložením ve styku. (lambda třecího obložení ~ 0.1, lambda pro ocel ~ 54). Proto se předpokládá, že veškeré teplo vzniklé třením je pohlceno kovovou částí brzdy/spojky.
Tento orientační výpočet používá pouze hmotnost kotouče (kužele, bubnu) m
(viz výpočet níže). Výpočet je správně, pokud je kotouč příjemce energie
(typicky kotoučová brzda).
Pro jiné konstrukční uspořádání (typicky spojka) je třecí energie absorbována
například skříní spojky a výsledek je samozřejmě neplatný.
Předpokládá se, že proces brždění / zapnutí spojky je krátký, tudíž není uvažováno s ochlazením v průběhu tohoto procesu. Z tohoto předpokladu vychází i výpočet oteplení povrchu třecí plochy, kde se uvažuje pouze s přestupem tepla do disku (bubnu, skříně...) na základě tepelné vodivosti materiálu.
Úlohy typu:
- jak změnit rozměry pro dosažení dovoleného pmax
- jak může být zatížená brzda / spojka pro dosažení dovoleného pmax
- jaká může být maximální síla Fn'
a další můžete snadno řešit pomocí funkce excelu "Hledání
řešení" (GoalSeek).
Pro nejčastější úlohy jsou předdefinované vstupy do této funkce a její
vyvolání.
Po výběru dotazu a zadání požadované hodnoty spustíte vyvolání funkce tlačítkem
"Najít".
K původní hodnotě měněného parametru se vrátíte stisknutím tlačítka "Zpět".
(funkčnost je časově omezena aby nedošlo k nechtěnému
přepsání hodnot).
Příklad:
Chcete spočítat úhel třecího segmentu pro diskovou brzdu,
který zajistí požadovaný maximální tlak "pmax".
Je jasné, že úhel třecího segmentu se může pohybovat pouze v nějakém rozmezí,
požadavek na pmax však není nijak omezen. Takže požadavek na velikou změnu pmax
může vést ke zcela nesmyslnému úhlu segmentu alfa.
Ze seznamu vyberte úlohu, kterou chcete řešit.
Zadejte požadovanou hodnotu, která má být dosažena změnou vstupního parametru a vyvolejte funkci "Hledání řešení" tlačítkem vpravo.
Rozměrové parametry jsou odhadnuté na
základě předchozích údajů. Po odškrtnutí talčítka vpravo můžete zadat vlastní
rozměry (viz. obrázek).
Hodnota hmotnosti je použita pro výpočet ΔT1
Hodnota plochy je využitá pro výpočet ochlazení v odstavci [8].
Upozornění:
Přednastavené hodnoty jsou zaokrouhleny tak, aby hodnoty dávaly smysl jak pro
palcové, tak pro metrické jednotky. Při přepnutí jednotek tak mohou být některé
výsledky (hmotnost, plocha, oteplení) vlivem zaoukrouhlení mírně odlišné.
Hodnota povrchu S' je použita jako přednastavená pro výpočet oteplení v odstavci [8] a není využita v tomto odstavci.
Plocha S' je počítána podle obrázku.

Třecí plocha je tvořena pásem, který je ovinut kolem brzdícího bubnu. Využití v průmyslových aplikacích, jednoduchá konstrukce. Vhodné pro manuální ovládání, kdy je možné poměrně malou ovládací silou dosáhnout vysokého brzdného účinku.

Pro výpočet a návrh brzdy/spojky jsou nutné dva základní parametry. Kroutící moment Mk a součinitel tření f.
Tyto parametry spolu s definicí rozměrů vedou k výpočtu maximálního tlaku na třecí plochu, výpočtu ovládací síly a při znalosti energetických a časových parametrů z [1] i k výpočtu oteplení.
V zeleném poli je moment Mk z odstavce [1]. Pokud potřebujete řešit pouze geometrii pro zadaný krouticí moment Mk, odškrtněte tlačítko vpravo a zadejte Mk, který má brzda / spojka přenést. Tím přerušíte spojení s odstavcem [1] a není tak počítáno oteplení a rychlost (výsledky jsou šedivé).
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Doporučená hodnota vychází ze zvoleného materiálu třecí plochy [1.44].
V této části definujete rozměry třecího elementu. Rozměry můžete kontrolovat na obrázku vpravo.
Plocha, kterou třecí segment doléhá na třecí plochu. Závislá na definici rozměrů třecího elementu.
Plocha brzdy/spojky, se kterou je ve styku třecí segment (označena čárkovanou čarou, pokud je to na nákresu viditelné).
Výsledky určují tahovou sílu pro jeden pás F1 a F2, která je nutná pro zajištění požadovaného třecího momentu Mk.
Většina výrobců třecích materiálů uvádí i maximální hodnotu třecí rychlosti, kterou je schopen materiál zvládnout. Doporučená hodnota vychází z volby materiálu [1.43]
Maximální tlak na nejvíce zatíženém místě obložení. Výrobci obložení většinou uvádějí jeho maximální hodnotu (viz doporučená hodnota vpravo). V případě překročení doporučené maximální hodnoty zkuste změnit geometrii, popřípadě typ obložení.
Někteří výrobci uvádějí pro třecí segmenty i maximální doporučenou hodnotu tepelného toku q.
Třecí obložení má špatnou tepelnou vodivost lambda v porovnáním s tepelnou vodivostí materiálů které jsou s obložením ve styku. (lambda třecího obložení ~ 0.1, lambda pro ocel ~ 54). Proto se předpokládá, že veškeré teplo vzniklé třením je pohlceno kovovou částí brzdy/spojky.
Tento orientační výpočet používá pouze hmotnost kotouče (kužele, bubnu) m
(viz výpočet níže). Výpočet je správně, pokud je kotouč příjemce energie
(typicky kotoučová brzda).
Pro jiné konstrukční uspořádání (typicky spojka) je třecí energie absorbována
například skříní spojky a výsledek je samozřejmě neplatný.
Předpokládá se, že proces brždění / zapnutí spojky je krátký, tudíž není uvažováno s ochlazením v průběhu tohoto procesu. Z tohoto předpokladu vychází i výpočet oteplení povrchu třecí plochy, kde se uvažuje pouze s přestupem tepla do disku (bubnu, skříně...) na základě tepelné vodivosti materiálu.
Úlohy typu:
- jak změnit rozměry pro dosažení dovoleného pmax
- jak může být zatížená brzda / spojka pro dosažení dovoleného pmax
- jaká může být maximální síla Fn'
a další můžete snadno řešit pomocí funkce excelu "Hledání
řešení" (GoalSeek).
Pro nejčastější úlohy jsou předdefinované vstupy do této funkce a její
vyvolání.
Po výběru dotazu a zadání požadované hodnoty spustíte vyvolání funkce tlačítkem
"Najít".
K původní hodnotě měněného parametru se vrátíte stisknutím tlačítka "Zpět".
(funkčnost je časově omezena aby nedošlo k nechtěnému
přepsání hodnot).
Příklad:
Chcete spočítat úhel třecího segmentu pro diskovou brzdu,
který zajistí požadovaný maximální tlak "pmax".
Je jasné, že úhel třecího segmentu se může pohybovat pouze v nějakém rozmezí,
požadavek na pmax však není nijak omezen. Takže požadavek na velikou změnu pmax
může vést ke zcela nesmyslnému úhlu segmentu alfa.
Ze seznamu vyberte úlohu, kterou chcete řešit.
Zadejte požadovanou hodnotu, která má být dosažena změnou vstupního parametru a vyvolejte funkci "Hledání řešení" tlačítkem vpravo.
Nejčastěji používané konstrukční uspořádání je na obrázku.
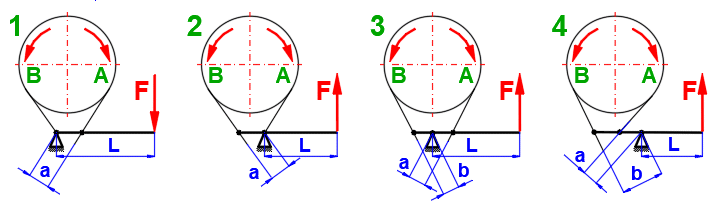
Vyberte typ konstrukce, smysl otáčení bubnu a zadejte požadované rozměry. Výsledkem je ovládací síla F.
Použití: Pro jeden směr otáčení, ruční ovládání.
Použití: Pro jeden směr otáčení, ruční ovládání
Výhoda: Poměrně malou silou F lze brzdit velký kroutící mornent. Pro a = b .
e^(f*alfa) je F = 0. Brždění by ale bylo trhavé, nevyhovující.
Proto se většinou navrhuje a > 2.5 * b.
Použití: Pro oba směry otáčení, pro a=b je F shodná pro oba směry.
Rozměrové parametry jsou odhadnuté na základě předchozích údajů. Po odškrtnutí talčítka vpravo můžete zadat vlastní rozměry (viz. obrázek).
Hodnota hmotnosti je použita pro výpočet ΔT1
Hodnota plochy je využitá pro výpočet ochlazení v odstavci [8].
Hodnota povrchu S' je použita jako přednastavená pro výpočet oteplení v odstavci [8] a není využita v tomto odstavci.
Plocha S' je počítána podle obrázku.

V této kapitole jsou uvedené některé doplňkové výpočty pro určení zatížení brzdy/spojky a výpočet oteplení.
Primární úlohou brzdy/spojky je zastavit / rozpohybovat definovanou hmotu (odebrat / přidat kinetickou energii Ek). V naprosté většině případů se jedná o dvě základní úlohy.
1. Zabrzdit / roztočit rotační součásti
2. Zabrzdit / rozpohybovat přímo se pohybující součásti
3. Kombinace předchozích bodů
Výpočty v tomto odstavci umožňují definovat 5 výpočtů pro každou úlohu. Zaškrtnutím / odškrtnutím tlačítka v záhlaví přidáte / odeberete součet Ek do závěrečného výsledku na řádku [6.6].
Častá úloha výpočtu Ek je řešení rotujícího válce. Zadejte rozměry a otáčky dle obrázku.
Občas je udávaná hmotnost rotující součásti a poloměr setrvačnosti. Pro výpočet Ek můžete použít tuto tabulku.
Pro rotující součásti je často udáván moment setrvačnosti. V tomto případě použijte pro výpočet Ek tuto tabulku.
Pro výpočet Ek zadejte hmotnost a rychlost pohybující se součástí. Pokud potřebujete přepočítat přímočarý pohyb na otáčky, zadejte průměr kola ve sloupci označeném D.
Podle nastaveného typu výpočtu [1.2] bude po stisknutí tlačítka přenesena hodnota Ek do [1.4] (brzdy) nebo [1.15] (spojky).
Ve většině případů je kromě kinetické energie (viz odstavec
6) zatížen systém brzdy/spojky i dodatečným kroutícím momentem, který vzniká
například z:
- třecí síly ložisek
- třecí síly mechanismů
- pohyb po nakloněné rovině
- aerodynamický odpor
- atd.
Uvedené výpočty zahrnují nejčastěji řešené úlohy.
Hodnotu zatěžovacího momentu ML přenesete do odstavce [1] stisknutím tlačítka ">> ML".
Výpočet zatěžujícího / odlehčovacího momentu vozidla, který vzniká valivým odporem a pohybem po nakloněné rovině. Ve výpočtu vyplňte požadované parametry.
Asfalt / Pneumatika (nákladní automobil) … (0.006-0.010)
Asfalt / Pneumatika (osobní automobil) … (0.010-0.015)
Asfalt / Pneumatika (motocykl) … (0.010-0.015)
Asfalt / Pneumatika (bicykl) … (0.002-0.005)
Dlažba / Pneumatika … (0.015-0.030)
Písek, štěrk / Pneumatika … (0.040-0.080)
Kolejnice / Ocelové kolo … (0.001-0.002)
Podle nastaveného typu výpočtu [1.2] bude po stisknutí tlačítka přenesena hodnota ML do [1.5] (brzdy) nebo [1.16] (spojky).
Dodatečný zatěžující / odlehčovací moment je závislý na hmotnosti zdvihaného zařízení. Ve výpočtu vyplňte požadované parametry.
Podle nastaveného typu výpočtu [1.2] bude po stisknutí tlačítka přenesena hodnota ML do [1.5] (brzdy) nebo [1.16] (spojky).
Dodatečný zatěžující / odlehčovací moment je závislý na hmotnosti, koeficientu tření f a úhlu nakloněné roviny. Ve výpočtu vyplňte požadované parametry.
=======Dynamické (v>0), Nemazané ========
Kalená ocel - Kalená ocel (0.1)
Kalená ocel - Litina (0.13-0.27)
Kalená ocel - Bronz (fosforový) (0.15)
Kalená ocel - Dřevo (dub) (0.4-0.5)
Litina - Litina (0.15-0.2)
Litina - Bronz (fosforový) (0.15-0.2)
Litina - Dřevo (dub) (0.3-0.5)
Bronz (fosforový) - Bronz (fosforový) (0.2)
Kůže - Litina (0.56)
Guma - Litina (0.8)
Guma - Beton (0.7)
Guma - Asfaltová cesta (0.7)
Azbest (tkanina) - Ocel (0.3-0.35)
Nylon - Ocel (0.3)
Polystyrene - Ocel (0.5)
=======Dynamické (v>0), Mazané ========
Kalená ocel - Kalená ocel (0.05-0.1)
Kalená ocel - Litina (0.05-0.15)
Kalená ocel - Bronz (fosforový) (0.09-0.15)
Kalená ocel - Dřevo (dub) (0.08)
Litina - Litina (0.07-0.1)
Litina - Bronz (fosforový) (0.07-0.1)
Litina - Dřevo (dub) (0.2)
Bronz (fosforový) - Bronz (fosforový) (0.07-0.1)
Kůže - Litina (0.15-0.35)
Guma - Litina (0.5)
Guma - Beton (0.3-0.5)
Guma - Asfaltová cesta (0.2-0.3)
Azbest (tkanina) - Ocel (0.08-0.12)
Jak při brždění, tak při rozběhu dochází při styku třecích ploch k přeměně kinetické energie v teplo. V předchozích odstavcích jsou uvedené vztahy pro výpočet maximálního momentu a maximálního tlaku na třecí plochy pro zadané rozměry brzdy/spojky. I v případě, že není přenášen maximální moment a není překročen maximální dovolený tlak, může dojít ke zničení brzdy/spojky nadměrným oteplením.
Rozjezd automobilu do kopce. Ačkoliv je spojka konstruována i pro tento případ (přenos většího zatížení), může řidič (chybně) vyrovnat zatěžující moment tím, že spojka zůstává dlouhodobě v záběru. V tomto případě je do systému spojky neustále přiváděno teplo vzniklé třením a po překročení mezních hodnot může dojít k poškození spojky.
V tomto odstavci můžete:
- vyřešit oteplení brzdy/spojky při jednorázovém zabrždění / sepnutí spojky.
- simulovat opakované brždění / sepnutí spojky.
Po výběru ze seznamu [8.2] jsou vyplněné hodnoty
velikosti povrchu a hmotnosti z příslušného odstavce typu brzdy/spojky
[2,3,4,5].
Pro rozumný výpočet (odhad) teplotní charakteristiky je však nutné stanovit
velikost povrchu a hmotnosti co nejpřesněji vzhledem k použité konstrukci
brzdy/spojky.
Jako příklad uvedeme rozdíl mezi diskovou brzdou a diskovou spojkou.
Disková brzda:
Tvořená kovovým diskem, který je bržděn třecími destičkami. Veškeré teplo je
akumulováno v kovovém disku, který teplo odevzdává okolnímu vzduchu. Pro výpočet
tepla je možné použít hodnoty plochy a hmotnosti z odstavce [2].
Disková spojka:
Tvořená tenkým diskem s třecím obložením, který zabírá do kovové konstrukce
spojky. Veškeré teplo je tak akumulováno v konstrukci
spojky. Parametry plochy a hmotnosti jsou zcela odlišné od navržených v odstavci
[2] a je nutné zadat vlastní hodnoty.
Pro zadání vlastních hodnot odškrtněte tlačítko vpravo.
Hodnota je přednastavená na základě výběru materiálu [1.54].
Podle volby typu výpočtu v odstavci [1] jsou přenesené hodnoty energie. Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnoty.
Pro výpočet nárůstu teploty jsou použity hodnoty z [8.4, 8.5, 8.7].
Při jednom cyklu brždění / sepnutí spojky dojde k přibližnému nárůstu teploty o teplotu ΔT. Hodnota je přibližná, podrobnější popis naleznete v teoretické části nápovědy.
Při tomto výpočtu je simulováno 100 kroků opakovaného brždění / sepnutí spojky se zadaným časovým intervalem [8.13]. Pro každý krok je spočítán odpovídající součinitel přestupu tepla alfa, který je pak použit pro výpočet teplot následujícího kroku. Většinou je tento postup vyhovující a rychle konverguje k ustálené teplotě.
Průběh teploty je zobrazen v grafu B [8.25]. X-ová souřadnice je v minutách.
V případě velké tepelné setrvačnosti brzdy/spojky (velká hmotnost) může být 100 kroků iterace nedostatečné. Tento případ rozeznáte z grafu B, kdy křivka nekonverguje k ustálené teplotě Max/Min. V tomto případě použijte kumulativní výpočet [8.17].
Zadejte teplotu okolního vzduchu.
Rychlost proudění vzduchu kolem tělesa brzdy/spojky výrazně ovlivňuje
přestup tepla.
Zkuste proto tuto hodnotu odhadnout co nejpřesněji.
Hodnota je přednastavena na základě výpočtu z [1]. Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
Zadejte časový interval mezi opakovaným použitím brzdy/spojky.
Na Grafu B můžete většinou vidět postupnou konvergenci k ustálené hodnotě
Min,Max.
Min, Max hodnota je brána z posledního (100) kroku postupné iterace.
Při tomto výpočtu odhadnete celkový nárůst teploty. Z tohoto nárůstu je spočítán odpovídající součinitel přestupu tepla alfa, který je použit pro celkový výpočet oteplení.
Po odškrtnutí tlačítka vpravo můžete zadat svůj odhad nárůstu teploty. Ve většině případů je to však zbytečné a doporučená hodnota v zeleném poli je dostatečně přesná.
Maximální teplota brzdy/spojky pro neomezený počet cyklů brždění / sepnutí spojky.
Můžete zadat přímo číslo cyklu, nebo nastavit posuvníkem vpravo. Průběh teploty vybraného cyklu je zobrazen v grafu.
Návrh diskové brzdy přední nápravy osobního automobilu + teplotní analýza.
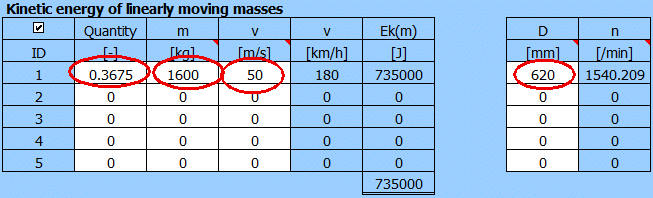
Hmotnost automobilu: m = 1600 kg
Počáteční rychlost v1 = 180 km/h (50 m/s)
Koncová rychlost v2 = 0
Klesání vozovky
a
= -5° (8.75%)
Průměrná hodnota decelerace a
= -7 m/s^2
Průměr kola = 620 mm
Rozložení brzdícího účinku 70% přední 30% zadní náprava.
Opakované brždění 180->0 km-h s periodou 180s
Doba brždění:
t = v1 / a; t = 50 / 7 => t = 7.14 s
v1-Počáteční rychlost; a-Akcelerace / Decelerace; t-čas
Výpočtové předpoklady:
- není zahrnutý aerodynamický odpor
- nedochází k prokluzu kol
- lineární průběh
V odstavci [1] zvolte jednotky výpočtu [1.1] a výpočet brzdy [1.2]
Nejprve je nutné vyřešit ztížení brzdy.

Pro výpočet kinetické energie Ek použijte odstavec [6], stisknutí tlačítka "Ek >>".
Výpočet Ek pro jeden brzdící kotouč. Přední náprava 70%
zatížení, jedno kolo => 0.7 / 2 = 0.35.
Pro osobní automobily použijeme koeficient 1.05 (který zahrnuje rotující bržděné
hmoty, jako kola, hřídele, ozubená kola atd..).
První sloupec 0.35 x 1.05 = 0.3675.
Výsledný Ek=735000 [J] a pro průměr kola 620mm => otáčky 1540 [/min].
Pro výpočet dodatečného zatěžovacího momentu ML použijte odstavec [7], stisknutí tlačítka "ML >>".
Celkovou hmotnost vozidla rozložíme na jedno kolo přední nápravy podle
předchozí úvahy m=1600*0.35=560 [kg].
Po vyplnění zbývajících údajů získáme dodatečný zatěžovací moment 123 [Nm] a
přeneseme do odstavce [1].
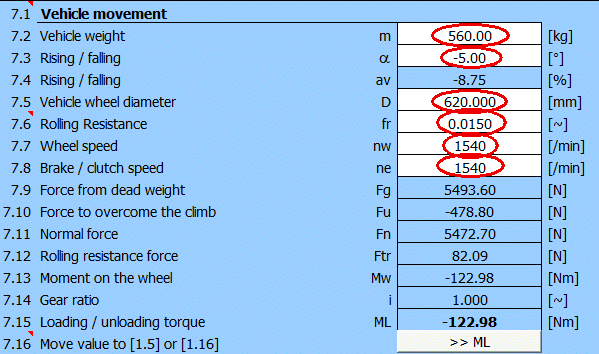
Po vyplnění všech údajů a volbě KA=1.1 máme definované parametry pro výpočet rozměrů diskové brzdy (t, Mk, Eh).

Předběžně je vhodné definovat (vybrat) v odstavci [1] materiál brzdového obložení a materiál brzdového kotouče.
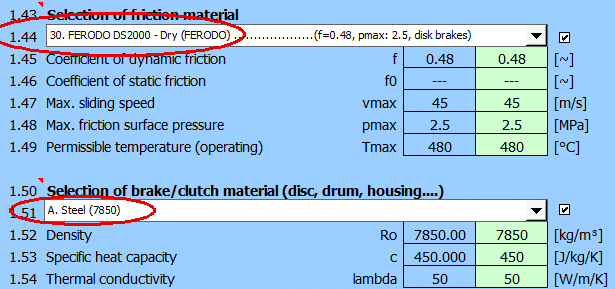
Po přepnutí do odstavce pro výpočet diskové brzdy/spojky [2] nastavte počáteční parametry [2.1-2.7].

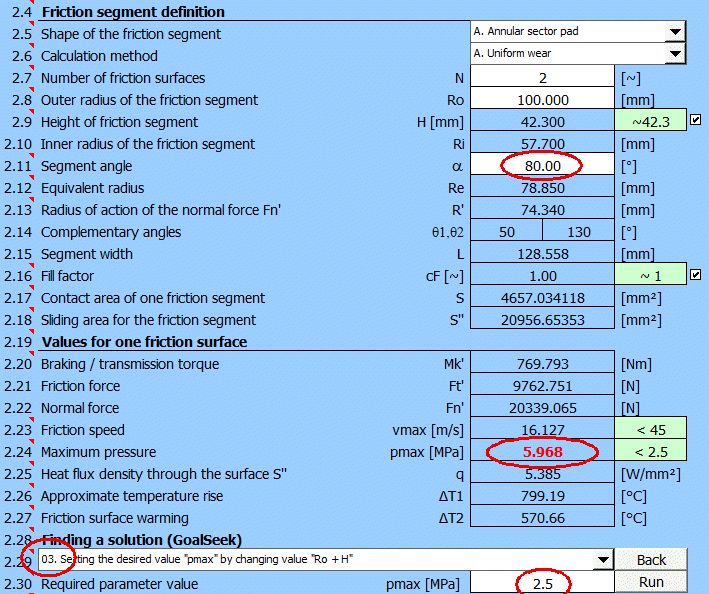
Zvolte úhel třecího segmentu alfa [2.11] = 80°.
Je pravděpodobné, že hodnota maximálního tlaku pmax [2.24] bude buď překračovat dovolenou hodnotu z [1.48], nebo bude příliš nízká a nevyužije se tak potenciál brzdy.
Vyberte proto na [2.29] "Hledání řešení" (03.) pro pmax, zadejte požadovanou
hodnotu 2.5 [MPa] (viz vybraný materiál) a stiskněte tlačítko "Najít".
Bude hledán minimální vnější poloměr třecího segmentu pro dosažení zadaného
tlaku pmax=2.5 [MPa].
Po vyhledání řešení získáte výsledky:

Po vhodné volbě hodnot Ro a H pak bude návrh diskové brzdy vypadat následovně.
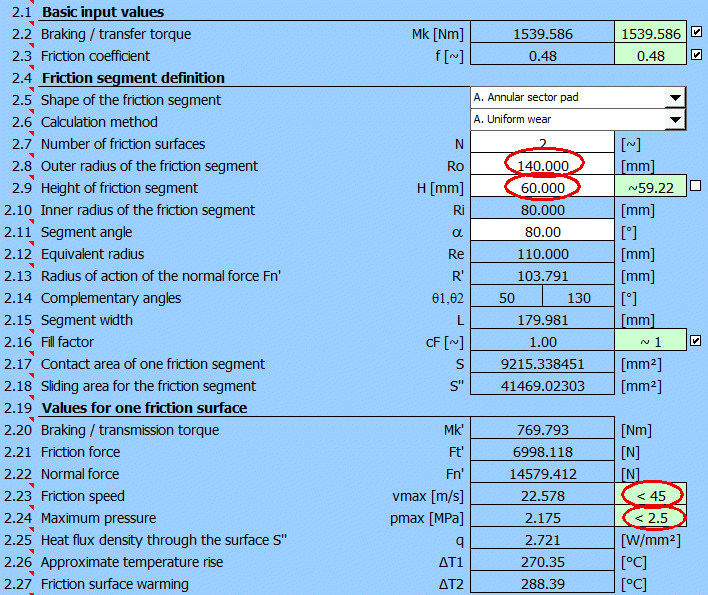
Návrh splňuje základní požadavky, kladené na třecí rychlost a tlak na obložení při splnění požadavku na bržděný moment Mk.
Nedílnou součástí návrhu brzdy by měla být i teplotní analýza. V odstavci
[2] je zahrnut i návrh rozměrů brzdícího kotouče. Ty jsou pro analýzu nutné.
Pro tento příklad použijte přednastavené (odhadnuté) hodnoty.

Po přechodu do odstavce [8] nastavte parametry následovně.
- [8.3] Jsou použité parametry disku z vybraného výpočtu diskové brzdy [2]
- [8.7] Je použita energie brždění z odstavce [1]
Zadejte teplotu vzduchu, rychlost proudění vzduchu (odhadem poloviční rychlost
vozidla na počátku brždění) a požadovaný časový interval
mezi bržděním.
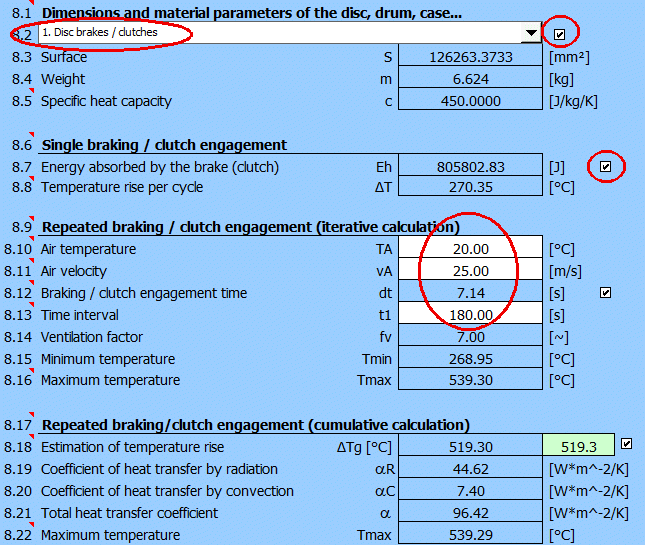
Výsledkem je graf nárůstu a poklesu teploty mezi jednotlivými brzdícími cykly.
Návrh diskové spojky osobního automobilu.
Hmotnost automobilu: m = 1600 kg
Výkonový diagram motoru
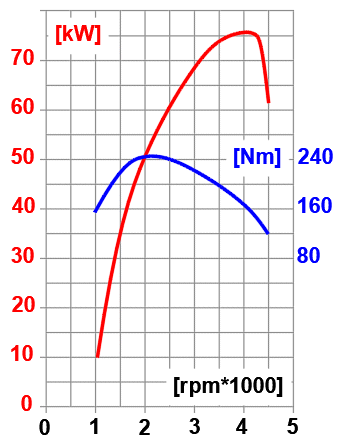
Z výkonového diagramu odhadnuto:
- zvolené otáčky pro rozjezd = 2500 [/min]
- výkon motoru pro 2500 [/min] = 60kW
Počáteční rychlost v1 = 0
Koncová rychlost v2 = 25 km/h (7 m/s) pro otáčky spojky 2500 rpm na I.
rychlostní stupeň
Stoupání vozovky
a
= +5° (8.75%)
Průměr kola = 620 mm
Výpočtové předpoklady a zjednodušení:
- není zahrnutý aerodynamický odpor
- nedochází k prokluzu kol
- výkon a otáčky pohonu jsou uvažovány jako konstantní v průběhu sepnutí spojky
V odstavci [1] zvolte jednotky výpočtu [1.1] a výpočet spojky [1.2].
Nejprve je nutné vyřešit zatížení spojky.
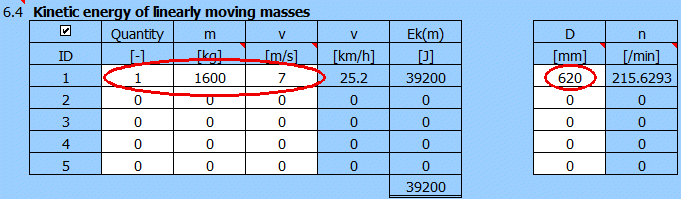
Pro výpočet koncové kinetické energie Ek použijte odstavec [6], stisknutí tlačítka "Ek >>".
Výpočet koncové Ek. Výsledný Ek=39200 [J] a pro průměr kola 620mm => otáčky 215 [/min].
Pro výpočet dodatečného zatěžovacího momentu ML použijte odstavec [7], stisknutí tlačítka "ML >>".
Vyplňte hmotnost, stoupání vozovky, průměr kola, otáčky kola, otáčky spojky.
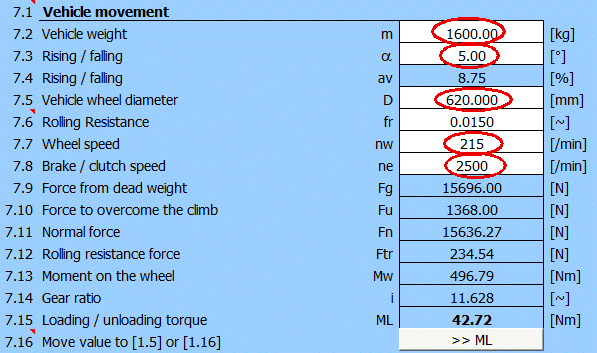
Po vyplnění údajů získáte dodatečný zatěžovací moment 42.7 [Nm]. Přeneste hodnotu do odstavce [1].
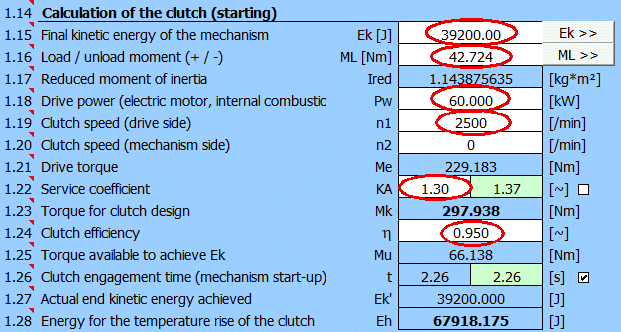
Po doplnění všech údajů a volbě KA=1.3 máme definované parametry pro výpočet rozměrů diskové spojky (t, Mk, Eh).
Předběžně je vhodné definovat (vybrat) v odstavci [1] materiál spojkového obložení a materiál spojkové skříně.
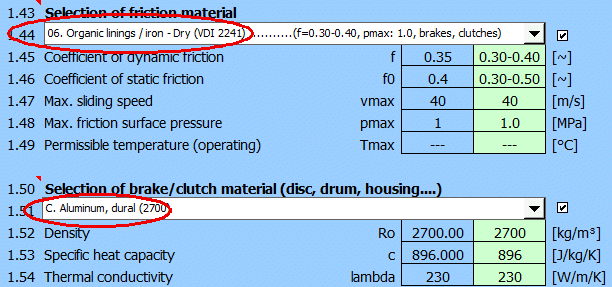
Po přepnutí do odstavce pro výpočet diskové brzdy/spojky [2] nastavte počáteční parametry [2.1-2.7].

Je pravděpodobné, že hodnota maximálního tlaku pmax [2.24] bude buď překračovat dovolenou hodnotu z [1.48] nebo bude příliš nízká a nevyužije se tak potenciál spojky.
Vyberte na [2.29] "Hledání řešení" (03.) pro pmax, zadejte hodnotu 1.0 [MPa] (viz vybraný materiál) a stiskněte tlačítko "Najít".
Bude hledán minimální vnější poloměr třecího segmentu pro dosažení zadaného
tlaku pmax=1.0 [MPa].
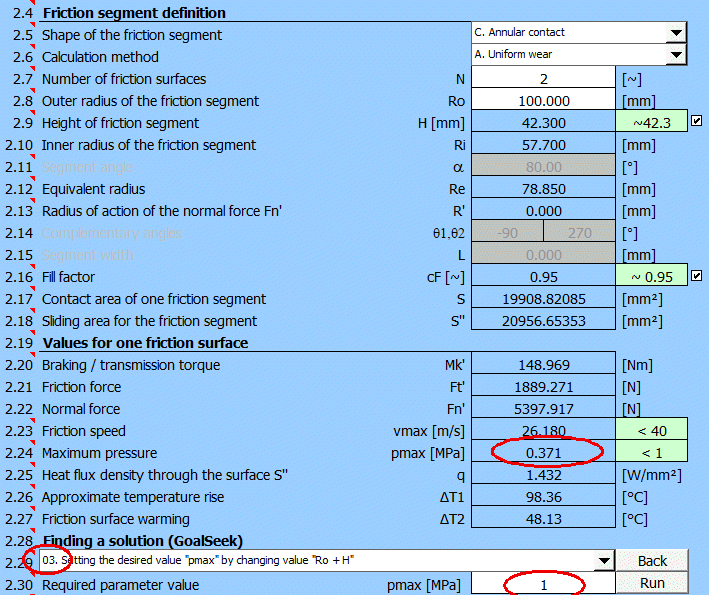
Po vyhledání řešení získáte výsledky:

Po vhodné volbě hodnot Ro a H pak bude návrh spojky vypadat následovně.
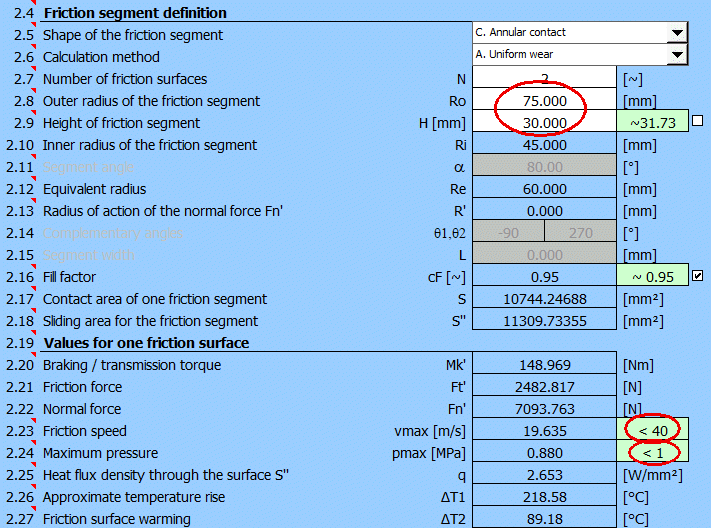
Návrh splňuje základní požadavky, kladené na třecí rychlost a tlak na obložení při splnění požadavku na bržděný moment Mk.
Výpočet tabulky ovládací síly F a brzdícího momentu Mk pro definovanou brzdu.
Rozměry brzdy dle obrázku [mm].
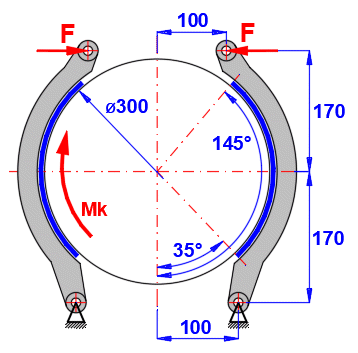
Koeficient tření brzdového obložení ............. f = 0.4 [~]
Šířka brzdového obložení .......................... w = 100 [mm]
Lepené obložení => ................................ cF = 1.0 [~]
Maximální tlak na brzdové obložení ...... pmax = 0.5 [MPa]
Zadejte rozměry brzdy podle zadání (pro vstup odškrtněte tlačítka vpravo).
Postupně měňte kroutící moment Mk [Nm] v rozsahu 300-1100.
Tabulka výsledků:
| ID | Mk [Nm] | F [N] | pmaxR [MPa] |
| 1 | 500 | 1932 | 0.24 |
| 2 | 600 | 2319 | 0.29 |
| 3 | 700 | 2705 | 0.34 |
| 4 | 800 | 3092 | 0.39 |
| 5 | 900 | 3478 | 0.43 |
| 6 | 1000 | 3865 | 0.48 |
| 7 | 1100 | 4251 | 0.53 |
Použitím funkce "Hledání řešení" na [4.24-4.26] pak naleznete i maximální moment Mk a maximální ovládací sílu F pro max. dovolený tlak pmax=0.5 [MPa].
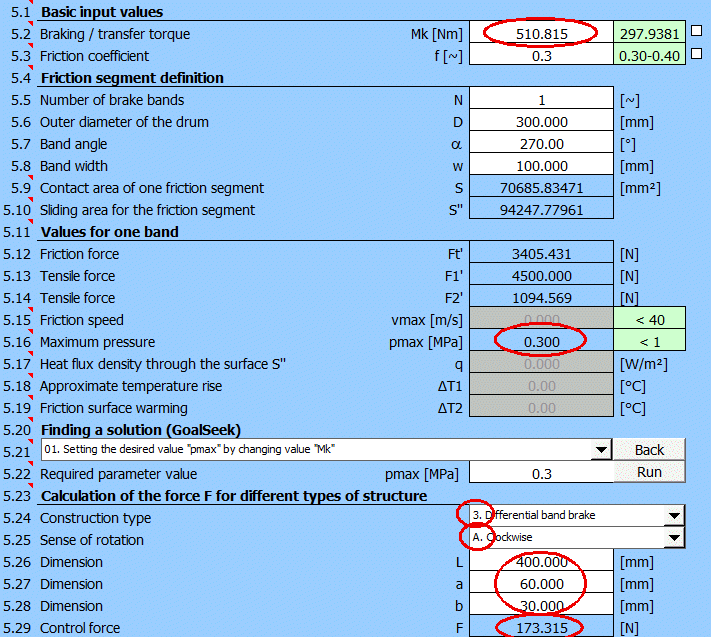
Pásová brzda se zadanými rozměry, zjistit max. kroutící moment Mk a ovládací sílu F.
Rozměry brzdy dle obrázku [mm]. D=300mm, L=400mm, a=60mm, b=30mm
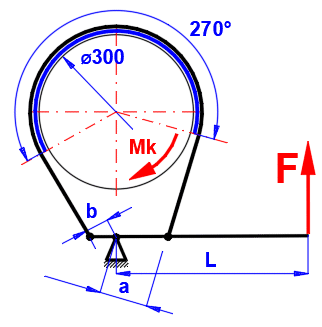
Koeficient tření brzdového obložení ........... f = 0.3 [~]
Šířka brzdového obložení ........................ w = 100 [mm]
Maximální tlak na brzdové obložení ...... pmax = 0.3 [MPa]
Zadejte rozměry brzdy podle zadání (pro vstup odškrtněte tlačítka vpravo).
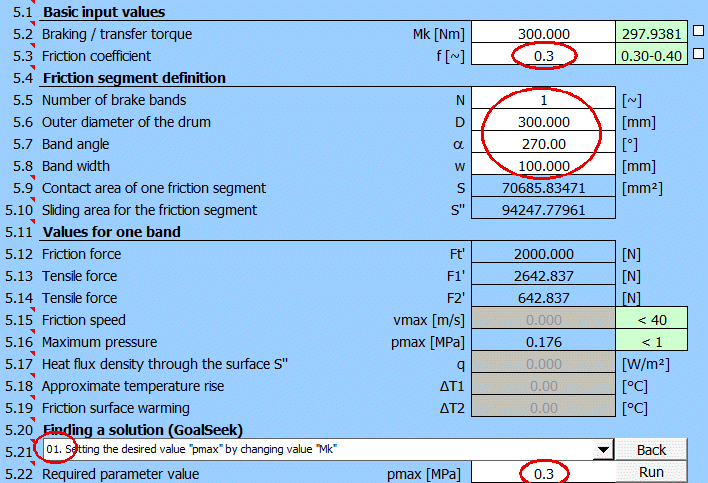
Vyberte na [5.21] "Hledání řešení" (01.) pro pmax, zadejte požadovanou hodnotu
0.3 [MPa] a stiskněte tlačítko "Najít" ("Run").
Bude vyhledán moment Mk pro dosažení zadaného
tlaku pmax=0.3 [MPa].
Po volbě typu ovládacího mechanismu a zadání rozměrů získáte celkové řešení. Maximální moment Mk a ovládací sílu F.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
Litrature:
[1] Clutches and Brakes Design and Selection Second Edition (William C. Orthwein)
[2] Shigley’s Mechanical Engineering Design (Richard G. Budynas, J. Keith Nisbett)
[3] Textbook of Machine Design (R.S. KHURMI, J.K. GUPTA)
[4] Brake Design and Safety Third Edition (Rudolf Limpert)
[5] Roloff / Matek - Maschinenelemente, Normung, Berechnung, Gestaltung
Standards:
VDI 2241-Blatt 1
Schaitbare fremdbetätigte Reibkupplungen und -bremsen.
Begriffe, Bauarten, Kennwerte, Berechnungen
Friction clutches and brakes Vocabulary, types, characteristic data,
calculations
VDI 2241-Blatt 2
Schaitbare fremdbetätigte Reibkupplungen und -bremsen,
Systembezogene Eigenschatten, Auswahlkriterien, Berechnungsbeispiele
Friction clutches and brakes Typ related properties, criteria for selection,
examples of calculations
SAE J866
Friction Coefficient Identification and Environmental Marking System for Brake
Linings
SAE J661
(R) BRAKE LINING QUALITY TEST PROCEDURE
Company cataloques: Ortlinghaus, Goizper, TAROX, FERODO...
^