Rolling bearings.

Table of Content:

• Control and syntax
• Information on the project
• Theory - Fundamentals
• Process of calculation
• Selection of bearing type, bearing loads
• Selection of bearing size
• Adjusted bearing life
• Auxiliary calculations
• Fluctuating bearing load
• Calculation of bearings with angular contact
• Graphic output
• Setting, change the language
• Workbook modifications

Rolling bearings.

This document can be used for the selection, calculation and check of rolling bearings of the company INA/FAG. The programme provides solutions to the following tasks:

1. Selection and check of a suitable bearing. The document includes a database of approx. 5,000 different rolling bearings INA/FAG in all basic types and design.
2. Calculation of basic bearing parameters (life, static safety, etc.).
3. Calculation of adjusted bearing life acc. to the new methodology of ISO 281.
4. Calculation of load with a pair of tapered roller bearings or a pair angular contact ball bearings resp.
5. Support of 2D and 3D CAD systems.

In addition to the above given basic calculations, the document also includes several other auxiliary calculations (e.g. a calculation of lubricant operational viscosity, calculation of mean loads for bearings loaded by variable loads, calculation of permitted bearing speed, etc.).

The programme uses data, procedures, algorithms and other information from specialised literature, catalogues of rolling bearings INA/FAG, ISO, ANSI, SAE standards and other sources.

Related standards: ISO 15, ISO 76, ISO 104, ISO 281, ISO 355, ISO 1132, ISO 5593, ISO 5753, ISO 3448, ISO 15312, DIN 615, DIN 620, DIN 625, DIN 628, DIN 630, DIN 635, DIN 711, DIN 715, DIN 720, DIN 722, DIN 728, BS 290, BS 292, BS 3134

Hint: When selecting a suitable type of bearing, you can use the comparative document "Selection of a rolling bearing".

 User interface.

 Download.

 Purchase, Price list.
 

Control, structure and syntax of calculations.

Information on the syntax and control of the calculation can be found in the document "Control, structure and syntax of calculations".

Information on the project.

Information on the purpose, use and control of the paragraph "Information on the project" can be found in the document  "Information on the project".

Theory - Fundamentals.

Rolling bearings are produced in a wide scope of different designs and sizes. They usually consist of two rings, rolling elements and a cage. The bearings are divided into several basic types according to their inner design, the shape of rolling bodies and directions of the forces that can be retained. A comparison of individual types of rolling bearings can be found in the document "Selection of a rolling bearing".

Basic types of rolling bearings are internationally standardized. Within the scope of each type the bearings are produced in various designs whose properties may differ from the basic design. Detailed technical parameters of rolling bearings are given in catalogues of individual producers.

Calculation of rolling bearings.

Selection of suitable dimensions of the bearing is determined by the amount, direction and type of load on the bearing and its speed. Depending on the type of load on the bearing in operation, the bearings may be divided into two groups for calculation purposes:

• Bearings loaded dynamically
  In case of a dynamic loading the loaded bearing rotates and selection of a suitable bearing is determined by its life due to contact fatigue of the material.
• Bearings loaded statically
  In case of a static loading the bearing is loaded at standstill, at very slow rotation or slow swinging movements. Selection of a suitable bearing is determined by its static load rating.

Basic bearing life.

The life of a rolling bearing is understood as the number of its revolutions (or the period of its operation at the given speed) to the moment when the first traces of fatigue of material on rolling elements or orbital paths appear. Practical tests show that the life of identical bearings differs under the same operational conditions. In order to assess the service life of bearings, the so-called basic life measurement has been introduced.

The basic life of rolling bearings is the life that is achieved or exceeded by 90% of identical bearings under the same operational conditions provided that commonly used materials were used, usual production quality achieved and bearings are operated under normal operational conditions. The basic life is defined by the equation:

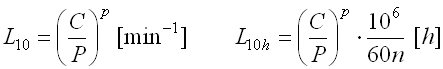
where:
C ... basic dynamic bearing load rating [N, lb]
P ... equivalent bearing dynamic load [N, lb]
n ... bearing speed [1/min]
p ... exponent (p=3 for ball bearings, p=10/3 for other bearings)

Basic dynamic load rating of the bearing is defined as a constant non-variable load at which the bearing reaches the basic life of 1 million revolutions. Values of dynamic loading capacities are given for each bearing in the respective catalogue.

Equivalent dynamic load rating of the bearing is defined exclusively as a radial load (with radial bearings) or axial load (with axial bearings), at which all bearings of the same type show the same life as reached under conditions of a real load. The amount of the equivalent load is described in the relation:

where:
F_r ... radial component of the real load [N, lb]
F_a ... axial component of the real load [N, lb]
X ... coefficient of radial dynamic load
Y ... coefficient of axial dynamic load

Values of the coefficients X, Y depend on the type, design and size of the bearing; with some types of bearings, also on the direction and amount of the real load. These values are given for each bearing in the respective catalogue.

Hint: Guiding values of the life can be found in par. [1.13].

Adjusted bearing life.

The basic life assesses the life of the rolling bearing only in view of loads acting on it and does not take into account any other effects such as operational conditions, production quality or properties of the materials used. Efforts to enhance the quality and reliability of the designs lead to the requirement to calculate the life of the bearing more precisely and therefore the standard ISO has introduced a modified equation of the life:

where:
a₁ ... coefficient of the life for the required reliability (see the table below)
a₂ ... coefficient of the life for the given material properties and level of production technology
a₃ ... coefficient of the life for the given operational conditions

Values of coefficient a₁

Due to the mutual dependence of coefficients a₂ and a₃ producers of bearings usually introduce the common value a₂₃. The value of this coefficient will depend, above all, on the quality of lubrication and according to recommendations in ISO 281 it is determined in dependence on the type of bearing using the respective diagram (see the picture).

Values of the coefficient a₂₃ for radial roller bearings

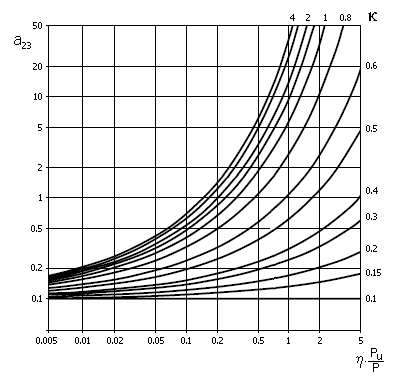
where:
k ... viscosity ratio (gives the rate between operational and rated lubricant viscosity k=n/n₁ - see the chapter on lubrication of bearings)
h ... coefficient of the level of contamination of the lubricant (see par. [3.10])
P .... equivalent dynamic load
P_U ... fatigue load limit (given for each bearing in the respective catalogue)

In case the producer does not give these values of limit fatigue loads with the bearings, you can use approximate values in calculations as given in the following theoretical relations:

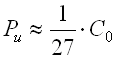
         ... for ball bearings

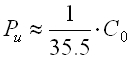
     ... for self-aligning ball bearings

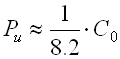
        ... for other bearings

Load of the bearing.

The external system of forces acting on the seating must be distributed with a calculation of the bearing into the forces acting in the radial and axial directions. The intersection of normal lines at contact points of rolling bodies and orbital paths with the axis of the bearing (see the illustration) is considered the centre of the acting forces.

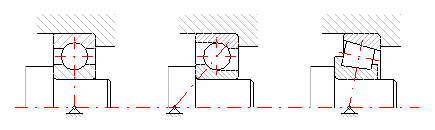
Additional dynamic forces (vibrations and surges) that increase loading on bearings usually occur with machines in operation. These additional forces cannot usually be calculated or measured precisely. Their effects are therefore expressed by various empirical factors that multiply the calculated radial and axial forces. In case of toothed gears, the amount of these additional forces depends on the accuracy of toothing and in case of machines connected to belt drives, on the type of belt and its prestressing. Values of the respective coefficients are usually given in documents of producers of belts and gears, orientation values can be found in par. [1.15].

Fluctuating load.
The above-mentioned calculations of the life of rolling bearings are based on the presumption that the bearing is operated under constant non-variable operational conditions. However, in practice this presumption is often not fulfilled. 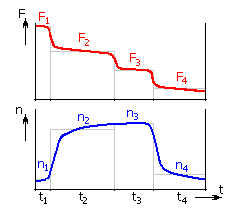In applications where the amount of direction of the load or speed, temperature, conditions of lubrication or level of contaminations varies over the course of time, it is not possible to determine the bearing life directly. In such cases it is necessary to divide the bearing working cycle into several time periods in which the operational conditions are approximately constant (see the picture).

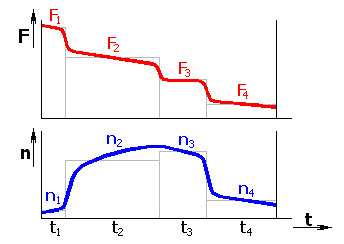
It is necessary to calculate the bearing life separately for each such period. The total bearing life can be determined using the relation

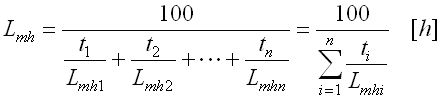
where:
L_mhi ... partial bearing life for individual time periods with constant operational conditions [h]
t_i ....... time portions of individual periods in the bearing’s total working cycle [%]

In an effort to design a bearing quickly, practical procedures use a simplified way of calculation of the bearing life for some types of loads. In this calculation the external load of the bearing is replaced by a virtual mean permanent load that shows the same effects on the bearing as an actually acting variable load. The procedures for determination of the mean load for some common types of loads are given in the table.

Calculation of the bearing mean load F_m

Fluctuating load with linear change of the amount, at constant speed
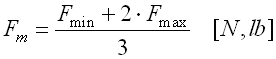Fluctuating load with sinusoidal course, at constant speed
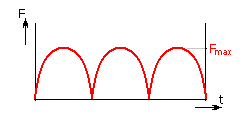Rotating load, at constant speed
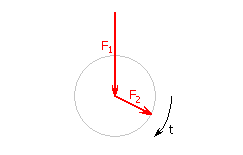Fluctuating load, at constant speed
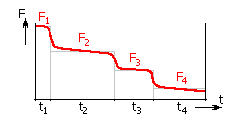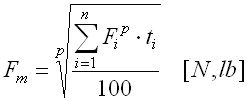Fluctuating load, at variable speed
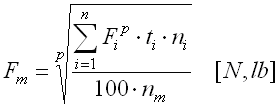	where mean speed:
Oscillating motion
	Oscillating motion is replaced by virtual rotation at the speed equal to the frequency of oscillation:
where: Fi ... partial non-variable load [N, lb] ni ... constant speed during acting of partial loads [1/min] ti ... time portions of acting of partial loads in the bearing’s total working cycle [%] p ... exponent (p=3 for ball bearings, p=10/3 for other bearings)

Note: The simplified calculation method gives sufficiently accurate results with calculations of basic life provided that a variable load of constant direction is applied. Use of the simplified calculation is not suitable in case of a load with variable amounts and directions and with calculations of modified life.

Effects of temperature on the bearing load rating.

Commonly produced and delivered rolling bearings are designed for operational temperatures up to 120 °C (100 °C for sealed bearings). In case of use of a bearing at permanently higher temperatures it is necessary to modify it during production to ensure its dimensional stability under operation. Bearings for use at high temperatures are produced with thermal treatment, usually with greater clearances and a differently designed cage, possibly with the use of special materials.

Requirements for the use, production and delivery of stabilized bearings must usually be consulted with the producer, where you can find detailed technical parameters of the bearing. For the purposes of preliminary designs it is possible to use the following orientation table.

Approximate load rating of stabilized bearings compared with common bearings of the same sizes

Safety of bearings at static load.

A bearing at static load is loaded by forces at standstill, at very slow speed or slow swinging movements. The load rating of the bearing is determined by permissible permanent deformations of orbital paths and rolling bodies. The coefficient of safety s₀ gives the standard of safety of static-loaded rolling bearings and is defined by the following relation:

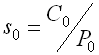
where:
C₀ ... basic bearing static load rating [N, lb]
P₀ ... equivalent bearing static load rating [N, lb]

Basic static load rating of the bearing is defined as the external load that causes a permanent deformation of 0.0001 of the diameter of the rolling body at the contact point of the most loaded rolling body. This permanent deformation usually has no adverse effects on the bearing function. Values of static load ratings are given for each bearing in the respective catalogues.

Equivalent static load rating of the bearing is defined exclusively as radial load (with radial bearings) and axial load (with axial bearings) respectively, which causes a permanent deformation in the bearing and this deformation is of the same size as under actual conditions of loading. The amount of the equivalent load is described by the relation

where:
F_r ... radial component of the real load [N, lb]
F_a ... axial component of the real load [N, lb]
X₀ ... coefficient of radial static load
Y₀ ... coefficient of axial static load

Values of the coefficient X₀,Y₀ depend on the type, design and size of the bearing. These values are given for each bearing in the respective catalogue.

Hint: Guide values of the coefficient of safety can be found in par. [1.14].

Friction and warming of bearings.

The friction moment of rolling bearings depends on many factors (design of the bearing, method of lubrication, speed, etc.) and it is very difficult to determine exactly. Practical calculations therefore use a simplified model with the use of an estimated coefficient of friction. Under the assumption of normal operational conditions and good lubrication an approximate friction moment can be calculated with rolling bearings operated at mean speed using the equation

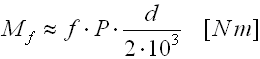
where:
P ... equivalent dynamic load of the bearing [N]
d ... diameter of the bearing hole [mm]
f ... coefficient of friction (depending on the type of bearing, f=<0.0010...0.0050>)

In case of sealed bearings the moment from the friction sealing must be added to the calculated friction moment. The resulting friction moment further determines the power loss N_R that is equal to the heat produced in the seating:

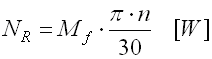
where:
n ... speed of the bearing [1/min]

Calculation of bearings with angular contact

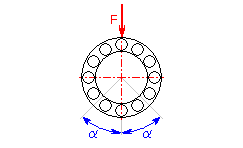
In case the shaft is seated in two single row angular contact ball bearings or in two tapered roller bearings, a mutual inner axial force is produced with radial load in the bearings. This force will naturally affect the bearing load rating and therefore it must be included in the calculation. The amount of the axial load of one bearing depends on the contact angle and arrangement of both bearings, on the amount of radial forces F_rA, F_rB and on the direction and amount of the external axial force K_a.

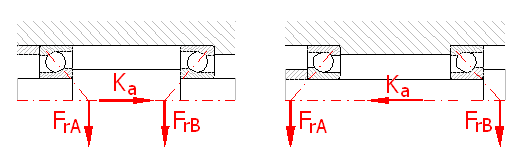
The calculation must also consider the seating as a unit and both bearings must be designed at the same time.

Operational conditions.

Required minimum load rating of the bearing.

Higher speeds create a danger of rolling elements slipping between the orbital paths of the rings with unloaded bearings due to centrifugal forces. This may adversely affect wear of the bearing and thus reduce its life. The bearing should be loaded by a certain minimum force under operation to ensure correct rolling. The amount and size of this force depends on the type, design and size of bearing and operational conditions. The relations for determining the minimum load are usually given in catalogues of individual producers.

Operating temperature.

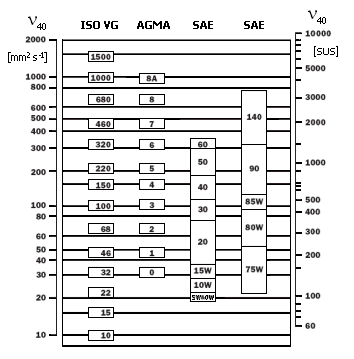
The heat that is produced by friction must be dissipated to achieve thermal balance. The operational temperature depends on many factors; its calculation is very complicated and leads to a system of non-linear equations. The following relation can be used for fast orientation:

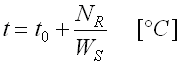
where:
t₀ ..... ambient temperature [°C]
N_R .... power loss [W]
W_S ... coefficient of cooling [W/°C]

The coefficient of cooling gives the amount of heat being dissipated into the ambient air at a temperature drop of 1 °C. For bearings seated in frame machines it can be determined approximately using the relation

where:
D ... outer diameter of the bearing [mm]
v ... velocity of air [m/s]  (v~1-2 for bearings inside the buildings, v~2-4 for bearings in the open air)

Limiting speed.

The speed of rolling bearings cannot be increased without any limitation. Centrifugal forces of the bearing increase its loading, inaccuracy of its run causes vibrations and friction in the bearing causes warming. Limit speed depends on the type, design and size of bearing, its accuracy, and the design of the cage, inner clearances and operational conditions in its seating and, above all, the highest permissible temperature of the lubricant.

No specific and generally applicable limit of permissible speed can be determined exactly for rolling bearings. Producers give in their dimensional tables guide values of limit speeds for individual bearings for the purposes of fast orientation. These values are based on practical experience and are applicable for bearings with normal clearances and produced at normal levels of accuracy provided that they are operated under normal conditions and with usual cooling. The given limit speeds can be exceeded in certain individual cases, however, it is advisable to consult this with the producer.

In addition to limit speeds, some producers also state in their catalogues of rolling bearings values of so-called thermal reference speeds. The reference speed gives the limit permissible speed of the bearing under exactly defined conditions and serves as an initial value for determining the permitted speed of the bearing for the given operational conditions.

where:
n_r ... reference speed [1/min]
f_p ... adjustment factor for the given type, size and load of bearing
f_v ... adjustment factor for the chosen conditions of lubrication

The method of determining adjustment factors is described in catalogues of individual producers or in ISO 15312. The reference speeds given in the dimensional tables are defined for the following operational conditions:

• Bearing temperature 70 °C
• Ambient temperature 20 °C
• load P=0.05*C₀
• Lubricant kinematic viscosity
  n = 12 [mm²/s] ... oil lubricated radial bearings
  n = 24 [mm²/s] ... oil lubricated thrust bearings
  n₄₀ = 100-200 [mm²/s] ... grease lubrication

Lubrication of rolling bearings.

The reason for lubricating rolling bearings is to create a carrying lubrication film on contacts between rolling bodies with orbital paths of the rings. In addition, the lubricant protects the bearing from corrosion, improves its sealing, exhibits cooling effects and lubricates the surfaces of the bearing with sliding friction.

Rolling bearings can be lubricated by plastic or liquid lubricants. Selection of a suitable lubricant is determined, above all, by the speed, operational temperature, position of the shafts, general concept of seating and economy of operation. If permitted by operational conditions, greases are preferred with rolling bearings.

Grease lubrication.

Grease lubrication is preferential particularly as regards easy operation, economy and sealing of bearings against dirt and moisture. It enables a simple arrangement of seating and is better suited for high and surge loading. Greases must show good lubrication capability and high chemical, thermal and mechanical stability. The market offers a wide range of suitable greases. In addition, most producers of rolling bearings offer their own ranges of lubricants.

ARCANOL Greases offered by FAG

Greases offered by INA

Grease has a limited life in the bearing. The reason is its leakage from the bearing and impairment of its properties over the course of time. Therefore, it is necessary to refill or replace the lubricant at certain time intervals. The refill intervals will depend on the type and size of bearing and operational conditions. The recommended refill periods are given for individual bearings in catalogues of the producers

Oil lubrication.

Lubrication of rolling bearings by oil is not so good and is usually used only in the following cases:

• Speed of the bearing is so high that refilling intervals for lubrication by grease would be too short
• Operational temperature is higher than the permissible temperature for greases
• The adjacent parts are lubricated by oil
• Lubrication by oil flow is required for intensive cooling of the bearing
• Lubrication of spherical roller bearings

Depending on the operational conditions and desired design of seating several different types of oil lubrication of rolling bearings are used (oil bath, circulation of oil, spraying of oil, oil mist). Bearings are usually lubricated by mineral oils. Kinematic viscosity is the decisive property of oil; it decreases with increasing temperature. Practical experience shows that in the case of common seating the viscosity of oil should not drop below 12 mm²/s at operational temperatures. The rated viscosity that is determined in dependence on the mean diameter and speed of the bearing is the guiding factor for the selection of an oil with suitable operational viscosity.

Rated viscosity n₁

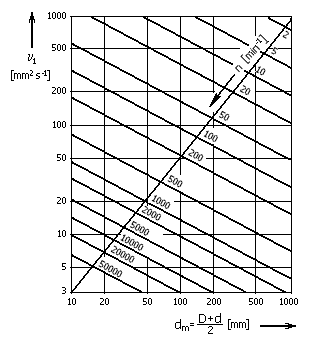
The qualitative standard of lubrication of rolling bearings is given in the viscosity ratio:

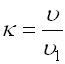
where:
n .... viscosity of the lubricant at operational temperatures [mm²/s]
n₁ ... rated viscosity [mm²/s]

For the viscosity ratio k<1 it is recommended to use a high-pressure oil with EP additives. Very long fatigue life can be achieved at k=3..4.

Viscosity of mineral oils n₄₀ at reference temperature 40 °C (~100 °F).

Hint: The auxiliary calculation in par. [4.1] can be used for fast determination of viscosity of the lubricant.

Production accuracy and matching of rolling bearings.

Accuracy of dimensions and run.

Accuracy of rolling bearings is understood as accuracy of their dimensions, shape and run (radial and axial run-out of the rings). Bearings are commonly produced at normal accuracy, which is not marked in the name of the bearing. Accuracy of bearings is standardized internationally, and markings of individual levels of accuracy can be found in the table:

Detailed information can be found in the respective catalogue of bearings.

Bearing clearance.

Clearance of the bearing is the amount of free shift of one ring against the other from one margin position to the other. Correct run of the bearing is influenced, above all, by its radial clearance. Bearings with normal radial clearance, C0, which is not marked in the name of the bearing, are designed for normal operational conditions. Smaller clearances, C2, or greater clearances, C3, C4, C5, are chosen for significantly different operational conditions.

Detailed information can be found in the respective catalogue of bearings.

Matching of rolling bearings.

Selection of correctly matching bearing rings on the shaft and in the body has great importance as for the life of the rolling bearing. When selecting suitable tolerances, the following conditions are critical:

• Amount and way of loading
• Dilatation of the seated parts
• Thermal conditions in the bearing
• Requirements for accuracy, installation and dismounting of bearings
• Material and rigidity of the parts

Orientation values for the selection of tolerances can be found in the following tables; exact data for individual types and sizes of bearings can be found in the respective catalogue.

Tolerances of diameters of shafts for radial bearings

Tolerances of diameters of holes for radial bearings

Tolerances of diameters of shafts and holes of bodies for axial bearings

Process of calculation.

Selection, calculation and check of a rolling bearing consist of the following steps:

1. Set up the desired calculation units (SI/Imperial). [1.1]
2. Select the desired type of bearing in the selection list [1.2]. When selecting a suitable type of bearing, you can use the comparative document "Selection of a rolling bearing".
3. Provided that the type of the bearing is produced in various designs, select the suitable design in the lists in par. [1.3].
4. In par. [1.7] enter the parameters of loading of the bearing. In case of bearings loaded by variable loads use the auxiliary calculation [5] to determine the mean load.
5. In case the bearing will be loaded by additional dynamic forces under operation, define the respective coefficients in par. [1.15].
6. Enter the desired life of the bearing [1.13] and safety at static loading of the bearing [1.14].
7. Activate the automatic search for a suitable bearing by pressing the button "Find first" in row [2.1]. In case the calculation cannot find any suitable bearing, select another type [1.2] or design of bearing [1.3] and repeat the calculation.
   Warning: For shafts seated in a pair of tapered roller bearings or angular contact ball bearings, use the special calculation in chapter [6] for selection of the bearings.
8. Check the parameters of the designed bearing in par. [2]; perform an additional calculation, if necessary, to arrive at the modified life of the bearing in par. [3] for known operational parameters. In case some recommended values are exceeded with the designed bearing or the bearing does not meet your requirements, use the button "Find next" to find another bearing. A suitable bearing can also be selected manually in the list [2.1].
9. Save the book with the suitable solution under a new name.

Selection of bearing type, bearing loads. [1]

In this paragraph perform selection of the desired type and design of bearing, define its loading and enter the desired physical properties of the bearing.

1.1 Calculation units.

Select the desired calculation units in the selection list. When switching over the units, all values will be recalculated immediately.

Warning: When setting units different from the units used in the respective catalogue of a producer of bearings, the respective table parameters of the bearing will be rounded during recalculation.

1.2 Bearing type.

Select the desired type of bearing in the selection list. A comparison of basic types of rolling bearings can be found in the document "Selection of a rolling bearing".

Warning: In case the shaft is seated in two single row angular contact ball bearings or in two tapered roller bearings, use the auxiliary calculation in par. [6] for selection and check of the bearings.

1.3 Bearing design.

Within the range of each type, rolling bearings may be produced in a different design with some properties different from the basic design. In case the producer delivers various designs of the selected type [1.2], the programme offers the respective selection lists in rows [1.4 .. 1.6]. Set up the desired design of the bearing in these lists.

1.7 Bearing load.

In this paragraph enter the radial and axial components of external loads of the bearing and its speed at constant non-variable operational conditions.

Hint: In case the actual load of the bearing is fluctuating, use the auxiliary calculation in par. [5] to determine the mean non-variable load. Detailed information on calculations of bearings operated under variable operational conditions can be found in the theoretical section of the Help.

1.13 Bearing life.

Enter the desired life of the bearing.

Guide values of the life of rolling bearings

In case of wheeled vehicles, their life is usually given in millions of driven kilometres.

For recalculation use the following relation:

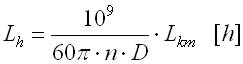
where:
n ... speed of the bearing [1/min]
D ... diameter of the vehicle wheel [m]

1.14 Static safety factor.

Enter the desired safety at static loading of the bearing.

Minimum permissible values of the static safety coefficient

Note: In case of axial spherical roller bearings it is recommended to use the minimum value of the coefficient s₀=4.

1.15 Additional dynamic forces.

Additional dynamic forces (vibrations and surges) that increase loading on bearings usually occur with machines in operation. These additional forces cannot usually be calculated or measured precisely. Their effects are therefore expressed by various empirical factors that multiply the calculated radial and axial forces.

In this paragraph define the individual factor depending on the type of machine used. The resulting factor of additional forces is calculated additionally in [1.11].

1.17 Additional forces from geared transmission.

In case of transmissions with toothed gears the amount of additional forces will depend on the accuracy of the toothing and machines connected to the transmission.

The factor of additional forces f_k, resulting from inaccuracy of toothing, should be entered in row [1.19]. The recommended values for the selected type of toothing [1.18] are given in the green field.

The factor of additional forces from the connected machines f_d should be entered in row [1.21]. The recommended values for the selected type of machine [1.20] are given in the green field.

Note: When ticking the checkboxes [1.19, 1.21] the calculation automatically introduces the mean values of factors.

1.22 Additional forces from belt drives.

In case of belt drives, the amount of additional forces will depend on the type of belt and its pre-stressing. The factor of additional forces f_p should be entered in row [1.24]. Data on its amount are usually given in materials from the producers of the belts. If the data are not available, use the recommended values that are given for the selected type of belt [1.23] in the green field. Higher values in the given range should be used for short lengths of shafts, surge loads or large pre-stressing of belts.

Note: When ticking the checkbox [1.24] the calculation automatically introduces the mean value of the factor.

Selection of bearing size. [2]

This paragraph can be used for selection of a bearing of a suitable size. Dimensions of the bearing should be selected in par. [2.1]. Physical properties, dimensional and operational parameters of the selected bearing are calculated in par. [2.2] in real time.

Hint: The programme provides a function of automatic searching for a bearing of a suitable size to facilitate the design. Automatic selection of the bearing can be activated using the buttons in row [2.1].

2.1 Bearing size.

In the selection list select a bearing with the desired dimensions. Individual bearings are listed in ascending order according to inner diameter. The table parameters of the bearing are arranged in columns in the following order:
- Main dimensions of the bearing (inner and outer diameter, width of the bearing)
- Basic dynamic and static load rating of the bearing (C, C0)
- Reference and limit speeds (nr, nmax)
- Marking of the bearing

Automatic selection of the bearing

The programme provides a function of automatic searching for a bearing of a suitable size to facilitate the design. After pressing the button "Find first" the programme finds the first bearing that meets the requirements for life and static safety as defined in par. [1.12]. In case some recommended values are exceeded with the proposed bearing or this bearing does not meet the desired requirements, use the button "Find next" to find another bearing.

When searching for a suitable bearing, the programme also checks any possible exceeding of the permitted load [2.9, 2.10]. In case the calculation cannot find a suitable bearing, select another type [1.2] or design of bearing [1.3] and repeat the calculation.

Note: For some types of bearings the producer gives only values for bearing limit speed with oil lubrication and grease lubrication (nO, nG).

2.2 Parameters of the selected bearing.

Basic parameters of the selected bearing are calculated additionally in this paragraph in real time. Physical properties and operational parameters of the bearing are given in the left part, its dimensions in the right part.

Hint: The meaning and a detailed description of individual parameters can be found in the theoretical section of the Help.

2.3 Basic dynamic load rating.

After unchecking the check box in this line, you can enter into the calculation your own values of the basic bearing capacity. In this way you may calculate the approximate comparison of the service life for an equivalent bearing supplied by another manufacturer.

Warning: The calculation is performed according to the methodology defined by the manufacturer for the primary bearing. As for the equivalent bearing supplied by another manufacturer, the compliance with the prescribed calculation procedure may not be guaranteed.

2.9, 2.10 Permissible radial or axial load.

Not all types of rolling bearings can carry combined loads. Some types are designed only for retaining radial forces, other types for axial forces; some types may carry only limited loads in the given direction. The recommended amounts of permitted loads are prescribed for the given types by producers and calculated additionally for the selected bearing in row [2.9] or [2.10] resp.

Note: In case the producer does not give any limitations to carrying combined loads for the given type and design of bearing, no values will be given in rows [2.9, 2.10].

2.13 Power loss.

Reference value which is valid for given type and size of the bearing with the assumption of standard operating conditions, load P/C≈0.1 and good type of lubrication.

Hint: More accurately value for the design type, lubrication type and load type is calculated on the line [4.13].

Operating parameters, adjusted bearing life. [3]

The adjusted life [3.12] and recommended amount of minimum load [3.6] are calculated additionally for the given operational parameters (lubrication) of the selected bearing in this paragraph.

3.1 Kinematic viscosity of the lubricant.

In row [3.3] enter the kinematic viscosity of the lubricant used at the operating temperature. In case of plastic lubricants the kinematic viscosity of its basic oil component is given.

Practical experience shows that in the case of common seating the viscosity of oil should not drop below 12 mm²/s at operating temperatures. The rated viscosity [3.2] that is determined in dependence on the mean diameter and speed of the bearing is the guiding factor for the selection of an oil with suitable operating viscosity. The qualitative standard of lubrication of rolling bearings is given in the viscosity ratio [3.4]. For the viscosity ratio k<1 it is recommended to use a high-pressure oil with EP additives. Very long fatigue life can be achieved at k=3..4.

Hint: Use the auxiliary calculation [4.1] to determine the operational viscosity of the lubricant.

Warning: Commonly produced and used rolling bearings are designed for operational temperatures up to 120 °C (100 °C for sealed bearings).

Note: Detailed information on lubrication of rolling bearings can be found in the theoretical section of the Help and catalogues of producers.

3.5 Requisite minimum load.

Higher speeds create a danger of rolling elements slipping between the orbital paths of the rings with unloaded bearings due to centrifugal forces. This may adversely affect wear of the bearing and thus reduce its life. The bearing should be loaded by a certain minimum force under operation to ensure correct rolling. The amount and size of this force depends on the type, design and size of bearing and operational conditions. The recommended amount of the minimum load is additionally calculated for the given bearing in row [3.6].

Note: In case the producer does not give any value of the minimal load for given type and design of the bearing, no value will be given in row [3.6].

3.7 Calculation of the adjusted rating life.

The basic life [2.5] assesses the life of the rolling bearing only in view of loads acting on it and does not take into account any other effects such as operational conditions, production quality or properties of the materials used. This paragraph includes the adjusted life of the selected bearing calculated for the given load, desired reliability and assumed operating viscosity and the level of contamination of the lubricant.

Note: Calculation of the adjusted life is performed according to the methodology of ISO 281.

Hint: Detailed information on calculating the adjusted life of rolling bearings can be found in the theoretical section of the Help.

3.8 Fatigue load limit.

After unchecking the check box in this line, you can enter into the calculation your own value of the fatigue load limit. In this way you may calculate the approximate comparison of the service life for an equivalent bearing supplied by another manufacturer.

Warning: The calculation is performed according to the methodology defined by the manufacturer for the primary bearing. As for the equivalent bearing supplied by another manufacturer, the compliance with the prescribed calculation procedure may not be guaranteed.

3.9 Required reliability.

Select the desired reliability in the selection list.

The reliability gives the percentage share of bearings from a group of identical bearings working under the same operational conditions that reach the calculated operation life. The basic life of rolling bearings [2.5] is determined for a reliability of 90%.

3.10 Contamination of the lubricant.

In row [3.11] enter the factor of the level of contamination of the lubricant. Its amount varies in the interval <0..1>; the recommended values for the selected level of contamination [3.10] are given in the green field.

Level of contamination of the lubricant is divided into several levels:

• Extreme cleanliness - Laboratory conditions (h=1)
• High cleanliness - Oil filtered through an extremely fine filter; typical for greases with sealed bearings
• Normal cleanliness - Oil filtered through a fine filter; typical for greases with bearings shields on both sides
• Slight contamination - Slightly contaminated lubricant
• Typical contamination - Typical conditions for bearings without integrated sealing; coarse oil filter, lubricant contaminated by particles rubbed from neighboring machine parts
• Severe contamination - Strongly contaminated ambient environment; arrangement of bearings with insufficient sealing
• Very severe contamination - h=0

Note: When ticking the checkbox [3.11] the calculation automatically introduces the mean value of the coefficient depending on the selected level of contamination of the lubricant [3.10].

Auxiliary calculations. [4]

This paragraph gives some auxiliary calculations for approximate determination of some operational parameters of rolling bearings (operating viscosity of the lubricant, length of relubrication intervals, desired oil flow, etc.).

4.1 Calculation of operating viscosity.

This paragraph is designed to determine the approximate kinematic viscosity of the selected lubricant at the operating temperature [4.2]. The calculation is divided into two parts:

• Determination of operating viscosity of mineral oils [4.3]
  Calculation of the operating viscosity is based on the known oil viscosity [4.5] at the reference temperature 40 °C (~100 °F).
• Determination of operating viscosity of other lubricants [4.7]
  Calculation of the operating viscosity is based on two known values of kinematic viscosity of the lubricant [4.9] at various temperatures [4.8].

Note: Exact values of operating viscosity can be found in the material sheets of the respective lubricants.

4.11 Bearing lubrication.

The desired oil flow [4.14] or the length of the relubrication interval [4.15] resp. are additionally calculated for the selected bearing [2.1] and the selected method of lubrication [4.12].

Note: The selected method of lubrication is also decisive in calculating the permissible speed of the bearing [4.16].

4.14 Desired oil volume flow.

The necessary flow of oil for cooling the bearing with circulatory lubrication is determined for the given warming of the bearing (power loss [4.13]) in this row. The calculated oil flow is a theoretical table value that is determined for the difference in temperatures at the oil inlet and outlet, DT=10 °C.

Note: The calculation does not take into account any external cooling of the bearing due to heat conduction, radiation or convection. Practical experience shows that under normal cooling conditions there will be sufficient oil flow approx. 20-40% lower, under very good cooling conditions up to 70% lower.

4.15 Relubrication interval.

The recommended length of the relubrication interval is determined for the given load and speed of the selected bearing. The given value is valid for loads C/P>3, normal lubrication conditions and operational temperature of the lubricant up to 70 °C (~160 °F). In case of higher temperatures the additional lubrication interval is shorter.

4.16 Calculation of permissible speed.

The permissible speed of the bearing is determined for the given load, method of lubrication [4.12] and viscosity of the lubricant [3.3] in this paragraph.

4.18 Temperature difference.

Enter the difference between mean bearing temperature and ambient temperature.

4.19 Difference of oil temperature.

Enter the difference between oil input temperature and oil output temperature.

Fluctuating bearing load. [5]

The used calculations of the life of rolling bearings are based on the presumption that the bearing is operated under constant non-variable operational conditions. However, in practice this presumption is often not fulfilled.

The auxiliary calculation in this paragraph is designed to determine the mean non-variable loading in applications where the bearing is exposed to a loading of a variable amount in a constant direction at a constant or variable speed.

When calculating the mean loading, proceed in the following steps:

1. Divide the working cycle into several time periods in which the operational conditions are approximately constant (see the picture).
2. In the selection list [5.1] set up the number of these time periods.
3. In the input table [5.2] define the operational conditions for individual time periods.
4. The mean non-variable loading is additionally calculated in par. [5.3]. Using the button "Transfer" then transfer data on the loading to the main calculation.

Warning: This calculation is approximate only and gives sufficiently accurate results with calculations of basic life provided that the variable loading has a constant direction. For calculations of a adjusted life (or if the bearing is exposed to a load of variable amounts and directions) it is more suitable to select a more complex method of calculating the life of rolling bearings. Detailed information on calculations of bearings working under variable operational conditions can be found in the theoretical section of the Help.

Calculation of bearings with angular contact. [6]

In case the shaft is seated in two single row angular contact ball bearings or in two tapered roller bearings, a mutual inner axial force is produced with radial load in the bearings. This force will naturally affect the bearing load rating and therefore it must be included in the calculation. The amount of the axial load of one bearing depends on the contact angle and arrangement of both bearings, on the amount of radial forces F_rA, F_rB and on the direction and amount of the external axial force K_a.

The calculation must also consider the seating as a unit and both bearings must be designed at the same time. In case of the design of bearings, proceed in the following steps:

1. Activation of a switch in Fig. [6.1] selects the respective arrangement of bearings and direction of action of the external axial force. The calculation assumes action of an external force in the shaft axis. In case the external axial force is acting on the bearing body, forces in the opposite direction in the shaft must be considered.
2. In the selection list [6.2] select the desired bearing type.
3. Enter the amount of the external axial force [6.3].
4. In the pop-up lists [6.5, 6.13] select the designs of both bearings.
5. Enter the respective radial loads [6.6, 6.14] for both bearings.
6. In the following step it is necessary to select both bearings step-by-step. In case the entered data are definite, the programme shows recommendations in rows [6.4] or [6.12] respectively, for which bearing must be designed the first.
7. Activate the automatic search for a suitable bearing using the buttons "Find first" in rows [6.7, 6.15]. The basic life of both bearings will be additionally calculated in rows [6.10, 6.18].
8. Using the buttons "Transfer" in rows [6.11, 6.19] you can transfer the selected bearings into the main calculation. Here check the parameters of the designed bearing in par. [2] and additionally calculate the adjusted life of the bearing in par. [3] for known operational parameters, if necessary.

Warning: Here the performed calculation of the bearings works with the following data from the introductory paragraph:
- speed of the bearing [1.8]
- desired life [1.13]
- additional dynamic forces defined in par. [1.15]
Therefore it is necessary to enter these data in par. [1].

Graphic output, CAD systems.

Information on options of 2D and 3D graphic outputs and information on cooperation with 2D and 3D CAD systems can be found in the document "Graphic output, CAD systems".

Setting calculations, change the language.

Information on setting of calculation parameters and setting of the language can be found in the document "Setting calculations, change the language".

Workbook modifications (calculation).

General information on how to modify and extend calculation workbooks is mentioned in the document "Workbook (calculation) modifications".