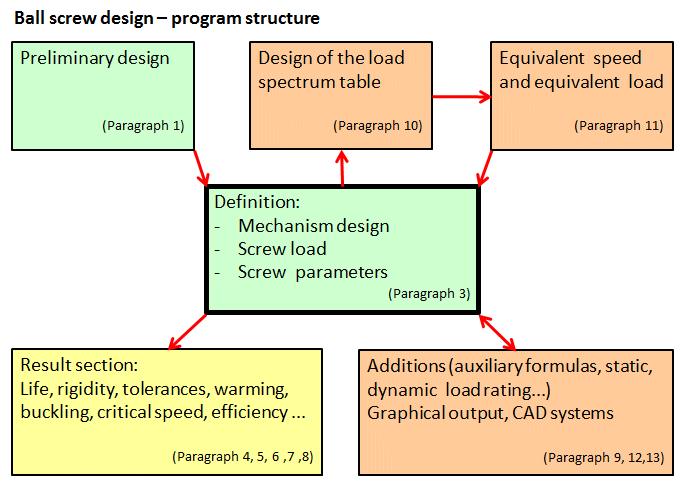
Das Programm ist für die Konstruktion, Berechnung und Kontrolle von Kugelschrauben ausgelegt. Das Programm löst die nachstehenden Aufgaben:
1. Vorentwurf (minimale Eingabeparameter, ausreichend zur Orientierung und Auswahl aus Katalogen)
2. Detaillierte Analyse (Belastung, Wahl der Abmessungen, Kontrolle der Parameter)
3. Definition der Lastspektrumtabelle (Geschwindigkeit, Drehmoment, Drehzahl und Leistung ...)
4. Berechnung der äquivalenten Belastung
5. Lebensdauerberechnung, Toleranzentwurf, Temperaturanalyse
6. Prüfung der Schraube auf Spannung/Druck, Verdrückung, Biegung, Streben und kritische Drehzahl
7. Entwurf der Schmierung und Berechnung des Wirkungsgrades
8. Das Programm enthält Schraubentabellen nach ISO und ANSI
9. Unterstützung der 2D CAD Systeme
In der Berechnung sind Daten, Verfahren, Algorithmen und Fachliteraturangaben und Angaben aus Normen AISC,ISO,DIN und BS verwendet.
Normenverzeichnis: ISO 3408-1:2006; ISO 3408-2: 1991; ISO 3408-3:2006; ISO 3408-4:2006; ISO 3408-5:2006;
ISO 286-2:2010
DIN ISO 3408; JIS B1192-1997; JIS B1192-2018; DIN 69051-5; ANSI B5.48
Firmenkataloge: THK, PMI, KSK, NSK, SKF, HIWIN, KURODA, NOOK, THOMSON, Steinmayer, MANESMAN
Anwenderoberfläche.
Zum Herunterladen.
Preisliste, Einkauf.
Die Informationen über die Syntax und die Bedienung der Berechnung finden Sie im Dokument"Steuerung, Struktur und Syntax der Berechnungen".
Die Informationen über den Zweck, die Anwendung und die Bedienung des Absatzes "Projektinformation " finden Sie im Dokument "Projektinformationen".
Kugelschrauben (KS) sind vielseitig einsetzbar. Zum Beispiel Antriebe von CNC-Maschinen, Antriebe von Spritzgussmaschinen, Ersatz für hydraulische Antriebe, Medizintechnik, Flug- und Automobiltechnik, Transporttechnik. Der Vorteil der KS ist der hohe Wirkungsgrad der Übersetzung (ca. + 90%), der Nachteil ist dann die fehlende Selbstsperrung.
Es wird ungefähr die folgende Typenaufteilung angewendet:
Universalschrauben, die in Bearbeitungszentren, Flugzeugtechnik, Automobiltechnik, Positioniergeräten usw. verwendet werden. Je nach Genauigkeitsgrad werden sie durch Schleifen oder Beringen hergestellt. Normalerweise in der Genauigkeitsklasse IT1-IT5 hergestellt. Die Muttern können mit oder ohne Vorspannung hergestellt werden. Die meisten Berechnungen im Programm beziehen sich auf diese universelle Gruppe.
Entwickelt für hohe Positioniergeschwindigkeiten (Arbeiten bis 30 m/min, Eilgang bis 80 m/min). Bearbeitung, Positionierung, Genauigkeit IT1, IT3, Vorspannung verwendet. Normalerweise mehrgängig.
Entwickelt für hohe Lasten, lange Nutzungsdauer. Eine größere Tragfähigkeit wird durch größere Kugeldurchmesser, eine größere Anzahl von Arbeitsgewinden und eine Profilanpassung sichergestellt. Hergestellt durch Schleifen mit der Anforderung einer höheren Genauigkeit (IT1) ohne Vorspannung.
Geringe Positioniergenauigkeit, geringere Geschwindigkeit, niedriger Preis, keine Vorspannung. Herstellung durch Walzen, Kreisen, Genauigkeit IT5, IT7, IT10. Verwendung für Transportmechanismen.
Diese Kategorie umfasst eine Reihe von KS wie profillose Schrauben (die Welle hat die Form einer geschliffenen gehärteten Stange), Schrauben mit einem Käfig (Kugeln befinden sich im Käfig ohne Übersetzer, stufenloser Gang, kurze Hübe), teleskopische Schrauben (mehrere gegenseitig eingeschraubte KS, kleiner Einbau) usw.
Je nach Ausführung handelt es sich um eine Ausführung mit einer externen Kugelführung (höhere Lärmentwicklung, mehrere Kugeln im Umlauf) und einer internen Kugelführung. Die Entnahme der Kugeln kann dann auf verschiedene Arten gelöst werden, meistens abhängig vom Hersteller und der Anstrengung, den bestmöglichen Drehzahlkoeffizient (d1 * nmax) zu erreichen.
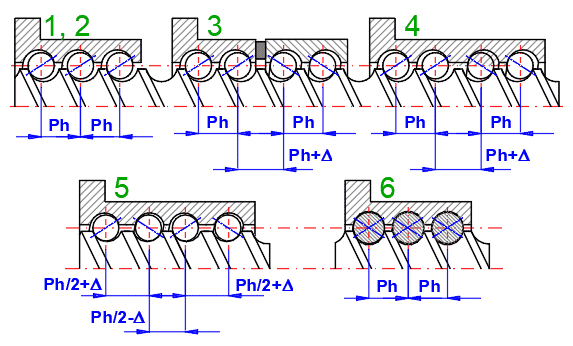
Die Muttern werden mit Spiel oder Vorspannung am Bolzen montiert, die zur Abgrenzung des Spiels dient. Der Nachteil der Vorspannung ist ein größerer Verschleiß, bei dem die Haltbarkeit mit zunehmender Vorspannung abnimmt.
1. Ohne Vorspannung
2. Vorspannung durch äußere Kraft auf Mutter/Schraube sichergestellt
3. Distanzring verschiebt die Gewinde der Mutter
4. Unterschiedliche Steigung im Muttergewinde
5. Durch gegenseitiges Verschieben der einzelnen Gewindegänge (bei mehrgängigen Gewinden)
6. Verwendung von größeren (und kleineren) Kugeldurchmessern (4-Punkte-Kontakt)
Üblicherweise wird ein Wert von 10 % der dynamischen Grundtragfähigkeit Ca verwendet. Einzelne Hersteller erlauben und empfehlen dann je nach Art und Bestimmungszweck der Schraube unterschiedliche Einstellungen.
Beispiel der Hersteller:
KSK
3 % Ca - für genaue Positionierung und weniger beanspruchte Schrauben geeignet
5 % Ca - für genaue Positionierung und durchschnittlich beanspruchte Schrauben geeignet
10 % Ca - für genaue Positionierung und höher beanspruchte Schrauben geeignet
THK
10% Ca
Stainmaier
8-10% Ca - für Muttern mit 2-Punkt-Kontakt
5-8% Ca - für Muttern mit 4-Punkt-Kontakt
Die geometrischen Hauptparameter der KS sind der Nenndurchmesser und die Gewindesteigung. Von diesen Parametern werden die Bauweise und die Verwendung abgeleitet. Von der Größe des Durchmessers hängen die Tragfähigkeit, Steifigkeit, Höchstdrehzahl ab, die Steigung mit der Drehzahl definiert dann die Vorschubgeschwindigkeiten. Andere geometrische Parameter, die die Funktionalität beeinflussen, umfassen Kugelgröße, Rillenkonstruktion, Genauigkeitsgrad, Ausführungsdurchmesser und Mutternlängen usw.
Andere wichtige Parameter wie Produktionsverfahren, Material, garantierte Genauigkeit und Schmierung bestimmen dann den spezifischen Einsatz in der vorgesehenen Konstruktion.
Obwohl Normen (ISO, ANSI) eine Reihe von Berechnungen oder Kontrollparametern enthalten, ist es immer ratsam, die Handbücher des bestimmten Herstellers mitzuberücksichtigen.
Hersteller von Schrauben mit Zollabmessungen bieten eher Standardkugelschrauben an. Dabei gilt, dass sowohl Zoll- als auch metrische Schrauben unter vergleichbaren Bedingungen die gleiche Tragfähigkeit und Nutzungsdauer aufweisen. Der größte Unterschied ist die angegebene Nutzungsdauer. Für Zollschrauben wird sie in Zoll des Vorschubs über die Nutzungsdauer angeführt, bei Herstellern von metrischen Schrauben dann in Umdrehungen über die Nutzungsdauer. Die Berechnung enthält beide Parameter.
Nach ANSI ist die dynamische Tragfähigkeit die Last, bei welcher der Bolzen die Nutzungsdauer von 1 Million Zoll Vorschub erreicht. Nach ISO wird die Lebensdauer mit 1 Million Umdrehungen berechnet.
Wenn also die Steigung weniger als 1 Zoll beträgt, ist die Tragfähigkeit gemäß der ANSI-Definition geringer als die Tragfähigkeit derselben Kugelschraube, ausgedrückt gemäß der ISO/DIN-Norm.
Umgekehrt gilt dies für eine Schraube mit einer Steigung von mehr als 1 Zoll. Bei einer Schraube mit einer Steigung von mehr als 1 Zoll ist die ANSI-Tragfähigkeit höher als die ISO-Tragfähigkeit, selbst wenn die Schraube selbst identisch ist. Um ANSI/ISO vergleichen zu können, muss die Umrechnung nach folgender Formel durchgeführt werden:
Pi [lbf] = Ca [N] / (4.44822 * (25.4 / Ph [mm])(1/3))
Wobei:
Ca [N] ...... Dynamische Tragzahl ISO
Pi [lbf] ...... Dynamische Tragzahl ANSI
Ph [mm] ... Steigung
In Normen, Literatur, Katalogen werden die Maße häufig nicht einheitlich bezeichnet. Aus diesem Grund führen wir hier die Bezeichnung für folgende Berechnung an.
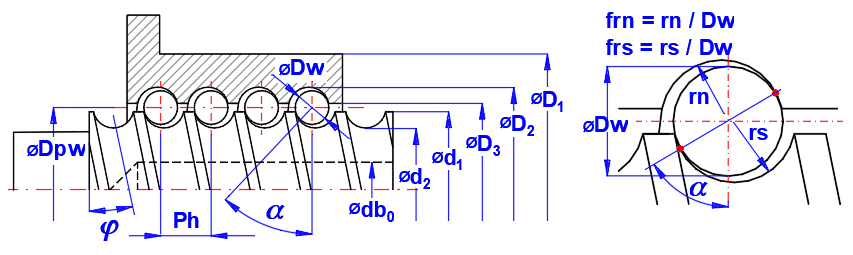
Größe des Drehzahlkennwert (Dn = d1 * ns)
Sein Wert wird hauptsächlich durch die Konstruktion der Kugelübertragung beeinflusst. Hochgeschwindigkeitsschrauben erfordern möglichst stufenlose Wege in den Übersetzern und möglichst genaue Kugelübergänge in den Übersetzer. Die Hersteller geben unterschiedliche Werte für unterschiedliche Bauweisen an, die von der Genauigkeit, der Art und Weise
der Übertragung der Kugeln (intern/extern) usw. abhängen. Meistens gilt, dass der Dn-Wert mit ansteigendem Schraubendurchmesser sinkt.
Beispiele für Dn
(Hersteller ...... Bereich)
KSK ............... 100000 - 125000
NSK ................ 80000 - 160000
Shuton .......... 100000 - 160000
PMI ................. 80000 - 220000
Steinmeyer ..... 120000 - 160000
Bei der Berechnung der Kugelschraube werden eine Reihe von Festigkeitsprüfungen und zusätzlichen Berechnungen durchgeführt. Ihre Liste und die verwendeten Formeln sind weiter unten zu entnehmen.
| Knicklast | Kritische Drehzahl | Durchbiegung | |
| Montage der Kugelumlaufspindel | Coeffb | Coeffncr | Coeffymax |
| Fest - Fest | 4 | 4.73 | 0.002604167 (1/384) |
| Fest - Stütze | 2 | 3.927 | 0.0054 |
| Stütze - Stütze | 1 | 3.14159 | 0.013020833 (5/384) |
| Fest - Freies Ende | 0.25 | 1.875 | 0.125 (1/8) |
y [m] = Coeffymax * (qm * Ls/1000)4) / ((Es * 1000000) * Ix)
Coeffymax ... Koeffizient [~]
qm ............. Eigengewichtbelastung [N/m]
Ls ............... Nicht unterstützte Länge der Kugelumlaufspindel [mm]
Es ............... Elastizitätsmodul [MPa]
Ix ............... Quadr. Trägheitsmoment [m]
t [MPa] = 16 * Mk / (p * (d2 / 1000)3) / 1000000
Mk ........ Drehmoment [Nm]
d2 ........ Innendurchmesser der Schraube [mm]
Ϭ [MPa] = 4 * F / (p * (d2 / 1000)2) / 1000000
F .......... Lastkraft [N]
Ϭred [MPa] = (Ϭ2 + 3 * t2)0.5
Fb = (Coeffb * p2 * Es * Ix) / Ls2
Coeffb ... Knickkoeffizient
ncr = (60 * Coeffncr2 / (2 * p)) * (Es * Ix * 9.81 / ((ros * 9.81 * 0.000000000001) * A * Ls4))0.5
Coeffncr ... Drehzahlkoeffizient
ros ........... Dichte [kg/m3]
Die statische Grundlast (C0a) entspricht in der Regel der zulässigen Axiallast der Kugelschraube. Abhängig von den Bedingungen muss der folgende statische Sicherheitskoeffizient gegen die maximal berechnete Last in Betracht genommen werden (unerwartete äußere Kraft durch Trägheit beim Start oder Stopp).
SFs = C0a / Fmax
Fmax ....... Maximale axiale Belastung [N]
C0a ......... Grundlegende statische axiale Tragzahl [N]
SFs .......... Sicherheitsfaktor
Seine Werte sollten größer sein als die folgenden Empfehlungen. Er wird nach dem angegebenen Belastungskoeffizient geschätzt [3.15].
Allgemeiner Maschinenbau
Keine Vibrationen oder Stößen ....... 1.0 - 3.5
Mit Vibrationen oder Stößen ........... 2.0 - 5.0
Werkzeugmaschinen
Keine Vibrationen oder Stößen ........ 1.0 - 4.0
Mit Vibrationen oder Stößen ............ 2.5 - 7.0
h = (1 - f * tan( f ))
/ (1 + f / tan( f ))
hr = (1 - f / tan( f )) /
(1 + f * tan( f ))
f .... Reibungskoeffizient
f ... Steigungswinkel
Fettschmierung: Generell werden Fette der Klasse 2 nach DIN51825 empfohlen. Während des normalen Betriebs nach 6-10 Monaten wieder auffüllen.
Ölschmierung: Im Allgemeinen werden für die Schmierung die gleichen Öle verwendet wie für Wälzlager. Empfohlene Viskosität min. 50mm2/s(cSt)
Bei der Berechnung kommen viele Normen und Informationen aus Fach- oder Firmenpublikationen zur Anwendung. In diesem Abschnitt finden Sie die verwendeten Formeln und Beziehungen ohne detaillierte Erläuterungen und Kommentare die den Originalquellen zu entnehmen sind. In den meisten Fällen werden diese Auszüge in der Originalsprache der Norm angegeben.
This part of specifies the technical acceptance conditions for ball screws and, in particular, the respective permissible deviations for the acceptance tests.
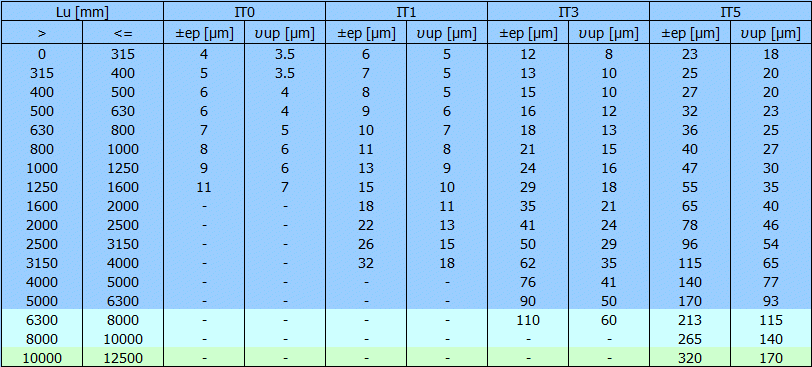
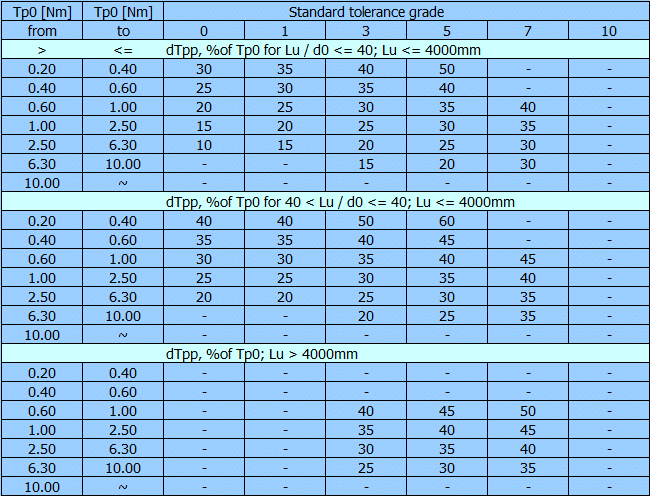
The typical tolerance grades for positioning and transport ball screws
| Type of ball screw | Standard tolerance grade |
| Positioning (type P) | 0 - 1 - 3 - 5 |
| Transport (type T) | 0 - 1 - 3 - 5 - 7 - 10 |
| Travel deviations per reference length | Positioning | Transport |
| Travel compensation c for useful travel Lu | Specified by user | C = 0 |
| Tolerance on specified travel ep | 1.1 | 1.2 |
| Permissible travel variation uup within useful travel | 2 | - |
| Permissible travel variation u300pwithin 300 mm travel | 3 | 3 |
| Permissible travel variation u2pp within 2p rad | 4 | - |
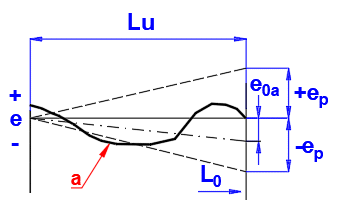
Checking of the mean travel deviations, esa and e0a, within the useful travel
Lu:
a) for the specified travel Ls
b) for the nominal travel L0
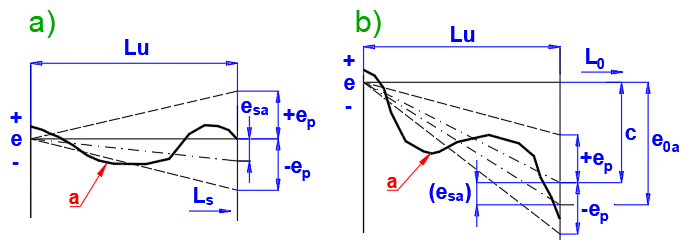
(a) Actual travel deviation
Permissible deviations
Checking of the mean travel deviation e0a, within the useful travel Lu:
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
ep = +- (Lu / 300 * u300p) [mm] |
|||||
Checking of the travel variation uu within the useful travel Lu
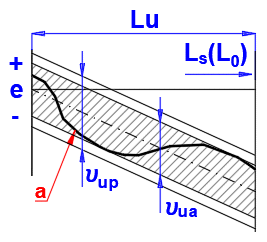
Permissible deviations

Checking of the travel variation u300pwithin 300 mm within an axial travel of 300 mm:
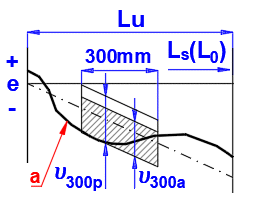
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
u300p [mm] |
|||||
| 3.5 | 6 | 12 | 23 | 52 x | 210 x |
x - Only for transport ball screws
Permissible travel variation u2pp within 2p rad
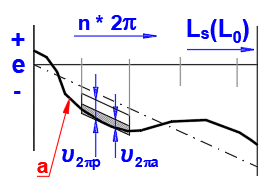
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
u300p [mm] |
|||||
| 3 | 4 | 6 | 8 | - | - |
Although is a detailed description of the measurement and the resulting values in the standard, it is advisable to consult with the manufacturer or use the company catalogs.
Positioning or transport ball screw. Measurement of dynamic preload drag torque, ΔTp:
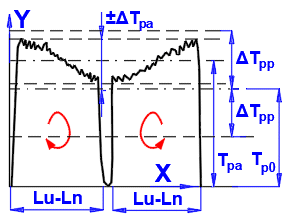
X - Travel
Y - Dynamic preload drag torque
Permissible deviations
Measurement of axial rigidity, Rnu:
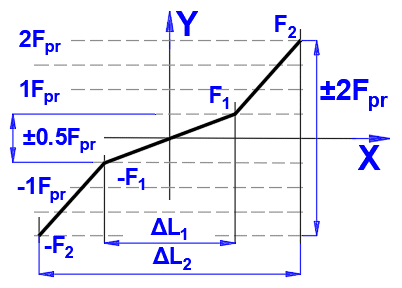
X ... Elastic deformation
Y ... Load
The axial load F1 = 0.5 * FPr or F2 = 2Fpr to the ball screw shaft in tension
and in compression.
Fpr is the preload and ΔL1 or ΔL2
are the elastic deformations (reversal range) caused by the axial test loads ±
F1 and ± F2 respectively.
Rigidity in the ranges ± F1:
Rnu1 = 2 * F1 / ΔL1 = Fpr / ΔL1
Rigidity in the range + F1 to + F2 and - F1 to - F2:
Rnu2 = 2 * (F2 - F1) / (ΔL2 - ΔL1) = 3 * Fpr / (ΔL2 - ΔL1)
Other test loads F may be used by agreement between the user and the manufacturer.
The static axial rigidity R [N/µm], constitutes the resistance to deformation and denotes the force ΔF [N], which is required to effect a component deflection ΔL by 1 µm in the axial direction of load application:
R = ΔF / ΔL
1 / Rbs = 1 / Rs + 1 / Rnu,ar
Static axial rigidity of ball screw shaft, Rs
The rigidity of the ball screw shaft follows from the elastic deflection of the ball screw shaft ΔL caused by an axial force ΔF and depends on the bearing arrangement.
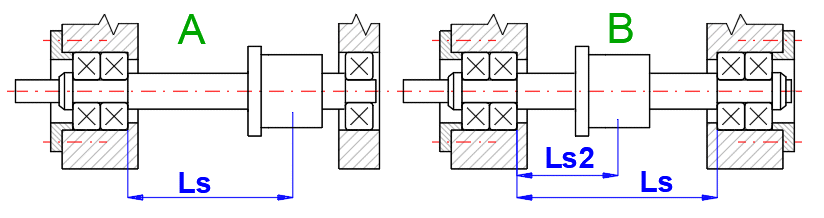

A. Rigid mounting of ball screw shaft at one end
Rs1 = (p * (dc2 - db02) * E) / (4 * Ls * 1000)
dc = Dpw - Dw * cos(a)
Dc = =Dpw + Dw * cos(a)
B. Rigid mounting of ball screw shaft at both ends
Rs2 = (p * (dc2 - db02) * E) / (4 * Ls2 * 1000) * (Ls / (Ls - Ls2))
minimum of rigidity at: Ls2 = Ls / 2
Static axial rigidity of ball nut unit with backlash: Rnu1
Static axial rigidity of nut body and screw shaft under resulting radial
components of load: Rns
Rns = ΔF / ΔLns
ΔLns = ΔF / Rns
Rns = (2 * p * i * Ph * E * tan(a)2) / (((D12 + Dc2) / (D12 - Dc2) + (dc2 + db02) / (dc2 - db02)) * 1000)
Static axial rigidity in ball / balltrack area: Rbt
The axial deflection in the ball / balltrack area is sufficiently approximated by the following equation:
ΔLns = (11)
According to Hertz the approach of the components is calculated from:
ΔLs,nb/t = (12)
Where for the screw shaft balltrack/ball contact applies:
Ʃρs = 4 / Dw - 1 / (frs * Dw) + 2 * cos(a) / (Dpw - Dw * cos(a))
For the nut bailtrack/ball contact applies:
Ʃρn = 4 / Dw - 1 / (frn * Dw) - 2 * cos(a) / (Dpw + Dw * cos(a))
The auxiliary values Ysn depend upon the ratio of the semi-major to the semi-minor axes of the contact ellipse cos(t). The following equation makes use of sin(t), which can be obtained by:
sin(t) = (1 - cos(t)2)0.5
Ys,n = 1.282 * (-0.154 * sin(t)0.25 + 1.348 * sin(t)0.5 - 0.194 * sin(t))
cos(ts) = abs[(-1 / (frs * Dw) - 2 * cos(a) / (Dpw - Dw * cos(a))) / Ʃρs]
cos(tn) = abs[(-1 / (frn * Dw) + 2 * cos(a) / (Dpw - Dw * cos(a))) / Ʃρn]
cEs,n = (11550 * (E0s,n + E0b) / (E0s,n * E0b))1/3
Es = En = Eb = 210000
ms = mn = mb = 10 / 3
E0s = E0n = E0b = E0
cEs = cEn = cEb =0.4643
FN = F / (i * z1 * cos(φ) * sin(a))
z1 = INTEGER ((Dpw * p) / (cos(φ) * Dw) - z2)
φ = arctan (Ph / (Dpw * p)
The rigidity characteristic k of one loaded turn of the ball screw is calculated from:
k = (z1 * sin(a)5/2 * cos(φ)5/2) / (cE3 * ck3/2)
ck = Ys * (Ʃρs)1/3 + Yn * (Ʃρn)1/3
Thus, the axial deflection due to Hertz stress exerted on a single nut can be calculated:
ΔLb/t = (F / (k * i))2/3
d(ΔLb/t) = 2/3 * F-1/3 * (1 / (k * i)2/3) * dF
The static axial rigidity of the ball/balltrack area Rb/t at the axial force F is:
Rb/t = dF / d(ΔLb/t) = 3/2 * (Fe * (i * k)2)1/3
1 / Rnu1 = 1 / Rb,t + 1 / Rn,s
Static axial rigidity of symmetrically preloaded ball nut unit: Rnu2,4
Static axial rigidity of nut body and screw shaft under preload, Rn/s,pr
As both nut bodies act like preloaded rings, the rigidity, Rn/s,pr of a double
nut is twice as high as that of a single nut:
Rn/s,pr = 2 * Rn/s
Static axial rigidity of ball/balltrack area under preload: Rn/t,pr
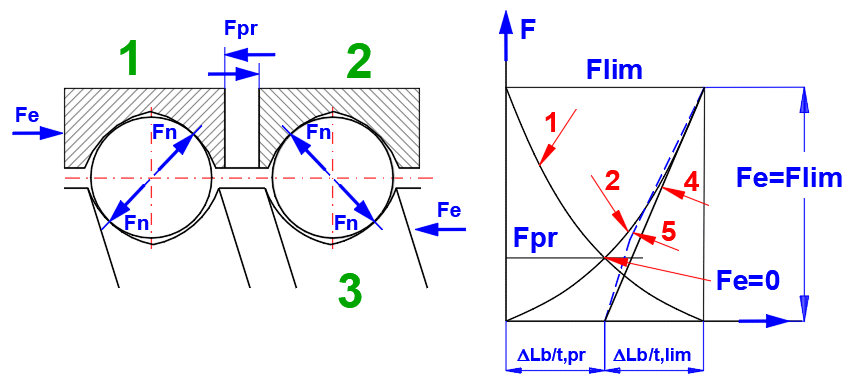
1. ball nut 1
2. ball nut 2
3. ball screw shaft
4. straight approximation line
5. actual curve
(5) Actual curve of the axial deflection in the ball/balltrack area of the
preloaded ball nut system if an additional external load between Fc = 0 and Fc =
Flim is applied.
Maximum deviation between 4 and 5 is approximately 6 %.
The following equation will furnish a guide value for symmetric double nuts:
Fpr = Fm / 23/2
Fm ..... Equivalent load (ISO 3408-5)
Fm = (Ʃ Fej3 * (nj / nm) * qj)(1/3) <j = 1 ... n>
The axial deflection of the ball/balltrack area due to the preload of a symmetrically preloaded nut system:
ΔLb/t,pr = (Fpr / (k * i))2/3
For 0 < Fe <= Flim, the rigidity Rb/t in the ball/balltrack area is determined as follows:
Flim = 23/2 * Fpr
Aproximation result
Rb/t = 23/2 * (Fpr * (k * i)2)1/3
Single or double ball nut preloaded by two-point-ball-contact: Rnu2
1 / Rnu2 = 1 / Rb/t + 1 / Rn/s,pr
Single ball nut preloaded by four-point-ball-contact: Rnu4
1 / Rnu4 = 1 / Rb/t + 1 / Rn/s,pr
As tolerances accumulate during the manufacturing process, differences occur
in rigidity evaluations.
The correction factor takes into account the following influences: machining
inaccuracies of balltrack (travel variations, groove, surface roughness, contact
angle, diameter).
Correction factor for accuracy far
| Accuracy class | far |
| 0, 1 | 0.60 |
| 3 | 0.55 |
| 5 | 0.50 |
| 7, 10 | 0.40 |
The static axial rigidity of the ball nut unit calculated with the
corresponding correction factor is:
Rnu,ar = far * Rnu
Calculations are based on the definition of the dynamic load capacity, under which the ball screw reaches 1 million revolutions. More specifically this means that 90% of a sufficiently large number of identical ball screws will reach this value or service life. This durability or capacity is usually marked as L10. For higher reliability than 90% it is necessary to use the appropriate “far” correction factor.
Basic formula for the nominal life calculation
L = (Ca / Fm)3 * 106
L ...... Life [revolutions]
Ca ... Basic dynamic axial load rating [N]
Fm ... Ekquivalent axial load [N]
and
Lh = L / (60 * nm)
Lh ..... Life [hodiny]
nm .... Equivalent rotational speed [/min]
L1,2 = (Ca / Fm1,2)3 * 106
L1,2 = (Ca / Fma1,2)3 * 106
Lr = (L1-10/9 + L2-10/9)-9/10
Lar = L * far; resp. Lar = Lr * far
far ... Reliability factor
| Reliability [%] | far |
| 90% | 1.00 |
| 95% | 0.62 |
| 96% | 0.53 |
| 97% | 0.44 |
| 98% | 0.33 |
| 99% | 0.21 |
In the same way, the modified life
Lm, Lhm is calculated:
Lm = (Cam / Fm)3 * 106
;Lhm = Lm / (60 * nm); Lm1,2 = (Cam / Fm1,2)3 * 106
...............
L = (Ca / (fw * Fm))3 * 106
fw ... Load factor
In the case of variable rotational speed and variable axial load, the equivalent values Fm and nm are used for the life calculation:
At variable rotational speed the following applies for the equivalent rotational speed nm [/min]:
nm = Ʃ (qj / 100) * nj <j = 1 ... n>
q ... Time [%]
n ... Rotational speed [/min]
At variable axial load and variable rotational speed, the following applies for the equivalent axial load Fm [N]:
Fm = (Ʃ Fj3 * (nj / nm) * (qj / 100))(1/3) <j = 1 ... n>
F ... Axial load, force [N]
Fm1,2 = (Ʃ F1,2j3 * (nj / nm) * (qj / 100))(1/3) <j = 1 ... n>
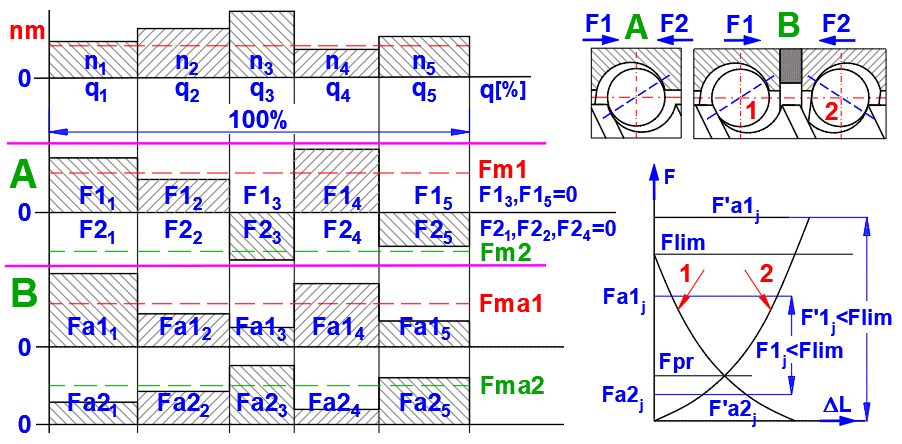
Due to the application of an external axial load to a preloaded ball screw (backlash elimination between nuts and screw shaft), one ball nut will be additionally loaded and the other relieved.
Flim = 23/2 * Fpr
The preloaded ball nut (1) or (2)
will be additionally loaded by an external axial load. The actual axial load to
this ball nut is
- for the external load F1j or F2j <= Flim, the following equation:
Fa1,2 = fop * Fpr * (1 + F1,2j / (23/2 * fop * Fpr)3/2
fop ... Operational preload factor (0.6)
F ... Axial load, force [N]
Fa .... Actual axial load [N]
Fpr ... Preload [N]
- for the external load F1j or F2j > Flim, then:
Fa1j = F1j , Fa2j = F2j and Fa1j = 0, Fa2j = 0
For the calculation for the equivalent actual axial load:
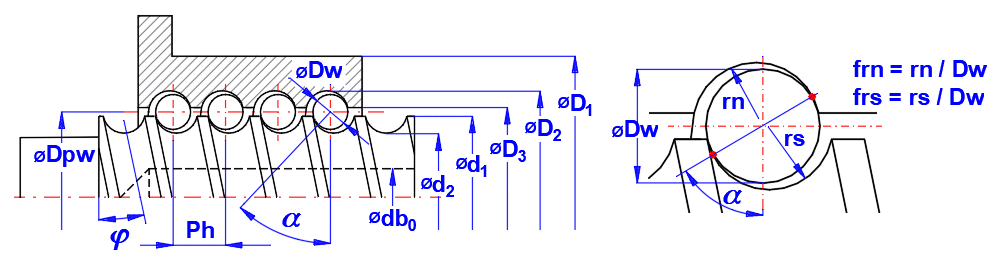
The basic axial load rating is calculated from the following equations:
C0a = k0 * z1 * i * sin(a)
* Dw2 * cos(φ)
z1 = INTEGER ((Dpw * p)
/ (cos(φ) * Dw) - zu)
φ
= arctan (Ph / (Dpw *
p)
k0 = 27.74 / (Dw * (( ρ11 +
ρ12) * ( ρ21 +
ρ22))0.5
ρ11 = ρ21
= 2 / Dw
ρ12 = -1 / (frs * Dw)
ρ22 = cos(a)
/ (Dpw / 2 - cos(a) * Dw / 2)
a ........ Contact angle [°]
φ
........ Lead angle [°]
i ......... Number of loaded turns
[~]
Dw ..... Ball diameter [mm]
Dpw ... Ball pitch circle diameter
In the case of optimal load distribution (parallel
load directions in ball screw shaft and in ball nut), the basic dynamic axial
load rating is derived from the following basic interrelations:
Ca = Ci * i0.86
Ci = Cs * (1 + (Cs / Cn)10/3)-0.3
Cs = fc * cos(a)0.86
* z12/3 * Dw1.8 * tan(a) * cos(φ)1.3
fc = 9.32 * f1 * f2 * (1 / (1 - 1 / (2 * frs)))0.41
f1 = 10 * (1 - sin(a) /
3)
f2 =
g0.3
* (1 -
g)1.39 / (1 +
g)1/3
g = Dw / Dpw *
cos(a)
Cs / Cn = f3 * ((2 - 1 / frn) / (2 - 1 / frs))0.41frn = rn / Dw
frs = rs / Dw
f3 = ((1 -
g) / (1
+ g))1.7233
C0am = C0a * fh0 * fac
Correction for surface hardness, fh0
fh0 = (AH / 654)3 ≤ 1.0
AH ... actual hardness [HV10]
Correction for accuracy, fac
| Accuracy class | fac |
| 0, 1, 3, 5 | 1.00 |
| 7 | 0.90 |
| 10 | 0.70 |
Cam = Ca * fh * fac * fm
Correction for surface hardness, fh
fh = (AH / 654)2 ≤ 1.0
AH ... actual hardness [HV10]
Correction for accuracy, fac is the same as for static axial load
Material factor fm
| Ball bearing steel | fm |
| Air melted | 1.00 |
| Vacuum degassed | 1.25 |
| Electro slag remelted | 1.44 |
| Vacuum remelted | 1.71 |
The following equations for the basic load rating and static thrust capacity are included to enable the user of this standard to determine the approximate size ball screw assembly necessary to meet requirements.
Imperial (Inch) System Symbols
Pi ...... Basic load rating (1 000 000 inches rated life), [lbf]
Pix .... Rated load at x inches rated life, [lbf]
Ti ...... Basic thrust capacity, [Ibf]
LIi ..... 1 000 000 inches rated life, [inches]
LIix ... X inches rated life, [inches]
di ...... Ball diameter, [inches]
n ....... Number of ball turns under a unidirectional load, [turns]
Li ...... Lead, [inches / revolution]
Z ....... Number of load carrying balls per turn, [balls
/ turn]
Pi = 4500 * Z2/3 * di1.8 * n0.86 * Li1/3 , [lbf]
Ti = 10 000 * n * Z * di2 , [lbf]
Pix = Pi * (LIi / LIix)1/3 , [lbf]
In der Regel ist der Entwurf nicht direkt lösbar und es ist eine laufende Konkretisierung der Parameter erforderlich. Für die häufigsten Lösungen, wenn Sie die Belastungskräfte, Vorschubgeschwindigkeiten und die Positioniergenauigkeit kennen, empfehlen wir folgende Vorgehensweise.
1. Wählen Sie in Absatz [1.0] die Einheiten aus und führen Sie den Vorentwurf durch. Überprüfen Sie die Genauigkeitsanforderungen.
2. In Absatz [3.0] die Schraubenparameter (Durchmesser, Steigung, Genauigkeit, Belastung ...) auf der Grundlage des Vorentwurfs auswählen / eingeben.
3. Wenn Sie die erschwerenden Parameter nicht genau kennen, fahren Sie mit den Absätzen [10.0] und [11.0] fort.
Hier können Sie eine Belastungstabelle [10.0] definieren und die äquivalente Belastung [11.0] berechnen.
(Für eine genaue Berechnung der Last ist es erforderlich, die Abmessungen der Schraube zu kennen, daher ist es angebracht, für ihre Schätzung den Vorentwurf anzuwenden)
4. Nach Eingabe / Änderung der Eingabeparameter [3.3-3.44] können Sie sofort die wichtigsten Parameter [3.45-3.57] überprüfen.
5. Eine detaillierte Liste aller Ergebnisse finden Sie im Kapitel Ergebnisse.
Der Entwurf der Kugelschraube ist nicht direkt und einfach lösbar. Beim Entwerfen muss eine Reihe häufig widersprüchlicher Anforderungen berücksichtigt werden, und die Lösung ist durch schrittweise Konkretisierung des Entwurfs gemeinsam mit der Kontrolle der Parameter der Schraube im Katalog des Herstellers (Lieferanten) zu finden.
Daher ist es in diesem Kapitel möglich, die Abmessungen der Schraube grob zu entwerfen, die Umdrehungen und den Vorschub zu entwerfen, die kritischen Umdrehungen zu überprüfen, die Schraube auf Knick zu überprüfen und die Genauigkeit und erforderliche Motorleistung zu bestimmen. In den nachstehenden Kapiteln kann man dann den Vorentwurf optimieren und alle Parameter im Detail entwerfen und überprüfen.
In einer Auswahlliste das benötigte Einheitssystem der Berechnung wählen. Beim Umschalten der Einheiten werden sofort alle Eingangswerte umgerechnet.
Gleichzeitig werden die Auswahltabellen so neu eingestellt, dass sie den ausgewählten Einheiten (ISO/ANSI) entsprechen.
Die meisten Aufgaben erfordern die Lösung der Geschwindigkeit des Wagens (Mitnehmers) in Abhängigkeit von Steigung, Umdrehungen der Schraube, Übersetzung und Motordrehzahl. Sie können dies in diesem Abschnitt lösen. Aktivieren Sie die Option rechts neben den Eingabezellen, um anzugeben, welcher Wert berechnet werden soll.
Der Bereich der Steigung Ph in Bezug auf den Durchmesser der Schraube d1 ist in der Tabelle [1.32] angegeben. Folgen Sie dem Bild bei der Auswahl der Werte.
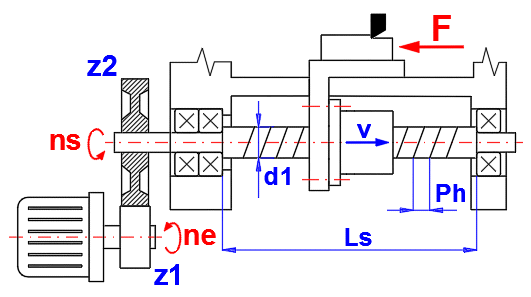
Standardreihe der Steigung - mm (ISO, JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardreihe der Steigung - inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Für Ihre Auswahl können Sie die Liste rechts verwenden.
Das Übersetzungsverhältnis ist definiert als das Verhältnis der Anzahl der Zähne i = z2/z1. Wenn Sie einen direkten Schraubenantrieb verwenden, ist i = 1.
1. Geben Sie die äquivalente Schraubenbelastung ein [1.9]. Geben Sie einfach Ihre Schätzung der Schraubenbelastung ein (Welches Gewicht heben Sie an, mit welcher Kraft drücken Sie, welche Kraft wirkt während der Bearbeitung ...). Vergessen Sie nicht, die Auswirkungen von Vibrationen und Stößen zu berücksichtigen, da bei starken Stößen und Vibrationen die Last 2x, 3x größer sein kann (siehe Koeffizient fw [1.11]).
2. Geben Sie die äquivalente Drehzahl ein [1.10]. Ungefähr die Drehzahl, bei welcher die Schraube meist beansprucht wird.
3. Geben Sie die erforderliche Haltbarkeit in Stunden ein [1.11]. (Für vorläufige Zwecke können Sie einen Wert von ca. 20.000 Stunden auswählen)
Basierend auf der angegebenen äquivalenten Lastkraft, Drehzahl und erforderlichen Haltbarkeit wird die erforderliche dynamische Tragfähigkeit "Ca-req" ("Pi-req" nach ANSI) berechnet. Der Durchmesser der Schraube richtet sich nach der dynamischen Tragfähigkeit. Der vorgeschlagene Schraubendurchmesser reicht vom Minimalwert des Durchmessers der Mutter mit fünf Gewinden bis zum Maximalwert des Durchmessers der Mutter mit einem Gewinde. Die Anzahl der Gewinde ist in Klammern nach dem Durchmesser angegeben.
Wenn die Schaltfläche aktiviert ist, werden die Werte aus Zeile [1.5] automatisch übertragen.
fw = 1.0 … 1.2 für nahezu keine Vibration, keine Stoßbelastung (v ≤ 0.25 m / s)
fw = 1.2 … 1.5 für leichte Vibration, Stoßbelastung (0.25 <v ≤ 1.00 m / s)
fw = 1.5 … 2.0 für mittlere Vibration, Stoßbelastung (1.00 <v ≤ 2.00 m / s)
fw = 2.0 … 3.5 für starke Vibrationen, Stoßbelastung (v> 2.00 m / s)
Man kann von mehreren Eingabemöglichkeiten wählen. Bei mm-Schrauben wird die Nutzungsdauer in Stunden verwendet (seltener in Umdrehungen der Schraube). Bei Zollschrauben dann die Nutzungsdauer in Zoll (oder in [m]) des Vorschubs. Bei einer Änderung wird der Eingabewert automatisch neu berechnet, sodass die erforderliche dynamische Tragfähigkeit gleich bleibt.
Orientierungswerte in Stunden sind in
der Tafel angeführt.
Maschinen für kurzzeitigen Betrieb 5000 - 10000
8-Stundenbetrieb 20000
16-Stunden-Betrieb 40000
Maschinen für durchgehenden Betrieb 80000
Basierend auf Belastung, Drehzahl und erforderlicher Nutzungsdauer wird die erforderliche dynamische Tragfähigkeit berechnet. Die ausgewählte Schraube sollte eine höhere Tragfähigkeit haben.
Dies ist ein Wert, der von einem ISO-Wert in einen ANSI-Wert umgerechnet wird. Mehr im theoretischen Teil der Hilfe.
Der vorgeschlagene Schraubendurchmesser reicht von einem Minimalwert mit fünf Muttergewinden bis zu einem Maximalwert des Durchmessers einer Schraube mit einem Gewinde.
Der Durchschnitt wird aufgrund der gemäß ISO3402-5 berechneten Ca-Tragfähigkeit entworfen.
Nach der Wahl der Art und Weise der Lagerung und Eingabe der Länge und des Durchmessers der Schraube (siehe Bilder) werden alle wichtigen Kontrollwerte berechnet. Sie können sofort den Wert des Geschwindigkeitsfaktors, die maximale Knickkraft und die maximal zulässige Drehzahl überprüfen. Gleichzeitig können Sie die Toleranzklasse der Schraube in Abhängigkeit von der erforderlichen Positioniergenauigkeit abschätzen.
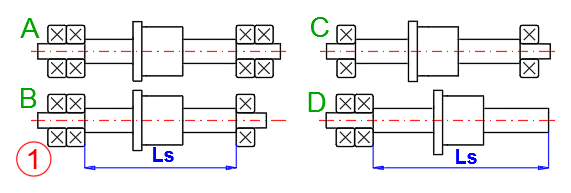
Wählen Sie die Art der radialen Lagerung der Kugelschraube wie abgebildet. Die Montagemethode beeinflusst die Knickbruchfestigkeit und die kritische Drehzahl. Bei einer rotierenden Mutter ist es nicht erforderlich, die kritische Drehzahl zu überprüfen.
Geben Sie die Länge des nicht abgestützten Teils der Schraube Ls ein (siehe Abbildung). Im Allgemeinen werden Längen empfohlen, die kleiner als 40 Schraubendurchmesser sind.
Standardbereich von ISO-Durchmessern [mm]
6, 8, 10, 12, 16, 20, 25, 32, 40, 50, 63, 80, 100, 125, 140, 160, 200
Vom Hersteller verwendete Durchmesser [mm]
4, 6, 8, 10, 12, 14, 15, 16, 20, 25, 28, 32, 36, 40, 45, 50, 63, 80, 100, 125, 140, 160, 200
Standardbereich von ANSI B5.48-1977-Durchmessern [in]
0.25, 0.3125, 0.375, 0.5, 0.625, 0.75, 0.875, 1, 1250, 1.5, 1.75, 2, 2.25, 2.5, 3, 3.5, 4, 4.5, 5, 6, 8
Größe des Drehzahlkennwert (Dn = d1 * ns)
Sein Wert wird hauptsächlich durch die Konstruktion der Kugelübertragung beeinflusst. Hochgeschwindigkeitsschrauben erfordern möglichst stufenlose Wege in den Übersetzern und möglichst genaue Kugelübergänge in den Übersetzer. Die Hersteller geben unterschiedliche Werte für unterschiedliche Bauweisen an, die von der Genauigkeit, der Art und Weise der Übertragung der Kugeln (intern/extern) usw. abhängen. Meistens gilt, dass der Dn-Wert mit ansteigendem Schraubendurchmesser sinkt.
Beispiele für Dn
(Hersteller ...... Bereich)
KSK ............... 100000 - 125000
NSK ................ 80000 - 160000
Shuton .......... 100000 - 160000
PMI ................. 80000 - 220000
Steinmeyer ..... 120000 - 160000
Wird zur Berechnung des Wirkungsgrades verwendet. Für den Vorentwurf kann ein Wert von 0.01 gewählt werden.
Abhängig von der Länge der Schraube Ls wird auch die Toleranz für einzelne Toleranzklassen bestimmt. Anhand der Werte aus der Tabelle können Sie auch die erforderliche Genauigkeit der Schraube abschätzen/auswählen.
ISO: Für Positionierschrauben (P-type) wird IT0-IT5, für Transportschrauben (T-type) dann IT1-IT10 angewendet.
ANSI: Verwendete Skala Class1 bis Class8.
Detaillierte Erklärung im theoretischen Teil und Kapitel [6.0].
Die Tabelle zeigt die Schraubendurchmesser und den Steigungsbereich gemäß ISO und ANSI. Mit Sternchen werden Durchschnittswerte markiert, die von einigen Herstellern über den Rahmen der ISO-Norm angeboten werden.
Nach Auswahl der Schraube aus der Tabelle wird der Wert des Durchmessers in Zeile [1.19] übertragen.
In diesem Absatz können Materialparameter definiert werden. In den allermeisten Fällen ist die Grundeinstellung für Stahl entsprechend. Zum Einstellen die Taste drücken. Nur ein Spezialist oder der Hersteller sollte diese Werte ändern.
In diesem Abschnitt definieren Sie alle Eingabeparameter der Übersetzung mit Kugelschraube. Beginnend mit Genauigkeit, Verlegung der Schraube, Belastung, Länge, Tragfähigkeit usw. Nach der Definition aller Parameter stehen alle Schraubenparameter im Kapitel "Ergebnisse" zur Verfügung, die in der Praxis ausgewertet und überwacht werden.
Verwenden Sie bei der Auswahl von Parametern die Hilfe für jeden Parameter. Vorteilhafterweise können Sie auch zusätzliche Berechnungen aus dem Kapitel "Zusätze" verwenden.
Nach Betätigen der Taste "[1.0]>>[3.0]" werden die Werte (Ph, Fm, nm, fw, L, Ls, d1) aus dem Vorentwurf in diesen Absatz übernommen.
Wenn die Auswahl aus Tabelle [3.26] eingestellt ist, wird die entsprechende Schraube d1 (oder die nächsthöhere) gefunden.
In diesem Abschnitt definieren Sie Genauigkeit, Konstruktion, Belastung und Haltbarkeit.
Auf der Grundlage des Bestimmungszwecks der Schraube und des Vorentwurfs sollten Sie in der Lage sein, die geeignete Toleranzklasse auszuwählen. Die Toleranzklassen IT0-IT5 werden für Schrauben verwendet, die zur Positionierung bestimmt sind, und die Toleranzklassen IT1-IT10 werden für Transportschrauben verwendet.
Die Wahl der Toleranzklasse beeinflusst in erster Linie die Positioniergenauigkeit, Toleranzen (Absatz [6.0]), in geringerem Maße die Tragfähigkeit, die erreichte Geschwindigkeit und natürlich den Preis.
Im Standardmaschinenbau arbeiten wir mit 90 % Zuverlässigkeit. Dies bedeutet, dass 90 % der Schrauben die deklarierte Beanspruchung bei der erforderlichen Nutzungsdauer aushalten. Es gibt jedoch Branchen, in denen eine höhere Zuverlässigkeit erforderlich ist (Luftfahrt, Raumfahrt, Kernenergiewirtschaft ...). Daher ist es möglich, die erforderliche Zuverlässigkeit einzustellen, die sich auf die erforderliche dynamische Tragfähigkeit auswirkt.
Wählen Sie die Art der radialen Lagerung der Kugelschraube wie abgebildet. Die Montagemethode beeinflusst die Knickbruchfestigkeit und die kritische Drehzahl. Bei einer rotierenden Mutter ist es nicht erforderlich, die kritische Drehzahl zu überprüfen.

In der Praxis werden zwei Methoden der axialen Lagerung der Enden verwendet. Im ersten Fall ist ein Ende fest verankert und das andere Ende ist in Richtung der Schraubenachse frei, im zweiten Fall sind beide Enden fest verankert. Der zweite Fall wird verwendet, wenn die Schraube vorgespannt werden muss (z. B. Eliminierung der Wärmeausdehnung, Erhöhung der axialen Steifheit usw.).
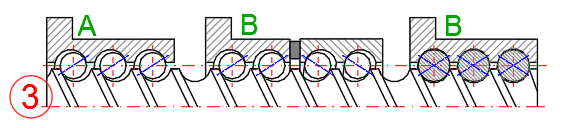
Es werden zwei Arten von Muttern verwendet.
A. Keine Vorspannung. Es wird davon ausgegangen, dass die Genauigkeit und Belastung nur in einer Bewegungsrichtung wichtig sind. Bei der Wahl der entgegengesetzten Bewegungsrichtung ist das Spiel zu berücksichtigen.
B. Mit Vorspannung. Die Mutter ist strukturell so ausgebildet, dass beim Übergang von einer Richtung in die andere kein Spiel vorhanden ist. Die Konstruktionslösung kann eine Reihe von Varianten aufweisen, und je nach Konstruktionsanforderungen ändert sich auch die Größe der Vorspannung (in der Regel muss dies mit dem Lieferanten abgestimmt werden).
Die vorgespannte Mutter und die Größe der Vorspannung beeinflussen dann die Berechnung der äquivalenten Schraubenbelastung. Dies können wir uns so vorstellen, dass die Vorspannung auch dann eine Kraft erzeugt, wenn die Mutter nicht belastet wird, diese Kraft muss bei der Berechnung der äquivalenten Belastung berücksichtigt werden.
Bei der Bestimmung der Kraft für die Berechnung der äquivalenten Belastung treten drei Fälle auf.
- Keine Belastungskraft. Die Vorspannkraft ist in beide Richtungen aufgeteilt.
- Die Ladekraft ist kleiner als Flim. Die Belastungskraft ist gemeinsam mit der Vorspannkraft proportional in beide Richtungen verteilt.
- Die Belastungskraft ist größer als Flim. Die Belastungskraft übersteigt die Vorspannkraft und wird nur in der entsprechenden Richtung berücksichtigt.
Eine ausführliche Beschreibung finden Sie in Absatz [11.0].
Geben Sie die Last in der einen und der anderen Richtung ein. Bei variabler Belastung dann die äquivalente Belastung, siehe Absatz [11.0].
Geben Sie die maximale axiale Belastung ein. Muss größer oder gleich Fma1, Fma2 sein.
Geben Sie die Drehzahl in einer und der anderen Richtung ein. Bei variablen Geschwindigkeiten dann die äquivalente Drehzahl, siehe Abschnitt [11.0].
Geben Sie die Höchstdrehzahl ein. Muss größer oder gleich nm1, nm2 sein.
Entsprechend der erforderlichen Positioniergenauigkeit und der erforderlichen Steifigkeit wird die Methode zum Zusammenpassen der Mutter an der Welle ausgewählt. Mit zunehmender Vorspannung nimmt die Haltbarkeit ab. Mutter mit Spiel – Einwegbelastung Last Fpr = 0.
Die Größe der Vorspannung wird normalerweise im Katalog angegeben oder kann mit dem Lieferanten abgestimmt werden. Im Allgemeinen werden die folgenden Vorspannungswerte verwendet, ausgedrückt in Prozent der dynamischen Tragfähigkeit der Ca-Schraube:
3 % Ca - für genaue Positionierung und weniger beanspruchte Schrauben geeignet
5 % Ca - für genaue Positionierung und durchschnittlich beanspruchte Schrauben geeignet
8 % Ca - für Muttern mit 2-Punkt-Kontakt
10 % Ca - für genaue Positionierung und höher beanspruchte Schrauben geeignet
fw = 1.0 … 1.2 für nahezu keine Vibration, keine Stoßbelastung (v ≤ 0.25 m / s)
fw = 1.2 … 1.5 für leichte Vibration, Stoßbelastung (0.25 <v ≤ 1.00 m / s)
fw = 1.5 … 2.0 für mittlere Vibration, Stoßbelastung (1.00 <v ≤ 2.00 m / s)
fw = 2.0 … 3.5 für starke Vibrationen, Stoßbelastung (v> 2.00 m / s)
Man kann von mehreren Eingabemöglichkeiten wählen. Bei mm-Schrauben wird die Nutzungsdauer in Stunden verwendet (seltener in Umdrehungen der Schraube). Bei Zollschrauben dann die Nutzungsdauer in Zoll (oder in [m]) des Vorschubs. Bei einer Änderung wird der Eingabewert automatisch neu berechnet, sodass die erforderliche dynamische Tragfähigkeit gleich bleibt.
Orientierungswerte in Stunden sind in
der Tafel angeführt.
Maschinen für kurzzeitigen Betrieb 5000 - 10000
8-Stundenbetrieb 20000
16-Stunden-Betrieb 40000
Maschinen für durchgehenden Betrieb 80000
Basierend auf Belastung, Drehzahl und erforderlicher Nutzungsdauer wird die erforderliche dynamische Tragfähigkeit berechnet. Die ausgewählte Schraube sollte eine höhere Tragfähigkeit haben.
Dies ist ein Wert, der von einem ISO-Wert in einen ANSI-Wert umgerechnet wird. Mehr im theoretischen Teil der Hilfe.
Wählen Sie in diesem Abschnitt die entsprechende Schraube (Mutter) aus oder geben Sie die entsprechenden Parameter aus dem Herstellerkatalog ein.
Geben Sie die Länge des nicht abgestützten Teils der Schraube Ls ein (siehe Abbildung). Im Allgemeinen werden Längen empfohlen, die kleiner als 40 Schraubendurchmesser sind.
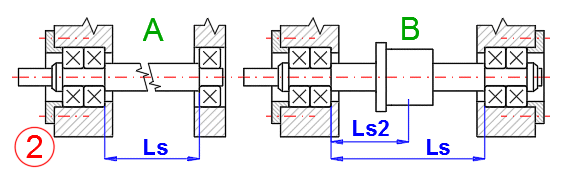
Geben Sie bei doppelseitiger axialer Halterung der Schraube (Variante B) auch die Koordinate der Mutter Ls2 ein.

Die Anzahl der Gewinde wird durch die Konstruktion der Mutter bestimmt und normalerweise vom Hersteller angegeben. Angewendet wird die Anzahl der Gewinde im Bereich von ungefähr 1,5 bis 6,0. Die Anzahl der Gewinde beeinflusst die Berechnung der statischen und dynamischen Tragfähigkeit, Steifigkeit und Länge der Mutter.
Geben Sie die Anzahl der nicht belasteten Kugeln ein. Es handelt sich um Rückführsysteme, bei denen die Kugeln nach einer Umdrehung und normalerweise zu = 3 zurückgeführt werden. Bei Rückführsystemen, bei denen die Kugeln vom letzten Gewinde zum ersten zurückgeführt werden, gilt zu = 0. Informationen zur konkreten Konstruktion finden Sie meistens im Herstellerkatalog.
Der Koeffizient drückt eine ungleichmäßige Lastverteilung bei mehreren Gewinden an einer Mutter aus. Wenn also die Mutter mehrere Gewinde hat, wird die Tragfähigkeit Ca nach der Formel Ca=Ca(1)*i^exp, wobei Ca(1) die Tragfähigkeit pro Gewinde ist. Ähnliches gilt für Pi (Zollschrauben).
Die Berechnung enthält zwei grundlegende Tabellen für Schraubenmaße. Millimeter (ISO) und Zoll (ANSI). Die Tabellen enthalten alle Kombinationen aus dem Durchmesser der Schraube und Steigung. Hersteller halten diese Grundabmessungen ein (oder bieten mehrere Schraubendurchmesser an). Die Wahl der Kugeldurchmesser ist jedoch beliebig. Basierend auf der Analyse einer großen Anzahl von Herstellerkatalogen haben wir auch eine Tabelle der eingesetzten Kugeldurchmesser und deren Zuordnung zu den Durchmessern von Schrauben erstellt. So entstand eine Reihe, die als leicht, mittel und schwer bezeichnet wird (Größe der Kugeln). Für welche auch die einschlägigen Werte nachberechnet wurden C0a,Ca,Ti,Pi.
Die Herstellerkataloge sind dann eine Untermenge dieser Tabellen, und es ist meistens möglich, eine konkrete Schraube zu finden, die den berechneten Parametern entspricht.
Wählen Sie die entsprechende Schraube aus der Liste. Sie sollte die Bedingung erfüllen, dass der Wert der dynamischen Tragfähigkeit Ca> Ca-reg [3.17] (bzw. Pi> Pi-reg [3.18] für Zollschrauben) ist. Gleichzeitig sollte der Wert der Steigung Ph aus dem Vorentwurf [1.0] beachtet werden, in welchem Sie die Bewegungsgeschwindigkeit der Mutter und damit die erforderliche Steigung Ph definieren.

Das innere Loch der Schraube dient zur Installation der Kühlung oder zur Änderung der kritischen Drehzahl. Die meisten Schrauben sind ohne Loch db0 = 0.
Der Durchmesser ist in der Regel eine Frage der Konstruktion des Herstellers. Natürlich kann er nicht beliebig gewählt werden. Die Grundbedingung lautet, dass der Durchmesser Dw nicht größer sein darf als die Steigung Ph.
0.600, 0.800, 1.000, 1.200, 1.250, 1.500, 1.588, 1.750, 2.000, 2.381, 2.500, 3.000, 3.175, 3.500, 3.969, 4.762, 5.000, 5.556, 6.000, 6.350, 7.144, 7.938, 8.000, 9.525, 10.000, 10.319, 12.700, 20.000, 20.638, 25.400, 30.000, 31.750, 38.100, 40.000, 44.450, 50.000
Standardreihe der Steigung - mm (ISO, JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardreihe der Steigung - inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Der Teilkreisdurchmesser wird aus dem Durchschnitt von d1 und Dw berechnet. Wenn Sie einen benutzerdefinierten Wert eingeben möchten, deaktivieren Sie die Schaltfläche rechts.
In den meisten Fällen beträgt er 45 °.
Die Schmiegung frn ist das Verhältnis des Kugellaufbahnradius der Kugelgewindemutter zum Nenndurchmesser der Kugel. Die Schmiegung frs ist das Verhältnis des Kugellaufbahnradius der Kugelgewindespindel zum Nenndurchmesser der Kugel.
Wenn Sie Ihre eigenen Schraubenparameter definieren, geben Sie die Tragfähigkeit aus dem Herstellerkatalog ein.
Der Wert wird nach DIN69051-5 vorgeschlagen.
Der Wechselschalter dient zur Anzeige (siehe Abbildung rechts), zur Berechnung der Mutterlänge [3.43] und des Arbeitswegs [3.44] sowie zur Ausgabe in CAD.
Nachdem Sie die Schaltfläche rechts deaktiviert haben, können Sie Ihren eigenen Wert eingeben.
In diesem Abschnitt werden die wichtigsten Werte aus dem Kapitel Ergebnisse aufgelistet.
In diesem Abschnitt sind die Lebensdauer gemäß ISO3408-5 (ANSI_B5.48) aufgeführt.
Wenn die Schraube nur in einer Richtung belastet wird (Fma1 oder Fma2 = 0; [3.8,3.9]) und keine vorgespannte Mutter verwendet wird, wird eine einfache Haltbarkeitsberechnung verwendet.
Dieser Teil enthält zwei Möglichkeiten.
- In beiden Richtungen beanspruchte Schraube (ohne vorgespannte Mutter).
- In einer sowie zwei Richtungen belastete Schraube mit vorgespannter Mutter. Die vorgespannte Mutter verursacht eine zusätzliche interne Belastung der Schraube (in beiden Richtungen), die auch bei der Belastung in einer Richtung berücksichtigt werden muss.
Die Berechnung berücksichtigt dann für die Berechnung der Haltbarkeit die Beanspruchung in beiden Richtungen. (Index 1,2 zeigt die Richtung an).
Dieser Absatz enthält die Steifigkeitsberechnung nach ISO3408-4.
Die Einstellungsänderung spiegelt sich in Absatz [3.0] wider.
In diesem Teil können Sie die Gesamtsteifigkeit von Schraube, Mutter, Lagern und Montageelementen lösen.
Die Steifigkeit der Stützlager variiert je nach Lagertyp und Vorspannung. Wenden Sie sich an den Lagerhersteller.
Die Steifigkeit des Montageteils der Mutter variiert je nach Maschinenkonstruktion.
Die Verformung wird für die maximale Kraft Fmax [3.10] und die volle Länge der Schraube Ls [3.20] berechnet.
Es handelt sich um laufende Werte für die Steifigkeitsberechnung. Details in ISO3408-4.
In diesem Abschnitt werden für Kugelgewindetriebe technische Abnahmebedingungen einschliesslich der für die Abnahmeprüfungen in der jeweiligen Toleranzklasse geltenden Toleranzen festgelegt.
Sie können die Toleranzklasse nach Bedarf ändern. Die Änderung wird auch in den Absätzen [3.0,5.0] berücksichtigt.
Der Nutzweg u ist der Hub plus Lange der Kugelgewindemutter.
Rechts befindet sich der aufgrund der Länge der Schraube und der Länge der Mutter geschätzte Wert. Nachdem Sie die Schaltfläche deaktiviert haben, können Sie Ihren eigenen Wert eingeben.
Die Tabelle stellt die wichtigsten Toleranzwerte für den gesamten Längenbereich Lu dar. Gleichzeitig werden die Spalte und Zeile für die aktuelle Länge und Toleranzklasse der Schraube markiert.
In der Tabelle sind die kompletten Toleranzen gemäß den Abbildungen rechts für den aktuellen Lu-Wert dargestellt.
Die Werte gelten nur für vorgespannte Muttern, Drehzahl 100 U/min und Viskosität ISO_grade100.
Für die Messungen werden die Werte F1=0.5*Fpr und F2=2*Fpr angewendet. Bei der Berechnung sind theoretische Werte eingesetzt. Nachdem Sie die Schaltfläche in [6.16] deaktiviert haben, können Sie Ihre eigenen Werte einsetzen.
Eine Wertetabelle gemäß ANSI_B5.48 ist verfügbar.
Zulässige Gesamtabweichung vom positiven zum negativen Fehlerwert über die gesamte Hublänge.
Maximal zulässige positive oder negative Neigung der gemessenen Kurve des Steigungsfehlers. Üblicherweise in Zoll (mm) des Fehlers pro 12 Zoll (300 mm) der Gewindelänge angegeben.
Gesamtabweichung von positiv nach negativ, Steigungsfehler pro Mutterumdrehung.
Während des Betriebs steigt die Temperatur von Schraube und Mutter, was sich auf die Genauigkeit auswirkt. Grundsätzlich wird dies auf drei Arten ggf. in einer Kombination davon gelöst.
- Lösung durch das Steuersystem des Schraubenantriebs (Mutter)
- Abkühlen der Schraube (Innenloch, Kühlflüssigkeit)
- durch Vorspannen der Schraube in axialer Richtung (nur für eine beidseitig befestigte Schraube)
In diesem Abschnitt können Sie die Ausdehnung der Schraube in Bezug auf den Temperaturanstieg und die Vorspannkraft ermitteln, die zur Beseitigung der Wärmeausdehnung erforderlich ist.
Wenn diese Option aktiviert ist, werden die Werte aus den Absätzen [3] und [2] ausgefüllt.
Geben Sie den Temperaturanstieg der Schraube während des Betriebs ein.
Anforderung für die Änderung der Wellenlänge mithilfe der Vorspannung. Die aktivierte Schaltfläche ergänzt automatisch den Wert aus [7.6].
In diesem Abschnitt werden die grundlegenden Kontrollberechnungen angeführt, die beim Entwurf der Kugelschraube verwendet werden. Die grünen Felder enthalten die empfohlenen Werte.
Die Eingabeparameter werden aus Absatz [3.0] eingelesen.
Sie können die Art der Lagerung ändern. Die Änderung wird auch in Absatz [3.0] berücksichtigt.
Je nach Ausführung können zusätzliche axiale Belastungen auftreten, die mitberücksichtigt werden müssen. Wenn sie auftreten, geben Sie ihren Wert ein.
Dieser Wert gibt die Durchbiegung der mit Eigengewicht belasteten Schraube für horizontal gelagerte Schrauben an.
Die empfohlene Maximaldurchbiegung ist für:
Allgemeinen Maschinenbau y = 0.0003 * Ls
Bau der Werkzeugmaschinen y = 0.0002 * Ls
Zur Kontrolle und Berechnung der Sicherheit wird Vergüteter und legierter Stahl mit der in [2.0] definierten Gleitgrenze Rp0.2 in Betracht genommen.
Bei gleichzeitiger Einwirkung von Zug / Druck und Torsion ist es notwendig, die kombinierte Beanspruchung zu lösen. Die reduzierte Spannung sollte geringer sein als die zulässige Zugspannung.
Die Grenzschlankheit SRc ist ein wichtiger Parameter eines konkreten Werkstoffes, der den Bereich der elastischen und der nicht elastischen Knickung unterscheidet und dadurch auch die Verwendung der entsprechenden Beziehungen. Es ist also empfehlenswert, diesen Parameter für einen konkreten Werkstoff zu überprüfen. Der empfohlene Wert ist also gemäß der allgemeinen Beziehung festgelegt:
SRcs = 0.5 * (E / (Rp02 * 0.5))0.5
SRc = (E *
p2
/ (Rp02 * 0.5))0.5
Der Schlankheitsgrad eines konkreten Trägers bestimmt, in welchem Bereich der Knickung sich der Träger befindet (der einfache Druck, die nicht elastische Knickung, die elastische Knickung) und dadurch wird auch die für die Bestimmung des Sicherheitskoeffizienten nötige Kontrollmethode festgesetzt.
A. SR < SRcs..............Bereiche
für den einfachen Druck. Empfohlene Sicherheit SF>1.75)
B. SRcs < SR < SRc.....Bereiche für die nicht elastische Knickung. Empfohlene
Sicherheit
SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
C. SRc < SR................Bereiche für die elastische Knickung. Empfohlene
Sicherheit SF>3.5)
Sie drückt das Verhältnis zwischen kritischer und wirkender Kraft aus. Der minimale Sicherheitskoeffizient (grüne Zelle) wird in Abhängigkeit vom Schlankheitsverhältnis empfohlen [8.21]
Die Drehzahl der Schraube sollte 80 % der kritischen Drehzahl nicht überschreiten.
Die Werte sollten größer sein als die folgenden Empfehlungen. Sie werden nach dem angegebenen Belastungskoeffizient geschätzt [3.15].
Allgemeiner Maschinenbau
Keine Vibrationen oder Stößen ....... 1.0 - 3.5
Mit Vibrationen oder Stößen ........... 2.0 - 5.0
Werkzeugmaschinen
Keine Vibrationen oder Stößen ........ 1.0 - 4.0
Mit Vibrationen oder Stößen ............ 2.5 - 7.0
Für schnell laufende, leistungsbedingt beanspruchte Schrauben wird eine Ölschmierung empfohlen. Für diese Kategorie der Schrauben ist dieser Abschnitt bestimmt. Aufgrund des Durchschnitts der Schraube und der Drehzahl werden die Viskosität und die Mindestmenge von Öl empfohlen. Gleichzeitig wird der Wirkungsgrad geschätzt.
Es wird empfohlen, Öle mit Verschleißschutzadditiven zu verwenden. Sie sind in der Lage auch unter extremen Reibungsbedingungen zu schmieren, wenn die Drehzahl für die Schmierung nicht ausreicht. EHD (elasto-hydrodynamic lubrication). Empfohlen wird das Getriebeöl der CLP-Klasse gemäß DIN51517-3 oder gleichwertig.
Sie können die Betriebstemperatur und die Ölsorte und nach Deaktivieren der Schaltflächen rechts Ihre eigenen Werte für die Ölviskositätsklasse ggf. die Viskosität auswählen.
Wenn die Schaltfläche [8.42] aktiviert ist, wird die Viskosität basierend auf der Betriebstemperatur und der ausgewählten Viskositätsklasse (VG2-VG1500) berechnet.
Wählen Sie in der Auswahlschaltfläche die Berechnung entweder für eine einzelne Schraube/Mutter oder für eine Schraube/Mutter + Lager aus.
Basierend auf den Schraubenabmessungen, der Schraubenbelastung, der Lagerbelastung, dem Öltyp und der Viskosität wird der Reibungskoeffizient geschätzt, der den Wirkungsgrad bestimmt. Nachdem Sie die Schaltfläche rechts deaktiviert haben, können Sie Ihren eigenen Koeffizienten eingeben.
Die Berechnung basiert auf der Schraubengeometrie und dem Reibungskoeffizienten [8.44]. Wenn Sie über keine Labormessungen verfügen, kann dies ein passender Parameter für andere spezialisierte Berechnungen sein (Erwärmung, Verlustwärme, Wärmeausdehnung usw.).
Normalbetrieb bezeichnet die Übersetzung von Rotationskraft in Axialkraft, Umkehrbetrieb bezieht sich dann auf die Übersetzung von Axialkraft in Rotationskraft.
In diesem Absatz finden Sie einige grundlegende Formeln, die beim Entwurf behilflich sein können.
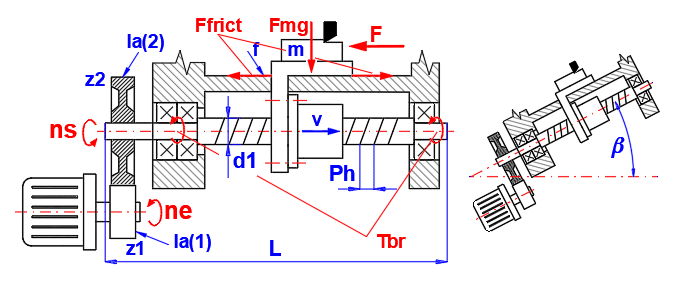
In diesem Absatz können Sie die Parameter des Mechanismus und das Lastspektrum von Schraube und Mutter genau definieren. Sie erhalten genaue Werte für Kräfte, Drehmomente und erforderliche Motorleistung. Sie können die resultierenden Kräfte und Drehzahlen in den Abschnitt Berechnung der äquivalenten Last [11] übertragen.
Bei der Definition des Mechanismus richten Sie sich nach der Abbildung.
Sie können dann eine Reihe von Parametern (Drehzahl, Kräfte, Drehmomente und Motorleistung) in der Grafik überwachen.
Die x-Achse drückt die Zeit aus.
Definieren Sie alle Parameter. Durch das Aktivieren der Schaltfläche auf [10.2] werden die Parameter der Schraube aus Absatz [3.0] automatisch übertragen. Nach dem Deaktivieren können Sie verschiedene Dimensionen definieren.
Die tatsächliche Länge der Schraube L wird aus dem eingegebenen Abstand zwischen den Lagern Ls geschätzt, der um 10 Durchmesser der Schraube erhöht wird. Dieser Wert wird nur zur Berechnung des Trägheitsmoments verwendet.
Die meisten Lagerungen werden entweder in horizontaler (0°) oder vertikaler Ebene (90°) konstruiert. Geben Sie die Ausrichtung des Mechanismus ein.
Geben Sie das Gesamtgewicht der Objekte ein, die von der Schraube bewegt werden.
Trägheitsmoment – von geradliniger Bewegung (Tisch, Werkstück ...) in Drehbewegung umgerechnet.
Trägheitsmoment der Schraubenwelle.
Trägheitsmoment aller Räder (rotierende Massen) auf der Schraubenseite. Sie können die Formeln aus Absatz [9] anwenden, um die Werte ungefähr zu berechnen.
Trägheitsmoment aller Räder (rotierende Massen) auf der Motorseite, einschließlich rotierender Massen des Motors (Informationen zum Motor finden Sie im Katalog des Motorherstellers). Sie können die Formeln aus Absatz [9] anwenden, um die Werte ungefähr zu berechnen.
Das Übersetzungsverhältnis ist definiert als das Verhältnis der Anzahl der Zähne i = z2/z1. Wenn Sie einen direkten Schraubenantrieb verwenden, ist i = 1. Auch in diesem Fall ist es angebracht, die rotierenden Massen auf der Motorseite (Motor, Kupplungen ...) zu definieren [10.11].
Trägheitsmoment aller rotierenden Massen auf den Antrieb (Motor) bezogen. Es wird zur Berechnung der Winkelbeschleunigung verwendet.
Entsprechend der erforderlichen Positioniergenauigkeit und der erforderlichen Steifigkeit wird die Methode zum Zusammenpassen der Mutter an der Welle ausgewählt. Mit zunehmender Vorspannung nimmt die Haltbarkeit ab. Mutter mit Spiel – Einwegbelastung Last Fpr = 0.
Die Größe der Vorspannung wird normalerweise im Katalog angegeben oder kann mit dem Lieferanten abgestimmt werden. Im Allgemeinen werden die folgenden Vorspannungswerte verwendet, ausgedrückt in Prozent der dynamischen Tragfähigkeit der Ca-Schraube:
3 % Ca - für genaue Positionierung und weniger beanspruchte Schrauben geeignet
5 % Ca - für genaue Positionierung und durchschnittlich beanspruchte Schrauben geeignet
8 % Ca - für Muttern mit 2-Punkt-Kontakt
10 % Ca - für genaue Positionierung und höher beanspruchte Schrauben geeignet
Zum Drehen der vorgespannten Mutter ist ein Drehmoment erforderlich, auch wenn die Mutter nicht axial belastet ist.
Wählen Sie den Reibungskoeffizienten in der Führung.
Für lineare Kugelführungen beträgt der Koeffizient f = 0.003-0.006.
Für die geschmierte Scherreibung kann man von folgenden Werten ausgehen.
f = 0.05-0.10 ... gehärteter Stahl / gehärteter Stahl
f = 0.05-0.15 ... gehärteter Stahl / Gusseisen
f = 0.09-0.15 ... gehärteter Stahl / Bronze (Leuchtstoff)
f = 0.07-0.10 ... Gusseisen / Gusseisen
f = 0.07-0.10 ... Gusseisen / Bronze (Leuchtstoff)
Geben Sie den Wirkungsgrad der Kugelübersetzung ein. Der empfohlene Wert befindet sich rechts von der Eingangszelle. Der Wert basiert auf der Schraubengeometrie und enthält keine weiteren Einflüsse. Für diesen Vorschlag ist er jedoch völlig ausreichend.
Geben Sie die Reibungsmomente der Lager ein. Der ungefähre Wert befindet sich rechts von der Eingangszelle.
Nach dem Drücken der Taste werden die berechneten Kräfte und Drehzahlen in die Tabelle übernommen, die für die Berechnung der äquivalenten Belastung und der äquivalenten Drehzahl in Absatz [11.0] vorgesehen ist.
Definieren Sie in der Tabelle schrittweise den Arbeitszyklus des Mechanismus.
Drehzahl: Geben Sie in der Spalte "neend" die Motorenddrehzahl schrittweise im einschlägigen Abschnitt ein.
Zeitabschnitt: Geben Sie in der Spalte "dt“ die Länge jedes Abschnitts in Sekunden ein.
Bearbeitungskraft: Geben Sie die externe Kraft in Spalte "F“ ein, wenn sie im jeweiligen Abschnitt wirkt (z. B. Bearbeitung).
Tabellenzeile1: neend=2000; dt=0.05; F=0 ............... Anlauf von 0 auf Betriebsdrehzahl 2000/min. (Beschleunigung)
Tabellenzeile2: neend=2000; dt=0.40; F=1000 .......... Arbeitszyklus der Bearbeitung bei der Drehzahl von 2000/min, Bearbeitungskraft 1000N
Tabellenzeile3: neend=0; dt=0.05; F=0 ............... Bremsung von Arbeitsdrehzahl auf 0. (Abbremsvorgang)
Tabellenzeile4: neend=0; dt=0.10; F=0 ............... Zeitverzögerung (z. B. zum Umrüsten des Werkzeugs)
Tabellenzeile5: neend=-2000; dt=0.05; F=0 ................ Anlauf für Rückwärtsfahrt auf Drehzahl -2000 / min (Beschleunigung)
Tabellenzeile6: neend=-2000; dt=0.40; F=0 ................ Rückwärtsfahrt bei Drehzahl von -2000/min, Bearbeitungskraft 0N
Tabellenzeile7: neend=0; dt=0.05; F=0 ............... Abbremsen auf Null-Drehzahl (Abbremsvorgang)
Tabellenzeile8: neend=0; dt=0.10; F=0 ............... Zeitverzögerung (z. B. zum Umrüsten des Werkzeugs)
Gesamtzeit des Arbeitszyklus 1,2 Sek.
Berechnungen der Nutzungsdauer der Schraube gehen von der Annahme aus, dass die Schraube unter konstanten Betriebsbedingungen arbeitet. In der Praxis ist diese Annahme jedoch nicht erfüllt. Daher können Sie diese Hilfsberechnung verwenden, welche die variable Belastung und die variable Drehzahl in die äquivalente Last umrechnet, die bei der Berechnung der Haltbarkeit verwendet wird.
Vorteilhafterweise können Sie den vorherigen Absatz [10] anwenden, der eine genaue Definition der Parameter des Mechanismus und des Lastspektrums ermöglicht, was zu einer genauen Definition der Kräfte und Drehzahl für diese Berechnung führt.
Wenn Sie die Berechnung in Absatz [10] nicht anwenden, gehen Sie wie folgt vor, um die äquivalente Belastung zu berechnen:
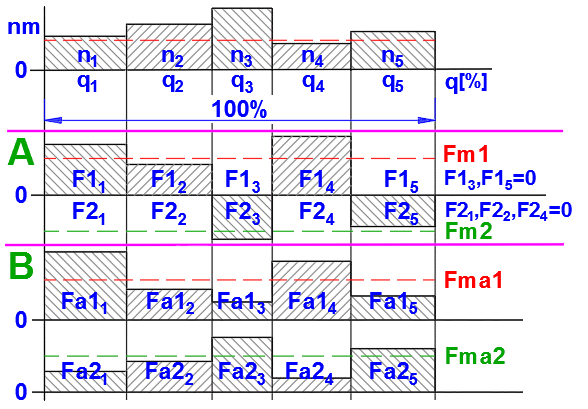
1. Teilen Sie den Arbeitszyklus der Schraube in mehrere Zeitabschnitte ein, in denen die Betriebsbedingungen ungefähr konstant sind (siehe Abbildung).
2. Stellen Sie die Anzahl dieser Zeitabschnitte in der Auswahlliste [11.2] ein.
3. Wählen Sie die Mutter Typ A oder B [11.3] und die Größe der Vorspannung [11.4].
4. Definieren Sie die Betriebsbedingungen für die einzelnen Abschnitte in der Eingabetabelle [11.7].
Anschließend können Sie die Berechnungsergebnisse in Absatz [3.0] übertragen.
Sie können die Verläufe der Eingangswerte in der Grafik rechts überwachen, wobei auch die äquivalente Belastung und die äquivalente Drehzahl (grün Richtung1, rot Richtung2) angezeigt werden.
Die X-Koordinate gibt den Prozentsatz der Belastung (Drehzahl) auf dem angegebenen Niveau an (gesamter Belastungszyklus = 100%).
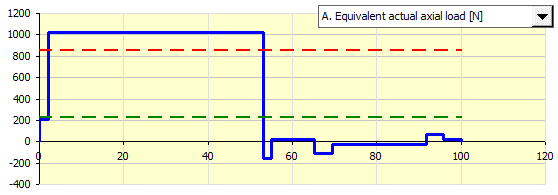
Nach dem Betätigen der Taste werden die Werte aus diesem Absatz in Absatz [3.0] verschoben.
Verschobene Werte: nm1,nm2,nmax,Fma1,Fma2,Fmax
Bei einer vorgespannten Mutter wird auch der Wert der Vorspannung Fpr übertragen [11.4]
Geben Sie die Anzahl der Belastungszustände ein. Im Falle der Übertragung aus dem vorherigen Absatz [10] wird diese automatisch eingestellt.
Es werden zwei Arten von Muttern verwendet.
A. Keine Vorspannung. Es wird davon ausgegangen, dass die Genauigkeit und Belastung nur in einer Bewegungsrichtung wichtig sind. Bei der Wahl der entgegengesetzten Bewegungsrichtung ist das Spiel zu berücksichtigen.
B. Mit Vorspannung. Die Mutter ist strukturell so ausgebildet, dass beim Übergang von einer Richtung in die andere kein Spiel vorhanden ist. Die Konstruktionslösung kann eine Reihe von Varianten aufweisen, und je nach Konstruktionsanforderungen ändert sich auch die Größe der Vorspannung (in der Regel muss dies mit dem Lieferanten abgestimmt werden).
Die vorgespannte Mutter und die Größe der Vorspannung beeinflussen dann die Berechnung der äquivalenten Schraubenbelastung. Dies können wir uns so vorstellen, dass die Vorspannung auch dann eine Kraft erzeugt, wenn die Mutter nicht belastet wird, diese Kraft muss bei der Berechnung der äquivalenten Belastung berücksichtigt werden.
Bei der Bestimmung der Kraft für die Berechnung der äquivalenten Belastung treten drei Fälle auf.
- Keine Belastungskraft. Die Vorspannkraft ist in beide Richtungen aufgeteilt.
- Die Ladekraft ist kleiner als Flim. Die Belastungskraft ist gemeinsam mit der Vorspannkraft proportional in beide Richtungen verteilt.
- Die Belastungskraft ist größer als Flim. Die Belastungskraft übersteigt die Vorspannkraft und wird nur in der entsprechenden Richtung berücksichtigt.

Entsprechend der erforderlichen Positioniergenauigkeit und der erforderlichen Steifigkeit wird die Methode zum Zusammenpassen der Mutter an der Welle ausgewählt. Mit zunehmender Vorspannung nimmt die Haltbarkeit ab. Mutter mit Spiel – Einwegbelastung Last Fpr = 0.
Die Größe der Vorspannung wird normalerweise im Katalog angegeben oder kann mit dem Lieferanten abgestimmt werden. Im Allgemeinen werden die folgenden Vorspannungswerte verwendet, ausgedrückt in Prozent der dynamischen Tragfähigkeit der Ca-Schraube:
3 % Ca - für genaue Positionierung und weniger beanspruchte Schrauben geeignet
5 % Ca - für genaue Positionierung und durchschnittlich beanspruchte Schrauben geeignet
8 % Ca - für Muttern mit 2-Punkt-Kontakt
10 % Ca - für genaue Positionierung und höher beanspruchte Schrauben geeignet
Begrenzungslast, bei welcher der Kontakt von Kugel und Bahn in unbelasteter Richtung unterbrochen wird.
Gemäß ISO3408-5 ist Fop = 0.6.
Da die Vorspannung während der Nutzungsdauer der Kugelschrauben abnimmt, wird die durchschnittliche Betriebsvorspannung auf 60 % der ursprünglichen Vorspannung eingestellt.
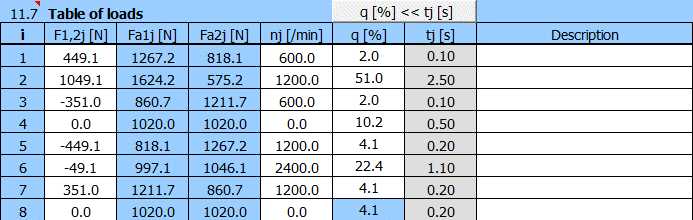
- in der ersten Spalte „F1,2“ geben Sie die Belastung der Mutter schrittweise ein. Positive Werte in einer Richtung, negative Werte in der anderen Richtung.
- in der zweiten Spalte "Fa1" und der dritten Spalte "Fa2" werden dann die Ist-Werte der Belastung (in der einen oder anderen Richtung) berechnet, die auch die Vorspannung der Mutter berücksichtigen [11.4].
- in der vierten Spalte geben Sie die entsprechende Drehzahl ein (immer ein positiver Wert, die Richtung wird von der Belastung gesteuert).
- in der fünften Spalte geben Sie den Prozentsatz der Auslastung für jede Belastung ein (die Summe muss 100 % betragen). Bei ungenügender Eingabe wird die letzte gültige Zelle rot markiert.
- In der sechsten (grauen) Spalte können Sie die Zeit der einzelnen Belastungen eingeben und nach Betätigen der Taste "q[%]<<tj[s]" wird die Zeit in der fünften Spalte in Prozent berechnet.
Index1 und Index2 geben äquivalente Belastungen (Drehzahl) in der einen oder anderen Richtung an.
In diesem Abschnitt können Sie die statische und dynamische Tragfähigkeit auf Grund der ISO- und ANSI-Abmessungen sowie der Parameter der Schraube und Mutter berechnen. Gleichzeitig können Sie die Tabelle der Schrauben (Abmessungen nach ISO, ANSI) mit den berechneten Werten ausfüllen.
Nach dem Betätigen der Taste werden die Werte aus diesem Absatz in den Absatz "Definition von Mechanismus, Belastung und Schraubenparametern" [3.0] verschoben.
Übertragene Werte: i, zu, d1, Dw, Ph, Dpw, , frn, frs
SI units: C0am, Cam
Imperial units: Ti, Pix
Dieser Abschnitt enthält allgemeine Eingabeparameter für die Berechnung C0a,Ca,C0am,Cam,Ti,Pi,Pix. Durch das Aktivieren der Schaltfläche auf [12.3] werden sie automatisch aus dem Hauptabsatz [3.0] übertragen. Nachdem Sie die Schaltfläche deaktiviert haben, können Sie Ihre eigenen Werte eingeben.
Übertragene Werte: i, zu, d1, Dw, Ph, Dpw, , frn, frs

Die Anzahl der Gewinde wird durch die Konstruktion der Mutter bestimmt und normalerweise vom Hersteller angegeben. Angewendet wird die Anzahl der Gewinde im Bereich von ungefähr 1,5 bis 6,0. Die Anzahl der Gewinde beeinflusst die Berechnung der statischen und dynamischen Tragfähigkeit, Steifigkeit und Länge der Mutter.
Geben Sie die Anzahl der nicht belasteten Kugeln ein. Es handelt sich um Rückführsysteme, bei denen die Kugeln nach einer Umdrehung und normalerweise zu = 3 zurückgeführt werden. Bei Rückführsystemen, bei denen die Kugeln vom letzten Gewinde zum ersten zurückgeführt werden, gilt zu = 0. Informationen zur konkreten Konstruktion finden Sie meistens im Herstellerkatalog.
Der Durchmesser ist in der Regel eine Frage der Konstruktion des Herstellers. Natürlich kann er nicht beliebig gewählt werden. Die Grundbedingung lautet, dass der Durchmesser Dw nicht größer sein darf als die Steigung Ph.
0.600, 0.800, 1.000, 1.200, 1.250, 1.500, 1.588, 1.750, 2.000, 2.381, 2.500, 3.000, 3.175, 3.500, 3.969, 4.762, 5.000, 5.556, 6.000, 6.350, 7.144, 7.938, 8.000, 9.525, 10.000, 10.319, 12.700, 20.000, 20.638, 25.400, 30.000, 31.750, 38.100, 40.000, 44.450, 50.000
Standardreihe der Steigung - mm (ISO, JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardreihe der Steigung - inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Die Norm ISO3408-5 verwendet den Wert von 0,86. Der Wert 0,7 wird von einigen Herstellern verwendet und geht von (ISO281,2007), (ISO/TR1281-1,2008), (Lundberg, et al.,1947) aus.
Die modifizierte Tragfähigkeit umfasst weitere Parameter wie Genauigkeit, Härte und Materialverarbeitung und wird in die Tabellen eingetragen ggf. in Absatz [3.0] übertragen.
Die Härteabweichung wird um den Faktor fh0, fh korrigiert
Der Basiswert ist 654HV10 (fh0, fh = 1.0). Die Verringerung der Härte wirkt sich auf fh0 und fh aus. Die Erhöhung der Härte hat keinen Einfluss auf die Berechnung.
Abhängig von der Toleranzklasse der Spindel müssen die statische Tragzahl C0 und die dynamische Tragzahl C mit den Korrekturfaktoren fac multipliziert werden.
Korrekturfaktoren fac
IT0, IT1, IT3, IT5 …… 1.0
IT7 ……………………...... 0.9
IT10 ………....…………… 0.7
Einfluss der Methode der Materialherstellung.
Stahl der Kugeln / Wert des Koeffizienten fm
Stähle auf Luft abgekühlt….......................……1.00
Stähle entgast ....….......................................1.25
Stähle elektrisch umgeschmolzen….................1.44
Stähle in Vakuum umgeschmolzen….…........….1.71
Berechnung der Grundtragfähigkeit nach ANSI.
Der Weg von 1.000.000 Zoll wird als Standardwert betrachtet.
Die Entfernung von 25.400 Metern wird als Grundwert angesehen.
Die Berechnung enthält zwei grundlegende Tabellen für Schraubenmaße. Millimeter (ISO) und Zoll (ANSI). Die Tabellen enthalten alle Kombinationen aus dem Durchmesser der Schraube und Steigung. Die Hersteller halten diese Grundabmessungen ein (oder bieten mehrere Durchmesser an). Die Wahl der Kugeldurchmesser ist jedoch beliebig. Basierend auf der Analyse einer großen Anzahl von Herstellerkatalogen haben wir auch eine Tabelle der eingesetzten Kugeldurchmesser und deren Zuordnung zu den Durchmessern von Schrauben erstellt. Dadurch entstand eine Reihe, die als leicht, mittel und schwer bezeichnet wird. Diese Kombinationen der Abmessungen kommen dann auch in den Herstellerkatalogen vor.
Nach dem Betätigen der Taste werden die entsprechenden Werte C0am, Cam (Ti, Pix für ANSI) in die Tabelle für die entsprechenden Abmessungen d1xPhxDw schrittweise eingetragen. Diese Berechnung und das Ausfüllen der Tabelle nimmt einige Zeit in Anspruch. Sie können die Fortschrittsanzeige im Arbeitsfenster sehen. Es wird nicht empfohlen, den Vorgang der Generierung der Tabelle zu unterbrechen.
Die Berechnung setzt den Grundwert der Anzahl der Arbeitsgewinde auf i = 1.0. Die Parameter zu, alpha, frn, frs, exp, AH, fac, fm, LIix werden nicht geändert. So können Sie modifizierte Tabellen für diese Parameter erhalten. Diese Generierung der Tabellen ist jedoch für erfahrene Konstrukteure mit detaillierten Kenntnissen der relevanten Problematik geeignet.
Die Grundeinstellungen der Parameter der generierten Tabellen sind: zu=0, alfa=45, frn=frs=0.55, exp=0.86, AH=654, fm=1, LIix=1000000.
Entwurf eines Arbeitstischantriebs mit einer Kugelschraube.
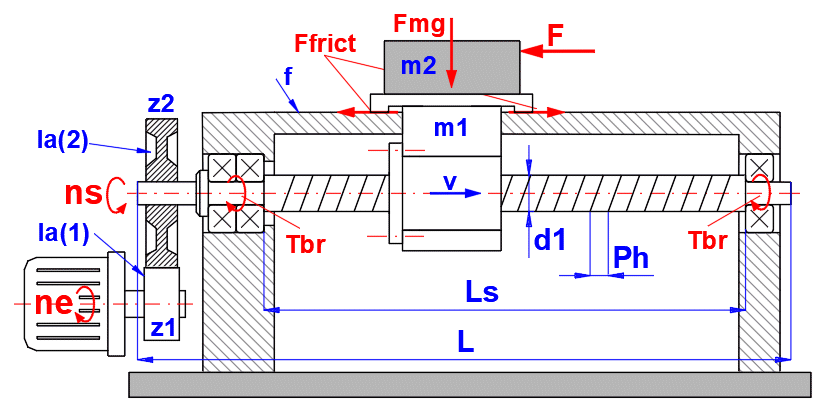
Tischgewicht: m1 = 60 kg
Werkstückgewicht: m2 = 40 kg
Kraft für die Bearbeitung: F = 1000 N.
Nutzweg: Lu = 1000 mm
Bearbeitungsgeschwindigkeit v = 400 mm/s
Eilgang: vmax = 800 mm/s
Lebensdauer: 20000h
Reibungskoeffizient der Führungsfläche: f = 0.05
Motordrehzahl: Nemax = 1500 /min
Positioniergenauigkeit: ± 0.1 mm bei max. Reise
Wiederholgenauigkeit: ± 0.02 mm
Montage der Kugelumlaufspindel: Fest - Stütze
Zunächst ist es angebracht, die Beziehung zwischen Tischgeschwindigkeit (v), Drehzahl (ns, ne) und Steigung der Schraube (Ph) in Absatz [1.0] zu lösen.

Für die erste Näherung können Sie die Werte aus dem Bild auswählen.

Als Nächstes schätzen wir die äquivalente Belastung Fm = 1000N, den Belastungskoeffizienten fw = 1,2 und geben die Nutzungsdauer Lh-req = 20000h ein. Die Nutzungsdauer erfüllen dann die Schrauben mit min. Nenndurchmesser 20-50 mm (entsprechend der Anzahl der aktiven Gewinde).
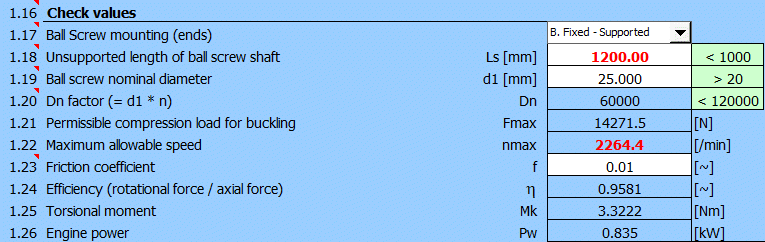
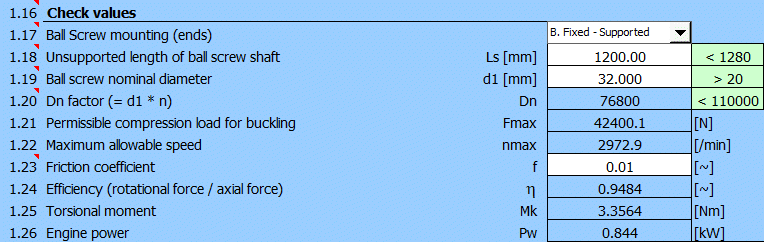
Wir schätzen den Montagebereich Ls = 1200 mm (1000 mm Bewegungslänge, 150 mm Länge der Mutter, 50 mm Montageüberlappungen). Für den nominalen Durchmesser der Schraube d1 = 25 mm wird der empfohlene Maximalwert von Ls <(40xd1) überschritten und vor allem wird die kritische Drehzahl (nmax) überschritten. Daher verwenden wir eine Schraube mit dem Durchmesser von d1 = 32 mm, welche die Grundkontrollen erfüllt.

Die erforderliche Genauigkeit für Lu> 1000 mm kann durch Auswahl des Genauigkeitsgrades IT3 erreicht werden.
Öffnen Sie Absatz [3.0] und übertragen Sie die Werte aus Absatz [1.0], indem Sie die Taste "[1.0] >> [3.0]" drücken.
Es ist auch notwendig, andere Antriebsparameter genauer zu definieren. Und zwar die Zeilen [3.3-3.7]. Feste Lagerung auf einer Seite, Unterstützung auf der anderen Seite und eine vorgespannte Mutter wird verwendet.
.
In den allermeisten Fällen kennen wir die Schraubenbelastung nicht im Detail. Hierzu ist die Berechnung aus den Absätzen [10.0] und [11.0] heranzuziehen.
In diesem Teil definieren wir die Belastung im Detail. Nach dem Aktivieren der Schaltfläche auf [10.2] werden die Werte aus Absatz [3.0] übertragen. Fügen Sie dann die verbleibenden Werte schrittweise hinzu.
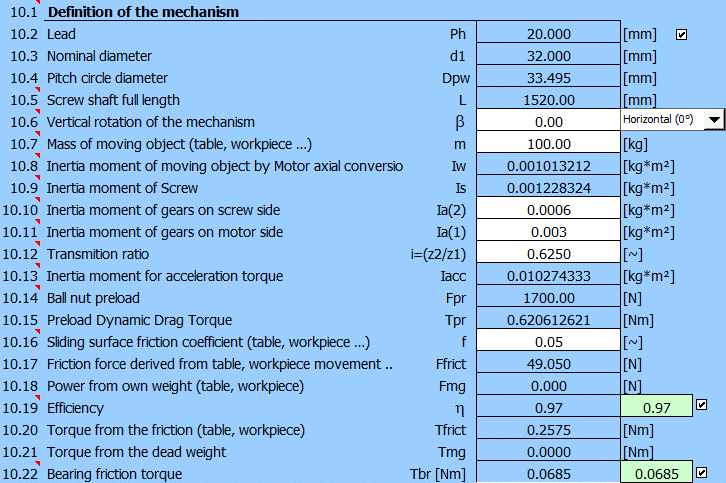
Ausrichtung des Mechanismus b=0
Gewicht m=40+60=100kg
Trägheitsmoment Ia(2),Ia(1) kann im Absatz [9.0] geschätzt werden.
![]()
![]()
Übersetzungsverhältnis i = 0.625 (siehe Absatz [1.0])
Reibungskoeffizient f = 0.05
Die Definitionstabelle sieht dann folgendermaßen aus:

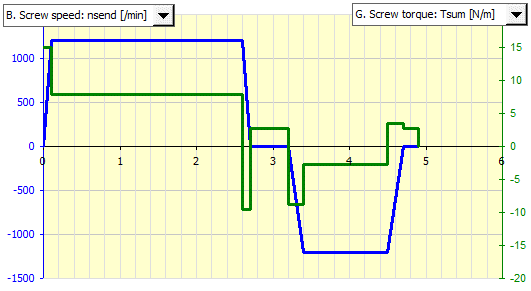
Tabellenzeile1: neend=750; dt=0.10; F=0 ............... Anlauf von 0 auf Betriebsdrehzahl 750/min. (Beschleunigung)
Tabellenzeile2: neend=750; dt=2.50; F=1000 .......... Arbeitszyklus der Bearbeitung bei der Drehzahl von 750/min, Bearbeitungskraft 1000N
Tabellenzeile3: neend=0; dt=0.10; F=0 ............... Bremsung von Arbeitsdrehzahl auf 0. (Abbremsvorgang)
Tabellenzeile4: neend=0; dt=0.50; F=0 ............... Zeitverzögerung (z. B. zum Umrüsten des Werkzeugs)
Tabellenzeile5: neend=-1500; dt=0.20; F=0 ................ Anlauf für Rückwärtsfahrt auf Drehzahl -1500 / min (Beschleunigung)
Tabellenzeile6: neend=-1500; dt=1.10; F=0 ................ Rückwärtsfahrt bei Drehzahl von -1500/min, Bearbeitungskraft 0N
Tabellenzeile7: neend=0; dt=0.20; F=0 ............... Abbremsen auf Null-Drehzahl (Abbremsvorgang)
Tabellenzeile8: neend=0; dt=0.20; F=0 ............... Zeitverzögerung (z. B. zum Umrüsten des Werkzeugs)
Die Drehzahl entspricht den Vorgaben, die Zeiten sind so vorgeschlagen, dass die Bedingung der maximalen Bewegungslänge Lu = 1000 mm (Zeile 2, Spalte ds) für die Tischgeschwindigkeit von 400 mm/s bzw. 800 mm/s für Rückwärtsfahren erfüllt wird.
Der Zeitzyklus beträgt 4,9 s. Die Grafik zeigt die Schraubengeschwindigkeit und die auf Mutter und Schraube wirkenden Kräfte.
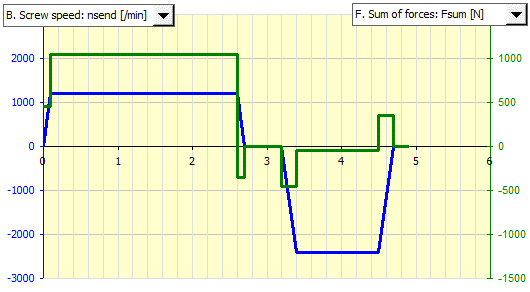
Da die Schraubenbelastung nicht konstant ist, muss die variable Belastung in eine äquivalente Belastung umgerechnet werden, die zur Berechnung der erforderlichen dynamischen Tragfähigkeit Ca herangezogen wird.
Drücken Sie in Zeile [10.23] die Taste "[10.0]>>[11.0]". Dadurch werden die Kräfte und Drehzahl in die Tabelle der Belastungen in Absatz [11.0] übertragen.
 =>
=>
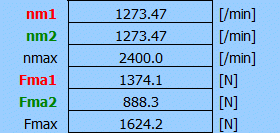
Es bleibt noch übrig, den Wert der Muttervorspannung einzugeben. Aus dem Vorentwurf kennen wir den Wert der erforderlichen dynamischen Tragfähigkeit Ca-req = 17000N [1.13]. Die Vorspannung der Mutter beträgt normalerweise 10 % Ca. Geben Sie in Zeile [11.4] den Wert Fpr = 1700N ein und in Zeile [11.6] den Koeffizinenten Fop = 0.6 gemäß ISO3408-5.
Drücken Sie die Taste "[11.0]>>[3.0]", um die berechneten Werte der äquivalenten Belastung und Drehzahl zurück in Absatz [3.0] zu übertragen.

Jetzt haben wir eine sehr genau definierte Schraubenbelastung und die erforderliche Tragfähigkeit.
Wir haben zwei Möglichkeiten, die Schraube auszuwählen.
Die Tabelle der Schrauben und ihrer Tragfähigkeiten wurde gemäß ISO3408-5 bzw. ANSI_B5.48 für Zoll-Einheiten generiert. Wenn Sie den jeweiligen Hersteller nicht direkt kennen, können Sie aus dieser Tabelle auswählen.
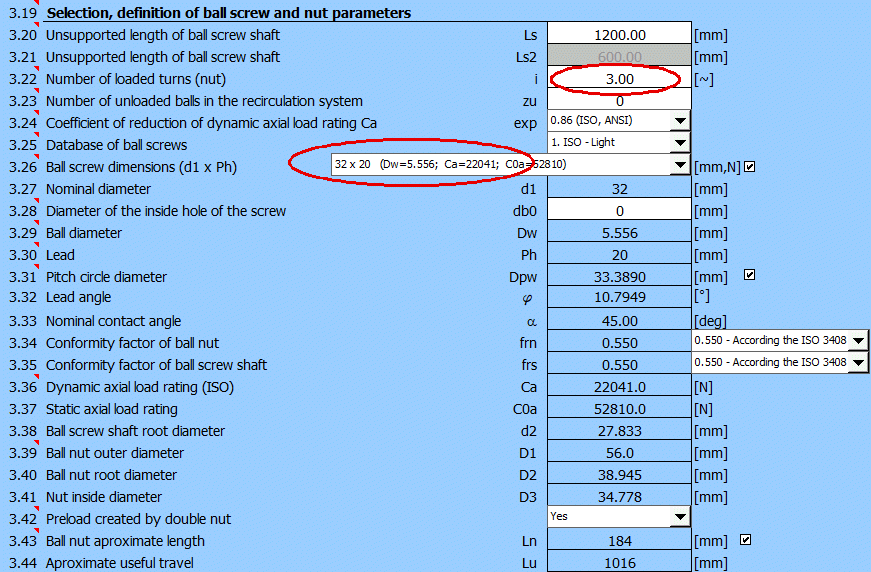
In der Auswahlliste sollte, aufgrund des Vorentwurfs, die Schraube mit Abmessungen 32x20(d1xPh) ausgewählt werden. Der Kugeldurchmesser Dw und die dynamische Tragfähigkeit Ca sind in Klammern angegeben. Die Grundtragfähigkeit Ca pro Arbeitsgewinde beträgt 8500N. Es ist daher notwendig, die Anzahl der Gewinde der Mutter i = 3 einzustellen. Der Wert der dynamischen Tragfähigkeit beträgt 22041 N, d. h. höher als der erforderliche Wert Ca-req = 20227 N.
Wenn Sie die Werte direkt aus dem Herstellerkatalog auswählen, ist am besten wie folgt vorzugehen.
- Wählen Sie die einschlägige Abmessung der Schraube aus der Tabelle aus (so werden die richtigen Abmessungen voreingestellt)
- Deaktivieren Sie die Schaltfläche rechts neben der Auswahlliste der Schraube.
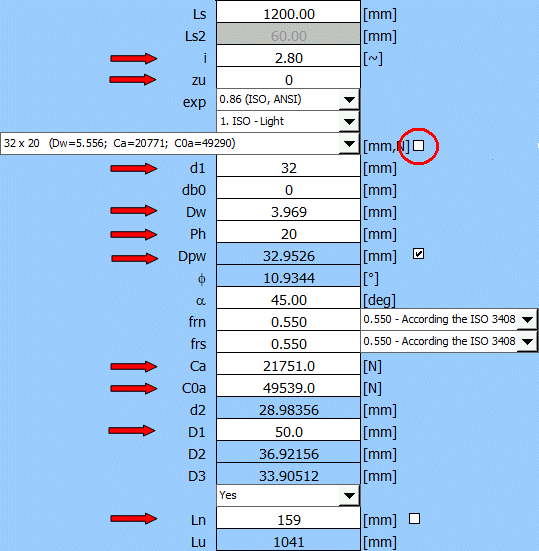
- Füllen Sie die markierten Zeilen mit den Werten aus dem Herstellerkatalog aus (einige Maße sind jedoch bereits korrekt ausgefüllt).
Ein Beispiel für angebotene Muttern in der erforderlichen Größe und Tragfähigkeit von mehreren Herstellern.
| ID | d1 x Ph | Dw | i | Ln | Ca | C0a | K | D1 | Manufact. |
| 1 | 32 x 20 | 3.969 | 2.8 | 159 | 21751 | 49536 | 842 | 50 | KSK |
| 2 | 32 x 20 | 5.556 | 2 | 177 | 31400 | 81100 | 790 | 55 | PMI |
| 3 | 32 x 20 | 3.969 | 3 | 178 | 19000 | 54300 | 680 | 50 | HIVIN |
| 4 | 32 x 20 | 4.763 | 4 | 216 | 31900 | 89140 | 940 | 54 | HIVIN |
| 5 | 32 x 20 | 5.000 | 4 | 70 | 29700 | 59800 | - | 53 | Thomson |
Am Ende des Absatzes [3.0] ist auch der Kurzauszug der Ergebnisse angeführt. Wird zur schnellen Orientierung verwendet, wenn Sie die ausgewählten Eingabeparameter abstimmen. Die kompletten Ergebnisse finden Sie dann im Kapitel "Ergebnisse".

Die Informationen über die Möglichkeiten der 2D- und 3D-graphischen Ausgabe und die Informationen über das Zusammenwirken mit den 2D- und 3D CAD-Systemen finden Sie im Dokument "Grafische Ausgabe, CAD - Systeme".
Nachdem Sie die Schaltfläche rechts deaktiviert haben, können Sie die Anzahl der Gewinde eingeben, die auf der Zeichnung der Schraube / Mutter dargestellt werden sollen.
Vorausgefüllte Werte gehen von der Berechnung aus.
Es wird angegeben, um welche Anzahl der Gewinde der linke Rand der Mutter in Bezug zum linken Anfang der Schraube versetzt wird.
Die Informationen über die Einstellung der Berechnungsparameter und der Spracheneinstellung finden Sie im Dokument "Einstellung der Berechnungen, Sprachenänderung".
Die allgemeinen Informationen darüber, wie man die Berechnungshefte ändern und erweitern kann, sind im Dokument "Benutzerspezifische Anpassungen der Berechnung" aufgeführt.
ISO 3408-1:2006
Ball screws - Part 1: Vocabulary and designation
Vis a billes - Partie 1: Vocabulaire et designation
ISO 3408-2: 1991
Ball screws - Part 2: Nominal diameters and nominal
leads. Metric series
Vis a billes - Partie 2: Diametres et pas hélicoIdaux, nominaux. Serie métrique
Kugeiroligewinde - Teil 2: Nenndurchmesser und Nennsteigungen. Metrische Reihe
ISO 3408-3:2006
Ball screws - Part 3: Acceptance conditions and acceptance tests
Vis a blues - Partie 3: Conditions et essals do reception
ISO 3408-4:2006
Ball screws - Part 4: Static axial rigidity
Vis a blues - Partie 4: Rigidite axiale statique
ISO 3408-5:2006
Ball screws -Part 5: Static and dynamic axial load ratings and operational life
Vis a billes - Partie 5: Charges axiales statiques et dynamiques de base et
durée de vie
ISO 286-2:2010
Část 2: Tabulky normalizovaných tolerančních tříd a mezních úchylek pro díry a
hřídele
Part 2: Tables of standard tolerance classes and limit deviations for holes and
shafts
Partie 2 : Tableaux des classes de tolerance normalisées et des écarts limites
des alesages et des arbres
Teil 2: Tabellen der Grundtoleranzgrade und GrenzabmaBe für Bohrungen und Wellen
DIN ISO 3408: the ISO standard has been adopted directly as the DIN standard
JIS B1192-1997 is similar to DIN ISO 3408
JIS B1192-2018 putting the JIS standard in harmonization with the ISO 3408
DIN 69051-5
Machine tools - Ball screws - Part 5: Mounting dimensions for ball nuts
Machines-outils - Vis a billes - Partie 5: Dimensions de raccordement pour
écrous
ANSI B5.48 - 2013
Ball Screws
Company cataloques: THK, PMI, KSK, NSK, SKF, HIWIN, KURODA, NOOK, THOMSON, Steinmayer, MANESMAN
^