Program je určen pro návrh, výpočet a kontrolu kuličkového šroubu. Program řeší následující úlohy:
Předběžný návrh (minimum vstupních parametrů, dostačující pro orientaci a výběr z katalogů)
Podrobná analýza (zatížení, volba rozměrů, kontrola parametrů)
Definice tabulky zatěžovacího spektra (rychlost, krouticí moment, otáčky a výkon...)
Výpočet ekvivalentního zatížení
Výpočet životnosti, návrh tolerancí, teplotní analýza
Kontrola šroubu na tah/tlak, otlačení, ohyb, vzpěr a kritické otáčky
Návrh mazání a výpočet účinnosti
Program obsahuje tabulky šroubů podle ISO a ANSI
Podpora 2DCAD systémů
Ve výpočtu jsou použita data,
postupy, algoritmy a údaje z odborné literatury a norem ANSI, ISO, DIN a JIS.
Seznam norem:
ISO 3408-1:2006; ISO 3408-2: 1991; ISO 3408-3:2006; ISO 3408-4:2006; ISO 3408-5:2006;
ISO 286-2:2010
DIN ISO 3408; JIS B1192-1997; JIS B1192-2018; DIN 69051-5; ANSI B5.48
Firemní katalogy: THK, PMI, KSK, NSK, SKF, HIWIN, KURODA, NOOK, THOMSON,
Steinmayer, MANESMAN
Uživatelské rozhraní.
Stáhnout.
Ceník, koupit.
Informace o syntaxi a ovládání výpočtu naleznete v dokumentu "Ovládání, struktura a syntaxe výpočtů".
Informace o účelu, použití a ovládání odstavce "Informace o projektu" naleznete v dokumentu "Informace o projektu".
Kuličkové šrouby (KŠ) mají široké spektrum využití. Například pohony CNC strojů, pohony vstřikovacích lisů, záměna za hydraulické pohony, zdravotní technika, letecká a automobilová technika, dopravní technika. Výhodou KŠ je vysoká účinnost převodu (cca+90%) nevýhodou pak absence samosvornosti.
Typové rozdělení se používá zhruba následující:
Univerzální šrouby používané v obráběcích centrech, letecké technice, automobilové technice, polohovací zařízení atd. V závislosti na stupni přesnosti jsou vyráběné broušením či kroužkováním. Obvykle vyráběné ve třídě přesnosti IT1-IT5. Matice mohou být s předepnutím nebo bez. Většina výpočtů v programu je vztažená právě k tétu univerzální skupině.
Určené pro vysoké rychlosti polohování (pracovní až 30m/min, rychloposuv až 80m/min). Obrábění, polohování, Přesnost IT1,IT3, použito předepnutí. Zpravidla vícechodé.
Určené pro vysoké zatížení, dlouhodobou trvanlivost. Větší únosnost ja zabezpečena většími průměry kuliček, větším počtem pracovních závitů, úpravou profilu. Vyráběné broušením s požadavkem na vyšší přesnost (IT1), bez předepětí.
Nízká přesnost polohování, nižší rychlost, nízká cena, bez předepnutí. Výroba válcováním, okružováním, přesnost IT5,IT7,IT10. Využití pro transportní mechanismy.
Do této kategorie spadá množství KŠ jako jsou bezprofilové šrouby (hřídel je ve formě broušené kalené tyče), šrouby s klecí (kuličky jsou v kleci bez převaděče, plynulý chod, krátké zdvihy), teleskopické (několik vzájemně zašroubovaných KŠ, malá zástavba) atd.
Podle konstrukce jde o konstrukci s vnějším vedením kuliček (větší hlučnost, více kuliček v oběhu) a vnitřím vedením kuliček. Odběr kuliček pak může být řešen několika způsoby, většinou závislých na výrobci a snahou o dosažení co nejlepšího otáčkového koeficientu (d1*nmax).
Matice jsou na šroub montovány s vůlí nebo s předepnutím, které slouží k vymezení vůle. Nevýhodou předepnutí je větší opotřebení, kdy se zvyšujícím se předepnutím klesá trvanlivost.
1.Bez předepnutí
2.Předepnutí zajištěné vnější silou na matici/šroub
3.Distanční kroužek posunující vzájemně závity matice
4.Rozdílné stoupání v závitu matice
5.Vzájemným posunutím jednotlivých chodů závitu (u vícechodých závitů)
6.Použití větších (a menších) průměrů kuliček (4-bodový kontakt)
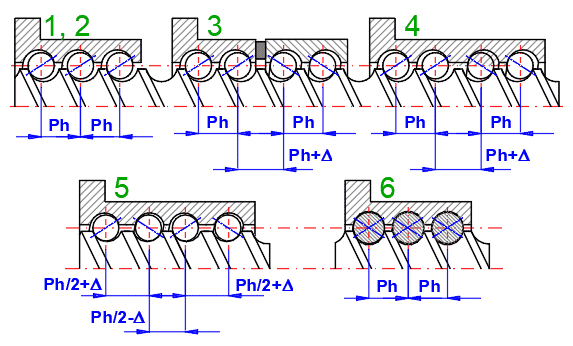
Většinou se používá hodnota 10% ze základní dynamické únosnosti Ca. Jednotliví výrobci pak umožňují a doporučují různé nastavení dle typu a určení šroubu.
Příklad výrobců:
KSK
3 % Ca - vhodné pro přesné polohování a méně zatížené šrouby
5 % Ca - vhodné pro přesné polohování a středně zatížené šrouby
10 % Ca - vhodné pro přesné polohování a více zatížené šrouby
THK
10% Ca
Stainmaier
8-10% Ca - pro matice s 2-bodovým kontaktem
5-8% Ca - pro matice se 4-bodovým kontaktem
Hlavní geometrické parametry KŠ je jmenovitý průměr a stoupání závitu. Od těchto parametrů se odvíjí konstrukce a použití. Na velikosti průměru závisí únosnost, tuhost, maximální otáčky, stoupání s otáčkami pak definuje rychlosti posuvu. Mezi další geometrické parametry, které ovlivňují funkčnost patří velikost kuliček, konstrukce drážek, stupeň přesnosti, průměry provedení a délky matice atd.
Další důležité parametry jako je způsob výroby, materiál, zaručená přesnost a mazání pak určují konkrétní nasazení v požadované konstrukci.
Ačkoliv normy (ISO,ANSI) předkládají řadu výpočtů či kontrolních parametrů, je vždy vhodné čerpat z manuálů konkrétního výrobce.
Výrobci šroubů v palcových rozměrech nabízí spíše standardní kuličkové šrouby. Přičemž palcové i metrické šrouby mají za srovnatelných podmínek i stejnou únosnost a životnost. Nejmarkantnějším rozdílem je tak uváděná životnost. Pro palcové šrouby je uváděná v palcích posunu na dobu životnosti, u výrobců metrických šroubů pak v otáčkách na dobu životnosti. Výpočet obsahuje oba parametry.
Přepočet:
Podle ANSI je dynamická únosnost zátěž, při které dosáhne šroub životnosti 1
milion palců posunu. Podle ISO je počítaná životnost na 1 milion otáček.
Pokud je tedy stoupání menší než 1 palec, je únosnost podle
definice ANSI menší než únosnost téhož kuličkového šroubu vyjádřená podle normy
ISO/DIN.
Opačně to pak platí pro šroub se stoupáním větším než 1 inch. V případě šroubu se
stoupáním větším než 1 inch bude únosnost dle ANSI vyšší než únosnost dle ISO,
i když samotný šroub je identický. Pro porovnání ANSI/ISO je nutné provést
přepočet dle vzorce:
Pi [lbf] = Ca [N] / (4.44822 * (25.4 / Ph [mm])(1/3))
kde:
Ca [N] ...... Dynamická únosnost ISO
Pi [lbf] ...... Dynamická únosnost ANSI
Ph [mm] ... Stoupání
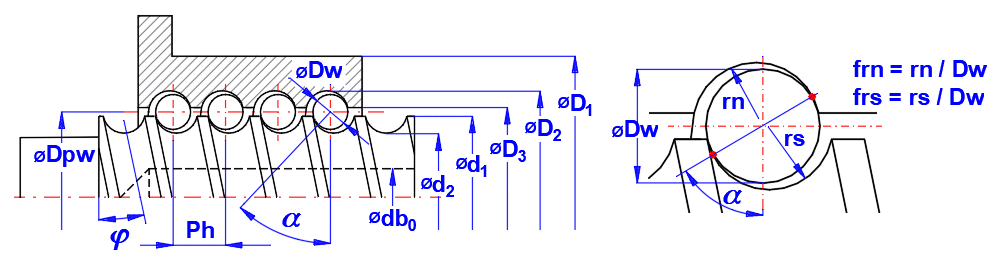
V normách, literatuře, katalozích bývá značení rozměrů často nejednotné. Proto zde uvádíme značení pro tento výpočet.
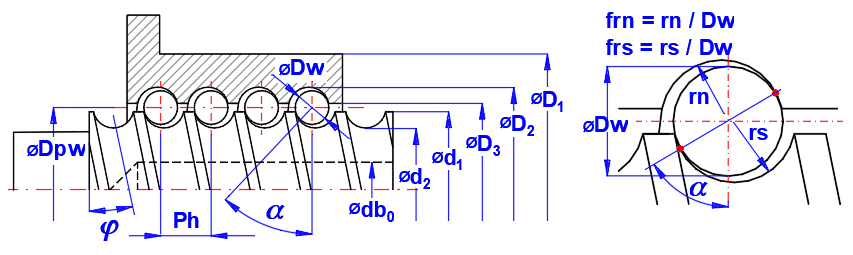
Velikost otáčkového faktoru (Dn = d1 * ns)
Jeho hodnota je ovlivněna především konstrukcí převodu kuliček. Pro vysoko
otáčkové šrouby je nutné co nejplynulejší dráhy v převodnících a co nejpřesnější
přechody kuliček do přechodníku. Výrobci uvádějí různé hodnoty pro různé
konstrukce, které jsou závislé na přesnosti, způsobu převodu kuliček
(interní/externí) atd.
Většinou platí, že se stoupajícím průměrem šroubu klesá hodnota Dn.
Příklady hodnot Dn
(Výrobce ...... rozsah)
KSK ............... 100000 - 125000
NSK ................ 80000 - 160000
Shuton .......... 100000 - 160000
PMI ................. 80000 - 220000
Steinmeyer ..... 120000 - 160000
Při výpočtu kuličkového šroubu se provádí řada pevnostních kontrol a doplňkových výpočtů. Jejich seznam a použité vzorce jsou níže.
| Vzpěr | Kritické otáčky | Průhyb | |
| Uložení kuličkového šroubu | Coeffb | Coeffncr | Coeffymax |
| Vetknutí - Vetknutí | 4 | 4.73 | 0.002604167 (1/384) |
| Vetknutí - Podpora | 2 | 3.927 | 0.0054 |
| Podpora - Podpora | 1 | 3.14159 | 0.013020833 (5/384) |
| Vetknutí - Volný konec | 0.25 | 1.875 | 0.125 (1/8) |
y [m] = Coeffymax * (qm * Ls/1000)4) / ((Es * 1000000) * Ix)
Coeffymax ... Koeficient [~]
qm ............. Zatížení od vlastní hmotnosti [N/m]
Ls ............... Nepodepřená délka
kuličkového šroubu [mm]
Es ............... Modul pružnosti [MPa]
Ix ............... Kvadr. moment setrvačnosti [m]
t [MPa] = 16 * Mk / (p * (d2 / 1000)3) / 1000000
Mk ........ Krouticí moment [Nm]
d2 ........ Vnitřní průměr šroubu [mm]
Ϭ [MPa] = 4 * F / (p * (d2 / 1000)2) / 1000000
F .......... Zatěžovací síla [N]
Ϭred [MPa] = (Ϭ2 + 3 * t2)0.5
Fb = (Coeffb * p2 * Es * Ix) / Ls2
Coeffb ... Koeficient vzpěru
ncr = (60 * Coeffncr2 / (2 * p)) * (Es * Ix * 9.81 / ((ros * 9.81 * 0.000000000001) * A * Ls4))0.5
Coeffncr ... Koeficient kritických otáček
ros ........... Hustota [kg/m3]
Základní statické zatížení (C0a) se obecně rovná přípustnému axiálnímu zatížení kuličkového šroubu. V závislosti na podmínkách je nutné vzít v úvahu následující statický koeficient bezpečnosti proti max. vypočtenému zatížení (neočekávaná vnější síla vyvolána setrvačností způsobenou startem nebo zastavením).
SFs = C0a / Fmax
Fmax ....... Maximální axiální zatížení [N]
C0a ......... Základní statická axiální únosnost [N]
SFs .......... Součinitel bezpečnosti
Jeho hodnoty by měly být větší než následující doporučení. Je odhadnut podle zadaného součinitele zatížení [3.15].
Obecné strojírenství
Bez vibrací nebo nárazů ............ 1.0 - 3.5
S vibracemi nebo nárazem ........ 2.0 - 5.0
Obráběcí stroje
Bez vibrací nebo nárazů ............ 1.0 - 4.0
S vibracemi nebo nárazem ........ 2.5 - 7.0
h = (1 - f * tan( f ))
/ (1 + f / tan( f ))
hr = (1 - f / tan( f )) /
(1 + f * tan( f ))
f .... Koeficient tření
f ... Úhel stoupání
Mazání tukem: Obecně se doporučují tuky stupně 2 dle DIN51825. Při běžném provozu doplňované po 6-10 měsících.
Mazání olejem: Všeobecně se pro mazání používají stejné
oleje jako pro valivá ložiska. Doporučená viskozita min. 50mm2/s(cSt)
Ve výpočtu je používána celá řada norem a informací z oborných či firemních publikací. V této části naleznete použité vzorce a vztahy bez podrobných vysvětlení a komentářů, které jsou v originálních zdrojích. Většinou jsou tyto výpisy uváděné v originálním jazyce normy.
Tato část specifikuje technické přejímací podmínky pro kuličkové šrouby a zejména příslušné přípustné odchylky pro přejímací zkoušky.
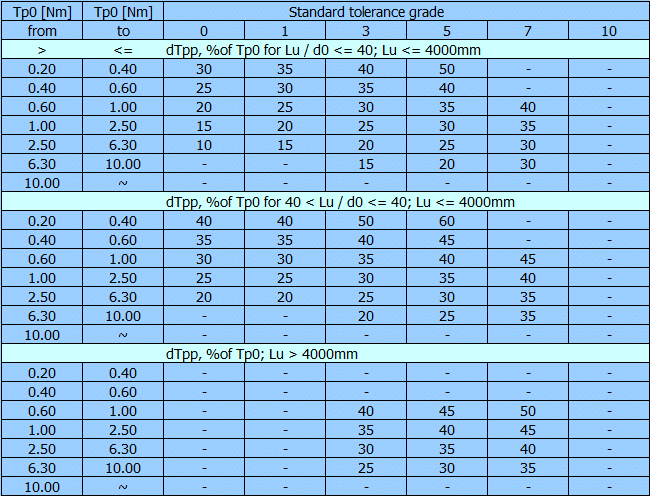
The typical tolerance grades for positioning and transport ball screws
| Type of ball screw | Standard tolerance grade |
| Positioning (type P) | 0 - 1 - 3 - 5 |
| Transport (type T) | 0 - 1 - 3 - 5 - 7 - 10 |
| Travel deviations per reference length | Positioning | Transport |
| Travel compensation c for useful travel Lu | Specified by user | C = 0 |
| Tolerance on specified travel ep | 1.1 | 1.2 |
| Permissible travel variation uup within useful travel | 2 | - |
| Permissible travel variation u300pwithin 300 mm travel | 3 | 3 |
| Permissible travel variation u2pp within 2p rad | 4 | - |
Checking of the mean travel deviations, esa and e0a, within the useful travel
Lu:
a) for the specified travel Ls
b) for the nominal travel L0
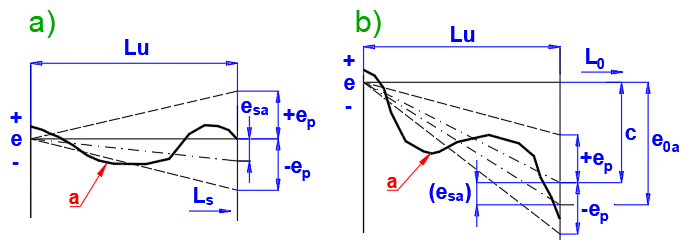
(a) Actual travel deviation
Permissible deviations
Checking of the mean travel deviation e0a, within the useful travel Lu:
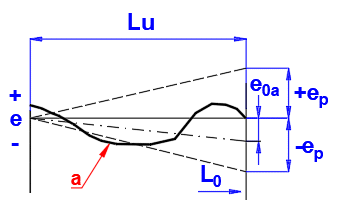
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
ep = +- (Lu / 300 * u300p) [mm] |
|||||
Checking of the travel variation uu within the useful travel Lu
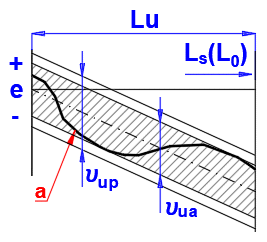
Permissible deviations

Checking of the travel variation u300pwithin 300 mm within an axial travel of 300 mm:
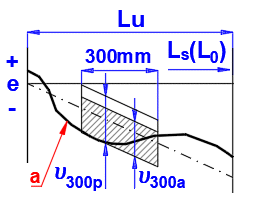
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
u300p [mm] |
|||||
| 3.5 | 6 | 12 | 23 | 52 x | 210 x |
x - Only for transport ball screws
Permissible travel variation u2pp within 2p rad
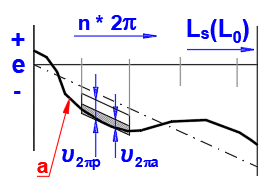
Permissible deviations
| Standard tolerance grade | |||||
| 0 | 1 | 3 | 5 | 7 | 10 |
|
u300p [mm] |
|||||
| 3 | 4 | 6 | 8 | - | - |
Although is a detailed description of the measurement and the resulting values in the standard, it is advisable to consult with the manufacturer or use the company catalogs.
Positioning or transport ball screw. Measurement of dynamic preload drag torque, ΔTp:
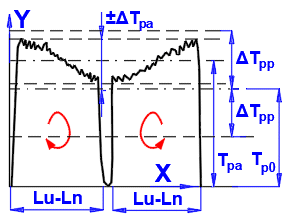
X - Travel
Y - Dynamic preload drag torque
Permissible deviations
Measurement of axial rigidity, Rnu:
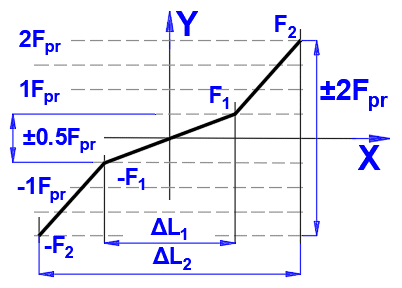
X ... Elastic deformation
Y ... Load
The axial load F1 = 0.5 * FPr or F2 = 2Fpr to the ball screw shaft in tension
and in compression.
Fpr is the preload and ΔL1 or ΔL2
are the elastic deformations (reversal range) caused by the axial test loads ±
F1 and ± F2 respectively.
Rigidity in the ranges ± F1:
Rnu1 = 2 * F1 / ΔL1 = Fpr / ΔL1
Rigidity in the range + F1 to + F2 and - F1 to - F2:
Rnu2 = 2 * (F2 - F1) / (ΔL2 - ΔL1) = 3 * Fpr / (ΔL2 - ΔL1)
Other test loads F may be used by agreement between the user and the manufacturer.
The static axial rigidity R [N/µm], constitutes the resistance to deformation and denotes the force ΔF [N], which is required to effect a component deflection ΔL by 1 µm in the axial direction of load application:
R = ΔF / ΔL
1 / Rbs = 1 / Rs + 1 / Rnu,ar
Static axial rigidity of ball screw shaft, Rs
The rigidity of the ball screw shaft follows from the elastic deflection of the ball screw shaft ΔL caused by an axial force ΔF and depends on the bearing arrangement.
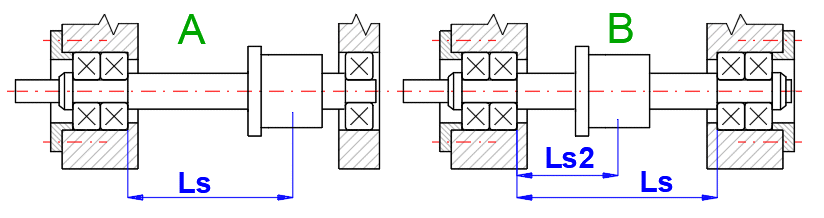

A. Rigid mounting of ball screw shaft at one end
Rs1 = (p * (dc2 - db02) * E) / (4 * Ls * 1000)
dc = Dpw - Dw * cos(a)
Dc = =Dpw + Dw * cos(a)
B. Rigid mounting of ball screw shaft at both ends
Rs2 = (p * (dc2 - db02) * E) / (4 * Ls2 * 1000) * (Ls / (Ls - Ls2))
minimum of rigidity at: Ls2 = Ls / 2
Static axial rigidity of ball nut unit with backlash: Rnu1
Static axial rigidity of nut body and screw shaft under resulting radial
components of load: Rns
Rns = ΔF / ΔLns
ΔLns = ΔF / Rns
Rns = (2 * p * i * Ph * E * tan(a)2) / (((D12 + Dc2) / (D12 - Dc2) + (dc2 + db02) / (dc2 - db02)) * 1000)
Static axial rigidity in ball / balltrack area: Rbt
The axial deflection in the ball / balltrack area is sufficiently approximated by the following equation:
ΔLns = (11)
According to Hertz the approach of the components is calculated from:
ΔLs,nb/t = (12)
Where for the screw shaft balltrack/ball contact applies:
Ʃρs = 4 / Dw - 1 / (frs * Dw) + 2 * cos(a) / (Dpw - Dw * cos(a))
For the nut bailtrack/ball contact applies:
Ʃρn = 4 / Dw - 1 / (frn * Dw) - 2 * cos(a) / (Dpw + Dw * cos(a))
The auxiliary values Ysn depend upon the ratio of the semi-major to the semi-minor axes of the contact ellipse cos(t). The following equation makes use of sin(t), which can be obtained by:
sin(t) = (1 - cos(t)2)0.5
Ys,n = 1.282 * (-0.154 * sin(t)0.25 + 1.348 * sin(t)0.5 - 0.194 * sin(t))
cos(ts) = abs[(-1 / (frs * Dw) - 2 * cos(a) / (Dpw - Dw * cos(a))) / Ʃρs]
cos(tn) = abs[(-1 / (frn * Dw) + 2 * cos(a) / (Dpw - Dw * cos(a))) / Ʃρn]
cEs,n = (11550 * (E0s,n + E0b) / (E0s,n * E0b))1/3
Es = En = Eb = 210000
ms = mn = mb = 10 / 3
E0s = E0n = E0b = E0
cEs = cEn = cEb =0.4643
FN = F / (i * z1 * cos(φ) * sin(a))
z1 = INTEGER ((Dpw * p) / (cos(φ) * Dw) - z2)
φ = arctan (Ph / (Dpw * p)
The rigidity characteristic k of one loaded turn of the ball screw is calculated from:
k = (z1 * sin(a)5/2 * cos(φ)5/2) / (cE3 * ck3/2)
ck = Ys * (Ʃρs)1/3 + Yn * (Ʃρn)1/3
Thus, the axial deflection due to Hertz stress exerted on a single nut can be calculated:
ΔLb/t = (F / (k * i))2/3
d(ΔLb/t) = 2/3 * F-1/3 * (1 / (k * i)2/3) * dF
The static axial rigidity of the ball/balltrack area Rb/t at the axial force F is:
Rb/t = dF / d(ΔLb/t) = 3/2 * (Fe * (i * k)2)1/3
1 / Rnu1 = 1 / Rb,t + 1 / Rn,s
Static axial rigidity of symmetrically preloaded ball nut unit: Rnu2,4
Static axial rigidity of nut body and screw shaft under preload, Rn/s,pr
As both nut bodies act like preloaded rings, the rigidity, Rn/s,pr of a double
nut is twice as high as that of a single nut:
Rn/s,pr = 2 * Rn/s
Static axial rigidity of ball/balltrack area under preload: Rn/t,pr
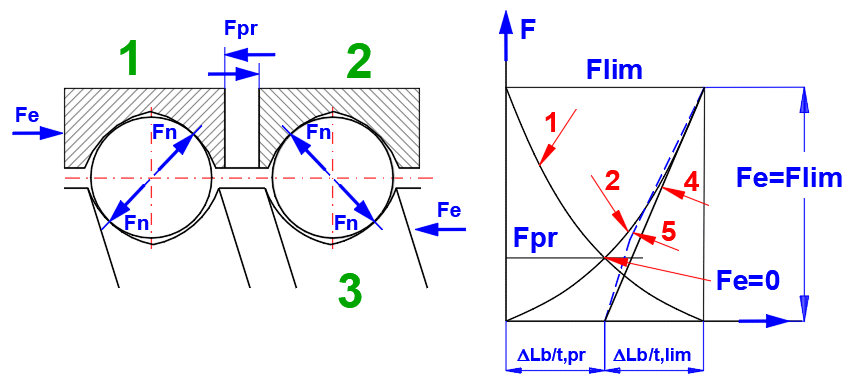
1. ball nut 1
2. ball nut 2
3. ball screw shaft
4. straight approximation line
5. actual curve
(5) Actual curve of the axial deflection in the ball/balltrack area of the
preloaded ball nut system if an additional external load between Fc = 0 and Fc =
Flim is applied.
Maximum deviation between 4 and 5 is approximately 6 %.
The following equation will furnish a guide value for symmetric double nuts:
Fpr = Fm / 23/2
Fm ..... Equivalent load (ISO 3408-5)
Fm = (Ʃ Fej3 * (nj / nm) * qj)(1/3) <j = 1 ... n>
The axial deflection of the ball/balltrack area due to the preload of a symmetrically preloaded nut system:
ΔLb/t,pr = (Fpr / (k * i))2/3
For 0 < Fe <= Flim, the rigidity Rb/t in the ball/balltrack area is determined as follows:
Flim = 23/2 * Fpr
Aproximation result
Rb/t = 23/2 * (Fpr * (k * i)2)1/3
Single or double ball nut preloaded by two-point-ball-contact: Rnu2
1 / Rnu2 = 1 / Rb/t + 1 / Rn/s,pr
Single ball nut preloaded by four-point-ball-contact: Rnu4
1 / Rnu4 = 1 / Rb/t + 1 / Rn/s,pr
As tolerances accumulate during the manufacturing process, differences occur
in rigidity evaluations.
The correction factor takes into account the following influences: machining
inaccuracies of balltrack (travel variations, groove, surface roughness, contact
angle, diameter).
Correction factor for accuracy far
| Accuracy class | far |
| 0, 1 | 0.60 |
| 3 | 0.55 |
| 5 | 0.50 |
| 7, 10 | 0.40 |
The static axial rigidity of the ball nut unit calculated with the
corresponding correction factor is:
Rnu,ar = far * Rnu
Výpočty jsou založené na definici dynamické únosnosti, což je zatížení, při kterém kuličkový šroub dosáhne trvanlivosti 1 milion otáček. Přesněji to znamená, že 90% dostatečně velkého počtu identických kuličkových šroubů dosáhne této trvanlivosti. Tato trvanlivost se obvykle značí jako L10. Pro vyšší spolehlivost než 90% je nutné použít příslušný korekční koeficient far.
L = (Ca / Fm)3 * 106
L ...... Trvanlivost [otáčky]
Ca .... Základní dynamická axiální únosnost [N]
Fm ... Ekvivalentní axiální zatížení [N]
Lh = L / (60 * nm)
Lh ..... Trvanlivost [hodiny]
nm .... Ekvivalentní otáčky [/min]
L1,2 = (Ca / Fm1,2)3 * 106
L1,2 = (Ca / Fma1,2)3 * 106
Lr = (L1-10/9 + L2-10/9)-9/10
Výpočet trvanlivosti La, Lhar pro spolehlivost vyšší než 90%
Lar = L * far; resp. Lar = Lr * far; Lhar = Lh * far
far ... Koeficient spolehlivosti
| Spolehlivost [%] | far |
| 90% | 1.00 |
| 95% | 0.62 |
| 96% | 0.53 |
| 97% | 0.44 |
| 98% | 0.33 |
| 99% | 0.21 |
Stejným způsobem je pak počítána modifikovaná trvanlivost Lm, Lhm:
Lm = (Cam / Fm)3 * 106 ;Lhm = Lm / (60 * nm); Lm1,2 = (Cam / Fm1,2)3 * 106
...............
L = (Ca / (fw * Fm))3 * 106
fw ... Součinitel zatížení
V případě proměnné rychlosti otáčení a proměnného axiálního zatížení se pro výpočet životnosti použijí ekvivalentní hodnoty Fm a nm:
Při proměnné rychlosti otáčení platí pro ekvivalentní rychlost otáčení nm [/min]:
nm = Ʃ (qj / 100) * nj <j = 1 ... n>
q ... Čas [%]
n ... Otáčky [/min]
Při proměnném axiálním zatížení a proměnné rychlosti otáčení platí pro ekvivalentní axiální zatížení Fm [N]:
Fm = (Ʃ Fj3 * (nj / nm) * (qj / 100))(1/3) <j = 1 ... n>
F ... Axiální zatížení, síla [N]
Fm1,2 = (Ʃ F1,2j3 * (nj / nm) * (qj / 100))(1/3) <j = 1 ... n>
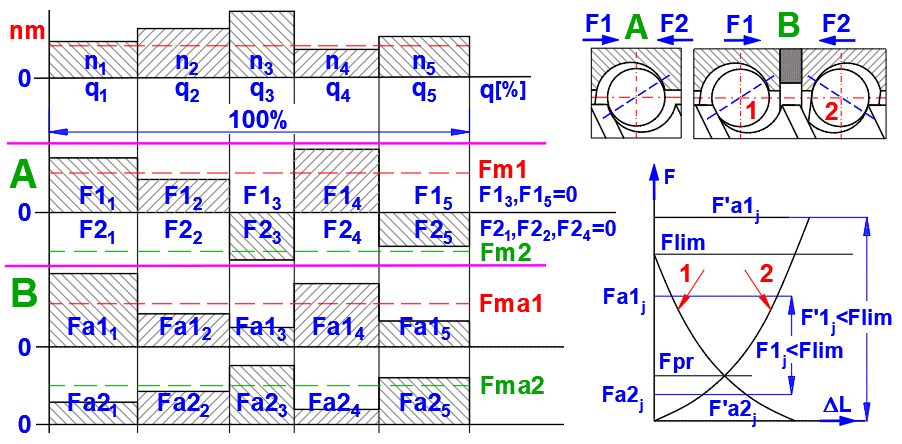
V důsledku působení vnějšího axiálního zatížení na předepjatý kuličkový šroub (eliminace vůle mezi maticemi a šroubem) bude jedna matice dodatečně zatížena a druhá uvolněna.
Flim = 23/2 * Fpr
Předepjatá matice (1) nebo (2) bude navíc zatížena vnějším axiálním
zatížením. Skutečné axiální zatížení této matice je
- pro vnější zatížení F1j nebo F2j <= Flim následující:
Fa1,2 = fop * Fpr * (1 + F1,2j / (23/2 * fop * Fpr)3/2
fop ... Operační koeficient předpětí (0.6)
F ...... Axiální zatížení, síla [N]
Fa .... Aktuální axiální síla [N]
Fpr ... Předpětí [N]
- pro vnější zatížení F1j nebo F2j > Flim pak:
Fa1j = F1j , Fa2j = F2j and Fa1j = 0, Fa2j = 0
Pro výpočet ekvivalentního aktuálního zatížení:
Základní axiální únosnost se počítá z následujících rovnic:
C0a = k0 * z1 * i * sin(a)
* Dw2 * cos(φ)
z1 = INTEGER ((Dpw * p)
/ (cos(φ) * Dw) - zu)
φ = arctan (Ph / (Dpw *
p)
k0 = 27.74 / (Dw * (( ρ11 +
ρ12) * ( ρ21 +
ρ22))0.5
ρ11 = ρ21
= 2 / Dw
ρ12 = -1 / (frs * Dw)
ρ22 = cos(a)
/ (Dpw / 2 - cos(a) * Dw / 2)
a ........ Úhel kontaktu [°]
φ ........ Úhel náběhu [°]
i ......... Počet zatížených závitů [~]
Dw ..... Průměr kuličky [mm]
Dpw ... Roztečný průměr [mm]
V případě optimálního rozložení zatížení (paralelní směry zatížení v kuličkovém šroubu a v kuličkové matici) je základní dynamické axiální zatížení odvozeno z následujících základních vzájemných vztahů:
Ca = Ci * i0.86
Ci = Cs * (1 + (Cs / Cn)10/3)-0.3
Cs = fc * cos(a)0.86
* z12/3 * Dw1.8 * tan(a) * cos(φ)1.3
fc = 9.32 * f1 * f2 * (1 / (1 - 1 / (2 * frs)))0.41
f1 = 10 * (1 - sin(a) /
3)
f2 = g0.3
* (1 - g)1.39 / (1 +
g)1/3
g = Dw / Dpw *
cos(a)
Cs / Cn = f3 * ((2 - 1 / frn) / (2 - 1 / frs))0.41frn = rn / Dw
frs = rs / Dw
f3 = ((1 - g) / (1
+ g))1.7233
C0am = C0a * fh0 * fac
Korekce tvrdosti povrchu, fh0
fh0 = (AH / 654)3 ≤ 1.0
AH ... skutečná tvrdost [HV10]
Korekce podle stupně přesnosti, fac
| Stupeň přesnosti | fac |
| 0, 1, 3, 5 | 1.00 |
| 7 | 0.90 |
| 10 | 0.70 |
Cam = Ca * fh * fac * fm
Korekce tvrdosti povrchu, fh0
fh = (AH / 654)2 ≤ 1.0
AH ... skutečná tvrdost [HV10]
Korekce podle stupně přesnosti, fac je stejná jako u statického axiálního zatížení.
Materiálový součinitel fm
| Ocel kuliček | fm |
| Chladnutí na vzduchu | 1.00 |
| Odplyněné | 1.25 |
| Elektricky přetavené | 1.44 |
| Přetavené ve vakuu | 1.71 |
The following equations for the basic load rating and static thrust capacity are included to enable the user of this standard to determine the approximate size ball screw assembly necessary to meet requirements.
Imperial (Inch) System Symbols
Pi ...... Basic load rating (1 000 000 inches rated life), [lbf]
Pix .... Rated load at x inches rated life, [lbf]
Ti ...... Basic thrust capacity, [Ibf]
LIi ..... 1 000 000 inches rated life, [inches]
LIix ... X inches rated life, [inches]
di ...... Ball diameter, [inches]
n ....... Number of ball turns under a unidirectional load, [turns]
Li ...... Lead, [inches / revolution]
Z ....... Number of load carrying balls per turn, [balls
/ turn]
Pi = 4500 * Z2/3 * di1.8 * n0.86 * Li1/3 , [lbf]
Ti = 10 000 * n * Z * di2 , [lbf]
Pix = Pi * (LIi / LIix)1/3 , [lbf]
Zpravidla není návrh přímo řešitelný a je nutné provádět průběžné zpřesňování parametrů. Pro nejčastější řešení, kdy znáte zatěžovací síly, rychlosti posuvu a přesnost polohování doporučujeme následující postup.
1. V odstavci [1.0] zvolte jednotky a proveďte Předběžný návrh. Zkontrolujte
požadavky na přesnost.
2. V odstavci [3.0] na základě předběžného návrhu zvolte / zadejte parametry
šroubu (průměr, stoupání, přesnost, zatížení...).
3. Pokud neznáte přesně ztěžující parametry, přejděte do odstavce [10.0] a [11.0].
Můžete zde definovat zatěžovací tabulku [10.0] a spočítat
ekvivalentní zatížení [11.0].
(Pro přesný výpočet zatížení je nutná znalost rozměrů šroubu,
proto je vhodné použít předběžný návrh pro jeho odhad)
4. Po zadání / změně vstupních parametrů [3.3-3.44] můžete okamžitě
kontrolovat nejdůležitější parametry [3.45-3.57].
5. Podrobný výpis všech výsledků je v Kapitole výsledků.
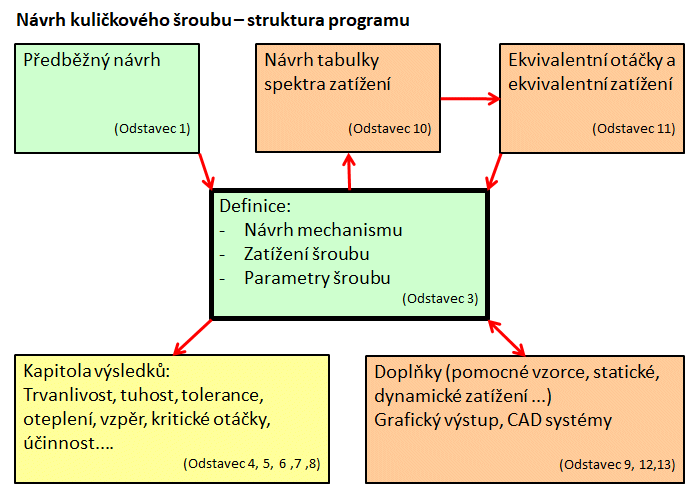
Návrh kuličkového šroubu není přímo a jednoduše řešitelný. Při návrhu je nutné brát do úvahy celou řadu často protichůdných požadavků a řešení je nutné hledat postupným zpřesňováním návrhu spolu s kontrolou parametrů šroubu v katalogu výrobce (dodavatele).
Proto je možné v této kapitole zhruba navrhnout rozměry šroubu, navrhnout otáčky, rychlost posuvu, zkontrolovat kritické otáčky, zkontrolovat šroub na vzpěr a zjistit přesnost a požadovaný výkon motoru. V dalších kapitolách je pak možné předběžný návrh optimalizovat a detailně navrhnout a zkontrolovat všechny parametry.
Ve výběrovém seznamu vyberte požadovanou soustavu jednotek výpočtu. Při přepnutí jednotek budou okamžitě přepočítány všechny vstupní hodnoty.
Zároveň dojde k přenastavení výběrových tabulek tak, aby odpovídaly vybraným jednotkám (ISO/ANSI).
Většina úloh vyžaduje řešení rychlosti vozíku (unašeče) v závislosti na stoupání, otáčkách šroubu, převodu a otáčkách motoru. To můžete řešit v této části. Zaškrtnutím volby napravo od vstupních buněk určíte, která hodnota se má spočítat.
Rozsah stoupání Ph vzhledem k průměru šroubu d1 je uveden v tabulce [1.32]. Při volbě hodnot se řiďte obrázkem.
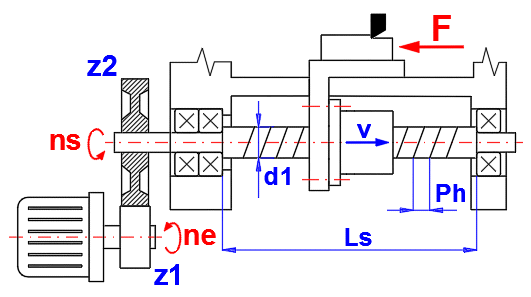
Standardni řada stoupání - mm (ISO, JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardni řada stoupání - inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Pro výběr je možné použít seznam napravo.
Převodový poměr je definován jako poměr počtu zubů i=z2/z1. Pokud používáte přímý pohon šroubu, je i=1.
1. Zadejte ekvivalentní zatížení šroubu [1.9]. Prostě zadejte váš odhad zatížení šroubu (Jakou hmotnost zdviháte, jakou silou vytlačujete, jaká síla
působí při obrábění....). Nezapomeňte zahrnout i vliv vibrací a rázů, kdy pro
silné rázy a vibrace může být zatížení i 2x,3x větší (viz koeficient fw [1.11]).
2. Zadejte ekvivalentní otáčky [1.10]. Zhruba otáčky, kdy je šroub nejvíce zatížen.
3. Zadejte požadovanou trvanlivost v hodinách [1.11]. (Pro předběžné účely můžete
zvolit hodnotu cca 20000 hodin)
Na základě zadané ekvivalentní zatěžovací síly, otáček a požadované trvanlivosti je spočítána požadovaná dynamická únosnost "Ca-req" ("Pi-req" podle ANSI). Podle dynamické únosnosti je vyhledán průměr šroubu. Navrhovaný průměr šroubu se pohybuje od minimální hodnoty průměru matice s pěti závity do maximální hodnoty průměru matice s jedním závitem. Počet závitů je uveden v závorce za průměrem.
Pokud je tlačítko zaškrtnuté, jsou automaticky přenesené hodnoty z řádku [1.5]
fw = 1.0 … 1,2 pro téměř žádné vibrace, žádné rázové
zatížení (v ≤ 0.25 m/s)
fw = 1.2 … 1,5 pro mírné vibrace, rázové zatížení (0.25 <v ≤ 1.00 m/s)
fw = 1.5 … 2.0 pro střední vibrace, rázové zatížení (1.00 <v ≤ 2.00 m/s)
fw = 2.0 … 3.5 pro silné vibrace, rázové zatížení (v > 2.00 m/s)
Je možné volit mezi několika možnostmi zadání. Pro mm šrouby je používána životnost v hodinách (méně často v otáčkách šroubu). Pro palcové šrouby pak životnost v palcích (popřípadě v[m]) posunu. Při změně je automaticky přepočítána vstupní hodnota tak, že požadovaná dynamická únosnost zůstává stejná.
Orientační hodnoty v
hodinách:
Stroje pro krátkodobý provoz 5000 - 10000
Stroje pro 8 hodinový provoz 20000
Stroje pro 16-ti hodinový provoz 40000
Stroje pro nepřetržitý provoz 80000
Na základě zatížení, otáček a požadované životnosti je vypočtena požadovaná dynamická únosnost. Vybraný šroub by měl mít únosnost vyšší.
Jedná se o hodnotu, která je převedena z ISO hodnoty na hodnotu dle ANSI. Více v teoretické části nápovědy.
Navrhovaný průměr šroubu se pohybuje
od minimální hodnoty s pěti závity matice do maximální hodnoty průměru matice s
jedním závitem.
Průměr je navrhován na základě únosnosti Ca počítané dle ISO3402-5.
Po volbě způsobu uložení a zadání délky a průměru šroubu (viz. obrázky) jsou dopočítány všechny důležité kontrolní hodnoty. Můžete tak ihned zkontrolovat hodnotu otáčkového faktoru, maximální vzpěrné síly a maximálních dovolených otáček. Zároveň můžete odhadnout i toleranční třídu šroubu v závislosti na požadované přesnosti polohování.
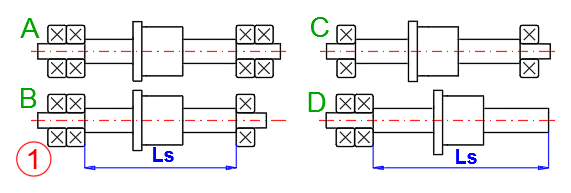
Vyberte způsob radiálního uložení kuličkového šroubu podle obrázku. Způsob uložení má vliv na vzpěrnou pevnost a na kritické otáčky. V případě rotující matice není nutné kontrolovat kritické otáčky.
Zadejte délku nepodepřené části šroubu Ls (viz obrázek). Obecně se doporučuje délka menší než 40 průměrů šroubu.
Standardní řada průměrů ISO [mm]
6, 8, 10, 12, 16, 20, 25, 32, 40, 50, 63, 80, 100, 125, 140, 160, 200
Průměry používané výrobci [mm]
4, 6, 8, 10, 12, 14, 15, 16, 20, 25, 28, 32, 36, 40, 45, 50, 63, 80, 100, 125,
140, 160, 200
Standardní řada průměrů ANSI B5.48-1977 [in]
0.25, 0.3125, 0.375, 0.5, 0.625, 0.75, 0.875, 1, 1250, 1.5, 1.75, 2, 2.25, 2.5,
3, 3.5, 4, 4.5, 5, 6, 8
Velikost otáčkového faktoru (Dn = d1 * ns)
Jeho hodnota je ovlivněna především konstrukcí převodu kuliček. Pro vysoko
otáčkové šrouby je nutné co nejplynulejší dráhy v převodnících a co nejpřesnější
přechody kuliček do přechodníku. Výrobci uvádějí různé hodnoty pro různé
konstrukce, které jsou závislé na přesnosti, způsobu převodu kuliček
(interní/externí) atd.
Většinou platí, že se stoupajícím průměrem šroubu klesá hodnota Dn.
Příklady hodnot Dn
(Výrobce ...... rozsah)
KSK ............... 100000 - 125000
NSK ................ 80000 - 160000
Shuton .......... 100000 - 160000
PMI ................. 80000 - 220000
Steinmeyer ..... 120000 - 160000
Slouží pro výpočet účinnosti. Pro předběžný návrh je možné volit hodnotu 0.01.
V závislosti na délce šroubu Ls je určena i tolerance pro jednotlivé toleranční třídy. Podle hodnot z tabulky tak můžete odhadnout/vybrat i požadovanou přesnost šroubu.
ISO: Pro polohovací šrouby (P-type) se používá IT0-IT5, pro transportní (T-type) pak IT1-IT10.
ANSI: Používaná stupnice Class1 až Class8.
Detailní vysvětlení v teoretické části a kapitole [6.0].
V tabulce jsou uvedené průměry šroubu a rozsah stoupání podle norem ISO a ANSI. Hvězdičkou jsou označené průměry, které jsou poskytovány některými výrobci nad rámec normy ISO.
Po výběru šroubu z tabulky je hodnota průměru přenesena do řádku [1.19].
V tomto odstavci je možné definovat materiálové parametry. V naprosté většině případů je vyhovující základní nastavení pro ocel. Nastavíte stisknutím tlačítka. Měnit tyto hodnoty by měl pouze specialista, či výrobce.
V tomto odstavci definujete všechny vstupní parametry převodu kuličkovým šroubem. Počínaje přesností, uložením šroubu, zatížením, délkou, únosností atd. Po definici všech parametrů jsou v "Kapitole výsledků" k dispozici všechny parametry šroubu, které se v praxi hodnotí a sledují.
Při volbě parametrů použijte nápovědu pro každý parametr. S výhodou můžete také použít doplňkových výpočtů z kapitoly "Kapitola doplňků".
Stisknutím tlačítka "[1.0]>>[3.0]" přenesete hodnoty (Ph, Fm, nm,
fw, L, Ls, d1) z
předběžného návrhu do tohoto odstavce.
Pokud je nastaven výběr z tabulky [3.26] je dohledán odpovídající šroub d1
(popřípadě nejbližší vyžší).
V této části definujete přesnost, konstrukci, zatížení a trvanlivost.
Na základě určení šroubu a na základě předběžného návrhu by jste měli být schopni zvolit odpovídající toleranční třídu. Pro šrouby určené k polohování se používají toleranční třídy IT0-IT5, Pro transportní účely pak toleranční třídy IT1-IT10.
Volba toleranční třídy má vliv především na přesnost polohování, tolerance (odstavec [6.0]), v menší míře pak na únosnost, dosahované rychlosti a samozřejmě na cenu.
V běžném strojírenství se pracuje se spolehlivostí 90%. To znamená, že 90% šroubů vydrží deklarovanou zátěž při požadované životnosti. Existují však odvětví, kdy je vyžadována spolehlivost vyšší (letectví, kosmonautika, jaderná energetika...). Proto je možné nastavit požadovanou spolehlivost, která ovlivňuje požadovanou dynamickou únosnost.
Vyberte způsob radiálního uložení kuličkového šroubu podle obrázku. Způsob uložení má vliv na vzpěrnou pevnost a na kritické otáčky. V případě rotující matice není většinou nutné kontrolovat kritické otáčky.

V praxi se používají dva způsoby axiálního uložení konců. V prvním případě je pevně ukotven jeden konec a druhý konec je volný ve směru osy šroubu, ve druhém případě jsou pevně ukotvené oba konce. Druhý případ se využívá v případě nutnosti předepnutí šroubu (například eliminace teplotní roztažnosti, zvýšení axiální tuhosti atd.).
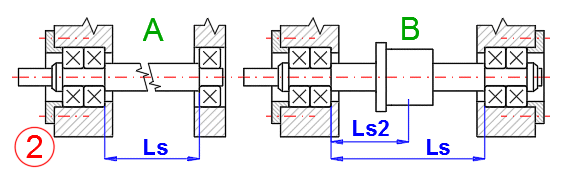
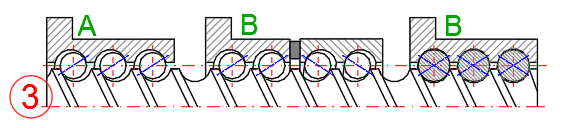
Jsou používány dva druhy matic.
A. Bez předepnutí. Předpokládá se, že přesnost a zatížení je důležité pouze v
jednom směru pohybu. Při volbě opačného směru pohybu je nutné počítat s vůlí.
B. S předepnutím. Matice je konstrukčne řešená tak, že není vůle při přechodu z
jednoho do druhého směru pohybu. Konstrukční řešení může mít řadu variant a
podle konstrukčních požadavků se mění i velikost předepnutí (Většinou je
nutné dohodnout s dodavatelem).
Matice s předepnutím a velikost předepnutí pak má vliv na výpočet ekvivalentního zatížení šroubu. Můžeme si to představit tak, že i když není matice zatížena, tak předepnutí vytváří sílu, kterou je nutné uvažovat při výpočtu ekvivalentního zatížení.
Při určení síly pro výpočet ekvivalentního zatížení pak nastávají tři případy.
- Nulová zatěžující síla. Síla předepnutí je rozdělena v jednom i druhém směru.
- Zatěžující síla je menší než Flim. Zatěžovací síla spolu se sílou předepnutí
je proporcionálně rozdělena do obou směrů.
- Zatěžující síla je větší než Flim. Zatěžující síla překoná sílu předepnutí a
je uvažována jen v příslušném směru.
Detailní popis viz odstavec [11.0]
Zadejte zatížení v jednom a druhém směru. V případě proměnlivého zatížení pak ekvivalentní zatížení, viz odstavec [11.0].
Zadejte maximální axiální zatížení. Musí být větší nebo rovné Fma1, Fma2.
Zadejte otáčky v jednom a druhém směru. V případě proměnlivých otáček pak ekvivalentní otáčky, viz odstavec [11.0].
Zadejte maximální otáčky. Musí být větší nebo rovné nm1, nm2.
Dle požadované přesnosti polohování a požadované tuhosti se volí způsob lícování matice na hřídel. S rostoucím předepnutím klesá trvanlivost. Matice s vůlí - Jednosměrné zatížení Fpr=0.
Velikost předepnutí bývá uvedena v katalogu, popřípadě je možné domluvit s
dodavatelem. Obecně se používají následující hodnoty předepnutí vyjádřeno v
procentech dynamické únosnosti šroubu Ca:
3 % Ca - Přesné polohování a méně zatížené šrouby
5 % Ca - Přesné polohování a středně zatížené šrouby
8 % Ca - Matice se 4-bodovým stykem
10 % Ca - Přesné polohování a více zatížené šrouby
fw = 1.0 … 1,2 pro téměř žádné vibrace, žádné rázové
zatížení (v ≤ 0.25 m/s)
fw = 1.2 … 1,5 pro mírné vibrace, rázové zatížení (0.25 <v ≤ 1.00 m/s)
fw = 1.5 … 2.0 pro střední vibrace, rázové zatížení (1.00 <v ≤ 2.00 m/s)
fw = 2.0 … 3.5 pro silné vibrace, rázové zatížení (v > 2.00 m/s)
Je možné volit mezi několika možnostmi zadání. Pro mm šrouby je používána životnost v hodinách (méně často v otáčkách šroubu). Pro palcové šrouby pak životnost v palcích (popřípadě v [m]) posunu. Při změně je automaticky přepočítána vstupní hodnota tak, že požadovaná dynamická únosnost zůstává stejná.
Orientační hodnoty v
hodinách:
Stroje pro krátkodobý provoz 5000 - 10000
Stroje pro 8 hodinový provoz 20000
Stroje pro 16-ti hodinový provoz 40000
Stroje pro nepřetržitý provoz 80000
Na základě zatížení, otáček a požadované životnosti je vypočtena požadovaná dynamická únosnost. Vybraný šroub by měl mít únosnost vyšší.
Jedná se o hodnotu, která je převedena z ISO hodnoty na hodnotu dle ANSI. Více v teoretické části nápovědy.
V této části vyberete odpovídající šroub (matici), popřípadě vyplňte odpovídající parametry z katalogu výrobce.
Zadejte délku nepodepřené části šroubu Ls (viz obrázek). Obecně se doporučuje délka menší než 40 průměrů šroubu.
V případě oboustraného axiálního uchycení šroubu (varianta B), zadejte ještě souřadnici matice Ls2.

Počet závitů je daný konstrukcí matice a většinou je výrobcem uváděn. Používá se počet závitů v rozsahu zhruba od 1.5-6.0. Počet závitů má vliv na výpočet statické a dynamické únosnosti, tuhosti a délky matice.
Zadejte počet nezatížených kuliček. Jedná se o vratné systémy, kdy jsou kuličky vracené po jedné otáčce a většinou zu=3. U vratných systémů, kde jsou kuličky vracené od konečného závitu do prvního je zu=0. Informaci o konkrétní konstrukci naleznete většinou v katalogu výrobce.
Součinitel vyjadřuje nerovnoměrné rozdělení zatížení v případě více závitů matice. Pokud má tedy matice závitů více, je únosnost Ca počítána podle vzorce Ca=Ca(1)*i^exp, kde Ca(1) je únosnost pro jeden závit. Opdobně pak pro Pi(palcové šrouby).
Výpočet obsahuje dvě základní rozměrové tabulky šroubů. Milimetrová(ISO) a palcová(ANSI). Tabulky obsahují všechny kombinace průměru šroubu a stoupání. Výrobci dodržují tyto základní rozměry (popřípadě nabízejí více průměrů šroubu). Volba průměrů kuliček je však libovolná. Na základě rozboru mnoha katalogů výrobců jsme připravili i tabulku používaných průměrů kuliček a jejich přiřazení k průměrům šroubů. Vznikla tak řada označená jako lehká, střední a těžká (velikost kuliček). Pro kterou byly dopočítány i příslušné hodnoty C0a, Ca, Ti, Pi.
Katalogy výrobců pak bývají podmnožinou těchto tabulek a většinou je možné dohledat i konkrétní šroub, který splňuje spočítané parametry.
Ze seznamu vyberte odpovídající šroub. Měl by splňovat podmínku, že hodnota dynamické únosnosti Ca>Ca-reg[3.17] (resp. Pi>Pi-reg[3.18] pro palcové šrouby). Zároveň by měla být dodržena hodnota stoupání Ph z předběžného návrhu[1.0], ve kterém definujete rychlost pohybu matice a tím i potřebné stoupání Ph.

Vnitřní otvor šroubu se používá pro instalaci chlazení, nebo pro změnu kritických otáček. Většina šroubů je bez otvoru db0=0.
Průměr je většinou konstrukční záležitostí výrobce. Je samozřejmé, že jej není možné volit libovolně. Základní podmínka je že průměr Dw nemůže být větší než stoupání Ph.
0.600, 0.800, 1.000, 1.200, 1.250, 1.500, 1.588, 1.750, 2.000, 2.381, 2.500, 3.000, 3.175, 3.500, 3.969, 4.762, 5.000, 5.556, 6.000, 6.350, 7.144, 7.938, 8.000, 9.525, 10.000, 10.319, 12.700, 20.000, 20.638, 25.400, 30.000, 31.750, 38.100, 40.000, 44.450, 50.000
Standardni řada stoupání - mm (ISO, JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardni řada stoupání - inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Roztečný průměr je dopočítán z průměru d1 a Dw. Pokud chcete zadat vlastní hodnotu odškrtněte tlačítko vpravo.
Ve většině případů je 45°.
Poměr (frs, frn) poloměru kuličkové dráhy hřídele kuličkového šroubu, rs nebo tělesa kulové matice, rn, k průměru kuličky, Dw
V případě, že definujete vlastní parametry šroubu, zadejte únosnost z katalogu výrobce.
Hodnota je navržena podle DIN69051-5.
Přepínač je použit pro zobrazení (viz obrázek vpravo), pro výpočet délky matice [3.43] a pracovní dráhy [3.44] a pro výstup do CAD.
Po odškrtnutí tlačítka vpravo můžete zadat vlastní hodnotu.
V této části jsou uvedené nejdůležitější hodnoty z kapitoly výsledků.
V tomto odstavci jsou uvedené hodnoty trvanlivosti podle ISO3408-5 (ANSI_B5.48).
Pokud je šroub namáhán pouze v jednom směru (Fma1 nebo Fma2 = 0; [3.8, 3.9]) a není použita předepjatá matice, je použit prostý výpočet trvanlivosti.
Tato část zahrnuje dvě možnosti.
- Obousměrně zatížený šroub (bez předepjaté matice).
- Jednosměrně i obousměrně zatížený šroub s předepjatou maticí. Předepjatá
matice přináší dodatečné vnitřní (obousměrné) zatížení šroubu, které je nutné
brát v úvahu i při jednosměrném zatížení.
Výpočet pak zohledňuje pro výpočet trvanlivosti obousměrné namáhání. (Index 1,2 označuje směr).
Tento odstavec obsahuje výpočet tuhosti podle ISO 3408-4.
Změna nastavení se promítne do odstavce [3.0].
V této části můžete řešit celkovou tuhost sestavy šroubu, matice, ložisek a montážních prvků.
Tuhost opěrného ložiska (ložisek) se liší v závislosti na typu ložiska a velikosti předpětí. Kontaktujte výrobce ložisek.
Tuhost montážní části matice se liší v závislosti na konstrukci stroje.
Deformace je počítána pro maximální sílu Fmax [3.10] a plnou délku šroubu Ls [3.20].
Jedná se o průběžné hodnoty pro výpočet tuhosti. Detaily v ISO 3408-4.
Tato část specifikuje technické přejímací podmínky pro kuličkové šrouby a zejména příslušné přípustné odchylky pro přejímací zkoušky.
Můžete změnit toleranční třídu podle potřeby. Změna se promítne i do odstavců [3.0, 5.0].
Část dráhy, na kterou se vztahuje specifikovaná úchylka (zdvih plus délka šroubové matice).
Napravo je hodnota odhadnutá na základě délky šroubu a délky matice. Po odškrtnutí tlačítka můžete zadat vlastní hodnotu.
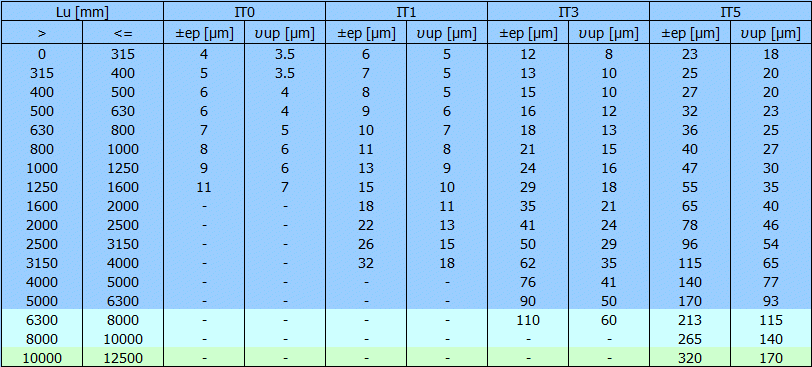
V tabulce jsou nejdůležitější toleranční hodnoty pro celý rozsah délek Lu. Zároveň je označen sloupec a řádek pro aktuální délku a toleranční třídu šroubu.
V tabulce jsou uvedené kompletní tolerance podle obrázků vpravo pro aktuální hodnotu Lu.
Hodnoty platí pouze pro předepnuté matice, otáčky 100/min a viskozitu ISO_grade100.
Pro měření se používají hodnoty F1=0.5*Fpr a F2=2*Fpr. Ve výpočtu jsou dosazené teoretické hodnoty. Po odškrtnutí tlačítka na [6.16] můžete dosadit hodnoty vlastní.
K dispozici je tabulka hodnot dle ANSI_B5.48
Celková přípustná odchylka od kladné do záporné hodnoty chyby po celé délce zdvihu.
Maximální přípustný kladný nebo záporný sklon měřené čáry chyby stoupání. Obvykle se uvádí v palcích(mm) chyby na 12 palců (300mm) délky závitu.
Celková odchylka od kladné do záporné, chyba stoupání pro jednu otáčku matice.
Při provozu vzrůstá teplota šroubu a matice, což má vliv na přesnost. V podstatě se řeší třemi způsoby, popřípadě jejich kombinací.
- řeší řídící systém pohonu šroubu (matice)
- chlazením šroubu (vnitřní otvor, chladicí kapalina)
- předepnutím šroubu v axiálním směru (pouze pro oboustraně upevněný šroub)
V tomto odstavci můžete zjistit roztažení šroubu vzhledem k nárůstu teploty a předepínací sílu, která je nutná pro eliminaci tepelné dilatace.
Při zaškrtnutí jsou vyplněné hodnoty z odstavce [3] a [2].
Zadejte zvýšení teploty šroubu při provozu.
Požadavek pro změnu délky hřídele pomocí předpětí. Zaškrtnuté tlačítko automaticky doplňuje hodnotu z [7.6]
V tomto odstavci jsou uvedené základní kontrolní výpočty používané při návrhu kuličkového šroubu. Zelená pole obsahují doporučené hodnoty.
Vstupní parametry jsou načteny z odstavce [3.0].
Můžete změnit způsob uložení. Změna se promítne i do odstavce [3.0].
V závislosti na konstrukci se může vyskytnout dodatečné axiální zatížení, které je nutné brát v úvahu. Pokud se vyskytne, zadejte jeho hodnotu.
Udává průhyb šroubu zatíženého vlastní vahou pro horizontálně uložené šrouby.
Doporučený maximální průhyb je pro:
Všeobecné strojírenství y = 0.0003 * Ls
Stavba obráběcích strojů y = 0.0002 * Ls
Pro kontrolu a výpočet bezpečnosti je uvažována zušlechtěná a legovaná ocel s mezí kluzu Rp0.2 definovanou ve [2.0].
V případě současného působení tahu / tlaku a krutu, je nutné řešit kombinované namáhání. Redukované napětí by mělo být menší než dovoleného napětí v tahu.
Mezní štíhlost SRc je důležitý
parametr konkrétního materiálu, rozlišující oblast pružného a nepružného vzpěru
a tím i použití odpovídajících vztahů. Je proto vhodné ověřit tento parametr pro
konkrétní materiál. Doporučená hodnota je určena podle obecného vztahu:
SRcs = 0.5*(E / (Rp02 * 0.5))^0.5
SRc = (E * 3.14^2 / (Rp02 * 0.5))^0.5
Štíhlostní poměr konkrétního šroubu
určuje, v jaké oblasti vzpěru šroub je (prostý tlak, nepružný vzpěr, pružný
vzpěr) a tím i kontrolní metodu použitou pro zjištění koeficientu bezpečnosti.
Mohou nastat 3 situace:
1. SR < SRcs .... Oblast prostého tahu / tlaku. Doporučená bezpečnost SF>1.75)
2. SRcs < SR < SRc ... Oblast nepružného vzpěru. Doporučená bezpečnost
SF=1.75*(1+(SR - SRcs) / (SRc - SRcs))
3. SRc < SR ... Oblast pružného vzpěru. Doporučená bezpečnost SF>3.5)
Vyjadřuje poměr mezi kritickou a působící silou. Minimální koeficient bezpečnosti (zelená buňka) je doporučen v závislosti na štíhlostním poměru [8.21]
Otáčky šroubu by neměly překročit 80% kritických otáček.
Jeho hodnoty by měly být větší než následující doporučení. Je odhadnut podle zadaného součinitele zatížení [3.15].
Obecné strojírenství
Bez vibrací nebo nárazů ............ 1.0 - 3.5
S vibracemi nebo nárazem ........ 2.0 - 5.0
Obráběcí stroje
Bez vibrací nebo nárazů ............ 1.0 - 4.0
S vibracemi nebo nárazem ........ 2.5 - 7.0
Pro rychloběžné, výkonově namáhané šrouby je doporučené mazání olejem. Pro tuto kategorii šroubů je určena tato část. Na základě průměru šroubu a otáček je doporučena viskozita oleje a jeho minimální množství. Zároveň je odhadnuta i účinnost.
Doporučuje se používat oleje s přísadami potlačujícími opotřebení. Mají schopnost mazat i v podmínkách mezního tření, když je nedostatečná rychlost pro mazání EHD (elasto-hydrodynamic lubrication). Doporučuje se převodový olej třídy CLP podle DIN51517-3 nebo ekvivalentní.
Můžete zvolit pracovní teplotu, typ oleje a po odškrtnutí tlačítek vpravo zvolit vlastní hodnoty třídy viskozity oleje resp. viskozitu.
Při zaškrtnutém tlačítku [8.42] je viskozita spočítána na základě pracovní teploty a zvolené třídy viskozity (VG2-VG1500).
Ve výběrovém tlačítku zvolte výpočet buď pro samostatný šroub/matice, nebo pro šroub/matice +ložiska.
Na základě rozměrů šroubu, zatížení šroubu, zatížení ložisek, typu oleje a viskozity je odhadnutý součinitel tření, který určuje účinnost. Po odškrtnutí tlačítka vpravo můžete zadat součinitel vlastní.
Výpočet ja založen na geometrii šroubu a součiniteli tření [8.44]. Pokud nemáte k dispozici laboratorní měření, může to být vhodný parametr pro další specializované výpočty (oteplení, ztrátové teplo, tepelná dilatace, atd.).
Normální provoz označuje převod rotační síly na axiální sílu, inverzní provoz pak převod axiální síly na sílu rotační.
V tomto odstavci naleznete některé základní vzorce, které mohou pomoci při návrhu.
V tomto odstavci můžete přesně definovat parametry mechanismu a zátěžové spektrum šroubu a matice. Získáte tak přesné hodnoty sil, momentů a potřebného výkonu motoru. Výsledné síly a otáčky můžete přenést do odstavce Výpočtu ekvivalentního zatížení [11].
Při definici mechanismu se řiďte obrázkem.
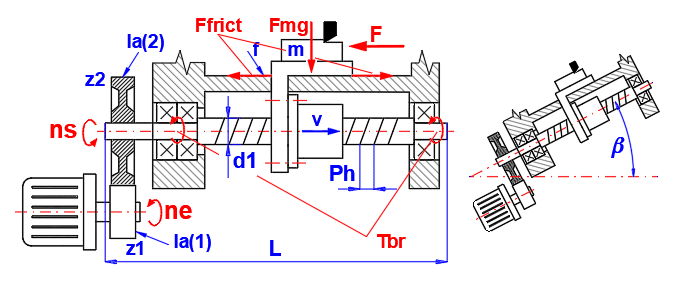
V grafu pak můžete sledovat řadu parametrů (otáčky, síly, momenty a výkon motoru).
X-ová osa vyjadřuje čas.
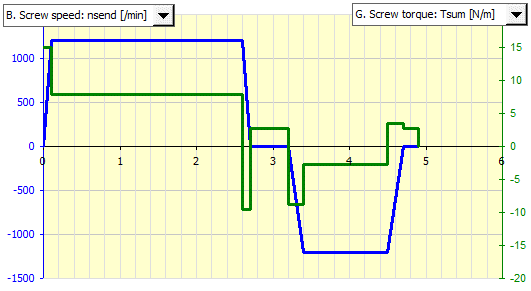
Definujte všechny parametry. Zaškrtnutím tlačítka na [10.2] jsou automaticky přenesené parametry šroubu z odstavce [3.0]. Po odškrtnutí můžete definovat rozměry rozdílné.
Skutečná délka šroubu L je odhadnuta ze zadané vzdálenosti mezi ložisky Ls, která je zvětšena o 10 průměrů šroubu. Slouží pouze k výpočtu momentu setrvačnosti.
Většina uložení je konstruována buď v horizontální(0°) a nebo vertikální rovině(90°). Zadejte natočení mechanismu.
Zadejte kompletní hmotnost objektů, se kterými šroub pohybuje.
Moment setrvačnosti převedený z přímočarého pohybu (stolu, obrobku...) na rotační.
Moment setrvačnosti hřídele šroubu.
Moment setrvačnosti všech kol (rotujících hmot) na straně šroubu. Pro přibližný výpočet hodnot můžete použít vzorce z odstavce [9].
Moment setrvačnosti všech kol (rotujících hmot) na straně motoru, včetně rotujících hmot motoru (informace o motoru hledejte v katalogu výrobce motoru). Pro přibližný výpočet hodnot můžete použít vzorce z odstavce [9].
Převodový poměr je definován jako poměr počtu zubů i=z2/z1. Pokud používáte přímy pohon šroubu, je i=1.0. Nicméně i v tomto případě je vhodné definovat rotující hmoty na straně motoru (motor, spojky....) [10.11].
Moment setrvačnosti všech rotujících hmot vztažených k pohonu (motoru). Je použit pro výpočet úhlového zrychlení.
Dle požadované přesnosti polohování a požadované tuhosti se volí způsob lícování matice na hřídel. S rostoucím předepnutím klesá trvanlivost. Matice s vůlí - Jednosměrné zatížení Fpr=0.
Velikost předepnutí bývá uvedena v katalogu, popřípadě je možné domluvit s
dodavatelem. Obecně se používají následující hodnoty předepnutí vyjádřeno v
procentech dynamické únosnosti šroubu Ca:
3 % Ca - Přesné polohování a méně zatížené šrouby
5 % Ca - Přesné polohování a středně zatížené šrouby
8 % Ca - Matice se 4-bodovým stykem
10 % Ca - Přesné polohování a více zatížené šrouby
Pro otáčení předepnuté matice je nutný krouticí moment i v případě, že matice není axiálně zatížena.
Zvolte součinitel tření ve vedení.
Pro lineární kuličková vedení je součinitel f=0.003-0.006.
Pro smykové, mazané tření je možné vycházet z následujících hodnot.
f = 0.05-0.10 ... Kalená ocel / Kalená
ocel
f =
0.05-0.15 ... Kalená ocel / Litina
f =
0.09-0.15 ... Kalená ocel / Bronz (fosforový)
f =
0.07-0.10 ... Litina / Litina
f =
0.07-0.10 ... Litina / Bronz (fosforový)
Zadejte účinnost kuličkového převodu. Doporučená hodnota je napravo od vstupní buňky. Hodnota vychází z geometrie šroubu a nezahrnuje další vlivy. Nicméně pro tento návrh je zcela postačující.
Zadejte třecí momenty ložisek. Přibližná hodnota je napravo od vstupní buňky.
Po stisknutí tlačítka budou přesunuté spočítané síly a otáčky do tabulky která je určena pro výpočet ekvivalentního zatížení a ekvivalentních otáček v odstavci [11.0].
V tabulce postupně definujte pracovní cyklus mechanismu.
Otáčky: Ve sloupci "neend" postupně zadejte koncové otáčky motoru
v daném úseku.
Časový úsek: Ve sloupci "dt" zadejte délku každého úseku v
sekundách.
Obráběcí síla: Ve sloupci "F" zadejte externí sílu, pokud v daném
úseku působí (například obrábění).
Řádek 1: neend=2000; dt=0.05; F=0 ............... Rozběh z 0 na pracovní
otáčky 2000/min.(akcelerace)
Řádek 2: neend=2000; dt=0.40; F=1000 .......... Pracovní cyklus obrábění
při otáčkách 2000/min, obráběcí síla je 1000N
Řádek 3: neend=0; dt=0.05; F=0
............... Zabrždění z pracovních otáček na 0.(decelerace)
Řádek 4: neend=0; dt=0.10; F=0
............... Časová prodleva (např. pro přenastavení nástroje)
Řádek 5: neend=-2000; dt=0.05; F=0 ................ Rozběh pro zpětný chod na
otáčky -2000/min(akcelerace)
Řádek 6: neend=-2000; dt=0.40; F=0 ................ Zpětný chod při otáčkách
-2000/min, obráběcí síla je 0N
Řádek 7: neend=0; dt=0.05; F=0
............... Zabrždění na nulové otáčky (decelerace)
Řádek 8: neend=0; dt=0.10; F=0
............... Časová prodleva (např. pro přenastavení nástroje)
Celkový čas pracovního cyklu 1.2 sec.
Výpočty trvanlivosti šroubu vychází z předpokladu, že šroub pracuje při stálých neproměnných provozních podmínkách. V praxi však tento předpoklad není splněn. Proto můžete použít tohoto pomocného výpočtu, který převede proměnné zatížení a proměnné otáčky na ekvivalentní zatížení použité ve výpočtu trvanlivosti.
S výhodou můžete použít předchozího odstavce [10], který umožňuje přesnou definci parametrů mechanismu a zátěžového spektra, jehož výsledkem je i přesná definice sil a otáček pro tento výpočet.
Pokud nevyužijete výpočtu z odstavce [10] postupujte při výpočtu ekvivalentního zatížení následovně:
1. Pracovní cyklus šroubu rozdělte do několika časových úseků, v nichž jsou
provozní podmínky přibližně konstantní (viz. obrázek).
2. Ve výběrovém seznamu [11.2] nastavte počet těchto časových úseků.
3. Zvolte typ matice A nebo B [11.3] a velikost předepnutí [11.4].
4. Ve vstupní tabulce [11.7] definujte provozní podmínky pro jednotlivé
úseky.
Výsledky výpočtu pak můžete přenést do odstavce [3.0].
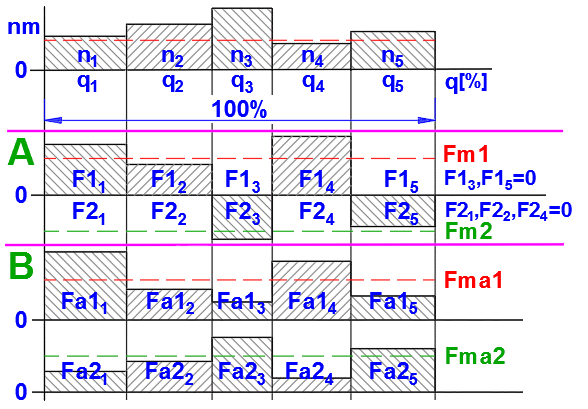
Průběhy vstupních hodnot můžete sledovat na grafu vpravo, s tím, že je zobrazeno i ekvivalentní zatížení a ekvivalentní otáčky (zelená směr1, červená směr2).
X-ová souřadnice udává procenta zatížení (otáček) na zadané úrovni (celý cyklus zatížení=100%).
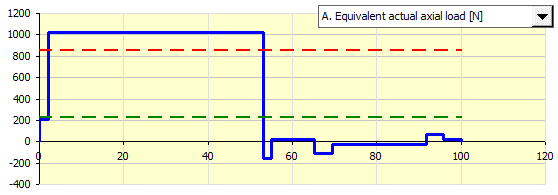
Po stisknutí tlačítka jsou hodnoty z tohoto odstavce přesunuty do odstavce [3.0].
Přesunuté hodnoty: nm1,nm2,nmax,Fma1,Fma2,Fmax
V případě předepnuté matice je přenesena i hodnota předpětí Fpr [11.4]
Zadejte počet zatěžovacích stavů. V případě přenosu z předchozího odstavce [10] je nastaveno automaticky.
Jsou používány dva druhy matic.
A. Bez předepnutí. Předpokládá se, že přesnost a zatížení je důležité pouze v
jednom směru pohybu. Při volbě opačného směru pohybu je nutné počítat s vůlí.
B. S předepnutím. Matice je konstrukčne řešená tak, že není vůle při přechodu z
jednoho do druhého směru pohybu. Konstrukční řešení může mít řadu variant a
podle konstrukčních požadavků se mění i velikost předepnutí (Většinou je
nutné dohodnout s dodavatelem).
Matice s předepnutím a velikost předepnutí pak má vliv na výpočet ekvivalentního zatížení šroubu. Můžeme si to představit tak, že i když není matice zatížena, tak předepnutí vytváří sílu, kterou je nutné uvažovat při výpočtu ekvivalentního zatížení.
Při určení síly pro výpočet ekvivalentního zatížení pak nastávají tři případy.
- Nulová zatěžující síla. Síla předepnutí je rozdělena v jednom i druhém směru.
- Zatěžující síla je menší než Flim. Zatěžovací síla spolu se sílou předepnutí
je proporcionálně rozdělena do obou směrů.
- Zatěžující síla je větší než Flim. Zatěžující síla překoná sílu předepnutí a
je uvažována jen v příslušném směru.

Dle požadované přesnosti polohování a požadované tuhosti se volí způsob lícování matice na hřídel. S rostoucím předepnutím klesá trvanlivost. Matice s vůlí - Jednosměrné zatížení Fpr=0.
Velikost předepnutí bývá uvedena v katalogu, popřípadě je možné domluvit s
dodavatelem. Obecně se používají následující hodnoty předepnutí vyjádřeno v
procentech dynamické únosnosti šroubu Ca:
3 % Ca - Přesné polohování a méně zatížené šrouby
5 % Ca - Přesné polohování a středně zatížené šrouby
8 % Ca - Matice se 4-bodovým stykem
10 % Ca - Přesné polohování a více zatížené šrouby
Limitující zatížení, při kterém dojde k přerušení kontaktu kuličky a dráhy v nezatíženém směru.
Podle ISO3408-5 je Fop=0.6.
Vzhledem k tomu, že předpětí se snižuje během provozní životnosti kuličkových
šroubů, je průměrné provozní předpětí nastaveno na 60% původního předpětí.
- v prvním sloupci "F1,2" zadejte postupně zatížení matice. Kladné hodnoty v jednom
směru, záporné hodnoty v opačném.
- ve druhém "Fa1" a třetím sloupci "Fa2" jsou pak dopočítané reálné hodnoty zatížení
(v jednom či druhém směru) které
berou do úvahy i předpětí matice [11.4].
- ve čtvrtém sloupci zadejte odpovídající otáčky (vždy kladná hodnota, směr jě
řízen zatížením).
- v pátém sloupci zadejte procenta využití pro každé zatížení (součet musí být
roven 100%). V případě nevyhovujícího zadání je poslední platná buňka označena
červeně.
- v šestém (šedivém) sloupci můžete zadat čas jednotlivých zatížení a po stisknutí
tlačítka "q[%]<<tj[s]" je čas rozpočítán na procenta v pátém sloupci.
Index1 a index2 značí ekvivalentní zatížení (otáčky) v jednom nebo druhém směru.
V tomto odstavci můžete spočítat statickou a dynamickou únosnost na základě rozměrů a parametrů šroubu a matice podle normy ISO a ANSI. Zároveň můžete vyplnit tabulku šroubů (rozměry dle ISO,ANSI) vypočtenými hodnotami.
Po stisknutí tlačítka jsou hodnoty z tohoto odstavce přesunuty do odstavce "Definice mechanismu, zatížení a parametrů šroubu" [3.0].
Přenášené hodnoty: i, zu, d1, Dw, Ph, Dpw, , frn, frs
SI jednotky: C0am, Cam
Imperial jednotky: Ti, Pix
V této části jsou společné vstupní parametry pro výpočet C0a,Ca,C0am,Cam,Ti,Pi,Pix. Zaškrtnutím tlačítka na [12.3] jsou automaticky přeneseny z hlavního odstavce [3.0]. Po odškrtnutí tlačítka můžete zadat vlastní.
Přenášené hodnoty: i, zu, d1, Dw, Ph, Dpw, , frn, frs

Počet závitů je daný konstrukcí matice a většinou je výrobcem uváděn. Používá se počet závitů v rozsahu zhruba od 1.5 do 6ti. Počet závitů má vliv na výpočet statické a dynamické únosnosti, tuhosti a délky matice.
Zadejte počet nezatížených kuliček. Jedná se o vratné systémy, kdy jsou kuličky vracené po jedné otáčce a většinou zu=3. U vratných systémů, kde jsou kuličky vracené od konečného závitu do prvního je zu=0. Informaci o konkrétní konstrukci naleznete většinou v katalogu výrobce.
Průměr je většinou konstrukční záležitostí výrobce. Je samozřejmé, že jej není možné volit libovolně. Základní podmínka je že průměr Dw nemůže být větší než stoupání Ph.
0.600, 0.800, 1.000, 1.200, 1.250, 1.500, 1.588, 1.750, 2.000, 2.381, 2.500, 3.000, 3.175, 3.500, 3.969, 4.762, 5.000, 5.556, 6.000, 6.350, 7.144, 7.938, 8.000, 9.525, 10.000, 10.319, 12.700, 20.000, 20.638, 25.400, 30.000, 31.750, 38.100, 40.000, 44.450, 50.000
Standardni řada stoupání mm (ISO,
JIS, DIN, BS...)
1; 2; 2.5 ; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40 [mm]
Standardni řada stoupání inch (ANSI)
0.08; 0.1; 0.125; 0.16; 0.2; 0.25; 0.333; 0.375; 0.4; 0.5; 0.75; 1.0 [in]
Norma ISO3408-5 používá hodnotu 0.86. Hodnota 0.7 je používána některými výrobci a vychází z (ISO281,2007), ( ISO/TR1281-1,2008), (Lundberg, et al.,1947)
Modifikovaná únosnost zahrnuje další parametry, jako je přesnost, tvrdost a zpracování materiálu a je vyplňována do tabulek, popřípadě přenesena do odstavce[3.0].
Odchylka tvrdosti je opravena součinitelem fh0,fh
Základní hodnota je 654HV10 (fh0, fh=1.0). Snížení tvrdosti ovlivňuje fh0 a fh. Zvýšení tvrdosti nemá na výpočet vliv.
Statická únosnost C0 a dynamická únosnost C musí být vynásobena korekčním součinitelem podle odpovídající toleranční třídy šroubu.
Hodnota součinitele fac
IT0, IT1, IT3, IT5 …… 1.0
IT7 ……………………...... 0.9
IT10 ………....…………… 0.7
Vliv způsobu výroby materiálu.
Ocel kuliček / hodnota součinitele fm
Oceli chladnutí na vzduchu…........……1.00
Oceli odplyněné....…........................1.25
Oceli elektricky přetavené…...............1.44
Oceli přetavené ve vakuu….…........….1.71
Výpočet základní únosnosti dle ANSI.
Jako základní hodnota je uvažována dráha 1000000 palců.
Jako základní hodnota je uvažována dráha 25400 metrů.
Výpočet obsahuje dvě základní rozměrové tabulky šroubů. Milimetrová(ISO) a palcová(ANSI). Tabulky obsahují všechny kombinace průměru šroubu a stoupání. Výrobci dodržují tyto základní rozměry (popřípadě nabízejí více průměrů). Volba průměrů kuliček je však libovolná. Na základě rozboru mnoha katalogů výrobců jsme připravili i tabulku používaných průměrů kuliček a jejich přiřazení k průměrům šroubů. Vznikla tak řada označená jako lehká, střední a těžká. Tyto kombinace rozměrů se pak vyskytují i v katalozích výrobců.
Po stisknutí tlačítka, jsou postupně do tabulky, vyplněny pro odpovídající rozměry d1xPhxDw i příslušné hodnoty C0am,Cam (Ti,Pix pro ANSI) . Tento výpočet a vyplnění tabulky trvá nějakou dobu. Ukazatel vyplnění vidíte v pracovním okně. Nedoporučujeme přerušovat proces generování tabulky.
Výpočet nastavuje základní hodnotu počtu pracovních závitů na i=1.0. Nemění parametry zu,alfa,frn,frs,exp,AH,fac,fm,LIix. Můžete tak získat modifikované tabulky pro tyto parametry. Nicméně přegenerování tabulek je vhodné pro zkušené konstruktéry s detailní znalostí příslušné problematiky.
Základní nastavení parametrů vygenerovaných tabulek je: zu=0, alfa=45, frn=frs=0.55, exp=0.86, AH=654, fm=1, LIix=1000000.
Návrh pohonu pracovního stolu kuličkovým šroubem.
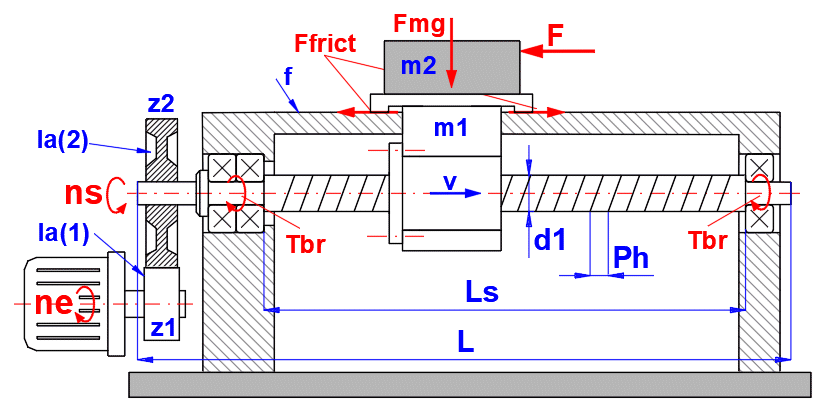
Hmotnost stolu: m1 = 60kg
Hmotnost obráběné součásti: m2 = 40 kg
Síla pro obrábění: F = 1000 N
Pracovní dráha: Lu = 1000 mm
Rychlost posuvu: v = 400 mm/s
Rychloposuv: vmax = 800 mm/s
Životnost: 20000h
Koeficient tření povrchu vedení: f = 0.05
Otáčky motoru: nemax = 1500 rpm
Přesnost polohování: ± 0.1 mm pro max. délku
Opakovaná přesnost: ± 0.02
mm
Uložení kuličkového šroubu (konce): Vetknutí - Podpora
Nejprve je vhodné řešit vzájemný vztah rychlosti stolu(v), otáček(ns,ne) a stoupání šroubu(Ph) v odstavci [1.0].

Pro první přiblížení je možné zvolit hodnoty z obrázku.

Dále odhadneme ekvivalentní zatížení Fm=1000N, součinitel zatížení fw=1.2 a zadáme životnost Lh-req=20000h. Životnost pak splňují šrouby s min. jmenovitým průměrem 20-50mm (podle počtu činných závitů).
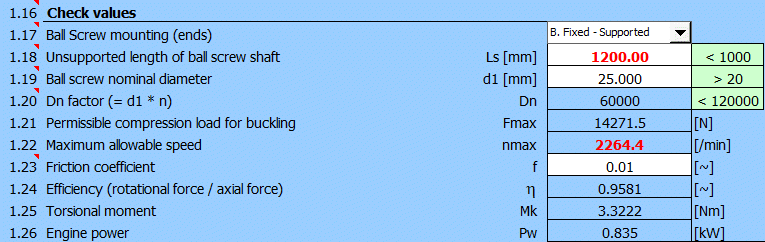
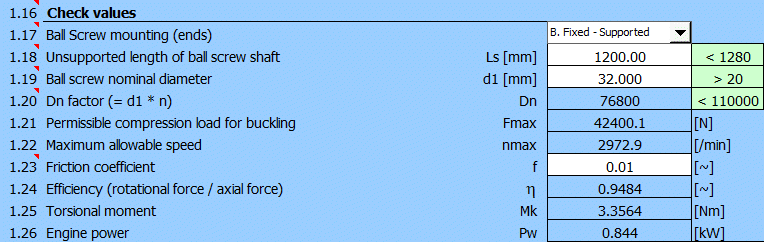
Odhadneme montážní rozpětí Ls=1200mm (1000mm délka pohybu, 150mm délka matice, 50mm montážní přesahy). Pro nominální průměr šroubu d1=25mm je překročena doporučená max. hodnota Ls<(40xd1) a hlavně jsou překročené kritické otáčky(nmax). Proto použijeme šroub o průměru d1=32mm, který splňuje základní kontroly.

Požadovanou přesnost pro Lu>1000mm je možné dosáhnout volbou stupně přesnosti IT3.
Otevřete odstavec [3.0] a přeneste hodnoty z odstavce [1.0] stisknutím tlačítka "[1.0] >> [3.0]".
Dále je nutné přesněji definovat další parametry pohonu. A to řádky [3.3-3.7]. Pevné uložení na jedné straně, druhá strana podpora a je použita matice s předepnutím.
.
Ve valné většině případů neznáme podrobně zatížení šroubu. Pro to je vhodné využít výpočtu z odstavců [10.0] a [11.0].
V této části definujeme podrobně zatížení. Po zaškrtnutí tlačítka na [10.2] jsou přeneseny hodnoty z odstavce [3.0]. Postupně pak doplňte zbývající hodnoty.
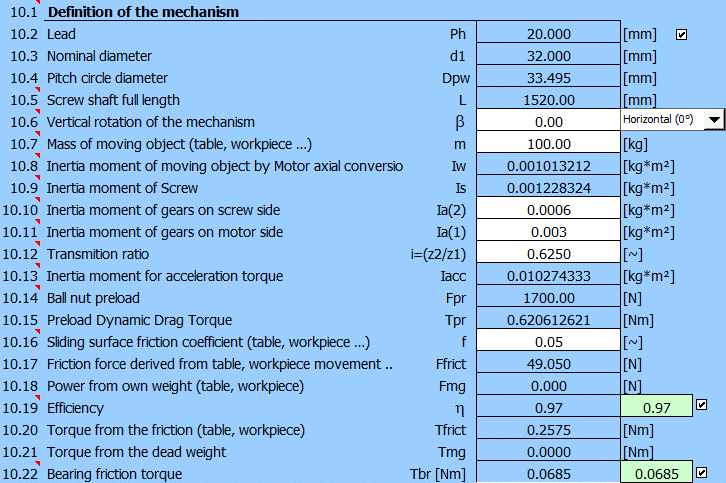
Natočení mechanismu b=0
Hmotnost m=40+60=100kg
Moment setrvačnosti Ia(2),Ia(1) je možné odhadnout v odstavci [9.0].
![]()
![]()
Převodový poměr i=0.625 (viz.odstavec [1.0])
Součinitel tření f=0.05
Definiční tabulka pak vypadá následovně:

Řádek 1: neend=750; dt=0.1; F=0 .............. Rozběh z 0 na pracovní
otáčky 750 /sec. (akcelerace)
Řádek 2: neend=750; dt=2.5; F=1000 ......... Pracovní cyklus obrábění při
otáčkách 750 /sec, obráběcí síla je 1000N
Řádek 3: neend=0; dt=0.1; F=0 .............. Zabrždění z pracovních otáček
na 0. (decelerace)
Řádek 4: neend=0; dt=0.5; F=0 .............. Časová prodleva (např. pro
přenastavení nástroje)
Řádek 5: neend=-1500; dt=0.2; F=0 .............. Rozběh pro zpětný chod na otáčky
-1500 /sec (akcelerace)
Řádek 6: neend=-1500; dt=1.1; F=0 .............. Zpětný chod při otáčkách -1500
/sec
Řádek 7: neend=0; dt=0.2; F=0 .............. Zabrždění na nulové otáčky
(decelerace)
Řádek 8: neend=0; dt=0.2; F=0 .............. Časová prodleva
Otáčky splňují zadání, časy jsou navržené tak, aby byla splňena podmínka
max. délky pohybu Lu=1000mm (řádek 2,sloupec ds) pro rychlost stolu 400mm/s resp.
800mm/s pro zpětný
chod.
Časový cyklus je 4.9s. V grafu jsou zobrazeny otáčky šroubu a síly působící na
matici a šroub.
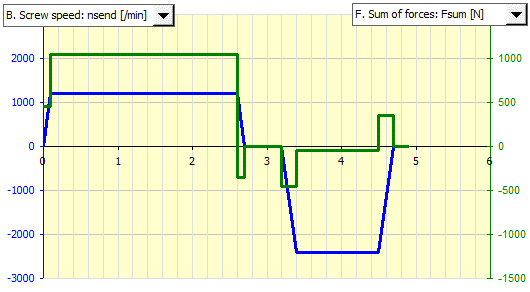
Jelikož není zatížení šroubu konstantní, je nutné převést proměnlivé zatížení na zatížení ekvivalentní, které je použito pro výpočet požadované dynamické únosnosti Ca.
Na řádku [10.23] stiskněte tlačítko "[10.0]>>[11.0]". Tím přenesete síly a otáčky do tabulky zatížení v odstavci [11.0].
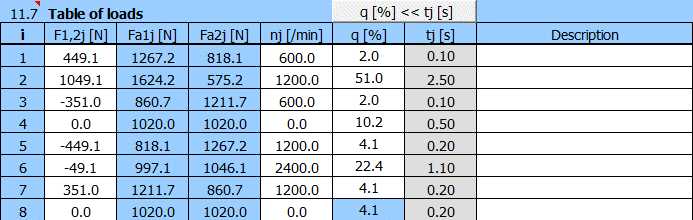 =>
=>
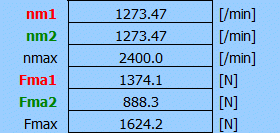
Zbývá zadat hodnotu předepnutí matice. Z předběžného návrhu známe hodnotu požadované dynamické únosnosti Ca-req=17000N [1.13]. Předepnutí matice bývá většinou 10%Ca. Zadáme na řádku [11.4] hodnotu Fpr=1700N a na řádku [11.6] podle ISO3408-5 zadáme součinitel Fop=0.6.
Vypočtené hodnoty ekvivalentního zatížení a otáček přenesete zpět do odstavce [3.0] stisknutím tlačítka "[11.0]>>[3.0]"

V tomto okamžiku máme velmi přesně definované zatížení šroubu a požadovanou únosnost.
Pro výběr šroubu máme dvě možnosti.
Tabulka šroubů a jejich únosností byla vygenerována podle ISO3408-5 resp. ANSI_B5.48 pro palcové jednotky. Pokud neznáte přímo konkrétního výrobce, je možné vybrat z této tabulky.
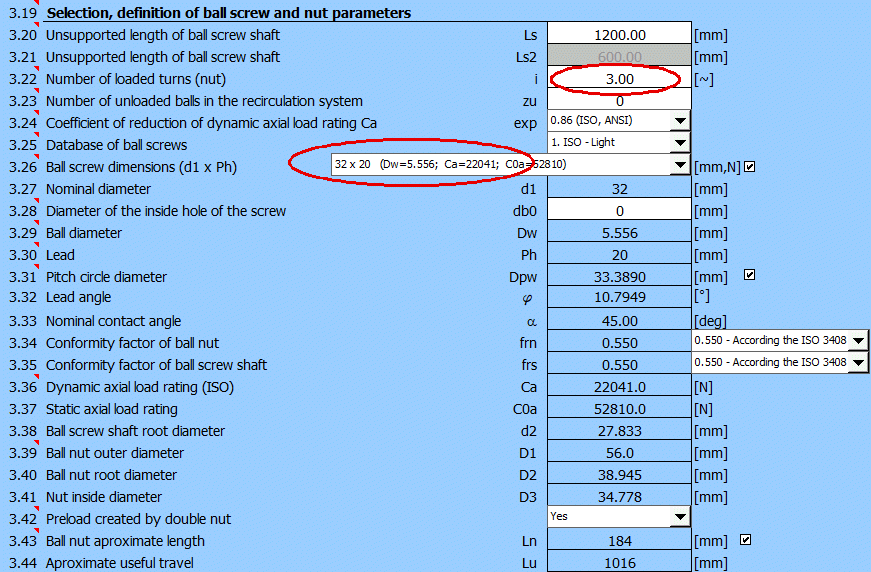
Ve výběrovém seznamu by měl být vybrán, na základě předběžného návrhu, šroub rozměru 32x20(d1xPh). V závorce je pak uveden průměr kuličky Dw a dynamická únosnost Ca. Základní únosnost Ca pro jeden pracovní závit je 8500N. Je tedy nutné nastavit počet závitů matice i=3. Hodnota dynamické únosnosti je 22041N, tedy větší hodnota než požadovaná hodnota Ca-req=20227N.
Pokud vybíráte hodnoty přímo podle katalogu výrobce je asi nejlepší následující postup.
- Vyberte příslušný rozměr šroubu z tabulky (tím přednastavíte správné
rozměry)
- Odškrtněte tlačítko napravo od výběrového seznamu šroubu.
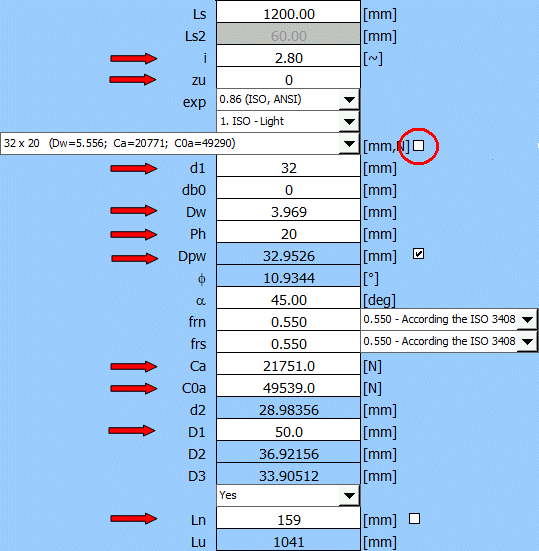
- Označené řádky vyplňte hodnotami z katalogu výrobce (řada rozměrů však již bude správně předvyplněna).
Příklad nabízených matic v požadovaném rozměru a únosnosti od několika výrobců.
| ID | d1 x Ph | Dw | i | Ln | Ca | C0a | K | D1 | Manufact. |
| 1 | 32 x 20 | 3.969 | 2.8 | 159 | 21751 | 49536 | 842 | 50 | KSK |
| 2 | 32 x 20 | 5.556 | 2 | 177 | 31400 | 81100 | 790 | 55 | PMI |
| 3 | 32 x 20 | 3.969 | 3 | 178 | 19000 | 54300 | 680 | 50 | HIVIN |
| 4 | 32 x 20 | 4.763 | 4 | 216 | 31900 | 89140 | 940 | 54 | HIVIN |
| 5 | 32 x 20 | 5.000 | 4 | 70 | 29700 | 59800 | - | 53 | Thomson |
V odstavci [3.0] je na konci i zkrácený výpis výsledků. Slouží pro rychlou orientaci v případě že ladíte vybrané vstupní parametry. Kompletní výsledky pak naleznete v "Kapitole výsledků".

Informace o možnostech 2D a 3D grafického výstupu a informace o spolupráci se 2D a 3D CAD systémy naleznete v dokumentu "Grafický výstup, CAD systémy".
Po odškrtnutí tlačítka vpravo můžete zadat počet závitů, který má být vykreslen na výkresu šroubu
/ matice.
Předvyplněné hodnoty vycházejí z výpočtu.
Udává o jaký počet závitů bude posunut levý okraj matice vzhledem k levému počátku šroubu.
Informace o nastavení parametrů výpočtu a nastavení jazyka naleznete v dokumentu "Nastavení výpočtů, změna jazyka".
Všeobecné informace o tom, jak je možné měnit a rozšiřovat sešity výpočtu, jsou uvedeny v dokumentu "Úpravy sešitu (výpočtu)".
ISO 3408-1:2006
Ball screws - Part 1: Vocabulary and designation
Vis a billes - Partie 1: Vocabulaire et designation
ISO 3408-2: 1991
Ball screws - Part 2: Nominal diameters and nominal
leads. Metric series
Vis a billes - Partie 2: Diametres et pas hélicoIdaux, nominaux. Serie métrique
Kugeiroligewinde - Teil 2: Nenndurchmesser und Nennsteigungen. Metrische Reihe
ISO 3408-3:2006
Ball screws - Part 3: Acceptance conditions and acceptance tests
Vis a blues - Partie 3: Conditions et essals do reception
ISO 3408-4:2006
Ball screws - Part 4: Static axial rigidity
Vis a blues - Partie 4: Rigidite axiale statique
ISO 3408-5:2006
Ball screws -Part 5: Static and dynamic axial load ratings and operational life
Vis a billes - Partie 5: Charges axiales statiques et dynamiques de base et
durée de vie
ISO 286-2:2010
Část 2: Tabulky normalizovaných tolerančních tříd a mezních úchylek pro díry a
hřídele
Part 2: Tables of standard tolerance classes and limit deviations for holes and
shafts
Partie 2 : Tableaux des classes de tolerance normalisées et des écarts limites
des alesages et des arbres
Teil 2: Tabellen der Grundtoleranzgrade und GrenzabmaBe für Bohrungen und Wellen
DIN ISO 3408: the ISO standard has been adopted directly as the DIN standard
JIS B1192-1997 is similar to DIN ISO 3408
JIS B1192-2018 putting the JIS standard in harmonization with the ISO 3408
DIN 69051-5
Machine tools - Ball screws - Part 5: Mounting dimensions for ball nuts
Machines-outils - Vis a billes - Partie 5: Dimensions de raccordement pour
écrous
ANSI B5.48 - 2013
Ball Screws
Company cataloques: THK, PMI, KSK, NSK, SKF, HIWIN, KURODA, NOOK, THOMSON, Steinmayer, MANESMAN
^