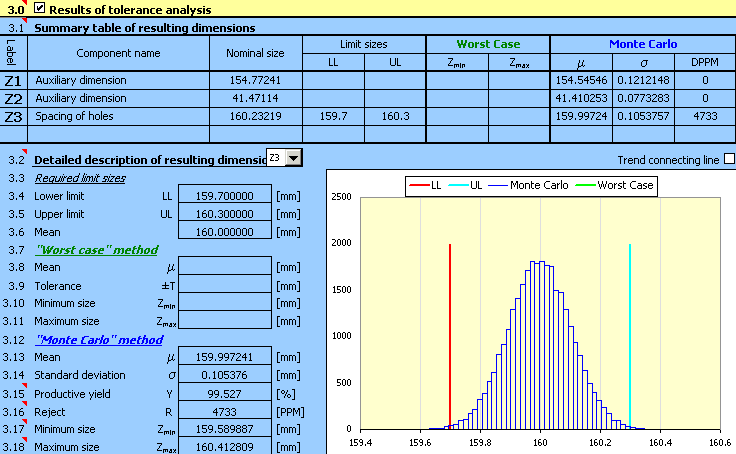
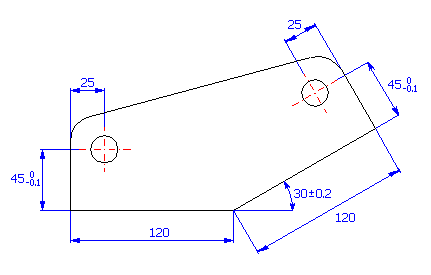
Tolerance analysis of a 2D dimensional chain using the "Monte Carlo" method.Tolerance analysis of a 2D dimensional chain using the "Monte Carlo" method.For the component (see the picture) design, the production tolerances of the dimensions are such that the required distance 160±0.3 mm between the centres of orifices is maintained for at least 99.5% of the manufactured components.
If we start from the graphical illustration of the dimensional chain
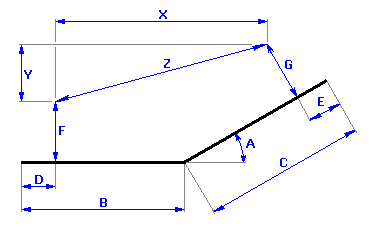
we can describe the resulting dimension for the given component using this relation:
where the following relations will hold for the auxiliary variables X, Y:
If the task was solved using the traditional "Worst Case" method, it would be necessary to use tolerances at approximately accuracy level 4 for dimensions B, C, D and E so that the required tolerance of the resulting dimension was kept. It is obvious that production with this accuracy would be disproportionately expensive. Therefore, it will be more convenient to use the statistic method of calculation in this case. These methods enable the manufacture of the component with significantly higher tolerances upon the occurrence of a small (pre-determined) percentage of rejects.
The solution of the task of the dimensional chain design can be divided into the following steps:
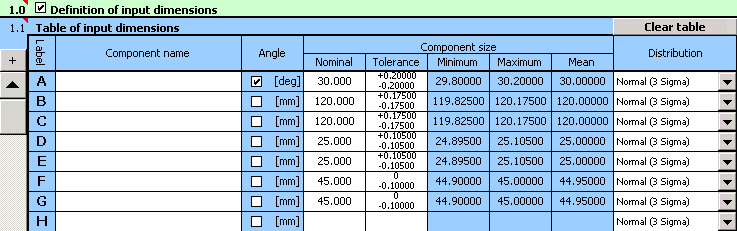
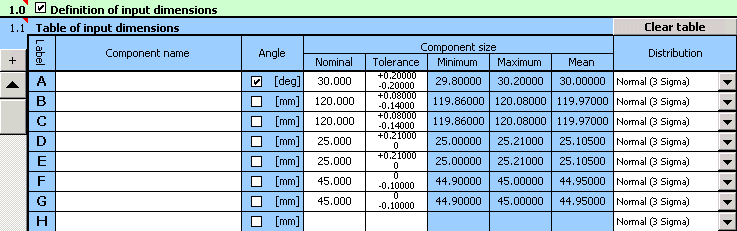
1) In Table [1.1], define all input dimensions (partial components) of the dimensional chain.
2) Further set the production tolerances for all dimensions. For dimensions with strictly set tolerances, set the rated dimensional deviations in the input table.
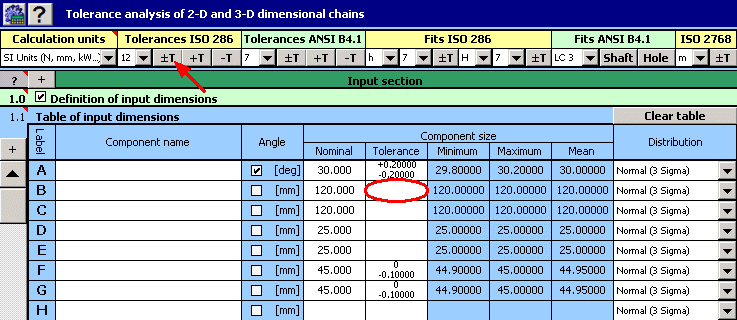
For the remaining dimensions, select a tentatively symmetrical tolerance at accuracy level 12.
3) In the list boxes, in the last column of the table, select a normal division with a production process capability level of 3s for all dimensions.
4) In Table [2.1], define the parameters of the resulting dimension (closed component) of the dimensional chain. To facilitate work and increase clear arrangement, we will divide the calculation relation into three parts (see above). We will use the first two lines of the table to define the auxiliary dimensions; the parameters of the searched resulting dimensions will be placed on Line "Z3". The above-mentioned calculation relations have to be modified in the form (syntax) required by Excel. Therefore, set the following text into the appropriate lines of the second column of the table:
Line 1 "Z1" ..... "=_B-_D+(_C-_E)*COS(RADIANS(_A))-_G*SIN(RADIANS(_A))"
Line 2 "Z2" ..... "=(_C-_E)*SIN(RADIANS(_A))+_G*COS(RADIANS(_A))-_F"
Line 3 "Z3" ..... "=(_Z1^2+_Z2^2)^0.5"
5) On line [2.5] check the switch next to the "Monte Carlo" calculation method. In List Box [2.6] further set the required number of simulations. To speed up the designing process, set smaller numbers of simulations in the initial steps of designing.
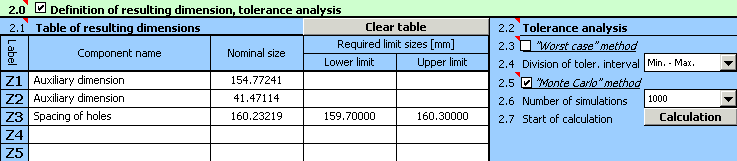
6) Press the button on Line [2.7] to run the calculation (tolerance analysis) of the dimensional chain. The parameters of the resulting dimension can be found in Paragraph [3].
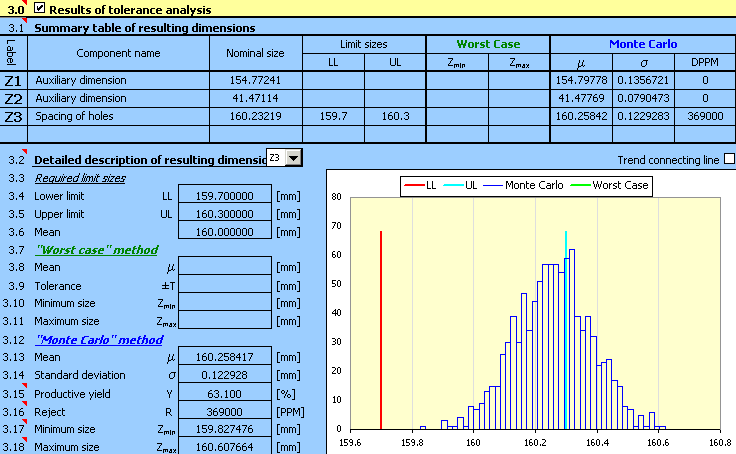
7) Expected production yield [3.15], better stated number of rejects [3.16] will be the decisive factor for the assessment of the design quality. The task assignment prescribes the maximum permissible number of 5,000 rejects per million pieces produced. The achieved results are higher by order of magnitude; therefore the designed tolerances are not suitable.
For an unsuitable design, the next logical step could be decreasing the sizes of the manufacturing tolerances used. On a closer view of the design, however, we discover that the main problem is not the selected size of tolerances, but rather the improper centring of the design. In the case of an optimally designed dimensional chain the mean dimension [3.13] should be close to the required dimension [3.6].
8) Therefore, in the next step we will adjust the position of the tolerance fields of dimensions B, C, D and E, while maintaining the originally designed values of the tolerances. By repeated adjustments of the deviations of the individual dimensions with a subsequent recalculation of the results, we will gradually achieve the solution
for which the design will be centred
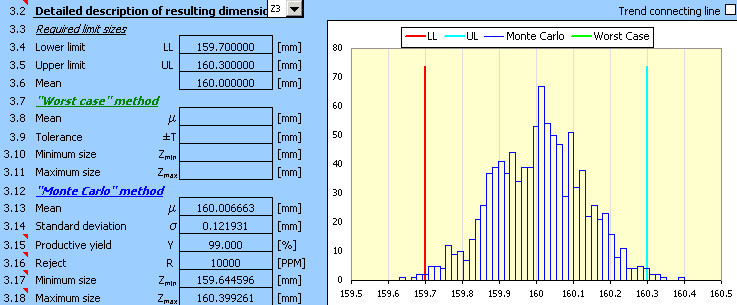
9) Although the design is already well centred, the required production yield has not yet been achieved. In the next step it will be necessary to decrease the tolerances designed tentatively in Step 2). After selecting the tolerances of dimensions B and C in accuracy level 11 and the centring of design, we will achieve the suitable solution
which meets the functional requirements set by the task assignment.
