Produktion und Zusammenstellung von Rollenlagern mit Hilfe der Methode der selektiven Montage.

Aufgabenstellung.

Für ein Rollenlager bestehend aus drei Einzelteilen mit den Abmessungen:

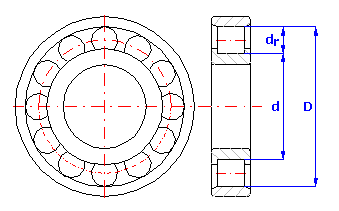
1. Äußerer Ring - Durchmesser D=160 mm
2. Innerer Ring - Durchmesser d=120 mm
3. Rollen - Durchmesser dr=20 mm sollen 

Sie die Produktionstoleranzen aller Einzelteile und die Parameter für die selektive Montage so vorschlagen, dass sich bei der Montage des Lagers ein Radialspiel von 60 mm bis 90 mm ergibt. Bei dem Lager wird weiter die Sicherstellung der Austauschbarkeit des Innenringes in der Art gefordert, dass im Fall eines Austausches des Ringes bei einer Reparatur des Lagers ein Radialspiel von 40 mm bis 105 mm garantiert ist.

Bemerkung: In der Praxis wird die Methode der selektiven Montage im allgemeinen nur bei der Fertigung von Produkten verwendet, bei denen keine Betriebsaustauschbarkeit der Einzelteile innerhalb des Produktes gefordert wird. Die Forderung nach der Sicherstellung der Austauschbarkeit eines von den Einzelteilen verringert deutlich die Vorteile der selektiven Montage. Die hier aufgeführte Aufgabe hat also einen rein theoretischen Charakter und soll nur die breiteren Verwendungsmöglichkeiten des Programms demonstrieren.

Lösung der Aufgabe.

Produktion von Rollenwälzlagern ist ein typisches Beispiel für die Verwendung der Methode der selektiven Montage. Bei der Lösung des aufgeführten Beispieles mit der klassischen "Worst Case" Methode wird zwar bei dem Lager eine vollständige Montage- wie auch Betriebsaustauschbarkeit aller Einzelteile gewährleistet, für die Einhaltung des geforderten radialen Spiels wäre es aber notwendig die Einzelteile des Lagers in der Genauigkeitsklasse 3 herzustellen. Es wird deutlich, dass die Produktion mit dieser Genauigkeitsklasse unangemessen teuer wäre. Bei der Verwendung der Methode der selektiven Montage kann man die Einzelteile mit einer bedeutend niedrigeren Genauigkeit herstellen. Die eigentliche Lösung der Aufgabe besteht aus zwei Teilen:

Vorschlag der Maßkette.

Die Größe des Radialspieles ist bei Rollenlagern durch die Beziehung c = D - d - 2*dr gegeben.

Die Lösung des Entwurfes und der Optimierung der Maßkette können wir dann in folgende Schritte einteilen:

1) Anhand der oben aufgeführten Beziehung definieren wir in der Tabelle [7.1] die Maßkette. Die Teilabmaße der Maßkette werden durch die bei der Montage des Lagers verwendeten Einzelteile gebildet. Das Schließmaß der Maßkette ist dann das geforderte Radialspiel.

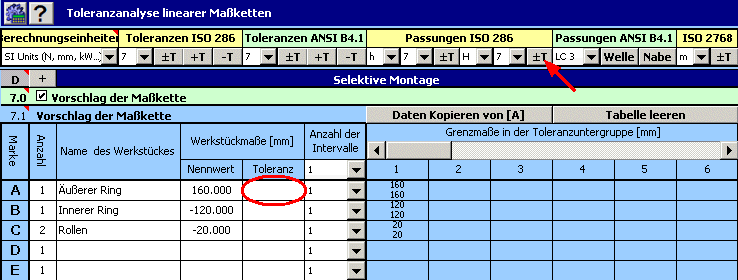
2) Für die einzelnen Abmaße geben wir dann die geforderten Produktionstoleranzen ein. Im Erstvorschlag verwenden wir bei allen Einzelteilen Toleranzen aus der 7. Genauigkeitsklasse. Für den Durchmesser der Rollen wählen wir dabei eine symmetrische Toleranz, für den Durchmesser des äußeren Ringes die Toleranz H7 und für den inneren Ring h7.

3) Für alle Einzelteile stellen wir vorläufig die Anzahl von Toleranzuntergruppen, in die gefertigten Teile einsortiert werden, auf 10 ein.

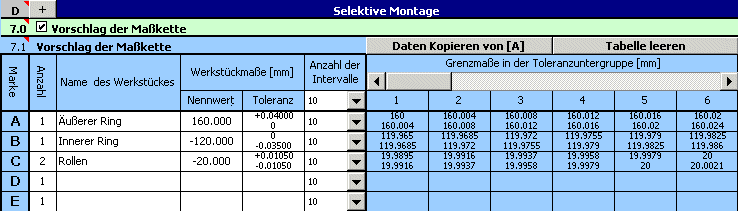
4) Im Abschnitt [8.1] berücksichtigen wir die Forderung nach der Betriebsaustauschbarkeit des Innenringes des Lagers.

5) Im Abschnitt [8.4] geben wir die Grenzwerte des geforderten Radialspiels bei der Montage des Lagers und beim Austausch des Innenringes ein.

6) In der Auswahlliste [8.9] wählen wir dann die Suche nach allen Montagekombinationen aus. Die eigentliche Suche der Kombinationen starten wir dann mit dem Button in der Zeile [8.10].

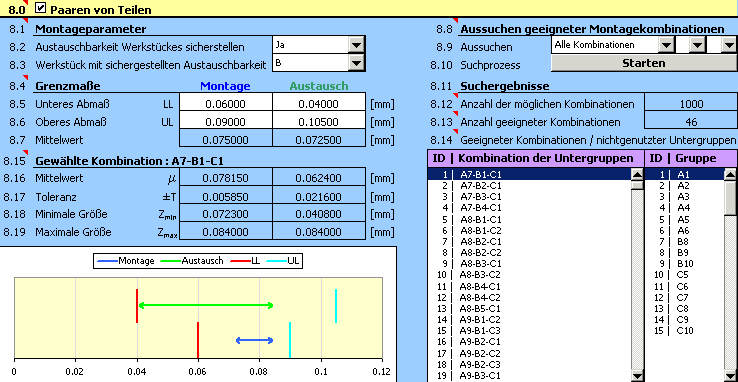
7) Die Qualität des Vorschlages beurteilen wir anhand der Ergebnisse im Abschnitt [8.11]. Es wird deutlich, dass der Vorschlag in diesem Fall ungeeignet ist. Aus der Tabelle der "nichtgenutzten Untergruppen" in der Zeile [8.14] geht hervor, dass für die Montage des Lagers mehr als die Hälfte der hergestellten Außenringe und der Rollen nicht verwendet werden könnte.

8) Für den ungeeigneten Vorschlag könnte der nächste logische Schritt in der Verkleinerung der Größe der verwendeten Produktionstoleranzen liegen. Bei näherem Beurteilen dieses Vorschlages stellen wir aber fest, dass das Hauptproblem hier nicht die gewählte Toleranzgröße ist, aber vielmehr die falsche Zentrierung des Vorschlages. Für die richtige Beurteilung dieses Aspektes des Vorschlages ist als maßgebender Hinweis der Erwartungswert des Schließmaßes, im Abschnitt [7.2] berechnet, zu sehen.

Für einen optimalen Lösungsvorschlag der Maßkette sollte sich der hier angegebener Wert so weit wie möglich der geforderten Dimension [8.7] annähern.

9) Im wiederholten Vorschlag korrigieren wir also bei Beibehaltung der Toleranzgrößen die Position der Toleranzfelder aller Einzelteile. Für den Durchmesser des Außenringes verwenden wir die Toleranz G7, für den Durchmesser des Innenringes die Toleranz g7.

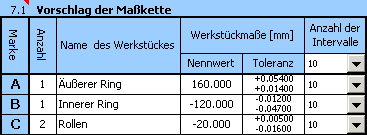
Die obere und untere Abweichung der Rollen korrigieren wir dann so, dass der resultierender Vorschlag möglichst gut zentriert ist.

10) Für einem so korrigierten Vorschlag der Maßkette suchen wir dann erneut alle geeigneten Montagekombinationen.

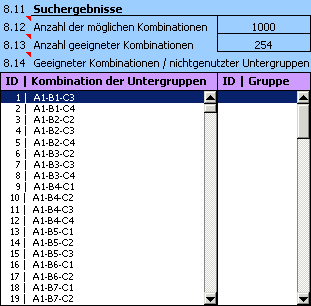
11) Aus den Suchergebnissen ist deutlich, dass nun bei der Montage des Lagers alle gefertigten Einzelteile verwendbar sind. Der Vorschlag ist aber nicht sehr effektiv, weil die Anzahl der geeigneten Montagekombinationen unnötig hoch ist. Eine Verringerung der Anzahl der annehmbaren Kombinationen können wir z.B. durch die Verringerung von Toleranzuntergruppen erreichen, in die gefertigte Teile einsortiert werden.

12) Durch schrittweise erfolgte Verringerung der Anzahl von Untergruppen kommen wir zum endgültigem Vorschlag der Maßkette,

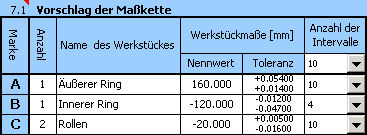
der für das gewählte Beispiel optimal erscheint.

Die resultierende Anzahl von 75 geeigneten Montagekombinationen ist für die Zwecke der selektiven Montage annehmbar.

Optimierung der Anzahl der zusammengesetzten Produkte.

Im vorhergehendem Teil der Aufgabe haben wir die Produktionstoleranzen der Einzelteile vorgeschlagen und haben alle annehmbaren Montagekombinationen gesucht, mit deren Hilfe ein Lager mit geeigneten Parametern zusammengesetzt werden kann. Bei der eigentlichen Montage des Lagers ist es aber nicht zweckmäßig die Lager nur mittels einer zufälligen Auswahl der Einzelteile im Rahmen zulässiger Montagekombinationen zusammenzusetzen. Wenn die Methode der selektiven Montage effektiv sein soll, muss die Aufgabe der optimalen Auswahl (Kombination) der Einzelteile gelöst werden. Die Einzelteile müssen so zusammengelegt werden, dass mit einer gegebenen Anzahl angefertigter Einzelteile eine maximal mögliche Anzahl von Produkten zusammengestellt werde kann, die die Funktionsanforderungen erfüllen.

Diese Aufgabe muss im Produktionsverlauf wiederholt gelöst werden, und zwar immer beim Auffüllen von Lagerbeständen vor dem Beginn der eigentlichen Montage. Das Wesentliche dieser Aufgabe ist die Festlegung des optimalen Montageablaufes zur Erreichung der maximalmöglichen Anzahl von zusammengesetzten Produkten. Bei der Lösung dieser Aufgabe müssen wir also aus der vorher gefundenen Menge der annehmbaren Kombinationen den optimalen Satz der bei der Montage verwendeten Kombinationen auswählen und gleichzeitig die Anzahl der Produkte festlegen, die im Rahmen jeder verwendeten Kombination zusammengesetzt worden sind.

Die Lösung der Aufgabe der Optimierung der Anzahl von zusammengesetzten Produkten wird in folgenden Schritten durchgeführt.

1) In der Tabelle [9.1] geben wir die Anzahl der gefertigten Einzelteile in einzelnen Toleranzsubintervallen ein.

Bemerkung: Die Grenzabmaße aller Toleranzsubintervalle sind in der Tabelle [7.1] aufgeführt.

2) In der Auswahlliste [9.3] wählen wir die geeignete Optimierungsmethode aus. Für das aufgeführte Beispiel wählen wir die "Basismethode" aus, die die besten Ergebnisse liefert. Diese Methode ist zwar wesentlich langsamer als die anderen Methoden, für kleine Anzahlen von Einzelteilen aus denen im gegebenem Beispiel das Lager zusammengesetzt ist, können wir sie aber ohne Probleme auch an einem weniger leistungsfähigem Computer verwenden.

Bemerkung: Ein Vergleich der Ergebnisse und der Geschwindigkeit der Berechnung, die beim gegebenen Beispiel bei der Verwendung verschiedener Optimierungsmethoden erreicht wurden, sind am Endes des Beispiels aufgeführt.

3) In der Auswahlliste [9.5] wählen wir das Feld "Massenverarbeitung" aus. Bei der Auswahl dieses Feldes führt das Programm nacheinander eine Optimierung für alle 10 Basislösungen. Die günstigste Lösung wird dann aus der Sicht der maximalen Anzahl der zusammengesetzten Produkte und der minimalen Anzahl der Montagekombinationen ausgewählt.

4) Mit dem Button in der Zeile [9.5] starten wir die Optimierung.

5) Die elementaren Qualitätsparameter des vorgeschlagenen Vorgehens bei der Montage sind im Abschnitt [9.6] aufgeführt,

die Details des optimierten Montageverlaufes sind in der Tabelle [9.12] aufgegliedert.

In der linken Spalte der Tabelle sind alle Montagekombinationen aufgeführt, die für das Zusammensetzten des Produktes verwendet wurden. In der rechten Spalte ist dann die Anzahl der im Rahmen jeder Kombination zusammengesetzten Produkte angegeben.

Vergleich der Ergebnisse der Optimierung und der Geschwindigkeit der Berechnung, die beim gegebenen Beispiel bei der Verwendung verschiedener Optimierungsmethoden erreicht wurden:

Bemerkung: Bei allen Optimierungsmethoden wurde die "Massenverarbeitung" verwendet. Die Berechnung wurde an einem Computer mit x86 Prozessor, 1800MHz, 256MB durchgeführt.