Entwurf und Optimierung einer linearen Maßkette mit Hilfe der "RSS" Methode.

Schlagen Sie bei einem Einzelteil (siehe Skizze) die Produktionstoleranzen der Abmaße so vor, dass bei einem technologisch resultierendem Maß die erlaubte Abweichung von ±0.0013" nicht überschritten wird.

Lösung der Aufgabe.

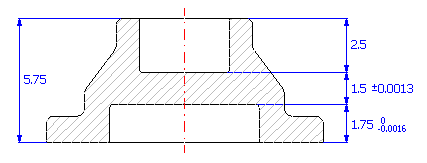
Wenn wir von der graphischen Darstellung der Maßkette ausgehen,

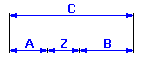
können wir beim gegebenen Einzelteil die Größe des resultierenden Abmaßes mit der Formel Z = C - A - B beschreiben.

Bei der Lösung dieser Aufgabe mit Hilfe der klassischen "Worst Case" Methode wäre es für die Einhaltung der geforderten Toleranz des resultierenden Abmaßes erforderlich bei den Abmaßen B und C die Toleranz ungefähr in der Genauigkeitsklasse 4 zu verwenden. Es wird deutlich, dass die Produktion mit dieser Genauigkeit unangemessen teuer wäre. In diesem fall wird es deshalb viel vorteilhafter sein, die statistische Methode der Berechnung zu verwenden. Diese Methode erlaubt die Fertigung dieses Teiles mit deutlich höheren Toleranzen bei kleinem (vorher festgelegten) Prozentsatz Ausschuss.

Vorschlag der Maßkette.

Die Lösung des Entwurfes und der Optimierung der Maßkette können wir in folgende Schritte einteilen:

1) Anhand der oben aufgeführten Beziehung definieren wir in der Tabelle [1.1] die Maßkette.

2) Für die einzelnen Abmaße geben wir dann die geforderten Produktionstoleranzen ein. Beim Abmaß A tragen wir die entsprechenden - durch die Aufgabenstellung gegebenen - Abweichungen ein.

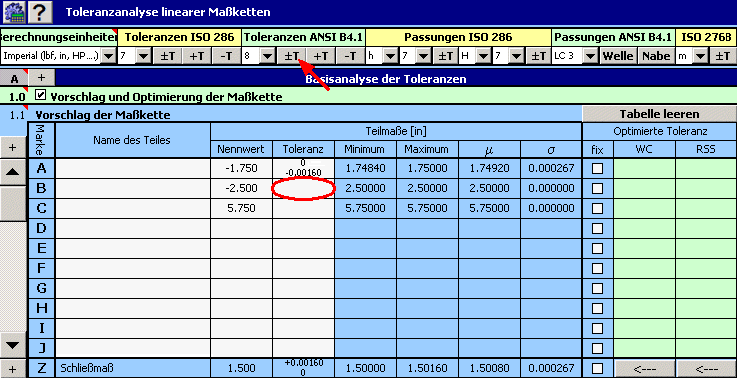
Bei den übrigen Abmaßen wählen wir vorläufig symmetrische Toleranzen im 8. Genauigkeitsgrad.

Bemerkung: Dieser Schritt ist zwar nicht unbedingt erforderlich, er stellt aber sicher, dass die optimierten Toleranzen im richtigen Verhältnis vorgeschlagen werden. Beim Vorschlag einzelner Toleranzen wird nämlich das Verhältnis deren Größen beibehalten, das durch die in der Eingabetabelle gegebenen Werte festgelegt ist.

3) In der 8. Spalte der Tabelle markieren wir das Kästchen beim Abmaß A, dessen Toleranz gegeben ist.

4) Im Abschnitt [1.3] geben wir die geforderten Grenzwerte des resultierenden Abmaßes ein.

5) In der Auswahlliste [1.7] wählen wir die Methode "Zentrierung und Optimierung", in der Liste [1.8] stellen wir die geforderte Genauigkeit (Anzahl der Dezimalstellen) für die vorgeschlagenen Toleranzen ein.

6) Mit Rücksicht auf verschiedene Möglichkeiten der Bearbeitung, die bei der Herstellung des Teiles verwendet werden können, stellen wir in der Auswahlliste [1.9] als die minimale erlaubte Toleranzgröße die Genauigkeitsstufe 6 ein. 

Tipp: Die Tabelle der mit normalem Aufwand erreichbaren Produktionstoleranzen für verschiedene Arten der Bearbeitung finden Sie in der Mappe "Toleranzen und Passungen".

7) In der Auswahlliste [1.10] stellen wir die geforderte Produktionsausbeute 99,9% ein, d.h. ein Produktionsprozess mit der maximalen Anzahl von 1000 Ausschussteilen pro eine Million gefertigte Teile.

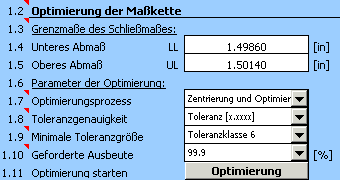
8) Mit dem Button in der Zeile [1.11] starten wir die Optimierung der Maßkette.

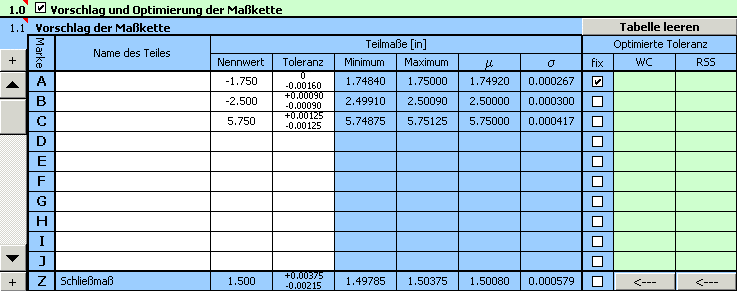
9) Die resultierenden Parameter des Vorschlages sind im Abschnitt [2.10] dargestellt,

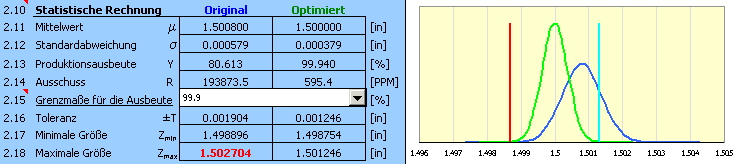
die optimierten Abweichungen der Fertigungsabmessungen sind in der 10. Spalte der Tabelle [1.1] aufgeführt.

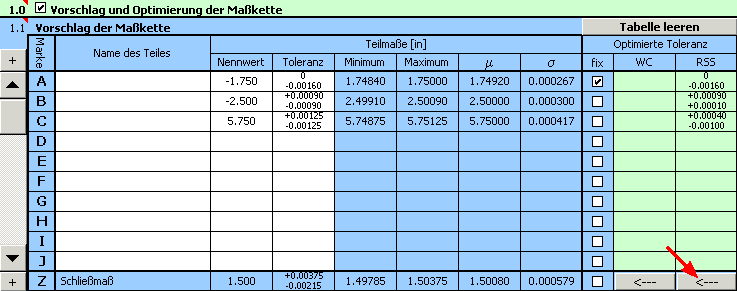
10) Die vorgeschlagenen Toleranzen lassen sich selbstverständlich weiter bearbeiten. Durch Drücken des Buttons in der unteren Zeile der Tabelle übertragen wir die vorgeschlagenen Toleranzen in die Eingabetabelle. Bei der Einhaltung der Größe der Toleranz können wir hier z.B. durch Feineinstellung die vorgeschlagenen Abweichungen in geeignetere Form bringen.

Die Ergebnisse der Berechnung werden für diese Korrektur identisch mit den für optimierte Toleranzen erreichten Ergebnissen sein.

Schlussbemerkung.

Die hier vorgeschlagene Lösung wird selbstverständlich nicht die einzige brauchbare Lösung dieser Aufgabe sein und muss auch nicht die Ideallösung sein. Bei der Auswahl einer geeigneten Lösung ist es notwendig, gründlich die gegenseitige Beziehung zwischen den gewählten Größen der Produktionstoleranzen und der zu erwartenden Produktionsausbeute zu bedenken. Durch eine Vergrößerung der verwendeten Toleranzen erreichen wir eine Senkung direkter, mit der Herstellung des Teiles verbundenen Kosten, andererseits wachsen die Kosten, die durch ein erhöhtes Vorkommen von mangelhaften Produkten verursacht werden. Die definitive Lösung muss dann so gewählt werden, dass die Gesamtkosten der Produktion so niedrig wie möglich sind.

Als Vergleich sind in der nachfolgenden Tabelle die Werte der zu erwartenden Produktionsausbeute für genormte Toleranzen der Abmaße B und C aufgeführt.