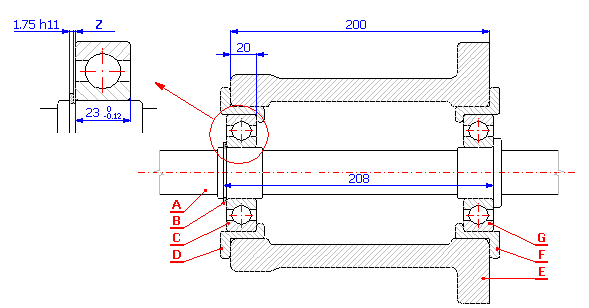
Schlagen Sie für das Beispiel einer Wellenlagerung im Gehäuse (siehe Skizze) die Produktionstoleranzen einzelner Teile so vor, dass bei der Montage ein Spiel in der Lagerung im Bereich von 0.05 bis 0.80 mm gewährleistet ist. Die vorgeschlagenen Toleranzen müssen dabei den folgenden technologischen Anforderungen der Produktion entsprechen.
- die Laufflächen im Gehäuses sollen gefräst werden
- die Bearbeitung der Welle und der Kugellagerbuchsen soll auf der Drehbank erfolgen
wo:
A ....... Welle
B ....... Sicherungsring 40 DIN 471
C,G .... Lager 6308 DIN 625 SKF
D,F .... Lagerbuchse
E ....... Gehäuse
Z ....... Spiel in der Lagerung <0.05 bis 0.80> mm
Wenn wir von der graphischen Darstellung der Maßkette ausgehen,
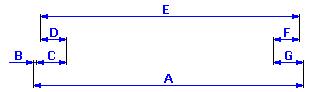
können wir bei der gegebenen Aufgabe die Größe des Spiels in der Lagerung mit der Formel Z = A - B - C + D - E + F - G beschreiben.
Beim eigentlichen Vorschlag der Fertigungstoleranzen müssen wir dann von den technologischen Forderungen der Produktion ausgehen. Die Größe der vorgeschlagenen Toleranzen der Einzelteile muss sich im Bereich der erreichbaren Produktionsgenauigkeit der gewählten Art der Verarbeitung bewegen. Beim Fräsen wird im Allgemeinen die Genauigkeit der Produktion im Bereich 9. bis 13. , beim Drehen im Bereich 6. bis 12. des Toleranzbandes erreicht.
Die Lösung des Entwurfes und der Optimierung der Maßkette können wir in folgende Schritte einteilen:
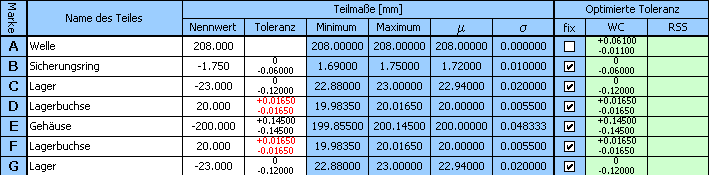
1) Anhand der oben aufgeführten Beziehung definieren wir in der Tabelle [1.1] die Maßkette. Die einzelnen Teilabmaße der Maßkette werden durch die Einzelteile gebildet, das geforderte Spiel in der Lagerung ist das Schließmaß.
2) Beim Teil mit der fest gegebenen, vom Hersteller vorgeschriebenen Toleranz (Lager, Sicherungsring) geben wir in der Tabelle die entsprechenden Abweichungen ein.
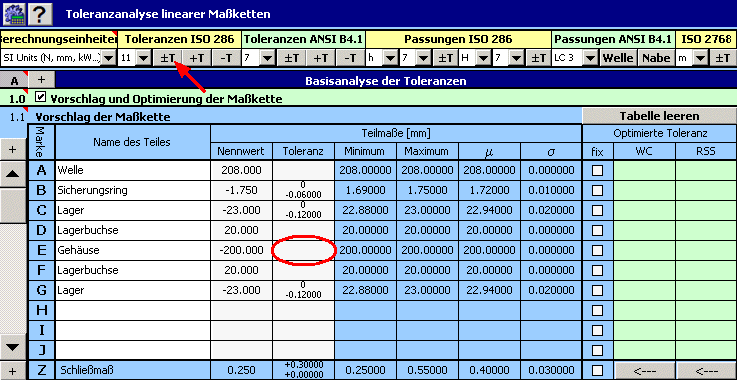
3) Die Laufflächen des Gehäuses werden gefräst, im ersten Vorschlag wählen wir deshalb für die Breite des Gehäuses die Toleranzgröße im 11. Genauigkeitsgrad.
4) Durch das Markieren entsprechender Kästchen in der 8. Spalte der Tabelle kennzeichnen wir alle Einzelteile mit fester Toleranz.
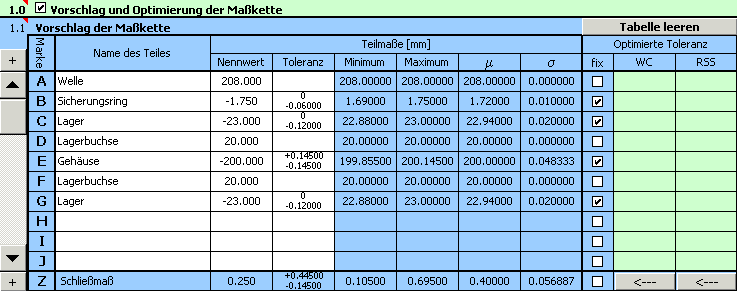
5) Im Abschnitt [1.3] geben wir die Grenzwerte des geforderten Spiels in der Lagerung ein.
6) In der Auswahlliste [1.7] wählen wir die Methode "Zentrierung und Optimierung", in der Liste [1.8] wählen wir "genormte Toleranzen" aus.
7) Für die Bearbeitung aller Einzelteile, bei denen wir im nächsten Schritt die Toleranzen vorschlagen wollen, wird Drehen verwendet. In der Auswahlliste [1.9] stellen wir deshalb als die minimale erlaubte Toleranzgröße die Genauigkeitsstufe 6 ein.

8) Mit dem Button in der Zeile [1.11] starten wir die Optimierung der Maßkette.
9) Die Parameter des resultierenden Spiels, die in dem optimierten Vorschlag der Toleranzen erreicht wurden, werden im Abschnitt [2.5] ausgegeben,
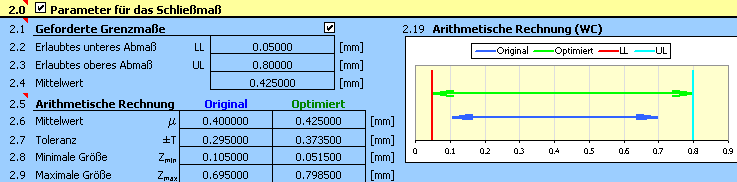
die optimierten Abweichungen der Fertigungsabmessungen sind in der 9. Spalte der Tabelle [1.1] aufgeführt.
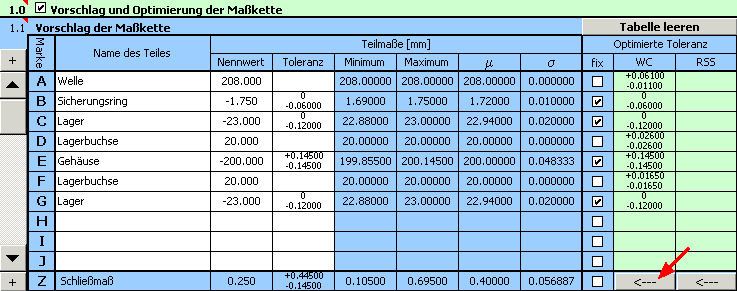
10) Für die hier aufgeführte Aufgabe wurde zwar bei der Optimierung eine funktionell geeignete Lösung gefunden, dieser Vorschlag ist aber aus der praktischen Sicht unbrauchbar. Die Breite der Lagerbuchsen wurde in den Zeile D und F vom Programm mit unterschiedlichen Toleranzen vorgeschlagen. Wenn aber die Produktion und Montage effektiv sein soll, muss eine gegenseitige Austauschbarkeit der beiden Lagerbuchsen gesichert sein.. Der weitere Schritt wird also die Beseitigung dieses Mangels sein.
11) Durch Drücken des Buttons in der unteren Zeile der Tabelle übertragen Sie die vorgeschlagenen Toleranzen in die Eingabetabelle. Hier vereinheitlichen wir dann die Toleranzen der Lagerbuchsen unter Verwendung des größeren vorgeschlagenen Wertes.
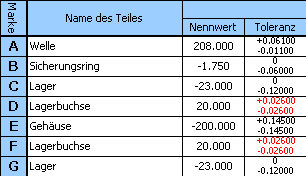
12) In der 8. Spalte der Tabelle markieren wir weiter das Kästchen in der Zeilen D und F und starten erneut die Optimierung mittels des Buttons in der Zeile [1.11].
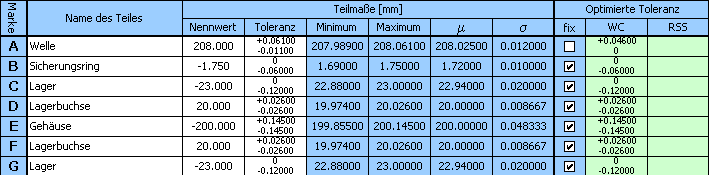
13) Das Ergebnis des Vorschlages ist nun eine absolut geeignete Lösung der Aufgabe, mit Toleranzen der Lagerbuchsen im 9. und der Welle im 7. Genauigkeitsgrad.
Die hier vorgeschlagene Lösung wird selbstverständlich nicht die einzige brauchbare Lösung dieser Aufgabe sein und muss auch nicht die Ideallösung sein. Es ist deshalb zweckmäßig (besonders bei einer Serienfertigung) mehrere Lösungen vorzuschlagen mit abweichender Genauigkeit bei der Einzelteilproduktion.
Eine andere Lösung dieser Aufgabe bekommen wir z. B. dann, wenn wir für die Toleranz der Lagerbuchsen im Schritt 11) den kleineren von den ursprünglich vorgeschlagenen Werten wählen.
Weitere geeignete Lösungen bekommen wir bei der Wahl abweichender Toleranz für die Breite des Gehäuses im Schritt 3). Ein Vergleich einiger geeigneter Vorschläge ist in der folgenden Tabelle aufgelistet:
| Lösung 1 | Lösung 2 | Lösung 3 | Lösung 4 | |
| Toleranzklasse | ||||
| Gehäuse | 11 | 11 | 10 | 10 |
| Lagerbuchsen | 9 | 8 | 10 | 9 |
| Welle | 7 | 8 | 8 | 9 |
| Lagerspiel [mm] | 0.053 - 0.793 | 0.061 - 0.789 | 0.062 - 0.788 | 0.073 - 0.777 |
Die definitive Lösung muss dann so gewählt werden, dass die Gesamtkosten der Produktion so niedrig wie möglich sind.