This workbook contains information defining the effect of temperature on some physical and mechanical properties of materials used in the engineering industry. Using this tool the following tasks can be solved:
The calculations use procedures, algorithms and data from various standards
and specialized literature.
List of standards: EN 1561, EN 1563, EN 16079, EN 1753, EN 10088-1, EN 10095, EN
10269, EN 10302
User interface.
Download.
Purchase, Price list.
Information on the syntax and control of the calculation can be found in the document "Control, structure and syntax of calculations".
This section focuses on the issue of thermal expansion of engineering materials. Paragraph [1] is for informative purposes only. Paragraph [2] is used to calculate the relevant material parameters depending on the selected temperature.
When a body is heated or cooled, its dimensions change. For bodies with one predominant dimension, this phenomena is referred to as thermal longitudinal expansion. The dependence of the elongation based on the type of material is expressed by the coefficient of longitudinal thermal expansion. In general, this physical phenomenon of material is defined by the following relation:
![]()
where:
L0 ... initial length of the body
DL ... change in length
DT ... change in temperature
However, this factor or coefficient does not have a constant value as it changes with the increasing temperature. The mathematical description of the curve of the thermal expansion coefficient based on temperature is a rather complex function. To achieve sufficiently accurate calculation of longitudinal expansion over a wider temperature range, it is usually necessary to use a quadratic or cubic computational relationship where the longitudinal expansion is described by two or more factors. For example, the quadratic relationship to calculate elongation is described by the following formula:
![]()
where:
a1,a2 ... coefficient of
thermal expansion
L ... initial length
DT ... change in temperature
However, even when using these complex relationships, a sufficiently accurate calculation covering the entire operating temperature range may not be guaranteed.
In "real life" engineering, the elongation of components is usually calculated using "linear" coefficients of thermal expansion. These linear coefficients are defined for a material which is heated starting with a precisely given initial temperature T0 until the final temperature T is reached. The thermal elongation of the component within the given temperature range may be determined using a linear relationship:
![]()
where:
a ... linear coefficient of thermal expansion for
heating starting with temperature T0 up to temperature T
L ... initial length
DT ... change in temperature T-T0
It is obvious that in order to achieve more accurate calculations of longitudinal expansion over a wider temperature range, it will be necessary to know more values of the linear expansion coefficient for the given material. In material databases or material sheets, it is usually possible to find one or more values of the coefficient for different temperature intervals "T0-T" for the given material. The purpose of this calculation is to find the approximate value of the linear coefficient of thermal expansion for any combination of start and end temperatures "T0-T".
The picture shows the usual curve of the coefficient of thermal expansion for individual material groups based on the relevant the temperature. Use the selection list to switch between individual groups.
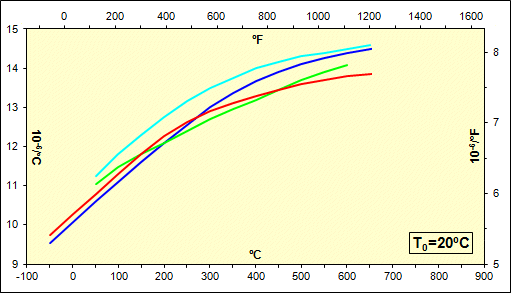
This paragraph is intended for the actual calculation of the linear coefficient of thermal expansion and for longitudinal elongation of the component.
First select the system of calculation units [2.1] and the corresponding material group [2.3]. After defining one known value of the coefficient in lines [2.5 - 2.8], a curve of the linear coefficient of thermal expansion is displayed in the diagram based on the given temperature range. The results of the calculation for the required temperature change [2.10, 2.11] are given in lines [2.12, 2.16].
Select the desired set of calculation units in the list. When the units are switched, all values are immediately recalculated.
In this section, you define the required parameters of your material.
In the selection list, choose the material group corresponding with your material.
This line specifies the range of usual values of the linear coefficient of thermal expansion for various materials selected from the given material group [2.3]. This coefficient is defined for a material heating process starting at 20° and ending at 100°C (68-212°F).
Enter one known value of the linear coefficient of thermal expansion in line [2.5] for material heating starting at temperature "T0" [2.6] until the temperature "T" [2.7] is reached.
After defining all known material parameters [2.2], the system displays a curve of the linear coefficient of thermal expansion for the given material based on the given temperature range. The displayed curve corresponds with the temperature change (heating) starting at the initial temperature "T0" until the indicated temperature is reached. Select the initial or starting temperature from the list at the bottom right of the graph.
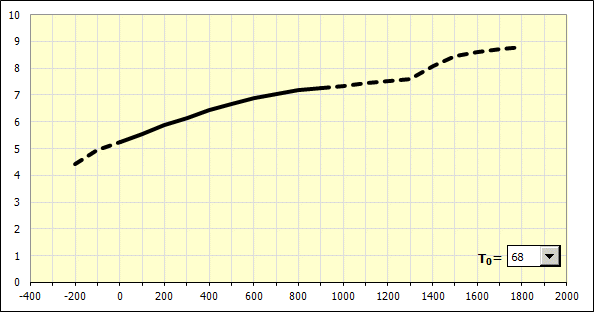
As for the material defined above, the basic value of the linear coefficient of thermal expansion for a heating process starting at 20° and ending at 100°C (68-212°F), is calculated on line [2.9].
In line [2.12] the actual calculation of the linear coefficient of thermal expansion for the material heating process starting with the initial temperature "TI" [2.10] and ending at "TE" [2.11] is performed.
The table shows informative values of the linear coefficient of thermal expansion for the selected materials.
Explanation of parameters:
a ... linear coefficient of thermal expansion [10-6/°C,
10-6/°F]
DT ... change in temperature (heating) of the
material for which the thermal expansion coefficient is defined [°C, °F]
In this part, the thermal elongation of a specific component made of the above-defined material is calculated for the temperature change described in lines [2.10, 2.11].
This paragraph is used to examine the mutual thermal expansion of a group of components made of different materials. The components must be arranged in a linear dimensional chain. The calculation allows you to compare the thermal extension of individual components or to compare two groups of components.
Calculation procedure:
1. Enter operating temperatures in line [3.1]
2. If the two groups of components which are being compared are not heated evenly, select the check box on line [3.2] and enter a different final temperature for the components belonging to group "B”
3. Define the parameters of the dimension chain in Table [3.3]
Column 1 - use the list to select the comparison group to which the component belongs
Column 3 - enter the length of the component
Column 4 - use the list to select the material group corresponding with the material of the component
Column 5 - enter the basic value of the linear coefficient of thermal expansion for heating from 20° to 100°C (68-212°F)
Column 6 - if you know the exact value of the coefficient of thermal expansion for the operating temperature change (e.g. from the material sheet), uncheck the check box and enter the value manually
4. The last two columns of the table show the calculated thermal extension of the individual components
5. The total extension of both comparison groups, including a graphical comparison, is available in Section [3.4]
This section focuses on the influence of the temperature on the modulus of elasticity of engineering materials. Paragraph [4] is for informative purposes only. Paragraph [5] is used to calculate the relevant modulus of elasticity depending on the selected temperature.
The data given here relates to the modulus of tensile elasticity. To determine the modulus of shear, it is possible to use the following conversion formula:
![]()
where:
E ... modulus of tensile elasticity
m ... Poisson's ratio
The picture shows the usual curves of the modulus of elasticity for individual groups of materials depending on the temperature. Use the selection list to switch between individual groups.
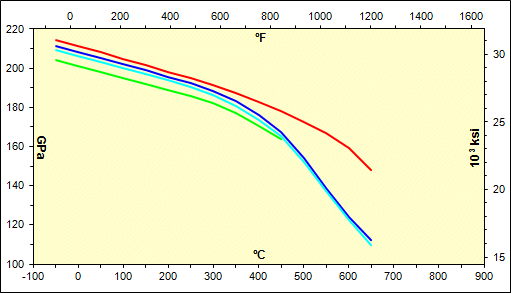
This paragraph is intended to calculate the actual tensile modulus of elasticity.
First select the system of calculation units [5.1] and the corresponding material group [5.3]. After defining one known value of the modulus of elasticity in the lines [5.5, 5.6], a curve of the modulus of elasticity as the function of temperature is displayed in the graph for the given material. The resulting calculated value of the modulus of elasticity for the required temperature [5.9] is given in line [5.10].
Select the desired set of calculation units in the list. When the units are switched, all values are immediately recalculated.
In this section, you define the required parameters of your material.
In the selection list, choose the material group corresponding with your material.
This line shows the range of usual modulus of elasticity for different materials from the given material group [5.3] at a temperature of 20°C (68°F).
Enter one known value of the modulus of elasticity at temperature "T" [5.6] in line [5.5].
After defining all material parameters in Section [5.2], a theoretical curve of the modulus of elasticity for the given material is displayed as the function of the temperature.
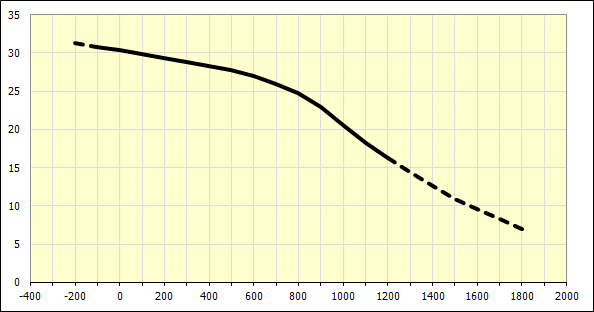
Line [5.8] calculates the basic value of the modulus of elasticity at a temperature of 20°C (68°F) and for the material defined above.
In line [5.10], the value of the modulus of elasticity is calculated for the required final temperature "TE" [5.9].
In this section, you may determine the corresponding value of the modulus of elasticity in shear for the above calculated value of the tensile modulus.
The table shows informative values of the tensile modulus of elasticity for the selected materials.
Explanation of parameters:
E ... Young's modulus [GPa, 103 ksi]
T ... material temperature for which the specified modulus of elasticity is
defined [°C, °F]
Information on setting of calculation parameters and setting of the language can be found in the document "Setting calculations, change the language".
General information on how to modify and extend calculation workbooks is mentioned in the document "Workbook (calculation) modifications".
EN 1561
Founding - Grey cast irons
Gießereiwesen - Gusseisen mit Lamellengraphit
Fonderie - Fontes à graphite lamellaire
Slévárenství - Litiny s lupínkovým grafitem
EN 1563
Founding - Spheroidal graphite cast irons
Gießereiwesen - Gußeisen mit Kugelgraphit
Fonderie - Fonte à graphite sphéroïdal
Slévárenství - Litina s kuličkovým grafitem
EN 16079
Founding - Compacted (vermicular) graphite cast irons
Gießereiwesen - Gusseisen mit Vermiculargraphit
Fonderie - Fontes à graphite vermiculaire (compacté)
Slévárenství - Litina s vermikulárním (kompaktním) grafitem
EN 1753
Magnesium and magnesium alloys - Magnesium alloy ingots and castings
Magnesium und Magnesiumlegierungen - Blockmetalle und Gussstücke aus
Magnesiumlegierungen
Magnésium et alliages de magnésium - Lingots et pièces moulées en alliages de
magnésium
Hořčík a slitiny hořčíku - Ingoty a odlitky ze slitin hořčíku
EN 10088-1
Stainless steels - Part 1: List of stainless steels
Nichtrostende Stähle - Teil 1: Verzeichnis der nichtrostenden Stähle
Aciers inoxydables - Partie 1 : liste des aciers inoxydables
Korozivzdorné oceli - Část 1: Přehled korozivzdorných ocelí
EN 10095
Heat resisting steels and nickel alloys
Hitzebeständige Stähle und Nickellegierungen
Aciers et alliages de nickel réfractaires
Oceli a niklové slitiny žáruvzdorné
EN 10269
Steels and nickel alloys for fasteners with specified elevated and/or low
temperature properties
Stähle und Nickellegierungen für Befestigungselemente für den Einsatz bei
erhöhten und/oder tiefen Temperaturen
Aciers et alliages de nickel pour éléments de fixation utilisés à température
élevée et/ou basse température
Oceli a niklové slitiny na upevňovací prvky pro použití při zvýšených a/nebo
nízkých teplotách
EN 10302
Creep resisting steels, nickel and cobalt alloys
Warmfeste Stähle, Nickel- und Cobaltlegierungen
Aciers et alliage à base de nickel et de cobalt résistant au fluage
Žáropevné oceli, niklové a kobaltové slitiny
ASM Handbook Volume 1: Properties and Selection: Irons, Steels, and
High-Performance Alloys
ASM International, 1990
Metals Handbook Desk Edition, 2nd Edition
ASM International, 1998
ASM Ready Reference: Thermal Properties of Metals
ASM International, 2002
Materials Science and Engineering Handbook, Third Edition
CRC Press LLC, 2001
Smithells Light Metals Handbook
Butterworth-Heinemann, 1998
CRC Materials Science and Engineering Handbook, 4th Edition
CRC Press, 2015
Military Handbook - MIL-HDBK-5H: Metallic Materials and Elements for
Aerospace Vehicle Structures
U.S. Department of Defense, 1998
Deutsches Kupferinstitut Berufsverband e.V,
Technische Broschüren und Datenblätter
Special Metals Corporation
High Performance Alloys Literature