The calculation is intended for the purposes of geometric and strength designs of helical tension cylindrical springs made of wires and rods of circular sections, exposed to a static loading. In addition to the design of geometric and strength parameters, the calculation co-operates with CAD systems. The application provides solutions of the following tasks:
Automatic design of the spring.
Selection of an optimal alternative of the spring design in view of strength, geometry and weight.
Strength check of the spring.
Calculation of working forces of a spring of known production and mounting dimensions.
Calculation of mounting dimensions for a known loading and production parameters of the spring.
The application includes a table of commonly used spring materials according to ISO, EN, ASTM/SAE, DIN, BS, JIS and others.
Support for 2D and 3D CAD systems.
The calculation is based on data, procedures and algorithms from specialized literature and standards EN 13906-2, DIN 2089-2, DIN 2097.
User interface.
Download.
Purchase, Price list.
Information on the syntax and control of the calculation can be found in the document "Control, structure and syntax of calculations".
Information on the purpose, use and control of the paragraph "Information on the project" can be found in the document "Information on the project".
A tension spring is a helical cylindrical spring with approximate constant stiffness which is able to receive external forces acting away from each other in its axis. Cold formed springs are preferably produced with prestressing, thus with close-coiled active coils. If necessary due to technical reasons, it is possible to use loose-coiled tension springs without prestressing, with gaps between the active coils. Hot formed springs shall be always without inner prestressing.
In view of spring function, there are four basic states of springs:
| State of the spring | Description of the spring state | index |
| free | the spring is not loaded | 0 |
| preloaded | the spring is exposed to the minimum operational loading | 1 |
| fully loaded | the spring is exposed to the maximum operational loading | 8 |
| limit | the spring is exposed to the limit operational loading | 9 |
The above-mentioned indexes are used in the calculation to specify individual parameters of the spring related to the given state of the spring.
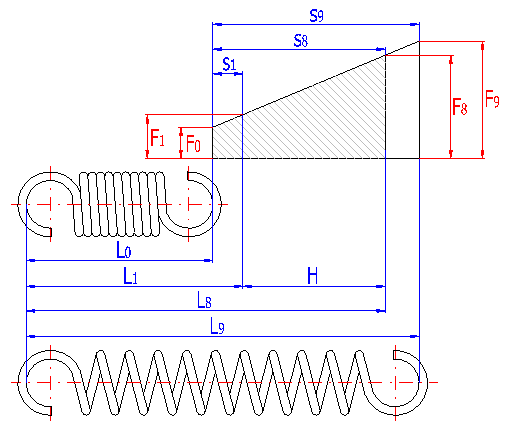
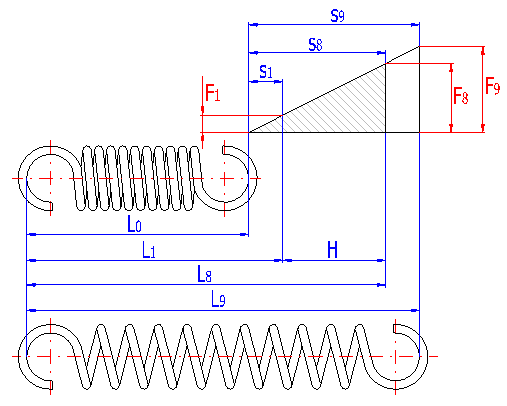
With regards to the manner of loading, the springs can be divided for purposes of calculations into springs exposed to static loading or loading with lower variability, with requirements of service life lower than 105 working cycles, and springs exposed to fatigue loading with requirements of service life higher than 105 working cycles. With regards to the considerable effects of the shape and design of fixing eyes on reduction of the spring's service life and impossibility of perfect shot peening of the spring, it is not advisable to use tension springs exposed to fatigue loading.
The task of spring design cannot be solved directly and allows considerable freedom in options of the design, dimensions or loading of the spring. Many springs of various designs and dimensions may meet requirements of the desired input parameters of the task. Therefore, it is necessary to proceed iteratively and successively evaluate individual designs of the spring. The calculation solves this problem by creating a table of optimum designs following the chosen qualitative standard. The solution procedure is given in the following items (the square brackets indicate the number of the paragraph).
In this paragraph, enter basic input parameters, characterizing the manner and mode of loading, design and method of seating of the spring and parameters of the working environment.
Tension springs are used in two basic designs:
Tension springs are used in many different designs. The most commonly used ends of springs are given in a list which can be used to choose a suitable solution according to the illustration. The type of design of the spring ends depends on the desired method of fixing the spring, its dimensions and the amount of loading.
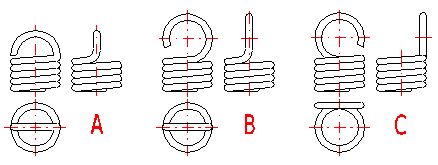
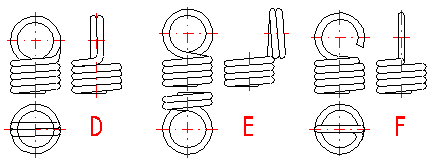
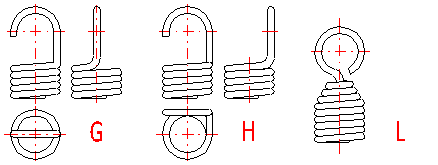
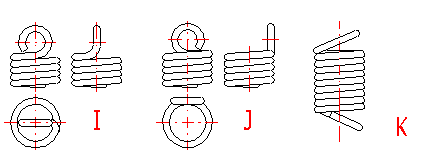
Tension springs are usually fixed using fixing eyes of several types (A .. J) with different heights of the eyes and differing properties. Fixing eyes are the best solution in the technological aspect, however, this brings certain problems in view of loading capacity of the spring. Loading of the spring creates a concentration of stress on the fixing eyes and this may be substantially higher than the calculated stress in the spring coils. This fact should be taken into account when designing the spring. When using fixing eyes it is advisable to design the spring with a sufficient level of safety [1.10] and check the loading capacity of the eyes in chapter [6]. The amount of concentration of the stress depends on the type, design and dimensions of the eye and it is very difficult to calculate it theoretically. In view of bending stress appearing in the fixing eye [6.1], small eyes (type I, J) or double eyes (type D, E) are the best solution. In view of concentration of stress in torsion at the point of transition of the coil into the loop [6.2] the full loops on the side (type C,E,I) are the best solution. With regards to the above-mentioned facts, it is not recommended to use tension springs with fixing eyes exposed to fatigue loading in any case.
For individual designs of fixing eyes, the following values of eye height are prescribed:
A) Half loop: LH = {0,55 .. 0,8} Di
B,C) Full loop: LH = {0,8 .. 1,1} Di
D,E) Double twisted full loop: LH ~ Di
F) Inside full loop: LH = {1,05 .. 1,2} Di
G,H) Raised hook: 1,2 Di < LH < 30 d
I,J) Small eye: 2 d < LH < 0,6 Di
K) Inclined full loop: LH = {0,35 .. 0,9} Di
With designs without fixing eyes (M .. O) the spring is fixed using end coils whose pitch does not change during functional deformation of the spring. These types of tension springs are suitable for possible use with fatigue loading.
A clockwise direction (in a dextrorsal helix) is preferably used with springs; a counterclockwise direction is used only if technically necessary.
End coils are the outer coils of the spring, co-axial with the active coils, whose pitch does not change during functional deformation of the spring. The end coils are used with tension springs without fixing eyes (design L .. O) for fixing the spring. Springs with fixing eyes do not have any end coils.
Choose the loading mode which best meets your entered data.
The temperature of the operational environment affects relaxation of the spring, appearing as reduction of the force developed by the spring with its deformation to a constant length, depending on time. It is advisable to take this fact into account with the design of the spring and increase the level of safety in a proper way with strength checks of the spring in case of temperatures over 80 °C. The operational temperature must also be reflected in selection of the spring material.
The service life of springs decreases significantly due to corrosion effects. Corrosion has very powerful effects particularly on springs exposed to fatigue loading. It is advisable to take this fact into account with the design of the spring and increase the level of safety in a proper way with strength checks of the spring in case of a corrosion-aggressive environment. It is also necessary to consider corrosion effects when selecting the spring material.
Minimum permissible ratio between the limit permissible stress in torsion of the chosen spring material and the actual maximum working stress in spring coils t8. For a non-corrosive atmosphere and working temperature of the ambient environment of the spring exceeding 80 °C, and with regards to the course and manner of loading tension springs, it is advisable to use a level of safety in the interval 1,05 .. 1,3. Springs working at higher temperatures or in an aggressive environment should be designed with a higher level of safety.
With helical springs, the stress appearing in the spring coils at the given loading is calculated for simple torsion. Additional bending stress appears in the coil due to its rounding. Therefore, the stress is corrected in the calculation using a correction coefficient. As several different coefficients are commonly used, choose from the list the correction coefficient which meets your local usage or recommendations of standards.
This paragraph can be used for selection of the spring material. Immediately after selection of material in the list, all information necessary for the design and calculation of the spring is displayed. If you need more detailed information on the chosen material, or you wish to define or modify its own material, switch over to the material sheet "Material".
From the selection list choose the required processing of the spring. The cold winding shall be used for springs of ordinary sizes with a diameter of the wire up to 16 mm. Hot forming shall be used for the production of heavily loaded springs of greater sizes with a diameter of the over10 mm.
Choose the spring material from the list. With regards to the complexity of the task to design a spring, this calculation is implemented as an internal function of the workbook. In addition to five user's materials, the list includes chosen materials of one standard. If you wish to use materials of another standard, choose the respective standard in the sheet "Material".
This paragraph includes information on recommended use of the chosen material. The spring material should be designed with regards to the manner of loading of the spring and operational conditions. If you must use a less suitable material, this fact should be reflected in increased level of safety in the design of the spring (see row [1.10]).
Properties of the chosen material described in rows [2.4, 2.6] are evaluated in five degrees (excellent, very good, good, poor, insufficient), the relative strength in row [2.5] in three degrees (high, medium, low).
All parameters of the material necessary for calculation and independent of the diameter of the used wire are displayed here.
This chapter includes the strength characteristics of the chosen material necessary for the design and calculation of the spring. The data characterizing strength of the material may be different for the same material depending on the diameter of the used wire. Therefore, the values given here depend on the diameter of the wire given in row [4.8].
This paragraph can be used for designing the spring. The task of designing the spring often has many various suitable solutions for the given input conditions. The application therefore proceeds iteratively with the spring design, and for the given input conditions it passes through individual designs of the spring and a set of most advantageous solutions is selected following the chosen qualitative standard. The chosen solutions are then offered in the form of a sorted table, in which you can choose a suitable design. The data on the chosen spring are then displayed immediately in the chapter of results.
This part can be used for entering of input data describing the basic parameters of the working cycle which have to be met by the designed spring. The first input column displays the desired value of the given parameter of the spring; the second column gives the permissible deviation from the desired value in the range 0-99%. If the designed spring has to meet the desired value of the given parameter, a zero deviation must be entered.
In this part it is necessary to specify various filters and marginal conditions of the design calculation. Their setting may significantly affect the course of the spring design and determine the speed, accuracy and quality of the design, the scope and number of suitable solutions and a qualitative standard for evaluation of the best designs.
If it is necessary to limit the outer diameter of the spring in its design, enable the check box at the beginning of the row and enter the maximum permissible value of the outer diameter of the spring in the input field.
If it is necessary to limit the inner diameter of the spring in its design, enable the check box at the beginning of the row and enter the minimum permissible value of the inner diameter of the spring in the input field.
Active coils of the spring are those coils whose pitch angle varies with functional deformation of the spring. In case of springs with fixing eyes, the number of active coils is equal to the total number of spring coils. When setting a fine division, the design calculation tests a higher number of different designs of the spring and is able to give a more accurate and higher quality solution. On the other hand, this naturally slows down the design calculation of the spring.
In the design of the spring, it is not possible to proceed without certain dimensional limitations. Some dimensions or ratios of individual dimensions of the spring are limited by the recommended values specified by the respective standards and producers. This creates a file of marginal conditions which must be taken into account during spring design.
Strictly following these marginal conditions may cause elimination of some advantageous solutions from the resulting design which may exceed some of the specified limits, even though they may be acceptable. Due to this reason, it is possible to set a filter of the design calculation in this row. Such filter specifies the percentage of exceeding the limit dimensions of the spring. This brings more suitable solutions, however, on the other hand it is then necessary to visually check the chosen solution in the chapter of results and consider acceptability of possible exceeding of the limit dimensions of the springs. Exceeding limit dimensions is indicated by a change in color of the parameter value to red in the chapter of results.
In case of loading of springs with fixing eyes, these eyes may be exposed to certain concentrations of stress which might be substantially higher than the calculated stress in the spring coils. Therefore, it is recommended to check these springs also in view of loading of the fixing eyes [6]. If the designed spring has to meet checks of loading capacity of fixing eyes, it is necessary to take this requirement into account when defining input data of the design calculation. One of the options is to enable this filter. The calculation then performs a preliminary check of loading of the eye when designing the spring, and the resulting design eliminates all solutions which do not meet the respective requirements. If this check is disabled, it is advisable to design the spring with a sufficiently overdesigned level of safety [1.10] to cover any possible stress concentrations appearing in the fixing eye.
The amount of stress concentrations also depends, among others, on the dimensions of the eye [6.2, 6.6], which are not known at the time of design, and the calculation can only estimate these dimensions. Therefore it is necessary to perform a consequential check of loading of the fixing eye in chapter [6] even if this filter is enabled.
If this filter of solutions is preset to "Yes", the resulting design includes only springs designed as preset in row [1.3]. Otherwise, the filter presents a calculation of a type of fixing eye based on the calculated height of the eye regardless of the setting in row [1.3]. The design then provides five options of designs of fixing eyes according to the calculated height and recommended limits:
1) Small eye (type I) for LH < 0,55 Di
2) Half loop (type A) for LH < 0,8 Di
3) Full loop (type B) for LH < 1,1 Di
4) Inner full loop (type F) for LH < 1,2 Di
5) Raised hook (type G) for LH > 1,2 Di
If this filter of solutions is set to "Yes", the resulting design eliminates all solutions with calculated levels of safety ss lower than the desired level of safety given in row [1.10].
If the filter is disabled, the resulting design includes all solutions with calculated levels of safety higher or equal to 1. Due to the fact that the desired levels of safety are usually more or less accurate estimations and only rarely reflect the accurately determined value, whose exceeding could lead to damage to the spring, experienced users can disable this filter during execution of the design and consider the level of safety of the designed spring directly in the table of the design or in the chapter of results in row [4.43].
Set in this row the criterion of evaluation of quality of individual suitable solutions of the spring design. The best solutions are then offered to the user in the table. The standard of quality can be chosen in the list according to the following description:
In some cases it is suitable to execute the design successively for all criteria and compare the designs.
The design calculation of the spring works on the iteration principle. This row can be used to set the number of iterations in the calculation and to affect the speed, accuracy and quality of the design. Generally, the more iterations, the slower the calculation and the more accurate the solution. However, it is advisable to take into account also other aspects when setting this row.
The speed of the design is affected by the capacity of the computer and the type of the design more than by the chosen number of iterations. Similarly, setting a high number of iterations does not always have to result in a more accurate solution for certain types of designs. Generally speaking, it is usually sufficient to set a low or medium number of iterations for common designs. Use of a high number of iterations is more important for very free designs, where all or the majority of parameters of the working cycle in paragraph [3.1] entered with a considerable permissible deviation and the desired diameter of the spring is not limited by filters in rows [3.8, 3.9].
This part can be used to initiate the design calculation and then to choose a suitable spring in the table of designed solutions. With regards to the complexity of the spring design, it is not possible to perform the design calculation automatically always with a change of one of the input parameters as with other calculations on the sheet. The design calculation is initiated once only when pressing the button in row [3.19]. Information on the course of the calculation is displayed in the dialogue.
After completion of the calculation, a table of designed solutions is filled in and sorted, and values of the best (chosen) solution are transferred automatically to the chapter of results. The table is sorted according to the criterion set in row [3.18]. The table of designed solutions can be re-sorted whenever using another sorting criterion.
If the design calculation was unsuccessful and no suitable solution was found, this fact is indicated by a warning message and the table of solutions remains in its original state. The following text gives some particular problems which may appear, and their possible remedies:
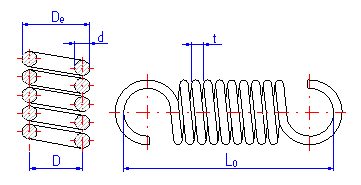
Meaning of parameters in the table:
| D | Mean spring diameter |
| De | Outer spring diameter |
| Di | Inner spring diameter |
| d | Wire diameter |
| n | Number of active coils |
| L0 | Free length of the spring |
| L1 | Length of the preloaded spring |
| L8 | Length of the fully loaded spring |
| F1 | Minimum working loading |
| F8 | Maximum working loading |
| t8 | Stress of the fully loaded spring |
| ss | Level of safety of a spring exposed to static loading |
| m | Weight of the spring |
| LH | Height of the fixing eye. The letter at the beginning indicates the type of eye design. |
| quality | A comparative value showing the quality of the solution with regards to the chosen qualitative standard [3.15]. The lower the given value, the higher the quality of the design. |
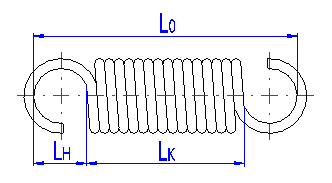
All necessary parameters describing the designed spring for the given loading and dimensions of the spring are shown in this paragraph. Entry data are transferred to the calculation from the table of solutions [3.20] of the chosen design of the spring or from some of the supplementary calculations [7,8,9]. For easier evaluation and checking of values of individual parameters of the spring, some data are completed with their recommended limit values (shown in green fields in the listing). Exceeding the recommended values is indicated by a change in color of the parameter to red. Critical values which might cause non-functionality or damage to the spring are indicated by a change in color of the whole field to red.
Parameters of the spring are divided in the listing into paragraphs according to the spring status; the strength check of the spring is given at the end of the chapter. Meanings of individual dimensional parameters of the spring can be seen in the illustration.
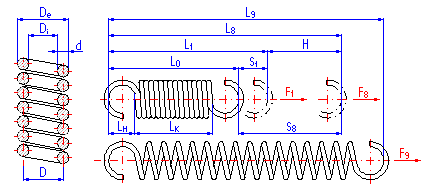
If it is necessary to tune some parameters of the designed spring (e.g. rounding of the designed dimensions), use some of the supplementary calculations [7,8,9] for this purpose.
Pressing the button in this row refreshes values in the listing of parameters of the spring with the data from the design of the spring chosen in the table of solutions [3.20].
This parameter gives the ratio D/d between the mean diameter of the spring and the diameter of the used wire.
The length of the spring section consisting only of active coils whose angle pitch does not change with functional deformation of the spring. In case of springs with fixing eyes, this section of the spring includes all coils. The meaning of this term can be seen in the illustration.
The height of the spring hook depends on its type and for individual types, their recommended limits are prescribed [1.3]. In case of springs without fixing eyes, this term means the distance between the end of active coils and the point of fixing of the spring (see the illustration).

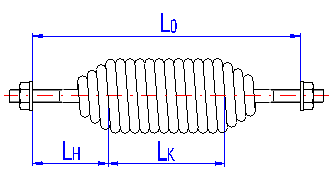
Parameters of a free spring are given by the spring design [1.2]. In case of prestressed springs, this prestressing is created in the course of production (winding) of the spring and its amount depends on the used wire, spring index and manner of winding. The spring is close-coiled; thus the pitch is equal to the wire diameter.
In case of springs without prestressing, the spring is loose-coiled. The pitch of the free spring must then be within the limits given in row [3.5] in the sheet "Options" (springs are usually designed with a pitch in the range 0.2*D < t < 0.4*D).
Resonance effects may appear in case of tension springs exposed to fatigue loading. To eliminate these effects, it is necessary to load the spring at an excitation frequency different from the characteristic frequency of the spring (by approx. +-15-20%).
With springs having ends of type A .. K (see [1.3]) the length of the wire is calculated including the approximate length of the fixing eyes.
With springs having ends of type A .. K (see [1.3]) the weight of the spring is calculated including the approximate weight of the fixing eyes.
The strength check of a compression spring is performed by comparison of the limit permissible stress in torsion of the chosen material [4.42] with the corrected stress of the spring in a fully loaded condition [4.41]. If the designed spring has to meet the strength check in the full extent, the resulting level of safety [4.43] must be higher or equal to the desired level of safety [1.10].
The stress in the spring coil is calculated for simple torsion and its calculated value is a theoretical value. In fact, the stress in the coil is higher because the curving of the coil causes an additional bending stress. Therefore, the stress is corrected using a corrective coefficient (see row [1.11]) for the purpose of a strength check.
This paragraph can be used for calculation of the spring parameters (designed in paragraph [4]) which is in specific operating conditions. The paragraph [5.1] is designed for the purpose of calculations of the length Lx of a spring loaded with a given operational force Fx. The paragraph [5.6] enables users to find the operational force which is necessary to extend the spring to the given length Lx.
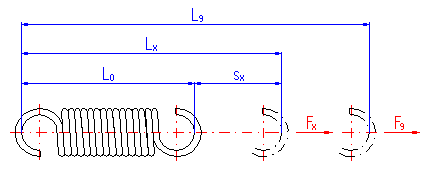
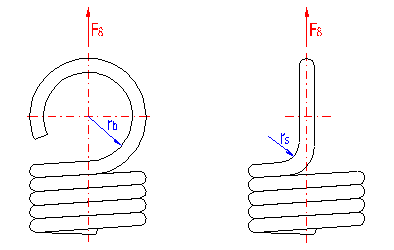
Loading of the spring creates a concentration of stress in the fixing eyes and this may be substantially higher than the calculated stress in the spring coils. It is therefore recommended to check such springs also in view of loading of the fixing eyes. This paragraph is designed just for this purpose.
The amounts of possible concentrations depend on the type, design and dimensions of the eye and it is very difficult to calculate them theoretically. Despite this, at least approximate calculations are used to provide some orientation information on any possible exceeding of strength limits of the chosen material of the spring. Two basic strength checks are performed with regards to the design of the fixing eye:
The amount of the bending stress which appears in the bend of the eye depends on the radius of the spring hook rb [6.2]. The amount of stress increases with an increasing radius and vice versa. Therefore, in view of the bending stress, a "Small eye" is the best solution (see [1.3], types I, J). The check itself is performed by a comparison of the calculated maximum bending stress in the fixing eye [6.3] with the permitted bending stress of the spring material [6.4]. Exceeding the permitted stress is indicated by a change in color of the parameter value to red. Any possible exceeding of the tensile strength Rm of the spring material is then indicated by a change in color of the whole field to red.
In the case of tension springs, the highest stress concentrations appear in points of transitions of coils to spring hook. The size of these stresses depends on the transition bend radius rs [6.6]. As it is very difficult and in some cases even impossible to calculate theoretically exact values of concentrations of actual stresses, the theoretical stress peak is usually calculated using a corrective coefficient which is given by the ratio of the mean and inner radius of the transition bend. Generally speaking, the size of stress in the transition bend decreases with an increasing radius of the bend and vice versa. The best solution of commonly used fixing eyes is, therefore, to use a "Full loop on side" (see[1.3], type C, E), where the transition of the coil to the eye is the smoothest.
The check itself is performed by a comparison of the calculated maximum stress in the transition bend [6.7] with the permitted torsional stress of the spring material [6.4]. Exceeding the permitted stress is indicated by a change in color of the parameter value to red. Any possible exceeding of the ultimate torsional strength Rms of the spring material is then indicated by a change in color of the whole field to red.
This paragraph includes the first of the supplementary calculations. This calculation includes three functions.
The design of a free spring determines its parameters [1.2].
In case of prestressed springs, this prestressing is created in the course of production (winding) of the spring and its size depends on the used wire, spring index and manner of winding The spring is close-coiled; thus the pitch is equal to the wire diameter. If the value of the prestressing is not known for the given spring (e.g. provided by producer), it is possible to use the automatic calculation. If the check box in row [7.17] is enabled, the amount of prestressing will be calculated automatically according to DIN 2089.
Springs without prestressing are loose-coiled. The pitch of a free spring must then be in the limits given in row [3.5] in the sheet "Options" (springs are usually designed with pitches in the range 0.2*D < t < 0.4*D). If the check box in row [7.17] is enabled, the pitch will be designed automatically as a mean value of the limit dimensions.
The height of the spring hook depends on its type and for individual designs of the eye, their recommended limits are prescribed (see [1.3]).
The calculation located in this paragraph includes two functions.
The height of the spring hook depends on its type and for individual designs of the eye, their recommended limits are prescribed (see [1.3]).
Parameters of unloaded spring are given by its design [1.2].
In case of prestressed springs, this prestressing is created in the course of production (winding) of the spring and its amount depends on the used wire, spring index and manner of winding. The spring is close-coiled; thus the pitch is equal to the wire diameter. If the value of prestressing is not known for the given spring (e.g. provided by the producer), it is possible to use the automatic calculation. If the check box in row [8.18] is enabled, the amount of prestressing will be calculated automatically according to DIN 2089.
Springs without prestressing are loose-coiled. The pitch of a free spring must then be in the limits given in row [3.5] in the sheet "Options" (springs are usually designed with pitches in the range 0.2*D < t < 0.4*D). If the check box in row [8.18] is enabled, the pitch will be designed automatically as a mean value of the limit dimensions.
The calculation located in this paragraph includes two functions.
The height of the spring hook depends on its type and for individual designs of the eye, their recommended limits are prescribed (see [1.3]).
Parameters of unloaded spring are given by its design [1.2].
In case of prestressed springs, this prestressing is created in the course of production (winding) of the spring and its amount depends on the used wire, spring index and manner of winding. The spring is close-coiled; thus the pitch is equal to the wire diameter. If the value of prestressing is not known for the given spring (e.g. provided by the producer), it is possible to use the automatic calculation. If the check box in row [9.16] is enabled, the amount of prestressing will be calculated automatically according to DIN 2089.
Springs without prestressing are loose-coiled. The pitch of a free spring must then be in the limits given in row [3.5] in the sheet "Options" (springs are usually designed with pitches in the range 0.2*D < t < 0.4*D). If the check box in row [9.16] is enabled, the pitch will be designed automatically as a mean value of the limit dimensions.
The service life of tension springs exposed to fatigue loading with the requirement of a service life more than 105 working cycles, depends very much on the shape of the fixing eyes. Additional stress appears particularly in points of transition of active coils into fixing eyes and the stress at these points is usually much higher than in active coils. The amount of concentration of the stress depends on the type, design and dimensions of the eye and it is very difficult to calculate it theoretically (in some cases it is even impossible). In addition to this, the distance of the coils prevents perfect shot peening of the spring. Due to these reasons, it is recommended to avoid use of tension springs exposed to fatigue loading. If it is necessary to use a tension spring with fatigue loading, it is advisable to avoid use of fixing eyes and choose another type of fixing of the spring (see [1.3], types M, N, O).
This paragraph is designed just for calculation and strength check of a tension spring exposed to fatigue loading. If you merely wish to check a spring designed using the design calculation in chapter [3], transfer the data on the designed spring to the calculation using the button in row [10.1]. The resulting data can then be transferred using the button in row [10.38] to the chapter of results [4], where some other parameters of the spring are calculated additionally.
The springs designed in chapter [3], which are optimized in view of the static strength check, will not probably meet requirements of the dynamic check. If you also wish to use the automatic design [3] for a spring exposed to fatigue loading, proceed as follows:
Choose the loading mode which best meets your entered data.
Two fields of fatigue stress of springs can be distinguished with springs exposed to fatigue loading. In the first field with limited service life of springs (lower than approx. 107 working cycles, the fatigue strength of the spring decreases with an increasing number of working cycles. In the field of unlimited service life (the desired service life of the spring is higher than 107 working cycles), the fatigue limit of the material and thus the strength of the spring remains approximately constant.
The level of safety gives the minimum permissible ratio between the fatigue strength in torsion of the spring and the actual maximum working stress t8in spring coils. For a non-corrosive atmosphere and working temperature of the immediate vicinity of the spring up to 80 °C, and with regards to the course and mode of loading, it is advisable to choose a level of safety of springs in an interval from 1.05 .. 1.25. To determine the level of safety, it is also necessary to consider suitability of the chosen material for fatigue loading. With materials unsuitable for fatigue loading it is advisable to increase the desired level of safety by up to 20%. Springs working at higher temperatures or in a corrosive environment should be designed with higher levels of safety. Particularly corrosion significantly decreases the service life of a spring exposed to fatigue loading.
With helical springs the stress appearing in the spring coil at the given loading is calculated for simple torsion. Additional bending stress appears in the coil due to its rounding. Therefore, the stress is corrected in the calculation using a correction coefficient. As several different coefficients are commonly used, choose from the list the correction coefficient which meets your local usage or recommendations of standards.
The height of the spring hook depends on its type and for individual designs of the eye, their recommended limits are prescribed (see [1.3]).
Parameters of free spring are given by the spring design [1.2].
In case of prestressed springs, this prestressing is created in the course of production (winding) of the spring and its amount depends on the used wire, spring index and manner of winding. The spring is close-coiled; thus the pitch is equal to the wire diameter. If the value of the prestressing is not known for the given spring (e.g. provided by the producer), it is possible to use the automatic calculation. If the check box in row [10.21] is enabled, the size of the prestressing will be calculated automatically according to DIN 2089.
Springs without prestressing are loose-coiled. The pitch of a free spring must then be in the limits given in row [3.5] in the sheet "Options" (springs are usually designed with pitches in the range 0.2*D < t < 0.4*D). If the check box in row [10.21] is enabled, the pitch will be designed automatically as a mean value of the limit dimensions.
The strength check of a spring exposed to fatigue loading is performed by comparison of the maximum fatigue strength of the used material specified for the given loading [10.36] with corrected stress of the spring in a fully loaded condition [10.31]. If the designed spring has to meet the strength check in the full extent, the resulting level of safety [10.37] must be higher or equal to the desired level of safety [10.5].
Maximum permissible stress of the spring material for infinite life and zero-to-maximum stress fluctuation.
Determination of the maximum fatigue strength of the spring is based on the ultimate fatigue strength of the chosen material and the given course of loading of the spring using a Goodman's fatigue diagram.
Information on options of 2D and 3D graphic outputs and information on cooperation with 2D and 3D CAD systems can be found in the document "Graphic output, CAD systems".
Information on setting of calculation parameters and setting of the language can be found in the document "Setting calculations, change the language".
When designing a spring, it is not possible to proceed without certain dimensional limitations. Some dimensions or ratios of individual dimensions of the spring are limited by recommended values determined by the respective standards (see e.g. DIN 2097) and various producers as well. This creates a file of marginal conditions which must be taken into account in the design of the spring.
Therefore, different recommended limit dimensions of the spring may be used which can be modified in this paragraph according to the user's requirements. Minimum values of individual parameters can be entered in the first column, maximum values in the second column. In case of setting more free marginal conditions (by decreasing the minimum or increasing the maximum values) the application selects a suitable solution from a wider range of suitable solutions. This increases the chance of finding a higher quality solution. On the other hand, this creates the risk that the chosen supplier will not be able to produce the designed spring.
If there are no special requirements for limit dimensions of the spring, the predefined setting can be used. Pressing the button in row [3.7] sets in input fields the implicit values corresponding to the file of marginal conditions for commonly delivered springs.
This parameter gives the ratio D/d between the mean diameter of the spring and the diameter of the used wire. According to DIN 2097, the permissible spring index is in an interval from 4 to 20.
According to DIN 2097 it is max. 200 mm. Commonly delivered are also springs with greater diameters.
Not prescribed by the standard, usually 1 to 15 with commonly produced springs.
According to DIN 2097 max. 1500 mm.
Not prescribed by the standard; with commonly produced springs without prestressing, made of a wire strengthened by drawing or heat, usually 0.2*D < t < 0.4*D.
A minimum of three active coils are prescribed by standard DIN 2097 for tension springs.
General information on how to modify and extend calculation workbooks is mentioned in the document "Workbook (calculation) modifications".
With calculation of springs, it is not possible to intervene in the design calculation of the spring using modifications and changes in the workbook. With regards to the complexity of the task of designing a spring, this calculation is implemented as an internal function of the workbook.
^