In diesem Teil werden einige theoretische Informationen und Formeln zusammengefasst, welche den Geometrieentwurf, Berechnung der Kraft- und Leistungsparameter und Festigkeitskontrollen der Evolventenverzahnung betreffen. Diese Unterlagen wurden in den folgenden Berechnungen angewendet.
Einige der wichtigsten Formeln für die Berechnung der Verzahnungsgeometrie sind unten angeführt. In den Formeln werden die Indexe 1 und 2 für das Ritzel und Rad verwendet (dies ist das Paar: Sonnenrad und Planetenträger, beziehungsweise Planetenträger und Hohlrad). Im Fall einer Innenverzahnung (Hohlrad) wird ein negativer Wert der Zähnezahl des Innenrades und damit auch ein negativer Wert des Achsabstandes und der Durchmesser verwendet.
Im Fall eines Planetengetriebes sind die einzelnen Räder voneinander gegenseitig abhängig und es ist das Getriebe als Einheit inkl. der entsprechenden begrenzenden Bedingungen (siehe weiter) zu lösen.
Parameter des Grundprofils: mn (Modul, DP für Fingerberechnung),
a (Eingriffswinkel), ha*, c*, rf* (Parameter
der Bearbeitungsmaschine)
Parameter der Ritzel und Rad: z1, z2 (Zähnezahl vom Ritzel und Rad), x1,
x2 (Einheitsverschiebung), b
(Schrägungswinkel am Zahngrundkreis), b (Verzahnungsbreite)
Durch Annähern oder Entfernen des Werkzeuges in Hinsicht auf die Radmitte ändert sich die Form und dadurch auch die Eigenschaften einer Evolventenverzahnung. So wird eine korrigierte Verzahnung, Verschiebungs-Verzahnung gebildet. In der Abbildung ist:
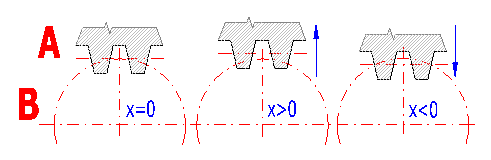
Durch eine Verzahnungskorrektur ist es möglich:
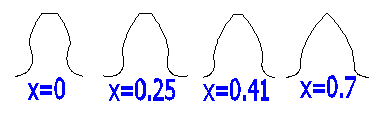
Beispiel eines Zahnprofils (z=10, a=20;
Bei einer Festlegung der Korrekturwerte sind die funktionellen Anforderungen auf die Verzahnung zuerst zu erfüllen, welche zu den Wichtigsten gehören
Zur Sicherung der funktionellen Anforderungen ist es dann möglich, weiter die
Höhenkorrekturen zwecks der Verbesserung eines oder mehreren wichtigen
Verzahnungsparameter zu optimieren. Von den oft verwendeten Optimierungsmethoden
ist es möglich, hier die Verzahnung auf den Ausgleich der Schlüpfe [5.14 - 5.17]
und auf Minimierung der Schlüpfe
Drehmoment
Mk [Nm] = Pw * 9550 / n .............. (SI units)
T [lb.in] =
Pw, PP ...
n ...........
Pw = Ft * v / 1000
Ft ... Tangentialkraft
v .... rychlost ozubeného hřebenu
Ft = Mk * 2000 / dw
dw ... Walzkreisdurchmesser
MK ...
Axialkraft
Fa = Ft * tan(b) / cos(awt)
Radialkraft
Fr = Ft *
Normalkraft
Fn = (Ft2 + Fa2 + Fr2)0.5
Biegemoment
Mo = Fa * (dw / 2000)
Die Verluste im Planetengetriebe können in Verluste durch Leerlauf und Verluste durch Belastung aufgeteilt werden. Die Verluste durch Leerlauf (durch Schmierung, unbelasteter Eingriff, Lager) sind sehr schwierig analytisch zu bestimmen und sind gewöhnlich wesentlich niedriger als die Verluste durch Belastung. Die Verluste bei Belastung entstehen bei der Leistungsübertragung und sind:
Es ist ungefähr möglich, den Verlustkoeffizienten nach der Formel
auszudrücken:
Geradverzahnung: zz = 0.5 • f •
p
• e • (1/z1 +- 1/z2)
Schrägverzahnung: zz
= 0.25 / cos(b) • f •
p • e •
(1/z1 +- 1/z2)
wobei:
z1, z2 – Zähnezahl
f – Reibungskoeffizient (0.04 - 0.08)
e – Eingriffskoeffizient
b – Schrägungswinkel am Zahngrundkreis
Zeichen (+) für Außenverzahnung, (-) für Innenverzahnung.
Die Verlustleistung kann aus der Beziehung bestimmt werden:
PVL = w • F • f • r
wobei:
w – Drehgeschwindigkeit
F – resultierende Lagerbelastung (Planetenträger, Fliehkraft)
f – Reibungskoeffizient (0.001 - 0.005)
r – mittlerer Lagerdurchmesser
Für die Berechnung der Verluste (des Wirkungsgrads) des Planetenradsatzes verwenden wir die Verluste im Vergleichsgetriebe (abgestellter Planetenträger), wobei:
wobei:
zz0/z1 – Verlustkoeffizient Sonnenrad – Planetenrad
zz1/z2 – Verlustkoeffizient Planetenrad – Hohlrad
z0,z2 – Zähnezahl des Sonnen- und Hohlrades
Für die Einzelfälle des Leistungsflusses gilt dann für die Berechnung der Verluste:
| z = ir • zr / (ir - 1) | Sonnenrad => Planetenrad (Planetenträger) |
| z = zr | Sonnenrad => Hohlrad |
| z = ir • zr / (ir - 1 + zr ) | Planetenrad (Planetenträger) => Sonnenrad |
| z = - zr / (ir - 1) | Planetenrad (Planetenträger) => Hohlrad |
| z = - zr / (ir - 1 - ir • zr) | Hohlrad => Planetenrad (Planetenträger) |
| z = zr | Hohlrad => Sonnenrad |
Die Planetenzahnradsätze bestehen aus einem System von Zahnrädern und einem Planetenträger. Die sogenannten Zentralzahnräder sind gleichachsig mit dem Planetenträger und der Zentralachse des Übersetzungmechanismus. Die Planetenräder sind dann Zahnräder gedreht gelagert am Planetenträger und sind im Eingriff mit den Zentralrädern oder untereinander. Die Planetenräder können eine oder mehrere Verzahnungen haben. Zwei- und mehrstufige Planetenräder haben mehrere Konstruktionsvarianten mit größeren Möglichkeiten, sind aber komplizierter und für die Fertigung teuerer.
Ein Beispiel eines einfachen Planetengetriebes mit einstufiger
Planetenradverzahnung ist unten angeführt. Dieser Grundtyp des Planetengetriebes
ist dann auch komplex in diesem Programm gelöst.
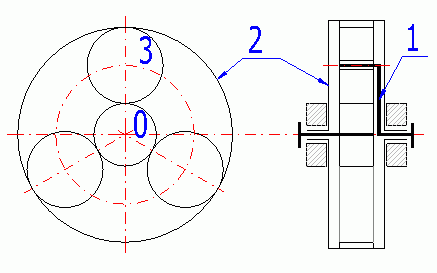
0 – Sonnenrad; 1 – Planetenträger; 2 – Hohlrad; 3 – Planetenrad.
Wenn bei einem einfachen Planetengetriebe alle drei Grundelemente (0, 1, 2) frei
sind, handelt es sich um ein Differentialgetriebe (2 Freiheitsgrade), welches es
ermöglicht, zwei Bewegungen in eine zusammenzusetzen / zu zersetzen. Dieses wird
zum Beispiel bei Bearbeitungsmaschinen (Zusammensetzen) oder beim
Differentialgetriebe für Fahrzeuge (Bewegungszersetzung) genutzt.
Wenn mit dem Rahmen eines der Grundelemente (0 oder 2) verbunden, entsteht ein Planetengetriebe (1 Freiheitsgrad) – ein Reduktor beim Antrieb in Richtung des Sonnenrads oder ein Multiplikator beim Antrieb in Richtung des Planetenträgers. Wenn mit dem Rahmen der Planetenträger verbunden, handelt es sich um ein normales Getriebe oder Vergleichsgetriebe.
Die Planetengetriebe können gegenseitig auf verschiedene Arten geschaltet werden. Das häufigste Verfahren ist die Schaltung nacheinander, wo das gesamte Übersetzungsverhältnis (Wirkungsgrad) durch ein Produkt der einzelnen Übersetzungsverhältnisse (Wirkungsgrade) gegeben ist. Bei den zusammengesetzten Getrieben wird sehr oft die Möglichkeit des Bremsens der einzelnen Elemente und damit die Schaltung der Getriebestufen genutzt.
• Platzeinsparung durch gleichachsige Anordnung der Antriebs- und
Abtriebswelle
• Niedrigeres Gewicht gegenüber dem normalen Getriebe
• Hoher Wirkungsgrad auch bei großen zu übertragenden Leistungen
• Niedrige radiale Belastung der Lager der Zentralelemente
• Kompakte Bauweise
• Kompliziertere Bauweise, höhere Anforderungen an die Genauigkeit der
Fertigung und Montage
• Höhere Herstellungskosten
• Einige begrenzende Bedingungen (Montierbarkeit)
In Bezug auf die angeführten Vorteile erfolgt der Einsatz von Planetengetrieben immer häufiger in einer ganzen Reihe von Bereichen (zum Beispiel Getriebe von Kraftfahrzeugen, Baumaschinen, Hebevorrichtungen, Schiffsgetriebe, Turbinenreduktoren etc.) Häufig ist auch die Verbindung eines Planetengetriebes mit einem Hydraulik- oder Reibungsgetriebe.
In den angeführten Formeln werden folgende Indexe verwendet.
Für:
- Sonnenrad – 0
- für Planetenrad – 1
- für Hohlrad – 2
Unter Berücksichtigung der Möglichkeit von Montage und Funktion des Planetenradsatzes ist es nicht möglich, willkürlich die Geometrie der Zahnräder zu wählen. Für eine korrekte Funktion sind etliche Bedingungen zu verfolgen und einzuhalten.
Die Planetenräder der Planetenzahnradsätze greifen in die Sonnenräder bzw. in andere Planetenräder ein. Im Fall dieser Berechnung kommt es zu einem gemeinsamen Eingriff des Planetenrads mit den Sonnenrädern (Planet, Hohlrad). Da das Planetenrad eine gemeinsame Achse mit dem Hohlrad hat, muss der Achsabstand zwischen den beiden Planetenrädern und den beiden Sonnenrädern gleich sein.
Für allgemein korrigierte Räder gilt also, dass
aw (0,1) = aw (1,2)
wo
wo
Für die einfachen Planetenräder und für eine gleichmäßige Verteilung ist die
folgende Bedingung zu erfüllen:
g = (abs (z0) + abs (z2))/P
Wobei:
g – muss eine willkürliche Ganzzahl sein
P – Anzahl Planetenräder
z – Zähnezahl
Diese Bedingung stellt ein Mindestspiel zwischen den Planetenrädern vmin (1 -
2 mm, 0,05 in) sicher.
Maximale Anzahl von Planetenrädern P = int(asin((da1+vmin)/(aw • 2)))
Es handelt sich um eine standardmäßige Verzahnungsberechnung, bei der in eine Zahnstange ein verzahntes Ritzel eingreift. Sowohl für das Ritzel, als auch für die Zahnstange kann das Profil des Herstellungswerkzeuges definiert werden.
In der Berechnung kann die Anzahl der Zähne vom Ritzel, der Eingriff- und Zahnneigungswinkel gewählt werden. Da es in diesem Fall keinen Sinn hat, die Zahnstange zu korrigieren, kann lediglich eine Korrektion des Ritzels gewählt werden (Achsabstand, Verbesserung der Eingriffsbedingungen, Verbesserung der Festigkeitsparameter).
In der Berechnung kann die Tangentialkraft eingegeben werden, was eigentlich eine Kraft ist, mit der die Zahnstange auf das Ritzel wirkt, und die Bewegungsgeschwindigkeit der Zahnstange (Umfangsgeschwindigkeit des Ritzels). Aus diesen beiden Werten werden anschließend die übertragene Leistung und das Ritzeldrehmoment berechnet. Da die Zahnstange für eine Vielzahl von unterschiedlichen Konstruktionslösungen angewendet werden kann, ist diese nachzuberechnen (abzuschätzen) und die Übersetzungsanforderungen auf diese zwei Werte umzurechnen.
Da es keine Normen für die Festigkeitsberechnung des Ritzels im Eingriff mit einer Zahnstange gibt, wird für die Festigkeitsberechnung die Norm ISO6336(ANSI/AGMA2001-D04) angewendet. Die Zahnstange ist hier durch ein Zahnrad mit einer hohen Anzahl an Zähnen (1000 Zähne) ersetzt.
Zur Festlegung der kritischen Drehzahl bei der Anwendung der Zahnstange gibt es keine genaue Methodik. Für eine grobe Schätzung kann eine Berechnung von zwei Zahnrädern angewendet werden (Ersatz der Zahnstange durch ein Zahnrad).
Für eine leichte Zahnstange, die mit keiner Konstruktion verbunden ist, benutzen Sie den Faktor sR/h=1, für eine mit einer Konstruktion verbundene Zahnstange den Faktor 20.
Für die Bestimmung des Lebensdauerkoeffizienten (YNT, ZNT) muss die Anzahl der Zyklen bekannt sein. Geben Sie die Anzahl der Belastungszyklen für das Ritzel und für die Zahnstange ein.
In den folgenden Absätzen wird die Art der Belastungsfähigkeitsberechnung beschrieben. Für die Berechnung wird die Norm ISO6336:2006 angewendet. In der Beschreibung werden die angewendeten Schlüsselformeln zum Verständnis der Berechnung und Bedienung dieses Programms angeführt. Dieser Text ersetzt keinesfalls die vollständige Lautung der angewendeten Normen.
This part of ISO 6336 presents the basic principles of, an introduction to, and the general influence factors for, the calculation of the load capacity of spur and helical gears.
Ft = 2000 * T1,2 / d1,2 = 19098 * 1000 * P / (d1,2
* n1,2) = 1000 * P / v
w1,2 = 2000 * v / d1,2
= n1,2 / 9549
Ft ... (nominal) transverse tangential load at reference cylinder per mesh
T1,2 ... nominal torque at the pinion (wheel)
d1,2 ... reference diameter of pinion (wheel)
P ... transmitted power
n1,2 ... rotation speed of pinion (wheel)
v ... tangential velocity (without subscript, at the reference circle
=tangential velocity at pitch circle)
w1,2 ... angular velocity of
pinion (wheel)
The application factor, KA, is used to modify the value of Ft to take into account loads additional to nominal loads, which are imposed, on the gears from external sources. The empirical guidance values in table B.1 ISO 6336-6 can be used (for industry gears and high speed gears).
(The internal dynamic factor KV makes allowance for the effects of gear tooth accuracy grade as related to speed and load.
There are three calculation methods (B2006), (C2006) a (C1996).)
Die Methode B eignet sich für alle Typen von Stirnzahnrädern. Sie ist relativ kompliziert und bei einer ungeeigneten Auswahl des Materials und des Genauigkeitsgrades im Hinblick auf die Belastung können die KV-Werte unrealistisch sein. Methode C kann mit gewissen Einschränkungen angewendet werden. Daher ist es möglich, in der Berechnung die Obergrenze von KV einzustellen (voreingestellt 5.0). Bei deren Überschreitung empfiehlt es sich, das gewählte Material und den Genauigkeitsgrad im Hinblick auf die Verzahnungsbelastung zu überprüfen.
Internal dynamic factor KV(B)
N = n1 / nE1
For N < NS (Subcritical range)
NS = 0.5 + 0.35 * ( Ft * KA / b )0.5
...... [ Ft * KA / b < 100 ]
NS = 0.85 ...... [ Ft * KA / b >= 100 ]
KV(B) = ( N * K ) + 1
K = ( CV1 * BP ) + ( CV2 * Bf ) + (
CV3 * BK )
BP = c' * fpb eff / ( Ft
* KA / b )
Bf = c' * fta
eff / ( Ft * KA / b )
BK = abs (1 + c' * Ca / ( Ft
* KA / b ))
For Ns < N < 1.15 (Main
resonance range)
KV(B) = ( CV1 * BP ) + ( CV2
* Bf ) + ( CV4 * BK )
+ 1
For N >= 1.5 (Supercritical range)
KV(B) = ( CV5 * BP ) + ( CV6
* Bf ) + CV7
For 1.15 < N < 1.5 (Intermediate range)
KV(B) = KV(N=1.5) + (
KV(N=1.15) - KV(N=1.5)) / 0.35 * (1.5 - N)
Coeficients
|
|
1.0 < eg <=2.0 | eg > 2.0 |
| CV1 | 0.32 | 0.32 |
| CV2 | 0.34 | 0.57 / (eg - 0.3) |
| CV3 | 0.23 | 0.096 / (eg - 1.56) |
| CV4 | 0.90 | (0.57 - 0.05 * eg ) / (eg - 1.44) |
| CV5 | 0.47 | 0.47 |
| CV6 | 0.47 | 0.12 / (eg - 1.74) |
| CV7 | 1.0 < eg <=1.5 | 0.75 |
| CV7 | 1.5 < eg <=2.5 | 0.125 * sin(p * (eg - 1.74)) + 0.875 |
| CV7 | eg > 2.5 | 1.0 |
| Cay1,2 | 1 / 18 * (sHlim1,2 / 97 - 18.45)2 + 1.5 | |
| Cay | 0.5 * (Cay1 + Cay2) | |
| Ca | Ca = Cay | |
Internal dynamic factor KV(C)
Method C supplies average values which can be used for industrial transmissions and gear systems with similar requirements in the following fields of application:
Method C can also generally be used, with restrictions for the following fields of application:
Method (C2006) is different from (C1996) by adding the
coefficient K3.
Example for input values KA * Ft / b = 100; v = 3 m / s; Q = 7 and straight
teeth.
1996.gif)
2006.gif)
KV(C..1996)
KVa,b = 1 + (K1 / ( Ft * KA
/ b ) + K2) * v * z1 / 100 * (u2 / (1 + u2))0.5
... [ eb
= 0; eb
>= 1.0]
KV(C..2006)
KVa,b = 1 + (K1 / ( Ft * KA
/ b ) + K2) * v * z1 / 100 * K3 * (u2 / (1 + u2))0.5
... [ eb
= 0; eb
>= 1.0]
KV = KVa - ea* ( KVa - KVb ) ... [0 < eb < 1.0]
Coeficients
| K1 (Accuracy grades as speclfled in ISO1328-1) | K2 | ||||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | All | |
| Spur gears eb = 0 | 2.1 | 3.9 | 7.5 | 14.9 | 26.8 | 39.1 | 52.8 | 76.6 | 102.6 | 146.3 | 0.0193 |
| Helical gears eb >=1.0 | 1.9 | 3.5 | 6.7 | 13.3 | 23.9 | 34.8 | 47.0 | 68.2 | 91.4 | 130.3 | 0.0087 |
| SRC = v * z1 / 100 * (u2 / (1 + u2))0.5 | |||||||||||
| K3 = 2.0 ...... [SRC <= 0.2] | |||||||||||
| K3 = -0.357 * SRC + 2.071 ...... [SRC > 0.2] | |||||||||||
nE1 = 30000 / ( p * z1 ) * ( cga / mred )0.5
mred = m*1 * m*2 / ( m*1
+ m*2 )
m*1,2 = J*1,2 / (rb 1,2)2
[kg/mm]
J*1,2 = J1,2 / b1,2
cga = c'
* (0.75 * ea
+ 0.25)
c' = c'th * CM * CR * CB * CE
* CFK * cos(b)
c'th = 1 / (0.04723 + 0.15551/zn1 + 0.25791/zn2
- 0.00635*x1 - 0.11654*x1/zn1 - 0.00193*x2
- 0.24188*x2/zn2 + 0.00529*x12 +
0.00182*x22)
c'th = 1 / (0.04723 + 0.15551/zn1 - 0.00635*x1 - 0.11654*x1/zn1 - 0.00193*x2 + 0.00529*x12 +
0.00182*x22) ... for internal gearing
CM = 0.8
CR = 1 + ln(bs / b) / (5 * e(sR/(5 * mn)))
...... [0.2 < bs < 1.2 ]
CB = 0.5 * (CB1 + CB2); CB1,2 = (1 +
0.5 * (1.2 - hf1,2 / mn)) * (1 - 0.02*(20 -
aPn))
CE = (( 2 * E1 * E2 ) / ( E1 + E2
)) / 206
CFK = (( Ft * KA / b ) / 100 )0.25......
[ CFK<= 1.0 ]
zn1,2 = z1,2 / cos(b)3
Main resonance of gear with idler gears, inner gears and planet gears are calculated by different process. Details in ISO6336-1.
This coefficient takes into account the effect of the non-uniform distribution of load over the gear face. Uneven load distribution is caused by an elastic deformation of gears and housing, manufacturing deviations and thermal distortion. Methods, principles and assumptions are given in standard ISO6336-1. Because the determination of the coefficient is dependent on a number of factors and primarily on the specific dimensions and design of the gearbox, is for the design purposes selected the coeficient KHb from graphs based on practical experiences. The calculation is in paragraph [18].
Detail description is in ISO6336-1. Here is just a selection of formulas, information and comments that are related to the calculation KHb.
a) KHb = (2 * Fby * cgb
/ (Fm / b))0.5 ...... [ Fby
* cgb / (2 * Fm / b) >= 1.0;
KHb >= 2.0 ]
b) KHb = 1 + Fby * cgb
/ (2 * Fm / b) ...... [ Fby
* cgb / (2 * Fm / b) < 1.0;
KHb > 1.0 ]
Fm = Ft * KA * KV
Fby = Fbx * yb
cgb = 0.85 * cga
b ...... gear width
yb ... Running-in allowance from graph
1) Fbx = Choosing your own values
2) Fbx = 1.33 * B1 * fsh
+ B2 * fma ....... [ Fbx >= Fbxmin
]
3) Fbx = abs( 1.33 * B1 * fsh - fHb6)
...... [ Fbx >= Fbxmin
]
4) Fbx = 1.33 * B1 * fsh +
fsh2 + fma + fca +fbe
B1, B2 coeficients, table 8, ISO6336-1
fHb6 ... Helix slope deviation for Q=6,
ISO1328-1
fsh ... Component of equivalent misatignment. It is possible to use several
methods (calculation, measurement, estimation). Used formula:
fsh = Fm / b * 0.023 * (abs(B' + K'
* l * s / d12 * (d1 / dsh)4 - 0.3) + 0.3) * (b / d1)2
... [s / l < 0.3]
fsh = Fm / b * 0.046 * (abs(B' + K'
* l * s / d12 * (d1 / dsh)4 - 0.3) + 0.3) * (bB / d1)2
... [s / l < 0.3]
fsh2, fca, fbe ... can be determined by ISO6336-1
B' = 1.0 ... for both spur and single helical gears, for the total transmitted
power
K' = arrangement coefficient, gray indicates the less deformed helix of a double
helical gear
| K' | with stiffening | without stiffening |
| A | 0.48 | 0.80 |
| B | -0.48 | -0.80 |
| C | 1.33 | 1.33 |
| D | -0.36 | -0.60 |
| E | -0.60 | -1.00 |
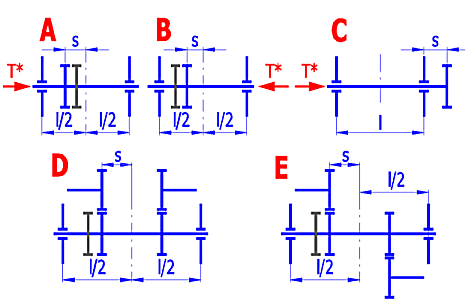
l, s .... picture
dsh ... shaft diameter
fma ... mesh misalignment. It is possible to use several
methods (calculation, measurement, estimation). Used formula:
fma = (fHb12 + fHb22)0.5
.
a) KHb = Acoef * (2 * Fby * cgb
/ (Fm / b))0.5 ...... [ Fby
* cgb / (2 * Fm / b) >= 1.0;
KHb > 1.0 ]
b) KHb = Acoef * (1 + Fby * cgb
/ (2 * Fm / b)) ...... [ Fby
* cgb / (2 * Fm / b) < 1.0;
KHb > 1.0 ]
Fm = Ft * KA * KV
Fby = Fb * 0.8
..... [Fb from ISO 1328]
cgb = 0.85 * cga
b ...... gear width
Acoef = 1.0 ..... Double-sided symmetrically supported gearing
Acoef = (0.9 + 0.15 * (b1 / d1)2 + 0.23 * (b1 / d1)3)
..... Double-sided non-symmetrically supported gearing
Acoef = (0.9 + (b1 / d1)2) ..... Overhung gearing
For the preliminary design is possible to use values from these graphs.
X Axis: Ratio gear width to gear diameter
Y Axis: Factor KHb ..... [min. value = 1.05]
Accuracy grade 7
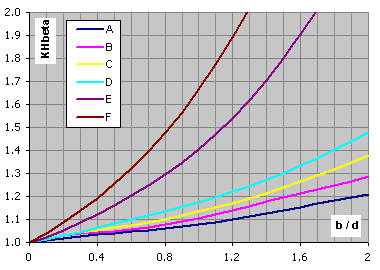
Not-hardended gears, VHV<370, design type A-F ... calculation paragraph [2.0]
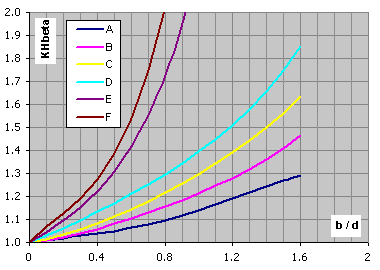
Hardended gears, VHV<=370, design type A-F ... calculation paragraph [2.0]
KFb = ( KHb )NF
NF = (b / h)2 / (1 + b / h + (b / h)2) ...... [když
b / h < 3; pak b / h = 3] ([if b / h < 3; then b / h = 3])
The smaller of the values b1/h1, b2/h2 is to be used as b/h.
KHa = KFa =
eg
/ 2 * (0.9 + 0.4 * (cga
* (fpb - ya)) / (FtH
/ b)) ...... [eg
<= 2.0]
KHa = KFa =
0.9 + 0.4 * (2.0 * (eg
- 1.0) / eg)0.5
* cga * (fpb
- ya) / (FtH /
b) ...... [eg
> 2.0]
Pro: (For:)
KHa >
eg
/ (
ea
* Ze2)
...... KHa =
eg
/ (
ea
* Ze2)
KHa <
1.0 ...... KHa
= 1.0
Pro: (For:)
KFa >
eg
/ (0.25 *
ea
+ 0.75) ...... KFa =
eg
/ (0.25 *
ea
+ 0.75)
KFa <
1.0 ...... KFa
= 1.0
fpb = fpt (ISO1328-1)
ya ... Material: St, St(cast),
V, V(cast), GGG(perl.), GGG(bai.), GTS(perl.)
ya = fpb * 160 /
σHlim [ v < 5m/s ]
ya
<= 12800 / σHlim [ 5m/s < v <= 10m/s ]
ya
<= 6400 / σHlim [ v > 10m/s ]
ya ... Material: GG,
GGG(ferr.)
ya = fpb 0.275
[ v < 5m/s ]
ya
<= 22 [ 5m/s < v <= 10m/s ]
ya
<= 11 [ v > 10m/s ]
ya ... Material:
Eh, IF, NT(nitr.), NV(nitr.), NV(nitrocar.)
ya = fpb 0.075
[ ya
<= 3 ]
This part of ISO 6336 specifies the fundamental formulae for use in the determination of the surface load capacity of cylindrical gears with involute external or internal teeth. It includes formulae for all influences on surface durability for which quantitative assessments can be made. lt applies primarily to oil-lubricated transmission, but can also be used to obtain approximate values for (slow-running) grease-lubricated transmissions, as long as sufficient lubricant is present in the mesh at all times.
Safety factor for surface durability (against pitting), SH
Calculate SH separately for pinion and wheel:
SH1,2 = σHG1,2 / σH1,2 > SHmin
σH1 = ZB * σH0 * (KA * KV * KHb
* KHa)0.5
σH2 = ZD * σH0 * (KA * KV * KHb
* KHa)0.5
The
nominal contact stress at the pitch point σH0
σH0 = ZH * ZE * Ze
* Zb * (Ft / (b * d1)
* (u + 1) / u)0.5
σHP = ZL * ZV * ZR * ZW * ZX * ZNT * σHlim / SHmin = σHG / SHmin
The pitting stress limit σHG
σHG = σHP * SHmin
ZH = (2 * cos(bb) * cos(awt) / (cos(at)2 * sin(awt)))0.5
M1 = tan(awt) /
((((da1 / db1)2 - 1.0)0.5 - 2 *
p / z1) * (((da2 / db2)2
- 1.0)0.5 - (ea
- 1.0) * 2 * p / z2))0.5
M2 = tan(awt) /
((((da2 / db2)2 - 1.0)0.5 - 2 *
p / z2) * (((da1 / db1)2
- 1.0)0.5 - (ea
- 1.0) * 2 * p / z1))0.5
Spur gears with, ea
> 1.0
ZB = 1.0 ... [ M1<= 1.0 ]
ZB = M1 .... [ M1 > 1.0 ]
ZD = 1.0 ... [ M2<= 1.0 ]
ZD = M2 .... [ M2 > 1.0 ]
Helical gears with, eb
>= 1.0
ZB = ZD = 1.0
Helical gears with, eb
< 1.0
ZB = M1 - eb
* (M1 - 1.0) ... [ ZB >= 0 ]
ZD = M2 - eb
* (M2 - 1.0) ... [ ZD >= 0 ]
(For internal gears, ZD shall be taken as equal to 1.0)
ZE = (p * ((1.0 - n12) / E1 + (1 - n22) / E2))-0.5
n1,2 ... Poisson's ratio
E1,2 ... modulus of elasticity
Ze = ((4.0 -
ea)
/ 3 * (1.0 - eb)
+ eb
/ ea)0.5
... [ 0 <= eb
< 1.0 ]
Ze = (1.0 /
ea)0.5
... [ eb
>= 1.0 ]
Zb = 1 / (cos(b))0.5
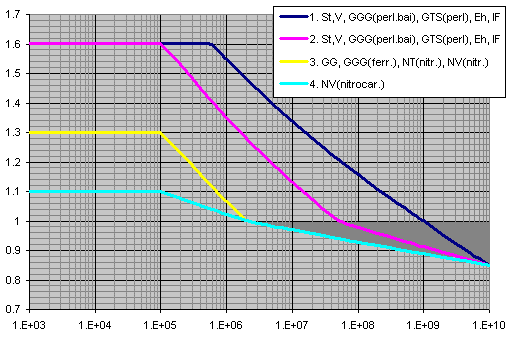
X axis ... number of cycles
Y axis ... ZNT
ZL = CZL + 4 * (1.0 - CZL) / (1.2 + 80 /
n50)2 = CZL
+ 4 * (1.0 - CZL) / (1.2 + 134 / n40)2
CZL = 0.83 ... [ σHlim < 850 ]
CZL = σHlim / 4375 + 0.6357 ... [
850 <= σHlim <= 1200 ]
CZL = 0.91 ... [ 1200 < σHlim ]
n50 (
n40) ... Nominal viscosity in 50°C (40°C) [mm2/s]
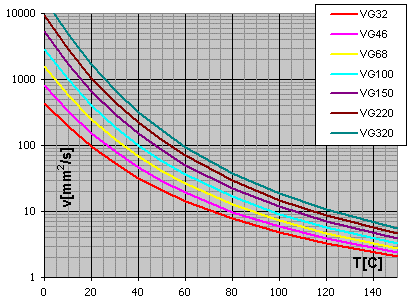
Diagram viscosity / temperature for viscosity index VI = 50
ZV = CZV + 2 * (1.0 - CZV) / (0.8 + 32 / v)0.5
CZV = CZL + 0.02
ZR = (3 / Rz10)CZR
CZR = 0.15 ... [ σHlim < 850 ]
CZR = 0.32 - 0.0002 * σHlim ... [
850 <= σHlim <= 1200 ]
CZR = 0.08 ... [ 1200 < σHlim ]
Rz10 = Rz * (10 / rred)(1/3)
rred = (r1
* r2) / (r1
+ r2)
r1,2 = 0.5 * db1,2 *
tan(awt)
The work hardening factor, ZW takes account of the increase in the surface durability due to meshing a steel wheel (structural steel, through-hardened steel) with a hardened or substantially harder pinion with smooth tooth flanks.
Pinion Surface-hardened, Gear through-hardened
ZW = 1.2 * (3 / RzH)0.15 ... [ HB < 130 ]
ZW = (1.2 - (HB - 130) / 1700) * (3 / RzH)0.15
... [ 130 <= HB <= 470 ]
ZW = (3 / RzH)0.15 ... [ HB > 470 ]
ZW for static stress
ZW = 1.05 ... [ HB < 130 ]
ZW = 1.05 - (HB - 130) / 680 ... [ 130 <= HB <= 470 ]
ZW = 1.0 ... [ HB > 470 ]
RzH = Rz1 * (10 / rred)0.33
* (Rz1 / Rz2)0.66) / (
n40 * v / 1500)0.33)
... [ 3 <= RzH <=16 ]
Through-hardened pinion and gear
ZW = 1.0 ... [ HB1/HB2 < 1.2 ]
ZW = 1.0 + A * (u - 1.0) ... [ 1.2 <= HB1/HB2
<= 1.7 ]
ZW = 1.0 + 0.00698 * (u - 1.0) ... [ 1.7 < HB1/HB2
]
A = 0.00898 * HB1/HB2 - 0.00829
ZW for static stress
ZW = 1.0
This part of ISO 6336 specifies the fundamental formulae for use in tooth bending stress calculations for involute external or internal spur and helical gears with a rim thickness sR > 0.5 * ht for external gears and sR >1.75 * mn for internal gears.
Safety factor for bending strength (safety against tooth breakage), SF
Calculate SF separately for pinion and wheel:
SF1,2 = σFG1,2 / σF1,2 >= SFmin
σF = σF0 * KA * KV * KFb * KFa
The nominal tooth root
stress σF0
σF0 = Ft / (b * mn) * YF * YS
* Yb * YB * YDT
σFP = σFlim * YST * YNT * YdrelT * YRrelT * YX / SFmin = σFG / SFmin
Tooth root stress limit σFG
σFG = σFP * SFmin
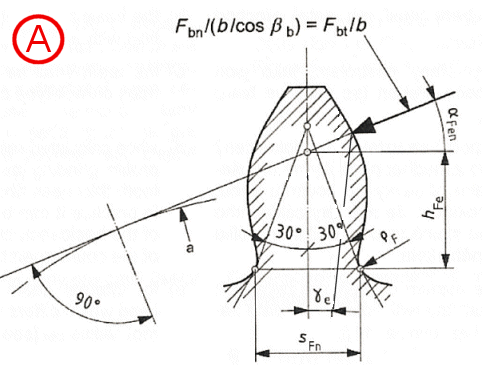
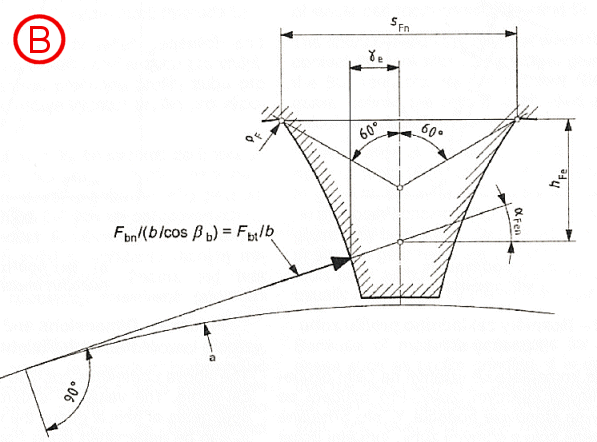
YF = (6 * hFe / mn * cos(aFen)) / ((sFn / mn)2 * cos(an))
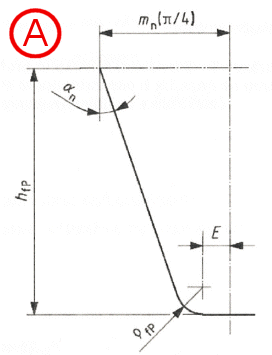
Dimensions and basic rack profile of the teeth (finished profile)
A...without undercut
B...with undercut
auxiliary values
E = p / 4 * mn - hfP
* tan(an) + spr / cos(an)
- (1 - sin(an) * rfP
/ cos(an)
spr = pr - q
spr = 0 when gears are not undercut
rfPv = rfP
... external gears
rfPv = rfP
+ mn * (x0 + hfp/mn - rfP/mn)1.95
/ (3.156 * 1.036z0) ... internal gears
x0 ... the pinion-cutter shift coefficient
z0 ... the number of teeth of the pinion cutter
G = rfPv / mn - hfP
/ mn + x
H = 2 / zn * (p / 2 - E / mn)
- T
T = p / 3 ... external gears
T = p / 6 ... internal gears
q = 2 * G / zn * tan(q)
- H
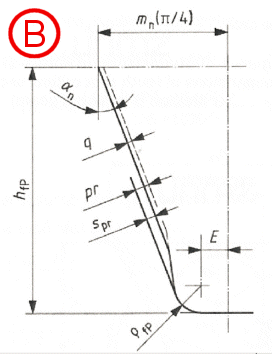
Determination of normal chordal dimensions of tooth root critical section for
Method B
A...external gears
B...internal gears
Tooth root normal chord sFn
sFn / mn = zn * sin(p/3 - q) + (3)0.5 * (G / cos(q)
- rfPv / mn) ...
external gears
sFn / mn = zn * sin(p/6 - q)
+ (G / cos(q)
- rfPv / mn) ...
internal gears
Radius of root fillet rF
rF / mn
= rfPv / mn + 2 * G2
/ (cos(q) * (zn * cos(q)2
- 2 * G))
Bending moment arm hFe
hFe / mn = 0.5 * ((cos(ge)
- sin(ge) * tan(aFen))
* den / mn - zn * cos(p/3
- q) - G / cos(q)
+ rfPv / mn)) ...
external gears
hFe / mn = 0.5 * ((cos(ge) - sin(ge) * tan(aFen)) * den / mn - zn * cos(p/6 - q) - (3)0.5 * (G / cos(q) - rfPv / mn))) ... internal gears
Parameters of virtual gears
bb = arcsin(sin(b)
* cos(an))
zn = z / (cos(bb))3
ean=
ea / (cos(bb))2
dn = mn * zn
pbn = p * mn *
cos(an)
dbn = dn * cos(an)
dan = dn + da - d
den = 2 * z / abs(z) * ((((dan / 2)2 - (dbn
/ 2)2)0.5 - p * d *
cos(b) * cos(an)
* (ean - 1) / abs(z))2
+ (dbn / 2)2)0.5
*The number of teeth z is positive for external gears and negative for internal gears
aen = arccos(dbn /
den)
ge = (0.5 * p
+ tan(an) * x) / zn +
inv(an) - inv(aen)
aFen = aen
- ge
The stress correction factor YS is used to convert the nominal
tooth root stress to local tooth root stress.
YS = (1.2 + 0.13 * L) * qs(1 / (1.21 + 2.3 / L))
L = SFn / hFe
qs = SFn / (2 * rF)
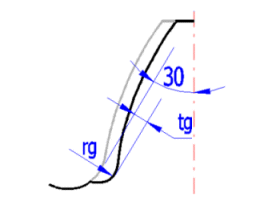
YSg = 1.3 * YS / (1.3 - 0.6 * (tg / rg)0.5) ... [ (tg / rg)0.5 < 2.0 ]
Yb = 1 - eb * b / 120 ... [if b > 30; b = 30]
external gears
YB = 1.0 ... [sR / ht >= 1.2]
YB = 1.15 * ln(8.324 * mn / sR) ... [0.5 < sR
/ ht < 1.2]
internal gears
YB = 1.0 ... [sR / mn >= 3.5]
YB = 1.6 * ln(2.242 * ht / sR) ... [1.75 < sR
/ mn < 3.5]
YDT = 1.0 ... [ean
<= 2.05] or [accuracy grade > 4]
YDT = -0.666 * ean
+ 2.366 ... [2.05 < ean
<= 2.5] and [accuracy grade <= 4]
YDT = 0.7 ... [ean
> 2.5] and [accuracy grade <= 4]
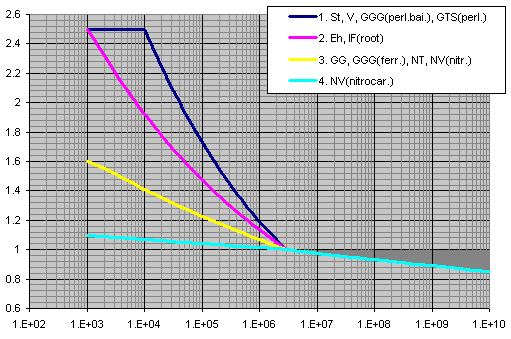
X axis ... number of cycles
Y axis ... YNT
YdrelT = Yd
/ YdT = (1 + (r'
* c*)0.5)
/ (1 + (r'
* cT*)0.5)
c* =
cP*
* (1 + 2 * qs)
cP*
= 1 / 5 = 0.2
cT*
= cP*
* (1 + 2 * 2.5)
Material: GG [σB=150MPa], GG, GGG(ferr.)[σB=300MPa]
r'
= 0.31
Material: NT, NV
r'
= 0.1005
Material: St, V, GTS, GGG(perl.), GGG(bai.)
r'
=
MAX(MIN(13100 / Rp0.2(2.1) - (MAX(600;Rp0.2)-600)(0.35)
/ 1600;0.32);0.0014)
Material: Eh, IF(root)
r'
= 0.003
Material: St, V, GGG(perl.), GGG(bai.)
YdrelT = (1 + 0.82 * (YS
- 1) * (300 / σ0.2)(1/4)) / (1 + 0.82 * (300 / σ0.2)(1/4))
Material: Eh, IF, IF(root)
YdrelT = 0.44 * YS +
0.12
Material: NT, NV
YdrelT = 0.20 * YS +
0.60
Material: GTS
YdrelT = 0.075 * YS +
0.85
Material: GG, GGG(ferr.)
YdrelT = 1.0
Rz < 1 mm
Material: V, GGG(perl.), GGG(bai.), Eh, IF
YRrelT = 1.12
Material: St
YRrelT = 1.07
Material: GG, GGG(ferr.), NT, NV
YRrelT = 1.025
1mm < Rz < 40 mm
Material: V, GGG(perl.), GGG(bai.), Eh, IF
YRrelT = 1.674 - 0.529 * (Rz + 1)0.1
Material: St
YRrelT = 5.306 - 4.203 * (Rz + 1)0.01
Material: GG, GGG(ferr.), NT, NV
YRrelT = 4.299 - 3.256 * (Rz + 1)0.0058
YRrelT = 1.0
YX = 1.0 ... All materials for static stress
YX ... Material: St, St(cast),
V, V(cast), GGG(perl.), GGG(bai.), GTS(perl.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.03 - 0.006 * mn
... [ 5 < mn < 30 ]
YX = 0.85 ... [ mn >=
30 ]
YX ... Material:
Eh, IF(root), NT, NV, NT(nitr.), NV(nitr.), NV(nitrocar.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.05 - 0.01 * mn
... [ 5 < mn < 25 ]
YX = 0.80 ... [ mn >=
25 ]
YX ... Material: GG,
GGG(ferr.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.075 - 0.015 * mn
... [ 5 < mn < 25 ]
YX = 0.70 ... [ mn >=
25 ]
This part of ISO 6336 describes contact and tooth-root stresses, and gives numerical values for both limit stress numbers. It specifies requirements for material quality and heat treatment and comments on their influences on both limit stress numbers.
The allowable stress numbers, σH lim, and the nominal stress numbers, σF lim, can be calculated by the following equation:
a) σHlim = A * x + B
b) σFlim = A * x + B
where x is the surface hardness HBW or HV and A, B are constants
The three material quality grades ML, MQ and ME, stand in relationship to
- ML stands for modest demands on the material quality and on the material heat
treatment process during gear manufacture.
- MQ stands for requirements that can be met by experienced manufacturers at
moderate cost.
- ME represents requirements that must be realized when a high degree of
operating reliability is required
In this calculation, except σHlim and σFlim, are proposed other material
parameters that are necessary for calculating the gearing. The values of Ro, E
and Poisson constant are commonly available. For the proposal of the tensile strength Rm
and yield strength Rp0.2 was used information from the ISO 1265 and specialized
literature. Parameters for the time-strength curves were obtained from ISO6336-2
and 3. These curves can be seen in a small graph in the calculation.
All calculated values are design and based on empirical experience. The exact
values for a concrete material you can obtain from your manufacturer or from
material tests.
Values HB for HB<=450 steel ball, HB>450 carbide ball
Values HB used recalculation HB=HV-HV/20
Values HRC used recalculation HRC=(100*HV-14500)/(HV+223)
Kv = (C / (C + vt))−B
C = 50 + 56 * (1.0 − B) ... [ 6 ≤ Av ≤ 12 ]
B = 0.25 * (Av − 5.0)0.667
vt max = [C + (14 − Av)]2
The empirical guidance values from table B.1 ISO 6336-6 are used.
Cp = (1 / p
* (((1 - mP2)
/ EP) + ((1 - mG2) /
EG)))0.5 ... [lb/in2]0.5
mP and mG
is Poisson’s ratio for pinion and gear, respectively; EP and EG is
modulus of elasticity for pinion and gear [lb/in2].
Cf = 1.0
Through hardened gears
CH = 1.0 + A * (mG - 1.0)
A = 0.00898 *(HBP / HBG) - 0.00829
HBP is pinion Brinell hardness number [HB]; HBG is gear Brinell hardness
number,[HB].
This equation is valid for the range 1.2 ≤ HBP / HBG ≤ 1.7 For HBP / HBG < 1.2,
A = 0.0 HBP / HBG > 1.7, A = 0.00698
Surface hardened/through hardened values
CH = 1.0 + B * (450 - HBG)
B = 0.00075 * (2.71828)-0.0112 * (fp)
fp is surface finish of pinion, microinches, Ra
if fp>64 ... CH = 1.0
Km = f (Cmf, Cmt)
Km = Cmf
Cmf = 1.0 + Cmc * (Cpf *
Cpm + Cma * Ce)
Cmc is 1.0 for gear with unmodified leads; Cmc is 0.8 for gear with leads
properly modified by crowning or lead correction.
Cpf = F / (10 * d) − 0.025 ... [F<=1.0]
Cpf = F / (10 * d) − 0.0375 + 0.0125 * F ... [1.0<F<=17.0]
Cpf = F / (10 * d) − 0.1109 + 0.0207 * F − 0.000228 * F2 ...
[17.0<F<=40.0]
Cpm = 1.0 ... [S1 / S < 0.175]
Cpm = 1.1 ... [S1 / S >= 0.175]
Cma = A + B * F + C * F2
| A | B | C | |
| 1…Open gearing | 0.247 | 0.0167 | -0.0000765 |
| 2…Commercial enclosed gearboxes | 0.127 | 0.0158 | -0.0001093 |
| 3…Precision enclosed gearbox | 0.0675 | 0.0128 | -0.0000926 |
| 4…Extra precision enclosed gearbox | 0.038 | 0.0102 | -0.0000822 |
Ce = 0.8 ... [gearing is adjusted at assembly; gearing is
improved by lapping]
Ce = 1.0 ... [for all other conditions]
KR = 1.50 [Fewer than one failure in 10 000]
KR = 1.25 [Fewer than one failure in 1000]
KR = 1.00 [Fewer than one failure in 100]
KR = 0.85 [Fewer than one failure in 10]
KR = 0.70 [Fewer than one failure in 2]
KB = 1.6 * ln(2.242 / mB) ... [for mB<1.2]
KB = 1.0 ... [for mB>=1.2]
mB = tR / ht
tR is gear rimthickness below the tooth root
[in]; ht is gear
tooth whole depth [in]
The contact stress number formula for gear teeth is:
sc = Cp (Wt * Ko * Kv * Ks * Km * Cf / (d * F * I))0.5
Allowable contact stress number
The relation of calculated contact stress number to allowable contact stress
number is:
sc ≤ (sac * ZN * CH) / (KT * SH * KR)
Pitting resistance power rating
The pitting resistance power rating is:
Pac = (p * np * F / 396 000) * I / (Ko * Kv * Ks * Km * Cf) * ((d * sac * ZN CH) / (Cp * SH * KT * KR))2
SH = sac / sc * (ZN * CH) / (KT * KR)
The fundamental formula for bending stress number in a gear tooth is:
st = Wt * Ko * Kv * Ks * (Pd * Km * KB / (F * J))
Allowable bending stress number
The relation of calculated bending stress number to allowable bending stress
number is:
st ≤ (sat * YN) / (SF * KT * KR)
Bending strength power rating
The bending strength power rating is:
Pat = (p * np * F / 396 000) * (F * J) / (Ko * Kv * Pd * Ks * Km * KB) * (sat * YN) / (SF * KT * KR)
SF = sat / st * YN / (KT * KR)
Transmitted tangential load
Wt = 33000 * P / vt = 2 * T / d = 396000 * P / (p
* np * d)
P is transmitted power [hp];
T is transmitted pinion torque [lb*in];
vt is pitch line velocity at operating pitch diameter,
[ft/min]
vt = p
* np * d / 12
This part of ANSI / AGMA 2001-D04 describes the allowable stress numbers sac and sat, for pitting resistance and bending strength.
Allowable stress numbers in this standard are determined or estimated from
laboratory tests and accumulated field experiences. They
are based on unity overload factor, 10 million stress cycles, unidirectional
loading and 99 percent reliability. For service life other than 10
million cycles, the allowable stress numbers are adjusted by the use of stress
cycle factors YN and ZN
The allowable stress numbers sac and sat can be calculated by the following equation:
a) sac = A * x + B
b) sat = A * x + B
where x is the surface hardness HBW and A, B are constants
These requirements are specified in this standard and are divided in three material quality grades 1,2 an 3.
In this calculation, except sac and sat, are proposed other material parameters that are necessary for calculating the gearing. The values of p, E and Poisson constant are commonly available. For the proposal of the tensile strength Rm and yield strength Rp0.2 was used information from the ISO 1265 and specialized literature. All calculated values are design and based on empirical experience. The exact values for a concrete material you can obtain from your manufacturer or from material tests.
Values HB for HB<=450 steel ball, HB>450 carbide ball
Values HB used recalculation HB=HV-HV/20
Values HRC used recalculation HRC=(100*HV-14500)/(HV+223)
^