V této části jsou shrnuty některé teoretické informace a vzorce, které se týkají návrhu geometrie, výpočtu silových a výkonostních parametrů a pevnostní kontroly evolventního ozubení. Tyto podklady byly použity v následujících výpočtech.
Některé nejdůležitější vzorce pro výpočet geometrie ozubení jsou uvedené níže. Ve vzorcích jsou použity indexy 1 a 2 pro pastorek a kolo (Planetové převody: centrální kolo / satelit, respektive satelit / korunové kolo). V případě vnitřního ozubení (Planetové převody: korunové kolo) je použita záporná hodnota počtu zubů vnitřního kola a tím i záporná hodnota osové vzdálenosti a průměrů.
V případě planetového převodu jsou na sobě navzájem jednotlivá kola závislá a je nutné řešit převod jako celek včetně příslušných omezujících podmínek (viz. dále).
Parametry základního profilu: mn (modul, DP pro palcový výpočet),
a
(úhel záběru), ha*, c*, rf* (parametry obráběcího nástroje)
Parametry pastorku a kola: z1, z2 (počet zubů pastorku a kola), x1, x2
(jednotkové posunutí),
b
(úhel sklonu zubů), b (šířka ozubení)
Volba součinitelů posunutí x1 a x2 je základní úloha při návrhu ozubeného soukolí, především u kol s přímými zuby. Posunutí má vliv nejen na geometrické, ale i na kinematické a pevnostní charakteristiky. Při návrhu korekcí je nutné nejprve splnit funkční požadavky a potom je možné korekce optimalizovat tak, aby zlepšovaly některé další parametry soukolí.
Přibližováním nebo oddalováním výrobního nástroje od středu kola se mění tvar a tím i vlastnosti evolventního ozubení. Vytváří se tak korigované ozubení. Na obrázku je:
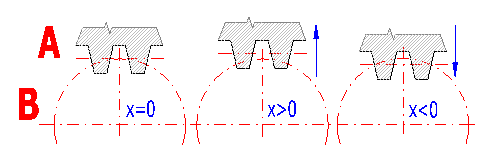
Korigováním ozubení je možné:
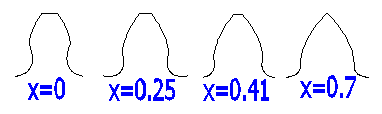
Příklad profilu zubu (z=10, a=20;
Při stanovení hodnot korekcí je třeba nejprve splnit funkční požadavky na ozubení, kde mezi nejdůležitější patří
Při zajištění funkčních požadavků je potom možné dále optimalizovat korekce
ke zlepšení jednoho či více
Kroutící moment, Torsional moment (Pinion) Krouticí moment (pastorek)
Drehmoment (Ritzel) Moment de torsion
Mk [Nm] = Pw * 9550 / n .............. (SI units)
T [lb.in] =
Pw, PP ... výkon [kW, HP] Transferred power Přenášený výkon Übertragene Leistung
Puissance transférée
n ........... otáčky [/min], Speed (Pinion) Otáčky pastorku Ritzel Drehzahl
Vitesse
Výkon (ozubený hřeben)Spur gear - Rack [mm / ISO] Čelní ozubení - ozubený
hřeben [mm / ISO] Stirnverzahnung - Zahnstange [mm / ISO] Denture droite - la
Crémaillère [mm / ISO]
Pw = Ft * v / 1000
Ft ... obvodová síla, Tangential force Obvodová síla Tangentialkraft Force
tangentielle
v .... rychlost ozubeného hřebenu
Obvodová síla,
Ft = Mk * 2000 / dw
dw ... Průměr valivé kružnice, Operating pitch diameter Průměr valivé kružnice
Walzkreisdurchmesser Diamètre opérationel du pas
MK ... Krouticí moment
Axiální síla, Axial force Axiální síla Axialkraft Force axiale
Fa = Ft * tan(b) / cos(awt)
Radiální síla, Radial force Radiální síla Radialkraft Force radiale
Fr = Ft *
Normálná síla, Normal force Normálná síla Normalkraft Force normale
Fn = (Ft2 + Fa2 + Fr2)0.5
Ohybový moment, Bending moment Ohybový moment Biegemoment Moment de flexion
Mo = Fa * (dw / 2000)
Ztráty v planetovém převodu je možné rozdělit na ztráty volnoběhem a ztráty zatížením. Ztráty volnoběhem (mazáním, nezatížený záběr, ložiska) je obtížné určit analyticky a jsou běžně podstatně nižší než ztráty zatížením. Ztráty při zatížení vznikají při přenosu výkonu a jsou to:
Přímé ozubení: zz = 0.5 • f • p • e • (1/z1 +- 1/z2)
Šikmé ozubení: zz = 0.25 / cos(b) • f • p • e • (1/z1 +- 1/z2)
kde:
z1, z2 - počty zubů
f - součinitel tření (0.04 - 0.08)
e
- součinitel záběru
b - úhel sklonu zubů
Znaménko (+) pro vnější ozubení, (-) pro vnitřní.
Ztrátový výkon je možné určit ze vztahu:
PVL = w • F • f • r
kde:
w
- úhlová
rychlost
F - výsledné zatížení ložiska (unašeč, odstředivá síla)
f - součinitel tření (0.001 - 0.005)
r - střední poloměr ložiska
Pro výpočet ztrát (účinnosti) planetového soukolí použijeme ztráty v porovnávacím převodu (zastavený unašeč) kde:
zr = zz0 / z1 + zz1 / z2; ir = z2 / z0
kde:
zz0/z1 -
součinitel ztrát centrální kolo-satelit
zz1/z2 -
součinitel ztrát satelit-korunové kolo
z0,z2 - počet zubů centrálního a korunového kola
Pro jednotlivé případy toku výkonu potom platí pro výpočet ztrát:
| z = ir • zr / (ir - 1) | Centrální kolo => Satelit (unašeč) |
| z = zr | Centrální kolo => Korunové kolo |
| z = ir • zr / (ir - 1 + zr ) | Satelit (unašeč) => Centrální kolo |
| z = - zr / (ir - 1) | Satelit (unašeč) => Korunové kolo |
| z = - zr / (ir - 1 - ir • zr) | Korunové kolo => Satelit (unašeč) |
| z = zr | Korunové kolo => Centrální kolo |
Planetová soukolí jsou tvořena soustavou ozubených kol a unašečem. Takzvaná centrální ozubená kola jsou souosá s unašečem a centrální osou převodového mechanismu. Satelity jsou pak ozubená kola otočně uložená na unašeči a jsou v záběru s centrálními koly či mezi sebou. Satelity mohou mít jedno dvě či více ozubení. Dvou a vícestupňové satelity mají více konstrukčních variant s většími možnostmi, jsou však složitější a výrobně dražší.
Příklad jednoduchého planetového převodu s jednostupňovým ozubením satelitu je uveden níže. Tento základní typ planetového převodu je pak také komplexně řešen v tomto programu.
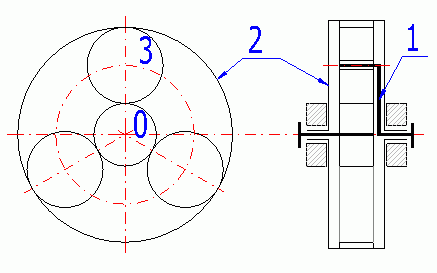
0 - Centrální kolo; 1 - Unašeč; 2 - Korunové kolo; 3 - Satelit.
Jestliže jsou u jednoduchého planetového převodu volné všechny tři základní členy (0, 1, 2), jedná se o diferenciál (2 stupně volnosti), který umožňuje skládat / rozkládat dva pohyby do jednoho. Toho se využívá například u obráběcích strojů (skládání) nebo u automobilového diferenciálu (rozkládání pohybu).
Jeli spojen s rámem jeden ze základních členů (0 nebo 2) vzniká planetový převod (1 stupeň volnosti) a to reduktor při pohonu směrem od centrálního kola nebo multiplikátor při pohonu směrem od unašeče. Pokud je s rámem spojen unašeč jedná se o normální převodovku neboli porovnávací převod.
Planetové převody je možné vzájemně řadit nejrůznějšími způsoby. Nejčastější způsob je řazení za sebou, kdy je celkový převodový poměr(účinnost) dán součinem dílčích převodových poměrů (účinností). U skládaných převodů je často používaná možnost brždění jednotlivých členů a tím řazení převodových stupňů.
Vzhledem k uvedeným výhodám je použití planetových převodů čím dále tím častější v celé řadě oblastí (například převodovky motorových vozidel, stavební stroje, zdihací zařízení, lodní převodovky, reduktory turbín atp.) Časté je také spojení planetového převodu s hydraulickým či třecím převodem.
V uvedených vzorcích jsou použity následující indexy.
Pro:
- centrální kolo - 0
- pro satelit - 1
- pro korunové kolo - 2
S ohledem na možnost montáže a funkci planetového soukolí není možné volit geometrii ozubených kol libovolně. Pro správnou funkci je nutné sledovat a dodržet několik následujících podmínek.
Satelity planetových soukolí zabírají s centrálními koly popřípadě s jinými satelity. V případě tohoto výpočtu dochází ke společnému záběru satelitu s centrálními koly (planeta, korunové kolo). Protože planetové kolo má společnou osu s korunovým kolem, musí být osová vzdálenost mezi satelitem a oběma centrálními koly shodná.
Pro obecně korigovaná kola tak platí že:
aw (0,1) = aw (1,2)
kde aw (0,1)=mt • (z0+z1)/2
• COS(alfat)/COS(alfawt(0,1))
kde aw (1,2)=mt • (z1+z2)/2
• COS(alfat)/COS(alfawt(1,2))
Pro jednoduché satelity a pro rovnoměrné rozložení satelitů je nutné splnit následující podmínku:
g = (abs (z0) + abs (z2))/P
Kde:
g - musí být libovolné celé číslo
P - počet satelitů
z - počet zubů
Tato podmínka zajišťuje minimální vůli mezi satelity vmin (1-2 mm, 0.05 in).
Maximální počet satelitů P = int(asin((da1+vmin)/(aw • 2)))
Jedná se o standardní výpočet ozubení, kdy do ozubeného hřebene zabírá ozubený pastorek. Jak pro pastorek, tak pro ozubený hřeben je možné definovat profil výrobního nástroje.
Ve výpočtu je možné zvolit počet zubů pastorku, uhel záběru a úhel sklonu zubů. Jelikož nemá v tomto případě smysl korigovat ozubený hřeben, je možné volit pouze korekci pastorku (osová vzdálenost, zlepšení záběrových podmínek, zlepšení pevnostních parametrů).
Ve výpočtu je možné zadat tečnou sílu, zož je vlastně síla, kterou působí ozubený hřeben na pastorek a rychlost pohybu ozubeného hřebene (obvodová ryclost pastorku). Z těchto dvou hodnot je pak dopočítán přenášený výkon a kroutící moment pastorku. Jelikož je možné ozubený hřeben použít pro řadu odlišných konstrukčních řešení, je pak třeba dopočítat (odhadnout) a převést požadavky převodu na tyto dvě hodnoty.
Jelikož neexistují žádné normy pro pevnostní výpočet pastorku v záběru s ozubeným hřebenem, je pro pevnostní výpočet použita norma ISO6336 (ANSI/AGMA 2001-D04). Ozubený hřeben je zde nahrazen ozubeným kolem s vysokým počtem zubů (1000 zubů).
Pro stanovení kritických otáček při použití ozubeného hřebenu není žádná přesná metodika. Pro hrubý odhad je možné použít výpočet dvou ozubených kol (náhrada ozubeného hřebene kolem).
Pro lehký hřeben, který není spojen s konstrukcí použijte koeficient sR/h=1, pro hřeben spojený s s konstrukcí pak 20.
Pro stanovení součinitele životnosti (YNT, ZNT) je nutné znát počet cyklů. Zadejte počet namáhacích cyklů pro pastorek a pro hřeben.
V následujících odstavcích bude popsán způsob výpočtu únosnosti. Pro výpočet je použita norma ISO 6336:2006 (ANSI/AGMA...). V popisu budou uvedeny použité klíčové vzorce spolu s poznámkami důležitými pro pochopení výpočtu a ovládání tohoto programu. Tento text v žádném případě nenahrazuje úplné znění použitých norem.
Tato část ISO 6336 uvádí základní principy, doporučené a obecné ovlivňující faktory pro výpočet únosnosti čelních kol s přímými a šikmými zuby.
Ft = 2000 * T1,2 / d1,2 = 19098 * 1000 * P / (d1,2
* n1,2) = 1000 * P / v
w1,2 = 2000 * v / d1,2
= n1,2 / 9549
Ft ... (jmenovité) tečné čelní zatížení na referenčním válci během záběru.
T1,2 ... jmenovitý točivý moment pro pastorek (kolo)
d1,2 ... referenční průrměr pastorku (kola)
P ... přendášný výkon
n1,2 ... frekvence otáčeni pastorku (kola)
v ... obvodová rychlost (bez indexu, na referenční kružnici = obvodová rychlost
na roztečné kružnici)
w1,2 ... úhlová rychlost pro
pastorek (kolo)
Aplikační faktor (Součinitel vnějších dynamických sil) KA se používá k úpravě hodnoty Ft kde bere v úvahu přídavná zatížení ke jmenovitému, které jsou způsobeny z externích zdrojů. Empirické směrné hodnoty, které je možné použít jsou v tabulce B.1 ISO 6336-6 (pro průmyslové a vysokorychlostní převody).
Vnitřní dynamický faktor (Součinitel vnitřních dynamických sil) KV bere v úvahu příspěvek efektu stupně přesnosti zubu v zárvislosti na rychlosti a zatížení.
K dispozici jsou tři výpočtové metody (B2006), (C2006) a (C1996).
Metoda B se hodí pro všechny typy čelních ozubených kol. Je poměrně komplikovaná a při nevhodné volbě materiálů vzhledem k zatížení jsou hodnoty KV mimo realitu. Metodu C je možné použít s určitými omezeními. Proto je ve výpočtu možné nastavit horní mez KV (přednastaveno 5.0). Při jejím překročení je vhodné zkontrolovat zvolený materiál vzhledem k zatížení ozubení.
Vnitřní dynamický faktor KV(B)
N = n1 / nE1
Pro N < NS (Podkritické pásmo)
NS = 0.5 + 0.35 * ( Ft * KA / b )0.5
...... [ Ft * KA / b < 100 ]
NS = 0.85 ...... [ Ft * KA / b >= 100 ]
KV(B) = ( N * K ) + 1
K = ( CV1 * BP ) + ( CV2 * Bf ) + (
CV3 * BK )
BP = c' * fpb eff / ( Ft
* KA / b )
Bf = c' * fta
eff / ( Ft * KA / b )
BK = abs (1 + c' * Ca / ( Ft
* KA / b ))
Pro Ns < N < 1.15 (Hlavní resonanční pásmo)
KV(B) = ( CV1 * BP ) + ( CV2
* Bf ) + ( CV4 * BK )
+ 1
Pro N >= 1.5 (Nadkritické pásmo)
KV(B) = ( CV5 * BP ) + ( CV6
* Bf ) + CV7
Pro 1.15 < N < 1.5 (Mezilehlé pásmo)
KV(B) = KV(N=1.5) + (
KV(N=1.15) - KV(N=1.5)) / 0.35 * (1.5 - N)
Koeficienty
|
|
1.0 < eg <=2.0 | eg > 2.0 |
| CV1 | 0.32 | 0.32 |
| CV2 | 0.34 | 0.57 / (eg - 0.3) |
| CV3 | 0.23 | 0.096 / (eg - 1.56) |
| CV4 | 0.90 | (0.57 - 0.05 * eg ) / (eg - 1.44) |
| CV5 | 0.47 | 0.47 |
| CV6 | 0.47 | 0.12 / (eg - 1.74) |
| CV7 | 1.0 < eg <=1.5 | 0.75 |
| CV7 | 1.5 < eg <=2.5 | 0.125 * sin(p * (eg - 1.74)) + 0.875 |
| CV7 | eg > 2.5 | 1.0 |
| Cay1,2 | 1 / 18 * (sHlim1,2 / 97 - 18.45)2 + 1.5 | |
| Cay | 0.5 * (Cay1 + Cay2) | |
| Ca | Ca = Cay | |
Vnitřní dynamický faktor KV(C)
Metoda C dává průměrné hodnoty, které je rožno použít pro průmyslové převody
a obdobné převodovky s podobnými požadavky v následujících oblastech použití:
Metoda C může být rovněž obecně použita s omezeními v následujících oblastech:
Metoda (C2006) se od (C1996) liší přidáním koeficientu K3 a pro vstupní hodnoty KA*Ft/b=100; v=3m/s; Q=7; přímé zuby vypadají hodoty následovně:
1996.gif)
2006.gif)
KV(C..1996)
KVa,b = 1 + (K1 / ( Ft * KA
/ b ) + K2) * v * z1 / 100 * (u2 / (1 + u2))0.5
... [ eb
= 0; eb
>= 1.0]
KV(C..2006)
KVa,b = 1 + (K1 / ( Ft * KA
/ b ) + K2) * v * z1 / 100 * K3 * (u2 / (1 + u2))0.5
... [ eb
= 0; eb
>= 1.0]
KV = KVa - ea* ( KVa - KVb ) ... [0 < eb < 1.0]
Koeficienty
| K1 (st. přesnosti dle ISO1328-1) | K2 | ||||||||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | All | |
| Přímé zuby eb = 0 | 2.1 | 3.9 | 7.5 | 14.9 | 26.8 | 39.1 | 52.8 | 76.6 | 102.6 | 146.3 | 0.0193 |
| Šikmé zuby eb >=1.0 | 1.9 | 3.5 | 6.7 | 13.3 | 23.9 | 34.8 | 47.0 | 68.2 | 91.4 | 130.3 | 0.0087 |
| SRC = v * z1 / 100 * (u2 / (1 + u2))0.5 | |||||||||||
| K3 = 2.0 ...... [SRC <= 0.2] | |||||||||||
| K3 = -0.357 * SRC + 2.071 ...... [SRC > 0.2] | |||||||||||
nE1 = 30000 / ( p * z1 ) * ( cga / mred )0.5
mred = m*1 * m*2 / ( m*1
+ m*2 )
m*1,2 = J*1,2 / (rb 1,2)2
[kg/mm]
J*1,2 = J1,2 / b1,2
cga = c'
* (0.75 * ea
+ 0.25)
c' = c'th * CM * CR * CB * CE
* CFK * cos(b)
c'th = 1 / (0.04723 + 0.15551/zn1 + 0.25791/zn2
- 0.00635*x1 - 0.11654*x1/zn1 - 0.00193*x2
- 0.24188*x2/zn2 + 0.00529*x12 +
0.00182*x22)
c'th = 1 / (0.04723 + 0.15551/zn1 - 0.00635*x1 - 0.11654*x1/zn1 - 0.00193*x2 + 0.00529*x12 +
0.00182*x22) ... pro vnitřní ozubení
CM = 0.8
CR = 1 + ln(bs / b) / (5 * e(sR/(5 * mn)))
...... [0.2 < bs < 1.2 ]
CB = 0.5 * (CB1 + CB2); CB1,2 = (1 +
0.5 * (1.2 - hf1,2 / mn)) * (1 - 0.02*(20 -
aPn))
CE = (( 2 * E1 * E2 ) / ( E1 + E2
)) / 206
CFK = (( Ft * KA / b ) / 100 )0.25......
[ CFK<= 1.0 ]
zn1,2 = z1,2 / cos(b)3
Kritické otáčky pro ozubení s vloženým kolem, ozubení vnitřní a planetové se stanovují odlišným způsobem. Podrobnosti v ISO6336-1.
Tento koeficient vyjadřuje vliv nerovnoměrnosti rozložení zatížení po šířce zubu. Tato nerovnoměrnost je způsobena elastickou deformací ozubených kol, uložení, výrobními úchylkami a tepelnými deformacemi. Metody, principy a předpoklady jsou uvedeny v normě ISO6336-1. Jelikož určení tohoto koeficientu je závislé na řadě faktorů a především na konkrétních rozměrech a konstrukci převodu, je pro účely návrhu volen koeficient KHb z grafů založených na praktických zkušenostech. Výpočet je uveden v odstavci [18].
Podrobný popis je v ISO6336-1. Zde je pouze výběr vzorců, informací a poznámek, které přímo souvisí se zde uvedeným výpočtem KHb.
a) KHb = (2 * Fby * cgb
/ (Fm / b))0.5 ...... [ Fby
* cgb / (2 * Fm / b) >= 1.0;
KHb >= 2.0 ]
b) KHb = 1 + Fby * cgb
/ (2 * Fm / b) ...... [ Fby
* cgb / (2 * Fm / b) < 1.0;
KHb > 1.0 ]
Fm = Ft * KA * KV
Fby = Fbx * yb
cgb = 0.85 * cga
b ...... šířka kola
yb ... přídavek na záběh z grafu
1) Fbx = Volba vlastní hodnoty
2) Fbx = 1.33 * B1 * fsh
+ B2 * fma ....... [ Fbx >= Fbxmin
]
3) Fbx = abs( 1.33 * B1 * fsh - fHb6)
...... [ Fbx >= Fbxmin
]
4) Fbx = 1.33 * B1 * fsh +
fsh2 + fma + fca +fbe
B1, B2 koeficienty, tabulka 8, ISO6336-1
fHb6 ... Úchylka sklonu zubu pro Q=6,
ISO1328-1
fsh ... Složka ekvivalentni nesouososti. Je možné stanovit několika způsoby
(výpočet, měření, odhad). Zde použit vzorec:
fsh = Fm / b * 0.023 * (abs(B' + K'
* l * s / d12 * (d1 / dsh)4 - 0.3) + 0.3) * (b / d1)2
... [s / l < 0.3]
fsh = Fm / b * 0.046 * (abs(B' + K'
* l * s / d12 * (d1 / dsh)4 - 0.3) + 0.3) * (bB / d1)2
... [s / l < 0.3]
fsh2, fca, fbe ... je možné stanovit dle ISO6336-1
B' = 1.0 ... pro obě čelní kola s přímými a šikmými zuby, pro celkový přenášený
výkon.
K' = koeficient rozložení, šedá označuje méně deformované ozubení v případě kola
s dvojitě šikmými zuby.
| K' | S vyztužením | Bez vyztužení |
| A | 0.48 | 0.80 |
| B | -0.48 | -0.80 |
| C | 1.33 | 1.33 |
| D | -0.36 | -0.60 |
| E | -0.60 | -1.00 |
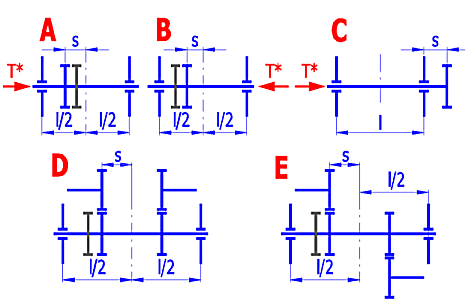
l, s .... viz. obrázek (picture)
dsh ... průměr hřídele (shaft diameter)
fma ... nesouosost záběru. Je možné stanovit několika způsoby (výpočet, měření,
odhad). zde použit vzorec:
fma = (fHb12 + fHb22)0.5
.
a) KHb = Acoef * (2 * Fby * cgb
/ (Fm / b))0.5 ...... [ Fby
* cgb / (2 * Fm / b) >= 1.0;
KHb > 1.0 ]
b) KHb = Acoef * (1 + Fby * cgb
/ (2 * Fm / b)) ...... [ Fby
* cgb / (2 * Fm / b) < 1.0;
KHb > 1.0 ]
Fm = Ft * KA * KV
Fby = Fb * 0.8
..... [Fb from ISO 1328]
cgb = 0.85 * cga
b ...... šířka kola
Acoef = 1.0 ..... Oboustraně symetricky uložené soukolí
Acoef = (0.9 + 0.15 * (b1 / d1)2 + 0.23 * (b1 / d1)3)
..... Oboustraně nesymetricky uložené soukolí
Acoef = (0.9 + (b1 / d1)2) ..... Letmo uložené soukolí
Pro účely předběžného návrhu je možné použít hodnot z následujících grafů.
Osa X: Poměr šířky kola k průměru kola .....
Osa Y: Součinitel KHb ..... [min. hodnota = 1.05]
Stupeň přesnosti 7
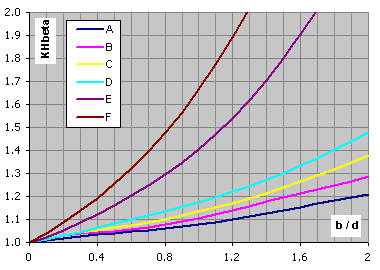
Netvrzená kola, VHV<370, konstrukce typu A-F ... výpočet odstavec [2.0]
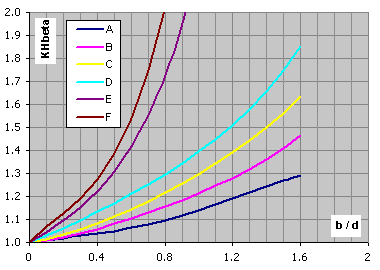
Tvrzená kola, VHV>=370, konstrukce typu A-F ... výpočet odstavec [2.0]
KFb = ( KHb )NF
NF = (b / h)2 / (1 + b / h + (b / h)2) ...... [když
b / h < 3; pak b / h = 3] ([if b / h < 3; then b / h = 3])
Menší z hodnot b1/h1, b2/h2 se
používá jako b/h.
KHa = KFa =
eg
/ 2 * (0.9 + 0.4 * (cga
* (fpb - ya)) / (FtH
/ b)) ...... [eg
<= 2.0]
KHa = KFa =
0.9 + 0.4 * (2.0 * (eg
- 1.0) / eg)0.5
* cga * (fpb
- ya) / (FtH /
b) ...... [eg
> 2.0]
Pro: (For:)
KHa >
eg
/ (
ea
* Ze2)
...... KHa =
eg
/ (
ea
* Ze2)
KHa <
1.0 ...... KHa
= 1.0
Pro: (For:)
KFa >
eg
/ (0.25 *
ea
+ 0.75) ...... KFa =
eg
/ (0.25 *
ea
+ 0.75)
KFa <
1.0 ...... KFa
= 1.0
fpb = fpt (ISO1328-1)
ya ... Material: St, St(cast),
V, V(cast), GGG(perl.), GGG(bai.), GTS(perl.)
ya = fpb * 160 /
σHlim [ v < 5m/s ]
ya
<= 12800 / σHlim [ 5m/s < v <= 10m/s ]
ya
<= 6400 / σHlim [ v > 10m/s ]
ya ... Material: GG,
GGG(ferr.)
ya = fpb 0.275
[ v < 5m/s ]
ya
<= 22 [ 5m/s < v <= 10m/s ]
ya
<= 11 [ v > 10m/s ]
ya ... Material:
Eh, IF, NT(nitr.), NV(nitr.), NV(nitrocar.)
ya = fpb 0.075
[ ya
<= 3 ]
Tato část ISO 6336 uvádí základní vzorce pro stanovení únosnosti povrchu čelnich kol s vnějším nebo vnitřním evolventním ozubenim. Obsahuje vzorce pro všechny vlivy na trvanlivost povrchu, kterou lze kvantitativně vyhodnotit. Platí v první řadě pro převodovky mazané olejem, ale lze je též použít pro získání přibližných hodnot pro (pomaluběžné) převodovky mazané tukem, dokud je záběr zubů trvale dostatečně mazán.
Faktor bezpečnosti pro trvanlivost povrchu (proti pittingu), SH
SH se stanovuje zvlášť pro pastorek i kolo:
SH1,2 = σHG1,2 / σH1,2 > SHmin
σH1 = ZB * σH0 * (KA * KV * KHb
* KHa)0.5
σH2 = ZD * σH0 * (KA * KV * KHb
* KHa)0.5
Jmenovité napětí v dotyku v roztečném bodě σH0
σH0 = ZH * ZE * Ze
* Zb * (Ft / (b * d1)
* (u + 1) / u)0.5
σHP = ZL * ZV * ZR * ZW * ZX * ZNT * σHlim / SHmin = σHG / SHmin
Mezní napětí při pittingu σHG
σHG = σHP * SHmin
ZH = (2 * cos(bb) * cos(awt) / (cos(at)2 * sin(awt)))0.5
M1 = tan(awt) /
((((da1 / db1)2 - 1.0)0.5 - 2 *
p / z1) * (((da2 / db2)2
- 1.0)0.5 - (ea
- 1.0) * 2 * p / z2))0.5
M2 = tan(awt) /
((((da2 / db2)2 - 1.0)0.5 - 2 *
p / z2) * (((da1 / db1)2
- 1.0)0.5 - (ea
- 1.0) * 2 * p / z1))0.5
Čelní soukolí s přímými zuby, ea
> 1.0
ZB = 1.0 ... [ M1<= 1.0 ]
ZB = M1 .... [ M1 > 1.0 ]
ZD = 1.0 ... [ M2<= 1.0 ]
ZD = M2 .... [ M2 > 1.0 ]
Čelní soukolí se šikmými zuby, eb
>= 1.0
ZB = ZD = 1.0
Čelní soukolí se šikmými zuby, eb
< 1.0
ZB = M1 - eb
* (M1 - 1.0) ... [ ZB >= 0 ]
ZD = M2 - eb
* (M2 - 1.0) ... [ ZD >= 0 ]
(Pro vnitřní ozubení musi byl ZD vždy rovno 1.0)
ZE = (p * ((1.0 - n12) / E1 + (1 - n22) / E2))-0.5
n1,2 ... Poissonovo číslo
E1,2 ... modul pružnosti
Ze = ((4.0 -
ea)
/ 3 * (1.0 - eb)
+ eb
/ ea)0.5
... [ 0 <= eb
< 1.0 ]
Ze = (1.0 /
ea)0.5
... [ eb
>= 1.0 ]
Zb = 1 / (cos(b))0.5
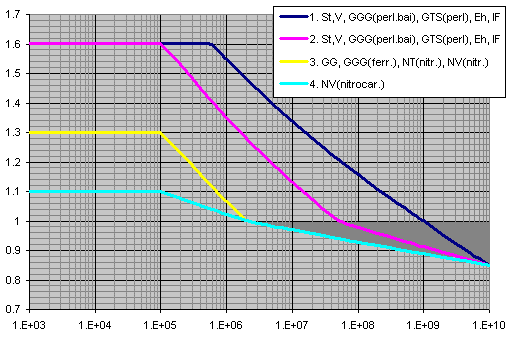
osa X ... počet cyklů
osa Y ... ZNT
ZL = CZL + 4 * (1.0 - CZL) / (1.2 + 80 /
n50)2 = CZL
+ 4 * (1.0 - CZL) / (1.2 + 134 / n40)2
CZL = 0.83 ... [ σHlim < 850 ]
CZL = σHlim / 4375 + 0.6357 ... [
850 <= σHlim <= 1200 ]
CZL = 0.91 ... [ 1200 < σHlim ]
n50 (
n40) ... jmenovitá viskozita při
50°C (40°C) [mm2/s]
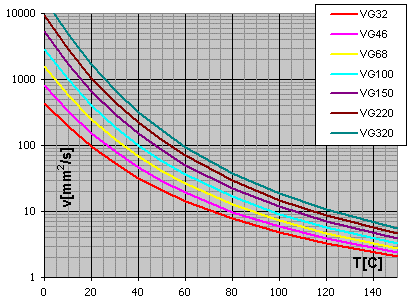
Graf viskozity na teplotě pro "viscosity index" VI = 50
ZV = CZV + 2 * (1.0 - CZV) / (0.8 + 32 / v)0.5
CZV = CZL + 0.02
ZR = (3 / Rz10)CZR
CZR = 0.15 ... [ σHlim < 850 ]
CZR = 0.32 - 0.0002 * σHlim ... [
850 <= σHlim <= 1200 ]
CZR = 0.08 ... [ 1200 < σHlim ]
Rz10 = Rz * (10 / rred)(1/3)
rred = (r1
* r2) / (r1
+ r2)
r1,2 = 0.5 * db1,2 *
tan(awt)
Faktor provozni tvrdosti ZW bere v úvahu nárůst trvanlivosti povrchu jako důsledek ocelového kola v záběru (konstrukční ocel, ocel k zušlechtění) s tvrdým nebo podstatně tvrdším pastorkem s hladkými boky zubu.
Povrchově kalený pastorek, kalené kolo
ZW = 1.2 * (3 / RzH)0.15 ... [ HB < 130 ]
ZW = (1.2 - (HB - 130) / 1700) * (3 / RzH)0.15
... [ 130 <= HB <= 470 ]
ZW = (3 / RzH)0.15 ... [ HB > 470 ]
ZW pro statické napětí
ZW = 1.05 ... [ HB < 130 ]
ZW = 1.05 - (HB - 130) / 680 ... [ 130 <= HB <= 470 ]
ZW = 1.0 ... [ HB > 470 ]
RzH = Rz1 * (10 / rred)0.33
* (Rz1 / Rz2)0.66) / (
n40 * v / 1500)0.33)
... [ 3 <= RzH <=16 ]
Kalený pastorek a kolo
ZW = 1.0 ... [ HB1/HB2 < 1.2 ]
ZW = 1.0 + A * (u - 1.0) ... [ 1.2 <= HB1/HB2
<= 1.7 ]
ZW = 1.0 + 0.00698 * (u - 1.0) ... [ 1.7 < HB1/HB2
]
A = 0.00898 * HB1/HB2 - 0.00829
ZW pro statické napětí
ZW = 1.0
Tato část ISO 6336 specifikuje základní vztahy používané pro výpočet napětí v ohybu zubů evolventních čelních ozubených kol s vnitřním nebo vnějším ozubením s přímými a šikmými zuby s tloušťkou věnce sR > 0.5 * ht pro vnější ozubení a sR >1.75 * mn pro vnitřní ozubeni.
Faktor bezpečnosti pro pevnost v ohybu (bezpečnost proti ulomení zubu), SF
SF se stanovuje zvlášť pro pastorek i kolo:
SF1,2 = σFG1,2 / σF1,2 >= SFmin
σF = σF0 * KA * KV * KFb * KFa
Jmenovité napětí v patě zubu σF0
σF0 = Ft / (b * mn) * YF * YS
* Yb * YB * YDT
σFP = σFlim * YST * YNT * YdrelT * YRrelT * YX / SFmin = σFG / SFmin
Mezní napětí v patě zubu σFG
σFG = σFP * SFmin
YF = (6 * hFe / mn * cos(aFen)) / ((sFn / mn)2 * cos(an))
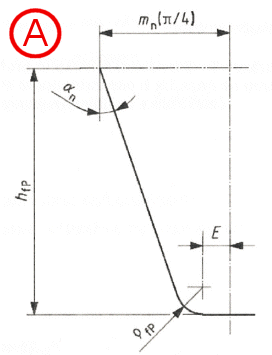
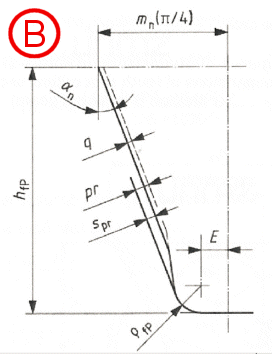
Rozměry základního profilu zubu (konečný stav)
A...bez podříznutí
B...s podříznutím
pomocné hodnoty
E = p / 4 * mn - hfP
* tan(an) + spr / cos(an)
- (1 - sin(an) * rfP
/ cos(an)
spr = pr - q
spr = 0 pokud není ozubení podříznuto
rfPv = rfP
... vnější ozubení
rfPv = rfP
+ mn * (x0 + hfp/mn - rfP/mn)1.95
/ (3.156 * 1.036z0) ... vnitřní ozubení
x0 ... posunutí nástroje
z0 ... počet zubů nástroje
G = rfPv / mn - hfP
/ mn + x
H = 2 / zn * (p / 2 - E / mn)
- T
T = p / 3 ... vnější ozubení
T = p / 6 ... vnitřní ozubení
q = 2 * G / zn * tan(q)
- H
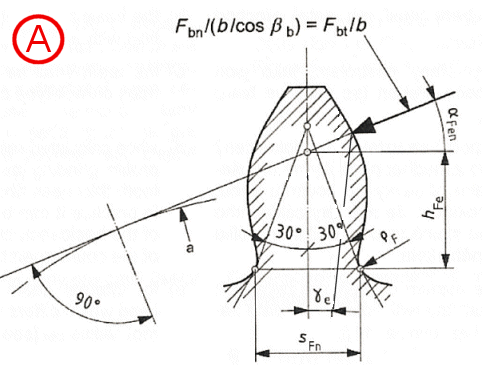
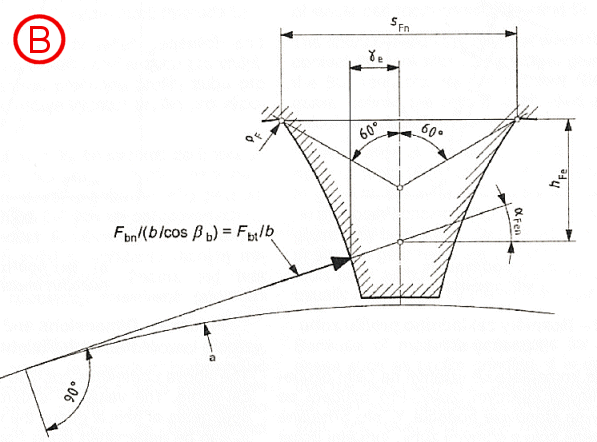
Stanovení kritického průřezu paty zubu na normále k ose zubu podle metody B
A...čelni kola s vnějším ozubením
B...čelni kola s vnitřním ozubením
Patní sečna sFn
sFn / mn = zn * sin(p/3 - q) + (3)0.5 * (G / cos(q)
- rfPv / mn) ...
vnější ozubení
sFn / mn = zn * sin(p/6 - q)
+ (G / cos(q)
- rfPv / mn) ...
vnitřní ozubení
Poloměr patního přechodu rF
rF / mn
= rfPv / mn + 2 * G2
/ (cos(q) * (zn * cos(q)2
- 2 * G))
Rameno ohybového momentu hFe
hFe / mn = 0.5 * ((cos(ge)
- sin(ge) * tan(aFen))
* den / mn - zn * cos(p/3
- q) - G / cos(q)
+ rfPv / mn)) ...
vnější ozubení
hFe / mn = 0.5 * ((cos(ge) - sin(ge) * tan(aFen)) * den / mn - zn * cos(p/6 - q) - (3)0.5 * (G / cos(q) - rfPv / mn))) ... vnitřní ozubení
Parametry virtuálních ozubených kol
bb = arcsin(sin(b)
* cos(an))
zn = z / (cos(bb))3
ean=
ea / (cos(bb))2
dn = mn * zn
pbn = p * mn *
cos(an)
dbn = dn * cos(an)
dan = dn + da - d
den = 2 * z / abs(z) * ((((dan / 2)2 - (dbn
/ 2)2)0.5 - p * d *
cos(b) * cos(an)
* (ean - 1) / abs(z))2
+ (dbn / 2)2)0.5
*Počet zubů z je kladný pro čelní kola s vnějším ozubením a záporný pro čelní kola s vnitřním ozubením
aen = arccos(dbn /
den)
ge = (0.5 * p
+ tan(an) * x) / zn +
inv(an) - inv(aen)
aFen = aen
- ge
Faktor koncentrace napeti YS je použit k přepočtu jmenovitého
napětí v ohybu na mistní napětí v patě zubu.
YS = (1.2 + 0.13 * L) * qs(1 / (1.21 + 2.3 / L))
L = SFn / hFe
qs = SFn / (2 * rF)
YSg = 1.3 * YS / (1.3 - 0.6 * (tg / rg)0.5) ... [ (tg / rg)0.5 < 2.0 ]
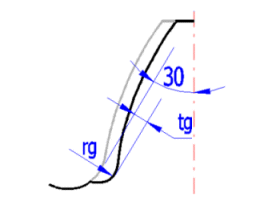
Yb = 1 - eb * b / 120 ... [if b > 30; b = 30]
vnější ozubení
YB = 1.0 ... [sR / ht >= 1.2]
YB = 1.15 * ln(8.324 * mn / sR) ... [0.5 < sR
/ ht < 1.2]
vnitřní ozubení
YB = 1.0 ... [sR / mn >= 3.5]
YB = 1.6 * ln(2.242 * ht / sR) ... [1.75 < sR
/ mn < 3.5]
YDT = 1.0 ... [ean
<= 2.05] or [stupeň přesnosti > 4]
YDT = -0.666 * ean
+ 2.366 ... [2.05 < ean
<= 2.5] and [stupeň přesnosti <= 4]
YDT = 0.7 ... [ean
> 2.5] and [stupeň přesnosti <= 4]
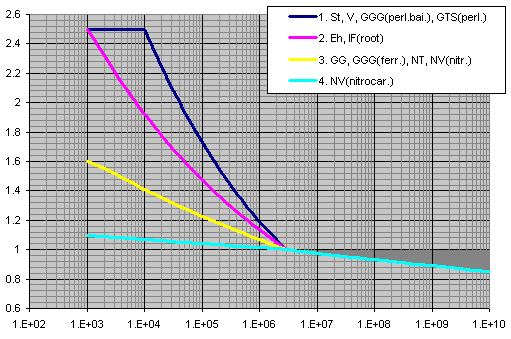
osa X ... počet cyklů
osa Y ... YNT
YdrelT = Yd
/ YdT = (1 + (r'
* c*)0.5)
/ (1 + (r'
* cT*)0.5)
c* =
cP*
* (1 + 2 * qs)
cP*
= 1 / 5 = 0.2
cT*
= cP*
* (1 + 2 * 2.5)
Material: GG [σB=150MPa], GG, GGG(ferr.)[σB=300MPa]
r'
= 0.31
Material: NT, NV
r'
= 0.1005
Material: St, V, GTS, GGG(perl.), GGG(bai.)
r'
=
MAX(MIN(13100 / Rp0.2(2.1) - (MAX(600;Rp0.2)-600)(0.35)
/ 1600;0.32);0.0014)
Material: Eh, IF(root)
r'
= 0.003
Material: St, V, GGG(perl.), GGG(bai.)
YdrelT = (1 + 0.82 * (YS
- 1) * (300 / σ0.2)(1/4)) / (1 + 0.82 * (300 / σ0.2)(1/4))
Material: Eh, IF, IF(root)
YdrelT = 0.44 * YS +
0.12
Material: NT, NV
YdrelT = 0.20 * YS +
0.60
Material: GTS
YdrelT = 0.075 * YS +
0.85
Material: GG, GGG(ferr.)
YdrelT = 1.0
Rz < 1 mm
Material: V, GGG(perl.), GGG(bai.), Eh, IF
YRrelT = 1.12
Material: St
YRrelT = 1.07
Material: GG, GGG(ferr.), NT, NV
YRrelT = 1.025
1mm < Rz < 40 mm
Material: V, GGG(perl.), GGG(bai.), Eh, IF
YRrelT = 1.674 - 0.529 * (Rz + 1)0.1
Material: St
YRrelT = 5.306 - 4.203 * (Rz + 1)0.01
Material: GG, GGG(ferr.), NT, NV
YRrelT = 4.299 - 3.256 * (Rz + 1)0.0058
YRrelT = 1.0
YX = 1.0 ... Pro statické napětí všech materiálů
YX ... Material: St, St(cast),
V, V(cast), GGG(perl.), GGG(bai.), GTS(perl.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.03 - 0.006 * mn
... [ 5 < mn < 30 ]
YX = 0.85 ... [ mn >=
30 ]
YX ... Material:
Eh, IF(root), NT, NV, NT(nitr.), NV(nitr.), NV(nitrocar.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.05 - 0.01 * mn
... [ 5 < mn < 25 ]
YX = 0.80 ... [ mn >=
25 ]
YX ... Material: GG,
GGG(ferr.)
YX = 1.0
... [ mn <= 5 ]
YX = 1.075 - 0.015 * mn
... [ 5 < mn < 25 ]
YX = 0.70 ... [ mn >=
25 ]
Tato část ISO 6336 popisuje napětí v dotyku a napětí v ohybu v patě zubu a uvádí pro ně číselné mezní hodnoty. Jsou specifikovány požadavky na kvalitu a tepelné zpracování materiálu, spolu s uvážením jejich vlivu na obě mezní hodnoty.
Dovolené hodnoty napětí v dotyku, σHlim a jmenovité napětí v ohybu σFlim je vypočítáno ze vztahu:
a) σHlim = A * x + B
b) σFlim = A * x + B
kde
x ... je tvrdost povrchu HBW nebo HV
A, B jsou konstanty
Použité vztahy jsou určeny pro tři stupně kvality materiálu ML, MQ a ME
- ML představuje nejmírnější požadavky na kvalitu materiálu a na proces jeho
tepelného zpracování během výroby ozubeného kola.
- MQ představuje požadavky, které může splnit zkušený výrobce při rozumných
výrobních nákladech.
- ME představuje požadavky, které musí být splněny při požadavku vysoké provozní
spolehlivosti.
V tomto výpočtu jsou kromě σHlim a σFlim navržené další materiálové parametry, které jsou pro výpočet ozubení nutné. Hodnoty Ro, E a poisonova konstanta jsou běžně dostupné. Pro návrh meze pevnosti v tahu Rm a meze kluzu Rp0.2 byly použity údaje z ISO 1265 a z odborné literatury. Parametry křivek pro časovou pevnost byly získané z ISO6336-2 a 3. Tyto křivky je možné vidět na malém grafu ve výpočtu.
Všechny počítané hodnoty jsou návrhové a získané na základě empirických zkušeností. Přesné hodnoty pro konkrétní materiál získáte nejlépe od výrobce, či na základě materiálových zkoušek.
Hodnoty HB pro HB<=450 ocelová kulička, HB>450 kulička z tvrdokovu
Hodnoty HB použitý přepočet HB=HV-HV/20
Hodnoty HRC použitý přepočet HRC=(100*HV-14500)/(HV+223)
Výtah je uváděn v originálním jazyce normy.
Kv = (C / (C + vt))−B
C = 50 + 56 * (1.0 − B) ... [ 6 ≤ Av ≤ 12 ]
B = 0.25 * (Av − 5.0)0.667
vt max = [C + (14 − Av)]2
The empirical guidance values from table B.1 ISO 6336-6 are used.
Cp = (1 / p
* (((1 - mP2)
/ EP) + ((1 - mG2) /
EG)))0.5 ... [lb/in2]0.5
mP and mG
is Poisson’s ratio for pinion and gear, respectively; EP and EG is
modulus of elasticity for pinion and gear [lb/in2].
Cf = 1.0
Through hardened gears
CH = 1.0 + A * (mG - 1.0)
A = 0.00898 *(HBP / HBG) - 0.00829
HBP is pinion Brinell hardness number [HB]; HBG is gear Brinell hardness
number,[HB].
This equation is valid for the range 1.2 ≤ HBP / HBG ≤ 1.7 For HBP / HBG < 1.2,
A = 0.0 HBP / HBG > 1.7, A = 0.00698
Surface hardened/through hardened values
CH = 1.0 + B * (450 - HBG)
B = 0.00075 * (2.71828)-0.0112 * (fp)
fp is surface finish of pinion, microinches, Ra
if fp>64 ... CH = 1.0
Km = f (Cmf, Cmt)
Km = Cmf
Cmf = 1.0 + Cmc * (Cpf *
Cpm + Cma * Ce)
Cmc is 1.0 for gear with unmodified leads; Cmc is 0.8 for gear with leads
properly modified by crowning or lead correction.
Cpf = F / (10 * d) − 0.025 ... [F<=1.0]
Cpf = F / (10 * d) − 0.0375 + 0.0125 * F ... [1.0<F<=17.0]
Cpf = F / (10 * d) − 0.1109 + 0.0207 * F − 0.000228 * F2 ...
[17.0<F<=40.0]
Cpm = 1.0 ... [S1 / S < 0.175]
Cpm = 1.1 ... [S1 / S >= 0.175]
Cma = A + B * F + C * F2
| A | B | C | |
| 1…Open gearing | 0.247 | 0.0167 | -0.0000765 |
| 2…Commercial enclosed gearboxes | 0.127 | 0.0158 | -0.0001093 |
| 3…Precision enclosed gearbox | 0.0675 | 0.0128 | -0.0000926 |
| 4…Extra precision enclosed gearbox | 0.038 | 0.0102 | -0.0000822 |
Ce = 0.8 ... [gearing is adjusted at assembly; gearing is
improved by lapping]
Ce = 1.0 ... [for all other conditions]
KR = 1.50 [Fewer than one failure in 10 000]
KR = 1.25 [Fewer than one failure in 1000]
KR = 1.00 [Fewer than one failure in 100]
KR = 0.85 [Fewer than one failure in 10]
KR = 0.70 [Fewer than one failure in 2]
KB = 1.6 * ln(2.242 / mB) ... [for mB<1.2]
KB = 1.0 ... [for mB>=1.2]
mB = tR / ht
tR is gear rimthickness below the tooth root
[in]; ht is gear
tooth whole depth [in]
The contact stress number formula for gear teeth is:
sc = Cp (Wt * Ko * Kv * Ks * Km * Cf / (d * F * I))0.5
Allowable contact stress number
The relation of calculated contact stress number to allowable contact stress
number is:
sc ≤ (sac * ZN * CH) / (KT * SH * KR)
Pitting resistance power rating
The pitting resistance power rating is:
Pac = (p * np * F / 396 000) * I / (Ko * Kv * Ks * Km * Cf) * ((d * sac * ZN CH) / (Cp * SH * KT * KR))2
SH = sac / sc * (ZN * CH) / (KT * KR)
The fundamental formula for bending stress number in a gear tooth is:
st = Wt * Ko * Kv * Ks * (Pd * Km * KB / (F * J))
Allowable bending stress number
The relation of calculated bending stress number to allowable bending stress
number is:
st ≤ (sat * YN) / (SF * KT * KR)
Bending strength power rating
The bending strength power rating is:
Pat = (p * np * F / 396 000) * (F * J) / (Ko * Kv * Pd * Ks * Km * KB) * (sat * YN) / (SF * KT * KR)
SF = sat / st * YN / (KT * KR)
Transmitted tangential load
Wt = 33000 * P / vt = 2 * T / d = 396000 * P / (p
* np * d)
P is transmitted power [hp];
T is transmitted pinion torque [lb*in];
vt is pitch line velocity at operating pitch diameter,
[ft/min]
vt = p
* np * d / 12
This part of ANSI / AGMA 2001-D04 describes the allowable stress numbers sac and sat, for pitting resistance and bending strength.
Allowable stress numbers in this standard are determined or estimated from
laboratory tests and accumulated field experiences. They
are based on unity overload factor, 10 million stress cycles, unidirectional
loading and 99 percent reliability. For service life other than 10
million cycles, the allowable stress numbers are adjusted by the use of stress
cycle factors YN and ZN
The allowable stress numbers sac and sat can be calculated by the following equation:
a) sac = A * x + B
b) sat = A * x + B
where x is the surface hardness HBW and A, B are constants
These requirements are specified in this standard and are divided in three material quality grades 1,2 an 3.
In this calculation, except sac and sat, are proposed other material parameters that are necessary for calculating the gearing. The values of p, E and Poisson constant are commonly available. For the proposal of the tensile strength Rm and yield strength Rp0.2 was used information from the ISO 1265 and specialized literature. All calculated values are design and based on empirical experience. The exact values for a concrete material you can obtain from your manufacturer or from material tests.
Values HB for HB<=450 steel ball, HB>450 carbide ball
Values HB used recalculation HB=HV-HV/20
Values HRC used recalculation HRC=(100*HV-14500)/(HV+223)