Le calcul est destiné à proposer les récipients sous pression et leurs parts. On peut calculer les déformations et les contraintes pour les coques de révolution soumises à une force axiale, une pression, une force radiale et un moment de flexion. Ce programme est destiné aux coques homogènes, de la même épaisseur et à partir du même matériau. En plus, le calcul permet de résoudre la liaison de deux coques dont les paramètres (épaisseur, matériau, dimensions) sont différents.
Le programme permet d’effectuer:
Le calcul utilise les données, les méthodes, les algorithmes et les informations de la littérature spécialisée (Roark formulas, Machinery's Handbook 26th, Teorie desek a skořepin [doc. Ing. Ladislav Šubrt, CSc.] et autres)
L’interface d’utilisateur.
A télécharger.
Tarif, Achat.
L'information sur la syntaxe et la commande du calcul peut être trouvée dans le document « commande, structure et syntaxe des calculs ».
L'information sur le but, l'utilisation et la commande du paragraphe « information sur le projet » peut être trouvée dans le document « information sur le projet ».
Les coques sont des éléments de construction plats dont l'épaisseur est
plusieurs fois moins importante que les deux dimensions restantes. Pour les
coques générales, la surface moyenne (la surface divisant l’épaisseur de la
coque en deux) peut prendre une forme quelconque. De plus, les coques peuvent
être arbitrairement chargées.
Selon la forme, on peut diviser les coques en :
Selon l’épaisseur, on peut diviser les coques en :
L’épaisseur de la coque est comparable avec le rayon de courbure minimum. Pour ce type de coque, il n’est pas possible de négliger les contraintes normales perpendiculaires à la surface moyenne de la coque et, en plus, il n’est pas possible de négliger les déformations des normales à la surface moyenne dues à des contraintes de cisaillement. Ainsi, la distribution non-linéaire des contraintes le long de l’épaisseur de la coque prend naissance. Il en résulte une solution analytique compliquée. C’est pourquoi on utilise, dans la plupart des cas, la méthode des éléments finis pour calculer numériquement ce type de coque.
Il s’agit du type de coque situé entre la coque à paroi épaisse et celle à paroi mince pour lequel la théorie des coques à paroi épaisse est trop compliquée et la théorie des coques à paroi mince ne donne pas des résultats suffisamment précis.
Dans ce cas, l'épaisseur de la paroi est trop petite par rapport au rayon de courbure minimum. Pour ces coques, il est possible de négliger l’influence des contraintes de cisaillement sur la déformation des normales à la surface moyenne. Cela, conjointement avec la possibilité de négliger certaines contraintes, permet d’utiliser une solution analytique simple de ce type de coque. Ce type de coque de révolution est calculé dans notre calcul.
Pour ces coques à paroi très mince, une déformation comparable ou supérieure à l’épaisseur de la paroi se produit. Ainsi, le point d’application des forces se déplace au cours du chargement. Une solution analytique est relativement compliquée. C’est pourquoi on utilise, dans la plupart des cas, la méthode des éléments finis pour calculer numériquement ce type de coque.
Il s’agit des coques pour lesquelles aucun moment intérieur (flexion, torsion) n’existe dans les parois. Elles ne sont soumises qu’à des forces normales, éventuellement à des forces de cisaillement. Ainsi, on obtient une charge uniformément répartie le long de l’épaisseur de la paroi. Une tension membranaire est favorable du point de vue de l’exploitation du matériau. C’est pourquoi vous devez, en concevant une coque, veiller à ce que cet état soit altéré aussi peu que possible.
Lors d'une solution analytique des coques à paroi mince, on procède au principe de l'élément extrait d’une coque générale – voir la figure.
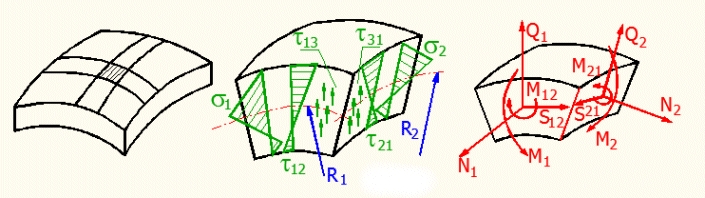
Vu que les coques à paroi épaisse ne sont pas envisagées, il est possible d’utiliser les formes linéaires des contraintes normales (s1, s2) ainsi que des contraintes de cisaillement (t12, t21). Pour les coques, ces contraintes ne sont pas égales à zéro au niveau de la surface moyenne. Il s’agit donc d’une superposition de la flexion et de la traction et d’une superposition de la torsion et du cisaillement uniformément réparti. Ainsi, la contrainte s1 est composée de la contrainte de membrane et de la contrainte de flexion.
Pour cet élément, on remplace la contrainte par les effets à force d’après le tableau suivant :
| Contrainte | Effet de forces intérieur résultant |
| s1 | N1-force normale |
| M1-moment de flexion | |
| s2 | N2-force normale |
| M2-moment de flexion | |
| t12 | S12-force de cisaillement |
| M12-moment de torsion | |
| t21 | S21-force de cisaillement |
| M21-moment de torsion | |
| t13 | Q1-effort tranchant (transversal) |
| t31 | Q2-effort tranchant (transversal) |
Comme l’élément extrait doit être en équilibre, il est possible de former un
système d'équations d’un équilibre pour le système des forces agissantes sur
l’élément. En plus, il est nécessaire de déduire les relations en matière de
déformation de la coque et les relations donnant l'interdépendance entre les
déformations et les effets de forces.
D’une façon générale, la solution de ces équations débouche sur un système d’équations aux dérivées partielles qui est difficilement résoluble. C’est pourquoi on définit des conditions simplificatrices variées pour les types de coque concrets. Cela ne donne que des résultats approximatifs, mais ces résultats sont toutefois suffisamment précis pour une utilisation pratique.
Toujours, les systèmes d’équations différentielles sont complétés par des conditions aux limites.
Dans la littérature, on peut trouver les solutions d’auteurs variés pour les différents types de coque. Les systèmes d’équations résultants varient souvent (en fonction des simplifications choisies), néanmoins les solutions des équations différentes ne varient que très peu (la variance estimée est inférieure à 10%).
Pour calculer les coques à paroi mince, on applique les conditions suivantes :
Dans la pratique, on peut rencontrer les coques de révolution ou les coques à symétrie de révolution probablement le plus souvent.
On considère comme des coques de révolution les coques dont la surface moyenne est celle de révolution. Quant aux chargements, aucune condition restrictive n’est définie. De nouveau, une solution générale est considérablement compliquée. Il existe avant tout pour une coque cylindrique qui est, évidemment, le type de coque le plus répandu.
Les coques à symétrie de révolution sont des coques de révolution qui sont chargées constamment sur les cercles parallèles. La solution de ce type de coque est beaucoup plus simple, elle dépend d’une seule coordonnée. Dans la littérature, on peut trouver les solutions pour les formes géométriques de base de coques, telles que le cylindre, la sphère, le cône, le tore etc.
Ce programme est destiné avant tout à calculer les coques à symétrie de révolution.
Dans la plupart des cas, on entend par « structures en coques » les structures établies par combinaison de deux et plus de coques ou par combinaison de coques avec autres éléments de construction. L’exemple typique d’une structure en coques peut être un récipient sous pression formé d’un récipient cylindrique avec le fond conique, une réduction du diamètre du tube à l’aide d’une pièce de réduction conique ou une bride sur le tube cylindrique.
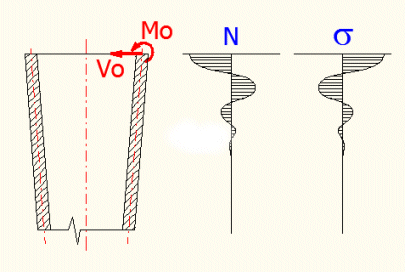
En principe, on peut dire que ces cas sont indéterminés statiquement. Cela veut dire que les effets de forces se produisent dans la liaison de deux coques que nous ne pouvons pas résoudre à l’aide des équations d’équilibre statique. Dans l'exemple suivant, on peut démontrer le problème de la liaison de la coque cylindrique et de celle sphérique dont l’ensemble est soumis à une surpression intérieure.
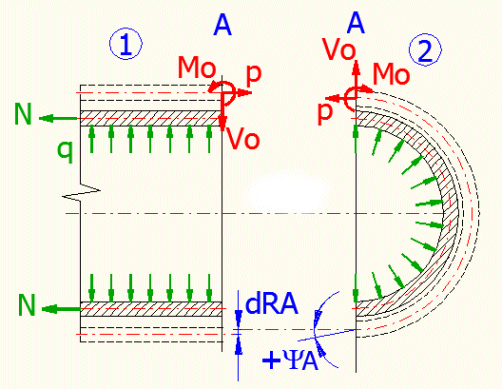
Si nous soumettions les différentes coques à une surpression intérieure, seulement des tensions membranaires se produiraient dans celles-ci et les coques se déformeraient en forme indiquée (hachurée). A l’endroit de la liaison des deux coques, les rayons se modifieraient différemment et un déplacement angulaire de la coque sphérique se produirait. Normalement, on calcule ce cas à l’aide de la méthode des forces en appliquant une force indéterminée « Vo », un moment « Mo » et une force « p » sur le bord de chaque coque.
Pour pouvoir « lier » les coques, il est nécessaire de définir de telles conditions qui garantissent l’exigence définissant la déformation résultante d‘une coque comme étant identique à la déformation résultante de l’autre coque. En résolvant ces équations, nous pouvons calculer les déformations et les contraintes à l’endroit de la liaison des coques. Dans la plupart des cas, il s‘agit de l’endroit avec la contrainte locale maximum qui nous intéresse.
Si aucun moment intérieur n’existe dans la coque, mais seulement les forces intérieures, la coque se trouve en état membranaire. Cet état est favorable et désirable du point de vue de la capacité portante de la coque. Le fait d’établir si la coque est ou n’est pas en état membranaire dépend de la forme, du montage et du mode de chargement de la coque. Il y a quelques règles de base relatives à la conception de la coque qui est destinée à être en état membranaire:
Si ces conditions ne sont pas remplies, l’état membranaire se dégrade. En conséquence, la contrainte augmente. On doit la compenser en utilisant une plus grande épaisseur de la paroi. On utilise souvent des renforts ou étrésillons différents qui retiennent une contrainte inopportune qui pourrait dégrader l’état membranaire.
Lors du calcul de la déformation (de la contrainte) d'une coque individuelle, procédez comme suit:
1...Choisissez le matériau de la coque, entrez les caractéristiques du
matériau [1.0].
2...Selon le type de coque, choisissez le paragraphe respectif du calcul [2.0,
3.0, 4.0, 5.0].
3...Choisissez le mode de chargement [2.1, 3.1, 4.1, 5.1].
4...Entrez les dimensions et les chargements de la coque et vérifiez les
résultats.
Lors du calcul de la déformation (de la contrainte) des coques liées, procédez comme suit :
1...Choisissez le type de liaison des coques [10.1] puis, confirmez en
enfonçant le bouton OK.
2...En fonction du choix, les paragraphes contenant les coques choisies sont
affichés [6.0, 7.0, 8.0, 9.0].
3...Entrez les caractéristiques du matériau, les dimensions et les chargements
des coques.
4...Dans le paragraphe [10.0], enfoncez le bouton « Résoudre
»
; ainsi vous démarrez l’itération.
5...Dans les paragraphes avec les coques choisies, vérifiez les résultats.
Dans ce paragraphe, sélectionnez les unités de calcul et choisissez le matériau de la coque vérifiée. Les caractéristiques du matériau sont automatiquement utilisées dans les paragraphes [2.0-5.0]. Dans les paragraphes [6.0-9.0], il est possible de joindre les caractéristiques du matériau différentes à chaque coque.
Sélectionnez le système d'unités de calcul dans la liste de sélection. En passant d'une unité à l'autre, toutes les valeurs seront immédiatement recalculées.
Choisissez le matériau de la coque correspondante dans la liste proposée. Si les constantes de matériau de votre matériau sont différentes des constantes de matériau indiquées à la ligne [1.3-1.8], décochez la case de la ligne [1.3] et insérez vos propres valeurs de matériau.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation de la coque cylindrique à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R/10. La déformation de la coque devrait être petite par rapport à son épaisseur.
Dans la liste déroulante, sélectionnez le chargement qui correspond à votre tâche. Après la sélection, le schéma de chargement respectif s’affiche. Les conditions de validité sont affichées à droite de la liste déroulante.
Remarques relatives aux différents modes de chargement:
3. Le point se trouve suffisamment loin du bord.
4. Où « y » doit être mesuré à partir de l’extrémité non chargée.
Entrez l’épaisseur de la coque, le rayon d’arrondi (rayon moyen) et la longueur de la coque. L’épaisseur de la coque devrait être inférieure à 1/10 du rayon.
Vous pouvez sélectionner si vous voulez entrer la force totale ou la force prise par rapport à un millimètre (un pouce) de la circonférence. Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après l’inversion, la valeur contenue dans le champ d’entrée est automatiquement convertie selon le diamètre actuel.
Entrez la surpression intérieure. En cas de surpression extérieure, entrez la valeur négative.
Entrez la vitesse de rotation en nombre de tours par minute.
Dans ces lignes, les résultats du calcul sont affichés.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation de la coques coniques à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R/10, ( t<r/10). La déformation de la coque devrait être petite par rapport à son épaisseur.
Dans la liste déroulante, sélectionnez le chargement qui correspond à votre tâche. Après la sélection, le schéma de chargement respectif s’affiche. Les conditions de validité sont affichées à droite de la liste déroulante.
Remarques relatives aux différents modes de chargement:
2... Il existe une discontinuité dans la charge due à
la pression du liquide au-dessous et au-dessus du niveau de liquide. Cela mène à
la contrainte de flexion dans cette zone. Pour « y » situés au-dessous du niveau
de liquide (y<d), s1max se trouve à la hauteur
y=3*d/4 et pour s2max est à
la hauteur Y=d/2.
4... « r » doit être une valeur positive et « r/t>10 »
afin que la condition du récipient sous pression reste en vigueur.
Entrez l’épaisseur de la coque [3.2]. Vu que le diamètre, la longueur et
l'angle du cône sont les variables dépendantes, ajustez, sur la ligne [3.3], les
variables dont les valeurs sont celles d’entrée. Puis, entrez ces valeurs
dimensionnelles.
Si vous choisissez, dans la ligne [3.1], le mode de chargement = 4 (force
tangentielle), il est possible d’entrer toutes les trois valeurs (R,y,a)
et le second rayon « r » est une variable dépendante.
Entrez le niveau de liquide et la masse volumique du liquide.
Vous pouvez sélectionner si vous voulez entrer la force totale ou la force prise par rapport à un millimètre (un pouce) de la circonférence. Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après l’inversion, la valeur contenue dans le champ d’entrée est automatiquement convertie selon le diamètre actuel.
Entrez la surpression intérieure. En cas de surpression extérieure, entrez la valeur négative.
Entrez la vitesse de rotation en nombre de tours par minute.
Dans ces lignes, les résultats du calcul sont affichés.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation de la coques coniques à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R2/10. La déformation de la coque devrait être petite par rapport à son épaisseur.
Dans la liste déroulante, sélectionnez le chargement qui correspond à votre tâche. Après la sélection, le schéma de chargement respectif s’affiche. Les conditions de validité sont affichées à droite de la liste déroulante.
Remarques relatives aux différents modes de chargement:
2. Il existe une discontinuité dans la charge due à la pression du liquide
au-dessous et au-dessus du niveau de liquide. Cela mène à la contrainte de
flexion dans cette zone. Le calcul est valable pour « y » situés au-dessous du
niveau de liquide (y<d). Pour y>d, le chargement 4 est utilisé où la force est
due à la masse du liquide.
4. L’angle « q0 » est un angle du bord inférieur du
récipient, il doit être plus grand que zéro.
5. Pour l’angle « q »<=90 deg.
Entrez l’épaisseur [4.2] et le rayon moyen de la coque sphérique [4.3], l’angle entre l’axe de la coque et le bord supérieur de la coque [4.4] et, éventuellement, l’angle entre l’axe de la coque et le bord inférieur de la coque [4.5].
Entrez le niveau de liquide et la masse volumique du liquide.
Vous pouvez sélectionner si vous voulez entrer la force totale ou la force prise par rapport à un millimètre (un pouce) de la circonférence. Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après l’inversion, la valeur contenue dans le champ d’entrée est automatiquement convertie selon le diamètre actuel.
Entrez la surpression intérieure. En cas de surpression extérieure, entrez la valeur négative.
Entrez la vitesse de rotation en nombre de tours par minute.
Dans ces lignes, les résultats du calcul sont affichés.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation des coques cylindriques et sphériques à paroi épaisse soumises à des chargements variés.
Dans la liste déroulante, sélectionnez le chargement qui correspond à votre tâche. Après la sélection, le schéma de chargement respectif s’affiche. Les conditions de validité sont affichées à droite de la liste déroulante.
Entrez les rayons extérieur et intérieur de la coque [5.2, 5.3] et, éventuellement, la longueur de la coque cylindrique [5.4].
Entrez le chargement par unité de surface [5.5].
Dans ces lignes, les résultats du calcul sont affichés. Sur la ligne [5.15], vous pouvez modifier le rayon sur lequel les valeurs calculées de la contrainte seront affichées.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation d’une longue coque cylindrique à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R/10. La déformation de la coque devrait être petite par rapport à son épaisseur. Une fois la coque soumise à un moment d’extrémité « Mo » et à une force « Vo », les contraintes (déformations) présentent un caractère oscillant exponentiellement amorti (voir la figure).
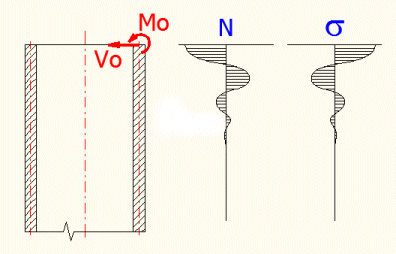
Cela veut dire que les effets de ces chargements s’éteignent vite et, à une distance suffisante de l’extrémité, ils ne se montrent plus. C’est pourquoi on divise les coques cylindriques en « longues » coques (le chargement d’une extrémité n’influence pas les déformations et les contraintes de l’autre extrémité) et en « courtes » coques (les effets du chargement d’extrémité ne suffisent pas de s’éteindre et influencent les déformations et les contraintes de l’autre extrémité). On peut considérer une coque cylindrique comme longue si sa longueur est supérieure à la valeur L indiquée dans la ligne [6.2] entre les conditions. Si nous acceptons une relativement faible précision (erreur ne dépasse pas 10%), il est possible d’envisager la valeur égale à 1/2L.
Formule du calcul de L: L=6/(3*(1-ny^2)/(R^2*t^2))^(1/4) où:
ny...coefficient de Poisson
R....rayon extérieur
t.....épaisseur de la coque
Dans la première partie du calcul, les données d’entrée sont affichées ; les résultats s’affichent dans la seconde partie. A droite en haut, vous trouvez les conditions aux limites les plus importantes ; les dimensions de référence de la coque et le chargement de la coque figurent au-dessous de ces conditions. Vous pouvez commuter entre les figures à l’aide du bouton « > » situé dans le coin supérieur droit de la figure.
Si le champ situé à droite de la cellule d’entrée est coché, les constantes du matériau sont reprises du paragraphe [1.0]. Si vous avez besoin d’entrer vos propres valeurs, décochez le champ et entrez le module de Young [6.2] et le coefficient de Poisson [6.3].
Entrez le rayon moyen [6.4] et l’épaisseur de la coque cylindrique [6.5].
Entrez le chargement par unité de surface [6.6]. Si la coque est soumise à la
surpression intérieure, la valeur est positive ; en cas de surpression
extérieure, entrez la valeur négative. Dans la ligne [6.7], on trouve la force
axiale totale produite sous l’action de la pression entrée sur la surface du
fond circulaire.
Dans la ligne [6.8], entrez la force par unité de longueur « p » ou la force
totale « P ». Vous pouvez sélectionner si vous voulez entrer la force totale ou
la force prise par rapport à un millimètre (un pouce) de la circonférence.
Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après
l’inversion, la valeur contenue dans le champ d’entrée est automatiquement
convertie selon le diamètre actuel. Si vous enfoncez le bouton « <-Pq »,
la valeur de la ligne [6.7] est reprise dans cette cellule d’entrée.
Sur la ligne [6.9], entrez la force circonférentielle (perpendiculaire à l’axe
de la coque) ; sur la ligne [6.10], entrez le moment.
La déformation de la coque en son extrémité (x=0) figure sur la ligne [6.12,
6.13]. Le champ d’entrée pour la coordonnée « x » (mesurée à partir du bord de
la coque dans le sens de son axe) est sur la ligne [6.14]. Ci-dessous, les
différents résultats pour la coordonnée entrée « x » sont affichés. En plus, la
coordonnée « x » peut être modifiée à l’aide d’une barre de défilement (scroll
bar) dont la gamme est 0 - valeur indiquée à droite de la barre de défilement
(la longueur minimale de la coque L est préréglée).
La liste déroulante à l'aide de laquelle vous pouvez ajuster le chargement
d'entrée (ou la somme des chargements d'entrée) est sur la ligne [6.15].
La fonctionnalité du second calcul est identique au premier calcul.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation d’une coque sphérique à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R/10. La déformation de la coque devrait être petite par rapport à son épaisseur. Une fois la coque soumise à un moment d’extrémité « Mo » et à une force « Vo », les contraintes (déformations) présentent un caractère oscillant exponentiellement amorti (voir la figure).
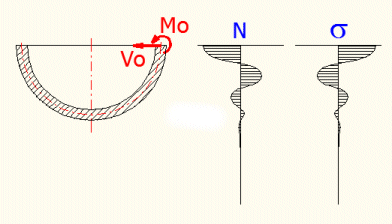
Cela veut dire que les effets de ces chargements s’éteignent vite et, à une distance suffisante du bord, ils ne se montrent plus.
Dans la première partie du calcul, les données d’entrée sont affichées ; les résultats s’affichent dans la seconde partie. A droite en haut, vous trouvez les conditions aux limites les plus importantes ; les dimensions de référence de la coque et le chargement de la coque figurent au-dessous de ces conditions. Vous pouvez commuter entre les figures à l’aide du bouton « > » situé dans le coin supérieur droit de la figure.
Si le champ situé à droite de la cellule d’entrée est coché, les constantes du matériau sont reprises du paragraphe [1.0]. Si vous avez besoin d’entrer vos propres valeurs, décochez le champ et entrez le module de Young [7.2] et le coefficient de Poisson [7.3].
Entrez l’angle « f » mesuré à partir de l’axe de la coque jusqu’à son bord [7.4] et l’épaisseur de la coque [7.5]. En plus, entrez le rayon moyen de la coque sphérique « R2 » [7.6] ou le rayon « R » [7.7] (distance entre l’axe et le bord). Sélectionnez le rayon voulu dans la liste déroulante sur la ligne [7.6]. L'autre valeur sera calculée.
Entrez le chargement par unité de surface [7.8]. Si la coque est soumise à la surpression intérieure, la valeur est positive ; en cas de surpression extérieure, entrez la valeur négative. Dans la ligne [7.9], on trouve la force tangentielle totale produite sous l’action de la pression entrée sur la surface du fond circulaire et la décomposition de cette force en ses composantes x et y [7.10, 7.11].
Dans la ligne [7.12], entrez la force par unité de longueur « P » ou la force totale « p ». Vous pouvez sélectionner si vous voulez entrer la force totale ou la force prise par rapport à un millimètre (un pouce) de la circonférence. Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après l’inversion, la valeur contenue dans le champ d’entrée est automatiquement convertie selon le diamètre actuel. Si vous enfoncez le bouton « <-Pq », la valeur de la ligne [7.9] est reprise dans cette cellule d’entrée.
Sur la ligne [7.13], entrez la force circonférentielle (perpendiculaire à l’axe de la coque) ; sur la ligne [7.14], entrez le moment.
La déformation de la coque en son extrémité (w=0)
figure sur la ligne [7.16, 7.17]. Le champ d’entrée pour l’angle w
(mesuré à partir du bord de la coque) est sur la ligne [7.18]. Ci-dessous, les
différents résultats pour l’angle entré « w
» sont affichés. En plus, l’angle « w » peut
être modifié à l’aide d’une barre de défilement (scroll bar) dont la gamme est 0
- valeur indiquée à droite de la barre de défilement.
La liste déroulante à l'aide de laquelle vous pouvez ajuster le chargement
d'entrée (ou la somme des chargements d'entrée) est sur la ligne [7.19].
La fonctionnalité du second calcul est identique au premier calcul.
Entrez l’angle « f » mesuré à partir de l’axe de la coque jusqu’à son bord [7.33] et l’épaisseur de la coque [7.34]. En plus, entrez le rayon moyen de la coque sphérique « R2 » [7.35] ou le rayon « R » [7.36] (distance entre l’axe et le bord). Sélectionnez le rayon voulu dans la liste déroulante sur la ligne [7.35]. L'autre valeur sera calculée.
A l’aide de deux boutons « <-f » situés à droite sur la ligne [7.33], il est possible d’entrer un tel angle « f » qui garantit que le rayon « R » [7.35] est identique au rayon « R » [7.6]. Cela nous permet de réaliser une « liaison » précise avec la coque sphérique du Premier calcul.
Avec ce calcul, il est possible de déterminer la contrainte et la déformation d’une longue coque conique à paroi mince soumise à des chargements variés. L’épaisseur t de la coque doit remplir t<R/10. La déformation de la coque devrait être petite par rapport à son épaisseur. Une fois la coque soumise à un moment d’extrémité « Mo » et à une force « Vo », les contraintes (déformations) présentent un caractère oscillant exponentiellement amorti (voir la figure).
Cela veut dire que les effets de ces chargements s’éteignent vite et, à une distance suffisante du bord, ils ne se montrent plus. C’est pourquoi on divise les coques coniques en « longues » coques (le chargement d’une extrémité n’influence pas les déformations et les contraintes de l’autre extrémité) et en « courtes » coques (les effets du chargement d’extrémité ne suffisent pas de s’éteindre et influencent les déformations et les contraintes de l’autre extrémité). On peut considérer une coque conique comme longue si sa longueur est supérieure à la valeur L indiquée dans la ligne [8.2] entre les conditions.
Pour calculer L (l’endroit où les effets du chargement d’extrémité sont
suffisamment amortis), on utilise les formules suivantes :
1) coefficient k = 2/sin(a)*((12*(1-ny^2)*R^2)/(t^2*(1/cos(a))^2))^(1/4)
2) coefficient mi = abs((kA-k)/(2^0.5))
3) R = RA-x*tan(a)
4) si le coefficient mi=4, on peut supposer que les effets du chargement
d’extrémité sont suffisamment amortis
où :
ny...coefficient de Poisson
R....rayon du cône, RA...(à l’origine)
t.....épaisseur de la coque
a.....demi-angle du cône
kA....coefficient k à l’origine de la coque
x......coordonnées sur l’axe du cône
En même temps, l’épaisseur de la coque doit remplir la condition R/(t*cos(a))>10 où R est le rayon envisagé le long de la coque dans l’intervalle x <0, L>.
Dans la première partie du calcul, les données d’entrée sont affichées ; les résultats s’affichent dans la seconde partie. A droite en haut, vous trouvez les conditions aux limites les plus importantes ; les dimensions de référence de la coque et le chargement de la coque figurent au-dessous de ces conditions. Vous pouvez commuter entre les figures à l’aide du bouton « > » situé dans le coin supérieur droit de la figure.
Si le champ situé à droite de la cellule d’entrée est coché, les constantes du matériau sont reprises du paragraphe [1.0]. Si vous avez besoin d’entrer vos propres valeurs, décochez le champ et entrez le module de Young [8.2] et le coefficient de Poisson [8.3].
Entrez le rayon d’arrondi (rayon moyen) « RA » [8.4], l’épaisseur de la coque [8.5] et le demi-angle du cône [8.6].
Entrez le chargement par unité de surface [8.7]. Si la coque est soumise à la surpression intérieure, la valeur est positive ; en cas de surpression extérieure, entrez la valeur négative. Dans la ligne [8.8], on trouve la force tangentielle totale produite sous l’action de la pression entrée sur la surface du fond circulaire et la décomposition de cette force en ses composantes x et y [8.9, 8.10].
Dans la ligne [8.11], entrez la force par unité de longueur « P » ou la force totale « p ». Vous pouvez sélectionner si vous voulez entrer la force totale ou la force prise par rapport à un millimètre (un pouce) de la circonférence. Sélectionnez le mode voulu à l’aide de l’inverseur dans cette ligne. Après l’inversion, la valeur contenue dans le champ d’entrée est automatiquement convertie selon le diamètre actuel. Si vous enfoncez le bouton « <-Pq », la valeur de la ligne [8.8] est reprise dans cette cellule d’entrée.
Sur la ligne [8.12], entrez la force circonférentielle (perpendiculaire à l’axe de la coque); sur la ligne [8.13], entrez le moment.
La déformation de la coque en son extrémité (x=0) figure sur la ligne [8.15, 8.16]. Le champ d’entrée pour la coordonnée « x » (mesurée à partir du bord de
la coque dans le sens de son axe) est sur la ligne [8.17]. Ci-dessous, les
différents résultats pour la coordonnée entrée « x » sont affichés. En plus, la
coordonnée « x » peut être modifiée à l’aide d’une barre de défilement (scroll
bar) dont la gamme est 0 - valeur indiquée à droite de la barre de défilement
(la longueur minimale de la coque L est préréglée).
La liste déroulante à l'aide de laquelle vous pouvez ajuster le chargement
d'entrée (ou la somme des chargements d'entrée) est sur la ligne [8.18].
La fonctionnalité du second calcul est identique au premier calcul.
Avec ce calcul, il est possible de déterminer les cours de la flexion, de la contrainte et du déplacement angulaire des plaques circulaires à paroi moyenne, y compris les valeurs maximales. Comme la tension membranaire (voir la partie théorique du calcul des plaques) n’est pas prise en compte pour ce type de calcul, il est nécessaire de contrôler la flexion maximale qui devrait être inférieure à la moitié de l’épaisseur de la plaque.
Si le champ situé à droite de la cellule d’entrée est coché, les constantes du matériau sont reprises du paragraphe [1.0]. Si vous avez besoin d’entrer vos propres valeurs, décochez le champ et entrez le module de Young [9.2] et le coefficient de Poisson [9.3].
Entrez le rayon extérieur [9.4] et l’épaisseur de la plaque [9.5]. L’épaisseur de la plaque devrait être inférieure à 1/5 du rayon (si nous demandons une précision élevée, l’épaisseur de la plaque devrait être inférieure à 1/10 du rayon).
Entrez le chargement par unité de surface [9.6], la force « P » agissant sur le cercle [9.7] dont le rayon est « ro » [9.8], la force « Vo » agissant sur la circonférence [9.9] et le moment «Mo » [9.10].
La déformation de la plaque en son extrémité (R=RA) figure sur la ligne [9.12, 9.13]. Le champ d’entrée pour la coordonnée « R » (mesurée à partir du centre de la plaque) est sur la ligne [9.14]. Ci-dessous, les différents résultats pour la coordonnée entrée « R » sont affichés. En plus, la coordonnée « R » peut être modifiée à l’aide d’une barre de défilement (scroll bar) dont la gamme est 0 - valeur « RA ».
La liste déroulante à l'aide de laquelle vous pouvez ajuster le chargement d'entrée (ou la somme des chargements d'entrée) est sur la ligne [9.15].
Dans les paragraphes précédents, les coques individuelles sont calculées. Dans la pratique, on peut rencontrer beaucoup plus souvent les problèmes relatifs à la liaison des formes de base des coques, éventuellement leur combinaison avec la plaque fixe (encastrement). Ces problèmes sont statiquement indéterminés et difficilement résolubles de façon analytique. Dans ce paragraphe, il est possible de calculer par approximations successives les chargements des extrémités de différentes coques de sorte que l'on obtienne les mêmes déformations aux extrémités des deux coques et que l’on puisse « lier » les coques. Ici, vous pouvez modifier trois paramètres et évaluer trois conditions. La solution utilise la fonction d’Excel « Goal seek... » (valeur cible en français) qui est utilisée de manière cyclique dans la modification de différents paramètres [10.4, 10.5, 10.6] de sorte que l’on obtienne le résultat auquel on veut aboutir [10.8, 10.10, 10.12] pour les équations [10.7, 10.9, 10.11]. Toutes les cellules portent un nom (ex. _Variable1, _Formula1, _dRA_06...). Il est donc désirable d’utiliser leurs noms dans les formules.
Procédé de solution:
Etapes successives du résolvant:
Voici un exemple d'explication.
Le tube dont l’épaisseur se change brusquement est soumise à une pression intérieure « q » et à une force axiale « N », le diamètre moyen du tube ne se change pas. Libérez les coques. Ensuite, soumettez les bords des deux coques à une force radiale « Vo », à une force axiale « p » et à un moment « Mo ». Pour cette coque, les conditions de déformation sont les suivantes : « dRA1=-dRA2 » et « YA1+YA2=0 ». (voir la figure).
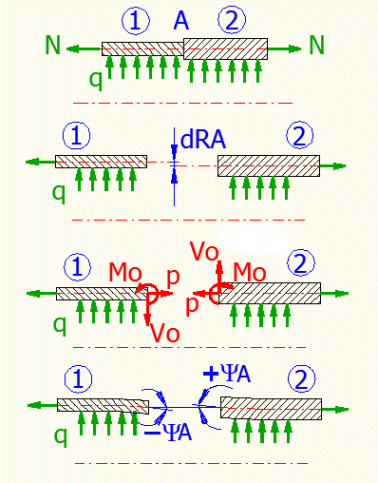
Procédé :
Comme la définition de la libération des coques et la définition des conditions aux limites peuvent être difficiles, on a préparé les solutions des cas les plus fréquents. Dans la liste déroulante, les types de coques liées, leurs chargements et leurs conditions aux limites sont enregistrés. Après la sélection, une figure s’affiche. En enfonçant le bouton « OK », vous ouvrez les paragraphes nécessaires à la solution de la liaison. En même temps, les différentes coques sont libérées (définition du chargement) et les conditions aux limites sont définies. On réalise ces démarches en écrivant les formules respectives dans les cellules correspondantes.
La libération des coques consiste à écrire les formules respectives dans les paramètres d’entrée des différentes coques (voir [10.1]). Après l’enfoncement de ce bouton, les formules de tous les paramètres d’entrée sont supprimées et remplacées par une valeur numérique. Utilisez cette commande avant de commencer à définir votre propre libération de la coque et vos propres conditions aux limites. En enfonçant ce bouton, vous réalisez la suppression des définitions non voulues provenant des calculs précédents.
Cette donnée définit le nombre d’utilisations de la fonction d’Excel « Goal seek... ». La gamme de valeurs d’entrée est 1-30. Normalement, la solution converge très vite (4-5 pas). La valeur préréglée (=10) est donc suffisante. Le pourcentage affiché dans le dialogue indique l’état du déroulement du calcul.
Utilisée dans l’approximation, la fonction « Goal seek... » peut bien trouver une solution satisfaisante, cependant elle met fin à la recherche des solutions prématurément dans le cas où les différences de résultats entre les différents pas sont faibles. La solution trouvée peut être ainsi entachée d’une erreur inutile. C’est pourquoi on peut augmenter la sensitivité de la solution, pour les cas prédéfinis, en multipliant le résultat par ce coefficient (« _Sensitivity »). Dans la plupart des cas, il n’est pas nécessaire de modifier ce paramètre, sa valeur est ajustée automatiquement lors du choix de [10.1].
Après le démarrage du procédé d’approximation, les valeurs dans ces champs sont
successivement modifiées de sorte que le résultat voulu [10.8-10.13] soit
atteint. Les différents paramètres (cellules) portent le nom « _Variable1 », «
_Variable2 » et « _Variable3 ». Liez ces variables au paramètre d’entrée que
vous voulez modifier dans le paragraphe respectif [6.0. 7.0. 8.0. 9.0]. Par ex.,
si vous ne connaissez pas la force « Vo » nécessaire à la déformation de la
coque, écrivez la formule « =_Variable1 » dans la cellule contenant la valeur «
Vo ».
Après l’enfoncement du bouton « <=0 », les valeurs sont remises à zéro.
Dans cette cellule (ces cellules), écrivez l’équation que vous voulez résoudre. Après le démarrage du procédé d’approximation, la valeur du paramètre [10.5] « _Variable1 » est modifiée de sorte que le résultat de l’équation écrite dans cette ligne corresponde à la valeur écrite dans la ligne suivante. Par ex., vous voulez que la modification du rayon de la coque cylindrique soit égale à zéro. A titre d’exemple, écrivez la formule « =_dRA_06 » (éventuellement « =_dRA_06*1000 » pour augmenter la sensitivité) dans cette cellule. Dans la cellule suivante [10.9], entrez le résultat voulu « 0 ».
Dans cette cellule (ces cellules), entrez le résultat voulu de l’équation de la ligne précédente. Si vous enfoncez le bouton « Résoudre », vous résolvez juste cette équation nonobstant les autres. Cela peut être utile dans le cas où vous faites des fautes en définissant les conditions, et la solution ne converge pas vers le résultat voulu.
A l’aide des différents calculs, il est possible de résoudre les liaisons des coques différentes. En pareil cas, il est nécessaire de libérer les différents éléments, de définir les conditions aux limites et d'écrire les formules (conditions) respectives dans le résolvant. Nous présentons ci-dessous quelques exemples parmi les plus fréquents de structures en coques.
Cet exemple de la liaison de la coque simule la liaison du tube avec une bride
(un problème très fréquent). Il peut aussi simuler le tube avec une nervure de
raidissement.
Entrez les dimensions de la coque [6.4, 6.5] et la valeur de la surpression « q
» [6.6]. Le chargement axial « p » [6.8] est égal à zéro.
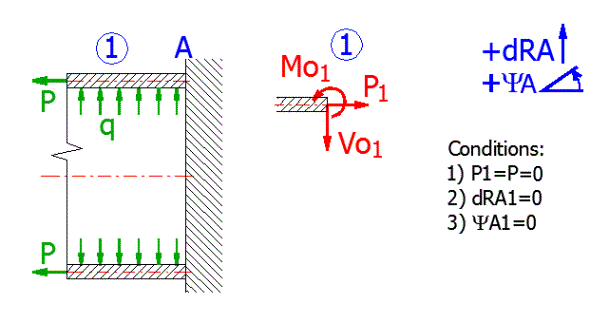
Libération de la coque:
A l’extrémité, la coque est soumise à une force et à un moment.
Conditions aux limites:
Entrez les dimensions de la coque [6.4, 6.5]. La surpression « q » [6.6] est égale à zéro, le chargement axial « p » [6.8] est égal à zéro et la valeur de la force circonférentielle « Vo » [6.9] est égale à (F/2).
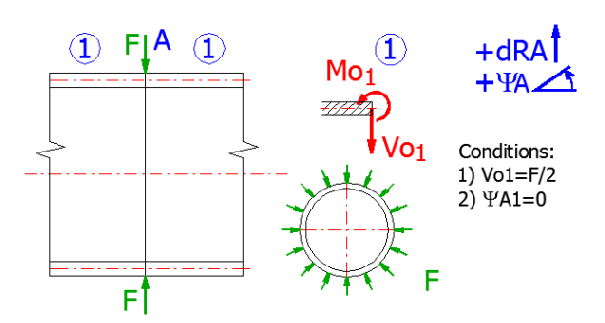
Libération de la coque:
A l’endroit où la coque est soumise à une force circonférentielle, il est
nécessaire de diviser la coque en deux éléments et de calculer sa moitié. La
moitié de la coque est donc soumise à la moitié de la force circonférentielle
d’origine. Et au point d’application de cette force, le déplacement angulaire
est égal à zéro.
Dans la cellule indiquant le moment « Mo » [6.10], liez « Paramètre modifié 1 »
; elle contiendra donc : « =_Variable1 ».
Conditions aux limites:
Le déplacement angulaire au point A est égal à 0. La formule dans la cellule
Equation 1 [10.8] est « =_Psi_06a*_Sensitivity ». Le résultat voulu Résultat1
dans la cellule [10.9] est égal à 0.
Entrez les dimensions de la coque cylindrique [6.4, 6.5] et les dimensions de la coque conique [8.4, 8.5, 8.6] (rayon RA=R). Entrez la surpression « q » [6.6, 8.7] et le chargement axial « p » [6.8]. Près de la partie conique, le chargement axial se décompose en une force parallèle à la surface de la coque et une force radiale agissant sur le bord de la coque.
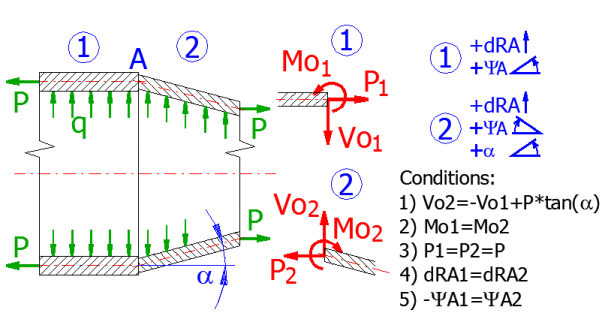
Libération des coques:
On libère les deux coques. Puis, on soumet leurs extrémités à une force
circonférentielle « Vo », à un moment « Mo » et à une force axiale « P » (pour
la coque conique, il faut augmenter la force circonférentielle Vo de la
composante radiale qui est le produit de la décomposition de la force parallèle
à la surface du cône).
Coque cylindrique:
Coque conique:
Conditions aux limites:
L'information sur l'arrangement des paramètres de calcul et de la langue peut être trouvée dans le document « Réglage des calculs, changement de langue ».
Les informations générales sur la façon dont vous pouvez modifier et prolonger les cahiers de travail sont mentionnées dans le document « Modifications du cahier de travail (calcul) ».